Tu sei qui
Schedulazione pannello

Una volta realizzato il pannello in ambiente di massa, opportunatamente ancorato a dei punti come descritto nei post precedenti, il passo finale è quello di definirlo geometricamente attraverso la misura dei suoi lati.
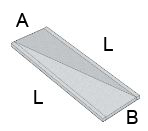
Il principio è quello di assegnare dei parametri alle quote del pannello, in modo tale da ottenere una schedule da applicare in seguito a una nuova famiglia: questa rappresenta la vera e propria sagoma mediante la quale una macchina a controllo numerico taglierà e piegherà il pannello in fase di produzione.

A un passo dal cantar vittoria, stamane, io e Stefano Guarnieri, ci siamo scontrati con varie difficoltà:
1_la massa non fornisce i valori dimensionali dei lati del pannello. Probabilmente perchè è concepita come una "spline" per punti, sebbene in questo caso sia una linea retta tra i due punti di riferimento.
2_se andiamo a quotare i lati del pannello (con una certa difficoltà, perchè vanno creati dei piani nei quali sono contenuti i lati A e B del pannello al fine di creare quote allineate nel corretto modo) otteniamo una quota nè "bloccabile" (giustamente, poichè la massa deve poter cambiare dimensioni) nè al momento parametrizzabile
3_altro tentativo è quello di creare, in sede di progetto, una partizione della superficie con dei montanti, dai quali (di volta in volta) ottenere la suddetta lunghezza dei lati A e B. Il limite di questa soluzione è che il calcolo non avviene in modo immediato, ma necessita di una misurazione "manuale" di volta in volta del pannello (una volta generata la geometria successiva).
Su questi ultimi due punti io e Stefano G. stiamo portando avanti varie ipotesi.
Di seguito illustro un tentativo di risolvere il punto 2 di sopra attraverso la parametrizzazione dei lati del pannello, esprimendo queste lunghezze in termini trigonometrici collegati ai parametri noti (VARIAZIONE,ANGOLO,RAGGIO).
1_Ragionamento i pianta:
Attraverso il teorema della corda, posso esprimere la distanza AB (tra i due punti di applicazione dell'istanza bilancia) come il doppio del RAGGIO (parametro che utilizzo per far ruotare la seconda istanza) moltiplicato per il seno di ß/2 (dove ß è il parametro ANGOLO che definisce la rotazione della seconda istanza).
Applico il teorema ai due punti estremi della trave. In qesto caso considero la trave non ruotata (parallela al pavimento) ed esprimo la sua lunghezza uguale a l (quindi metà trave= l/2)
Poichè anche la trave ha una rotazione, non devo considerare il valore l/2, bensì la proiezione a terra della metà della trave.
La proiezione a terra di l/2 necessita un legame con la rotazione della trave stessa: va espressa quindi in funzione della VARIAZIONE dell'altezza.
Quindi ottengo la lunghezza della proiezione l'/2 attraverso il teorema di pitagora.
RISULTATO: Ho descritto la lunghezza delle proiezioni a terra dei lati A (A'B') e B (A''B'') del pannello. Ora devo mettere in relazione questa proiezione con la VARIAZIONE tra la prima e la seconda istanza
2_Ragionamento in alzato:
Conoscendo la proiezione di A, cioè A'B', ricavo la lunghezza di A attraverso il teorema di pitagora:
la lunghezza del lato A, nel disegno chiamata d (segmento che unisce le due estremità delle due travi) corrisponde alla radice della somma tra il quadrato della proiezione di A (cioè A'B') e il quadrato di V (che sarebbe l'incremento della variazione, cioè la differenza tra il parametro seconda_variazione e prima_variazione).
Lo sesso ragionamento per il lato B, utilizzando la proiezione A''B''.
RISULTATO: Ho descritto la lunghezza dei lati Ae B del pannello in funzione dei soli parametri VARIAZIONE,ANGOLO,RAGGIO.
Ecco la formula (la semplicità non è il suo forte):
In questo modo posso conoscere già le dimensioni di ogni pannello nel momento in cui imposto le regole matematiche di variazione dei parametri. La massa diviene solamente uno strumento per "rappresentare" il pannello nel modello concettuale (non una superficie o solido dal quale estrarre dati). Ovviato in questo modo il problema di "quotare" i lati della massa.
Theme by Danetsoft and Danang Probo Sayekti inspired by Maksimer
