Prendo in considerazione un telaio con 2 travi (rigide assialmente) parallele incastrate agli estremi messe in orizzontale, inserisco tra le due travi 5 elementi infinitamente rigidi (assialmente e flessionalmente) con passo costante. Applicando una forza pari ad F su ogni traverso ottengo la seguente situazione:
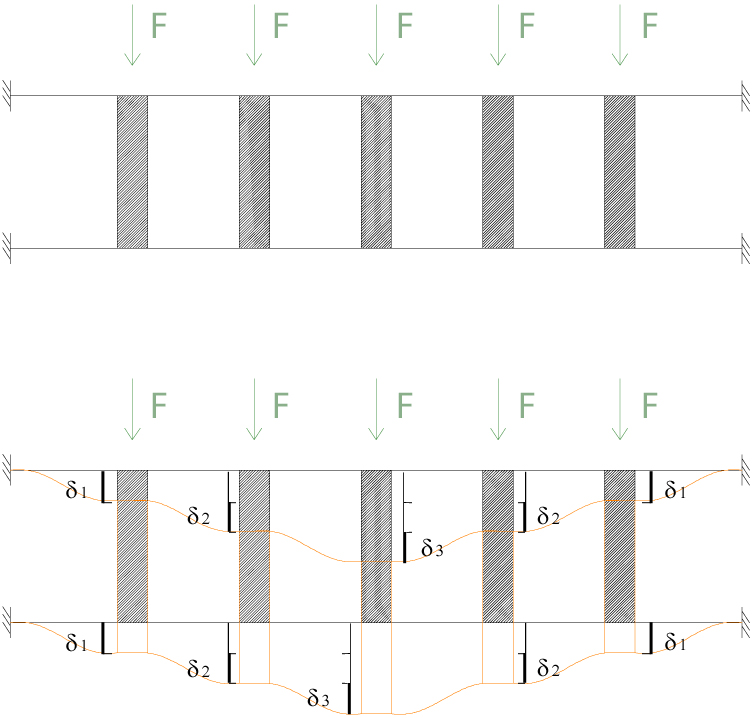
nella seconda immagine vediamo la deformazione dovuta alle forze applicate. Specifico che la struttura è simmetrica e che entrambe le travi hanno la stessa rigidezza.
Ora calcolo i tagli nei vari tratti delle travi ricordando che, per simmetria, il taglio nel primo tratto della trave superiore è uguale al taglio nel primo tratto della trave inferiore, al taglio dell'ultimo tratto della trave superiore e all'ultimo tratto della trave inferiore. T= (12 EI / l^3)*d1
Sempre per simmetria: il taglio nel secondo tratto della trave superiore=taglio nel secondo tratto trave inferiore. T= (12 EI / l^3)*d2
Nel primo traverso, per equilibrio ottengo quindi l'equazione F + [(24 EI / l^3)*d2] - [(24EI / l^3)*d1] = 0
d1 e d2 sono incognite, non posso ancora risolvere quindi proseguo i calcoli avanzando dall'estremità del telaio verso il centro.
Il taglio nel secondo tratto di trave è T= (12 EI / l^3)*d2
Nel terzo tratto di trave abbiamo T= (12 EI / l^3)*d3
Nel secondo traverso per equilibrio ottengo l'equazione F + [(24 EI / l^3)*d3] - [(24EI / l^3)*d2] = 0
Le incognite sono sempre due (d2 e d3), analizzo il terzo e quarto tratto dove come incognita avrò solo d3.
Il taglio nel terzo tratto (superiore e inferiore) di trave è uguale al quarto tratto. T= (12 EI / l^3)*d3
Nel terzo traverso (quello centrale) per l'equilibrio ottengo l'equazione F - [(48EI / l^3)*d3] = 0
Posso quindi stabilire che d3 = Fl^3 / 48 EI
Sostituendo il valore di d3 nell'equazione precedente troverò che d1 = 5 Fl^3 / 48 EI ; d2 = Fl^3 / 16 EI
Sostituisco i valori trovati nelle equazioni del taglio e trovo i valori riportati nell'immagine:
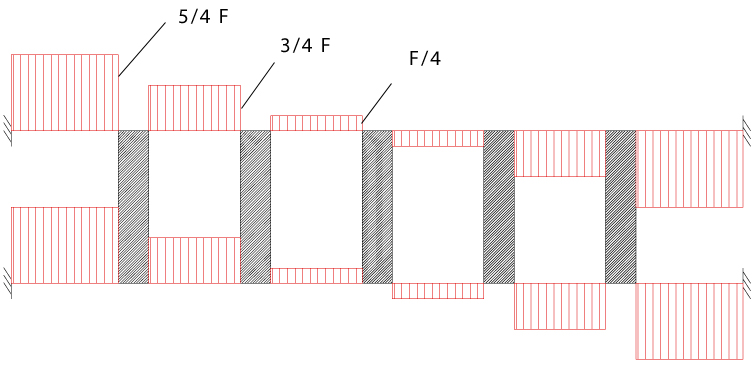
Posso quindi calcolare i momenti con i valori riportati nell'immagine:
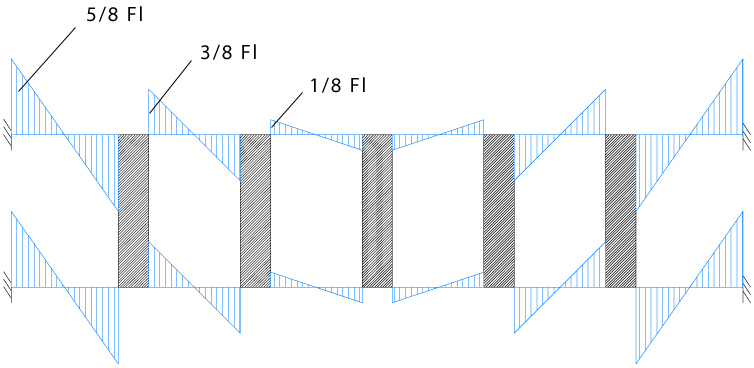
___________________________
Se considero il momento d'inerzia della trave inferiore 9 volte maggiore del momento d'inerzia della trave superiore dovrò chiaramente differenziare i calcoli. C'è sempre una simmetria tra il primo e l'ultimo tratto superiore così come c'è sempre simmetria tra il primo ed ultimo tratto nella trave inferiore.
Considero quindi che il taglio nel primo tratto è dato da (12 EI / l^3)*d1 (trave superiore) più (108 EI / l^3)*d1 (trave inferiore con I maggiore). Nel secondo tratto ho un taglio dato da (12 EI / l^3)*d2 più (108 EI / l^3)*d2.
Nel primo traverso per l'equilibrio quindi ottengo che F + [(120 EI / l^3)*d2] - [(120 EI / l^3)*d1] = 0
Nel secondo traverso per l'equilibrio ottengo che F + [(120 EI / l^3)*d3] - [(120 EI / l^3)*d2] = 0
Nel terzo traverso per l'equilibrio ottengo che F - [(240 EI / l^3)*d3] = 0
Quindi d3 = Fl^3 / 240 EI
Sostituisco il valore di d3 nell'equazione precedente e trovo d1 = Fl^3 / 48 EI ; d2 = Fl^3 / 80 EI
Il valore del taglio è riportato nell'immagine qui sotto:

Il valore del momento nei vari tratti è riportato nell'immagine qui sotto:
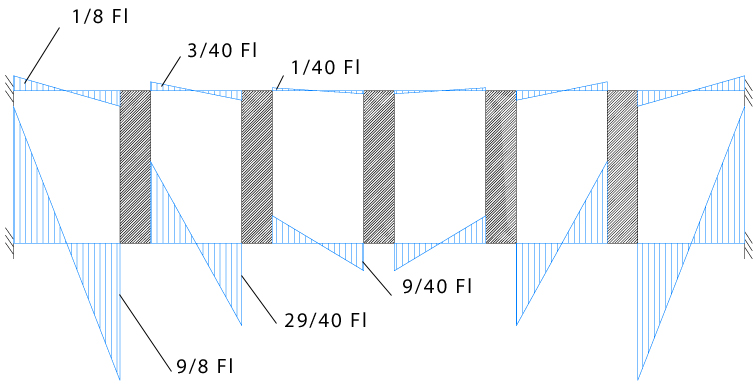
Commenti recenti