1 Planimetria generale architettonico – Terni - fuori scala
L’edificio scelto per la progettazione strutturale fa parte di un progetto architettonico sviluppato in un area residenziale nel paese di Terni; questo è composto da una destinazione residenziale con tipologia a “torre”, con nucleo di distribuzione verticale centrale e una distribuzione delle residenze e spazi comuni con affaccio sui lati corti dell’edificio.
La destinazione d’uso si compone di un piano terra che accoglie spazi di relazione, magazzini, locali tecnici, accoglienza, lavanderia e servizi, e ulteriori 5 piani di residenze studenti fornite di spazi accessori comuni per lo studio.
2 Planimetrie - fuori scala
L’edificio ha una struttura in telai piani di cemento armato, solai latero-cementizi, nucleo centrale costituito da setti in cemento armato che supportano le scale e il vano ascensore, così come si evince dalle planimetrie in figura 1.2.
Le tipologie residenziali sono composte secondo le dimensioni della maglia strutturale e sono quindi componibili in alzato in maniera randomica secondo la miglior disposizione degli spazi interni del progetto.
3 Alzati – fuori scala
Dagli alzati, rappresentati in figura 1.3, si nota come il progetto si componga di prospetti tecnologicamente analoghi a due a due composti l’uno da una “griglia” di prospetto in cui si inseriscono le aperture e le logge di ogni residenza o spazio comune composto da due diversi pacchetti tecnologici di tamponatura (tamponatura tipo 1 e 2), e l’altro composto da una disposizione quasi randomica delle bucature costituito da un unico pacchetto tecnologico (tamponatura tipo 2).
La particolarità dei due prospetti a griglia sarà presa in considerazione come “vincolo architettonico” nell’elaborazione del progetto strutturale per poter avere il risultato di una maglia composta dalla stessa dimensione in prospetto della trave e del pilastro (come si nota nella figura 2.3 in cui si rappresenta l’ipotesi di disegno dell’impalcato).
2. ANALISI DEI CARICHI
2.1Pacchetti tecnologici – fuori scala
Nella figura 2.1 sono riportati tutti i pacchetti tecnologici che si utilizzano nella redazione del progetto strutturale compresi i calcoli del carico permanente strutturale (G1), il carico permanente non strutturale (G2), il carico della tramezzatura (g2 che da normativa ricava il valore di G2 delle stesse tramezzature ripartite al mq), ed il carico delle tamponature tipo 1 e 2.
La sezione del solaio in latero-cemento è stata pre-dimensionata attraverso la tabella di normativa DM 09/01/1996, di seguito riportata:
Riassumendo, di seguito vengono riportati in tabella tutti i carichi che agiscono sui solai dimensionati e calcolati nel capitolo 1.
2.3 Tabella carichi solaio
3. PROGETTO DEL SOLAIO
Per quanto riguarda il dimensionamento per il solaio controterra, calcolati i carichi che gravano sullo stesso si dimensionano i Cupolex del vespaio areato mediante la scheda tecnica del prodotto: sovraccarico permanente = 1,39 KN/m + accidentale = 1,2 KN/m
3.1 Scheda tecnica Cupolex – solaio controterra
3.2 Ipotesi di impalcato del piano tipo
3.3 Individuazione aree funzionali
Si individuano le aree funzionali sull’impalcato in modo da poter poi ricavare le “sezioni” dei “modelli di solaio” di cui si andranno a calcolare poi le combinazioni di carico per ottenere l’inviluppo (tratteggio nero in figura 3.3).
Devono essere calcolati gli inviluppi delle tre “sezioni” dell’impalcato con le seguenti combinazioni di carico SLU che si riportano in figura 3.4:
3.4 Combinazione di carico SLU delle sezioni
Gli inviluppi che risultano dalle combinazioni di carico sono calcolati comprendendo anche il valore del momento nelle cerniere agli estremi del modello che sintetizza la tensione che la trave principale oppone alla deformazione dovuta dal travetto, calcolata con un valore pari a ql2/24.
Gli inviluppi del momento sono inoltre stati riportati, in figura 3.4, comprendendo già il contributo del taglio agente sulla sezione calcolato pari a (0,9 x d).
Attraverso i valori espressi dall’inviluppo del momento nel modello 1 si ricava tramite la tabella che segue l’armatura minima longitudinale che dovrà essere disegnata e verificata (calcolando agli appoggi anche l’azione del taglio nel calcolo della stessa armatura longitudinale).
3.5 Tabella calcolo armatura longitudinale - modello 1
Nella tabella 3.5 sono inoltre riportate le lunghezze d’ancoraggio per le barre utilizzate come armatura, appositamente dimensionate secondo gli Eurocodici2.
Il disegno che segue riporta graficamente quanto già espresso dalla tabella vista in precedenza:
Si verificano le sezioni dei travetti con le rispettive armature longitudinali a SLU ricavando Mrd di tutte le sezioni prese in esame nella tabella 3.5:
Con le stesse sezioni di cui sopra si vanno a verificare gli SLE per le tensioni in modo da verificare il buon esercizio durante la vita nominale della struttura.
dove:
4.2 Verifiche SLE
Dopo avere dimensionato e verificato le armature longiutdinali sia per Stato Limite Ultimo che per Stato Limite di Esercizio, si va ora a verificare se le sezione agli appoggi è verificata a taglio in modo da poter individuare se necessaria la presenza di eventuali fasce piene.
4.3 Verifica SLU a taglio
Da tali risultati si evince un Taglio resistente sempre maggiore di quello di progetto comportando così una non necessità di fasce piene.
Con la medesima procedura indicata per il progetto della sezione e della sua armatura longitudinale per il modello 1, si va a calcolare il modello 2 del solaio, come riportato in figura 4.4, con le correzioni riviste durante la revisione:
4.4 Impalcato piano tipo – sezione modello 2
4.5 Combinazioni di carico e inviluppi – modello 2
4.6 Tabella lunghezza di ancoraggio
SPECIFICA INDICAZIONI PER LA LUNGHEZZA D’ANCORAGGIO
Per il dimensionamento della lunghezza di ancoraggio si sono calcolati i valori in condizione di buona aderenza, ovvero se la barra si ancora in un punto dove il momento è minimo, e cattiva aderenza, ovvero nel caso l’ancoraggio capitasse la dove il momento è massimo o elevato quindi più prossimo a fessurazione. Inoltre data la presenza di barre che corrono longitudinalmente per tutta la sezione è stato necessario dividerli poichè da mercato le lunghezze massime sono di 12 metri, dato ciò si è calcolato inoltre il valore di sovrapposizione di tali barre cercando di spezzarle la dove il momento è minimo.
Per il predimensionamento della struttura si tengono conto i limiti geometrici imposti dalla normativa:
TRAVI
per travi emergenti, larghezza di base > 20 cm;
per travi a spessore, larghezza di base uguale alla larghezza del lato del pilastro ortogonale alla stessa con l’aggiunta per ogni lato della trave dell’altezza della trave stessa, il risultato comunque non maggiore di 2bc dove bc è la dimensione ortogonale alla trave del pilastro;
il rapporto b/h della trave >0.25;
Le zone critiche si estendono, per CD”A”, per una lunghezza pari a 1,5 volte l’altezza della sezione della trave, misurata a partire dalla faccia del nodo trave-pilastro o da entrambi i lati a partire dalla sezione di prima plasticizzazione. Per travi che sostengono un pilastro in falso, si assume una lunghezza pari a 2 volte l’altezza della sezione misurata da entrambe le facce del pilastro.
PARETI e SETTI
lo spessore delle pareti deve essere non inferiore al valore massimo tra 150 mm, (200 mm nel caso in cui nelle travi di collegamento siano da prevedersi, ai sensi del § 7.4.4.6, armature inclinate), e 1/20 dell’altezza libera di interpiano;
devono essere evitate aperture distribuite irregolarmente, a meno che la loro presenza non venga specificamente considerata nell’analisi, nel dimensionamento e nella disposizione delle armature;
in assenza di analisi più accurate si può assumere che l’altezza delle zone critiche sia la maggiore tra: la larghezza della parete e 1/6 della sua altezza.
5.1 Predimensionamento travi e pareti
SCALE
Il progetto prevede scale composte mediante solette rampanti, per questo, secondo limiti geometrici, si predimensionano le stesse con uno spessore compreso tra i 15 e i 20 cm, comprendendo tra i margini anche l’ingombro dovuto dal copriferro.
5.2 Carichi pacchetto scale – soletta rampante
PILASTRI
La dimensione minima della sezione trasversale non deve essere inferiore a 250 mm;
in assenza di analisi più accurate si può assumere che la lunghezza della zona critica sia la maggiore tra: l’altezza della sezione, 1/6 dell’altezza libera del pilastro, 45 cm, l’altezza libera del pilastro se questa è inferiore a 3 volte l’altezza della sezione;
Oltre al predimensionamento per limiti geometrici dati da normativa, si va a predimensionare la geometria della sezione dei pilastri ancorati alle fondazioni tramite il seguente procedimento:
attraverso la verifica SLU per azione di compressione pura sull’elemento, data da normativa:
Nu = 0.8 x Ac x fcd + As x fyd
si ricava:
Ac = Nd/(0.7 x fcd) in cui viene trascurato il contributo dell’armatura
dove Nd è pari alla somma di tutti i carichi che gravano sui pilastri del piano terra comprendendo anche la somma dei carichi dovuti al peso proprio della struttura (travi principali, travi secondarie e pilastri), il tutto calcolato attraverso la combinazione SLU determinata interamente sfavorevole.
Il coefficiente di riduzione 0.7 viene applicato per tenere conto della riduzione della resistenza della sezione dovuta all’azione di momento (dovuto alle relative eccentricità) sulla stessa.
2. si disegnano quindi le aree di influenza di ogni elemento pilastro, per ogni impalcato che comprende la struttura, ed ognuna di queste aree si suddivide ulteriormente per il calcolo dei diversi carichi dovuti a: G1, G2, Q1, Q2neve che si differenziano a seconda della destinazione e del pacchetto tecnologico di cui tale impalcato si costituisce (il tutto meglio esplicato in figura 5.4).
Per quanto riguarda l’area delle scale, queste vengono calcolate come contributo del carico dell’impalcato tramite il calcolo riportato nella figura 5.2 e riportato poi nella tabella sottostante che riassume tutti i carichi che influenzano il calcolo del predimensionamento dei pilastri:
5.3 Tabella riassuntiva dei carichi
5.4 Aree di influenza e delle destinazioni d’uso, dei pilastri
3. il progetto prevede degli affacci sui lati corti composti secondo un ordine randomico di logge, per poter ottimizzare i calcoli e velocizzare il predimensionamento, si sono studiate delle combinazioni, riportate in figura 5.5, in cui si evidenziano le differenze tra gli impalcati e si riportano nel giusto ordine tra i pilastri piano per piano.
5.5 Combinazioni carichi logge
5.6 Tabella dei carichi Ned (SLU) degli impalcati
4. dimensionate le aree di ogni pilastro alla base dell’edificio, si procede con il calcolo della capacità di resistenza a compressione della sezione attraverso la formula:
Nrd = fcd Ac
secondo normativa per la presso-flessione: per le strutture in CD “A” la sollecitazione di compressione non deve eccedere, il 55% della resistenza massima a compressione della sezione di solo calcestruzzo.
Quindi:
Nrd * 0.55 > Ne
dove Ne è la combinazione (SLU) per le azioni sismiche:
5.7 Tabella delle verifiche della sezione predimensionata dei pilastri
NODI TRAVE-PILASTRO
Sono da evitare per quanto possibile eccentricità tra l’asse della trave e l’asse del pilastro concorrenti in un nodo. Nel caso che tale eccentricità superi 1/4 della larghezza del pilastro la trasmissione degli sforzi deve essere assicurata da armature adeguatamente dimensionate allo scopo.
Il modello 3d della struttura è realizzato secondo lo schema strutturale di progetto, a questo vengono assegnate le sezioni per ogni elemento che lo compone.
Queste sezioni vengono definite nel software secondo la geometria e i materiali scelti, andando a diversificare diversi valori del modulo elastico per gli elementi (travi, pilastri, pareti) per contemplare il contributo della fessurazione della sezione:
6.2 Tabella sezioni di progetto
Assegnate le sezioni a tutti gli elementi del modello si uniscono questi in gruppi che identificano il piano della struttura e la sezione comune, per migliorare il metodo di selezione degli elementi nel software:
6.2 Tabella gruppi
7. CENTRO DI MASSA DEGLI IMPALCATI
Realizzato il modello 3d della struttura, si devono ora inserire tutti i carichi delle combinazioni SLU (capitolo successivo) e le azioni sismiche riferite ai centri di massa degli impalcati con le relative combinazioni sismiche da normativa.
Si procede quindi con il calcolo del baricentro di massa per ogni impalcato presente nella struttura, andando a dividere lo stesso in aree rettangolari in cui si identificano i carichi G1, G2, Q1 e Q2 relativi secondo la combinazione SLU sismica:
Wi = G1 + G2 + Q1 x Ψ21 +Q2 x Ψ22
Avendo la struttura impalcati differenti per ogni piano della stessa si identifica un “layer” di travi principali e secondarie uguali per ogni piano e si vanno a identificare i “layers” di tutti gli altri impalcati diversi tra loro, compresa la copertura:
7.1 Aree dell’impalcato per il calcolo del centro di massa
Per quanto riguarda le tamponature, queste si calcolano considerando nell’impalcato metà della loro altezza in alzato e metà della restante tamponatura del piano precedente, come in figura 7.2:
7.2 Aree dell’impalcato per il calcolo del centro di massa e sezione schematica
Definite le aree e le distanze del centro di massa delle stesse da un sistema di assi cartesiani riferiti all’impalcato, si va a calcolare il peso Wi dalla formula vista prima e il momento statico Sx e Sy che si ricava da:
Si = Wi x di
Dal quale si può ricavare:
Xm = ∑ Six/Wtot Ym = ∑ Siy/Wtot
7.3 Stralcio tabella calcolo dei pesi degli impalcati
Le coordinate del centro di massa dell’impalcato.
Calcolati tutti i centri di massa degli impalcati, da normativa si va ad introdurre per cautela un valore minimo di eccentricità che tiene conto della semplificazione che tutti gli accidentali sono stati considerati uniformemente distribuiti.
Eix = +/- 0.05 Xm
Eiy = +/- 0.05 Ym
Con l’introduzione del valore di eccentricità addizionale si ricavano in tutto 4 (combinazioni) differenti centri di massa per ogni impalcato di cui PER IL PROGETTO, andiamo a considerare solo il più sfavorevole.
7.4 Tabella centro di massa impalcati
7.5 Centri di massa degli impalcati
I centri di massa di ogni impalcato vengono caricati nel modello 3d ed inclusi all’interno dei rispettivi impalcati sintetizzati nello stesso tramite il comando DIAPHRAGM impostanto su di essi il valore della massa per i 3 gradi di libertà X, Y e per Z si imposta l’inerzia rotazionale Ip calcolata mediante:
8CENTRO DI RIGIDEZZA DEGLI IMPALCATI-9INVILUPPO SLU NON SISM.
8. CENTRO DI RIGIDEZZA DEGLI IMPALCATI
Ricavati centri di massa di tutti gli impalcati, si ricava il centro di rigidezza dell’impalcato tipo (poiché tutti gli impalcati hanno la stessa tipologia di struttura), per poter poi capire quale tra i centri di massa trovao è il più distante dal centro di rigidezza e quindi il più sfavorevole per quanto riguarda la torsione della struttura.
8.1 Impalcato e distanze dei “telai piani” dal sistema di riferimento cartesiano
Si identificano tutti i telai, verticali e orizzontali dell’impalcato tipo e degli stessi, si identificano gli elementi di cui sono composti nelle tabelle che seguono (figura 8.2 e 8.3):
8.2 Tabella elementi strutturali
Come mostra lo stralcio della tabella in figura 8.3, per ogni telaio viene calcolata la rigidezza secondo un modulo elastico stabilito in precedenza e l’inerzia di ogni elemento secondo l’asse riferito alla direzione del telaio.
Per il calcolo della rigidezza si tiene conto di un modello di telaio piano shear-type per cui la rigidezza è sintetizzata in:
K = (12E x∑ I)/h3
8.3 Stralcio tabella calcolo rigidezze telai
Le coordinate vengono ricavate mediante:
Xc = (∑ Kvi * dvi)/ Kvtot
Yc = (∑ Koi * doi)/ Kotot
8.4 Tabella calcolo coordinate centro di rigidezza
8.5 Centri degli impalcati
9. INVILUPPO SLU NON SISMICO
Per ricavare i carichi per il calcolo dell’inviluppo SLU non sismico di tutti gli elementi della struttura in esame di procede con il calcolo di tutti i carichi areali, lineari e puntuali che gravano sugli elementi strutturali, partendo quindi dall’area di influneza delle travi principali e secondarie e dala peso proprio degli elementi strutturali verticali:
9.1 Area di influenza travi principali e secondarie sugli impalcati
Per le travi secondarie si considera un area di influenza con interasse pari a 50 cm per ogni fronte dell’elemento stesso.
Come già fatto per il calcolo dei carichi per le aree di influenza dei pilastri, si vanno a localizzare i carichi G1, G2, Q1, Q2, calcolandoli come carichi linearmente distribuiti sulle travi.
Si localizzano inoltre i carichi concentrati degli elementi pilastri e setti che dovranno essere anch’essi caricati sul modello 3d e il carico areale da localizzare sulla superficie della soletta rampante delle scale.
Essendo la struttura composta da impalcati tutti differenti l’uno dall’altro, come già fatto per il predimensionamento dei pilastri, si localizzano tutte le varianti del piano in dei “moduli delle aree di influenza” sia per le travi primarie che secondarie, in modo da poter velocizzare il calcolo:
Ricavati i centri di tutti gli impalcati si deve ora definie quale tra i 4 centri di massa moltiplicati per l’eccentricità addizionale sia il più sfavorevole, per ogni impalcato.
Per fare ciò si effettuano due verifiche:
la distanza maggiore tra i centri di massa e il centro delle regidezze (la distanza maggiore sarà il caso più sfavorevole);
calcolo degli spostamenti maggiori dei punti dell’impalcato, ricavari mediande l’assegnazione di una forza orizzontale in direzione X e Y su ogni centro di massa (il centro di massa che genera spostamenti maggiori sarà il caso più sfavorevole);
1° verifica
8.6 Centro di massa più distante dal Centro delle Rigidezze (CR)
2° verifica
Si definiscono in SAP i 4 centri di massa ricavati, si assegna loro la massa per i tre gradi di libertà (figura 8.8) e il constraints – diaphram insieme a tutti i punti che giacciono sull’impalcato (figura 8.7) e si assegna loro, una volta ciascuno, le forze orizzontali nelle due direzioni X e Y e si verificano gli spostamenti (figura 8.9):
8.7 Assegnazione del constraints – diaphram
8.8 Assegnazione delle masse al centro di massa
8.8 Assegnazione delle masse al centro di massa
8.9 Deformazione
Da ogni configurazione deformata si localizzano 4 punti dell’impalcato e si studiano i loro spostamenti:
8.10 Schema della verifica
8.11 Tabella degli spostamenti
Dalle due verifiche risulta che la condizione più sfavorevole per tutti gli impalcati è assegnare il centro di massa al punto definito dall’eccentricità ex + , ey –
Ricavati i carichi che gravano su tutti gli elementi della struttura si procede con l’assegnazione di ogn’uno di questi al proprio elemento nell modello 3D, andando a definire quelle che sono le combinazioni di carico per l’inviluppo SLU non sismico.
Ai fini della progettazione strutturale dell’edificio in esame, si riducono le combinazioni per semplificare il calcolo a solo 3 di queste (figura 9.5)
9.5 Combinazioni per SLU non sismico
La prima combinazione presenta una situazione di “tutto caricato” con ogni carico moltiplicato, secondo normativa per la combinazione SLU, con coefficiente γ sfavorevole;
Le due combinazioni a seguire sono combinazioni a scacchiara in cui gli elementi selezionati in rosso sono carichi da esplicitare con coefficiente sfavorevole e i restanti con coefficiente favorevole, queste “scacchiere” inoltre si alternano tra gli impalcati.
Nel modello 3D in SAP si procede con la definizione di tutti i tipi di carico (esplicitando se moltiplicati per coefficienti favorevoli o sfavorevoli per le tre combinazioni) e l’assegnazione ad ogni elemento dei propri carichi siano essi puntuali, lineari o areali.
9.6 Sintesi definizione e assegnazione dei carichi nel modello 3D
(Le classi dei carichi definiti nella figura 9.6 si riferiscono a carichi linearmenti distribuiti, escludendo i carichi puntuali su setti e pilastri e quelli areali sulla soletta rampante che costituisce le scale.
La normativa classifica le strutture a seconda di tipologie di deformazioni, dobbiamo quindi calcolare il fattore q0 , che identifica la capacità di dissipazione della struttura e quindi configura uno spettro di progetto minimizzato rispetto allo spettro elastico, che secondo la normativa viene tabellato secondo le “tipologie strutturali”.
Si procede quindi con 2 analisi per capire se la natura della struttura sia o meno suscettibile alla torsione:
Analisi del modo 1 e 2 per quantificare la massa partecipante all’analisi modale;
Analisi del rapporto r/ls > 0,8 che da normativa, esplicitato per ogni impalcato della struttura identifica se la struttura sia deformabile torsionalmente o meno.
Si analizza attraverso l’analisi modale il modello 3d della struttura:
10.1 Modello “9” 3D – struttura
ricavando:
10.2 Deformazioni della struttura del modo 1 e 2 (modello 9)
10.3 Tabella delle masse partecipanti nei modi (modello 9)
Attraverso le deformazioni del modo 1 e 2 si riscontra un comportamento suscettibile alla torsione, questo poiché la struttura presenta un nucleo molto rigido dato dalle pareti del corpo di distribuzione dell’edificio.
Quindi si procede intervenendo sugli elementi strutturali cercando di irrigidire il perimetro dell’edificio modificando la sezione delle travi e dei pilastri e l’orientamento di tutti i pilastri della struttura.
Si realizza il modello “13” composto da travi perimetrali più rigide, le sezioni e l’orientamento dei pilastri sul perimetro che orientano il centro delle rigidezze più vicino al centro di massa dei vari impalcati:
10.4 Modello “13” 3D – struttura
ricavando:
10.5 Deformazioni della struttura del modo 1 e 2 (modello 13)
10.6 Tabella delle masse partecipanti nei modi (modello 13)
Nel nuovo modello si riscontra un comportamento diverso, che garantisce una buona partecipazione della massa nella deformazione del modo 1 e 2.
Nell’analisi del rapporto r/ls > 0,8 si riscontra quanto descritto dalla tabella seguente:
10.7 Tabella r/ls 0,8 (modello 13)
Nella tabella 10.7 sono riportati i delta degli spostamenti e delle rotazioni del centro di massa di ogni impalcato generati da una forza Fi ricavata da:
Fi = Fh x zi (Wi/∑zj x Wj)
dove:
Fh = forza equivalente al sisma presa come 5000 KN;
zi = altezza dell’impalcato da terra;
Wi = peso dell’impalcato;
Zj e Wj = rispettivamente l’altezza da terra dell’impalcato e il peso dello stesso.
Si ricava poi il taglio di piano tramite la somma delle forze applicate fino all’impalcato in esame e si calcola la Rigidezza flessionale per x e y e la rigidezza torsionale mediante:
Kfx = Taglio di piano / delta spostamento in x;
Kfy = Taglio di piano / delta spostamento in y;
Kt = Taglio di piano / delta rotazione in z;
con le rigidezze ricavate si esplicita r2:
r2 x= Kt/Krx r2 x= Kt/Krx
e si calcola:
ls = √((L2+B2)/12)
infine:
r/ls > 0,8
CONSIDERAZIONI:
La struttura del modello 13 viene verificata non suscettibile a torsione nelle due analisi descritte nel capitolo 10.
La struttura del modello 13 viene verificata non suscettibile a torsione nelle due analisi descritte nel capitolo 10, andranno ora fatte ulteriori cosiderazioni sulla dimensione delle sezioni degli elementi modificati per rendere la struttura non suscettibile a torzione:
Le sezioni delle travi 40x70 possono essere ridotte in sezioni 30x70 modificando di poco le percentuali di massa partecipante nei modi 1 e 2 della analisi modale;
I pilastri 40 x 60 che congiungono le travi suddette devone essere ingranditi fino a 40x70 per aumentare la probabilità presenza di cerniera plastica nel nodo trave pilastro;
Tutte le sezioni sono state razionalizzate con un numero complessivo di 2 tipi di pilastri e 3 tipi di travi per semplificare il progetto delle stesse sezioni in fase di dimensionamento.
10.8 Modello “17” 3D – struttura e sezioni degli elementi
Si effettua ora il calcolo dei nuovi centri di massa e di rigidezza, mutati a causa della variazione delle sezioni degli elementi strutturali, così come il valore della massa in x e y e dell’inerzia rotazionale in z:
10.9 Schema impalcato tipo – quote telai
10.10 Tabella sezioni di progetto
10.11 Tabella centro rigidezza – (Modello 17)
10.12 Tabella centri massa – (Modello 17)
10.13 Centri degli impalcati – (Modello 17)
Si effettua ora l’analisi modale del nuovo modello (17) di struttura corretto delle precisazioni sopra elencate:
10.14 Deformazioni della struttura del modo 1 e 2 (modello 17)
10.15 Tabella delle masse partecipanti nei modi (modello 17)
Nel nuovo modello 17 le percentuali di massa nei primi due modi ha un valore che soddisfa i paramentri della tipologia di struttura, per confermare questa ipotesi si effettua nuovamente il calcolo del rapporto r/ls > 0,8:
10.16 Tabella r/ls > 0,8 (modello 13)
Dalla tabella 10.16 si evince che il rapporto r/ls >0,8 è soddisfatto per ogni piao della struttura, quindi il modello 17 non è suscettibile a torsione, si procede ora con il verificare se la struttura di progetto è regolare sia in pianta che in alzato tramite le indicazioni riportare nel capitolo 7.2.2 della normativa, per capire in che tipologia strutturale ricade l’edificio oggetto di progettazione:
10.17.1 Stralcio di normativa, capitolo 7.2.2
Per la regolarità in pianta:
VERIFICATO, data la disposizione dei centri di massa di tutti gli impalcati della struttura;
VERIFICATO, 24,4/18,45 = 1,32 < 4;
VERIFICATO, nella struttura in esame non vi sono parti di essa che aggettano;
VERIFICATO, tutti gli orizzontamenti possono essere considerati infinitamente rigidi (ipotesi di progetto).
Per la regolarità il altezza:
e. VERIFICATO, ogni elemento strutturale verticale si estende per tutta l’altezza della struttura;
f. Attraverso i dati della tabella sottostante e per il fatto che la struttura ricade nella tipologia citata dalla nota in noramtiva per cui le strutture a nucleo in c.a. con sezione costante dello stesso con più del 50 % di assorbimento da parte del nucleo dell’azione sismica alla base (questo concetto è meglio rappresentato nelle considerazioni successive).
10.17.2 Stralcio di normativa, capitolo 7.2.2
Gli scostamenti superano il 30% previsto da normativa, ma ai fini progettuali si considera la struttura regolare in altezza;
g. VERIFICATO, dato che la struttura ricade in CD “A”;
h. VERIFICATO, nella struttura non vi è alcun restringimento della sezione orizzontale.
10.18 Impalcato tipo (modello 17)
Preso atto della regolarità in pianta e in sezione della struttura, si procede con l’analisi della tipologia strutturale escludendo la possibilità di ricadere in strutture suscettibili a torsione, si analizza l’ipotesi di tipologie a telai o a setti, per fare ciò si analizzano le azioni, valutando in percentuale a quale dei due elementi, telai o pareti, è affidata la resistenza a tali azioni:
per le strutture a telai, questi devono resistere per una percentuale ≥ 65% alle azioni agenti sulla struttura;
per le strutture a pareti, queste devono resistere per una percentuale ≥ 65% alle azioni agenti sulla struttura;
per strutture miste le azioni verticali devono essere affidate in maggioranza ai telai, per le azioni orizzontali ci sono due sottocategorie della stessa tipologia strutturale:
- miste equivalenti a telai, quando questi resistono per ≥ 50% alle azioni orizzontali agenti sulla struttura;
- miste equivalenti a pareti, quando queste resistono per ≥ 50% alle azioni orizzontali agenti sulla struttura.
10.19 Carico Wi applicato al modello 3D per l’analisi della tipologia strutturale (modello 17)
Calcolando quindi il peso di ogni impalcato della struttura e applicando tale “forza peso” in direzione orizzontale, prima in x e poi in y sul modello 3D si ricavano, mediante una section cut di tutti i punti alla base degli elementi, le reazioni vincolari di ogni elemento, infine sommando queste per tutti gli elementi a telaio e per tutte le pareti si ricava:
10.20 Tabella reazioni vincolari e percentuali delle azioni sugli elementi strutturali
Dalla tabella si deduce che la struttura analizzata ricade nella tipologia di struttura a pareti non accoppiate.
Il fattore di struttura q0 è tabellato dalla normativa a seconda della classe di duttilità nel quale si sta progettando (CD “A”) e a seconda della tipologia strutturale, quindi:
10.21 tabella di normativa per il calcolo del fattore di struttura q0
Dalla tabella si ricava q0 = 4,4
Con il valore del fattore di struttura si calcola q = q0 x KR
dove: KR = fattore riduttivo che dipende dalle caratteristiche di regolarità in altezza della struttura, con valore di 1 per strutture regolari in altezza e valore di 0,8 per strutture non regolari in altezza;
q0 = il massimo valore del fattore di struttura.
q = 4,4 per componenti orizzontali;
q = 1,5 per componenti verticali (valore da normativa per tutte le strutture tranne i ponti).
Ricavato il valore di q possiamo ora disegnare lo spettro elastico e trovare poi lo spettro di progetto, tramite delle formule in normativa che permettono di tracciare il grafico dello spettro tramite la conoscenza della topografia, dell’altezza del sito, della zona sismica, della vita nominale, del coefficiente d’uso dell’edificio, della categoria del sottosuolo, e dello stato limite che si vuole analizzare:
10.22 calcolo spettro di progetto della struttura
10.23 spettro di progetto
Per ottenere i valori delle accellerazioni agenti sulla struttura, avendo lo spettro di progetto occorre sapere il periodo proprio della struttura (T) che si può ricavare tramite l’analisi modale sul modello 3D:
10.24 analisi modale e periodi propri della struttura nei modi 1 e 2
Analizzando i primi due modi di tale analisi si ricavano i due periodi propri della struttura per x e per y con cui ricavare le accellerazioni dallo spettro:
Modal T1=0.67; T2=0.64
La normativa odierna ed il prossimo aggiornamento della stessa introducono due formule per verificare il giusto valore del periodo proprio di una struttura:
T=CxH^3/4 = 0.71
T=2√d = 0.77 e 0.72
La forza sismica equivalente E da applicare al modello 3D secondo combinazione si ricava dalla normativa tramite la formula:
Fh = Sd(Ti) x W x λ/g
In cui Sd è l’ordinata dello spettro di progetto secondo il periodo proprio della struttura, W è il peso della struttura, λ è un coefficiente pari a 1 se la struttura è più di tre orizzontamenti e g è la forza di gravità.
10.25 tabella calcolo della forza sismica “E”
Tale forza sismica va ora divisa per ogni piano della struttura e applicata sui baricentri di massa del modello 3D di ogni impalcato della struttura:
Fi = Fh x zi x Wi x ∑ zj x Wj
In cui Fh è la forza equivalente, zi e zj è la distanza da terra dell’impalcato in esame, Wj è il peso dell’impalcato.
10.26 tabella calcolo delle forze iesime di ogni piano
La normativa identifica come combianziona sismica:
E + G1 + G2 + P + Ψ21*Qk1 + Qk2…
In cui E, forza equivalente viene a sua volta combinata in altre 8 combinazioni di carico che tengono conto della varibilità spaziale del moto e alle diverse componenti dell’azione sismica:
1.0 Ex + 0.30 Ey + 0.30 Ez
(trascurando per il progetto il contributo di Ez)
Si ricavano 8 combinazioni differenti da applicare alla struttura sguendo la combinazione sismica precedente:
Esplicitati i carichi che gravano sulla struttura e applicati questi al modello 3D secondo le combinazioni sismiche e non sismiche degli SLU, si definiscono 3 inviluppi:
Inviluppo SLU non sismico;
Inviluppo SLU sismico;
Inviluppo degli inviluppi.
11.1 tabella inviluppi del modello 3D
Si esportano quindi gli inviluppi necessari per la progettazione delle “travate” della struttura.
Per progettare tali travate occorre ottimizzare le stesse in range che le tassonomizzano per dimensione della sezione, tipo (principali e secondarie) e sollecitazioni (massime o minime).
Ottimizzazione delle travate:
30x70 principali;
30x70 secondarie;
30x60 principali;
30x60 secondarie;
30x50 principali;
30x50 secondarie.
11.2.1 Impalcato piano tipo, selezione sezioni 30x50 principali
11.2.2 Esempio classificazione delle travate 30x50 principali
Ricavati i diagrammi dei momenti dall’inviluppo degli inviluppi si procede con la traslazione di tali diagrammi per i massimi e i minimi dello stesso per includere l’azione del taglio secondo:
a1= 0.9*d*(cotθ – cotα)/2
Si procede con la progettazione a flessione dell’armatura longitudinale delle travate, calcolando la lunghezza della zona critica e includendo i limiti geometrici e di armatura sismica e non sismica imposta dalla normativa vigente e il valore del taglio agente sugli appoggi (nodo trave-pilastro) lato inferiore (dall’inviluppo degli inviluppi), e dei momenti in campata suepriore se esistenti:
11.3 Tabella limiti geometrici travi
11.4 Progetto a flessione dell’armatura longitudinale
Per ogni range si identifica la travata con sollecitazioni massime e minime in modo da dimensionare l’armatura longitudinale e trasversale minima e massima e ricavare successivamente, con l’aggiunta dei ferri, tutte le armature delle altre travate;
Per la definizione delle armature longitudinali si calcolano le lunghezze di ancoraggio e di sovrapposizione dei ferri, nonché il valore del copriferro dato dalla classe di calcestruzzo di progetto e dalle condizioni ambientali nel quale si progetta la struttura, e si riportano graficamente:
11.5 Tabella lunghezze di ancoraggio e sovrapposizione
* il disegno dei ferri e delle lunghezze aggiuntive date dalle sovrapposizione o dagli ancoraggi rispettano i limiti imposti dalla normativa:
1. la sovrapposizione dei ferri deve avvenire quando il momento è minimo e non si possono effettuare ancoraggi inferiormente in presenza di appoggi;
2. non si possono prevedere sovrapposizioni o ancoraggi di ferri nella stessa sezione sia superiormente che inferiormente;
3. non si effettuano sovrapposizioni o ancoraggi nei nodi, se vincolati dalla geometria della travata il ferro longitudinale va ripiegato nel nodo, incluso nelle staffe dello stesso, e non può ritornare in zona critica della trave da cui proviene, con una lunghezza di ancoraggio calcolata con una resistenza pari a 1.25*fyk;
4. non si può ancorare in zona critica, ogni ferro deve oltrepassare la zona critica di ogni trave.
11.6 Progetto delle travate
* per il disegno dei ferri si rappresenta il diagramma a “gradoni” secondo le resistenze delle armature progettate calcolando Mrd(Φ) = 0.9*d*fyd*A(Φ) di ogni ferro longitudinale incluso nella progettazione.
Per le verifiche dell'armatura longitudinale delle travi in SLU sismico la normativa richiede che il rapporto geometrico di ARMATURA TESA (p) deve essere compreso tra 1,4/fyk e pcomp.+3.5/fyk.
Nel caso in cui l'inviluppo è caratterizzato da presenza di momento sia superiore che inferiore, l'armatura compressa quale sarebbe? Come calcoliamo il pcomp.?
Per la definizione dell’armatura trasversale si effettuano due diversi tipi di progettazione:
Progettazione armature trasversale per SLU non sismico;
Progettazione armature trasversali per SLU sismico.
1. La progettazione non sismica avviene tramite l’esportazione del diagramma del taglio dall’inviluppo non sismico, seguendo i range di travate già classificati precedentemente:
11.8 Diagrammi del taglio dell’inviluppo SLU non sismico delle travate 30x50 principali, sezione 1
Rispettando i limiti imposti dalla normativa per la quantità di armatura trasversale e il passo da rispettare, si progettano le armature da disegnare nelle travate e se ne verificano le sezioni:
11.9 Calcoli armatura trasversale per SLU non sismico delle travate 30x50 principali, sezione 1
2. La progettazione sismica dell’armatura trasversale delle travate segue un iter processuale differente da quello eseguito per la progettazione non sismica, prendendo in considerazione minimi di normativa differenti e ricavando il calcolo del taglio agente massimo e minimo di ogni trave presente nella travata, secondo un sottoschema della trave stessa che prende in considerazione le combinazioni di carico sismico come carichi uniformemente distribuiti sulla stessa e due momenti concordi applicati agli estremi della trave che equivalgono ai momenti resistenti delle sezioni della stessa trave maggiorati di un γRd per sovradimensionare la resistenza della sezione. Il sottoschema presenta un modello matematico di una trave appoggiata-appoggiata con 4 combinazioni di carico che prevedono:
11.10 Combinazioni di carico per il calcolo del taglio agente nel sottomodello per la progettazione dell’armatura a taglio delle travi
Le quattro combinazioni riportate in figura 11.10 prevedono la presenza o meno dei carichi accidentali Qk e gli effetti di oscillazione del sisma che generano i momenti resistenti MRd,A e MRd,B.
Con il valore del taglio ricavato dal sottomodello e seguendo i minimi da normativa si può progettare l’armatura trasversale delle travate, verificando la stessa con la procedura seguita per la progettazione in zona non sismica, seguendo però delle opportune verifiche specifiche per la zona critica delle travi in cui la normativa specifica dei diversi limiti di armatura trasversale e passo della stessa più restrittivi:
11.11 Tabella calcolo del taglio minimo e massimo dal sottomodello
11.12 Tabella minimi di normativa sismici per la progettazione armatura trasversale, progetto e verifica della stessa
La progettazione dell’armatura trasversale delle travate prende in considerazione entrambi i dimensionamenti andando a disegnare le armature lungo la travata e nelle zone critiche seguendo le indicazioni del dimensionamento più restrittivo tra i due effettuati.
11.13 Progetto armatura trasversale delle travate 30x50 principali, sezione 1
Le travate ora dimensionate a SLU vanno verificate per gli SLE a tensione e fessurazione, seguendo l’iter processuale già esposto e rappresentato per la verifica dei travetti del solaio nei capitoli precedenti.
Vengono qui di seguito riportate le tabelle dei calcoli da effettuare per gli SLE:
11.14 Tabella verifica SLE-tensioni delle travate 30x50 principali, sezione 1
11.15 Tabella verifica SLE-fessurazioni delle travate 30x50 principali, sezione 1
L’edificio scelto per la progettazione strutturale fa parte di un progetto architettonico sviluppato in un area residenziale nel paese di Terni; questo è composto da una destinazione residenziale con tipologia a “torre”, con nucleo di distribuzione verticale centrale e una distribuzione delle residenze e spazi comuni con affaccio sui lati corti dell’edificio.
La destinazione d’uso si compone di un piano terra che accoglie spazi di relazione, magazzini, locali tecnici, accoglienza, lavanderia e servizi, e ulteriori 5 piani di residenze studenti fornite di spazi accessori comuni per lo studio.
L’edificio ha una struttura in telai piani di cemento armato, solai latero-cementizi, nucleo centrale costituito da setti in cemento armato che supportano le scale e il vano ascensore, così come si evince dalle planimetrie in figura 1.2.
Le tipologie residenziali sono composte secondo le dimensioni della maglia strutturale e sono quindi componibili in alzato in maniera randomica secondo la miglior disposizione degli spazi interni del progetto.
Dagli alzati, rappresentati in figura 1.3, si nota come il progetto si componga di prospetti tecnologicamente analoghi a due a due composti l’uno da una “griglia” di prospetto in cui si inseriscono le aperture e le logge di ogni residenza o spazio comune composto da due diversi pacchetti tecnologici di tamponatura (tamponatura tipo 1 e 2), e l’altro composto da una disposizione quasi randomica delle bucature costituito da un unico pacchetto tecnologico (tamponatura tipo 2).
La particolarità dei due prospetti a griglia sarà presa in considerazione come “vincolo architettonico” nell’elaborazione del progetto strutturale per poter avere il risultato di una maglia composta dalla stessa dimensione in prospetto della trave e del pilastro (come si nota nella figura 2.3 in cui si rappresenta l’ipotesi di disegno dell’impalcato).
2. ANALISI DEI CARICHI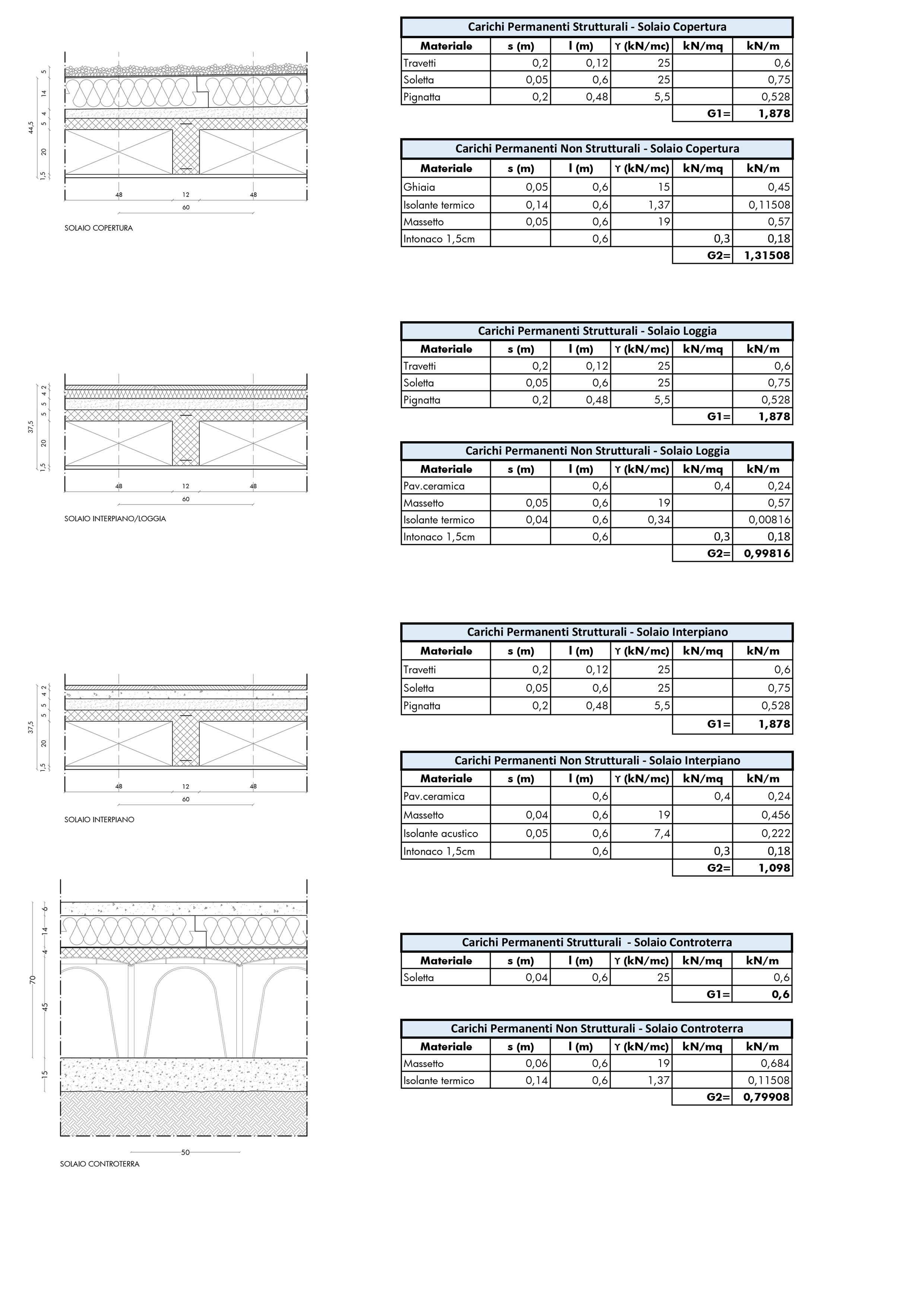
2.1Pacchetti tecnologici – fuori scala
Nella figura 2.1 sono riportati tutti i pacchetti tecnologici che si utilizzano nella redazione del progetto strutturale compresi i calcoli del carico permanente strutturale (G1), il carico permanente non strutturale (G2), il carico della tramezzatura (g2 che da normativa ricava il valore di G2 delle stesse tramezzature ripartite al mq), ed il carico delle tamponature tipo 1 e 2.
La sezione del solaio in latero-cemento è stata pre-dimensionata attraverso la tabella di normativa DM 09/01/1996, di seguito riportata:
2.2 Materiali utilizzati, copriferro, pre-dimensionamento solaio e analisi carichi variabili (Q)
Riassumendo, di seguito vengono riportati in tabella tutti i carichi che agiscono sui solai dimensionati e calcolati nel capitolo 1.
2.3 Tabella carichi solaio
3. PROGETTO DEL SOLAIO
Per quanto riguarda il dimensionamento per il solaio controterra, calcolati i carichi che gravano sullo stesso si dimensionano i Cupolex del vespaio areato mediante la scheda tecnica del prodotto: sovraccarico permanente = 1,39 KN/m + accidentale = 1,2 KN/m
3.1 Scheda tecnica Cupolex – solaio controterra
3.2 Ipotesi di impalcato del piano tipo
3.3 Individuazione aree funzionali
Si individuano le aree funzionali sull’impalcato in modo da poter poi ricavare le “sezioni” dei “modelli di solaio” di cui si andranno a calcolare poi le combinazioni di carico per ottenere l’inviluppo (tratteggio nero in figura 3.3).
Devono essere calcolati gli inviluppi delle tre “sezioni” dell’impalcato con le seguenti combinazioni di carico SLU che si riportano in figura 3.4:
3.4 Combinazione di carico SLU delle sezioni
Gli inviluppi che risultano dalle combinazioni di carico sono calcolati comprendendo anche il valore del momento nelle cerniere agli estremi del modello che sintetizza la tensione che la trave principale oppone alla deformazione dovuta dal travetto, calcolata con un valore pari a ql2/24.
Gli inviluppi del momento sono inoltre stati riportati, in figura 3.4, comprendendo già il contributo del taglio agente sulla sezione calcolato pari a (0,9 x d).
Attraverso i valori espressi dall’inviluppo del momento nel modello 1 si ricava tramite la tabella che segue l’armatura minima longitudinale che dovrà essere disegnata e verificata (calcolando agli appoggi anche l’azione del taglio nel calcolo della stessa armatura longitudinale).
3.5 Tabella calcolo armatura longitudinale - modello 1
Nella tabella 3.5 sono inoltre riportate le lunghezze d’ancoraggio per le barre utilizzate come armatura, appositamente dimensionate secondo gli Eurocodici2.
Il disegno che segue riporta graficamente quanto già espresso dalla tabella vista in precedenza:
3.6 Progetto armatura longitudinale - modello 1
.
4. VERIFICA DELLE SEZIONI
Si verificano le sezioni dei travetti con le rispettive armature longitudinali a SLU ricavando Mrd di tutte le sezioni prese in esame nella tabella 3.5:
4.1 Verifiche SLU
Con le stesse sezioni di cui sopra si vanno a verificare gli SLE per le tensioni in modo da verificare il buon esercizio durante la vita nominale della struttura.
dove:
4.2 Verifiche SLE
Dopo avere dimensionato e verificato le armature longiutdinali sia per Stato Limite Ultimo che per Stato Limite di Esercizio, si va ora a verificare se le sezione agli appoggi è verificata a taglio in modo da poter individuare se necessaria la presenza di eventuali fasce piene.
Da tali risultati si evince un Taglio resistente sempre maggiore di quello di progetto comportando così una non necessità di fasce piene.
Dimensionamento modello 2
Con la medesima procedura indicata per il progetto della sezione e della sua armatura longitudinale per il modello 1, si va a calcolare il modello 2 del solaio, come riportato in figura 4.4, con le correzioni riviste durante la revisione:
4.4 Impalcato piano tipo – sezione modello 2
4.5 Combinazioni di carico e inviluppi – modello 2
4.6 Tabella lunghezza di ancoraggio
SPECIFICA INDICAZIONI PER LA LUNGHEZZA D’ANCORAGGIO
Per il dimensionamento della lunghezza di ancoraggio si sono calcolati i valori in condizione di buona aderenza, ovvero se la barra si ancora in un punto dove il momento è minimo, e cattiva aderenza, ovvero nel caso l’ancoraggio capitasse la dove il momento è massimo o elevato quindi più prossimo a fessurazione. Inoltre data la presenza di barre che corrono longitudinalmente per tutta la sezione è stato necessario dividerli poichè da mercato le lunghezze massime sono di 12 metri, dato ciò si è calcolato inoltre il valore di sovrapposizione di tali barre cercando di spezzarle la dove il momento è minimo.
4.7 Verifiche SLU – modello 2
4.10 Progetto della sezione – modello 2
5. PREDIMENSIONAMENTO DELLA STRUTTURA
Per il predimensionamento della struttura si tengono conto i limiti geometrici imposti dalla normativa:
TRAVI
PARETI e SETTI
5.1 Predimensionamento travi e pareti
SCALE
Il progetto prevede scale composte mediante solette rampanti, per questo, secondo limiti geometrici, si predimensionano le stesse con uno spessore compreso tra i 15 e i 20 cm, comprendendo tra i margini anche l’ingombro dovuto dal copriferro.
5.2 Carichi pacchetto scale – soletta rampante
PILASTRI
Nu = 0.8 x Ac x fcd + As x fyd
si ricava:
Ac = Nd/(0.7 x fcd) in cui viene trascurato il contributo dell’armatura
dove Nd è pari alla somma di tutti i carichi che gravano sui pilastri del piano terra comprendendo anche la somma dei carichi dovuti al peso proprio della struttura (travi principali, travi secondarie e pilastri), il tutto calcolato attraverso la combinazione SLU determinata interamente sfavorevole.
Il coefficiente di riduzione 0.7 viene applicato per tenere conto della riduzione della resistenza della sezione dovuta all’azione di momento (dovuto alle relative eccentricità) sulla stessa.
2. si disegnano quindi le aree di influenza di ogni elemento pilastro, per ogni impalcato che comprende la struttura, ed ognuna di queste aree si suddivide ulteriormente per il calcolo dei diversi carichi dovuti a: G1, G2, Q1, Q2neve che si differenziano a seconda della destinazione e del pacchetto tecnologico di cui tale impalcato si costituisce (il tutto meglio esplicato in figura 5.4).
Per quanto riguarda l’area delle scale, queste vengono calcolate come contributo del carico dell’impalcato tramite il calcolo riportato nella figura 5.2 e riportato poi nella tabella sottostante che riassume tutti i carichi che influenzano il calcolo del predimensionamento dei pilastri:
5.3 Tabella riassuntiva dei carichi
5.4 Aree di influenza e delle destinazioni d’uso, dei pilastri
3. il progetto prevede degli affacci sui lati corti composti secondo un ordine randomico di logge, per poter ottimizzare i calcoli e velocizzare il predimensionamento, si sono studiate delle combinazioni, riportate in figura 5.5, in cui si evidenziano le differenze tra gli impalcati e si riportano nel giusto ordine tra i pilastri piano per piano.
5.5 Combinazioni carichi logge
5.6 Tabella dei carichi Ned (SLU) degli impalcati
4. dimensionate le aree di ogni pilastro alla base dell’edificio, si procede con il calcolo della capacità di resistenza a compressione della sezione attraverso la formula:
Nrd = fcd Ac
secondo normativa per la presso-flessione: per le strutture in CD “A” la sollecitazione di compressione non deve eccedere, il 55% della resistenza massima a compressione della sezione di solo calcestruzzo.
Quindi:
Nrd * 0.55 > Ne
dove Ne è la combinazione (SLU) per le azioni sismiche:
5.7 Tabella delle verifiche della sezione predimensionata dei pilastri
NODI TRAVE-PILASTRO
5.9 Predimensionamento della struttura
6. MODELLO 3D
6.1 Modello 3d struttura
Il modello 3d della struttura è realizzato secondo lo schema strutturale di progetto, a questo vengono assegnate le sezioni per ogni elemento che lo compone.
Queste sezioni vengono definite nel software secondo la geometria e i materiali scelti, andando a diversificare diversi valori del modulo elastico per gli elementi (travi, pilastri, pareti) per contemplare il contributo della fessurazione della sezione:
6.2 Tabella sezioni di progetto
Assegnate le sezioni a tutti gli elementi del modello si uniscono questi in gruppi che identificano il piano della struttura e la sezione comune, per migliorare il metodo di selezione degli elementi nel software:
6.2 Tabella gruppi
7. CENTRO DI MASSA DEGLI IMPALCATI
Realizzato il modello 3d della struttura, si devono ora inserire tutti i carichi delle combinazioni SLU (capitolo successivo) e le azioni sismiche riferite ai centri di massa degli impalcati con le relative combinazioni sismiche da normativa.
Si procede quindi con il calcolo del baricentro di massa per ogni impalcato presente nella struttura, andando a dividere lo stesso in aree rettangolari in cui si identificano i carichi G1, G2, Q1 e Q2 relativi secondo la combinazione SLU sismica:
Wi = G1 + G2 + Q1 x Ψ21 +Q2 x Ψ22
Avendo la struttura impalcati differenti per ogni piano della stessa si identifica un “layer” di travi principali e secondarie uguali per ogni piano e si vanno a identificare i “layers” di tutti gli altri impalcati diversi tra loro, compresa la copertura:
7.1 Aree dell’impalcato per il calcolo del centro di massa
Per quanto riguarda le tamponature, queste si calcolano considerando nell’impalcato metà della loro altezza in alzato e metà della restante tamponatura del piano precedente, come in figura 7.2:
7.2 Aree dell’impalcato per il calcolo del centro di massa e sezione schematica
Definite le aree e le distanze del centro di massa delle stesse da un sistema di assi cartesiani riferiti all’impalcato, si va a calcolare il peso Wi dalla formula vista prima e il momento statico Sx e Sy che si ricava da:
Si = Wi x di
Dal quale si può ricavare:
Xm = ∑ Six/Wtot Ym = ∑ Siy/Wtot
7.3 Stralcio tabella calcolo dei pesi degli impalcati
Le coordinate del centro di massa dell’impalcato.
Calcolati tutti i centri di massa degli impalcati, da normativa si va ad introdurre per cautela un valore minimo di eccentricità che tiene conto della semplificazione che tutti gli accidentali sono stati considerati uniformemente distribuiti.
Eix = +/- 0.05 Xm
Eiy = +/- 0.05 Ym
Con l’introduzione del valore di eccentricità addizionale si ricavano in tutto 4 (combinazioni) differenti centri di massa per ogni impalcato di cui PER IL PROGETTO, andiamo a considerare solo il più sfavorevole.
7.5 Centri di massa degli impalcati
I centri di massa di ogni impalcato vengono caricati nel modello 3d ed inclusi all’interno dei rispettivi impalcati sintetizzati nello stesso tramite il comando DIAPHRAGM impostanto su di essi il valore della massa per i 3 gradi di libertà X, Y e per Z si imposta l’inerzia rotazionale Ip calcolata mediante:
Ip = M x ρ^2
8. CENTRO DI RIGIDEZZA DEGLI IMPALCATI
Ricavati centri di massa di tutti gli impalcati, si ricava il centro di rigidezza dell’impalcato tipo (poiché tutti gli impalcati hanno la stessa tipologia di struttura), per poter poi capire quale tra i centri di massa trovao è il più distante dal centro di rigidezza e quindi il più sfavorevole per quanto riguarda la torsione della struttura.
8.1 Impalcato e distanze dei “telai piani” dal sistema di riferimento cartesiano
Si identificano tutti i telai, verticali e orizzontali dell’impalcato tipo e degli stessi, si identificano gli elementi di cui sono composti nelle tabelle che seguono (figura 8.2 e 8.3):
8.2 Tabella elementi strutturali
Come mostra lo stralcio della tabella in figura 8.3, per ogni telaio viene calcolata la rigidezza secondo un modulo elastico stabilito in precedenza e l’inerzia di ogni elemento secondo l’asse riferito alla direzione del telaio.
Per il calcolo della rigidezza si tiene conto di un modello di telaio piano shear-type per cui la rigidezza è sintetizzata in:
K = (12E x∑ I)/h3
8.3 Stralcio tabella calcolo rigidezze telai
Le coordinate vengono ricavate mediante:
Xc = (∑ Kvi * dvi)/ Kvtot
Yc = (∑ Koi * doi)/ Kotot
8.4 Tabella calcolo coordinate centro di rigidezza
8.5 Centri degli impalcati
9. INVILUPPO SLU NON SISMICO
Per ricavare i carichi per il calcolo dell’inviluppo SLU non sismico di tutti gli elementi della struttura in esame di procede con il calcolo di tutti i carichi areali, lineari e puntuali che gravano sugli elementi strutturali, partendo quindi dall’area di influneza delle travi principali e secondarie e dala peso proprio degli elementi strutturali verticali:
9.1 Area di influenza travi principali e secondarie sugli impalcati
Per le travi secondarie si considera un area di influenza con interasse pari a 50 cm per ogni fronte dell’elemento stesso.
Come già fatto per il calcolo dei carichi per le aree di influenza dei pilastri, si vanno a localizzare i carichi G1, G2, Q1, Q2, calcolandoli come carichi linearmente distribuiti sulle travi.
Si localizzano inoltre i carichi concentrati degli elementi pilastri e setti che dovranno essere anch’essi caricati sul modello 3d e il carico areale da localizzare sulla superficie della soletta rampante delle scale.
Essendo la struttura composta da impalcati tutti differenti l’uno dall’altro, come già fatto per il predimensionamento dei pilastri, si localizzano tutte le varianti del piano in dei “moduli delle aree di influenza” sia per le travi primarie che secondarie, in modo da poter velocizzare il calcolo:
9.3 Moduli aree di influenza variabili
9.4 Stralcio tabelle carichi SLU non sismici
Ricavati i centri di tutti gli impalcati si deve ora definie quale tra i 4 centri di massa moltiplicati per l’eccentricità addizionale sia il più sfavorevole, per ogni impalcato.
Per fare ciò si effettuano due verifiche:
1° verifica
8.6 Centro di massa più distante dal Centro delle Rigidezze (CR)
2° verifica
Si definiscono in SAP i 4 centri di massa ricavati, si assegna loro la massa per i tre gradi di libertà (figura 8.8) e il constraints – diaphram insieme a tutti i punti che giacciono sull’impalcato (figura 8.7) e si assegna loro, una volta ciascuno, le forze orizzontali nelle due direzioni X e Y e si verificano gli spostamenti (figura 8.9):
8.7 Assegnazione del constraints – diaphram
8.8 Assegnazione delle masse al centro di massa
8.8 Assegnazione delle masse al centro di massa
8.9 Deformazione
Da ogni configurazione deformata si localizzano 4 punti dell’impalcato e si studiano i loro spostamenti:
8.10 Schema della verifica
8.11 Tabella degli spostamenti
Dalle due verifiche risulta che la condizione più sfavorevole per tutti gli impalcati è assegnare il centro di massa al punto definito dall’eccentricità ex + , ey –
Ricavati i carichi che gravano su tutti gli elementi della struttura si procede con l’assegnazione di ogn’uno di questi al proprio elemento nell modello 3D, andando a definire quelle che sono le combinazioni di carico per l’inviluppo SLU non sismico.
Ai fini della progettazione strutturale dell’edificio in esame, si riducono le combinazioni per semplificare il calcolo a solo 3 di queste (figura 9.5)
9.5 Combinazioni per SLU non sismico
La prima combinazione presenta una situazione di “tutto caricato” con ogni carico moltiplicato, secondo normativa per la combinazione SLU, con coefficiente γ sfavorevole;
Le due combinazioni a seguire sono combinazioni a scacchiara in cui gli elementi selezionati in rosso sono carichi da esplicitare con coefficiente sfavorevole e i restanti con coefficiente favorevole, queste “scacchiere” inoltre si alternano tra gli impalcati.
Nel modello 3D in SAP si procede con la definizione di tutti i tipi di carico (esplicitando se moltiplicati per coefficienti favorevoli o sfavorevoli per le tre combinazioni) e l’assegnazione ad ogni elemento dei propri carichi siano essi puntuali, lineari o areali.
9.6 Sintesi definizione e assegnazione dei carichi nel modello 3D
(Le classi dei carichi definiti nella figura 9.6 si riferiscono a carichi linearmenti distribuiti, escludendo i carichi puntuali su setti e pilastri e quelli areali sulla soletta rampante che costituisce le scale.
10. ANALISI LINEARE ELASTICA
La normativa classifica le strutture a seconda di tipologie di deformazioni, dobbiamo quindi calcolare il fattore q0 , che identifica la capacità di dissipazione della struttura e quindi configura uno spettro di progetto minimizzato rispetto allo spettro elastico, che secondo la normativa viene tabellato secondo le “tipologie strutturali”.
Si procede quindi con 2 analisi per capire se la natura della struttura sia o meno suscettibile alla torsione:
Si analizza attraverso l’analisi modale il modello 3d della struttura:
10.1 Modello “9” 3D – struttura
ricavando:
10.2 Deformazioni della struttura del modo 1 e 2 (modello 9)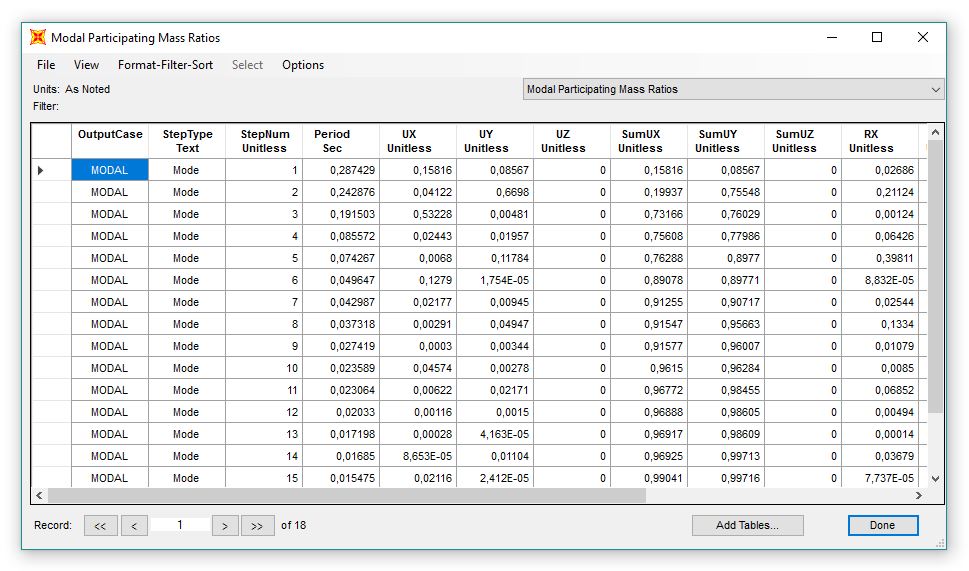
10.3 Tabella delle masse partecipanti nei modi (modello 9)
Attraverso le deformazioni del modo 1 e 2 si riscontra un comportamento suscettibile alla torsione, questo poiché la struttura presenta un nucleo molto rigido dato dalle pareti del corpo di distribuzione dell’edificio.
Quindi si procede intervenendo sugli elementi strutturali cercando di irrigidire il perimetro dell’edificio modificando la sezione delle travi e dei pilastri e l’orientamento di tutti i pilastri della struttura.
Si realizza il modello “13” composto da travi perimetrali più rigide, le sezioni e l’orientamento dei pilastri sul perimetro che orientano il centro delle rigidezze più vicino al centro di massa dei vari impalcati:
10.4 Modello “13” 3D – struttura
ricavando:
10.5 Deformazioni della struttura del modo 1 e 2 (modello 13)
10.6 Tabella delle masse partecipanti nei modi (modello 13)
Nel nuovo modello si riscontra un comportamento diverso, che garantisce una buona partecipazione della massa nella deformazione del modo 1 e 2.
Nell’analisi del rapporto r/ls > 0,8 si riscontra quanto descritto dalla tabella seguente:
10.7 Tabella r/ls 0,8 (modello 13)
Nella tabella 10.7 sono riportati i delta degli spostamenti e delle rotazioni del centro di massa di ogni impalcato generati da una forza Fi ricavata da:
Fi = Fh x zi (Wi/∑zj x Wj)
dove:
Fh = forza equivalente al sisma presa come 5000 KN;
zi = altezza dell’impalcato da terra;
Wi = peso dell’impalcato;
Zj e Wj = rispettivamente l’altezza da terra dell’impalcato e il peso dello stesso.
Si ricava poi il taglio di piano tramite la somma delle forze applicate fino all’impalcato in esame e si calcola la Rigidezza flessionale per x e y e la rigidezza torsionale mediante:
Kfx = Taglio di piano / delta spostamento in x;
Kfy = Taglio di piano / delta spostamento in y;
Kt = Taglio di piano / delta rotazione in z;
con le rigidezze ricavate si esplicita r2:
r2 x= Kt/Krx r2 x= Kt/Krx
e si calcola:
ls = √((L2+B2)/12)
infine:
r/ls > 0,8
CONSIDERAZIONI:
La struttura del modello 13 viene verificata non suscettibile a torsione nelle due analisi descritte nel capitolo 10.
CONSIDERAZIONI:
La struttura del modello 13 viene verificata non suscettibile a torsione nelle due analisi descritte nel capitolo 10, andranno ora fatte ulteriori cosiderazioni sulla dimensione delle sezioni degli elementi modificati per rendere la struttura non suscettibile a torzione:
10.8 Modello “17” 3D – struttura e sezioni degli elementi
Si effettua ora il calcolo dei nuovi centri di massa e di rigidezza, mutati a causa della variazione delle sezioni degli elementi strutturali, così come il valore della massa in x e y e dell’inerzia rotazionale in z:
10.9 Schema impalcato tipo – quote telai
10.10 Tabella sezioni di progetto
10.11 Tabella centro rigidezza – (Modello 17)
10.12 Tabella centri massa – (Modello 17)
10.13 Centri degli impalcati – (Modello 17)
Si effettua ora l’analisi modale del nuovo modello (17) di struttura corretto delle precisazioni sopra elencate:
10.14 Deformazioni della struttura del modo 1 e 2 (modello 17)
10.15 Tabella delle masse partecipanti nei modi (modello 17)
Nel nuovo modello 17 le percentuali di massa nei primi due modi ha un valore che soddisfa i paramentri della tipologia di struttura, per confermare questa ipotesi si effettua nuovamente il calcolo del rapporto r/ls > 0,8:
10.16 Tabella r/ls > 0,8 (modello 13)
Dalla tabella 10.16 si evince che il rapporto r/ls >0,8 è soddisfatto per ogni piao della struttura, quindi il modello 17 non è suscettibile a torsione, si procede ora con il verificare se la struttura di progetto è regolare sia in pianta che in alzato tramite le indicazioni riportare nel capitolo 7.2.2 della normativa, per capire in che tipologia strutturale ricade l’edificio oggetto di progettazione:
10.17.1 Stralcio di normativa, capitolo 7.2.2
Per la regolarità in pianta:
Per la regolarità il altezza:
e. VERIFICATO, ogni elemento strutturale verticale si estende per tutta l’altezza della struttura;
f. Attraverso i dati della tabella sottostante e per il fatto che la struttura ricade nella tipologia citata dalla nota in noramtiva per cui le strutture a nucleo in c.a. con sezione costante dello stesso con più del 50 % di assorbimento da parte del nucleo dell’azione sismica alla base (questo concetto è meglio rappresentato nelle considerazioni successive).
10.17.2 Stralcio di normativa, capitolo 7.2.2
Gli scostamenti superano il 30% previsto da normativa, ma ai fini progettuali si considera la struttura regolare in altezza;
g. VERIFICATO, dato che la struttura ricade in CD “A”;
h. VERIFICATO, nella struttura non vi è alcun restringimento della sezione orizzontale.
10.18 Impalcato tipo (modello 17)
Preso atto della regolarità in pianta e in sezione della struttura, si procede con l’analisi della tipologia strutturale escludendo la possibilità di ricadere in strutture suscettibili a torsione, si analizza l’ipotesi di tipologie a telai o a setti, per fare ciò si analizzano le azioni, valutando in percentuale a quale dei due elementi, telai o pareti, è affidata la resistenza a tali azioni:
per le strutture a telai, questi devono resistere per una percentuale ≥ 65% alle azioni agenti sulla struttura;
per le strutture a pareti, queste devono resistere per una percentuale ≥ 65% alle azioni agenti sulla struttura;
per strutture miste le azioni verticali devono essere affidate in maggioranza ai telai, per le azioni orizzontali ci sono due sottocategorie della stessa tipologia strutturale:
- miste equivalenti a telai, quando questi resistono per ≥ 50% alle azioni orizzontali agenti sulla struttura;
- miste equivalenti a pareti, quando queste resistono per ≥ 50% alle azioni orizzontali agenti sulla struttura.
10.19 Carico Wi applicato al modello 3D per l’analisi della tipologia strutturale (modello 17)
Calcolando quindi il peso di ogni impalcato della struttura e applicando tale “forza peso” in direzione orizzontale, prima in x e poi in y sul modello 3D si ricavano, mediante una section cut di tutti i punti alla base degli elementi, le reazioni vincolari di ogni elemento, infine sommando queste per tutti gli elementi a telaio e per tutte le pareti si ricava:
10.20 Tabella reazioni vincolari e percentuali delle azioni sugli elementi strutturali
Dalla tabella si deduce che la struttura analizzata ricade nella tipologia di struttura a pareti non accoppiate.
Il fattore di struttura q0 è tabellato dalla normativa a seconda della classe di duttilità nel quale si sta progettando (CD “A”) e a seconda della tipologia strutturale, quindi:
10.21 tabella di normativa per il calcolo del fattore di struttura q0
Dalla tabella si ricava q0 = 4,4
Con il valore del fattore di struttura si calcola q = q0 x KR
dove: KR = fattore riduttivo che dipende dalle caratteristiche di regolarità in altezza della struttura, con valore di 1 per strutture regolari in altezza e valore di 0,8 per strutture non regolari in altezza;
q0 = il massimo valore del fattore di struttura.
q = 4,4 per componenti orizzontali;
q = 1,5 per componenti verticali (valore da normativa per tutte le strutture tranne i ponti).
Ricavato il valore di q possiamo ora disegnare lo spettro elastico e trovare poi lo spettro di progetto, tramite delle formule in normativa che permettono di tracciare il grafico dello spettro tramite la conoscenza della topografia, dell’altezza del sito, della zona sismica, della vita nominale, del coefficiente d’uso dell’edificio, della categoria del sottosuolo, e dello stato limite che si vuole analizzare:
10.22 calcolo spettro di progetto della struttura
10.23 spettro di progetto
Per ottenere i valori delle accellerazioni agenti sulla struttura, avendo lo spettro di progetto occorre sapere il periodo proprio della struttura (T) che si può ricavare tramite l’analisi modale sul modello 3D:
10.24 analisi modale e periodi propri della struttura nei modi 1 e 2
Analizzando i primi due modi di tale analisi si ricavano i due periodi propri della struttura per x e per y con cui ricavare le accellerazioni dallo spettro:
Modal T1=0.67; T2=0.64
La normativa odierna ed il prossimo aggiornamento della stessa introducono due formule per verificare il giusto valore del periodo proprio di una struttura:
T=CxH^3/4 = 0.71
T=2√d = 0.77 e 0.72
La forza sismica equivalente E da applicare al modello 3D secondo combinazione si ricava dalla normativa tramite la formula:
Fh = Sd(Ti) x W x λ/g
In cui Sd è l’ordinata dello spettro di progetto secondo il periodo proprio della struttura, W è il peso della struttura, λ è un coefficiente pari a 1 se la struttura è più di tre orizzontamenti e g è la forza di gravità.
10.25 tabella calcolo della forza sismica “E”
Tale forza sismica va ora divisa per ogni piano della struttura e applicata sui baricentri di massa del modello 3D di ogni impalcato della struttura:
Fi = Fh x zi x Wi x ∑ zj x Wj
In cui Fh è la forza equivalente, zi e zj è la distanza da terra dell’impalcato in esame, Wj è il peso dell’impalcato.
10.26 tabella calcolo delle forze iesime di ogni piano
La normativa identifica come combianziona sismica:
E + G1 + G2 + P + Ψ21*Qk1 + Qk2…
In cui E, forza equivalente viene a sua volta combinata in altre 8 combinazioni di carico che tengono conto della varibilità spaziale del moto e alle diverse componenti dell’azione sismica:
1.0 Ex + 0.30 Ey + 0.30 Ez
(trascurando per il progetto il contributo di Ez)
Si ricavano 8 combinazioni differenti da applicare alla struttura sguendo la combinazione sismica precedente:
10.27 tabella combinazioni di E secondo normativa
11. PROGETTO DELLE TRAVI
Esplicitati i carichi che gravano sulla struttura e applicati questi al modello 3D secondo le combinazioni sismiche e non sismiche degli SLU, si definiscono 3 inviluppi:
11.1 tabella inviluppi del modello 3D
Si esportano quindi gli inviluppi necessari per la progettazione delle “travate” della struttura.
Per progettare tali travate occorre ottimizzare le stesse in range che le tassonomizzano per dimensione della sezione, tipo (principali e secondarie) e sollecitazioni (massime o minime).
Ottimizzazione delle travate:
11.2.1 Impalcato piano tipo, selezione sezioni 30x50 principali
11.2.2 Esempio classificazione delle travate 30x50 principali
Ricavati i diagrammi dei momenti dall’inviluppo degli inviluppi si procede con la traslazione di tali diagrammi per i massimi e i minimi dello stesso per includere l’azione del taglio secondo:
a1= 0.9*d*(cotθ – cotα)/2
Si procede con la progettazione a flessione dell’armatura longitudinale delle travate, calcolando la lunghezza della zona critica e includendo i limiti geometrici e di armatura sismica e non sismica imposta dalla normativa vigente e il valore del taglio agente sugli appoggi (nodo trave-pilastro) lato inferiore (dall’inviluppo degli inviluppi), e dei momenti in campata suepriore se esistenti:
11.3 Tabella limiti geometrici travi
11.4 Progetto a flessione dell’armatura longitudinale
Per ogni range si identifica la travata con sollecitazioni massime e minime in modo da dimensionare l’armatura longitudinale e trasversale minima e massima e ricavare successivamente, con l’aggiunta dei ferri, tutte le armature delle altre travate;
Per la definizione delle armature longitudinali si calcolano le lunghezze di ancoraggio e di sovrapposizione dei ferri, nonché il valore del copriferro dato dalla classe di calcestruzzo di progetto e dalle condizioni ambientali nel quale si progetta la struttura, e si riportano graficamente:
11.5 Tabella lunghezze di ancoraggio e sovrapposizione
* il disegno dei ferri e delle lunghezze aggiuntive date dalle sovrapposizione o dagli ancoraggi rispettano i limiti imposti dalla normativa:
1. la sovrapposizione dei ferri deve avvenire quando il momento è minimo e non si possono effettuare ancoraggi inferiormente in presenza di appoggi;
2. non si possono prevedere sovrapposizioni o ancoraggi di ferri nella stessa sezione sia superiormente che inferiormente;
3. non si effettuano sovrapposizioni o ancoraggi nei nodi, se vincolati dalla geometria della travata il ferro longitudinale va ripiegato nel nodo, incluso nelle staffe dello stesso, e non può ritornare in zona critica della trave da cui proviene, con una lunghezza di ancoraggio calcolata con una resistenza pari a 1.25*fyk;
4. non si può ancorare in zona critica, ogni ferro deve oltrepassare la zona critica di ogni trave.
11.6 Progetto delle travate
* per il disegno dei ferri si rappresenta il diagramma a “gradoni” secondo le resistenze delle armature progettate calcolando Mrd(Φ) = 0.9*d*fyd*A(Φ) di ogni ferro longitudinale incluso nella progettazione.
11.7 Progetto delle travate
DOMANDA:
Per le verifiche dell'armatura longitudinale delle travi in SLU sismico la normativa richiede che il rapporto geometrico di ARMATURA TESA (p) deve essere compreso tra 1,4/fyk e pcomp.+3.5/fyk.
Nel caso in cui l'inviluppo è caratterizzato da presenza di momento sia superiore che inferiore, l'armatura compressa quale sarebbe? Come calcoliamo il pcomp.?
Per la definizione dell’armatura trasversale si effettuano due diversi tipi di progettazione:
1. La progettazione non sismica avviene tramite l’esportazione del diagramma del taglio dall’inviluppo non sismico, seguendo i range di travate già classificati precedentemente:
11.8 Diagrammi del taglio dell’inviluppo SLU non sismico delle travate 30x50 principali, sezione 1
Rispettando i limiti imposti dalla normativa per la quantità di armatura trasversale e il passo da rispettare, si progettano le armature da disegnare nelle travate e se ne verificano le sezioni:
11.9 Calcoli armatura trasversale per SLU non sismico delle travate 30x50 principali, sezione 1
2. La progettazione sismica dell’armatura trasversale delle travate segue un iter processuale differente da quello eseguito per la progettazione non sismica, prendendo in considerazione minimi di normativa differenti e ricavando il calcolo del taglio agente massimo e minimo di ogni trave presente nella travata, secondo un sottoschema della trave stessa che prende in considerazione le combinazioni di carico sismico come carichi uniformemente distribuiti sulla stessa e due momenti concordi applicati agli estremi della trave che equivalgono ai momenti resistenti delle sezioni della stessa trave maggiorati di un γRd per sovradimensionare la resistenza della sezione. Il sottoschema presenta un modello matematico di una trave appoggiata-appoggiata con 4 combinazioni di carico che prevedono:
11.10 Combinazioni di carico per il calcolo del taglio agente nel sottomodello per la progettazione dell’armatura a taglio delle travi
Le quattro combinazioni riportate in figura 11.10 prevedono la presenza o meno dei carichi accidentali Qk e gli effetti di oscillazione del sisma che generano i momenti resistenti MRd,A e MRd,B.
Con il valore del taglio ricavato dal sottomodello e seguendo i minimi da normativa si può progettare l’armatura trasversale delle travate, verificando la stessa con la procedura seguita per la progettazione in zona non sismica, seguendo però delle opportune verifiche specifiche per la zona critica delle travi in cui la normativa specifica dei diversi limiti di armatura trasversale e passo della stessa più restrittivi:
11.11 Tabella calcolo del taglio minimo e massimo dal sottomodello
11.12 Tabella minimi di normativa sismici per la progettazione armatura trasversale, progetto e verifica della stessa
La progettazione dell’armatura trasversale delle travate prende in considerazione entrambi i dimensionamenti andando a disegnare le armature lungo la travata e nelle zone critiche seguendo le indicazioni del dimensionamento più restrittivo tra i due effettuati.
11.13 Progetto armatura trasversale delle travate 30x50 principali, sezione 1
Le travate ora dimensionate a SLU vanno verificate per gli SLE a tensione e fessurazione, seguendo l’iter processuale già esposto e rappresentato per la verifica dei travetti del solaio nei capitoli precedenti.
Vengono qui di seguito riportate le tabelle dei calcoli da effettuare per gli SLE:
11.14 Tabella verifica SLE-tensioni delle travate 30x50 principali, sezione 1