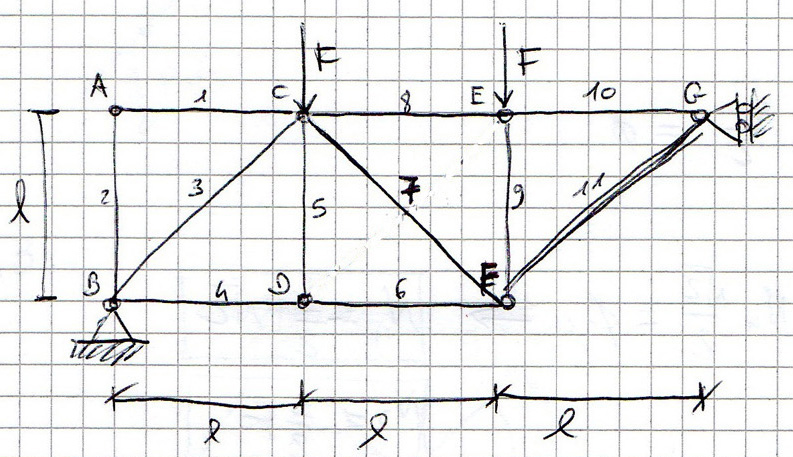
In questo esercizio ci troviamo di fronte ad una struttura reticolare asimmetrica.

Come fatto per l' esercizio precedente prima di tutto dobbiamo verificare che la struttura sia isostatica:

Passo 1

Per verificare l' isostaticità dobbiamo vedere se il numero dei vincoli (esterni e interni) e quello dei gradi di libertà è uguale:

V = l

Il numero di gradi di libertà è dato dal prodoto del numero delle aste per i gradi di libertà di ogni elemento:

l = 11 (aste) x3 (gradi di libertà) =33

Il numero di vincoli è dato dalla somma dei vincoli interni e esterni:

I vincoli esterni sono una cerniera, che blocca 2 gradi di libertà, e un carrello che blocca 1 gdl.

V_e = 3

Calcoliamo i vincoli interni con la formula: V_i = 2*(n -1) dove n è il numero di aste che arriva alla cerniera:

A-G = 2(2-1) = 2

B-D-E = 2(3-1) = 4

F = 2(4-1) = 6

C = 2(5-1) = 8

Avrò percio V_i = 30 che sommato al contributo di V_e da V = 33 = l     VERIFICATO!

Passo 2

Calcolo ora le reazioni vincolari con l' equilibrio alla traslazione e alla rotazione:

Sostituisco i vincoli con le loro reazioni e imposto le equazioni di equilibrio:

- Equilibrio alla traslazione orizzontale

U_B - U_G = 0 ----> U_B = U_G

- Equilibrio alla traslazione verticale

V_B - 2F = 0 ----> V_B = 2F = 20 kN

- Equilibrio alla rotazione in B

- F*l - F*2l + U_G*l = 0 ----> U_G = 30 kN = U_B

Disegno ora la struttura equilibrata:

 

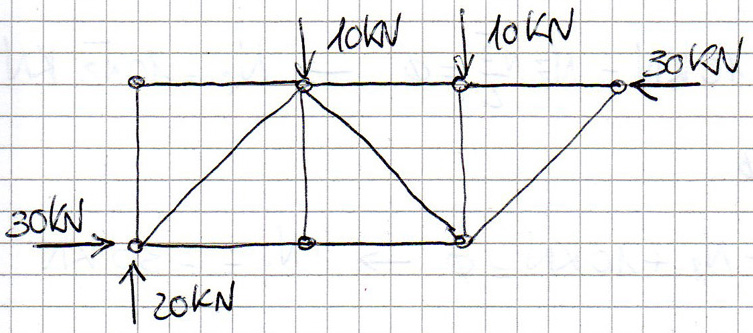
Passo 3

Calcolo ora le azioni di contatto con il metodo dei nodi. Isoliamo cioè ogni nodo e calcoliamo l' equilibrio:

Nodo A

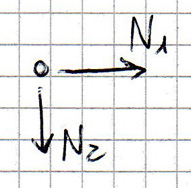
- Equilibrio alla traslazione orizzontale  N₁ = 0

- Equilibrio alla traslazione verticale  N₂ = 0

Nodo B

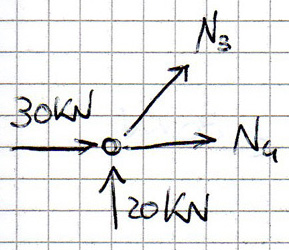
- Eq. trasl. orizzontale  30 kN + N₄ + N₃* √2/2 = 0

- Eq. trasl. verticale  20 kN + N₃* √2/2 = 0 ----> N₃ = -20√2 kN

                                                                          N₄ = - 10 kN

Nodo D

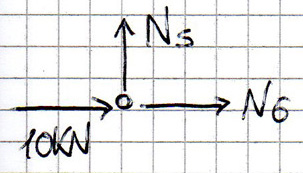
- Eq. trasl. orizzontale  10 kN + N₆ = 0 ----> N₆ = 10 kN

- Eq. trasl. verticale   N₅ = 0

Nodo C

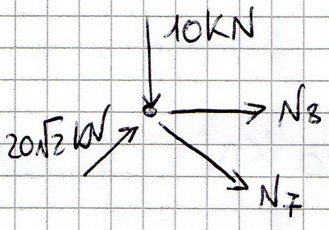
- Eq. trasl. orizzontale  20 kN + N₈ + 10 kN = 0 ----> N₈ = -30 kN

- Eq. trasl. verticale  20 kN - 10 kN - N₇*√2/2 = 0 ----> N₇ = 10√2 kN

Nodo F

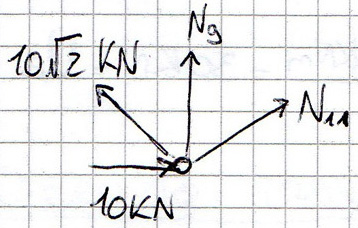
- Eq. trasl. orizzontale   10 kN + N₁₁*√2/2 - 10 kN = 0 ----> N₁₁ = 0

- Eq. trasl. verticale   N₉ + 10 kN = 0 ----> N₉ = -10 kN

Nodo G

- Eq. trasl. orizzontale   N₁₀ = - 30 kN

Posso disegnare ora la struttura con gli sforzi assiali di ogni asta:

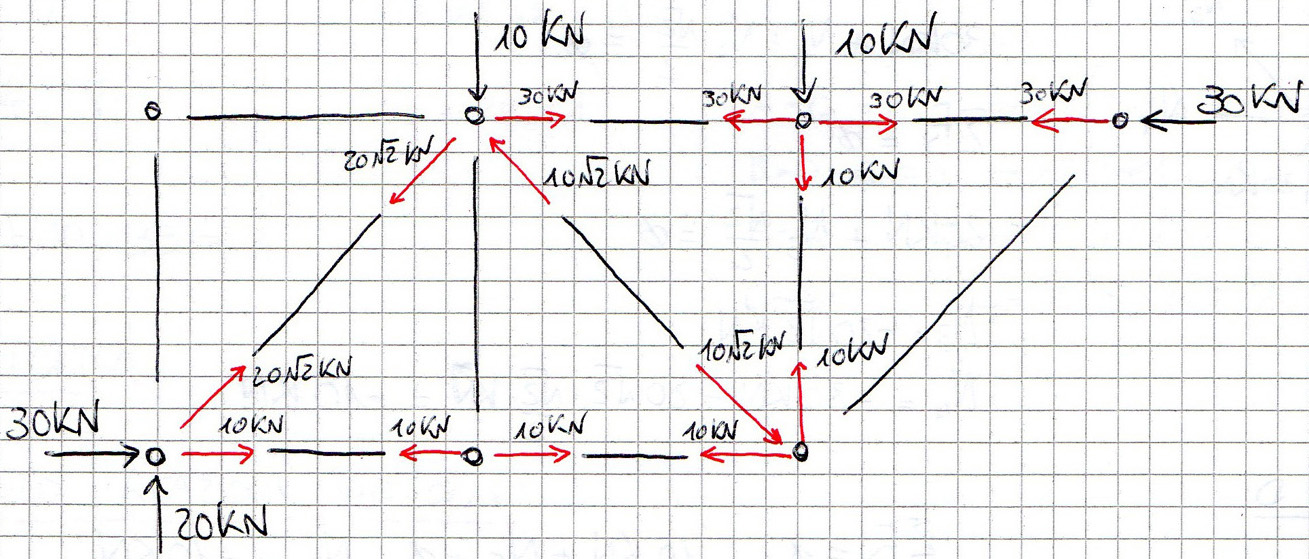
Possiamo notare come alcune aste nella struttura sono scariche.

Passo 4

A questo punto verifico se i calcoli sono giusti tramite SAP2000:

Reazioni vincolari.

Diagramma sforzo assiale.