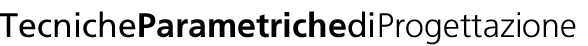Componente: sezione parametrica della seduta

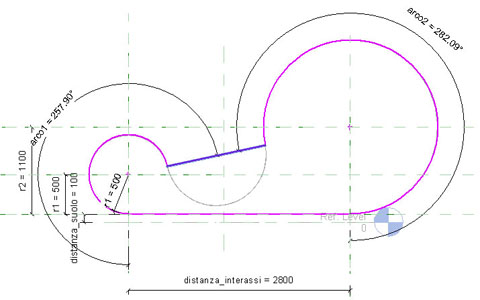
Cominciamo ad entrare nel vivo della progettazione della famiglia Seduta: abbiamo bisogno anzitutto di realizzare la componente SezioneSedia i cui parametri andranno a modificarne i raggi delle circonferenze terminali, la profondità della concavità superiore e inferiore che collega tangenzialmente le circonferenze, il loro interasse e l'altezza dal suolo del componente.

È stato piuttosto impegnativo giungere alla parametrizzazione del componente per via della geometria da gestire: si è rivelata infatti molto più complessa del previsto rispetto il suo schizzo a mano poi facilmente portato in CAD.

Le prime difficoltà sono nate dall'impossibilità di poter ancorare il centro della circonferenza, poi risolte attraverso una brevissima ricerca con argomento "pin center circle revit" che ha portato alla pagina http://www.revitclinic.com/revit-tutorial-articles/38-how-to-pin-lock-circles-in-revit-architecture-2012.html dove illustra come selezionando una circonferenza nel pannello Properties sia sufficiente spuntare la casella Center Mark Visible.

Quindi si è pensato successivamente di disegnare tutta la sezione direttamente nell'oggetto Extrusion ma si è rivelato scomodo in una fase successiva per via dei numerosi archi che Revit non è ingrado di gestire in maniera del tutto adeguata.

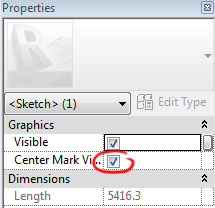
Dopo una serie di ragionamenti e prove la soluzione definitiva (per questo primo passaggio) si sviluppa a partire dall'oggetto come Extrusion dell'oggetto bordato di nero e Void Extrusion dell'oggetto in grigio.

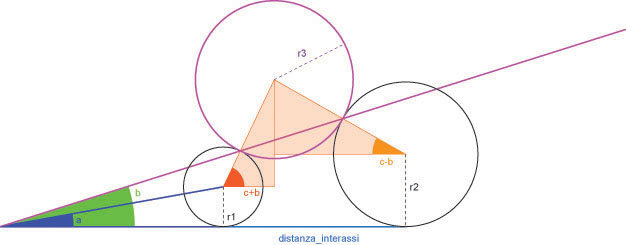
La soluzione è suggerita da una serie di ricerche sul web riguardo "circle tangent to two circles" che mi hanno portato alla pagina http://en.wikipedia.org/wiki/Homothetic_center#Tangent_circles_and_antihomologous_points che purtroppo non fornisce l'equazione per definire la circonferenza del Void Extrusion nello spazio. Cio che voglio trovare è l'angolo c e il raggio r3.

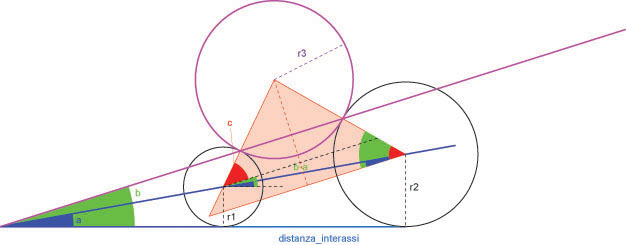
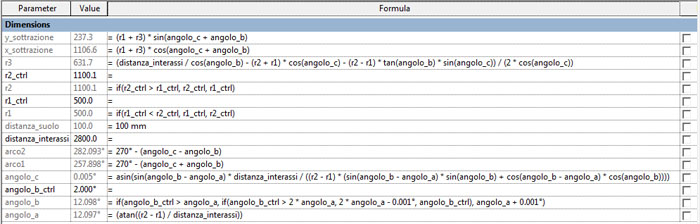
A partire da questa configurazione purtroppo non sono in grado di stabilire delle equazioni utili alla risoluzione del problema. Ho bisogno dunque di "giocare" po' con la trigonometria tenendo conto che l'angolo b è una scelta di progetto (per motivi di correttezza della geometria a<b<2a) che l'angolo a è calcolabile a partire dal  raggio delle circonferenze r1 e r2 e dalla distanza dei loro assi verticali come:

atan((r2 - r1) / distanza_interassi).

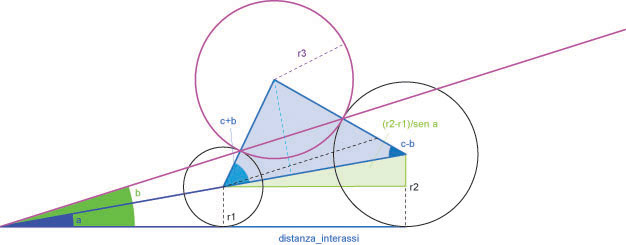Ora siamo in grado di stabilire 2 equazioni per la risoluzione del problema:

- una lega l'ipotenusa (nota) del tringolo verde chiaro al coseno di (c+b) per r1+r3 e di (c-b) per r2+r3

- l'altra uguaglia il seno di (c+b) per r1+r3 a quello di (c-b) per r2+r3

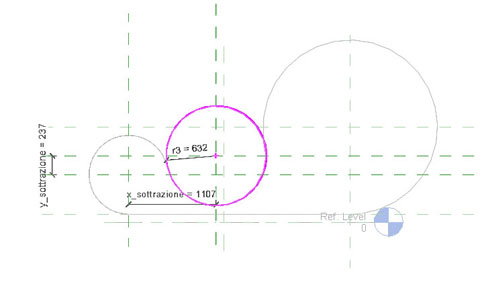
Le incognite del sistema sono però 3: sin(c),cos(c) e r3: abbiamo bisogno di un altra equazione. La ricaviamo da quest'altra configurazione: