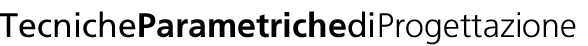Tu sei qui
modellare forme complesse_camera obscura 2.0

Una delle nozioni che abbiamo appreso dal corso di progettazione parametrica è che esistono molteplici strade per ottenere lo stesso obiettivo.
Post di Marco Campani e Federica Causarano
Dopo il nostro primo approccio alla camera oscura a Trondheim ( http://design.rootiers.it/2012/node/1187 ) e dopo i consigli del professore, siamo ripartiti alla carica con un nuovo tentativo.
Abbiamo abbandonato l’approccio delle masse e dei componenti adattativi e cercato di capire il funzionamento geometrico del modello. Ci siamo resi conto che il modo migliore per realizzarlo non è quello di controllare la faccia piana lunga, ma invece capire quali sono le conseguenze che la rotazione del quadrato superiore comporta rispetto alla base ed alla sommità della struttura.
Al momento di rotazione 0 (ovvero un cubo) i listelli sono perfettamente verticali, perpendicolari alla base.
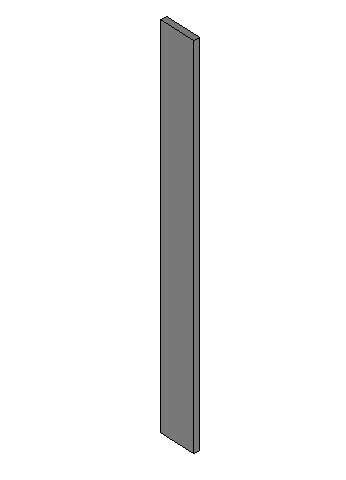
Di conseguenza, se visti dall’alto la base superiore e la base inferiore coincidono.
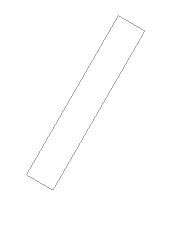
Applicando una rotazione alla parte superiore, accade che le facce (verticali) che compongono il listello non hanno più tutti angoli di 90°, ma diventano parallelepipedi. In pianta, quindi, le due basi non coincidono.
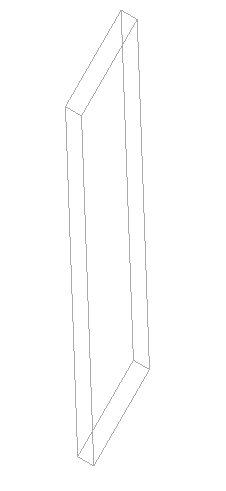
La prospettiva trae in inganno: l’immagine che sembra una vista 3d in wireframe in realtà è una pianta, e anche l’elemento in 3d è ripreso dalla stessa angolazione dell’elemento verticale precedente.
Siamo comunque sicuri che applicando questo tipo di “spostamento” della base superiore, tutte le facce che si andranno a formare saranno piane, in quanto non andiamo a distorcere una delle basi.
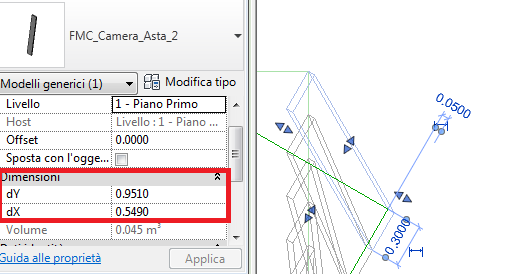
Quindi abbiamo capito che dovevamo creare una famiglia con due parametri di istanza - il ΔX e il ΔY- da poter gestire all’interno del progetto per posizionare correttamente le nostre aste.
Andiamo quindi a creare la nostra famiglia:
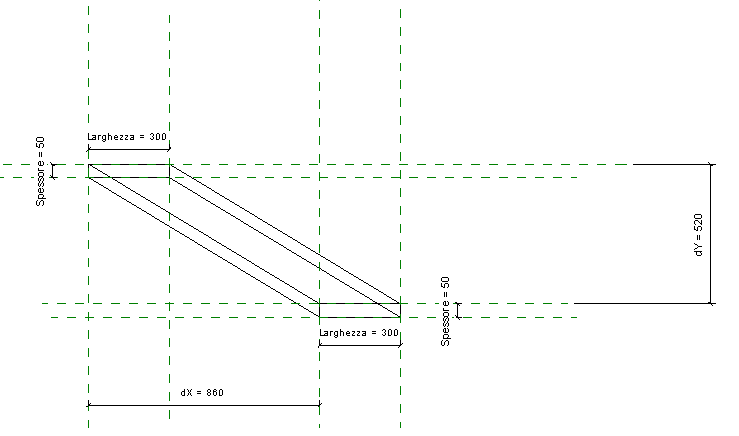
Si tratta di una semplice “unione di solidi”
che ha come base superiore ed inferiore lo stesso rettangolo individuato dai parametri di tipo “Spessore” e “Larghezza”. L’Altezza del solido è invece controllata dall’omonimo parametro di tipo. Come preannunciato, oltre ai precedenti parametri di tipo abbiamo introdotto i nuovi parametri d’istanza dX e dY che individuano la posizione del rettangolo a terra. Con essi utilizziamo un vertice del rettangolo superiore come punto di applicazione, così da poter disegnare i pannelli giustapposti in sommità e poi variare uno ad uno le posizioni della base. Tra i parametri si può notare che “Spessore” e “Larghezza” sono bloccati, operazione necessaria affinché la modifica dei parametri d’istanza non comporti la modifica delle dimensioni del rettangolo di base.
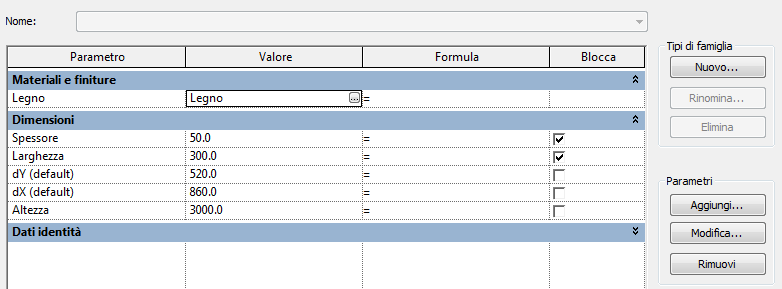
A questo punto rimane da capire quali valori debbano assumere ΔX e ΔY, e soprattutto in che rapporto sono con il numero del pezzo.
Siamo costretti quindi ad abbandonare la teoria parametrica e buttarci a capofitto in un modello reale. Scegliamo quindi delle dimensioni su cui basare il nostro modello:
L’altezza della camera oscura è 3m
Il lato del quadrato è sempre 3m
La rotazione è di 30°.
Il lato della camera oscura è composto da 10 listelli di 30 cm di larghezza cadauno.
Ovviamente da bravi parametrizzatori utilizzeremo questi dati (di cui alcuni sono già inseriti nella famiglia stessa) per generare uno specifico modello, ma potrebbero essere soggetti a variazione, con conseguente aggiornamento del modello.
La scelta dell’applicazione reale deriva da un problema nelle famiglie che non possiamo affrontare in Revit, di cui discuteremo a breve, e da un problema trigonometrico che prevede il cambio di funzione in un determinato momento.
Partiamo dal secondo:
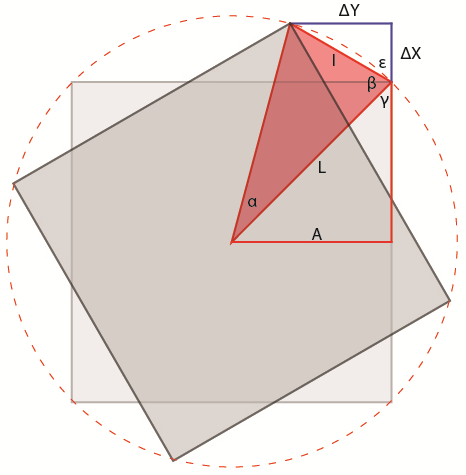
La figura mostra gli spostamenti che deve compiere la base del primo pezzo.
Assumendo come dato l’angolo α e l’apotema del quadrato A, la prima cosa da fare è trovare il raggio della rotazione del singolo pezzo, L, che varierà a seconda del numero del pezzo.
Tramite il teorema di Pitagora, possiamo assumere che L2 sarà uguale ad (A2 + (A – n × Larghezza)2). Assumendo il primo pezzo come pezzo 0, si avrà, come si vede in figura, che L0 è la metà della diagonale del quadrato. I successivi L1, L2, etc. saranno sempre minori in quanto si andrà a prendere il pezzo successivo, togliendo a uno dei cateti la larghezza del pezzo ruotato precedentemente. Ogni pezzo, quindi, ruota in maniera differente, con traiettorie di rotazione concentriche.
Dato che α è noto, possiamo semplicemente ricavare β tramite la somma degli angoli interni di un triangolo isoscele, β= (π – α)/2.
Seguendo le regole trigonometriche I= (L × cos β) × 2
e γ = arcsin (A/L).
Infine ε = π – γ – β.
Una volta trovati I e ε, si possono facilmente ricavare i cateti blu che rappresentano ΔX e ΔY, ovvero
ΔX = I × cosε
ΔY = I × sinε
Tramite un foglio elettronico calcoliamo uno per uno i valori che devono assumere i pannelli:
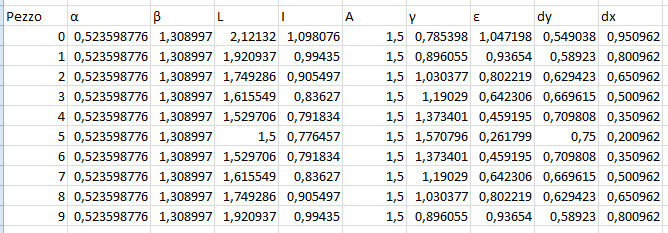
Ci accorgiamo subito di un errore: fino al pezzo numero 5, le misure date sono corrette. Dal pezzo 6 in poi, le misure sono specchiate e ritornano a ritroso quelle precedenti. L’errore è dovuto alla formula che calcola l’angolo γ = arcsin (A/L). Il pannello numero 6 ha effettivamente lo stesso raggio L del pannello numero 4, ma il suo angolo γ si calcola con la formula γ = (arccos (A/L) + π/2), come si può constatare dalla figura:
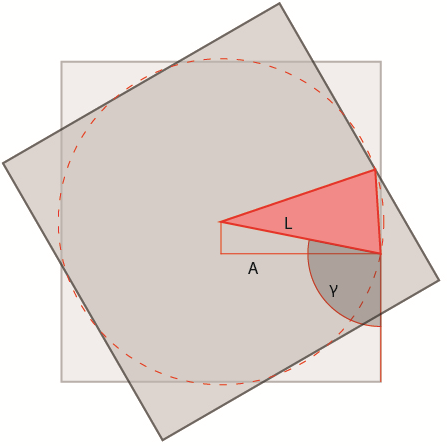
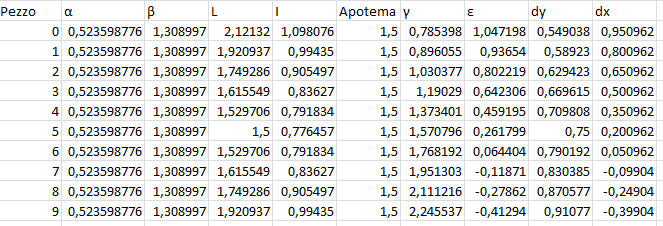
Una volta superati i listelli del primo quarto, continuando a utilizzare la stessa formula calcolavamo l’angolo al centro e non quello che ci interessava. Modificando la formula dal listello 6 in poi, abbiamo tutte le distanze necessarie:
A questo punto possiamo tornare in Revit e posizionare la nostra famiglia nel progetto. Facendo varie copie affiancate e cambiando i parametri di istanza otteniamo il seguente risultato:

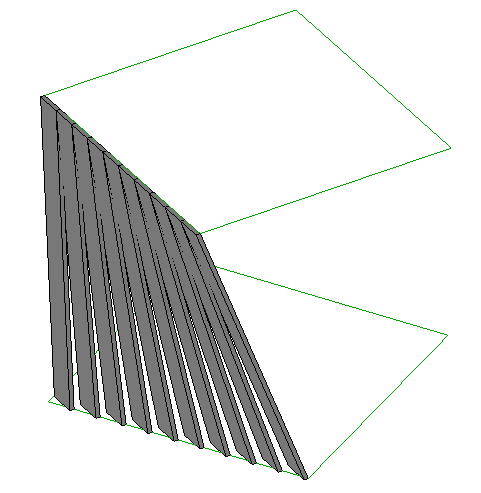
Torniamo invece al primo problema relativo alle famiglie. Nel progetto, come si può notare dalle tabelle, alcuni valori sono negativi, e ovviamente Revit non consente distanze negative. Per realizzarli nel modello abbiamo dovuto quindi specchiare manualmente le aste che avevano valori negativi e ed assegnar loro il valore calcolato in valore assoluto.
Completate le pareti della camera oscura facciamo le nostre osservazioni:
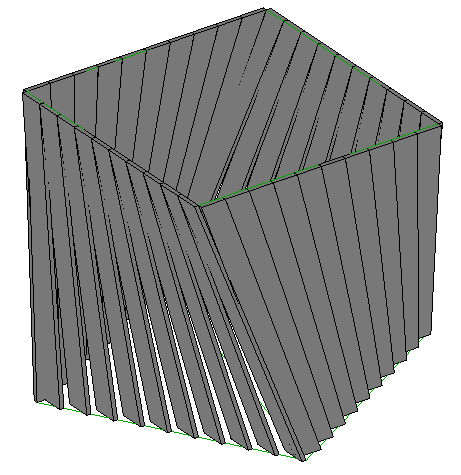
Ci sembra che alcuni pannelli si “fondano” tra di loro, soprattutto negli angoli e tra gli spigoli laterali. È anche vero però che il nostro modello ipotizza pezzi che si toccano in sommità, mentre il modello reale lascia un piccolo spazio tra i listelli (forse proprio perché si sono accorti di questi conflitti proprio come noi?)

Inoltre lo spazio è assai maggiore nella congiunzione tra le pareti:

Per ora siamo arrivati a questo punto, prossimamente inizieremo lo studio dei pezzi TOP e BOTTOM e del loro distanziatore!
A presto!!
Marco e Federica
| Allegato | Dimensione |
|---|---|
| 4.64 MB | |
| 244 KB |