Applicazione del sw Mathematica: minimizzazione di superfici

A seguito della lezione del prof D’Autilia dello scorso lunedì, abbiamo, seguendo le sue istruzioni, scritto un codice per minimizzare una superficie a partire da una funzione nota. La risoluzione di tale sistema prevede la conoscenza delle equazioni Weiestrass.
Tali equazioni hanno espressione:

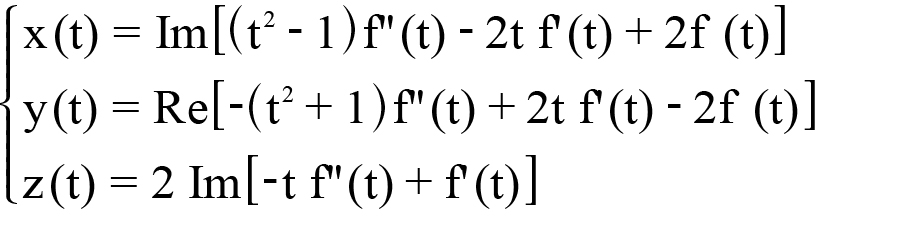
Per la risoluzione di funzioni polinomiali si può usare il seguente procedimento:
scelta la funzione, definiamo t, come parametro complesso.
t=u+I*v
funzione=t^3

Calcoliamo la derivata parziale rispetto u. Empiricamente abbiamo visto che derivando rispetto u otteniamo una soluzione analoga a quella ottenuta svolgendo il conto manualmente.

d1u=D[funzione,u]
3 (u + I v)^2  [la soluzione verrà espressa sempre in corsivo, come in questo caso]

d2u=D[d1u,u]
6 (u + I v)

Infine applichiamo la soluzione secondo Weiestrass, per scrivere le tre componenti della funzione parametrica. Per  permettere al software di risolvere l’espressione proposta, dobbiamo limitare la ricerca della soluzione all’insieme dei numeri reali.

xt=Expand[Simplify[Im[ComplexExpand[(t^2-1)*d2u-2*t*d1u+2*funzione]],Element[{u,v},Reals]]]
-6 v + 6 u^2 v - 2 v^3

yt=Expand[Simplify[Re[ComplexExpand[-(t^2+1)*d2u+ 2*t*d1u-2*funzione]],Element[{u,v},Reals]]]
-6 u – 2 u^3 v – 6 u v^2

zt=Expand[Simplify[2*Im[ComplexExpand[(-t*d2u)+d1u]],Element[{u,v},Reals]]]
-12 u v

Infine, visualizziamo il risultato ottenuto:
ParametricPlot3D[{xt,yt,zt},{u,-4,4 },{v,-4,4 } , PlotStyle->Directive[Orange,Specularity[White,50],PlotPoints->100]]

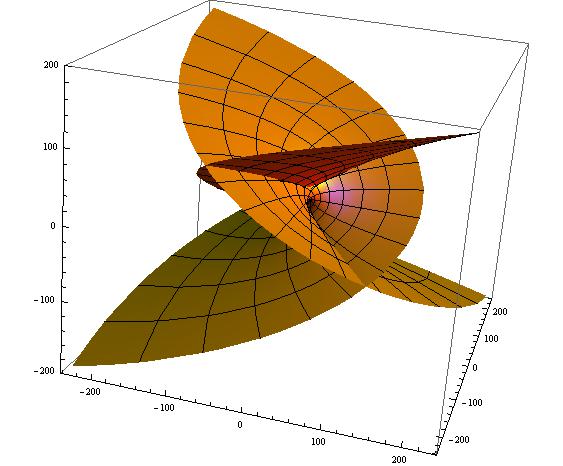
Successivamente abbiamo calcolato la superficie minima per una generica funzione.
Per una maggiore facilità nel confronto dei risultati proponiamo la stessa funzione.

Il procedimento è sostanzialmente analogo a quello precedente; la differenza è, come vedremo, nella determinazione delle derivate.

ta=u+I*v;
funzionea=ta3

Per il calcolo della derivata usiamo la seguente espressione:

Quindi otteremo:
d1ua=D[funzionea,u]
d1va=D[funzionea,v]
d1=1/2 (d1ua-I*d1va)
3 (u + I v)^2

d2au=D[d1,u];
d2av=D[d1,v];
d2=1/2 (d2au-I*d2av)
6 (u + I v)

xta=Expand[Simplify[Im[ComplexExpand[(t^2-1)*d2-2*t*d1+2*funzionea]],Element[{u,v},Reals]]]
-6 v + 6 u2 v - 2 v3

yta=Expand[Simplify[Re[ComplexExpand[-(t^2+1)*d2+2*t*d1-2*funzionea]],Element[{u,v},Reals]]]
-6 u – 2 u3 v – 6 u v2

zta=Expand[Simplify[2*Im[ComplexExpand[(-t*d2)+d1]],Element[{u,v},Reals]]]
-12 u v

ParametricPlot3D[{xta,yta,zta},{u,-dim,dim},
{v,-dim,dim},PlotStyle->Directive[Gray,Specularity[White,10]],Mesh->None,PlotPoints->10]

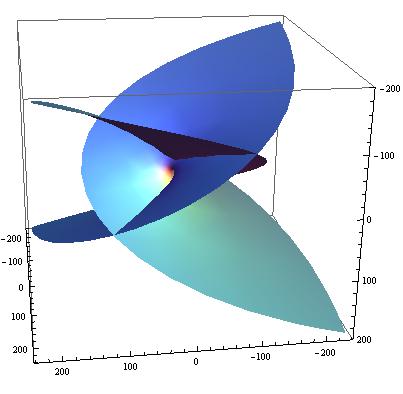
Come si può vedere le due soluzioni sono analoghe.
Di seguito proponiamo solo alcuni dei grafici ottenuti sostituendo la funzione di partenza.

f = Cos[t]^3

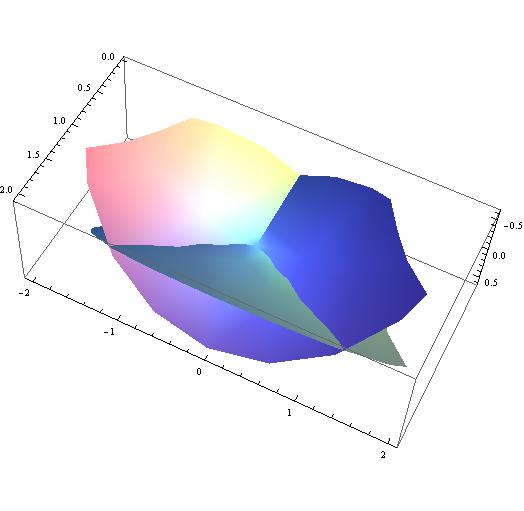
f = E^t;