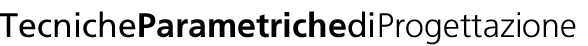tema d'esame: proposta per il MOMA PS1

Un muro di calcestruzzo (più o meno) uniforme di quattro metri d’altezza è concesso a Tadao Ando e pochi altri: non essendo questo il caso ho deciso di lavorare con quello che recinge il cortile del Moma ps1 per renderlo quantomeno gradevole nella fruizione dello spazio esterno.

 

Tra un rozzo modello analogico e diversi schizzi quello che vi mostro di seguito (fig.1)  mi è sembrato il più  convincente: un nastro continuo che talora ombreggia e talvolta offre una seduta, se non ospita fontanelle o sistemi d’irrigazione.

1.

Per l’individuazione della geometria di partenza ho utilizzato il software Surface Evolver, e più precisamente sono rimasta affascinata dall’esempio della goccia su un piano (disponibile online e nella documentazione fornita al momento dell’installazione): l’evoluzione avviene a volume costante, tenendo in considerazione l’energia di contatto e un angolo interno di contatto, tra il corpo e il piano appunto. L’effetto della forza gravitazionale può anche essere impostato come parametro.

Ciò che è necessario esplicitare nello script di partenza (oltre a vertices, edges, faces e bodies, ognuno definito in funzione del precedente) sono i vincoli: in questo caso non solo il contatto tra la goccia e il piano xy, ma anche tra questa e un piano verticale parallelo a yz (il muro di calcestruzzo, ricordate?).  Di seguito lo script commentato.

gravity_constant 0

PARAMETER angle = 180 // angolo interno tra piano e superficie, in gradi

 

#define T  (-cos(angle*pi/180))  // tensione virtuale della faccia sul piano

constraint 1    /* contatto con il piano orizzontale*/

formula: x3 = 0

energy:  // energia di contatto

e1: -T*y

e2: 0

e3: 0

 

constraint 2    /* contatto con il piano verticale */

formula: x1 = 0.0

energy:  // energia di contatto

e1: -T*y

e2: 0

e3: 0

 

vertices

1   0.0  0.0 0.0  constraint 1 2  /* i vertici che rimarranno fissi sui piani */

2   6.0  0.0 0.0  constraint 1

3   6.0  12.0 0.0  constraint 1

4   0.0  12.0 0.0  constraint 1 2

5   0.0  0.0 1.0  constraint 2

6   6.0  0.0 1.0

7   6.0  12.0 1.0

8   0.0  12.0 1.0  constraint 2

9   20.0  20.0 0.0  fixed   /* vertici dei piani: fixed indica che non si evolveranno */

10  20.0 -2.0 0.0  fixed

11  0.0 -2.0 0.0  fixed

12  0.0  20.0 0.0  fixed

13  0.0 -2.0 4.0  fixed

14  0.0  20.0 4.0  fixed

 

edges  /* definiti dai vertici che uniscono */

1   1 2    constraint 1 /* i 7 che rimarranno vincolati ai piani */

2   2 3    constraint 1

3   3 4    constraint 1

4   4 1    constraint 1 2

5   5 6

6   6 7  

7   7 8

8   8 5    constraint 2

9   1 5    constraint 2

10  2 6  

11  3 7

12  4 8    constraint 2

13  9 10   fixed no_refine  /* gli spigoli dei piani, i quali non evolveranno */

14 10 11   fixed no_refine

15 11 12   fixed no_refine

16 12  9   fixed no_refine

17 12 14   fixed no_refine

18 14 13   fixed no_refine

19 13 11   fixed no_refine

 

faces  /* facce definite da spigoli orientati */

1   1 10 -5  -9

2   2 11 -6 -10

3   3 12 -7 -11

//4   4  9 -8 -12

5   5  6  7   8

// 6   2  3  4   1

7  13 14 15  16  density 0 fixed no_refine /* anche qui le facce che non evolveranno */

8  15 17 18 19   density 0 fixed no_refine

bodies  /* un corpo definito dalle sue facce orientate */

1   1 2 3 5   volume 216 density 1

read

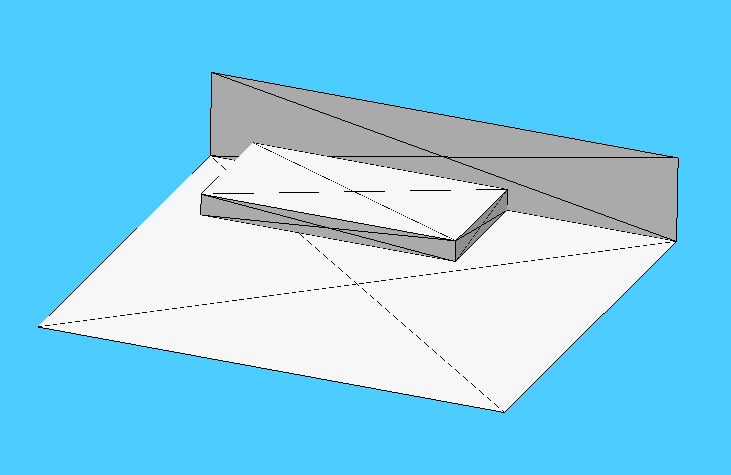
Questo è il file .fe (l’estensione del software) che ho lanciato con Surface Evolver; al comando s ( > show) questa è l’immagine prodotta (fig. 2).

2. 
 

I tentativi per ottenere un’evoluzione esteticamente piacevole sono stati numerosi, cercando di bilanciare di volta in volta i comandi d’evoluzione fondamentali:

r _ refine - rifinisce la triangolazione: gli spigoli sono divisi in due e le facce in quattro; ereditano gli attributi degli elementi genitori

u _ equiangulation - cerca di pulire la triangolazione: per ogni quadrangolo (ovvero due facce triangolari con uno spigolo in comune) si testa se la suddivisione lungo l’altra diagonale può produrre triangoli più simili.

g _ gradient descent iteration step - è il comando che permette l'evoluzione, la ricerca della superficie ottima attraverso la tecnica della discesa del gradiente.

I parametri da controllare, oltre ovviamente la sequenza di comandi, sono principalmente le dimensioni del volume iniziale e l'angolo di contatto tra questo e il piano. Il primo in particolare influisce non poco sulla mesh che andremo ad esportare: essendo ogni faccia divisa nello stesso numero di parti ogni volta che si esegue il comando refine, in poco tempo otteniamo zone in cui la distribuzione di mesh è più fitta, altre in cui lo è meno; queste attenzioni saranno importanti nel momento in cui vorremo lavorare la mesh al di fuori di Surface Evolver.

Giunta ad un risultato soddisfacente, ho esportato la mesh in formato .3ds; per fare questo evolver fornisce uno script, 3ds.cmd appunto. E’ possibile chiamarlo digitando:

Enter command: read "3ds.cmd"

Dopodiché viene chiesto di specificare il nome del file, che sarà salvato nella cartella di origine.

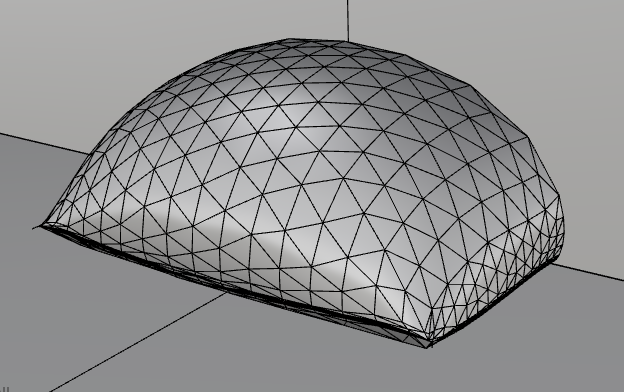
Questa è la superficie esportata da Surface Evolver, e aperta con Rhinoceros. (fig. 3)

3. 

L’intento è ora di tagliare un nastro di spessore variabile da questa superficie, i cui bordi sono identificati da curve proiettate. Queste, come vedremo più avanti, saranno proiettate anche sui piani orizzontali e verticali (muro di fondo e pavimento) così da suggerire l’idea di un nastro continuo.

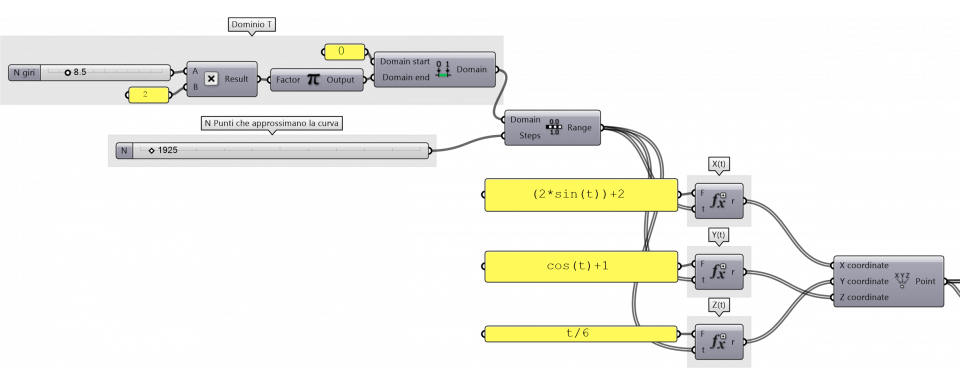
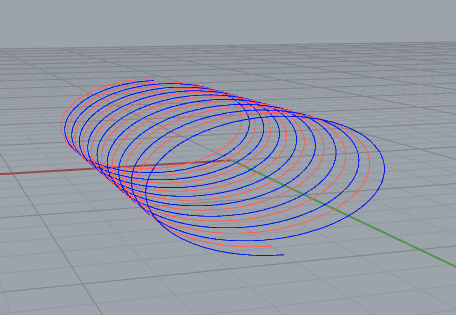
La curva che ho scelto di proiettare è un’elica ellittica, di equazione parametrica          

             x = 2 * sin(t) + 2

    c       y = cos(t) + 1

             z = t / 6

L’equazione della curva è stata portata in Rhinoceros attraverso Grasshopper, grazie ad una semplice definizione realizzata da Fabio durante il corso; il funzionamento è semplice: la curva è costruita interpolando punti, le cui coordinate x, y e z sono definite da equazioni in funzione del parametro t. (fig.4)

4.

La curva è stata quindi copiata alla distanza che definisce lo spessore del nastro da proiettare (i bordi, va da sé, sono due). (fig.5)

5. 

A questo punto entrambe le curve sono state proiettate sulla superficie con una proiezione sferica: vale a dire, scelto un centro di proiezione, da questo sono stati tracciati i raggi che uniscono i punti delle curve con la mesh iniziale.

Le curve sono state analogamente proiettate sulle porzioni di piano sottese dalla curva che segna intersezione piano – superficie. (fig.6)

6. 

Individuati così i punti di intersezione raggio/superficie è possibile interpolarli per ricostruire la curva sulla superficie. Questa e le operazioni successive ho ritenuto più comodo e veloce farle  direttamente in Rhinoceros (quindi ho dovuto effettuare un bake dei punti) per questioni di gestione di liste e controllo locale della geometria.

Le curve sono state quindi semplificate (rebuild) con dieci punti di controllo e usate, a coppie, come binari di uno sweep doppio; la curva di profilo che costruisce la superficie è un segmento che unisce un’estremità delle due curve. (fig 7, in verde le curve di profilo)

7. 

Da qui il procedimento è finalizzato alla costruzione: il risultato dello sweep (fig. 8) è una superficie ad unica curvatura, che può essere facilmente sviluppata e ritagliata su un materiale flessibile: il progetto è pensato con un materiale plastico, magari un tipo di bioplastica (questo potrebbe esserne un esempio?), ma ai fini della realizzazione di un modellino anche la carta può funzionare.

8. 

Le porzioni di nastro curve sono state sviluppate e numerate (con una microdefinizione in grasshopper che sfrutta il text tag e una serie di numeri) quindi stampate e ritagliate (fig. 9). Sono state stampate anche le proiezioni delle eliche sui piani, in forma di pianta e prospetto, unite per piegare il foglio e far da base al modello (fig. 10).

9. 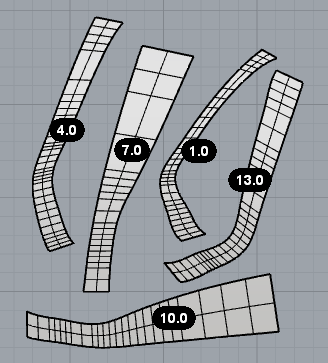     10. 

A questo punto montare le fasce con delle piccole linguette è stato relativamente semplice: è proprio la giacitura dell’intersezione nastro – piano che conferisce alla carta la giusta inclinazione, cosicché l’occhio possa ricostruire la curvatura originale. (fig. 11, fig. 12)

11. 

12. 

Questo non è solamente vero a prima vista: ho condotto sulla mesh iniziale e sul prodotto finale una zebra analysis di Rhinoceros, un’analisi che valuta la continuità e la levigatezza di una superficie usando una mappa rigata. Il risultato ottenuto mostra che i due oggetti sono, se non perfettamente coincidenti, quantomeno paragonabili. (fig. 13)

13.