L'obiettivo dell'esercitazione è analizzare la deformabilità di una trave a sbalzo maggiormente sollecitata attraverso l'utilizzo di tre tecnologie costruttive differenti: ACCIAO - LEGNO - CLS.

Si prende in esame una pianta destinata ad uso residenziale e tramite l'orditura del solaio si trova:

• Area di Influenza    = 20 mq
• Luce                        = 4 m
• Interasse                 = 5 m

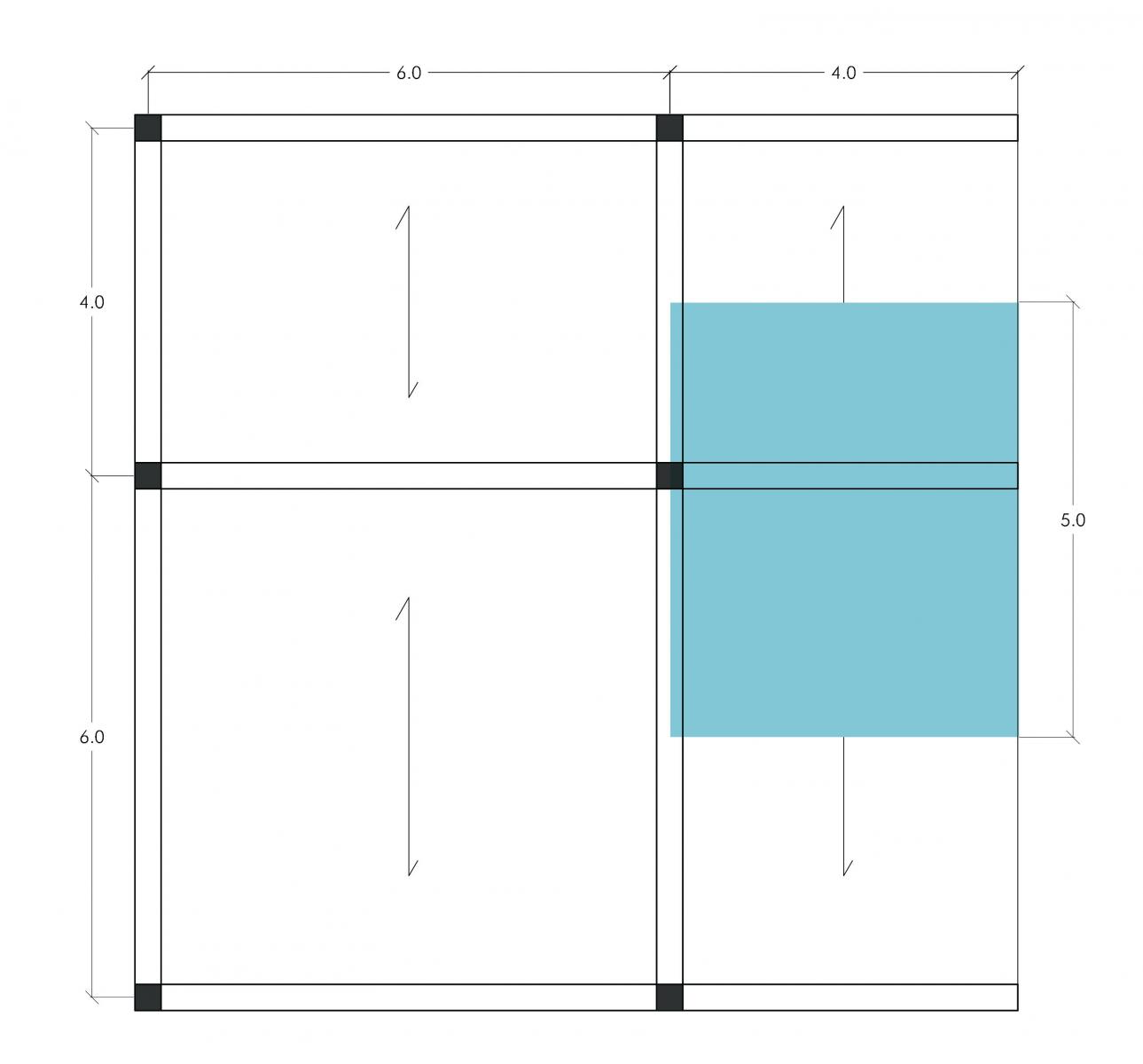
Per prima cosa bisogna trovare le stesse informazioni come nell'esercitazione 2, ovvero, calcolare il dimensionamento della trave. In questo caso però il momento flettente massimo, M_max,  sarà calcolato non più con l'equazione di una trave doppiamente appoggiata ma con l'equazione di una mensola ad incastro:

                                                      M_max = (q_u l²)/2                            

Dopo aver dimensionato la sezione si deve effettuare la verifica a deformabilità controllando l'abbasamento massimo della trave in rapporto alla sua luce. Questo si effettua allo Stato Limite di Esercizio SLE, stato subito dopo il quale la struttura non si rompe, ma a causa di spostamenti e deformazioni cambia nella sua conformazione limitando la possibilità d’utilizzo dell’edificio. 

Si calcolano perciò nuovamente i carichi incidenti sulla struttura moltiplicando il coefficiente di combinazione ψ al q_a :

                                                    q_e = (q_{s +} q_{p +} q_a x ψ) x i 

Nel caso dell'acciaio e del cemento armato si tiene conto del peso propro della trave, dunque si moltiplica al q_e, mentre nel caso del legno no pechè è un materiale leggero e quindi viene trascurato il valore del peso proprio.

Si trova il modulo elastico E ed il momento di Inerzia I_x per poter calcolare successivamente l'abbassamento massimo ν_max :

                                                     ν_max = (q_e l⁴)/8EI_x   

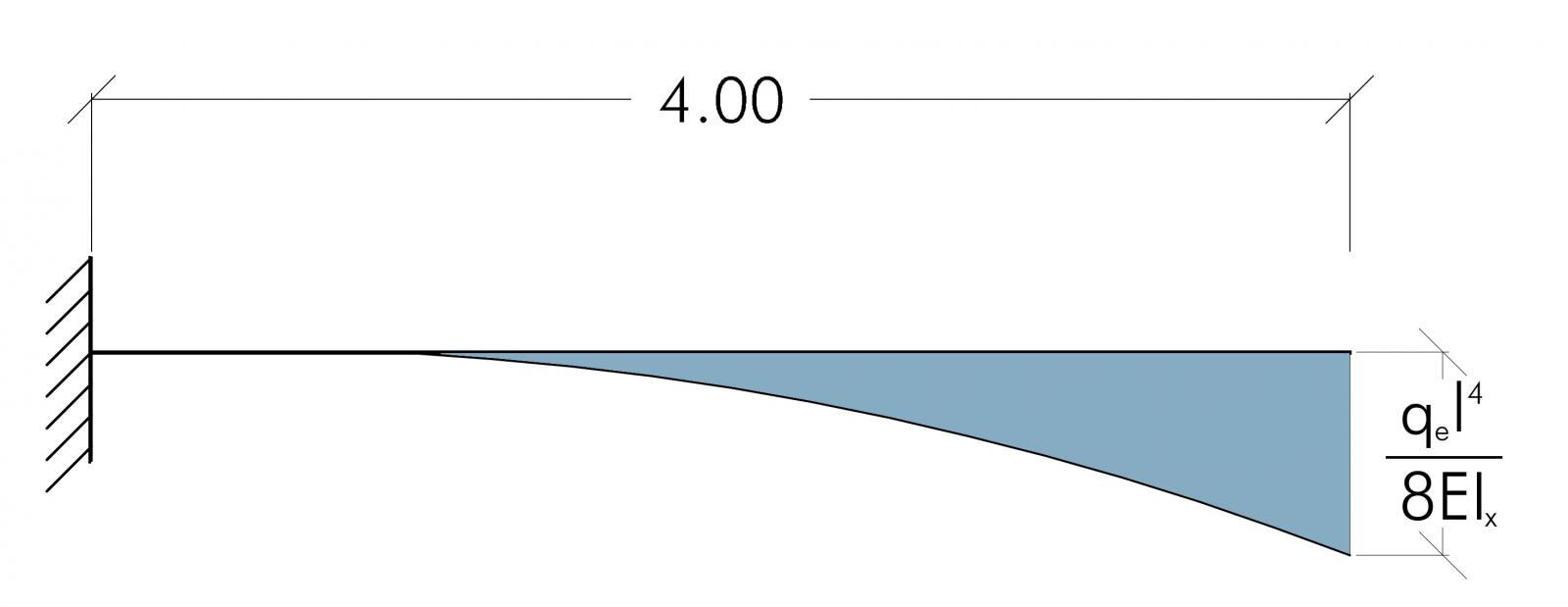
Si può così verificare se il rapporto tra la luce della trave e il suo abbassamento massimo sia maggiore a 250, come imposto dalla normativa. 

Si riprende la stessa tecnologia del solaio studiati nell'esercitazione 2:

SBALZO TRAVE ACCIAIO

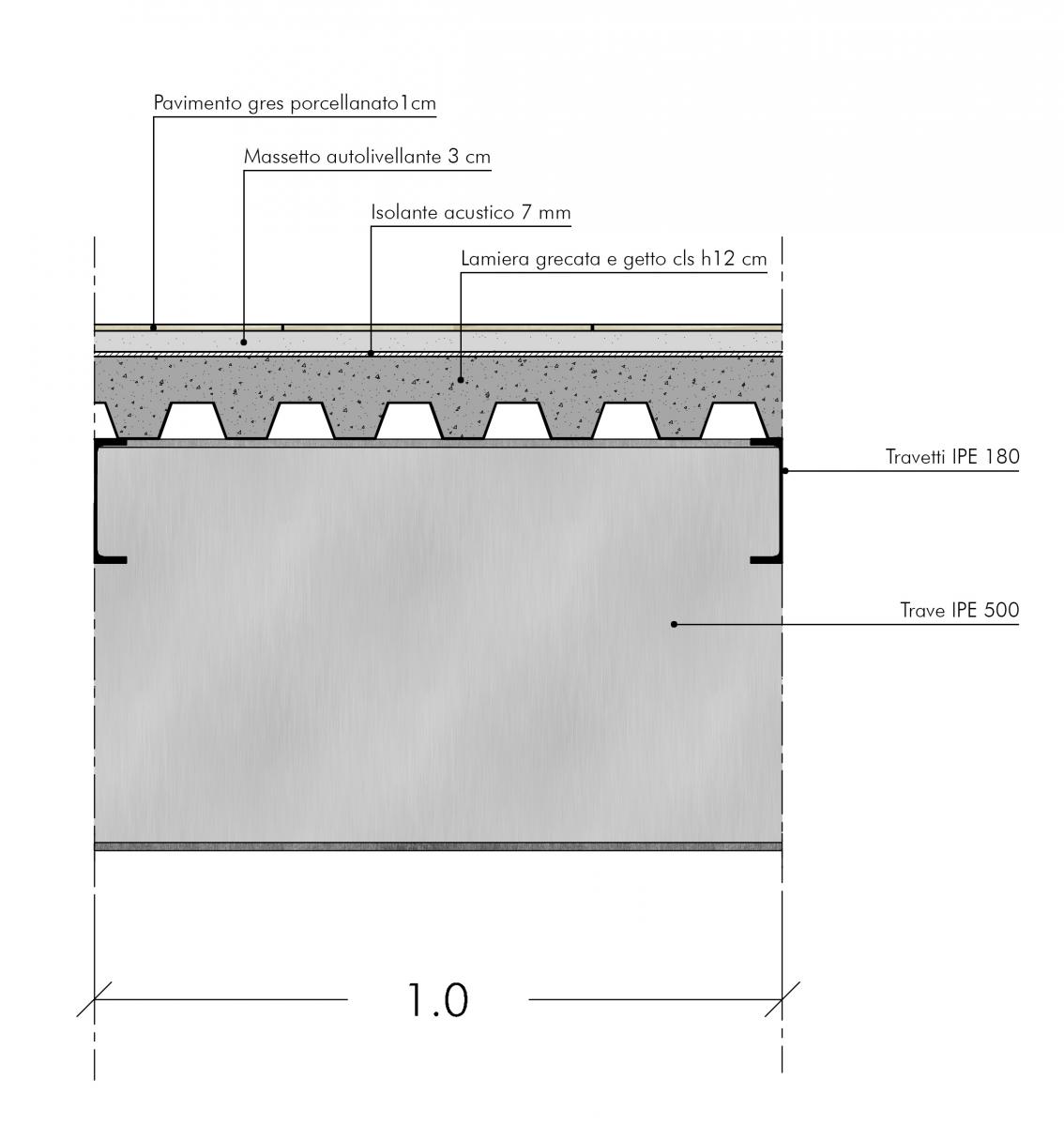
q_P =  0,19 + 0,6 + 0,03 + 1,0 + 0,5 =  2,32 KN/m²

• pavimentazione in gres porcellanato: 0,19 KN/m²
• massetto di tipo tradizionale: 0,03 m x 20 KN/m³ = 0,6 KN/m²
• isolamento acustico ACUSTIC SYSTEM 7: 0,03 KN/m²
• tramezzi: 1,0 KN/m²
• impianti: 0,5 KN/m²

q_s = 2,44  + 0,188 = 2,628 KN/m²

• lamiera grecata mod. E/S 4000 e getto di calcestruzzo h 12 cm :  2,44 KN/m²
• travetto IPE 180 :  0,188 KN/m > 0,188 (KN/m)  / 1 (m_interasse) = 0,188 KN/m²

^​q_a =  2 KN/m²   ambienti ad uso residenziale

Calcolo il q_u e trovo M_{max .} 

Scelgo la classe di resistenza dell'acciaio f_yk = 275 MPa e trovo  f_yd e W_xmin .

Il valore W_xmin è 1511,45 cm³, dunque trovo sulla tabella dei profilati IPE il valore successivamente maggiore a quest'ultimo per definire il W_x di design, che è uguale a 1930,0 cm³ IPE 500.

Si aggiunge il peso della trave al q_s:

q_s = 2,44  + 0,188 + 0,181 = 2,8 KN/m²

• lamiera grecata mod. E/S 4000 e getto di calcestruzzo h 12 cm :  2,44 KN/m²
• travetto IPE 180 :  0,188 KN/m > 0,188 (KN/m)  / 1 (m_interasse) = 0,188 KN/m²
• trave IPE 300 :  0,907 KN/m > 0,907 (KN/m)  / 5 (m_interasse) = 0,181 KN/m²

​Calcolo ora il q_e  e nonostante il carico sia stato modificato, il rapporto tra la luce di libera inflessione e l'abbassamento massimo è maggiore di 250.

l/νmax=412,846 > 250  

Il dimensionamento risulta corretto.

SBALZO TRAVE LEGNO

q_P =  0,216 + 0,6 + 0,03 + 1,0 + 0,5 + 0,9 =  3,306 KN/m²

• pavimentazione in parquet di rovere:  0,03 m x 7,2 KN/m³  = 0,216 KN/m²
• massetto di tipo tradizionale: 0,03 m x 20 KN/m³ = 0,6 KN/m²
• isolamento acustico ACUSTIC SYSTEM 7: 0,03 KN/m²
• caldana: 0,04 m x 24 KN/m³ = 0,96 KN/m²
• tramezzi: 1,0 KN/m²
• impianti: 0,5 KN/m²

^​q_s =  0,21 + 0,036 =  0,246  KN/m²

• assito:  0,21 KN/m²
• travetti :  1m x 0,20m x 0,30m x 0,6 KN/m³ = 0,036 KN/m²

 q_a =  2 KN/m²   ambienti ad uso residenziale

Calcolo il q_u e trovo M_{max .} 

Scelgo il legno lammellare GL24h con f_mk = 24 con k_mod= 0,60 e γ_m= 1,45.

Posso calcolare la tensione di progetto f_d = 9,93

Imposto una base di 40 cm trovando così un h_min = 70,72 cm e la ingegnerizzo portandola a un H = 75 cm. Ottengo una trave 40x70cm.

In questo caso, come già detto, il legno è un materiale leggero e quindi il peso proprio della trave viene trascurato.

Calcolo il q_e = 23 KN/m e il rapporto tra la luce l e l'abbassamento risulta  > 250.

l/vmax= 617,86 >250.

Il dimensionamento risulta corretto.

SBALZO TRAVE C.A.

q_P =  0,19 + 0,6 + 0,03 + 0,13 + 1,0 + 0,5 =  2,45 KN/m²

• pavimentazione in gres porcellanato: 0,19 KN/m²
• massetto di tipo tradizionale: 0,03 m x 20 KN/m³ = 0,6 KN/m²
• isolamento acustico ACUSTIC SYSTEM 7: 0,03 KN/m²
• intonaco: 0,13 KN/m²
• tramezzi: 1,0 KN/m²
• impianti: 0,5 KN/m²

q_s = 3,19  +  0,053 = 3,243 KN/m²

• pignatta 20x40x25 + caldana 5 cm :  3,19 KN/m²
• rete elettrosaldata (maglia 15cmx15cm  ø8): 5,3 Kg/m² = 0,053 KN/m²

^​q_a =  2 KN/m²   ambienti ad uso residenziale

Calcolo il q_u e trovo M_{max .} 

Per l'acciaio scelgo la classe B450C che ha una resistenza di snervamento f_yk = 450 MPa e trovo: f_yd = 391,30 N/mm²

Per trovare invece la tensione di progetto del calcestruzzo scelgo come classe di resistenza f_ck (C 40/50) e trovo: f_cd = 17 N/mm²

Si trova  h_u, impostando una base di 45 cm, si aggiunge il valore δ per trovare H_min =62,65 cm. 

Questo valore si ingegnerizza portandolo alla decina superiore dunque : H = 70 cm.

Calcolo il q_e = 41,34 KN/m e il rapporto tra la luce l e l'abbassamento risulta  > 250.

l/vmax= 816,74 >250.

Il dimensionamento risulta corretto.