In questa esercitazione si ipotizza la progettazione di un graticcio di 15x27 m, con 6 appoggi simmetricamente disposti, sul quale gravano 5 piani da 12 kN/m2 , mediante l'utilizzo del software SAP2000.
Inizio considerando il modello di piastra continua.
1. Creo una griglia di dimensioni x=15m e y=27m e disegno una superficie rettangolare
[New Model / Grid Only]
[draw rectangular area]
2. Discretizzo l'area in modo da ottenere un insieme di piccole parti che lavorano insieme al fine di ottenere un risultato più accurato. Quindi procedo con la suddivisione del rettangolo in geometrie di massimo 0,5x 0,5m
[ edit / edit areas / divide areas ]
3. Assegno i vincoli creando degli sbalzi di 3m.
[ assign / joint / restraints ]
4. Scelgo il materiale da utilizzare ovvero un calcestruzzo C35/45 e definisco la sezione dell'area dando un'altezza di 1m
[define / materials/ concrete/ C35/45 ]
[ define / section properties / area section / shell]
Analisi dei carichi
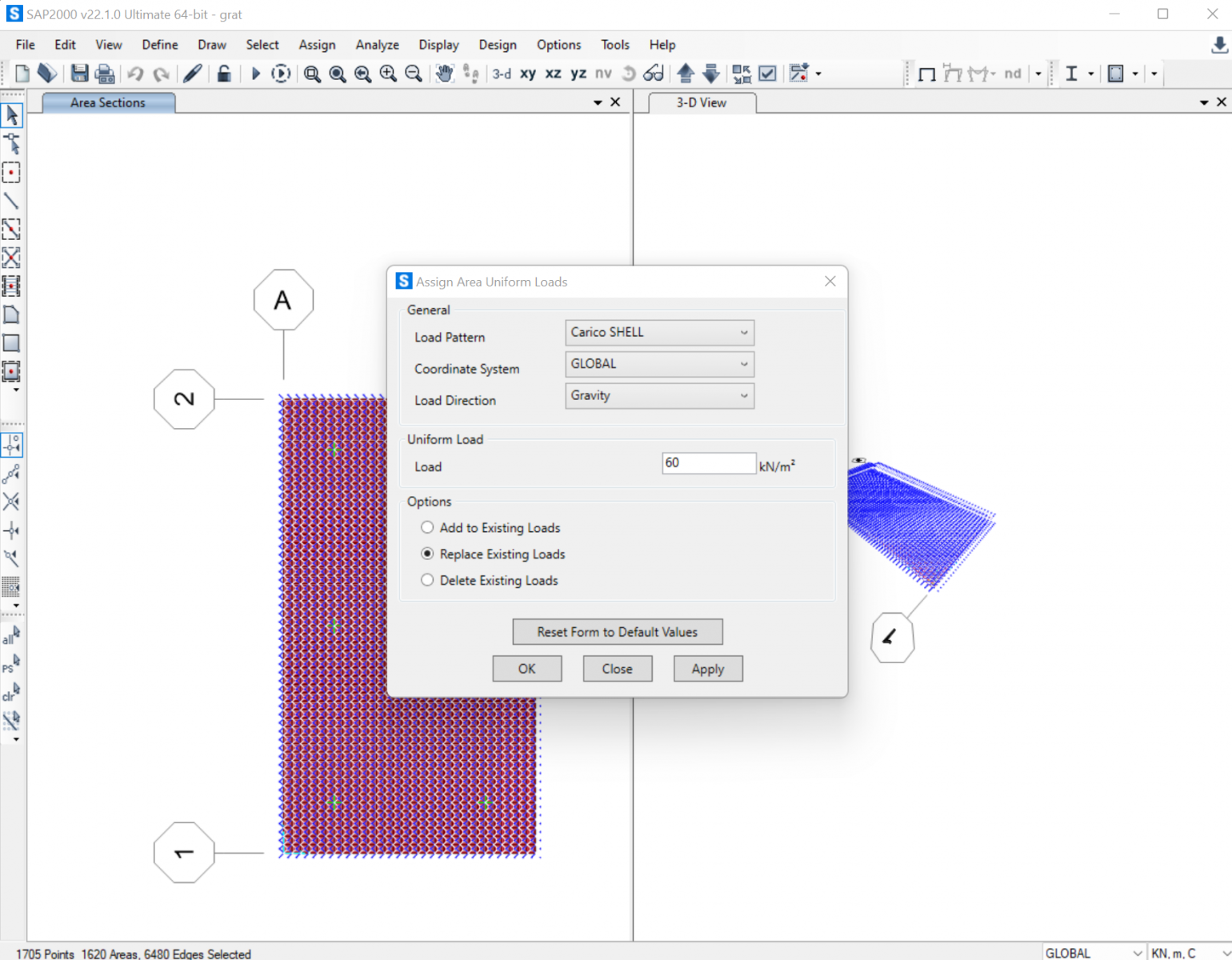
Calcolo il peso che il graticcio vede portare: 12 kN/m2 x 5 (numero di piani) = 60 kN/m2 e lo assegno alla struttura sotto il nome di "Carico Shell" (per il momento non considero ancora il peso proprio della struttura)
[ define / define load pattern/ Carico SHELL ]
5. Assegno alla piastra il carico definito in precedenza come carico uniformemente distribuito.
[ assign / area loads / uniform shell ]
6. Faccio l'analisi considerando unicamente il Carico Shell e osservo i risultati del momento M11 e M22
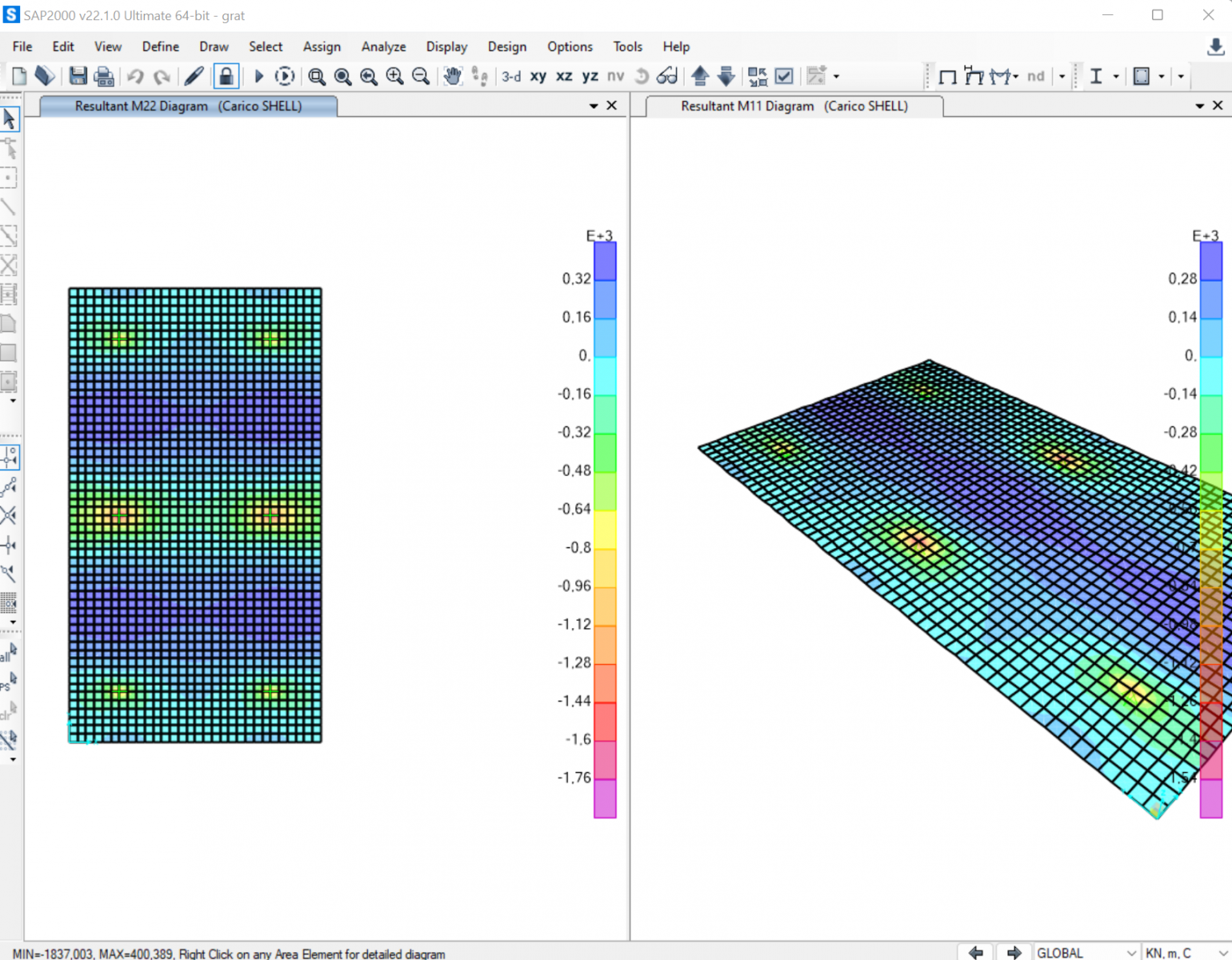
7. Considero il momento massimo presente - Mmax= 1837 kN*m - e procedo con il dimensionamento delle travi del graticcio
Ricordiamo che non abbiamo considerato il peso proprio della struttura nè il fatto che il graticcio non è una piastra continua, quindi arrotonciamo il momento Mmax = 2000 kN*m per trovare l'altezza minima.
Hmin = 78,86 cm
Volendo avere un passo di travi pari ad 1,5m e la base di queste pari a 40cm, considero il carico raddoppiato.
8. Torno su SAP e considero un graticcio di dimensioni 15x27m con passo di 1,5m tra le travi e vincoli posizionati come in precedenza per garantire uno sbalzo di 3m su ogni lato.
9. Procedo definendo e assegnando le travi precedentemente dimensionate ovvero T= 0,4x 1,7m
[ define / section properties / frame section ]
10. Ricordiamo che il graticcio lavora con nodi rigidi quindi bisogna fare in modo di considerare ogni intersezione tra due travi come un nodo rigido.
[ edit / edit lines / divide frames / break at intersection]
Analisi dei carichi
Apiano = 15x27= 405m2
npiano = 5
Qpiani = 12 * 5 = 60 kN/m2
Qtot = 405 * 60 = 24300 kN
CARICHI LINEARI :
Qltot = 60 * 1,5 = 90 kN/m
Qltravi = 90/2 = 45 kN/m (tranne travi di bordo)
Qltravi di bordo = 90/4 = 22,5 kN/m
11. Assegno i carichi alle travi
[ assign / frame loads / distribuited ]
12. Creo la combinazione dei carichi precedentemente inseriti e del peso proprio per far partire poi l'analisi della struttura
[ run now]
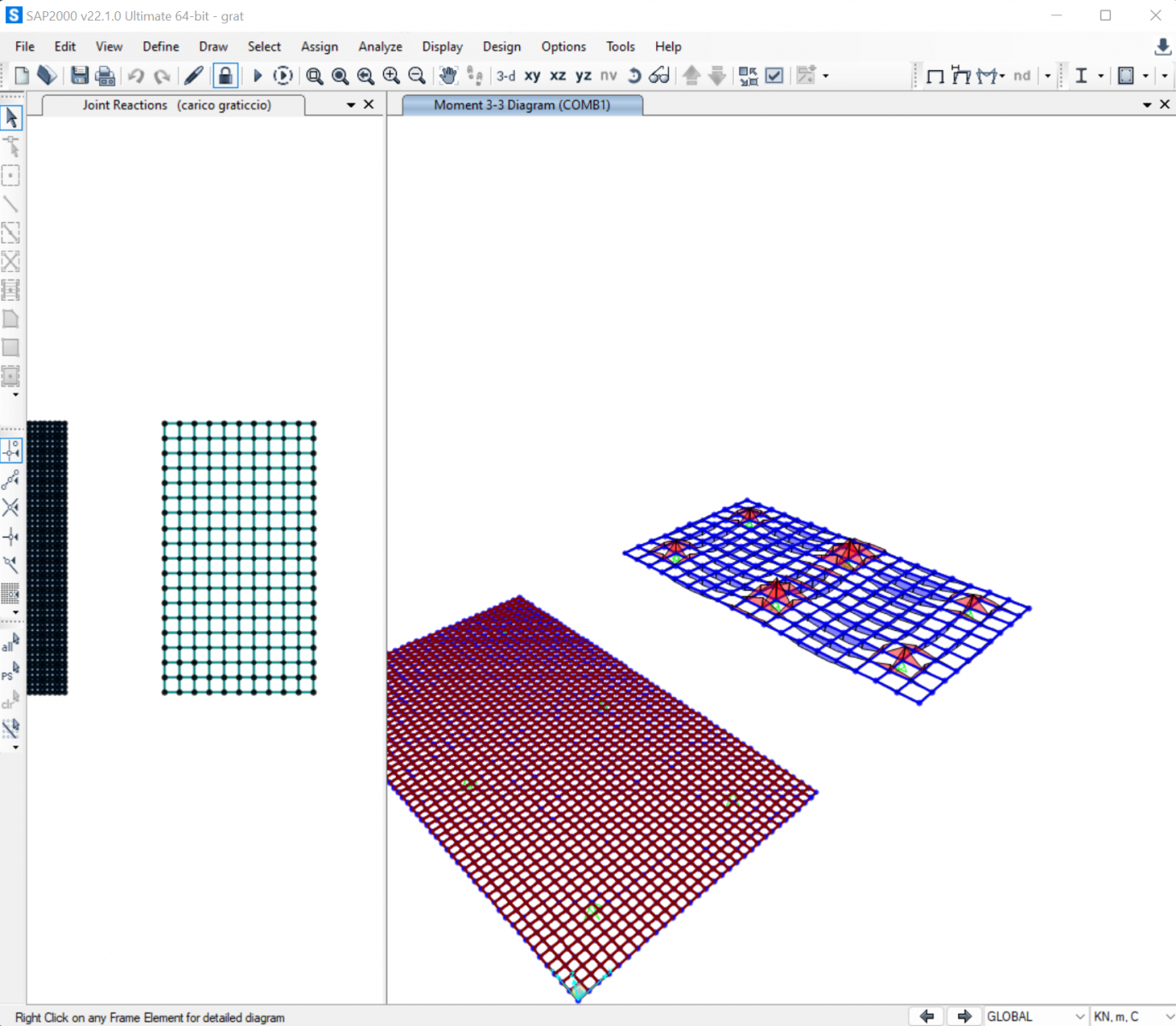
13. Osservo i risultati e noto che il momento massimo è il momento M33 pari a 3118 kN*m in corrispondenza dei vincoli in posizione centrale
14. Verifico la struttura e noto che Hmin =1,50m e che avendo utilizzato travi con H= 1,70m la trave è verificata.
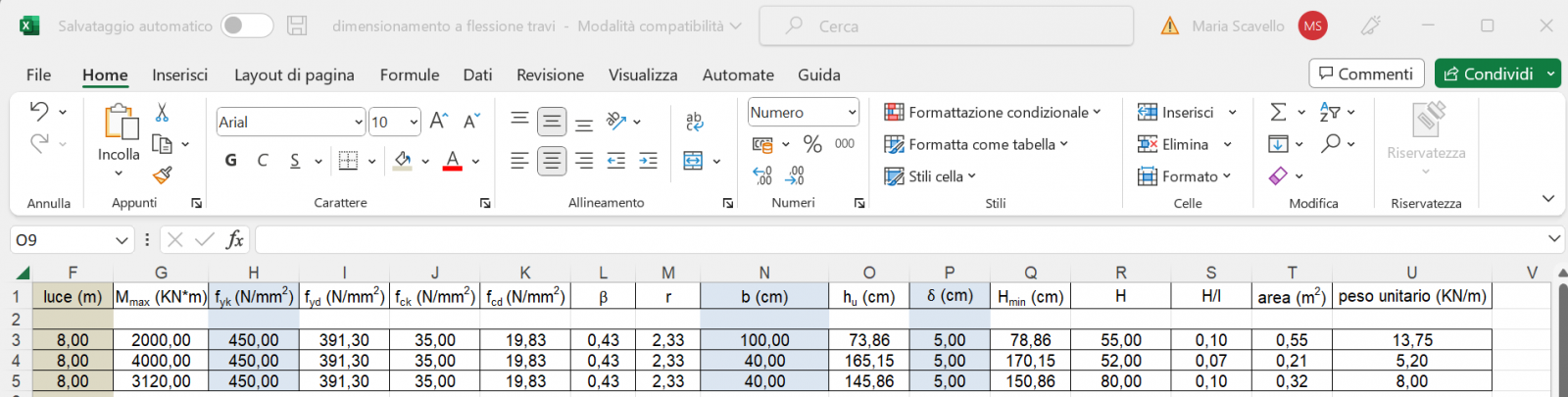
15. Decido di ridimensionare le travi con H=1,50 m per evitare ingombri inutili e spreco di materiale. Così facendo Mmax=2977 kN*m
Verifica a torsione
16. Una volta trovato il valore Tmax su SAP - Tmax =62 kN*m - verifico che questo sia minore di ftd.
La verifica a torsione è soddisfatta.
successivamente discretizzo l'area in tanti moduli più piccoli, in modo tale da ottenere risultati di calcolo migliori: il modulo scelto è di 0,50mx0,50m. 
L'operazione successiva prevede l'inserimento di vincoli alle estremità, alle quali assegno 4 cerniere. Momentaneamente le posiziono alle estremità della piastra, pur sapendo che la sollecitazione sarà maggiore in questo caso e che per ridurla occorre posizionarle più internamente.
Definisco un'altezza iniziale della piastra di 1m di altezza e definisco il materiale da utilizzare: scelgo un calcestruzo C35/45 in quanto per progettare una struttura speciale non si utilizza un calcestruzzo ordinario.
Inizio a svolgere l'ANALISI DEI CARICHI, calcolando che il singolo piano ha un carico di 12KN/m2 e che i piani sono 4. 12KNx4= 48KN/m2. Questo corrisponde al peso che dovrà sostenere il graticcio, non tenendo conto del peso proprio (16,5m x 27m=.445,5m2 e 445,5m2x48KN/m2= 21.384 KN Peso Proprio). Assegno quindi il Carico Shell alla piastra. 
Fsccio partire una prima analisi e vado a vedere l'effetto dei momenti M11 ed M22 che si sviluppano lungo le due direzioni. Il colore serve a capire dove il momento è maggiore e minore: vediamo che nei due casi il momento maggiore si trova lungo due direzioni diverse. 
Decido di progettare quindi un graticcio di 16,5m x 27m, che abbia una maglia interna con una luce di 1,5m e lo disegno accanto alla piastra. Ad esso inserisco i vincoli ai bordi esterni ed utilizzo delle cerniere. 
Discretizzo la struttura in quanto il graticcio lavora con dei nodi rigidi ed è necessario che nel punto d'intersezione delle travi ci sia sempre un nodo. Successivamente assegno una sezione alle travi tramite il comando Frame Section e la chiamo Gr.
Aggiungo i carichi che agiscono sul graticcio, considerando il peso proprio ed il Carico Shell.
Assegno quindi i carichi all'interno della struttura: 
Creo una combinazione di carico con il peso proprio ,che ha un fattore moltiplicativo di 1,3, e il carico shell. Successivamente mando l'analisi.
Il momento massimo è di circa 8000 KNxm. Mi rendo conto che in questo modo l'altezza della trave è eccessiva, quindi per contenere il momento cambio i vincoli e faccio in modo che ci sia un aggetto di 1,5m. 
Come ultima operazione faccio la verifica a torsione.
Il valore max del momento è di 90 Knxm, quindi lo inserisco nella tabella e verifico che il valore di Tmax sia minore di ftd - La struttura è verificata. 
