Lo scopo dell'esercitazione è quello di dimensionare gli elementi appartenenti ad un telaio piano (ovvero composto da travi che collaborano con i pilastri), di cui sono state precedentemente stabile le dimensioni, in tre differenti tecnologie costruttive: acciaio, calcestruzzo armato e legno.
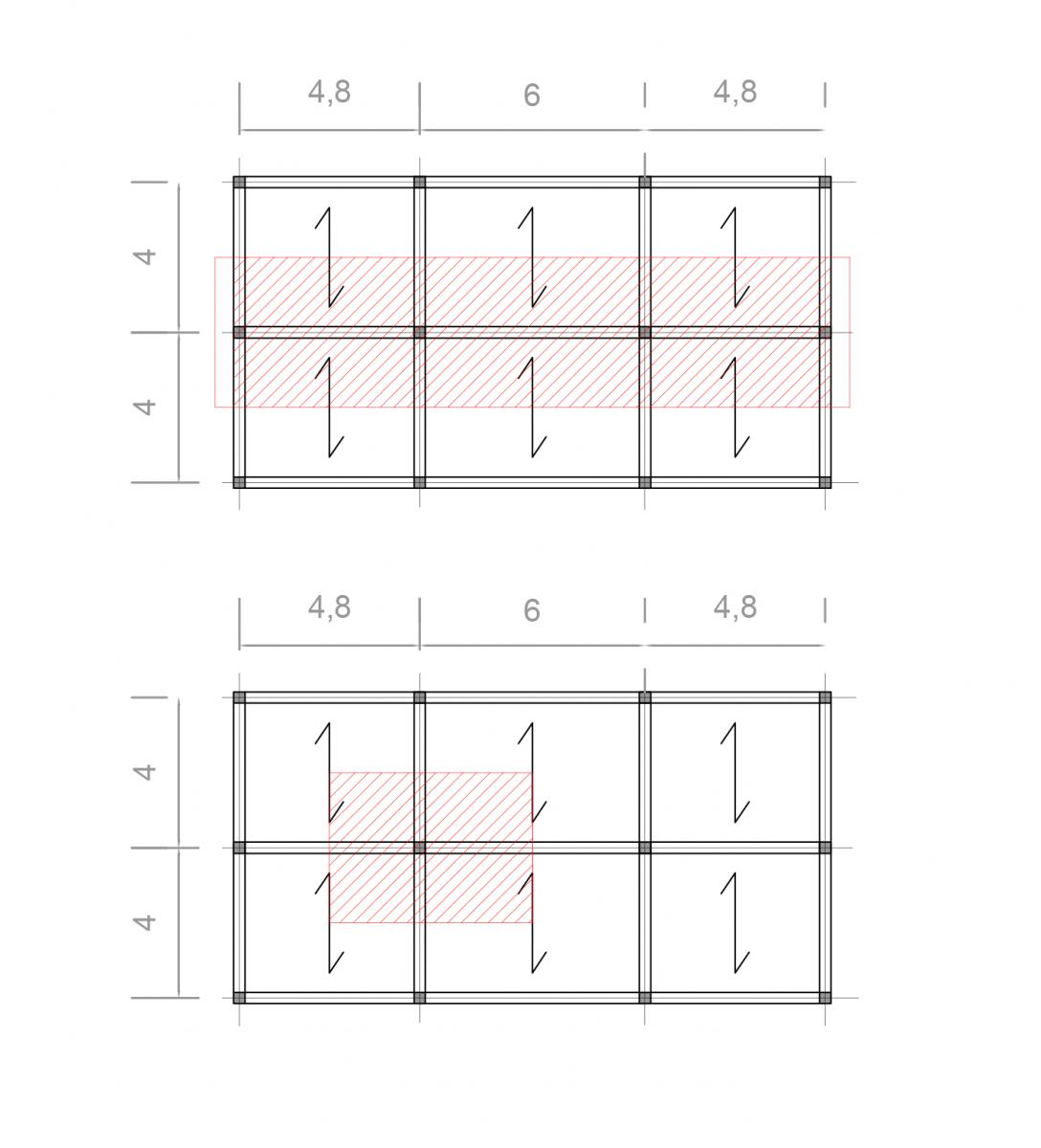
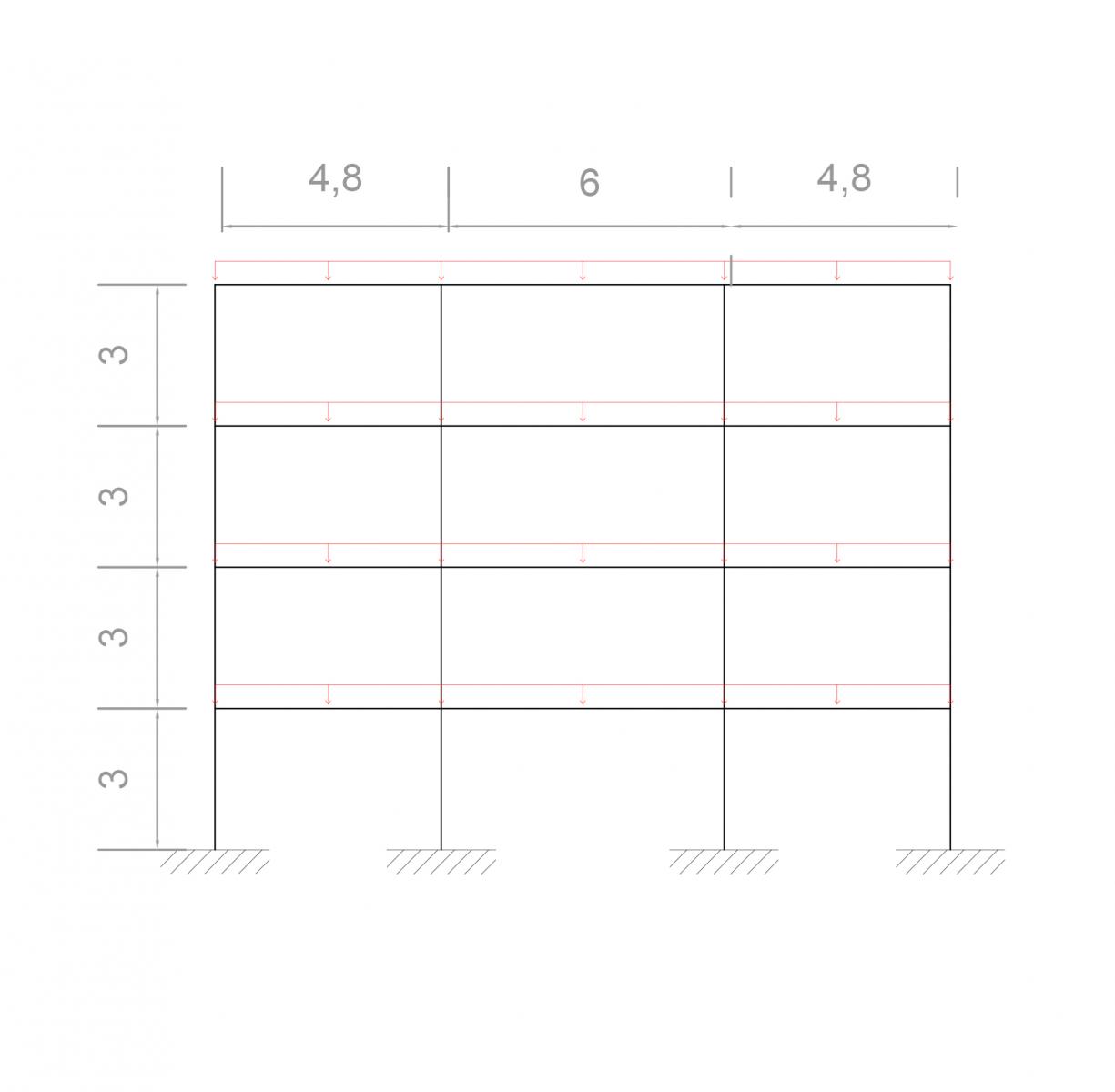
TRAVI
Per poter procedere al dimensionamento delle travi che "compongono" la carpenteria é necessario conoscere il carico q gravante sulle stesse. A tal fine l'analisi dei carichi consente di conoscere l'entità della forza agente sull' elemento, costituita dalla combinazione di tre "tipi" di carico:
CARICO STRUTTURALE(qs): peso proprio di tutti gli elementi strutturali
CARICO PERMANENTE(qp): peso proprio di tutti gli elementi non strutturali, compresa l'incidenza a mq dei tramezzi (1kN/mq) e degli impianti (0,5kN/mq)
CARICO ACCIDENTALE(qa): dipende dalla destinazione d'uso dell'edificio e del solaio stesso.
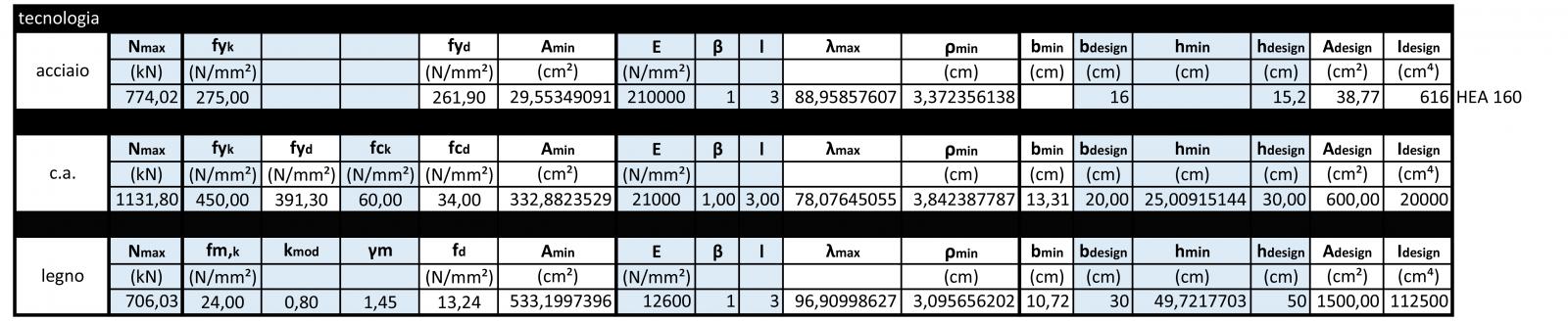
Le seguenti tabelle mostrano rispettivamente l'analisi dei carichi per le tre tecnologie:
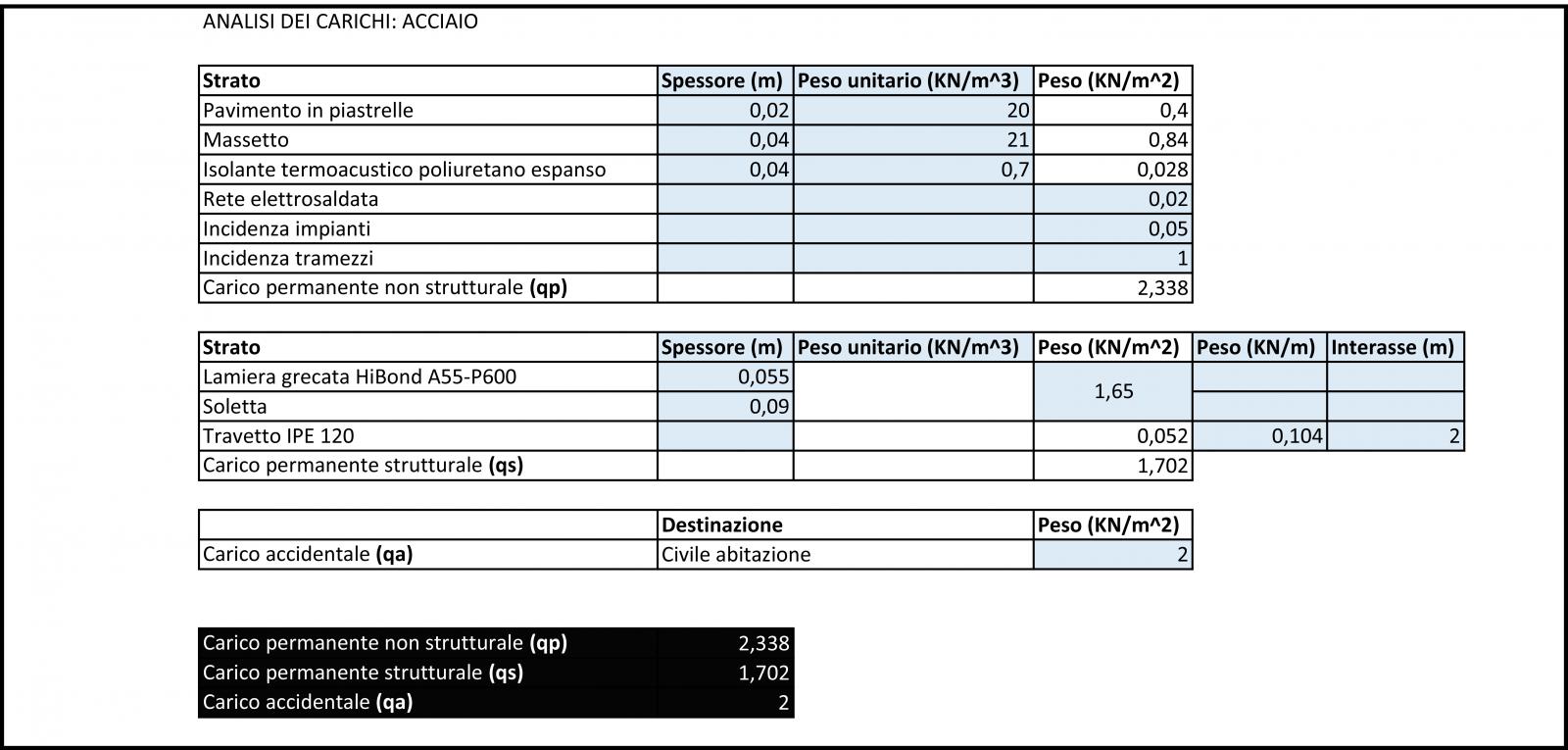
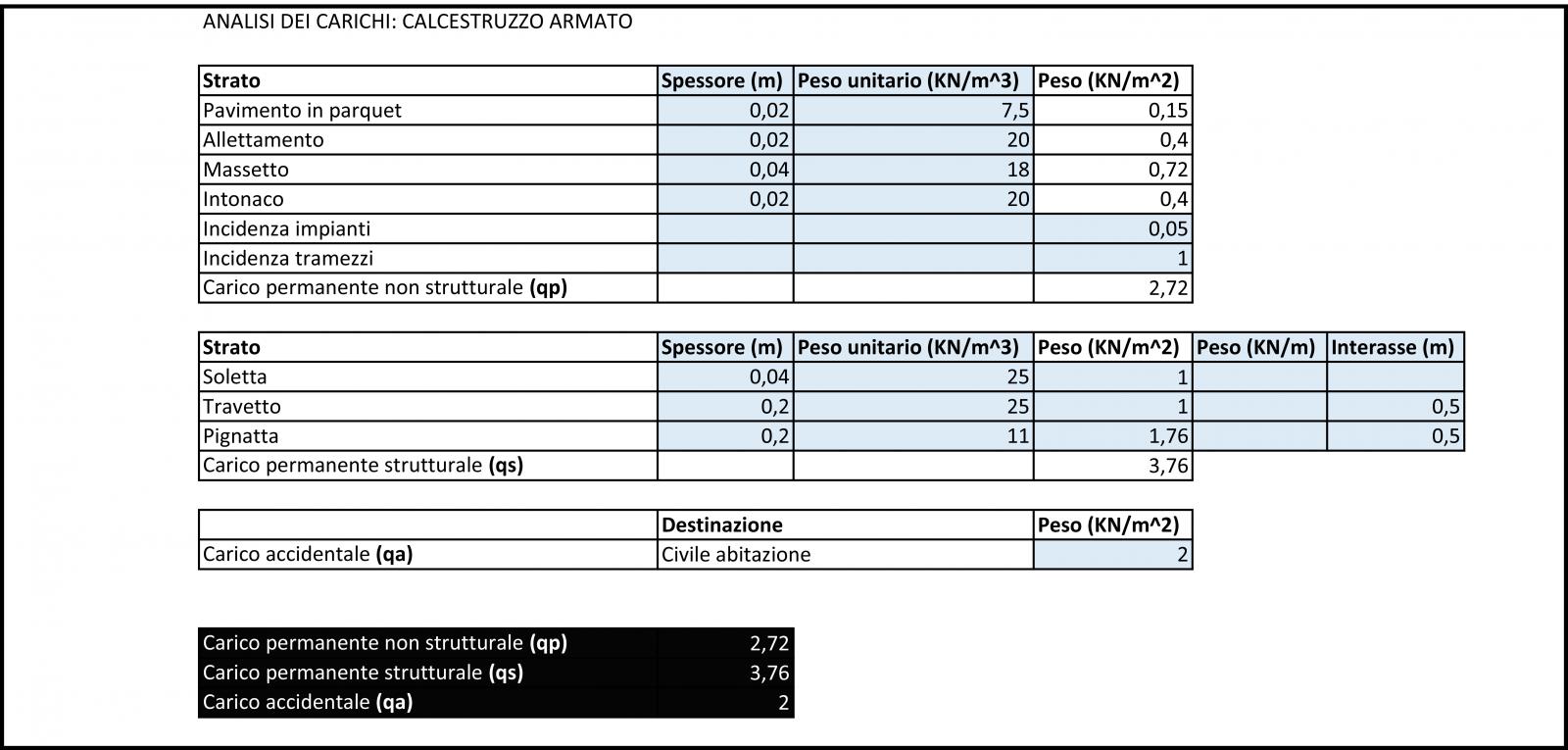
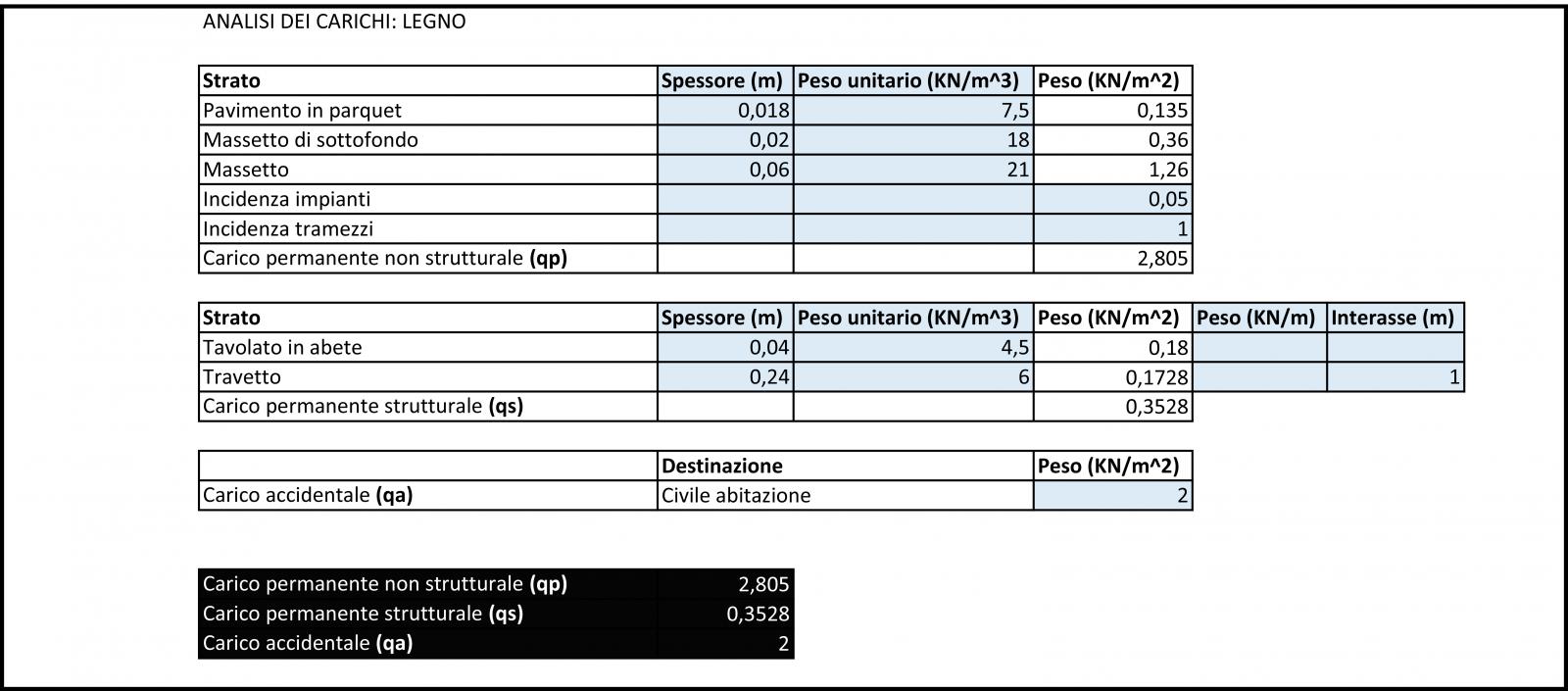
Prendendo in analisi un mq di solaio sono stati distinti elementi strutturali da elementi non strutturali e il relativo carico è stato calcolando moltiplicando il peso specifico del materiale (espresso in kN/m3) per la quantità di volume (m3/m2) di materiale stesso contenuta in un mq di solaio.
Per quanto riguarda i carichi accidentali invece, essi sono previsti dalla normativa attualmente vigente (NTC 2008-Norme tecniche per le costruzioni-D.N.14 gennaio 2008) nella quale questi vengono distinti in base alla destinazione d'uso dell'edificio.
Il carico totale a mq di solaio è stato calcolato tramite la formula prevista dalla normativa per la combinazione di carico allo stato limite ultimo:
q=gG1 qs+gG2 qp+ gQ qa
I valori di g (rispettivamente 1,3 per qs e 1,5 per qp e qa) rappresentano dei coefficienti di sicurezza che, maggiorando il momento, consentono di tener conto dell'aleatorietà dei valori di carico determinati. Il carico di cui sopra comunque, agisce su 1 mq di solaio, mentre per poter determinare le sollecitazioni agenti sugli elementi strutturali è necessario conoscere il carico agente sulla trave espresso in kN/m.
A questo scopo è stato sufficiente moltiplicare il carico di cui sopra per l'interasse relativo all'area di influenza della trave.
CALOCOLO MOMENTO MASSIMO
Lo schema statico del telaio piano è stato approssimato in ambito di pre dimensionamento a quello di una trave doppiamente appoggiata, quindi il nodo trave pilatro non viene visto come un nodo rigido bensì come un vincolo semplice di appoggio.
La sollecitazione massima flessionale massima è stata quindi calcolata come M= ql2/8.
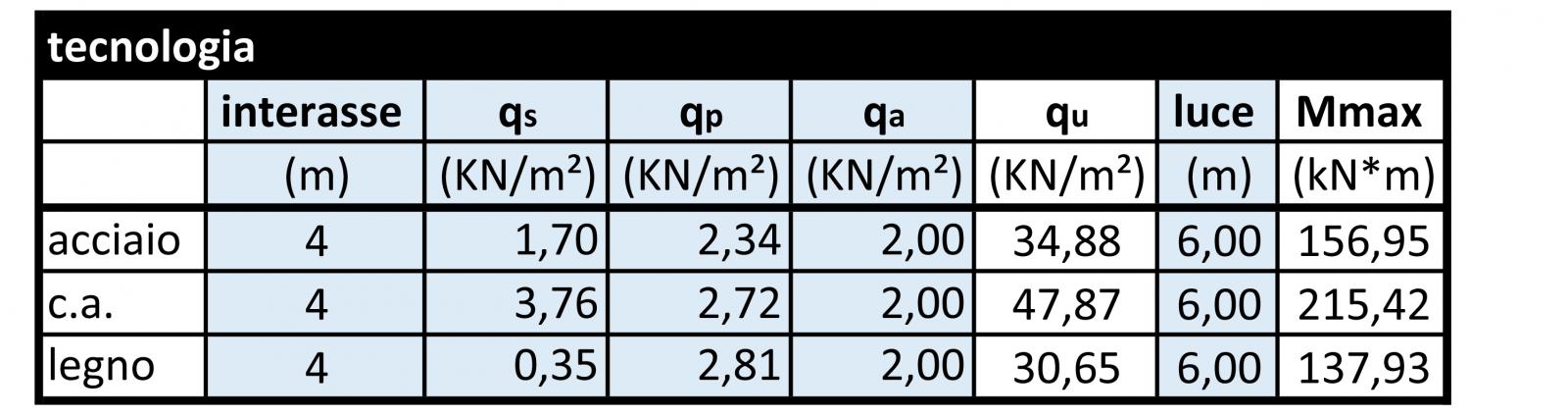
DIMENSIONAMENTO
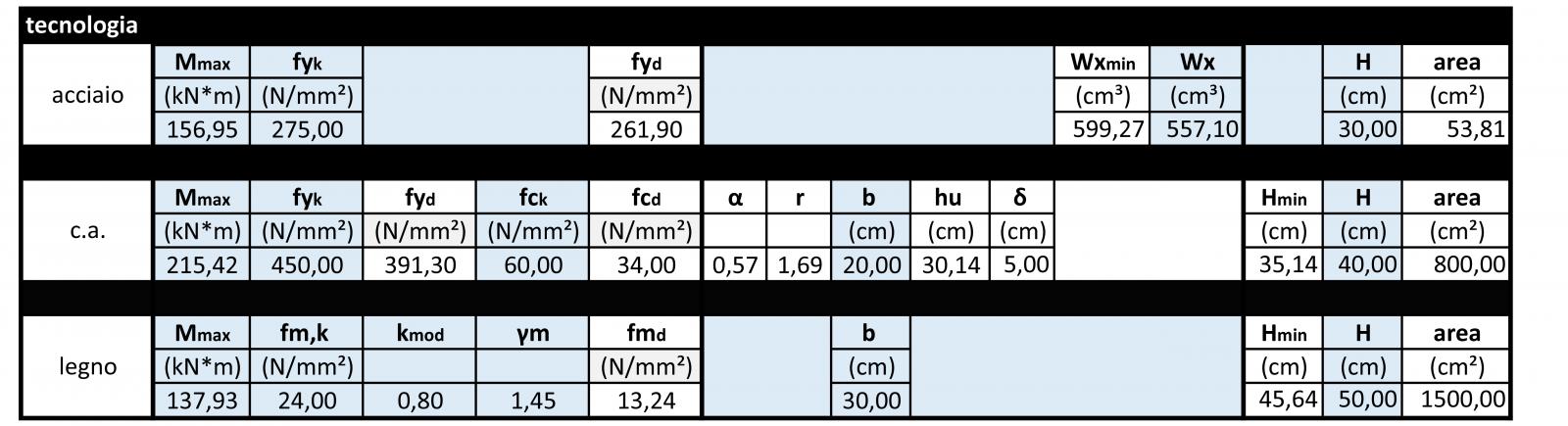
CALCOLO SFORZO NORMALE MASSIMO
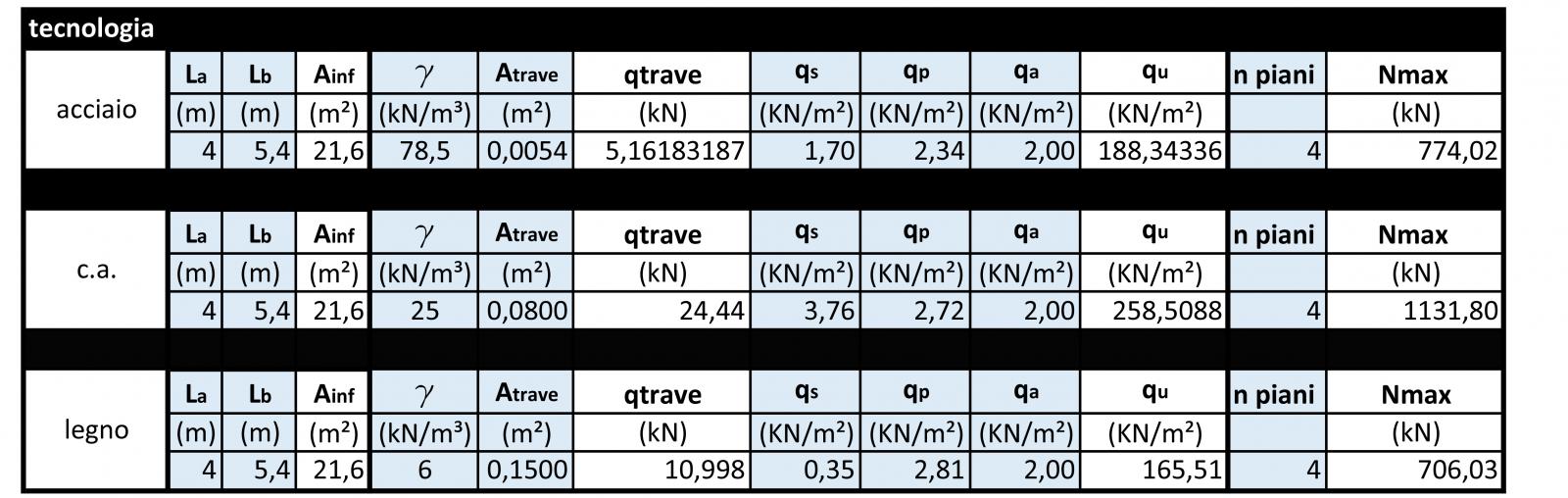
DIMENSIONAMENTO
Una volta ottenuto il valore massimo dello sforzo normale agente sul pilastro, il metodo di pre dimensionamento adottato mira a calcolare i valori di area e momento di inerzia minimi della sezione.
Quindi il calcolo dell'area consiste nell'eguagliare tensioni massime con resistenza a compressione del materiale
smax = fcd
N/Amin=fcd
Per cui l'area minima affinchè non si verifichi lo schiacciamento del materiale risulta essere uguale al rapporto tra sollecitazione e resistenza:
Amin=N/fcd
Il momento di inerzia minimo di ottiene invece mettendo in relazione il valore massimo della tensione agente sulla sezione e il valore critico della tensione dell'elemento. Quest'ultimo un particolare è la tensione associata allo sforzo normale critico, il cosiddetto carico critico euleriano, ultimo valore di carico oltre la quale non è più possibile l'equilibrio e si innesca l'instabilità.
Ncritico= p2E Imin /(l β)2
Nell'esercitazione il calcolo del momento di inerzia minimo avviene partendo da tre dati da inserire: il valore del modulo di elasticità E, il valore di β (che tiene conto di come il pilastro è vincolato), e l che è l'altezza del pilastro. Con questi dati è possibile calcolare due importanti parametri: snellezza massima dell'elemento e raggio di inerzia minimo della stesso. Quest'ultimo dato è fondamentale perché nelle sezioni in acciaio consente la scelta del profilo direttamente dal profilario, mentre nel caso di sezioni rettangolari, permette di calcolare la base minima della sezione.
l e r risultano quindi uguali a:
l = p (E/fcd)0,5
rmin= l0/lmax che nelle sezioni rettangolari vale rmin=(1/12b)0.5
Da qui è possibile calcolare la base minima come b=2(3rmin)0,5
Calcolata la base, il valore dell'altezza è semplicemente pari al rapporto tra area minima e base minima.
Una volta calcolate le dimensioni della sezione il momento di inerzia minimo della stessa viene fornito dai profilari per le sezioni in acciaio, ed è pari a I=bh3/12 per le sezioni rettangolari.
Per poter determinare mediante il programma di calcolo “SAP” i valori massimi di sollecitazione agenti sulla struttura prima di tutto occorre disegnarla, assicurandoci di stare lavorando con il sistema di unità di input idoneo.
Abbiamo copiato a questo punto il file tre volte per poter lavorare sulla stessa struttura modificando solo i materiali assegnati. Per ciò che concerne l’acciaio e il calcestruzzo, i materiali sono preinseriti e abbiamo dovuto unicamente selezionare i profili scelti in fase di calcolo, per l’acciaio, e dimensionare correttamente la sezione per il calcestruzzo armato. Diversamente ci siamo dovute comportare per la struttura in legno non essendo, infatti, tale materiale presente nella libreria installata. Abbiamo quindi creato un nuovo materiale specificando la sua natura ortotropa, il peso specifico e il modulo elastico (questi ultimi due cambiano a seconda del tipo di legno).
Sono stati poi inseriti da comando le densità di carico agenti sulle travi. Non abbiamo invece previsto di sottoporre le strutture all’analisi delle sollecitazioni orizzontali causate dall’azione del vento.
Abbiamo quindi ottenuto i seguenti diagrammi:
ACCIAIO
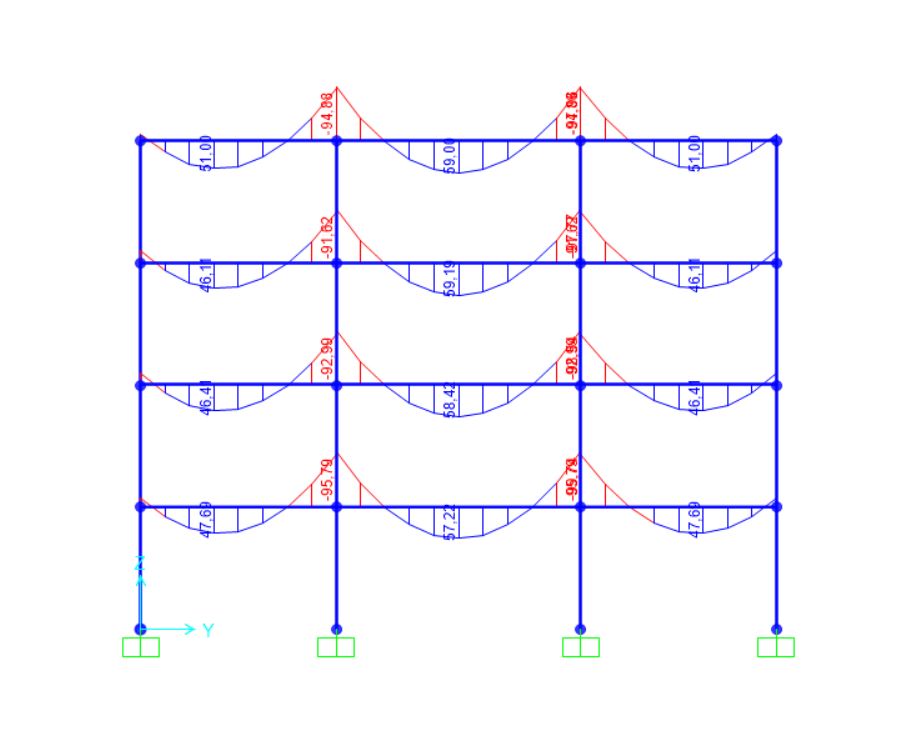
Diagramma dei momenti sulla trave
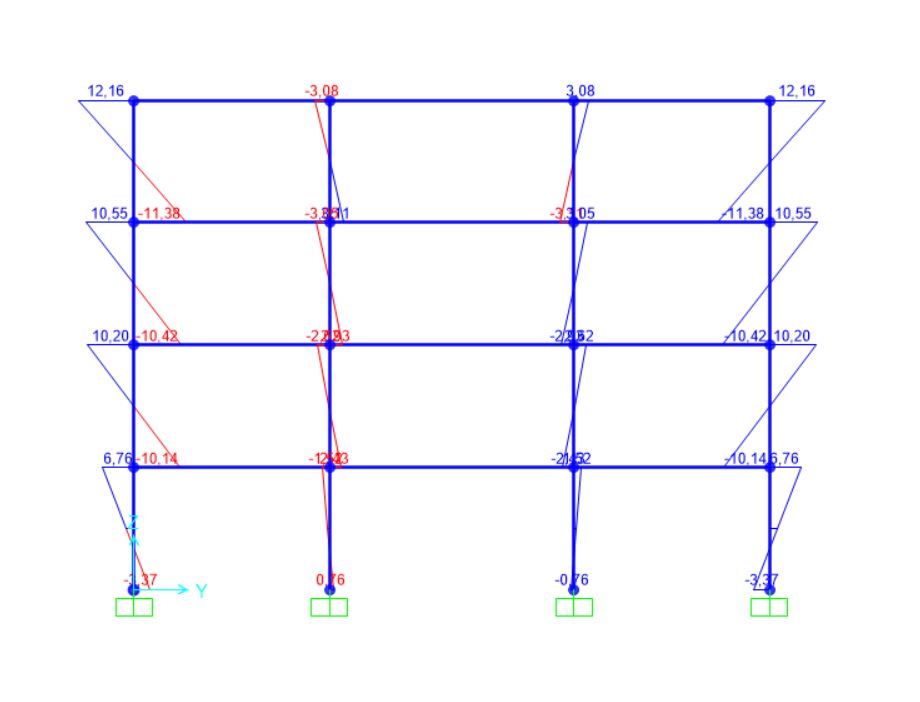
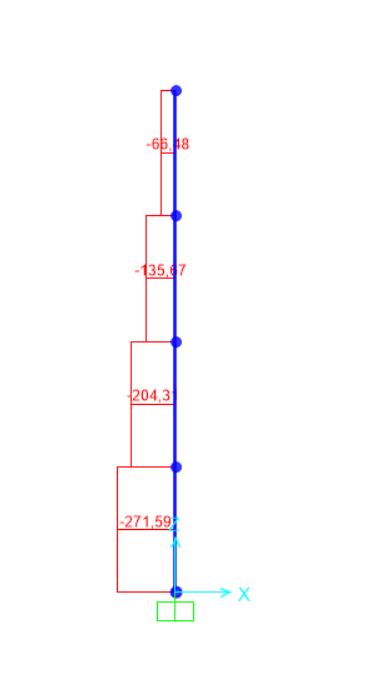
Diagrammi delle sollecitazioni sulla pilastrata
CALCESTRUZZO ARMATO
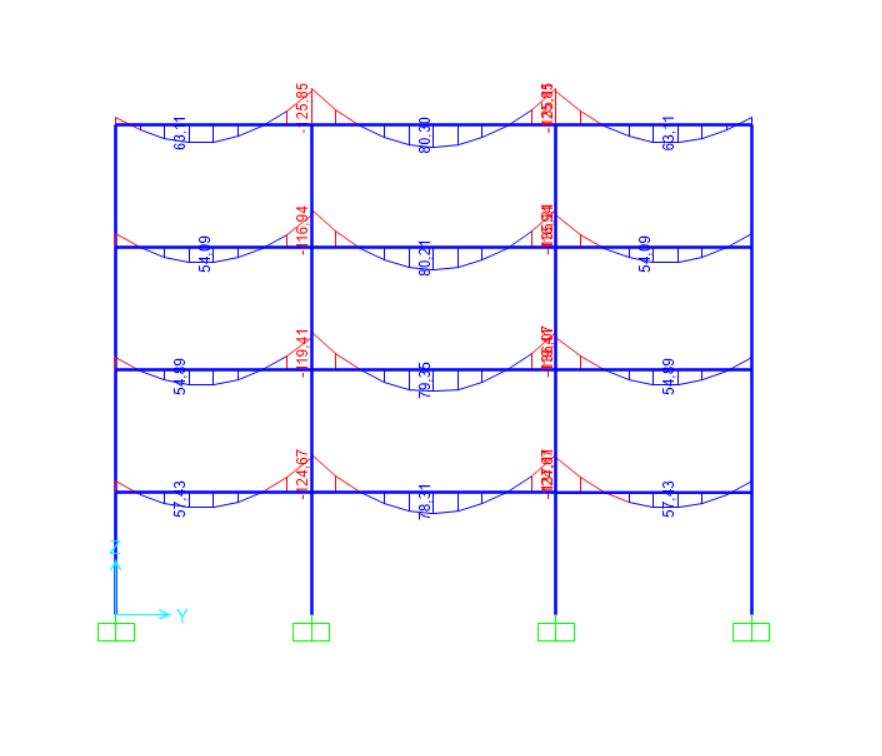
Diagramma dei momenti sulla trave
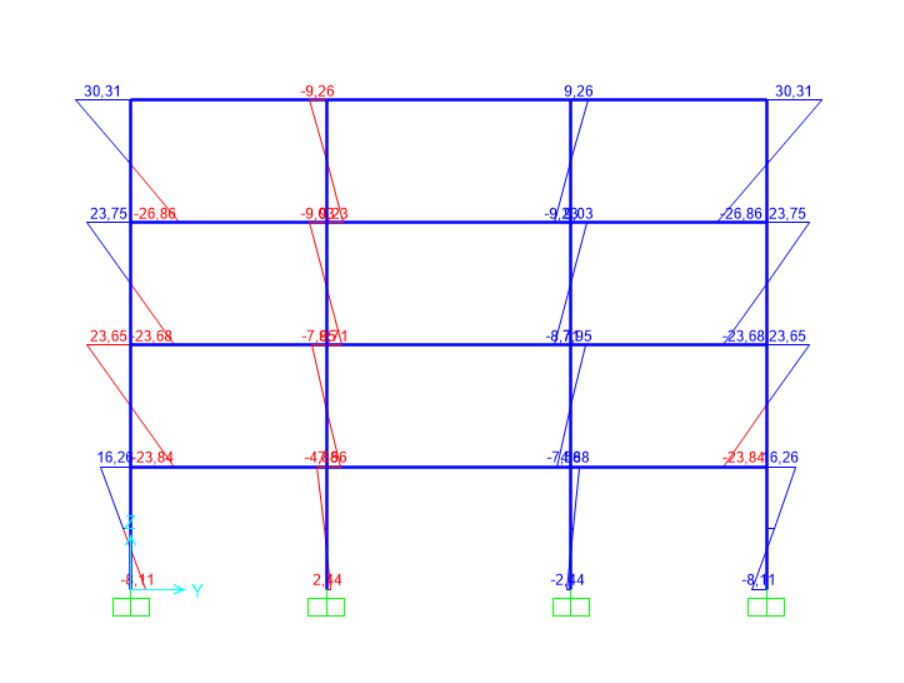
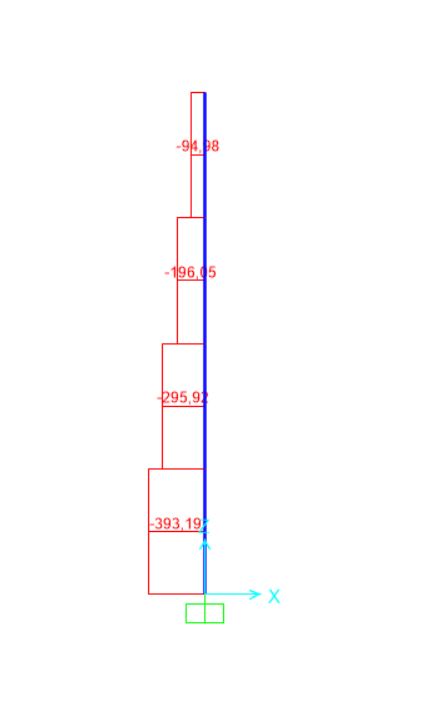
Diagrammi delle sollecitazioni sulla pilastrata
LEGNO
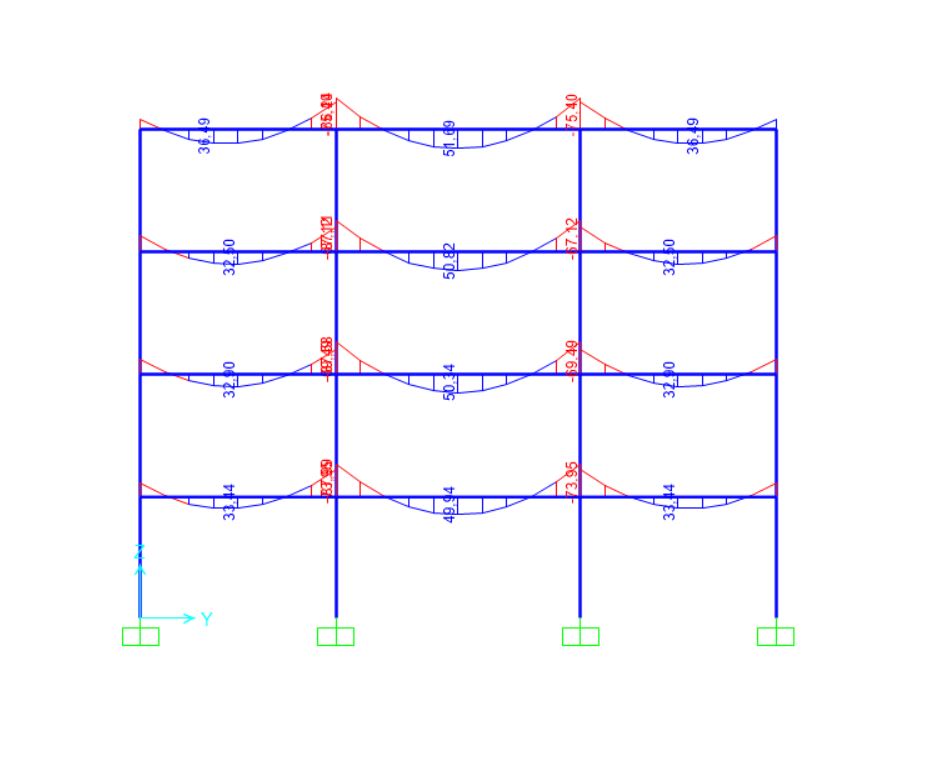
Diagramma dei momenti sulla trave
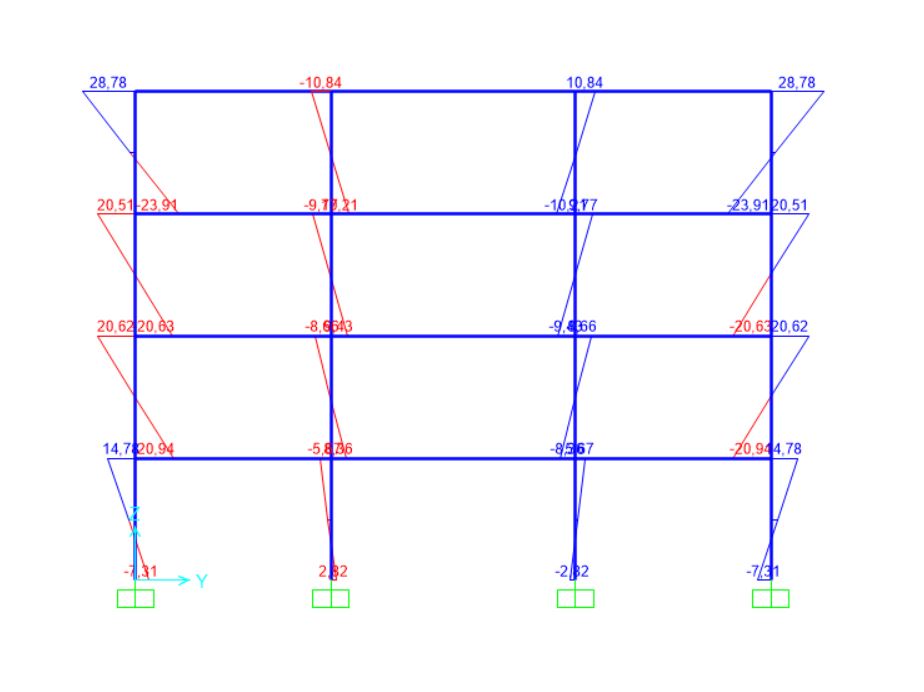
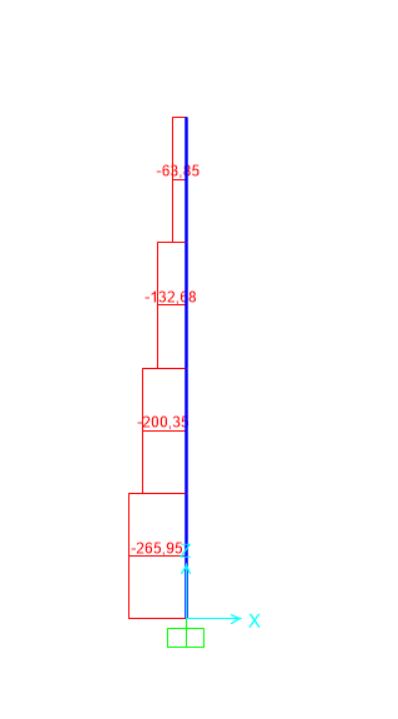
Diagrammi delle sollecitazioni sulla pilastrata
VERIFICA
Una volta terminata l'analisi in SAP della struttura è stata fatta la verifica degli elementi precedentemente progettati ma sostituendo le sollecitazioni di progetto con quelle ottenute dall'analisi.
Il metodo di verifica utilizzato mette a confronto le tensioni agenti sulla sezione più sollecitata con le tensioni ammissibili.
In generale quindi:
smax ≤ fcd
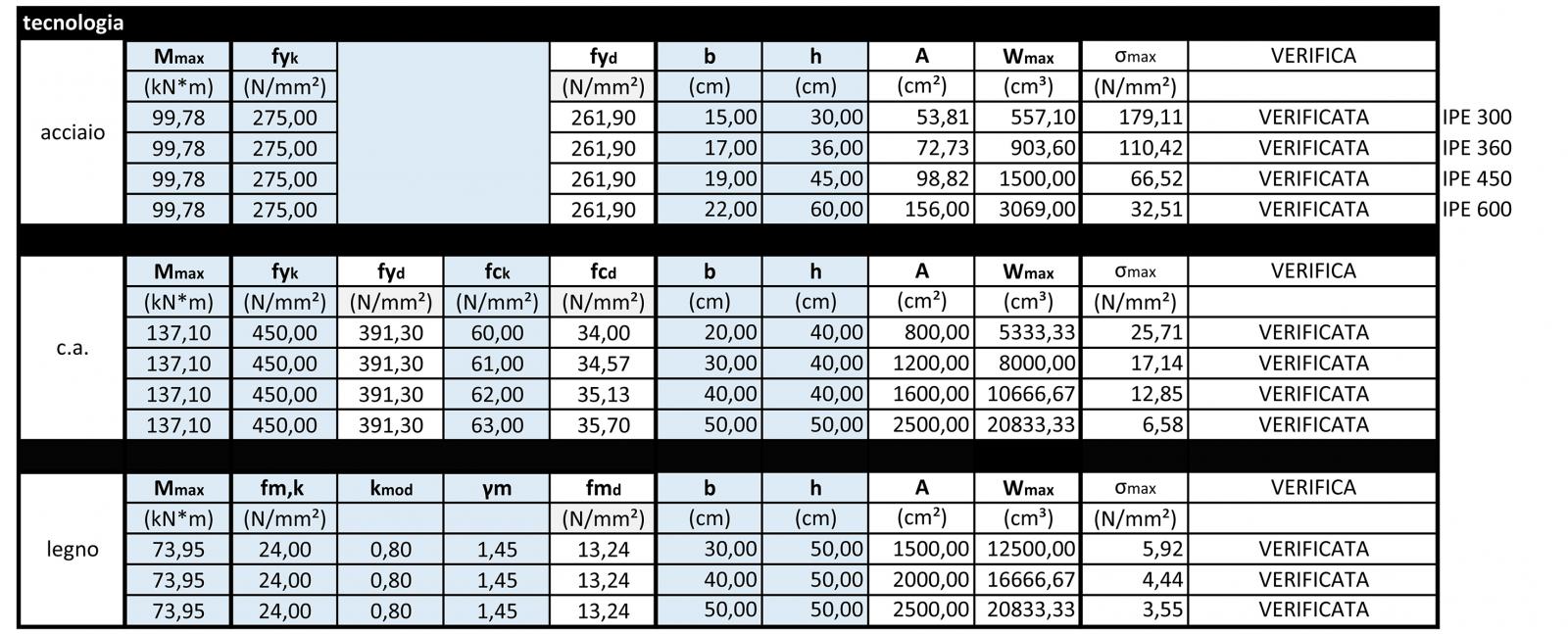
Per quanto riguarda la trave, la tensione massima è stata calcolata in funzione della sollecitazione massima agente sulla sezione, quindi come il rapporto tra momento massimo e modulo di resistenza a flessione massimo:
smax= Mmax/Wmax
Mmax/Wmax≤ fcd
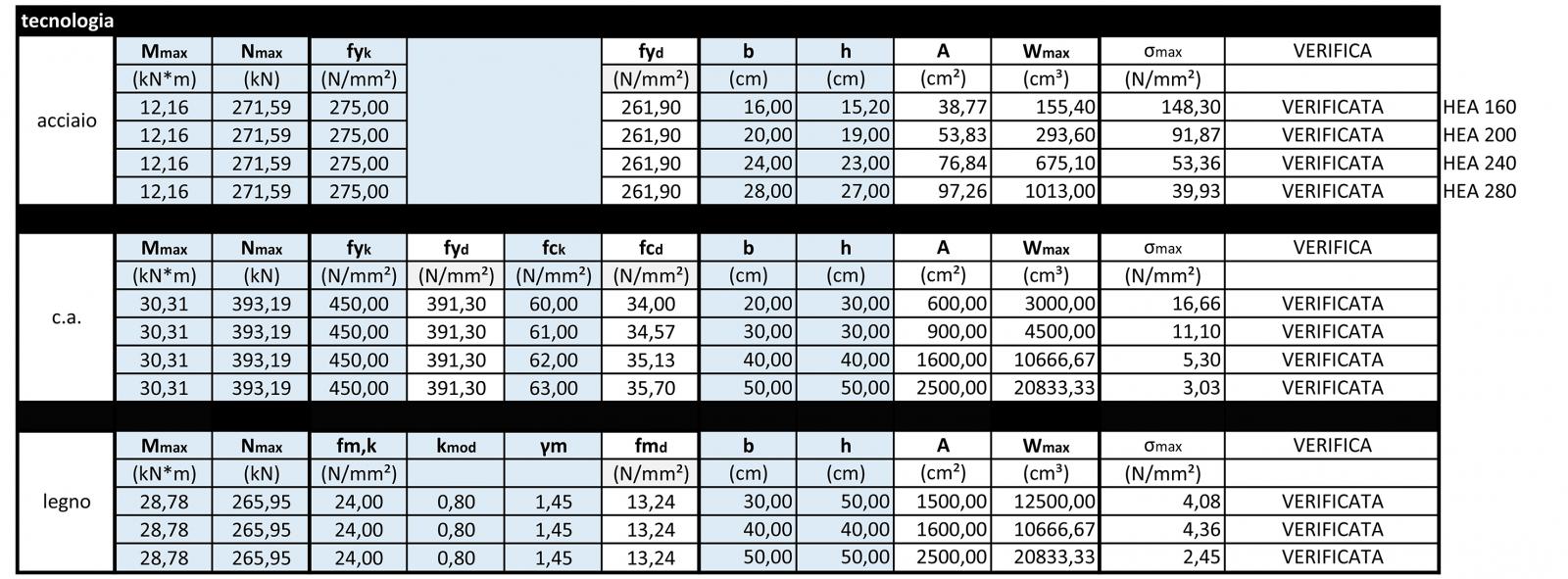
In riferimento al pilastro invece, la tensione massima è fornita dalle due diverse sollecitazioni agenti sullo stesso, ovvero sforzo normale di compressione e momento flettente trasmesso dalla trave al pilastro.
La tensione massima è quindi pari a:
smax= N/A+Mmax/Wmax
Da cui la verifica di una sezione presso-inflessa:
N/A+Mmax/Wmax≤ fcd
Commenti recenti