LINEA ELASTICA

Inviato da francesca.marino il Gio, 04/04/2013 - 21:41

L'esercitazione ci richiede di risolvere una struttura iperstatica con il metodo della linea elastica e verificare i dati ottenuti con Sap.

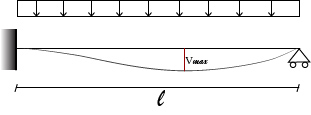
Calcolare il valore dell'abbassamento massimo V ed il punto in cui si trova sulla seguente trave iperstatica.

Abbiamo a nostra disposizione 8 equazioni con 8 incognite, tra cui equazioni di bilancio, equazioni delle deformate, e legame costitutivo elastico.

$\left\{\begin{matrix}N'+q_{1}=0 & & \\ T'+q_{2}=0 & & \\ M'+T=0 & & \end{matrix}\right.$ [1] $\left\{\begin{matrix}\varepsilon=u' & & \\ \varphi =v' & & \\ \chi =\varphi ' & & \end{matrix}\right.$ [2] $\left\{\begin{matrix}N=EA\varepsilon & & \\ M=EI\chi & & \end{matrix}\right.$ [3]

considerando solo l'abbassamento V possiamo combinare le varie equazioni:

$\frac{dT}{ds}+q_{2}=0$ [4] $T=-\frac{dM}{ds}$ [5]

$\frac{d}{ds}\left ( -\frac{dM}{ds} \right )+q_{2}=0$ [6] $-\frac{d^{2}M}{ds^{2}}+q_{2}=0$ [7] $\frac{d^{2}M}{ds^{2}}=q_{2}$ [8]

$\chi =\frac{d\varphi }{ds}$ [9] $\varphi =\frac{dv}{ds}$ [10]

$\chi =\frac{d}{ds}\left ( \frac{dv}{ds} \right )=\frac{d^{2}v}{ds^{2}}$ [11] $M=EI\chi =EI\frac{d^{2}v}{ds^{2}}$ [12]

$\frac{d^{2}}{ds^{2}}\left ( EI\frac{d^{2}v}{ds^{2}} \right )=q_{2}$ [13]

consideriamo EI=costante

$EI\frac{d^{4}v}{ds^{4}}=q_{2}$ [14] $\frac{d^{4}v}{ds^{4}}=\frac{q_{2}}{EI}$ [15] EQUAZIONE DELLA LINEA ELASTICA

Per trovare il valore di V(s) integriamo 4 volte l'equazione ottenuta

$\frac{d^{3}v}{ds^{3}}=\frac{q_{2}}{EI}s+C_{1}$ [16]

$\frac{d^{2}v}{ds^{2}}=\frac{q_{2}}{EI}\frac{s^{2}}{2}+C_{1}s+C_{2}$ [17]

$\frac{dv}{ds}=\frac{q_{2}}{EI}\frac{s^{3}}{6}+C_{1}\frac{s^{2}}{2}+C_{2}s+C_{3}$ [18]

$v\left ( s \right )=\frac{q_{2}}{EI}\frac{s^{4}}{24}+C_{1}\frac{s^{3}}{6}+C_{2}\frac{s^{2}}{2}+C_{3}s+C_{4}$ [19]

Si ottengono cosi quattro costanti che dipendono dai vincoli, andando ad applicare le condizioni ai bordi possiamo trovarci il valore di ognuna.

Nell'incastro s=0 abbiamo ABBASSAMENTO e ROTAZIONE nulli

v(0)=0 sostituendo nell'equazione v(s) otteniamo

$C_{4}=0$ [20]

$\varphi \left ( 0 \right )=0$ [21] $\varphi$ [22] è la derivata prima dell'abbassamento, sostituendo in dv/ds otteniamo

$C_{3}=0$ [23]

Nel carrello S=l non c'è ABBASSAMENTO ed ha MOMENTO nullo

v(l)=0 sostituendo in v(s)

$v\left ( l \right )=-\frac{ql^{4}}{24EI}+C_{1}\frac{l^{3}}{6}+C_{2}\frac{l^{2}}{2}=0$ [24]

il carico diventa negativo per la convenzione dei segni

$M\left ( l \right )=0$ [25] $M=\frac{d^{2}v}{ds^{2}}$ [26]

$M\left (l \right )=-\frac{ql^{2}}{2EI}+C_{1}l+C_{2}=0$ [27]

$C_{2}=\frac{q_{2}l^{2}}{2EI}-C_{1}l$ [28] sostituendo nel'abbassamento v(l)

$-\frac{q_{2}l^{4}}{24EI}+C_{1}\frac{l^{3}}{6}+\left ( \frac{q_{2}l^{2}}{2EI}-C_{1}l \right )\frac{l^{2}}{2}=0$ [29]

$-\frac{q_{2}l^{4}}{24EI}+C_{1}\frac{l^{3}}{6}+ \frac{q_{2}l^{4}}{4EI}-C_{1} \frac{l^{3}}{2}=0$ [30]

$-\frac{q_{2}l^{4}+6q_{2}l^{4}}{24EI}+C_{1}\frac{l^{3}-3C_{1}l^{3}}{6}=0$ [31]

$\frac{5q_{2}l^{4}}{24EI}-\frac{C_{1}l^{3}}{3}=0$ [32]

$C_{1}=\frac{5q_{2}l^{4}}{24EI}*\frac{3}{l^{3}}=\frac{5}{8}\frac{q_{2}l}{EI}$ [33]

$C_{2}=\frac{q_{2}l^{2}}{2EI}-\left ( \frac{5q_{2}l}{8EI} \right )l=\frac{4q_{2}l^{2}-5q_{2}l^{2}}{8EI}=-\frac{q_{2}l^{2}}{8EI}$ [34]

Trovate le costanti possiamo trovare l'abbassamento massimo richiesto dal problema. Siccome la rotazione è la derivata dello spostamento, in corrispondenza della rotazione nulla abbiamo l'abbassamento massimo

$\varphi =\frac{dv}{ds}=-\frac{q_{2}s^{3}}{6EI}+C_{1}\frac{s^{2}}{2}+_{2}s+C_{3}$ [35]

$\varphi =-\frac{q_{2}s^{3}}{6EI}+\frac{5q_{2}ls^{2}}{16EI}-\frac{q_{2}l^{2}s}{8EI}=0$ [36]

$\varphi =s\left ( -\frac{q_{2}s^{2}}{6EI}+\frac{5q_{2}ls}{16EI}-\frac{q_{2}l^{2}}{8EI} \right )$ [37]

Affinchè la rotazione sia nulla avremo

$s=0$ [38]

$s=\left ( \frac{5q_{2}l^{2}}{16EI}\pm \sqrt{\frac{25q_{2}^{2}l^{2}}{256E^{2}I^{2}}-4\frac{q{_{2}}^{2}l^{2}}{48E^{2}I^{2}}} \right )*\frac{3EI}{q_{2}}$ [39]

$S=0,57$ [40]

$v\left ( 0,57 \right )=\frac{q_{2}\left ( 0,57 \right )^{4}}{24EI}+\frac{5q_{2}l\left ( 0,57 \right )^{3}}{48EI}-\frac{q_{2}l\left ( 0,57 \right )^{2}}{16EI}=-\frac{0,25q_{2}l^{2}}{48EI}$ [41]

$l=1\rightarrow v\left ( 0,57 \right )=-0,00536\frac{q_{2}}{EI}$ [42]

Considerando il valore di v(s) possiamo determinare il momento ed il taglio per ogni sezione $M=EI\frac{d^{2}v}{ds^{2}}=-\frac{q_{2}s^{2}}{2}+\frac{5q_{2}l}{8}s-\frac{q_{2}l^{2}}{8}$ [43]

$M\left ( 0 \right )=-\frac{q_{2}l^{2}}{8}$ [44] $M\left ( l \right )=-\frac{q_{2}s^{2}}{2}+\frac{5q_{2}l}{8}s-\frac{q_{2}l^{2}}{8}$ [45]

Il momento è nullo nei punti

$s_{1}=0$ [46]

$s_{2}=\frac{l}{4}$ [47]

$T=-M\left ( s \right )=q_{2}s-\frac{5q_{2}l}{8}$ [48]

$T\left ( 0 \right )=-\frac{5q_{2}l}{8}$ [49] $T\left ( l \right )=q_{2}l-\frac{5q_{2}l}{8}=\frac{3}{8}q_{2}l$ [50]

Il taglio è nullo nel punti

$T\left ( \frac{5}{8}l \right )=0$ [51]

RISOLUZIONE IN SAP

Apriamo un nuovo file di tipo grid, con unità di misura kn, m, C, e GRIGLIA x=2 , Y= 1, Z=1 e spaziatura 1. Disegnare la struttura sulla griglia e posizionare un punto a 0.57, dato che dal calcolo a mano abbiamo visto che l’abbassamento massimo avviene in questo punto della struttura.