


La Cacciata di Adamo ed Eva dal Giardino del Paradiso - Alexandre Cabanel
Chissà a che livelli arrivò la frustrazione di Adamo ed Eva nell'ascoltare la sentenza di Dio, riguardante il loro definitivo allontanamento dal Paradiso Terrestre. Allora erano forse inconsapevoli del fatto che, a causa di quel gesto di superbia, avevano perduto per sempre i doni preternaturali, i quali, tra le altre cose, li mettevano al riparo da ignoranza e inettitudine. Sicuramente non immaginavano di aver abbandonato, col loro atto, una parte del genere umano alle frustrazioni causate dal burrascoso rapporto con la meccanica e la statica. Diverse generazioni di studenti di architettura hanno convissuto con lo spauracchio degli esami di queste due discipline. Spauracchio che puntualmente si acuiva nel momento in cui venivano pronunciate due parole: LINEA ELASTICA.
Nonostante il senso di inquietudine che ancora mi pervade, proverò in questo post a spiegare come affrontare un sistema iperstatico, tramite l'utilizzo, appunto, dell'equazione della linea elastica. Iniziamo.

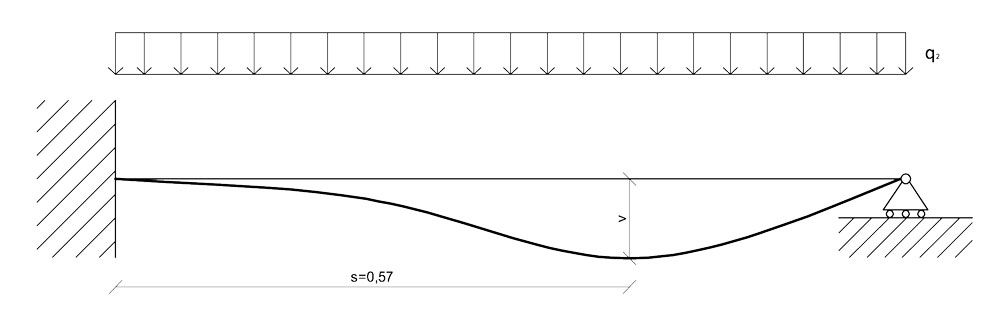
Questo era il sistema iperstatico assegnato, in cui dovevamo trovare il valore dello spostamento verticale v e ricavare un disegno della deformata, da verificare poi in SAP2000.
Scriviamo innanzitutto le equazioni relative al modello della trave di Bernoulli.
Equazioni differenziali di bilancio:
Equazioni del legame costitutivo:
Equazioni di congruenza:
Eliminiamo dal sistema le equazioni relative allo sforzo normale, dato che non prendiamo in considerazione l'analisi della deformata assiale, e mettiamo a sistema le rimanenti:
Partiamo dalla 2° equazione:
Sostituendo nella precedente:
Imponiamo che q2 sia costante, e,integrando 4 volte l'equazione differenziale ottenuta qui sopra, possiamo ricavare l'equazione esplicitata in v(s), che ci permetterà poi di ricavare tutte le altre incognite:
Scriviamo quindi le condizioni al bordo nei punti s=0 e s=L, per trovare i valori delle varie costanti c.
Per s=0:
Per la condizione s=L, mettiamo a sistema le 2 equazioni:
Sapendo che lo spostamento v ha un massimo o un minimo dove la pendenza della tangente alla deformata è nulla, poniamo l'equazione della rotazione pari a 0, per trovare un valore accettabile di s:
Supponiamo inoltre che la sezione della trave sia costante e dello stesso materiale, cosicchè possiamo sostituire ad I la formula del momento di inerzia di una sezione generica:
Consideriamo solo s=0,57, in quanto s<1, e lo andiamo a sostituire nell'equazione differenziale precedente per trovare v(s):
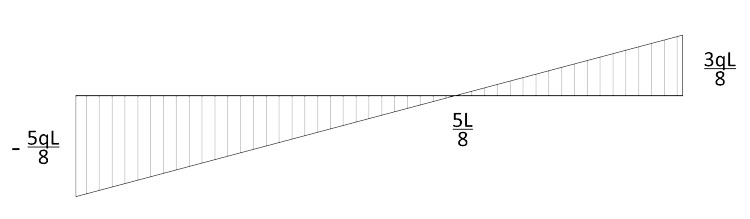
Disegniamo i diagrammi del taglio e del momento, da confrontare poi con quelli di SAP2000, impostando q2=-q e calcolando i relativi valori:
Per le condizioni al bordo, M è nullo in:
Troviamo anche i valori del taglio, sapendo che esso è la derivata del momento, consapevoli del fatto che nel punto in cui il taglio è nullo, il momento è invece massimo:

Dopo la parte dei calcoli manuali (poco piacevole, a dir la verità), portiamo il tutto su SAP2000, verificando di non aver sbagliato nulla.
Apriamo innanzitutto un nuovo file basato su griglia e andiamo nella vista 2D xz. Tramite lo strumento POINT inseriamo un punto in corrispondenza del vmax che usciva fuori dai precedenti calcoli (0,57L), e, grazie allo snap dei 3 punti, disegniamo la nostra trave (DRAW-FRAME):
Ora assegniamo una sezione generica IPE alla trave in acciaio (DEFINE-SECTION PROPERTIES-FRAME SECTIONS):

Dopo aver assegnato i vincoli e rimosso l'analisi del carico proprio della struttura, come al solito, impostiamo la densità di carico q2 per la trave:

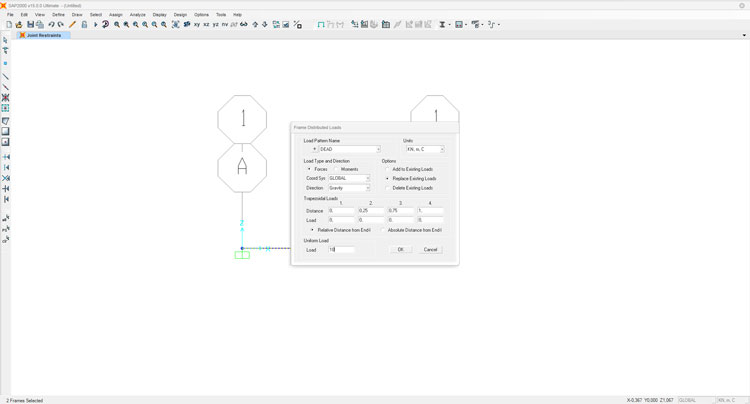

Ora non ci resta che avviare l'analisi della deformata, ricordandoci prima di rimuovere dall'analisi il MODAL:


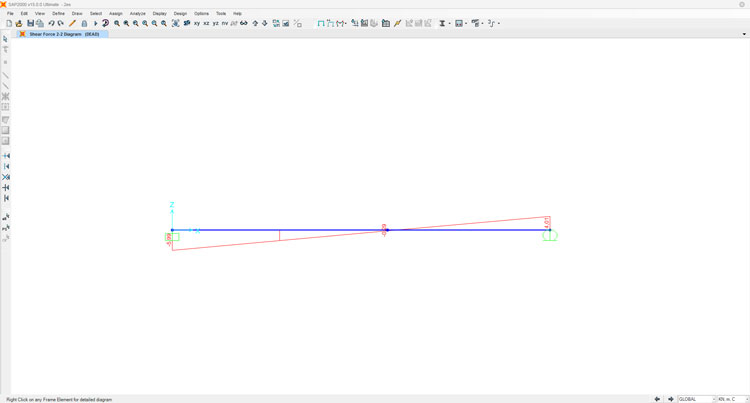
In ultimo, lasciamo che SAP2000 ci calcoli i diagrammi del momento flettente e del taglio, per verificare di averli disegnati correttamente in precedenza: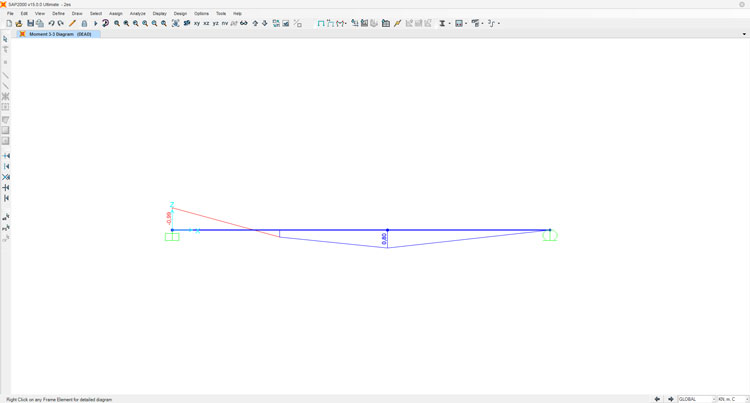
Links
[1] http://www.codecogs.com/eqnedit.php?latex=\left\{\begin{matrix}\frac{dN}{ds}@plus;q1=0 \\ \frac{dT}{ds}@plus;q2=0 \\ \frac{dM}{ds}@plus;T=0 \end{matrix}\right.
[2] http://www.codecogs.com/eqnedit.php?latex=\left\{\begin{matrix}M=EI\chi \\ N=\varepsilon AE \end{matrix}\right.
[3] http://www.codecogs.com/eqnedit.php?latex=\left\{\begin{matrix}\varepsilon (s)=u's=\frac{du}{ds} \\ \chi (s)=\varphi s=\frac{d\varphi }{ds} \\ \varphi =\frac{dv}{ds} \end{matrix}\right.
[4] http://www.codecogs.com/eqnedit.php?latex=\left\{\begin{matrix}\frac{dT}{ds}@plus;q_{2}=0 \\ \frac{dM}{ds}@plus;T=0 \\ M=EI\chi \\\chi =\frac{d\varphi }{ds} \\ \varphi =\frac{dv}{ds} \end{matrix}\right.
[5] http://www.codecogs.com/eqnedit.php?latex=T=-\frac{dM}{ds}\Rightarrow \frac{d}{ds}\left ( -\frac{dM}{ds} \right )@plus;q_{2}=0\Rightarrow -\frac{d^{2}M}{ds^{2}}@plus;q_{2}=0
[6] http://www.codecogs.com/eqnedit.php?latex=\varphi =\frac{dv}{ds}\Rightarrow \chi =\frac{d}{ds}\left ( \frac{dv}{ds} \right )=\frac{d^{2}v}{ds^{2}}=0\Rightarrow M=EI\frac{d^{2}v}{ds^{2}}
[7] http://www.codecogs.com/eqnedit.php?latex=-\frac{d^{2}}{ds^{2}}\left&space;(&space;EI\frac{d^{2}v}{ds^{2}}\right&space;)+q_{2}\Rightarrow&space;-\frac{d^{4}v}{ds^{4}}+\frac{q_{2}}{EI}=0\Rightarrow\frac{d^{4}v}{ds^{4}}=&space;\frac{q_{2}}{EI}
[8] http://www.codecogs.com/eqnedit.php?latex=\int \frac{d^{3}v}{ds^{^{3}}}=\frac{q_{2}}{EI}s@plus;c_{1}
[9] http://www.codecogs.com/eqnedit.php?latex=\int \int \frac{d^{2}v}{ds^{2}}=\frac{q_{2}s^{2}}{2EI}@plus;c_{1}s@plus;c_{2}
[10] http://www.codecogs.com/eqnedit.php?latex=\int \int \int \frac{dv}{ds}=\frac{q_{2}s^{3}}{6EI}@plus;c_{1}\frac{s^{2}}{2}@plus;c_{2}s@plus;c_{3}
[11] http://www.codecogs.com/eqnedit.php?latex=\upsilon&space;(s)=\frac{q_{2}s^{4}}{24EI}+c_{1}\frac{s^{3}}{6}+\frac{c_{2}s^2}{2}+c_{3}s+c_{4}
[12] http://www.codecogs.com/eqnedit.php?latex=v(0)=0\Rightarrow c_{4}=0
[13] http://www.codecogs.com/eqnedit.php?latex=\frac{dv}{ds}(0)=0\Rightarrow c_{3}=0
[14] http://www.codecogs.com/eqnedit.php?latex=\left\{\begin{matrix}v(L)=\frac{q_{2}L^{4}}{24EI}@plus;c_{1}\frac{L^{3}}{6}@plus;c_{2}\frac{L^{2}}{2} \\ \frac{d^{2}v}{ds^{2}}(L)=\frac{q_{2}L^{2}}{2EI}@plus;c_{1}L@plus;c_{2} \end{matrix}\right.
[15] http://www.codecogs.com/eqnedit.php?latex=\left\{\begin{matrix}\frac{q_{2}L^{4}}{24EI}@plus;c_{1}\frac{L^{3}}{6}@plus;c_{2}\frac{L^{2}}{2}=0 \\ \frac{q_{2}L^{2}}{2EI}@plus;c_{1}L@plus;c_{2}=0 \end{matrix}\right.
[16] http://www.codecogs.com/eqnedit.php?latex=\left\{\begin{matrix}\frac{q_{2}L^{4}}{24EI}@plus;c_{1}\frac{L^{3}}{6}@plus;c_{2}\frac{L^{2}}{2}=0 \\ c_{2}=-\frac{q_{2}L^{2}}{6EI}-c_{1}L \end{matrix}\right.
[17] http://www.codecogs.com/eqnedit.php?latex=\left\{\begin{matrix}\frac{q_{2}L^{4}}{24EI}@plus;c_{1}\frac{L^{3}}{6}@plus;\frac{L^{2}}{2}\left ( -\frac{q_{2}L^{2}}{6EI}@plus;c_{1} \frac{L}{2}\right )=0 \\ c_{2}=-\frac{q_{2}L^{2}}{6EI}-c_{1}L \end{matrix}\right.
[18] http://www.codecogs.com/eqnedit.php?latex=\left\{\begin{matrix}\frac{q_{2}L^{4}}{24EI}@plus;c_{1}\frac{L^{3}}{6}-\frac{qL^{4}}{4EI}\left-c_{1} \frac{L^{3}}{2}=0 \\ c_{2}=-\frac{q_{2}L^{2}}{6EI}-c_{1}L \end{matrix}\right.
[19] http://www.codecogs.com/eqnedit.php?latex=\left\{\begin{matrix}-\frac{5qL^{4}}{24EI}-\frac{c_{1}L^{3}}{3}=0 \\ c_{2}=-\frac{q_{2}L^{2}}{6EI}-c_{1}L \end{matrix}\right.
[20] http://www.codecogs.com/eqnedit.php?latex=\left\{\begin{matrix}c_{1}=-\frac{5qL}{8EI} \\ c_{2}=-\frac{q_{2}L^{2}}{6EI}-c_{1}L \end{matrix}\right.
[21] http://www.codecogs.com/eqnedit.php?latex=\left\{\begin{matrix}c_{1}=-\frac{5qL}{8EI} \\ c_{2}=-\frac{q_{2}L^{2}}{6EI}-\left ( -\frac{5qL}{8EI} \right )L \end{matrix}\right.
[22] http://www.codecogs.com/eqnedit.php?latex=\left\{\begin{matrix}c_{1}=-\frac{5qL}{8EI} \\ c_{2}=\frac{qL^{2}}{8EI} \end{matrix}\right.
[23] http://www.codecogs.com/eqnedit.php?latex=\varphi =\frac{dv}{ds}=\frac{q_{2}s^{3}}{6EI}@plus;\frac{c_{1}s^{2}}{2}@plus;c_{2}s^{2}=0
[24] http://www.codecogs.com/eqnedit.php?latex=\varphi =\frac{dv}{ds}=\frac{q_{2}s^{3}}{6EI}@plus;\left ( -\frac{5q_{2}L}{8EI} \right )\frac{s^{2}}{2}@plus;\frac{q_{2}L^{2}}{8EI}s^{2}=s\left ( \frac{q_{2}s^{2}}{6EI}-\frac{5q_{2}Ls}{16EI}@plus; \frac{q_{2}L^{2}}{8EI} \right )=0
[25] http://www.codecogs.com/eqnedit.php?latex=I=\frac{bh^{3}}{12}
[26] http://www.codecogs.com/eqnedit.php?latex=\frac{12q_{2}s^{2}}{6Ebh^{3}}-\frac{60q_{2}Ls}{16Ebh^{3}}@plus;\frac{12q_{2}L^{2}}{8Ebh^{3}}=0\Rightarrow \frac{q_{2}}{Ebh^{3}}\left ( 2s^{2} -\frac{15Ls}{4}@plus;\frac{3L^{2}}{2}\right )=0\Rightarrow \frac{\frac{15L}{4}\pm \sqrt{\left ( \frac{225L^{2}}{16}-12L^{2} \right )}}{4}=\frac{\frac{15L}{4}\pm \sqrt{\left ( \frac{33L^{2}}{16} \right )}}{4}=0
[27] http://www.codecogs.com/eqnedit.php?latex=x_{1}= 1,29L\; \; \; \; \; \; \; \; \; \; x_{2}=0,57 L
[28] http://www.codecogs.com/eqnedit.php?latex=v(s)=\frac{q_{2s^{4}}}{24EI}@plus;c_{1}\frac{s^{3}}{6}@plus;c_{2}\frac{s^{2}}{2}@plus;c_{3}s@plus;c_{4}\Rightarrow \frac{q_{2}\left ( 0,57L \right )^{4}}{24EI}-\frac{5q_{2}L}{8EI}\cdot \frac{\left( 0,57L \right )^{3}}{6}@plus;\frac{q_{2}L^{2}}{8EI}\cdot \frac{\left( 0,57L \right )^{2}}{2}\Rightarrow \frac{0,1q_{2}L^{4}}{24EI}-\frac{0,9q_{2}L^{4}}{48EI}@plus;\frac{0,32q_{2}L^{4}}{16EI}=\frac{0,26q_{2}L^{4}}{4Ebh^{3}}
[29] http://www.codecogs.com/eqnedit.php?latex=M(s)=EI\frac{d^{2}v}{ds^{2}}=EI\left ( -\frac{qs^{2}}{2EI}@plus;\frac{5qLs}{8EI}-\frac{qL^{2}}{8EI} \right )=-\frac{qs^{2}}{2}@plus;\frac{5qLs}{8}-\frac{qL^{2}}{8}
[30] http://www.codecogs.com/eqnedit.php?latex=M(0)=-\frac{qL^{2}}{8}
[31] http://www.codecogs.com/eqnedit.php?latex=M(L)=-\frac{qL^{2}}{2}@plus;\frac{5qL^{2}}{8}-\frac{qL^{2}}{8}
[32] http://www.codecogs.com/eqnedit.php?latex=\left\{\begin{matrix}s=L \\ s=\frac{L}{4} \end{matrix}\right.
[33] http://www.codecogs.com/eqnedit.php?latex=M'(s)=-qs@plus;\frac{5qL}{8}\Rightarrow T=-M'=qs-\frac{5qL}{8}
[34] http://www.codecogs.com/eqnedit.php?latex=T(0)=-\frac{5qL}{8}
[35] http://www.codecogs.com/eqnedit.php?latex=T(L)=\frac{3qL}{8}
[36] http://design.rootiers.it/strutture/taxonomy/term/2
[37] http://design.rootiers.it/strutture/taxonomy/term/16