2014 Geometrie costruttive | elica circolare con Grasshopper e Mathematica

Prima di capire come creare un elica circolare su Grasshopper e Mathematica, introduco l'esercizio del Prof. D'Autilia (sicuramente ho sbajato la derivata della radice quadrata)... comunque il ragionamento deve essere giusto.

Trovare T, N, B e K
Prendo a e b come numeri reali e positivi, in cui a è il raggio del cerchio dell’elica e b è una costante che determina la “densità” dei passi dell’elica.

Inoltre se:
b>0, l’elica ha la forma di una vite destrorsa;
se:
b<0 l’elica ha la forma di una vite sinistrorsa.

Considero la curva dell'elica:
P(t)=(a cos(t), a sin(t), bt) con t appartenente ai numeri reali

Il vettore velocità è dato dalla derivata prima di P(t)--> P’(t)=(-a sin(t), a cos(t), b)
Il vettore accelerazione è dato dalla derivata seconda--> P’’(t)=(-a cos(t), -a sin(t), 0)

1)Calcolo versore tangente T(t)= P’(t)/| P’(t) |
Coordinate del versore tangente--> T(t) =(-a sin(t)/(a^2+b^2)^(1/2); a cos(t)/(a^2+b^2)^(1/2);b/ (a^2+b^2)^(1/2))

2)Calcolo versore normale N(t)= T’(t)/| T’(t) |
T’=-a cos(t)/(2√a^2+b^2)
|T’|=a/√a^2+b^2 ---> Nx(t)=-cos(t)
Le coordinate del versore normale sono --> N(t)=(-cos(t), -sin(t),0)

3)Calcolo versore ortogonale B(t)= T’(t)^ N(t)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Le coordinate del prodotto vettoriale sono-->B(t)= (-b sin(t)/√a2+b2; -b cos(t)/√a2+b2; -a/√a2+b2)

4) Calcolo versore curvatura K(t)= T’(t)/|P’(t)|)
T’(t)= (-a cos(t)/ √a2+b2; -a sint)/ √a2+b2; 0 )
P’(t)=(-a sin(t), a cos(t), b)
Le coordinate del versore curvatura sono--> (-acos(t)/ a2+b2; -a sint)/ a2+b2; 0)

 

Modello su Mathematica

elica[a_][t_] := {a*Sin[t], a*Cos[t], t/3}

ParametricPlot3D[elica[a][t], {a, -1, 1}, {t, 0, 15}]

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

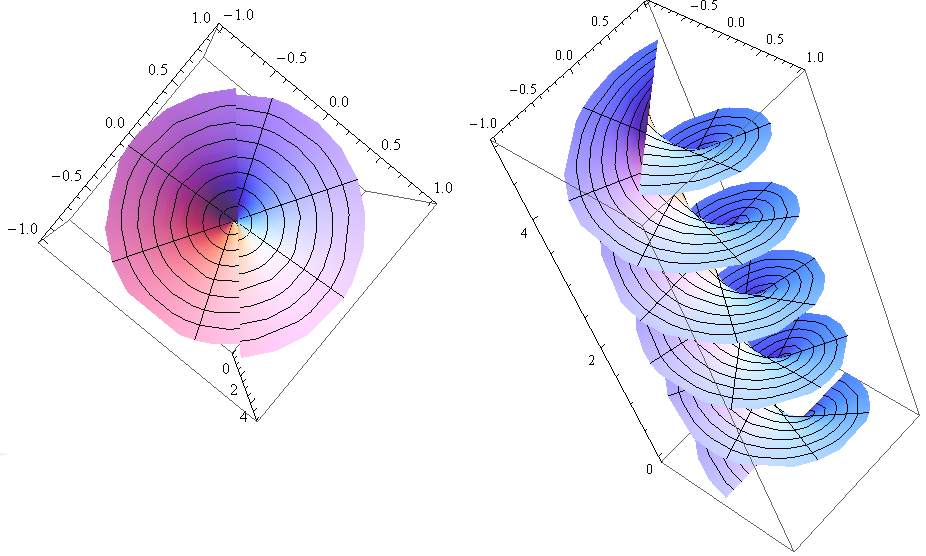
elica[a_][t_] := {Sin[t], Cos[t], t/3}  (è probabile che qui vi dia un errore, fate finta di niente)

Ora definiamo il versore tangente:

In[36]:= tangente[gamma_][t_] :=
 Simplify[D[gamma[tt],
     tt]/(D[gamma[tt], tt].D[gamma[tt], tt])^(1/2)] /. tt -> t

In[37]:= tangente[elica][t]

Output dell'input 37 dà come risultato la tangente.

Definisco il versore normale dell'elica che per errore ho chiamato binormale su Mathematica:

In[38]:= binormale[gamma_][t_] :=
 Simplify[Cross[D[gamma[tt], tt], D[gamma[tt], {tt, 2}]]/
    (Cross[D[gamma[tt], tt], D[gamma[tt], {tt, 2}]].
       Cross[D[gamma[tt], tt], D[gamma[tt], {tt, 2}]])^
     (1/2)] /. tt -> t

In[39]:= binormale[elica][t]

Definisco il versore ortogonale al versore tangente e al versore normale dell'elica (che per errore ho chiamato normale):

In[40]:= normale[gamma_][t_] :=
 Simplify[Cross[binormale[gamma][tt], tangente[gamma][tt]]] /. tt -> t

Il comando cross è la matrice

In[41]:= normale[elica][t]

In[64]:= Manipulate[
 Show[ParametricPlot3D[elica[t], {t, 0, 10 Pi},   PlotRange -> {{-4, 4}, {-4, 4}}],
  Graphics3D[{PointSize[0.003], Red, Point[elica[k]]}],
  Graphics3D[{Thick, Green,    Arrow [{elica[k], elica[k] + tangente[elica][k]/6}]}],
  Graphics3D[{Thick, Blue,    Arrow [{elica[k], elica[k] + normale[elica][k]/6}]}],
  Graphics3D[{Thick, Orange,    Arrow [{elica[k], elica[k] + binormale[elica][k]/6}]}]],
 {k, 0.1, 10 Pi}]

A seguire un video dell'elica (ancora da inserire):

https://www.youtube.com/watch?v=85ctpBBTs6w&feature=c4-overview&list=UUjOKiICWvgGhfTWR_9HDlZw

 

Modello su Grasshopper

A seguire un immagine del "processo" per la creazione di un'elica su grasshopper:

 

 

 

 

 

 

 

 

 

 

 

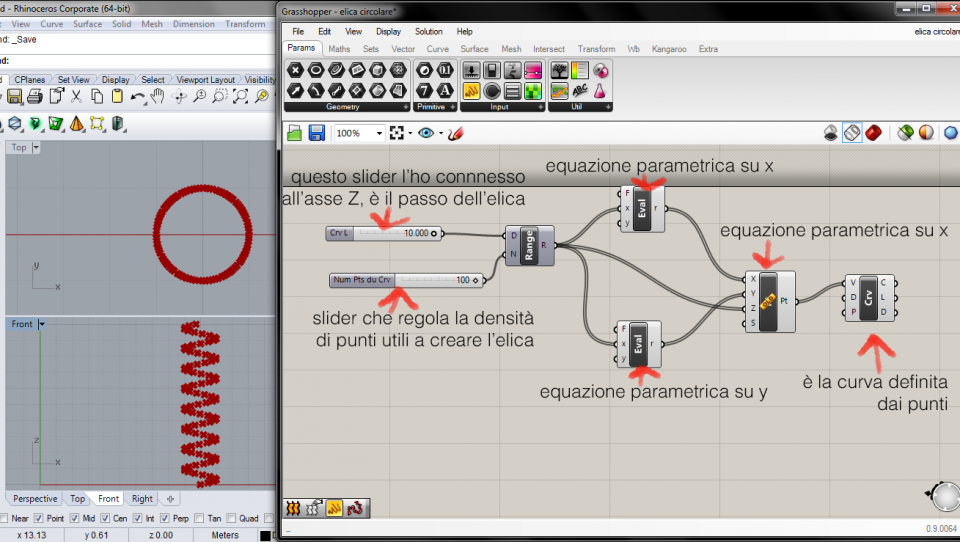
La nostra curva in grasshopper è stata scritta esattamente così, come in mathematica:

P(t)=(a cos(t), a sin(t), bt)

Nel comando EVALUATE (in alto),cliccando due volte sul "bottone", ho inserito l'equazione parametrica a cos(t); nel comando EVALUATE (in basso), inserisco l'equazione a sin(t); l'asse zeta bt è stato definito dallo slider CrvL.

Usando il comando POINT XYZ, collego il comando punto alle sue coordinate, ovvero:

Nel comando EVALUATE (in alto), ho inserito l'equazione parametrica a cos(t), collego il tutto alla coordinata X del comando POINT XYZ;

nel comando EVALUATE (in basso), inserisco l'equazione a sin(t), collego l'equazione alla coordinata Y del comando POINT XYZ;

collego lo slider Crv L con la coordinata Z del comando POINT XYZ.

Dopodichè collego all'output del comando POINT XYZ il comando CRV per avere la curva definita dai punti.

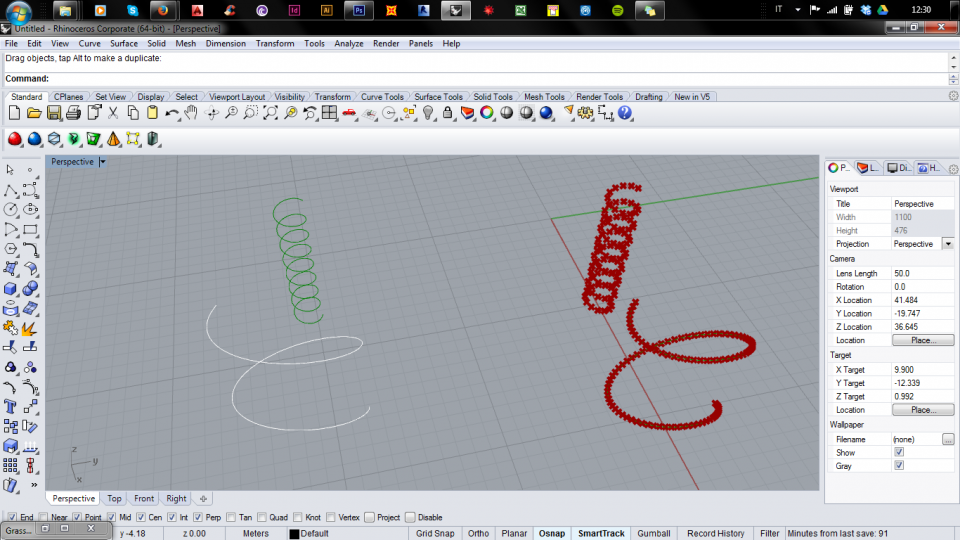
L'elica è pronta:

Una volta fatta l'elica circolare, è possibile fare altre forme modificando i parametri attraverso EVALUATE.