11 CLICK

- Per risolvere una struttura iperstatica, senza utilizzare la linea elastica, posso applicare il metodo delle forze che mi consente di ricondurre la prima ad una struttura isostatica equivalente.

- Per trasformare una iperstatica in uno schema equivalente isostatico devo declassare uno o più vincoli; per completarne la rappresentazione corretta, evidenzio inoltre la reazione vincolare che veniva fornita dal vincolo precedente e che il nuovo non fornisce. Ottengo, in questo modo, una incognita iperstatica e una struttura che presenta in contemporanea la rappresentazione statica e quella cinematica delle forze (interno ed esterne, agenti e reagenti) che entrano in gioco nel problema in analisi.

- Lo schema isostatico ottenuto va ulteriormente arricchito di una o più condizioni, rappresentate da equazioni di tipo cinematico (relative agli spostamenti), perchè la natura cinematica dello schema iperstatico di partenza deve essere uguagliata perfettamente se si vogliono trovare i relativi risultati di sollecitazioni, deformazioni e reazioni vincolari.

- Queste equazioni cinematiche consentono di determinare le incognite iperstatiche scelte per l'equivalenza tra gli schemi; queste incognite possono rappresentare sia forze interne/azioni di contatto che forze esterne.

- prendiamo un esempio:

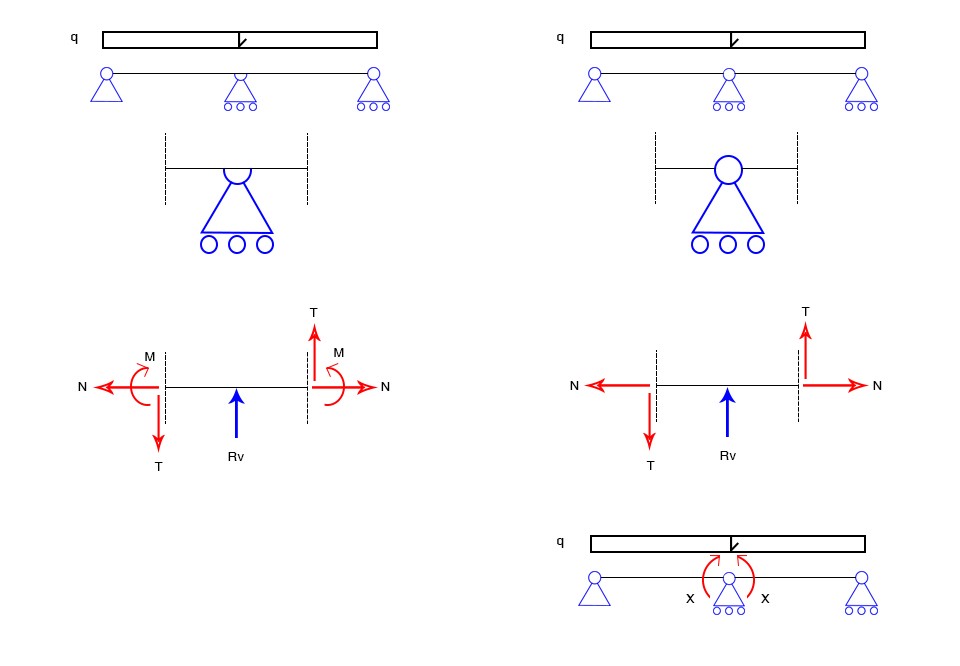
il carrello presente in mezzeria nella struttura iperstatica è passante, la trave è continua; il vincolo viene declassato ad un carrello che spezza la continuità della trave, individuando due elementi separati.

- Se si eseguono due tagli di Cauchy e si vanno ad analizzare le sezioni di mezzeria di entrambi gli schemi, si rende palese come le due situazioni non si equivalgano, proprio perchè la continuità della trave del primo non è stata mantenuta nel secondo.

- Nello schema iperstatico, la continuità implica che tutte le forse di contatto si trasferiscano; nello schema isostatico, avendo una cerniera interna che separa tratto sinistro e destro della trave e che permette la rotazione relativa di questi ultimi, non si ha la trasmissione del momento di continuità.

- Devo quindi aggiungerne la rappresentazione nello schema isostatico, tramite una coppia di forze, che determinano l'ingognita iperstatica di questo problema.

- Lo schema proposto va ancora arricchito per risultare equivalente al primo; sapendo di dover rappresentare un elemento che nasce come unico, posso esprimerne la continuità in termini cinematici, ovvero:

Ubs = Ubd >> Ubs - Ubd = 0 >> traslazione orizzontale relativa non consentita

Vbs = Vbd >> Vbs - Vbd = 0 >> spostamento verticale relativo non consentito

PHIbs = PHIbd >> la rotazione nel tratto di sinistra è uguale a quella di destra perchè impongo la continuità, ma avendo una cerniera interna so di avere la possibilità che si generi rotazione relativa...

- Quindi, avendo stabilito come ingognita iperstatica un momento di contatto a rapprensentare un vincolo di continuità, devo associarvi l'equazione cinematica relativa allo spostamento a cui questa incognita si oppone e che riproponga l'effetto del vincolo che c'era nel problema di partenza: in questo caso, perciò, impongo che la rotazione relativa nel punto sia uguale a zero.

- Grazie a questa equazione, la cinematica dello schema iperstatico è stata ripristinata e posso determinare il valore dell'ingognita X, in modo da trovare le informazioni necessarie a risolvere la struttura.