11 CLICK

11 CLICK

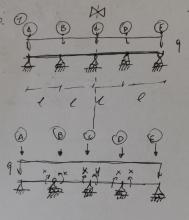
1- Riconoscere la tipologia di struttura presa in analisi in questo caso    abbiamo un tipo di trave continua su     più appoggi.

2- Riconosciamo la simmetria della struttura:
   -vincoli
   -trave
   -geometria
 "Simmetria perfetta": in questo caso nonostante a sinistra ci sia una cerniera, la struttura risulta  simmetrica     in quanto non è presente forza assiale la cerniera si comporta come un carrello.

3- Visto che è simmetrico, non è iperstatico 3 volte ma 2.

4- Riconduciamo la nostra struttura, ad una  sottostrutture nota in questo caso la riconduciamo in una trave doppiamente appoggiata.

5- Per ottenere una struttura equivalente introduciamo delle cerniere interne aggiungendo una coppia di forze concentrate ad ognuna di esse,    che mi permettono di ristabilire la continuità del momento.

6- Dobbiamo imporre che la rotazione relativa di ogni cerniera interna,sia equivalente a zero ( o si annulla ).
   - Δ(Φ)=0  
   - Δ(Φ)= (Φs)-(Φd)

7- Prendiamo in considerazione il tratto AB (trave doppiamente appoggiata)
   per trovare (Φbs) ed applichiamo il principio delle sovrapposizioni degli effetti (non è un principio perchè è dimostrabile).

8- Studiamo l'effetto del carico(q) e la Forza concentrata X per trovare (Φbs).

9- Ripetiamo lo stesso procedimento nel tratto BC, dove si aggiunge la  componente (y), alla fine otteniamo un equazione contenente 2 incognite  (X e Y) ovvero l'equazione di Δ(Φb).

10- Procediamo con gli stessi passaggi per ottenere Δ(Φc), in cui
    otteniamo sempre le incognite (X e Y), studiando il tratto BC,CD.

11- Infine poniamo a sistema le 2 equazioni trovate, per poi ricavare i valori di X e Y, in questo modo abbiamo i valori delle incognite iperstatiche,e possiamo procedere con lo studio della struttura (reazioni vincolari, taglio e momento).