11 Click

 

Il metodo delle forze viene utilizzato per risolvere strutture iperstatiche che vengono ricondotte a strutture isostatiche di riferimento (più semplici da studiare) equivalenti alla struttura di partenza.

 

1- Struttura una volta iperstatica: 3 gradi di libertà, 4 gradi di vincolo.

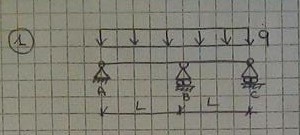
2- Per far sì che la struttura iperstatica analizzata sia facile da calcolare, scelgo una struttura isostatica equivalente e la sua reazione vincolare che sarà l'incognita X da trovare.

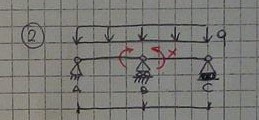
3- Eseguendo il taglio di Cauchy, si può notare che X equivale al momento flettente interno della trave. La forza interna può essere legata ad un vincolo di continuità: se la trave è continua, la forza passa.

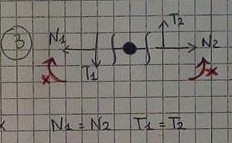
4- Scelta la struttura isostatica di riferimento, prendo in considerazione i diagrammi delle deformate per ogni tratto:

AB:                                                                        BC:
-> trave con carico distribuito                        -> trave con carico distribuito      
-> trave con forza X                                          -> trave con forza X

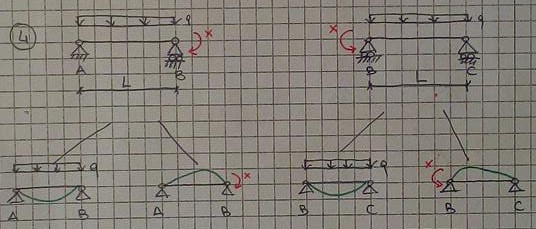
5- Nei diagrammi delle deformate conosco il valore delle rotazioni della trave, rispettivamente:

-> Φ_Bs: ql³/24EI
-> Φ_Bs: xl/3EI
-> Φ_Bd: ql³/24EI
-> Φ_Bd: xl/3EI

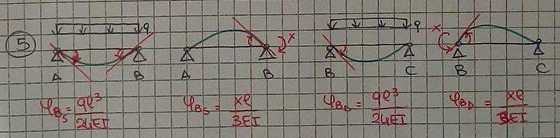
6- Impongo che ΔΦ (rotazione relativa) sia uguale a zero (perchè la trave in quel punto non può ruotare)
-> ΔΦ_B = 0               =>        Φ_Bs - Φ_Bd = 0

7- Sommo le rotazioni nel punto B:
-> Φ_Bs = (ql³/24EI) - (xl/3EI)
-> Φ_Bd = (-ql³/24EI) + (xl/3EI)

Φ_Bs - Φ_Bd = (ql³/24EI) - (xl/3EI) - [(-ql³/24EI) + (xl/3EI)] = 0

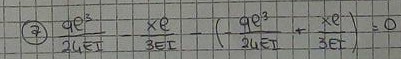
8- Trovo il valore dell'incognita X:
-> x=ql²/8

9- Trovato il valore della forza interna X, con il principio di sovrapposizioine degli effetti, è possibile calcolare il momento della trave iperstatica:

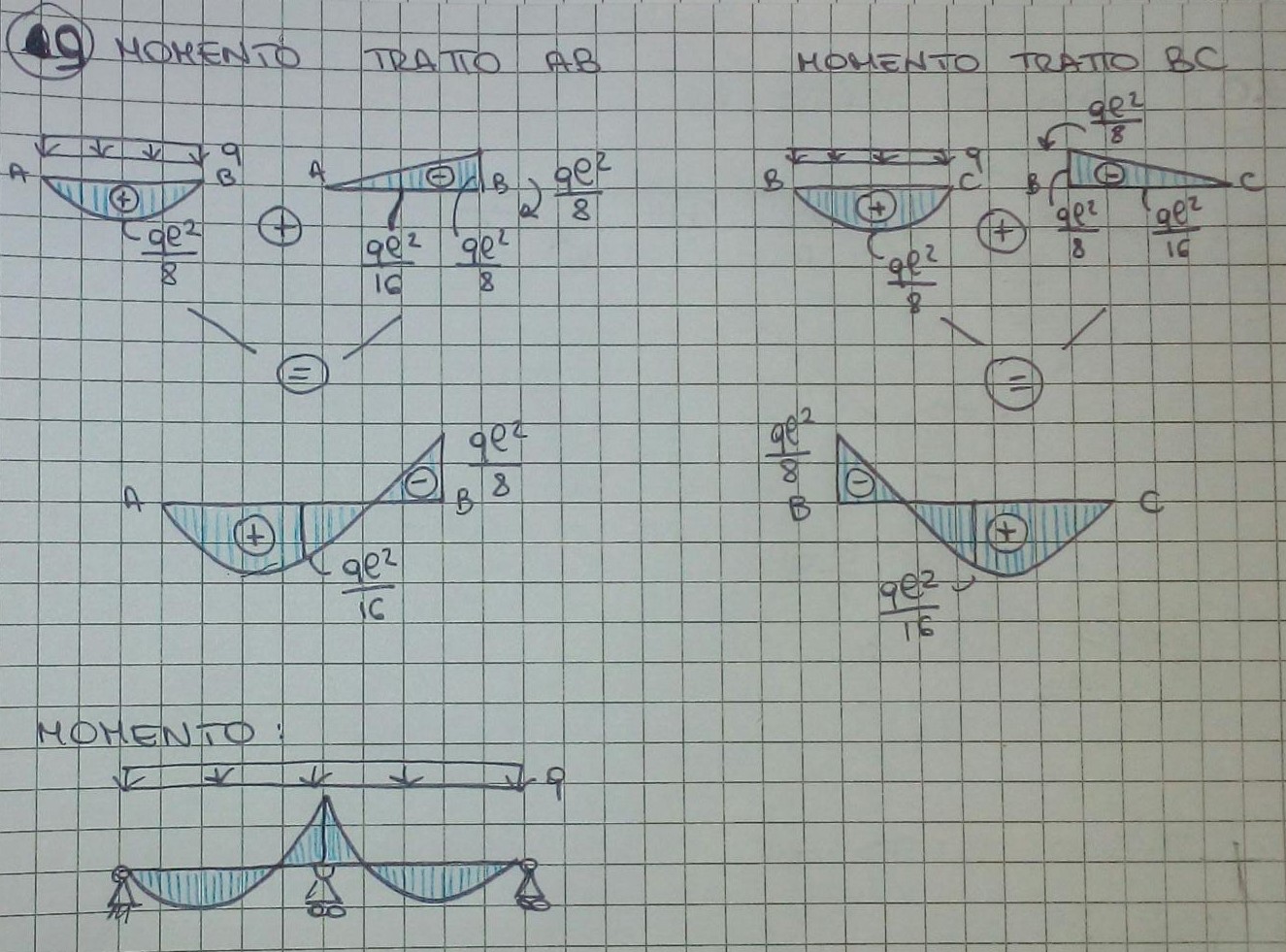
10- il taglio:

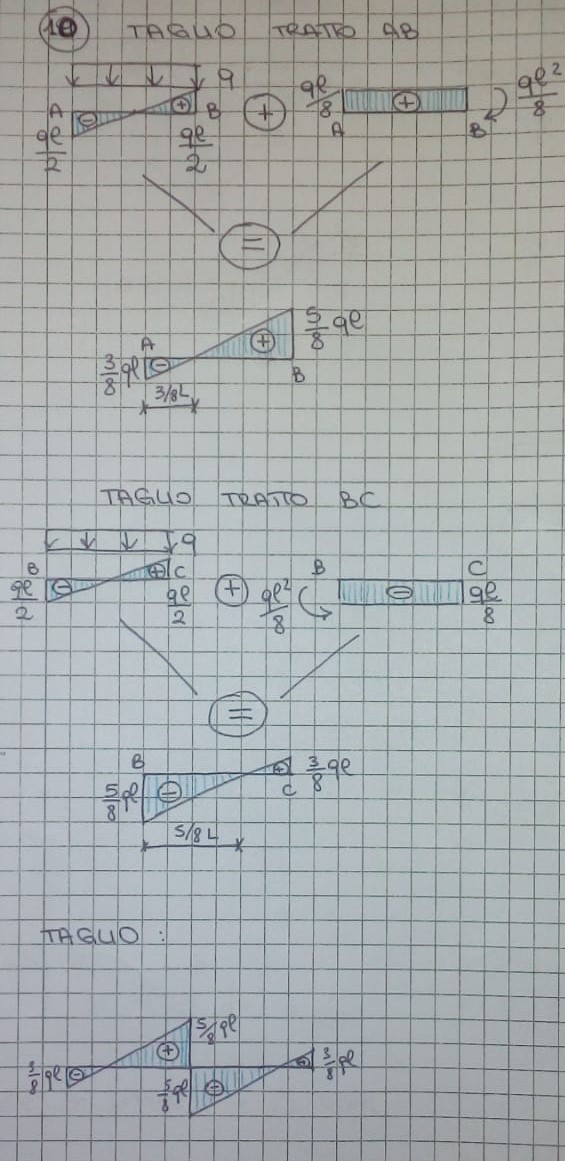
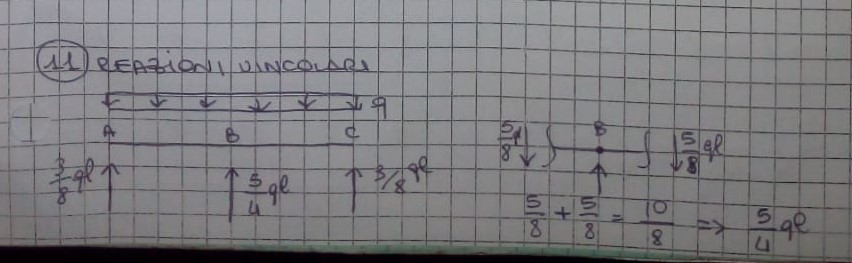
11- per poi trovare il valore delle reazioni vincolari: