11 click

1) Prendo in considerazione la struttura, e noto che si tratta di una struttura 4 volte iperstatica (essendo una trave unica con due cerniere e 3 carrelli

2) L'intera struttura è simmetrica (geometria, vincoli, carico). Posso quindi studiarla più semplicemente analizzandone solo una parte.

3) La metà della struttura che prendo in esame è quindi non più 4 volte iperstatica, ma 1 volta iperstatica (1 cerniera e 2 carrelli).

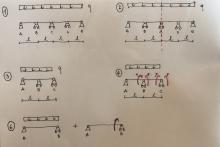
4) Trasformo la struttura, che prima era unica, in aste distinte. (Non si tratta più di una trave continua).
Questo implica l'inserimento di rotazioni interne sulle cerniere, per ripristinare le condizioni cinematiche.

5) Analizzo il punto B. La rotazione relativa deve essere pari a zero. Φb (d) = Φb (s)

6) Analizzo il tratto AB. Posso studiare la struttura, tramite il principio della sovrapposizione, in un primo momento visualizzandola come trave doppiamente appoggiata con carico distrubuito, e poi come una trave doppiamente appoggiata con momento applicato nel vincolo B.

7) Risolvo la struttura doppiamente appoggiata trovando i valori di N,T,M

8) Trovo il valore di X sfruttando il metodo della linea elastica. X= ql²/8. Il valore di X corrisponde alla rotazione relativa Φb (s)

9) Svolgo il procedimento analogo per il tratto BC

10) Trovo il valore di Y sfruttando il metodo della linea elastica.

11) Metto a sistema le due equazioni e mi trovo i valori di X e Y. Posso quindi risolvere la struttura iperstatica.