11 click

1 - E' possibile risolvere una struttura Iperstatica con il METODO DELLE FORZE, riconducendo questa ad una struttura isostatica equivalente.

2 - Prendo come esempio la seguente struttura iperstatica con il suo schema equivalente:

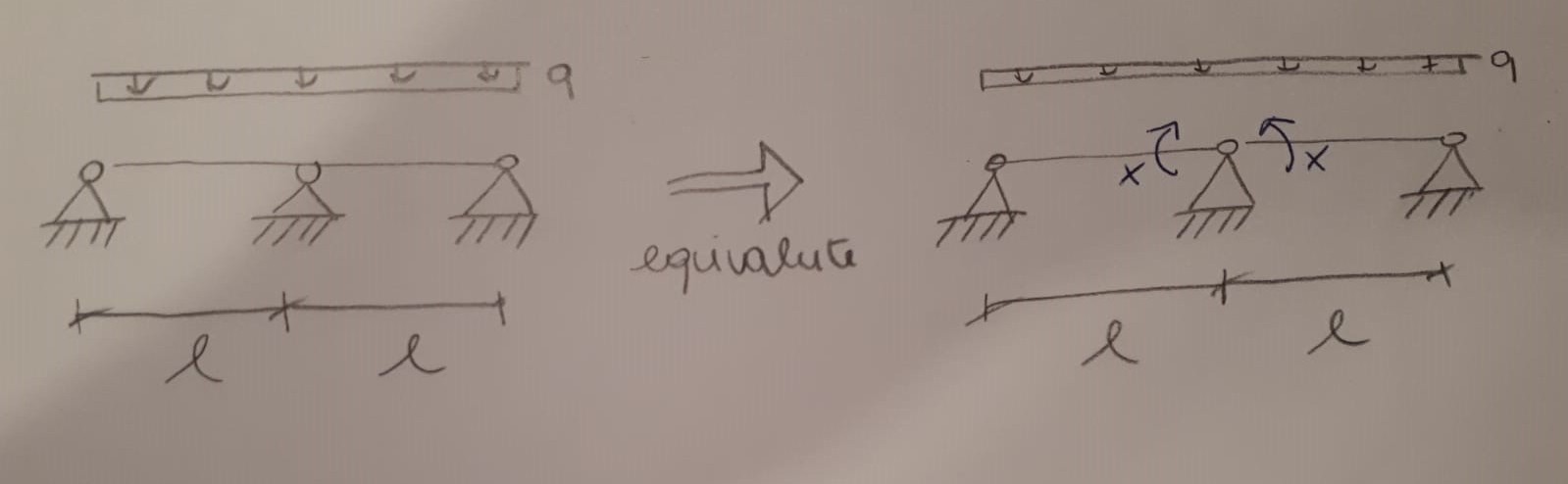
3 - Applicando il taglio di Cauchy ci si rende conto di come i due vincoli in mezzeria si comportino in modo differente: il secondo schema infatti si tratta di una struttura discontinua con una cerniera interna la quale non fa passare il momento. 

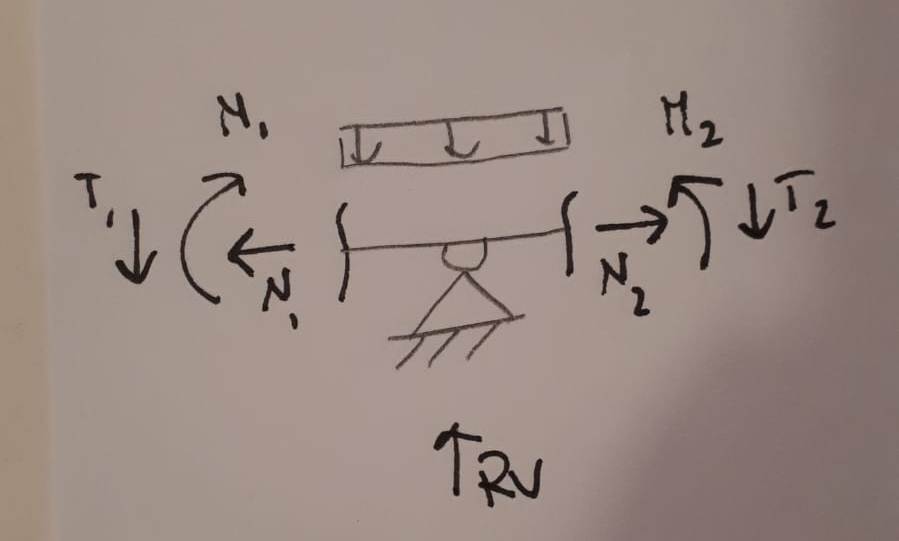
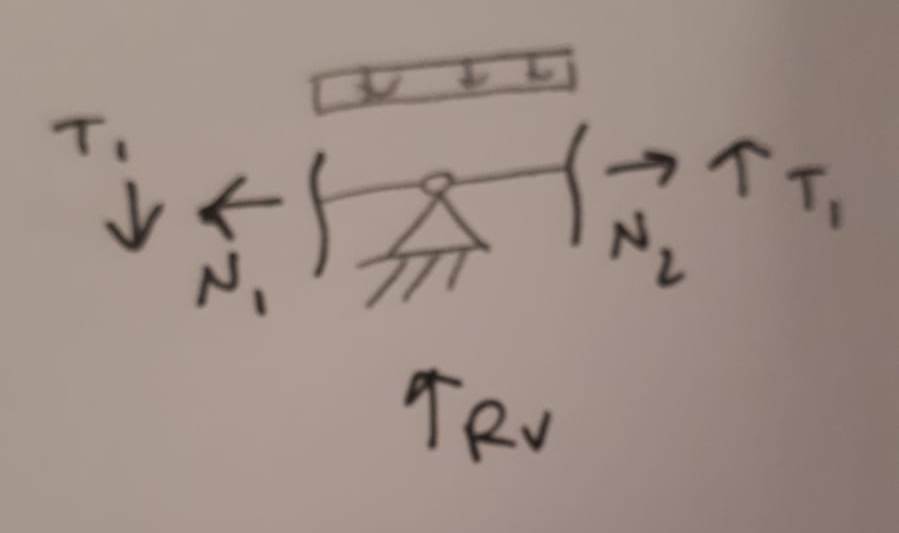
3 - In base a quante volte la struttura è iperstatica "cambio" uno o più vincoli, in questo caso la struttura è una volta iperstatica e cambio il vincolo in mezzeria con una cerniera interna.

4 - La struttura può essere equivalente solo se introduco anche la cinematica relativa al vincolo in mezzeria, per questo motivo è stata applicata al vincolo interno una coppia di forze X (incognita iperstatica).

5 - Per studiare la struttura equivalente la frammento in due parti (2 travi appoggiate) ed essendo soggette a due carichi differenti se studio separatamente: 

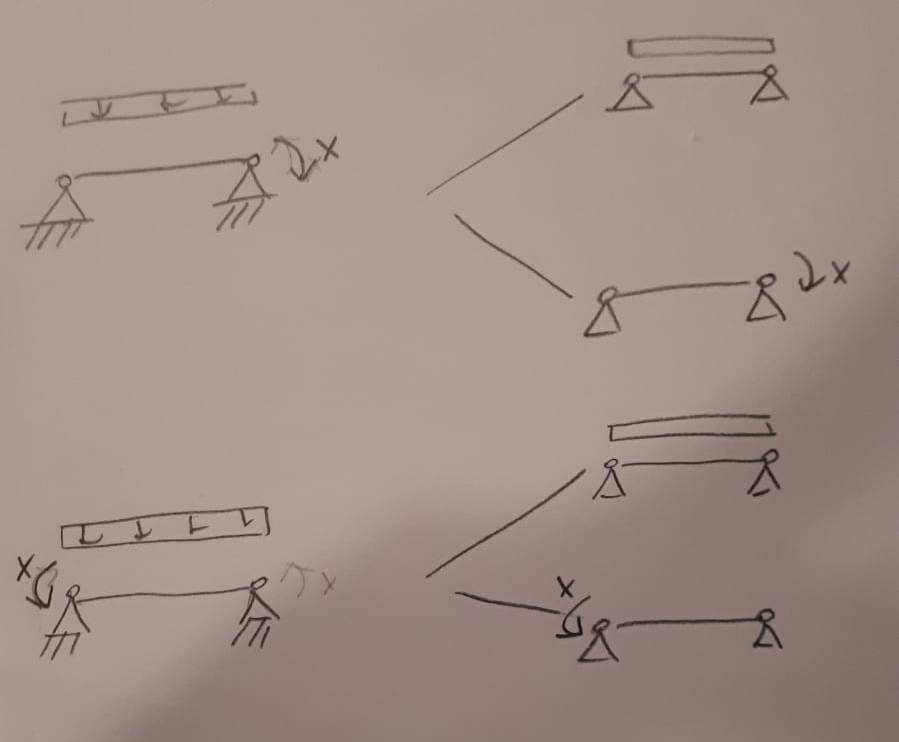
6 - Essendo la prima struttura iperstatica devo considerare lo schema equivalente come un'unica struttura ed imporre la continuità:

7 - Traslazioni orizzontali: Ubs=Ubd quindi Ubs - Ubd = 0 

8 - Traslazioni verticali: Vbs=Vbd quindi Vbs - Vbd = 0

9 - Mi rendo conto che ciò che cambia sono le rotazioni. Impongo Rbs=Rbd, essendo la struttura iperstatica continua, ed ottengo Rbs - Rbd = 0

10 - Conoscendo i valori delle rotazioni e impondendo l'equazione Rbs - Rbd = 0 posso ricavarmi l'incognita iperstatica X affinchè la struttura semplice isostatica sia equivalente alla struttura iperstatica.