11 Click

Per risolvere strutture iperstatiche semplici si può ricorrere al metodo delle forze. 

La struttura iperstatica può essere semplificata e risolta trasformandola in una struttura isostatica equivalente. 

Per prima cosa ricavo i gradi di iperstaticità dalla struttura di partenza, questo numero corrisponderà al numero di incognite iperstatiche e di conseguenza al numero di equazioni cinematiche di cui ho bisogno per trasformare la struttura in isostatica e risolverla. Il metodo delle forze, infatti, consiste proprio nel porre come incognite del problema alcune reazioni vincolari.

Le incognite iperstatiche possono essere forze concentrate oppure coppie di forze, e possono essere forze esterne o forze interne/azioni di contatto, che si generano nel momento in cui declasso uno o più vincoli. Affinché la struttura isostatica sia equivalente, dovrò porre ogni tipo di spostamento (verticale, orizzontale o rotazione) uguale a zero.

Nella Fig. 1.1 possiamo vedere un esempio di struttura una volta iperstatica, le due immagini successive Fig. 1.2 e 1.3 raffigurano due diverse rappresentazioni isostatiche equivalenti della stessa struttura iperstatica, in cui x è sempre l’incognita iperstatica.

In entrambi i casi si generano forze esterne, ma nel primo caso è una forza concentrata, mentre nel secondo caso una coppia di forze. Questo dipende da quale vincolo decido di declassare.

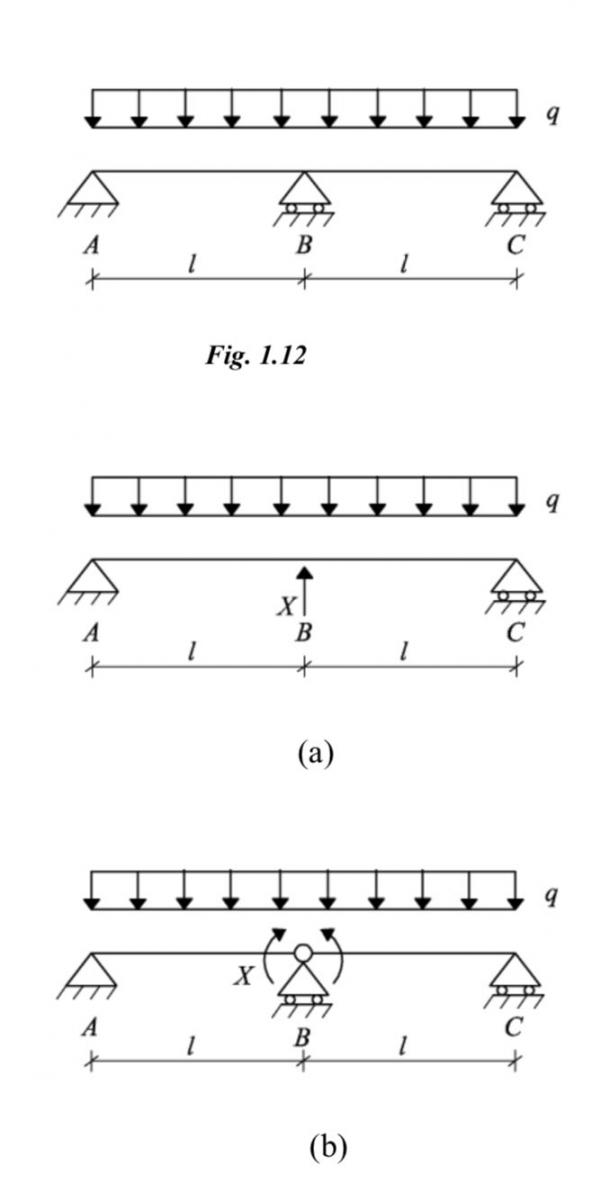
Un altro esempio è la trave continua su tre appoggi (Fig. 1.12), anch’essa una volta iperstatica, seguita da due diverse rappresentazioni isostatiche (a, b). In entrambi i casi l’incognita iperstatica x è una forza interna o azione di contatto, nel caso (a) una forza concentrata, nel caso (b) due coppie di forze uguali ed opposte.

In questo esempio vediamo bene come il declassare il carrello abbia portato ad avere una trave non più continua come quella di partenza, perciò è permessa la rotazione relativa ed il momento non è più trasmesso in tutta la trave, ma vi sono due diverse situazioni a destra e sinistra di B, che posso studiare eseguendo un taglio di Cauchy.

Una volta trovata l’incognita iperstatica grazie all’equazione cinematica imposta possiamo proseguire con il disegno dei diagrammi.

Queste strutture possono essere studiate come due strutture diverse secondo il principio di sovrapposizione degli eventi. Si può, cioè, studiare per parti la stessa struttura, in una considerando la struttura con carico distribuito agente e nell’altra considerando la stessa struttura solo con la forza generalizzata agente. 

Risolte queste strutture semplificate, posso sommare le reazioni vincolari e/o i diagrammi e trovare la soluzione per la struttura iniziale.