TRAVI RETICOLARI- STRUTTURA SIMMETRICA
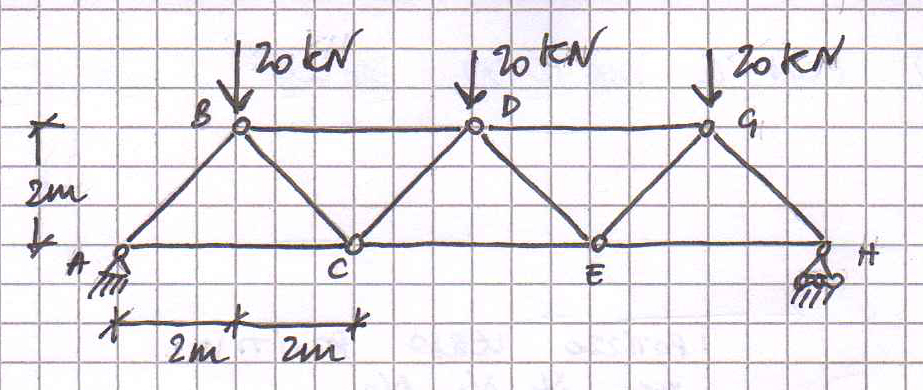
a. Verifica dell’isostaticità della struttura
La struttura è isostatica se il numero dei vincoli è pari al numero dei gradi di libertà della struttura: V=l.
Il numero dei gradi di libertà si calcola moltiplicando il numero degli elementi (11aste) per 3 che è il numero di gradi di libertà di ciascun elemento: l=11*3=33.
La struttura presenta 3 vincoli esterni : Ve=3 poiché si sommano i due gradi di libertà bloccati dalla cerniera ad 1 grado di libertà bloccato dal carrello.
Il numero dei vincoli interni si calcola: Vi=2*(n-1) dove n rappresenta il numero di aste che convergono nella cerniera interna.
Vi A= Vi H= 2*(2-1)=2
Vi B= Vi G= 2* (3-1)=4
Vi C= Vi D=Vi E= 2*(4-1)=6
Vi= 2*2 + 4*2 + 6*3= 30
V= Ve+Vi= 3+30=33=l quindi la struttura è isostatica.
b. Calcolo delle reazioni vincolari
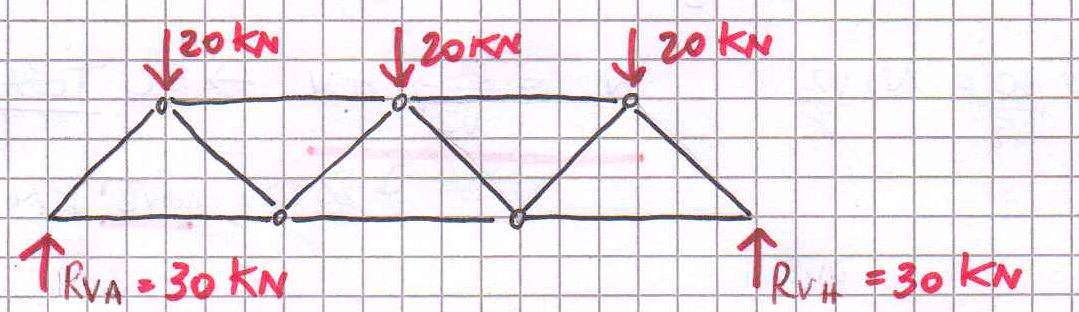
∑Fy= 3F-yA-yH=0
Poiché la struttura è simmetrica yA=yH e quindi (3/2)F=yA=yH= 30KN
c. Calcolo delle azioni di contatto
c.1 Metodo delle sezioni di Ritter
Seziono la struttura in modo tale da tagliare almeno 3 aste che non concorrano nello stesso nodo e ipotizzo gli sforzi normali uscenti dalle sezioni delle aste (sto ipotizzando quindi che tutte le aste siano tese cioè che si tratti di tiranti); in questo modo se mi verranno risultati negativi potrò dedurre facilmente che la mia ipotesi non era corretta e che lo sforzo normale ha verso opposto e cioè verso entrante rispetto alla sezione dell’asta che sarà quindi compressa (puntone).
Sezione 1
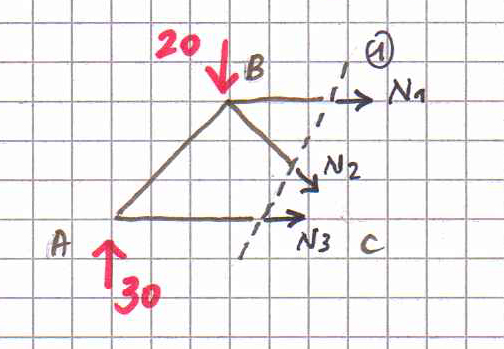
Imposto l’equazione dell’equilibrio a rotazione del nodo in cui concorrono più aste (C); in questo modo N2 e N3 , che hanno la retta d’azione passante per C, hanno braccio nullo perciò avrò un’unica incognita con un valore facilmente calcolabile.
∑Mc= -(3/2)F*2l + F*l - N1*l=0
N1=-2F=-40KN
Il risultato negativo ci mostra che l’asta BD, che avevo ipotizzato essere tesa, è in realtà compressa. BD è un puntone.
∑Mb= -(3/2)F*l + N3*l =0
N3= (3/2)F= 30KN AC è un’ asta tesa.
N2 è disposta lungo la diagonale di un quadrato, perciò la sua componente orizzontale è uguale alla sua componente verticale: N2x=N2y=N2*(√2/2).
∑Fy=(3/2)F – F – N2(√2/2)=0
N2=(√2/2)F=10√2 KN BC è un’asta tesa.
Sezione 2.
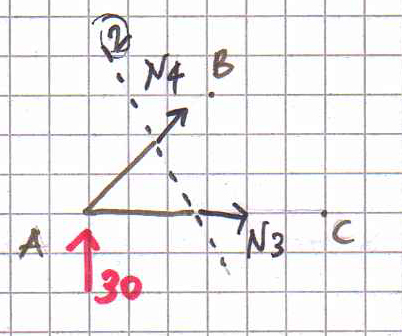
Anche N4 è disposta lungo la diagonale di un quadrato, perciò la sua componente orizzontale è uguale alla sua componente verticale: N4x=N4y=N4*(√2/2).
∑Fx= N3 + N4(√2/2) = 0 N3 è noto ed è pari a (3/2)F quindi
N4= -3*(√2/2)F= -30√2 KN AB è un’asta compressa.
Sezione 3.
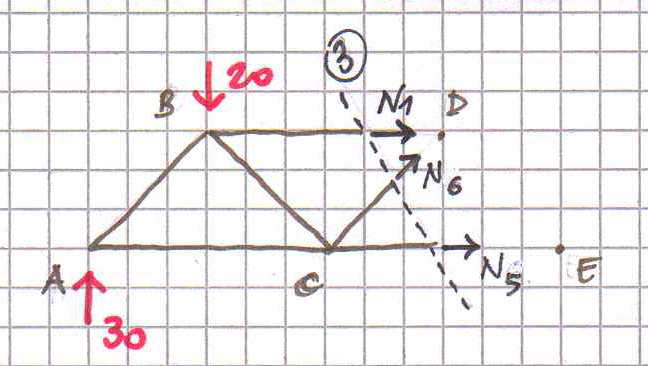
∑Md= N5*l + 2F*l – (3/2)F*3l= 0
N5=(5/2)F = 50 KN CE è un’asta tesa.
N6 è disposta lungo la diagonale di un quadrato, perciò la sua componente orizzontale è uguale alla sua componente verticale: N6x=N6y=N6*(√2/2).
∑Fy = (3/2)F – F + N6*(√2/2) =0
N6= - (√2/2)F = -10*√2 KN CD è un’asta compressa.
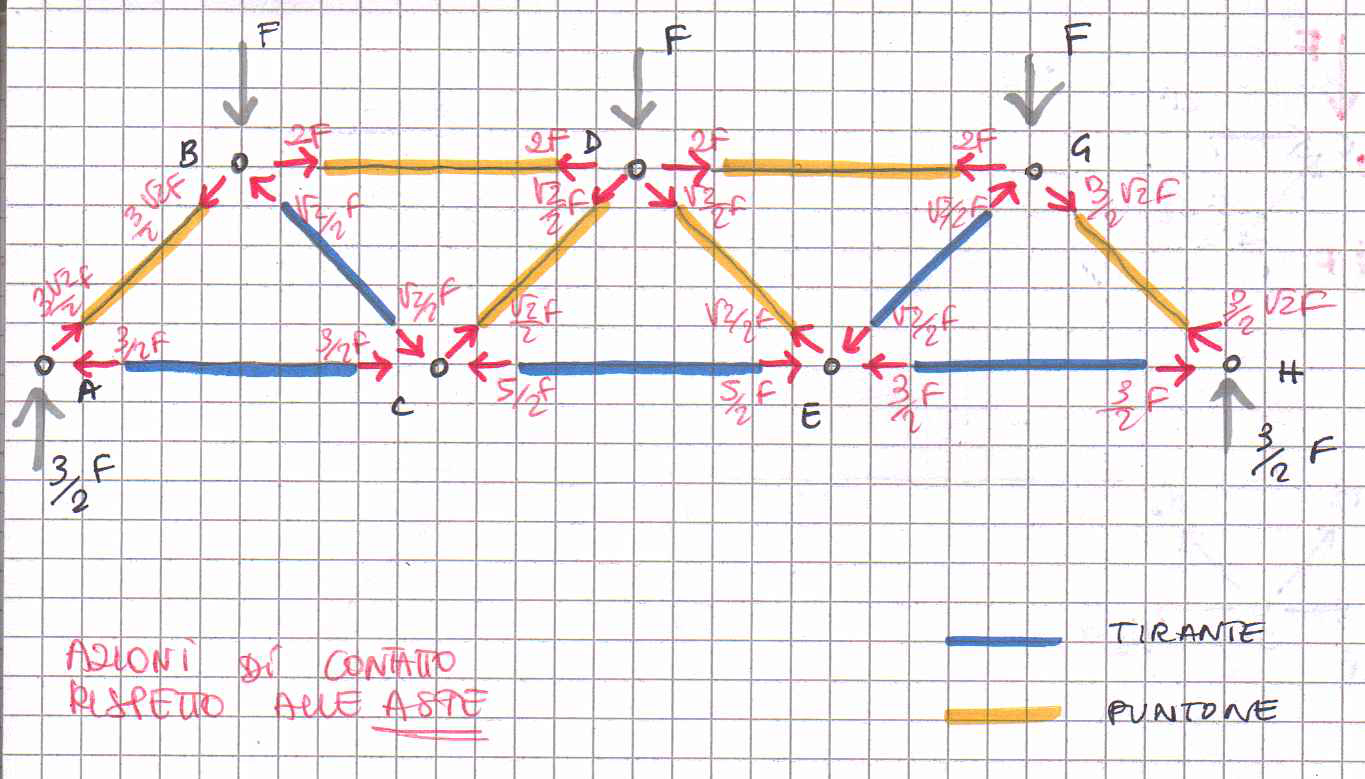
Poiché la struttura è simmetrica rispetto all’asse segnato nella figura, possiamo dedurre che anche le azioni di contatto sono simmetriche rispetto all’asse.
c.2 Metodo dei nodi.
Nel modello delle travature reticolari le forze sono considerate agenti solo sui nodi perciò ciascun nodo per essere in equilibrio deve avere la risultante delle forze orizzontali e la risultante delle forze verticali nulle.
Nodo A.
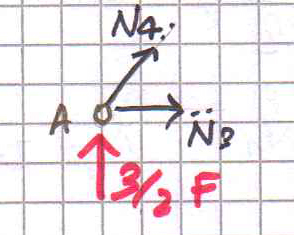
Nel nodo A agiscono la reazione vincolare della cerniera, N3 ed N4 (scompongo N4 lungo le sue componenti orizzontale e verticale come nel punto precedente dell’esercizio).
∑Fx = N3 + N4*(√2/2) =0
∑Fy = (3/2)F + N4*(√2/2) = 0 N4= -3*(√2/2)F = -30√2 KN N3= (3/2)F= 30KN
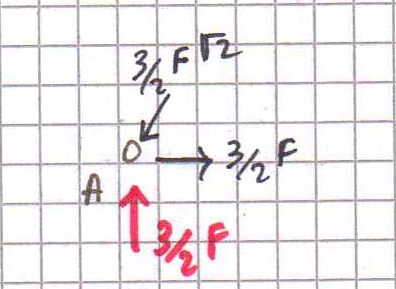
Uno sforzo normale di compressione sul nodo equivale ad uno sforzo di compressione sull’asta (ciò vale anche per lo sforzo normale di trazione).
Quindi AC è un’ asta tesa mentre AB è un’asta compressa.
Si può ottenere lo stesso risultato con il metodo geometrico e cioè scomponendo la reazione vincolare lungo la direzione delle due aste con la regola del parallelogramma e sapendo l’angolo di inclinazione delle aste (45°).
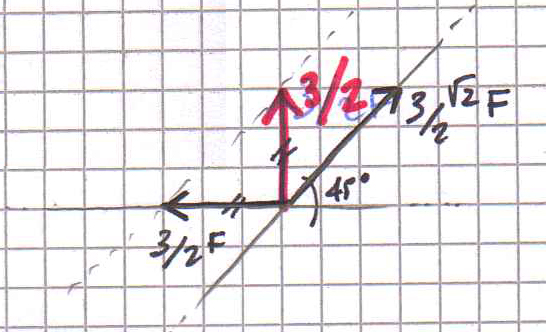
Nodo B.
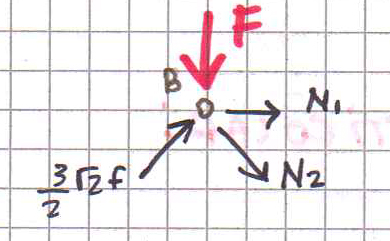
Nel nodo B agiscono F, N3(che ora è nota), N1 e N2 (scompongo N2 lungo le sue componenti orizzontale e verticale come nel punto precedente dell’esercizio).
∑Fy = (3/2)F – F – (√2/2)N2 = 0
N2= (√2/2)F = 10√2 KN
∑Fx = (3/2)F + N1 + (√2/2)N2 = 0 (3/2)F + N1 + (√2/2)*(√2/2)F = 0
N1= -2F = -40 KN

BD è un’asta compressa mentre BC è un’asta tesa.
Nodo C.

Nel nodo C agiscono N3 ed N2(ormai note) e N5 ed N6 da calcolare (dopo aver scomposto come al solito N6 ed N2 lungo le loro componenti orizzontale e verticale).
∑Fy = N6*(√2/2) + F/2 = 0
N6 = -F*(√2/2) = -10√2 KN
∑Fx = N5 – (3/2)F – N6*(√2/2) – F/2 = 0
N5 = 5/2= 50 KN
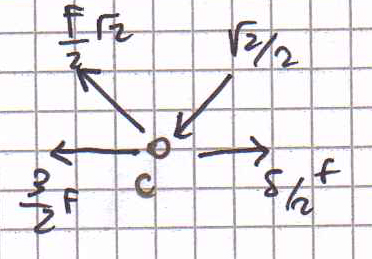
CE è un’asta tesa mentre CD è compressa.
Come possiamo vedere, il risultato ottenuto con il metodo dei nodi è uguale a quello ottenuto con il metodo delle sezioni di Ritter.
Ecco uno schema riassuntivo dell'azione dello sforzo normale sull’intera struttura.
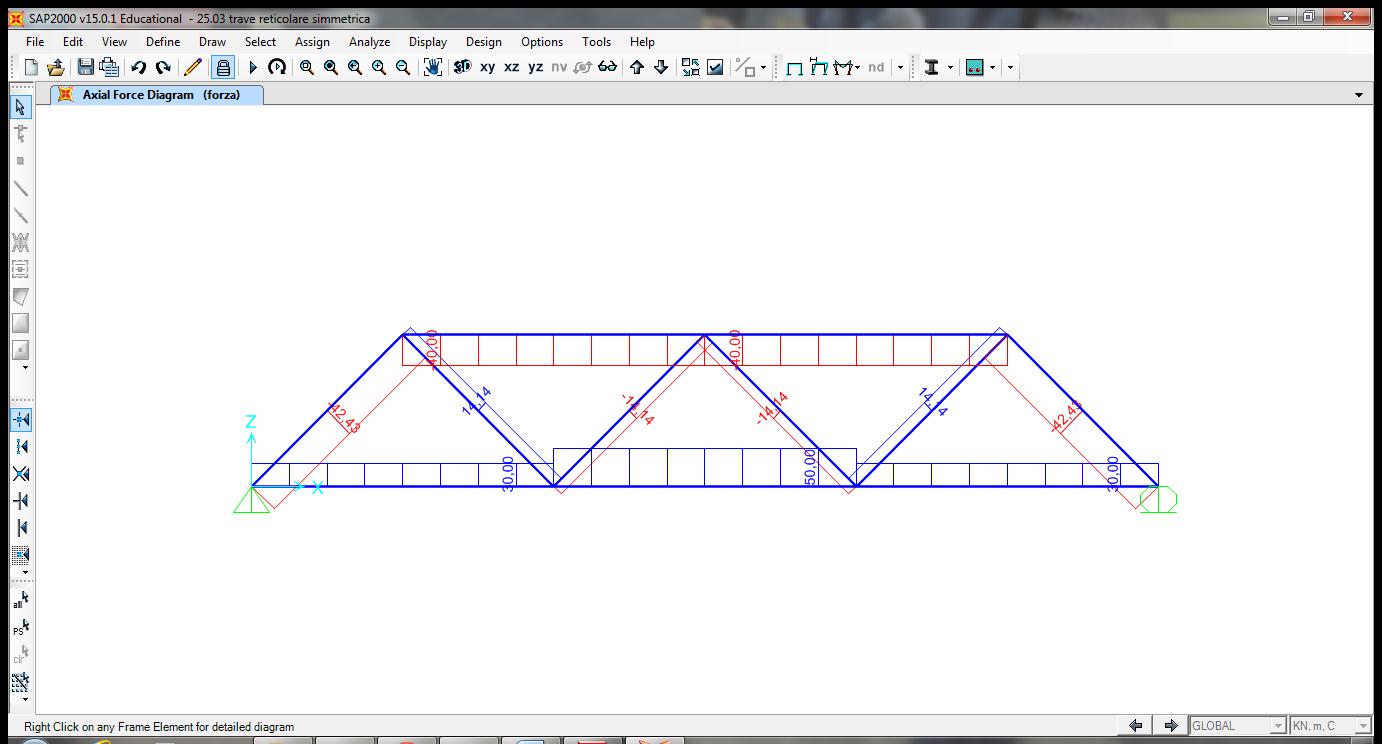
d. Verifica su SAP 2000.
Dopo aver disegnato la struttura partendo da una griglia e aver assegnato i vincoli esterni, bisogna assegnare le cerniere interne. Per fare ciò bisogna selezionare tutte le aste e dire a SAP che il momento nella sezione iniziale e finale di ciascuna asta è nullo.
Successivamente ho definito il carico concentrato e l’ho assegnato ai nodi B,D e G.
Il diagramma dello sforzo normale mi conferma che i miei calcoli sono corretti.
TRAVI RETICOLARI- STRUTTURA ASIMMETRICA
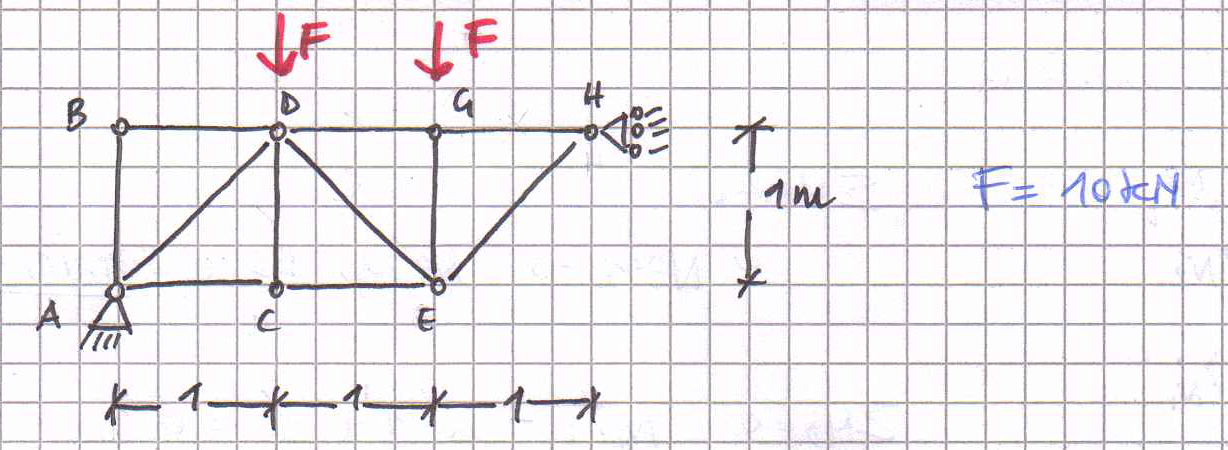
a. Verifica dell’isostaticità della struttura
l=11*3=33.
Ve=3 poiché si sommano i due gradi di libertà bloccati dalla cerniera ad 1 grado di libertà bloccato dal carrello.
Vi=2*(n-1)
Vi A= Vi D= Vi E = 2*(3-1)=4
Vi B= Vi H= 2* (2-1)=2
Vi C= 2*(5-1)=8
Vi G= 2*(4-1)=6
Vi= 4*3 + 2*2 + 8 + 6= 30
V= Ve+Vi= 3+30=33=l quindi la struttura è isostatica.
b. Calcolo delle reazioni vincolari
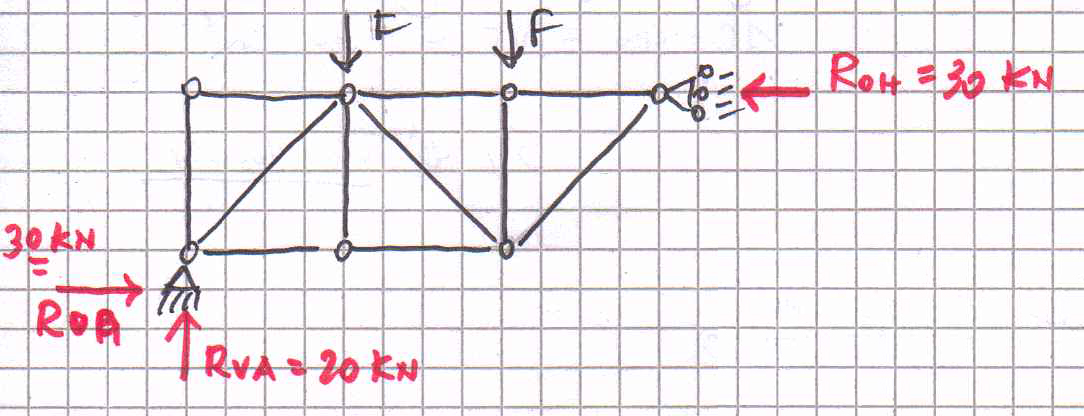
∑Fy= 2F-yA=0 yA=2F=20 KN
∑Fx = xA – x H= 0 xA=xH
∑Ma = F*l + F*2l – xH*l = 0 l=1m
F + 2F – xH = 0 xH = xA = 3F = 30 KN
c. Calcolo azioni di contatto
Applico il metodo che mi sembra più opportuno per rendermi più facili e veloci i calcoli.
Sezione 1.
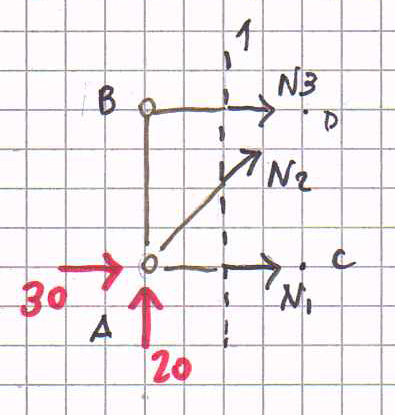
∑Ma = N3*l = 0
N3 = 0 BD è scarica.
∑Md= N1*l – yA*l + xA = 0 N1 – 20 + 30 = 0
N1= -10 KN AC è un’asta compressa.
∑Fy = F + N2*(√2/2) = 0
N2 = -20√2 KN AD è un’asta compressa.
Sezione 2.
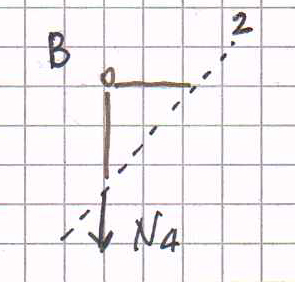
∑Fy = N4 = 0 AB è scarica.
Sezione 3.
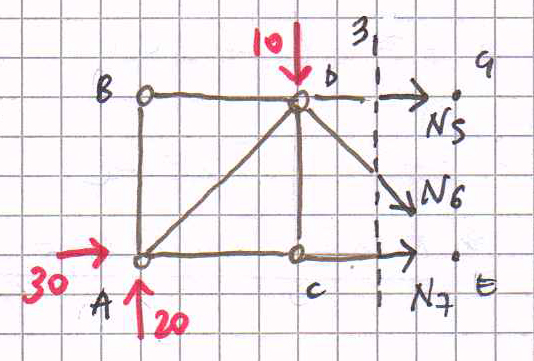
∑Me = -N5*l + F*l – yA*2l = 0
N5= -30 KN DG è un’asta compressa.
∑Md = N7*l – yA*l + xA*l = 0
N7= -10 KN CE è un’asta compressa.
∑Fy = N6*(√2/2) + F – yA = 0
N6= 10√2 KN DE è un’asta tesa.
Equilibrio al nodo D.
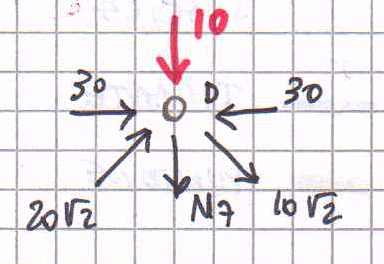
Sul nodo D agiscono F, N3 ed N5 (uguali e contrarie), N2 ed N6 (già note ma da scomporre lungo le loro componenti) e N7 da calcolare.
∑Fy = N7 + F + N6y – N2y = 0 N7 + 10 + 10 – 20 = 0
N7= 0 CD è scarica.
Sezione 4.
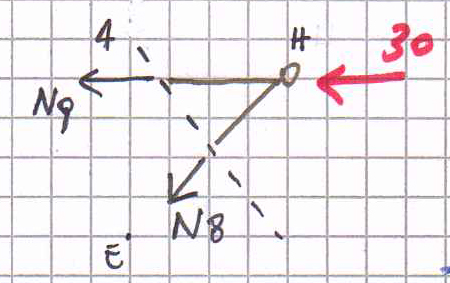
∑Me = xH*l + N9*l = 0
N9= -30 KN GH è un’asta compressa.
∑Fy = N8*(√2/2) = 0
N8= 0 EH è scarica.
Equilibrio al nodo G.
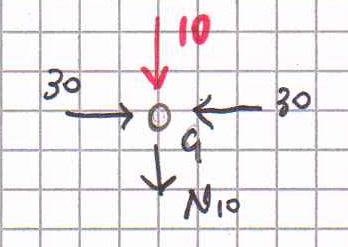
Sul nodo G agiscono F, N5 ed N9 (uguali e contrarie) ed N10 da calcolare.
∑Fy = N10 + F = 0
N10 = -10 GE è un’asta compressa.
Schema riassuntivo della situazione complessiva.
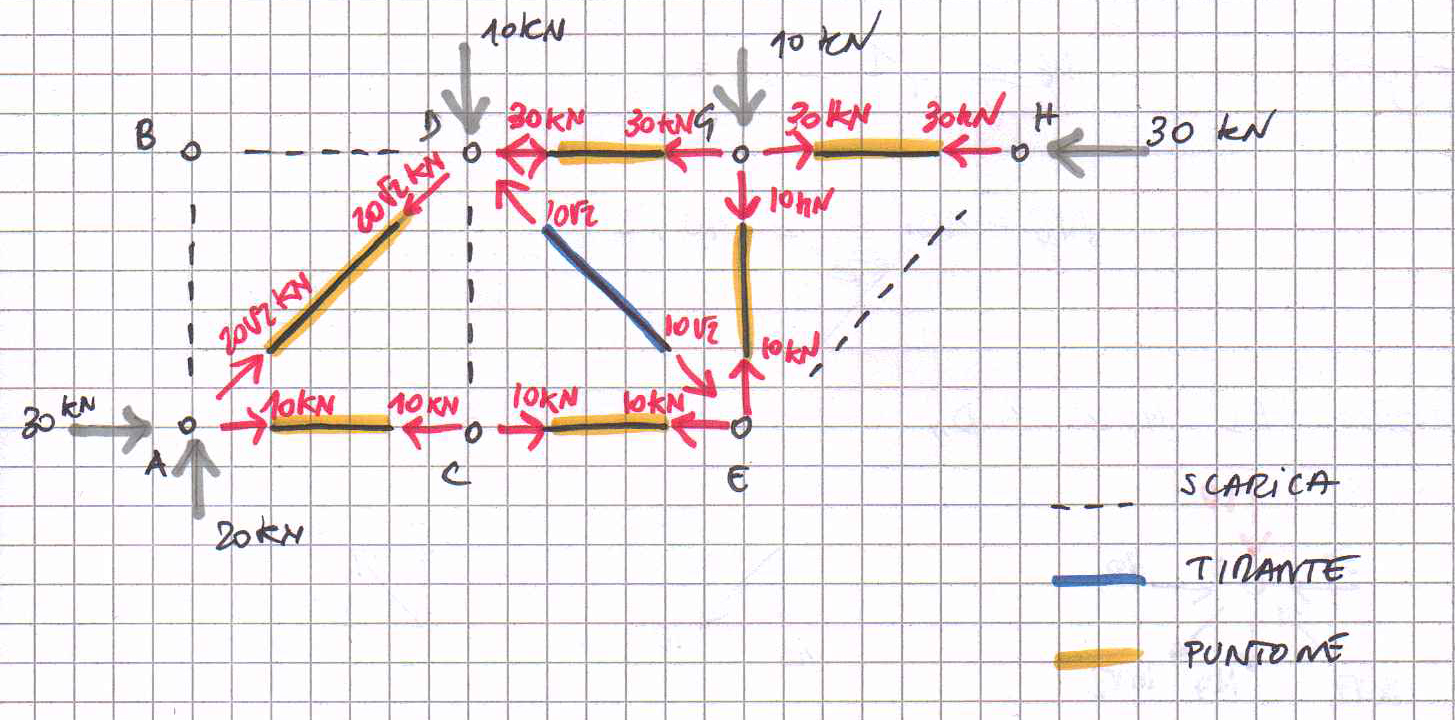
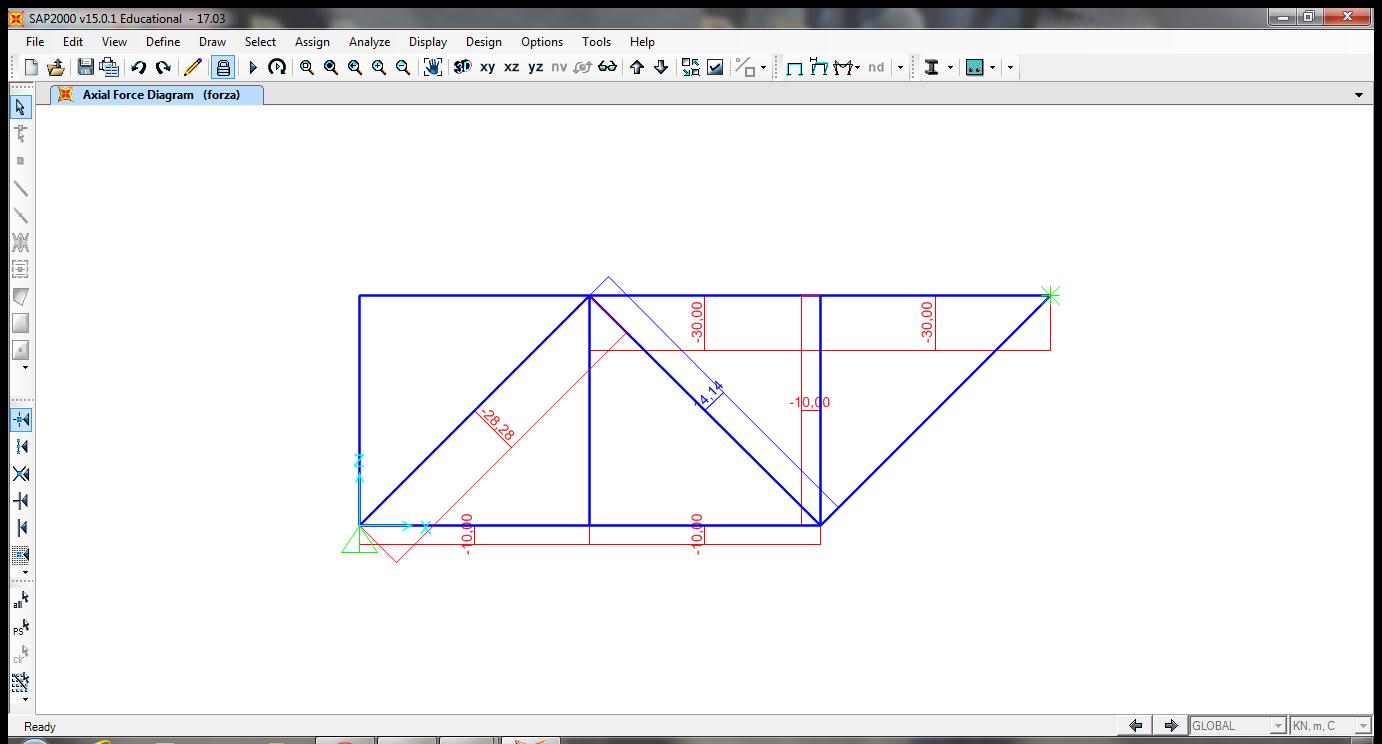
d. Verifica su SAP 2000.
Dopo aver disegnato la struttura partendo da una griglia e aver assegnato i vincoli esterni ( facendo attenzione a bloccare la traslazione lungo l’asse x per il carrello che da default bloccherebbe la traslazione lungo z), bisogna assegnare le cerniere interne. Per fare ciò bisogna selezionare tutte le aste e dire a SAP che il momento nella sezione iniziale e finale di ciascuna asta è nullo.
Successivamente ho definito il carico concentrato e l’ho assegnato ai nodi D e G.
Il diagramma dello sforzo normale mi conferma che i miei calcoli sono corretti.
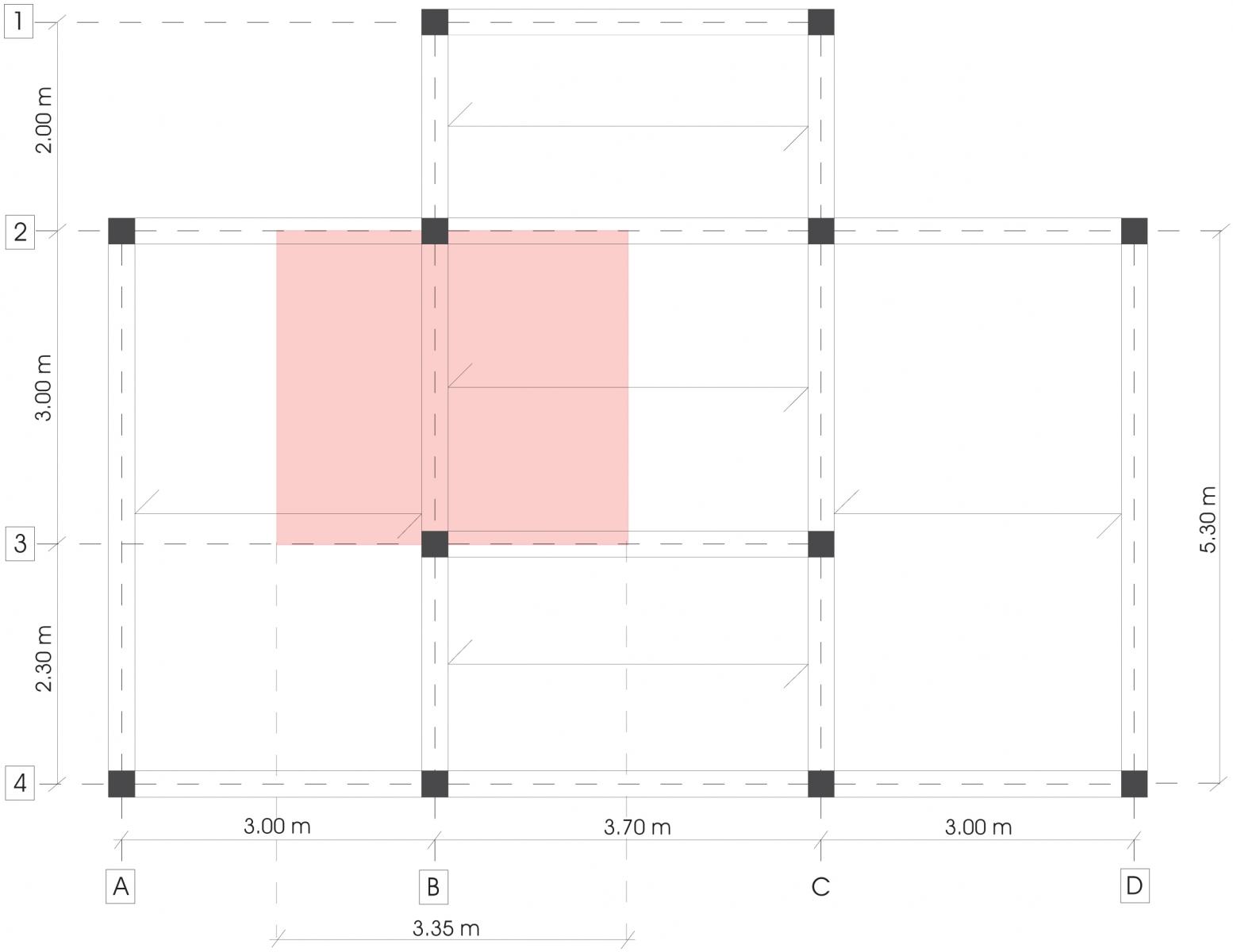
DIMENSIONAMENTO TRAVE
Ho scelto di dimensionare la struttura di un edificio residenziale unifamiliare su due livelli progettato durante il laboratorio di costruzione dell’architettura al primo anno della triennale.
Dopo aver disegnato l’impalcato e quotato luci ed interassi ho scelto di dimensionare la trave B 2-3 perché è quella che porta un’area di solaio maggiore. La sua area di influenza è A= luce * interasse= 3*3,35=10,05 mq.
1 ANALISI DEI CARICHI
Il carico del solaio comprende il carico strutturale qs (che equivale al peso proprio della struttura), il sovraccarico permanente qp (che equivale al peso proprio degli elementi e strati non strutturali che compongono il solaio e considera anche l’incidenza dei tramezzi e degli impianti) e il sovraccarico accidentale qa (che tiene conto del peso di mobili e persone e quindi dipende dalla funzione ed è tabellato nelle norme tecniche).
Il carico Q=qs+qp+qa considera un carico “spalmato” su un area (KN/mq) mentre noi sappiamo risolvere e calcolare strutture dove il carico è su metro lineare quindi dobbiamo moltiplicare il carico totale Q per l'interasse.
2 DIMENSIONAMENTO TRAMITE IL FOGLIO EXCEL
Una volta progettato il solaio, decisi materiali e spessori e calcolati i conseguenti carichi permanenti e strutturali (il sovraccarico accidentale, come abbiamo detto, è dato dalla normativa), possiamo calcolare il momento massimo come il momento in mezzeria di una trave doppiamente appoggiata M=(Q*l^2)/8 dove l è la luce che abbiamo come dato di progetto.
Inserendo nel foglio gli opportuni coefficienti di sicurezza specifici di ciascun materiale, otteniamo il valore della tensione di progetto fd e le indicazioni per dimensionare e successivamente verificare l’elemento strutturale fd=fy/coeff sicurezza dove fy è il valore di crisi di ciascun materiale.
LEGNO
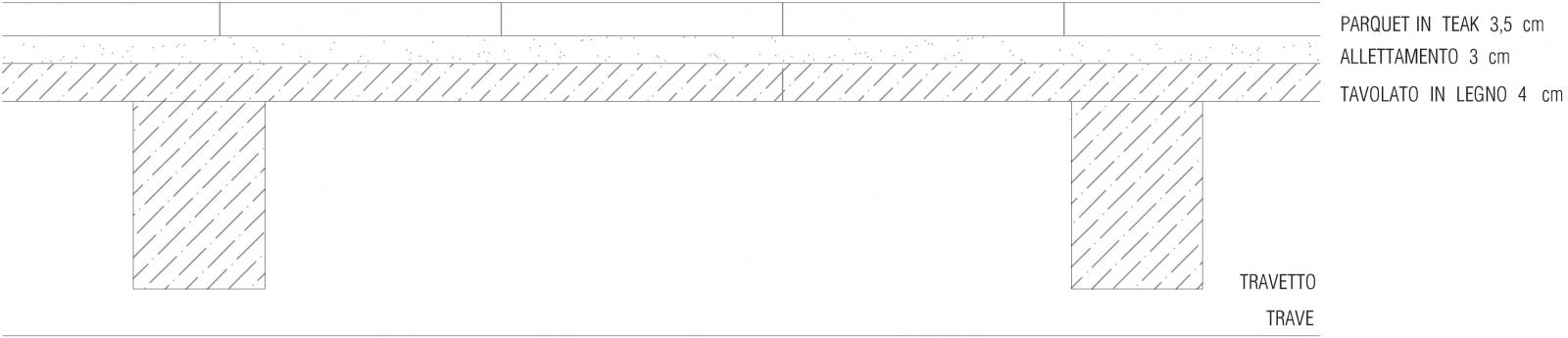
Inizieremo con il dimensionamento di un travetto poiché per calcolare il carico strutturale del solaio portato dalla trave abbiamo bisogno di conoscere il peso del travetto che occorre quindi dimensionare.
TRAVETTO
2.a Analisi dei carichi agenti su 1mq di solaio:
Carico strutturale
Tavolato Peso= volume* peso specifico= (0,04*1*1)mc * 5,25 KN/mc = 0,21 KN
qs=P/A=0,21KN/1mq= 0,21 KN/mq
Oppure qs= peso specifico*spessore= 5,25KN/mc * 0,04 m= 0,21 KN/mq
Sovraccarico permanente
Allettamento in cls qp= 18KN/mc * 0,03m= 0,54 KN/mq
Pavimento in teak spessore di 3,5 cm qp 6,3KN/mc*0,035 m= 0,22KN/mq
Incidenza impianti qp= 0,5 KN/mq
Incidenza tramezzi qp = 1 KN/mq
qp= 0,54+0,22+0,5+1= 2,26 KN/m
Sovraccarico accidentale
qa = 2 KN/mq per civile abitazione
2.b Carico totale a metro lineare Q= (qs+qp+qa)*interasse=(0,21+2,26+2)*1= 4,47KN/m
2.c Calcolo del momento massimo
M= (Q*l^2)/8 = 7,65 KN*m
Dove l è la luce del travetto = 3,7m
2.d Scelgo la classe di resistenza del legno lamellare
Scelgo una classe di resistenza intermedia GL 28h che corrisponde a una resistenza a flessione Fk= 28 N/mmq.
2.e Tensione di progetto
Dividendo fk per il coefficiente di sicurezza del legno lamellare(1,45) e moltiplicandolo per un ulteriore coefficiente di sicurezza che tiene conto della durata del carico Kmod (0,5) ottengo il valore della tensione di progetto fd.
Fd= 28*0,5/1,45 = 9,66 N/mmq
Come possiamo vedere il valore della tensione di progetto, che di solito è dato dal valore di crisi diviso per un coefficiente di sicurezza, è ulteriormente dimezzato rispetto al valore di resistenza a flessione poiché, per un materiale viscoso come il legno, bisogna tener conto anche degli effetti del tempo e dell’umidità che incidono profondamente sulle prestazioni del materiale.
Ora, inserendo un valore di base (b=14cm), otteniamo il valore dell’altezza minima che dovrà avere il travetto h= ((6*M*1000)/(b*fd))^5= 18,43 cm.
Ipotizzo quindi un travetto con un’altezza maggiore h=20cm e b=14cm e procedo con la verifica.
2.f Verifica
Qtr a metro lineare= area sez*peso specifico = 0,14m*0,2m*4,5KN/mc =0,126 KN/m
Qtr a mq= qtr/interasse=0,0126/1=0,0126 KN/mq
Aggiungo quindi al calcolo del carico strutturale anche il peso del travetto e ottengo che per la base scelta di 14cm avrei bisogno di un travetto alto minimo 18,68cm che è un valore minore rispetto ai 20 cm del travetto ipotizzato, il dimensionamento del travetto è quindi corretto. ->TRAVETTO IN LEGNO 14X20cm

TRAVE interasse 3.35m e luce 3m
2.a Analisi carichi
Carico strutturale
Carico Tavolato+ carico travetto qs= 0,21 KN/mq + 0,126 KN/mq = 0,336 KN/mq
Sovraccarico permanente
Allettamento + pavimento + impianti + tramezzi qp= 0,54+0,22+0,5+1=2,26 KN/mq
Sovraccarico accidentale
qa = 2 KN/mq per civile abitazione
2.b Carico totale a metro lineare
Q= (qs+qp+qa)*interasse=( 0,336 + 2,26 + 2) * 3,35 = 15,40 KN/m
2.c Calcolo del momento massimo
M= (Q*l^2)/8 = 17,32 KN*m
Dove l è la luce della trave è l = 3m
2.d Scelgo la classe di resistenza del legno lamellare
Scelgo una classe di resistenza intermedia GL 28h che corrisponde a una resistenza a flessione Fk= 28 N/mmq.
2.e Tensione di progetto
Fd= 28*0,5/1,45 = 9,66 N/mmq
Ora, inserendo un valore di base (b=20cm), otteniamo il valore dell’altezza minima che dovrà avere la trave h= ((6*M*1000)/(b*fd))^5= 23,20 cm.
Ipotizzo quindi una trave con un’altezza maggiore h=25cm e b=20cm e procedo con la verifica.
2.f Verifica
Qtr a metro lineare= area sez*peso specifico = 0,25m*0,2m*4,5KN/mc =0,225 KN/m
Qtr a mq= qtr/interasse=0,225/3,35=0,067 KN/mq
Aggiungo quindi al calcolo del carico strutturale anche il peso della trave stessa e ottengo che per la base scelta di 20cm avrei bisogno di una trave alta minimo 23,37 che è un valore minore rispetto ai 25 cm della trave ipotizzata, il dimensionamento della trave è quindi corretto. ->TRAVE IN LEGNO 20X25cm

ACCIAIO
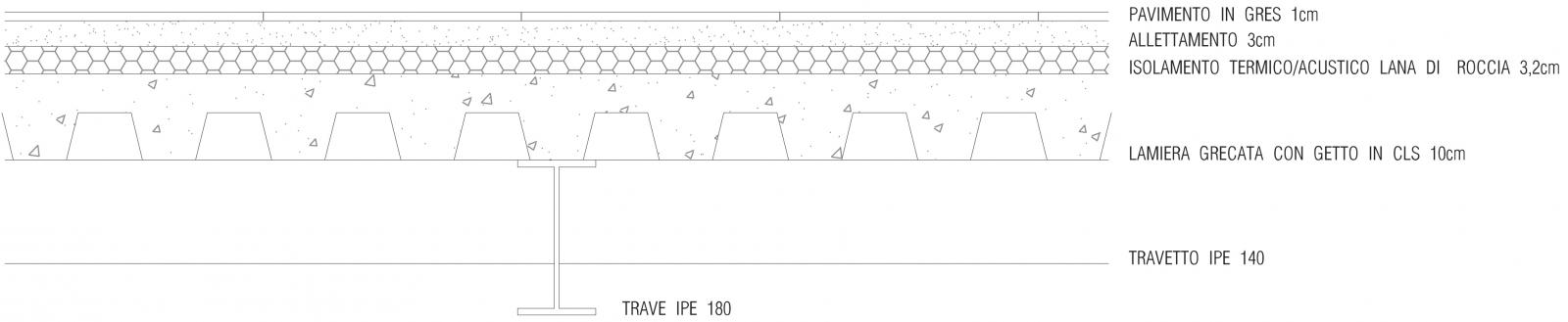
TRAVETTO
2.a Analisi dei carichi agenti su 1mq di solaio:
Carico strutturale
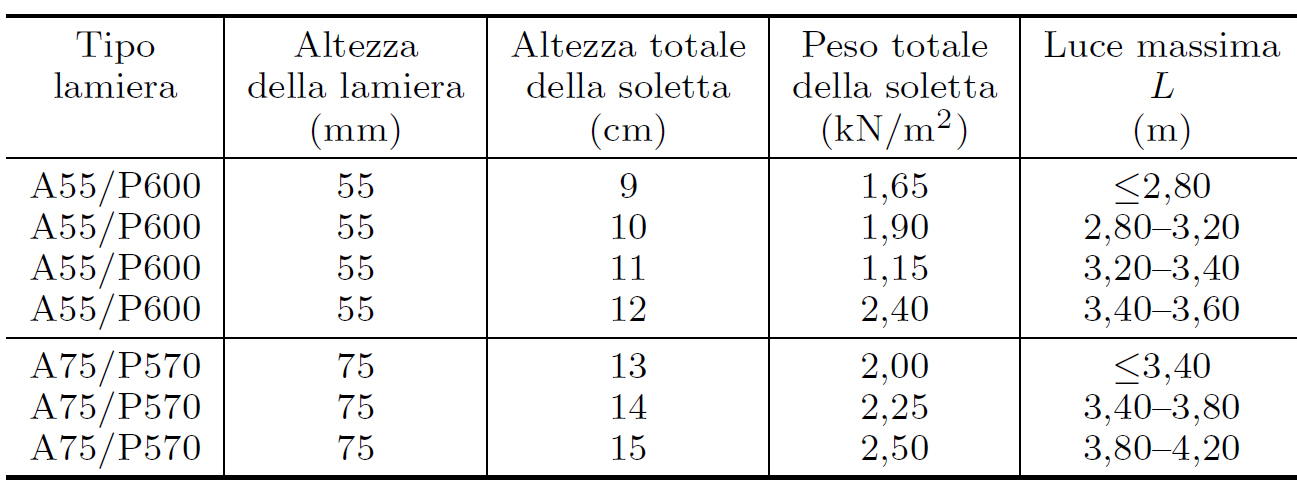
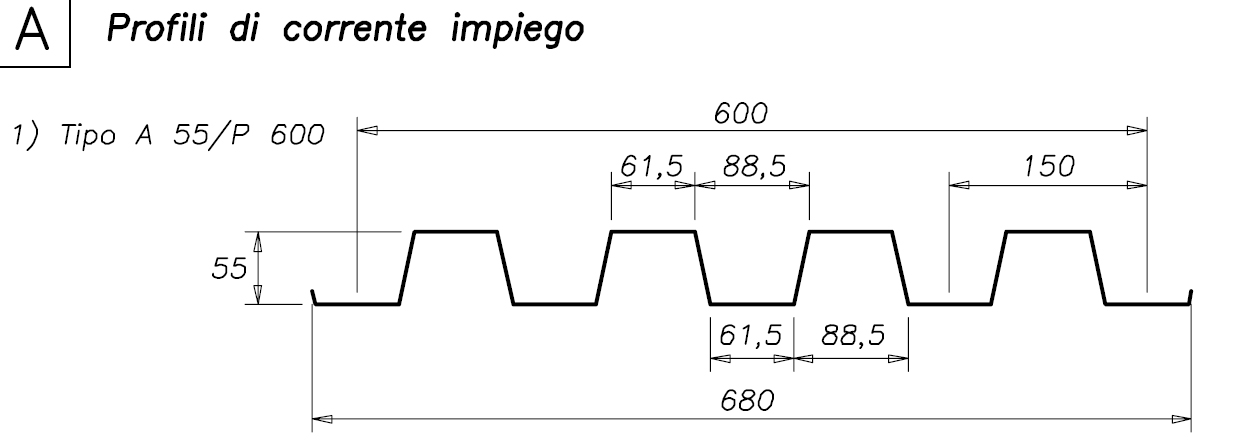
Lamiera grecata con getto di cls qs = 1,9 KN/mq (vedi tabella per luce max 3m)
Sovraccarico permanente
Isolamento acustico in lana di roccia per uno spessore di 3,2 cm
qp=27kg/mq=0,27KN/mq
Allettamento in cls qp= 18KN/mc * 0,03m= 0,54 KN/mq
Pavimento in gres spessore di 1 cm qp = 0,2KN/mq
Incidenza impianti qp = 0,5 KN/mq
Incidenza tramezzi qp = 1 KN/mq
qp=0,54+0,04+0,5+1=2,51KN/mq
Sovraccarico accidentale
qa = 2 KN/mq per civile abitazione
2.b Carico totale a metro lineare
Q= (qs+qp+qa)*interasse=( 1,9 + 2,51 + 2) * 1 = 6,41 KN/m
2.c Calcolo del momento massimo
M= (Q*l^2)/8 = 10,97 KN*m
Dove l è la luce del travetto = 3,7m
2.d Scelgo la classe di resistenza dell’acciaio
Scelgo una classe di resistenza bassa Fe 360 S 235 che corrisponde a una tensione di snervamento di Fy= 235 N/mmq.
2.e Tensione di progetto
Dividendo fy per il coefficiente di sicurezza dell’acciaio (1,15) ottengo il valore della tensione di progetto fd e dividendo il momento per fd ottengo il modulo di resistenza Wx.
Fd= 235/1,15 = 204,34 N/mmq
Wx = M/fd*1000= 53,68 cm^3
Ipotizzo quindi un travetto con un modulo di resistenza maggiore: IPE 140 e procedo alla verifica .
2.f Verifica
Qtr a metro lineare= 12,9 kg/m= 0,129 KN/m
Qtr a mq= qtr/interasse=0,129/1=0,129 KN/mq
Aggiungo quindi al calcolo del carico strutturale anche il peso del travetto e ottengo un modulo di resistenza Wx= 54, 55cm^3 che è un valore minore rispetto a Wx= 77,3 cm^3 dell’IPE 140, il dimensionamento del travetto è quindi corretto.
->TRAVETTO IN ACCIAIO IPE140

TRAVE interasse 3.35m e luce 3m
Carico strutturale
Lamiera grecata con getto di cls qs = 1,9 KN/mq
Travetto qs= 0,129 KN/mq
qs= 1,9+0,129= 2,029 KN/mq
Sovraccarico permanente
Isolamento acustico +allettamento+paviemento in gres+impianti+ tramezzi
qp=0,27+0,54+0,2+0,5+1=2,51KN/mq
Sovraccarico accidentale
qa = 2 KN/mq per civile abitazione
2.b Carico totale a metro lineare
Q= (qs+qp+qa)*interasse=( 2,029 + 2,51 + 2) * 3,35 = 21,90 KN/m
2.c Calcolo del momento massimo
M= (Q*l^2)/8 = 24,64 KN*m
Dove l è la luce della trave è l=3m.
2.d Scelgo la classe di resistenza dell’acciaio
Scelgo una classe di resistenza bassa Fe 360 S 235 che corrisponde a una tensione di snervamento di Fy= 235 N/mmq.
2.e Tensione di progetto
Fd= 235/1,15 = 204,34 N/mmq
Wx = M/fd*1000= 120,60 cm^3
Ipotizzo quindi un travetto con un modulo di resistenza maggiore IPE 180 e procedo alla verifica .
2.f Verifica
Qtr a metro lineare= 18,8 kg/m= 0,188 KN/m
Qtr a mq= qtr/interasse=0,188/3,35=0,056 KN/mq
Aggiungo quindi al calcolo del carico strutturale anche il peso del travetto e ottengo un modulo di resistenza Wx= 120,63cm^3 che è un valore minore rispetto a Wx= 146 cm^3 dell’IPE 180, il dimensionamento della trave è quindi corretto.
->TRAVE IN ACCIAIO IPE 180

CLS ARMATO
TRAVE interasse 3.35m e luce 3m

Carico strutturale
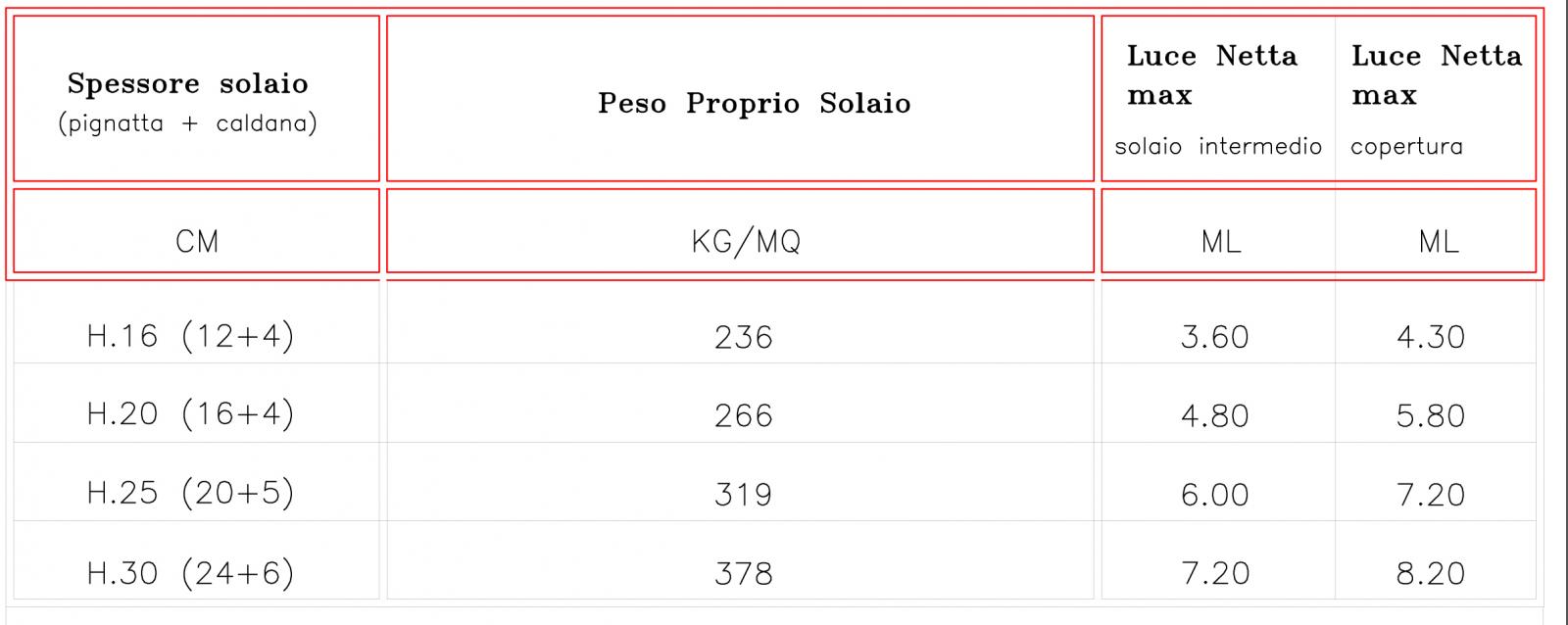
Pignatte (16 cm) + caldana (4cm)
(vedi tabella per luci tra 3.60 e 48.0 m) qs = 2,66 KN/mq
Sovraccarico permanente
Intonaco+ Isolamento acustico +allettamento+paviemento in gres+impianti+ tramezzi
qp=0,3+0,27+0,54+0,2+0,5+1=2,81KN/mq
Sovraccarico accidentale
qa = 2 KN/mq per civile abitazione
2.b Carico totale a metro lineare
Q= (qs+qp+qa)*interasse=( 2,66 + 2,81 + 2) * 3,35 = 25,02 KN/m
2.c Calcolo del momento massimo
M= (Q*l^2)/8 = 28,15 KN*m
Dove l è la luce della trave è l=3m.
2.d Scelgo la classe di resistenza dell’acciaio
Per l’acciaio da calcestruzzo armato sono previste solo due categorie B450A e B450C che hanno lo stesso valore di tensione di snervamento fy=450 N/mmq ma una differente duttilità cioè si rompono a seguito di due diverse deformazioni e perciò sono associate a due diversi coefficienti di sicurezza.
Scelgo l’acciaio B450C, il più duttile che ha un coefficiente di sicurezza più basso pari 1,15.
2.e Tensione di progetto dell’acciaio
Fd_f= 450/1,15 = 391,30 N/mmq
2.f Tensione di progetto del calcestruzzo
Inserisco il valore di resistenza cilindrica del calcestruzzo armato fck=40N/mmq
Fd_c = 40*0,85/1,6 dove 1,6 è il coefficiente di sicurezza del calcestruzzo armato.
2.g Altezza utile
Inserendo un ipotetico valore di base b =20 cm, otteniamo il valore di altezza utile hu che corrisponde alla distanza tra il lembo compresso della sezione e l’asse dell’armatura tesa.
hu = r √(M/ fD_c x b) = 18,63 cm
L’altezza totale H=hu+delta=18,63+5=23,63 cm dove delta è la misura del copriferro che di solito misura 5cm.
Ipotizzo una trave di base b=20cm e un’altezza maggiore rispetto a quella ottenuta H=25cm e procedo con la verifica.
2.h Verifica
Qtr a metro lineare= A*peso specifico=1,18KN/m
Qtr a mq= qtr/interasse=1,18/3,35=0,352 KN/mq
Aggiungo quindi al calcolo del carico strutturale anche il peso della trave e ottengo un’altezza totale H= 24,06 cm che è un valore minore rispetto a H= 25 cm scelta, il dimensionamento della trave è quindi corretto.

TRAVE RETICOLARE SPAZIALE - 4x6 campate con modulo di 2m
Per poter analizzare su Sap una travatura reticolare spaziale, dobbiamo disegnare la struttura in maniera molto accurata e perciò disegnamo prima il modello su Autocad e poi lo importeremo su Sap.
Per far sì che Sap riesca ad analizzare in maniera corretta la struttura, bisogna prestare attenzione ad alcune impostazioni di disegno: disegnare le aste su un layer nuovo che chiameremo “aste”, iniziare a disegnare dal punto d’origine (di coordinate 0,0,0) in modo tale da permettere una facile importazione su Sap; disegnare una struttura che sia chiusa (assicurarsi cioè che in ogni modulo non manchino aste)e che sia composta da elementi “singoli”, il che vuol dire che bisogna disegnare le linee che stilizzano le aste della travatura in modo tale che non ci siano linee doppie o sovrapposte.
1. DISEGNO SU AUTOCAD-2D
1.a Disegno il modulo base (un quadrato di lato 2m e una diagonale)
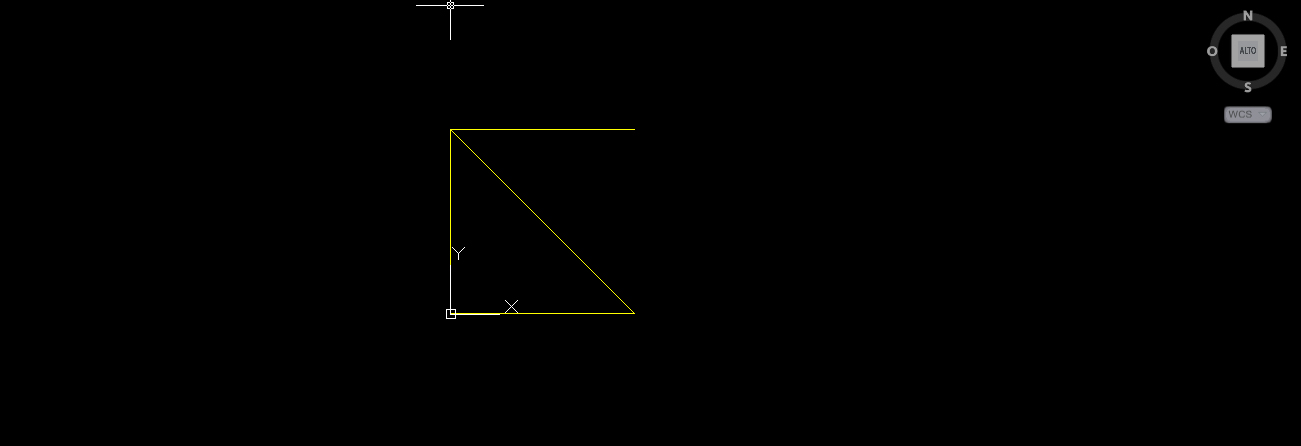
2. AUTOCAD 3D
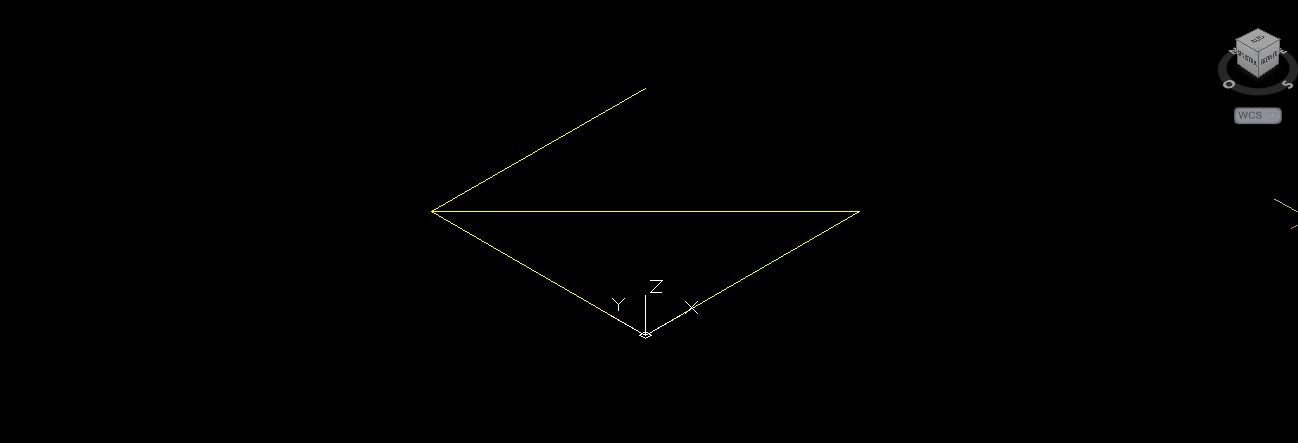
Con il comando “orbita” mi porto nella visualizzazione 3D e imposto la vista assonometrica SO, in questo modo mi rendo conto di aver disegnato il modulo base in pianta quindi lo seleziono e con il comando “ruota 3D” lo ruoto in modo tale da averlo in alzato(l’asse di rotazione è l’asse x e l’angolo di rotazione è 90°).
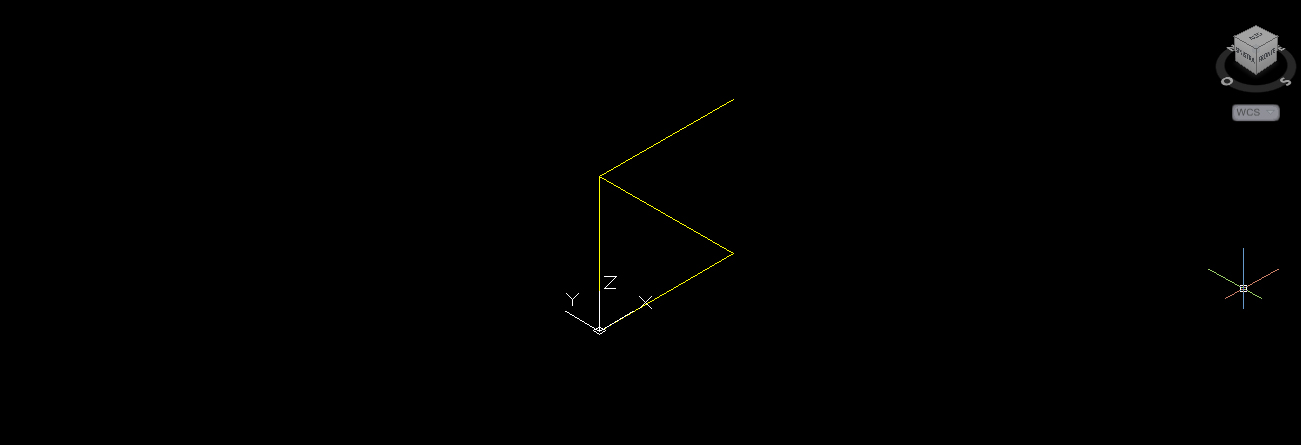
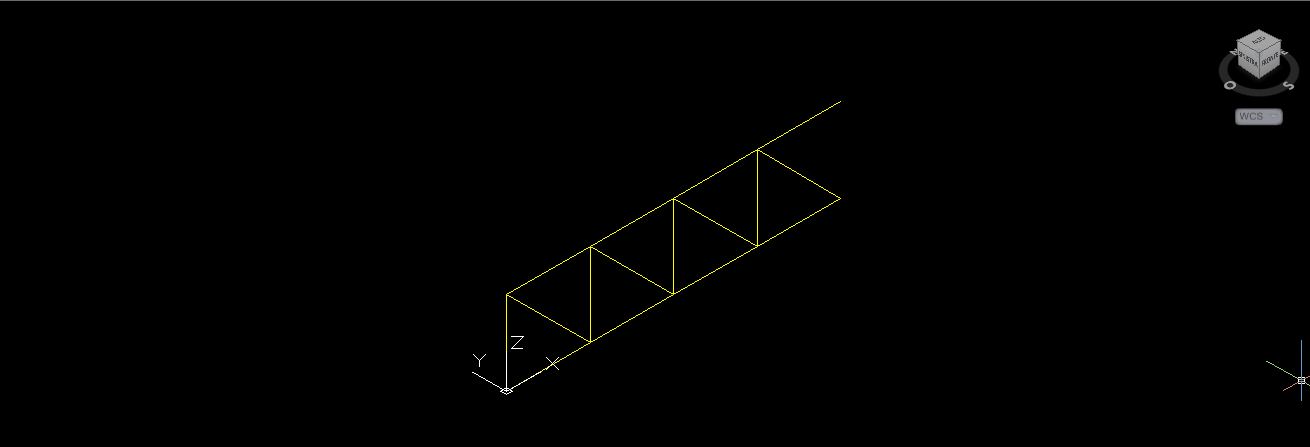
2.a Seleziono il modulo base e con il comando “serie” creo una riga con 4 colonne e una distanza di 2m tra le colonne; come possiamo vedere non è stata disegnata l’asta verticale di destra perché altrimenti avrei avuto una sovrapposizione delle linee verticali mentre in questo modo sono sicura che si tratti di tutte aste singole. Ora mi basta disegnare con il comando “linea” l’ultima asta verticale di dx per chiudere il modulo della larghezza della piastra.
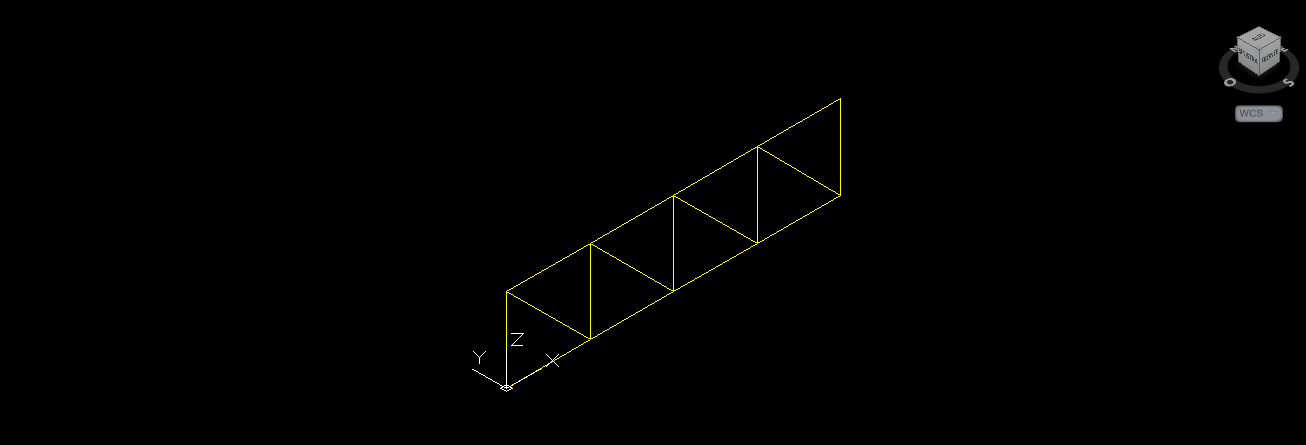
2.b Disegno le due linee orizzontali mancanti e la diagonale in modo tale da avere il modulo base anche nel piano yz.
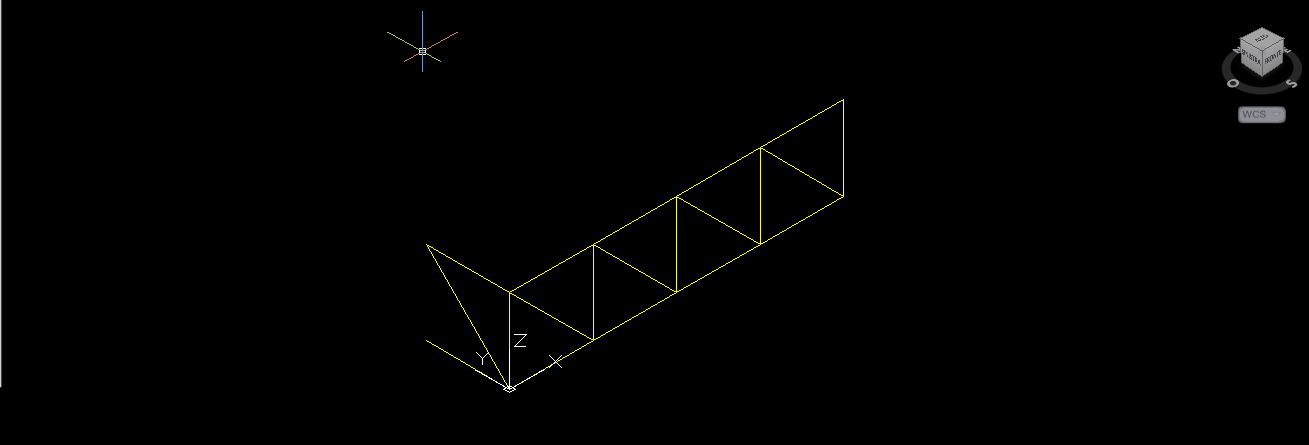
2.c Seleziono le 3 linee appena disegnate e con il comando “serie” creo una linea con 5 colonne e una distanza di 2m tra le colonne.

2.d Disegno la diagonale superiore e inferiore.
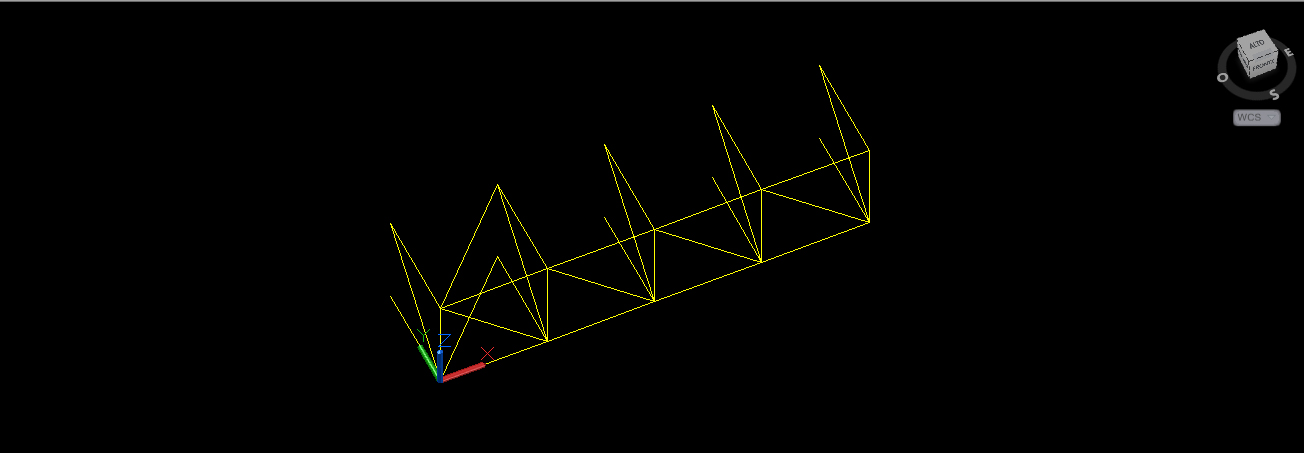
2.e Seleziono le diagonali appena create e con il comando “serie” creo una riga con 4 colonne e una distanza di 2m tra le colonne.
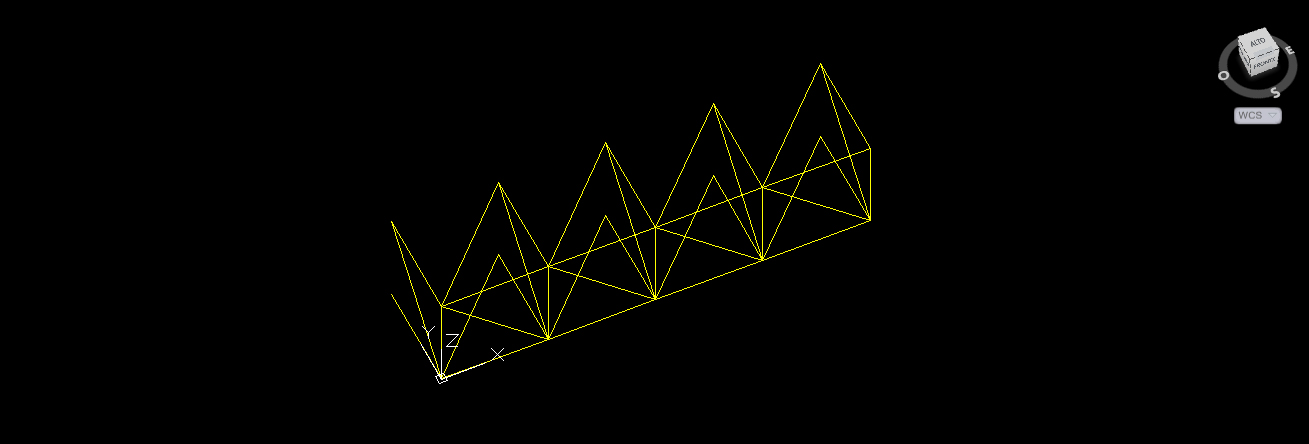
2.f Imposto un nuovo ucs per 3 punti in modo tale da avere l’asse x lungo la direzione della lunghezza della piastra. Seleziono tutti gli elementi disegnati e con il comando “serie” creo una riga con 7 colonne. Scelgo di realizzare 7 colonne e non 6 perché è più facile cancellare le aste in più che chiudere la struttura disegnando tutte le aste mancanti.

2.g Cancello le aste in più.
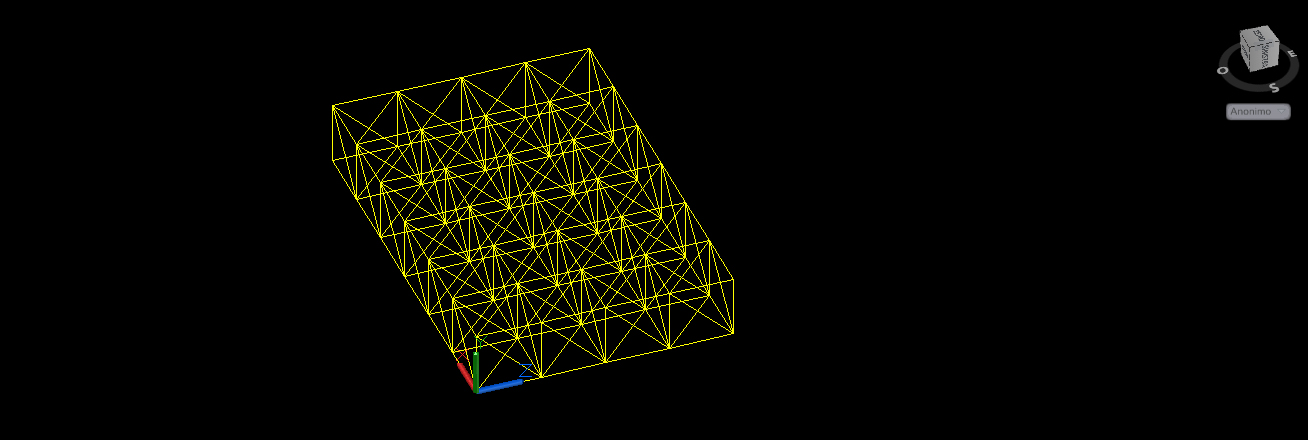
3. ESPLODERE LA STRUTTURA
È importante ricordarsi di esplodere la struttura in modo tale che non ci siano polilinee ma solo linee, in questo modo le aste su Sap saranno elementi lineari singoli e potranno essere facilmente analizzati dal programma.
4. SALVATAGGIO
Salvare il file in formato DXF2000
5. IMPORTARE SU SAP
Prima di importare il file occorre impostare le unità di misura poiché devono coincidere con quelle usate per disegnare su Autocad la struttura e perciò sceglieremo Kn,m,C.
Importare file di Autocad_dxf e nelle opzioni di importazione cercare il layer “aste” nel menu a tendina di frames. In questo modo le linee disegnate su autocad verranno lette come delle aste su sap.
6. ASSEGNAZIONE VINCOLI
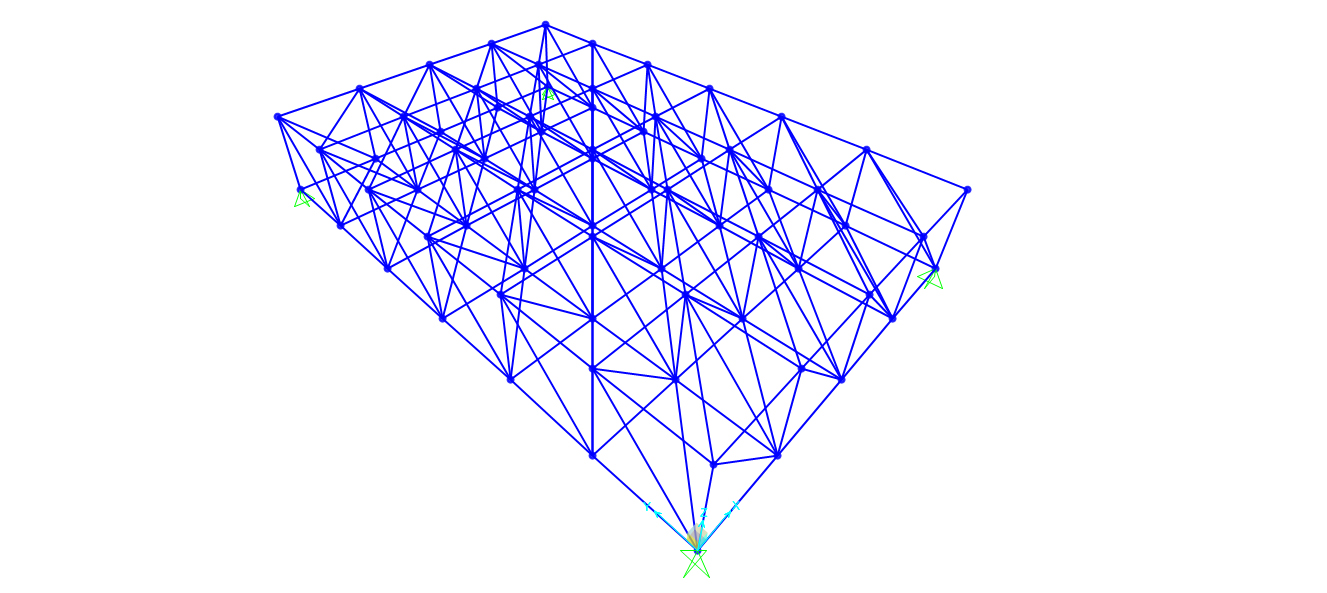
6.1 ESTERNI Seleziono i quattro nodi alle quattro estremità della pianta, i punti in cui la mia struttura poggia sui pilastri, e assegno a ciascun nodo una cerniera: Assaign->Joints->restraints e scelgo il vincolo della cerniera.
6.2 INTERNI Ora devo specificare a Sap che si tratta di una struttura reticolare in cui tutte le aste sono collegate da cerniere interne. Ciò equivale a dire a Sap che su ciascuna asta il momento iniziale e il momento finale sono nulli. Quindi seleziono l’intera struttura->assaign->frame->releases e assegno il valore nullo all’inizio e alla fine del moment 22 e del moment 33.
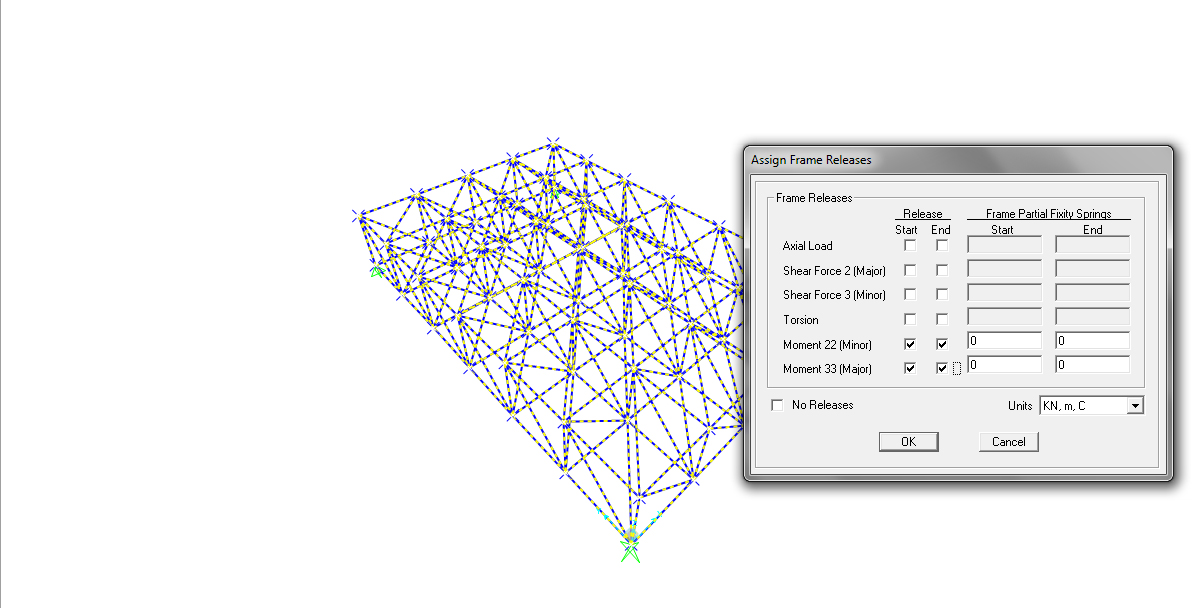

7. DEFINIRE MATERIALE E SEZIONE
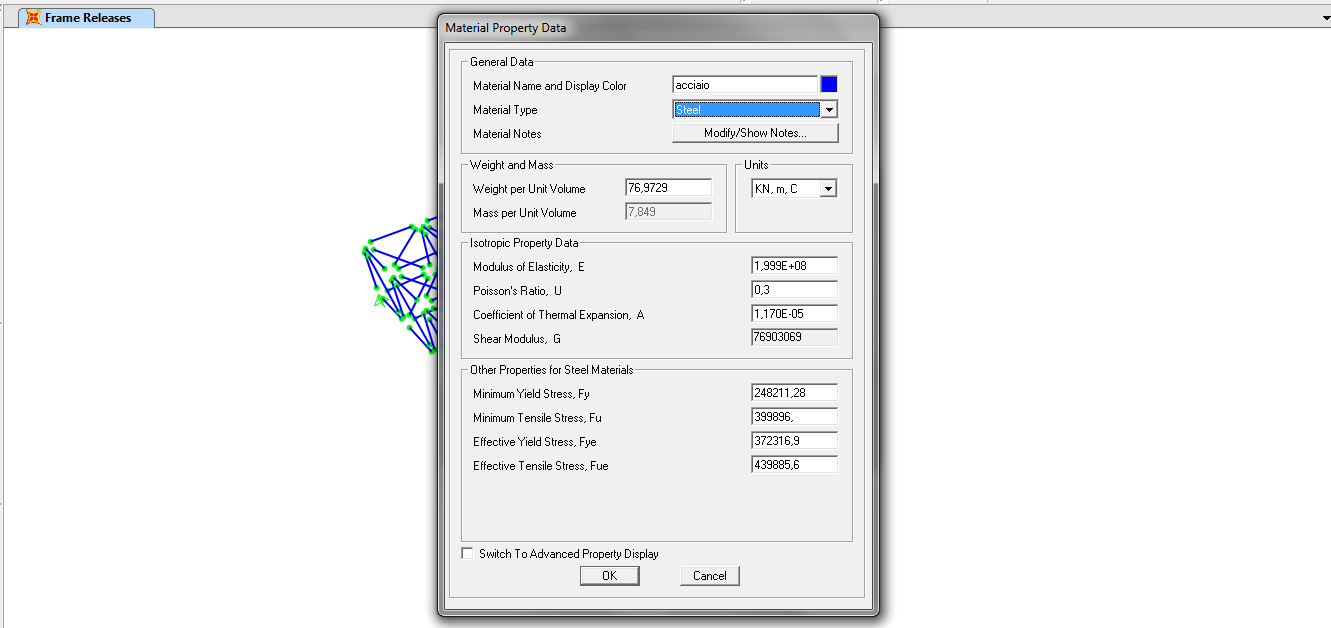
7.1 MATERIALE
Define->material->add new material che rinomino “acciaio”, scelgo “steel” nel menu a tendina del material type e lascio le caratteristiche fisiche e meccaniche predefinite.
7.2 SEZIONE
Define->sectione properties->frame sections->add new property e scelgo la sezione “pipe” che rinomino come “tubolare” e a cui attribuisco il materiale “acciaio” che ho precedentemente definito.
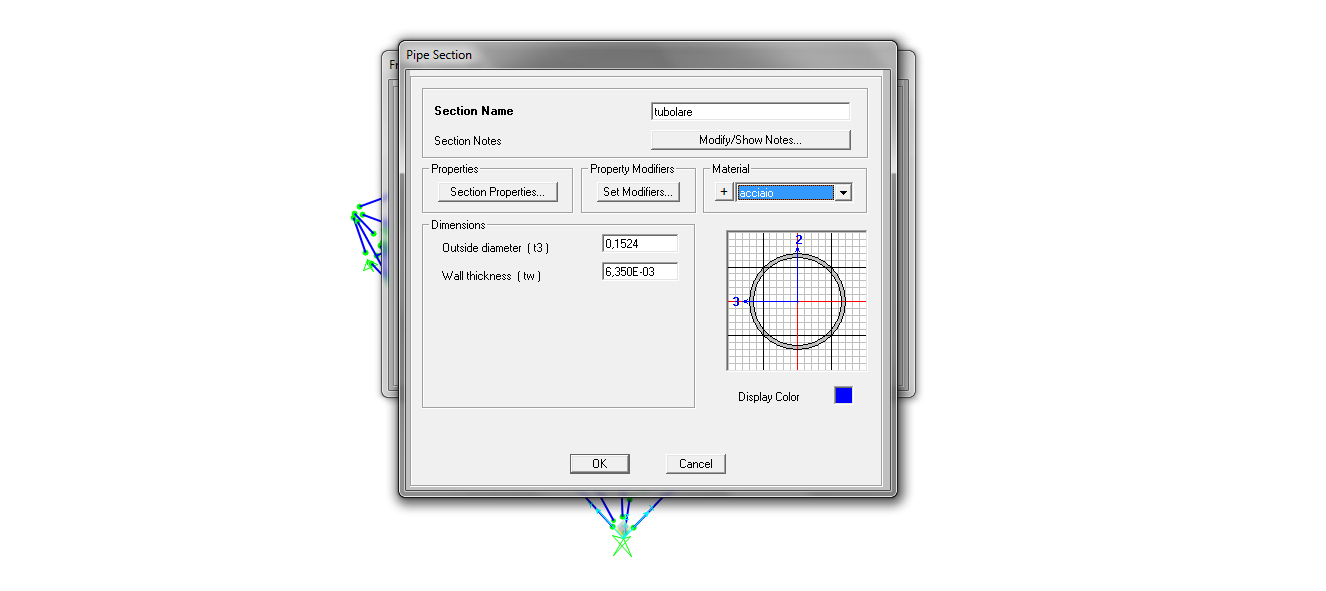
8. ASSEGNAZIONE MATERIALE E SEZIONE
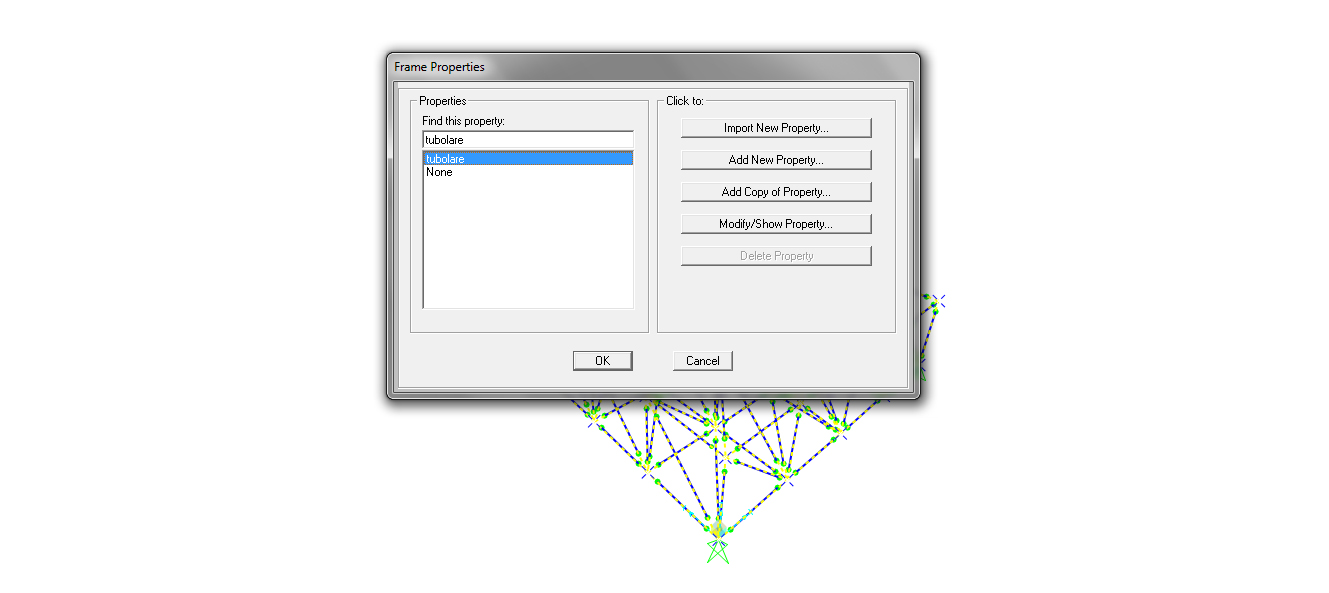
Seleziono l’intera struttura->assaign->frame->frame sections e scelgo la sezione che ho appena definito(in questo modo sto assegnando non solo la sezione ma anche il materiale).
9. DEFINIRE IL CARICO
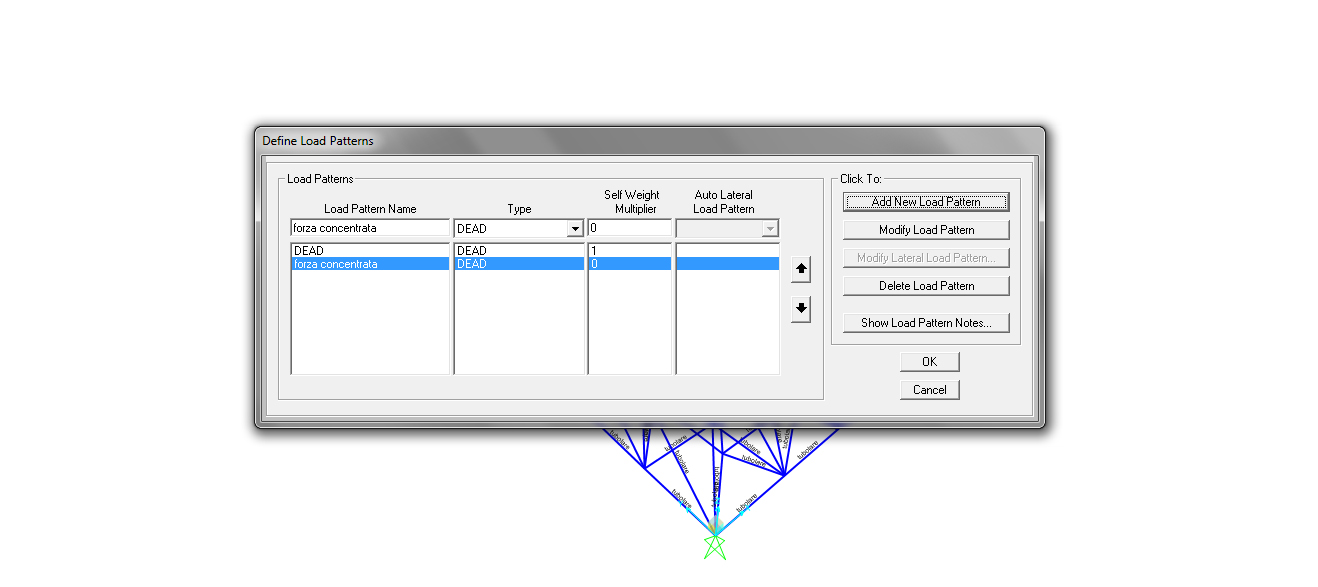
Define->load patterns->add new load pattern che rinomino “forza concentrata” e a cui imposto il valore “0” nel self weight multiplier.
10. ASSEGNAZIONE CARICO
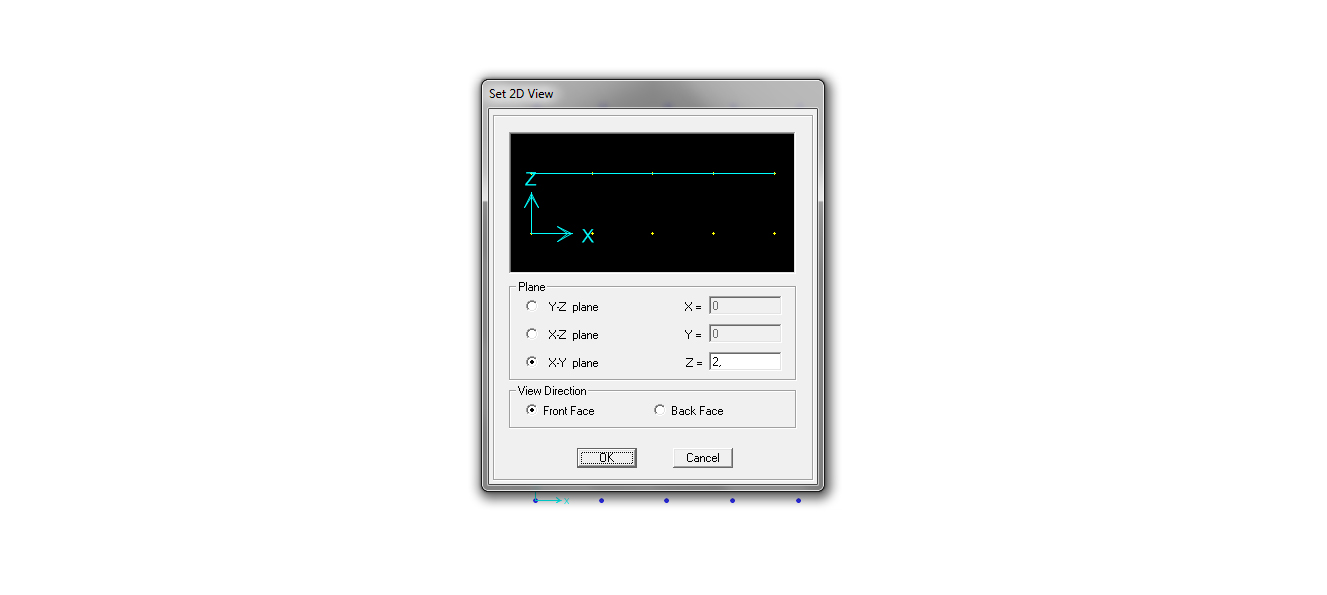
Devo assegnare il carico solo ai nodi superiori quindi, per avere una più facile visualizzazione d’insieme e per poter selezionare i giusti nodi, mi metto sul piano xy, clicco set display options e imposto la visualizzazione in modo tale che i nodi siano visibili e le aste siano nascoste.

Dopo di che vado su view->set 2D view->seleziono il piano superiore (quello con la z=2). Ora posso selezionare tutti i nodi che visualizzo sul piano xy e sono sicura che Sap ha selezionato solo quelli superiori.
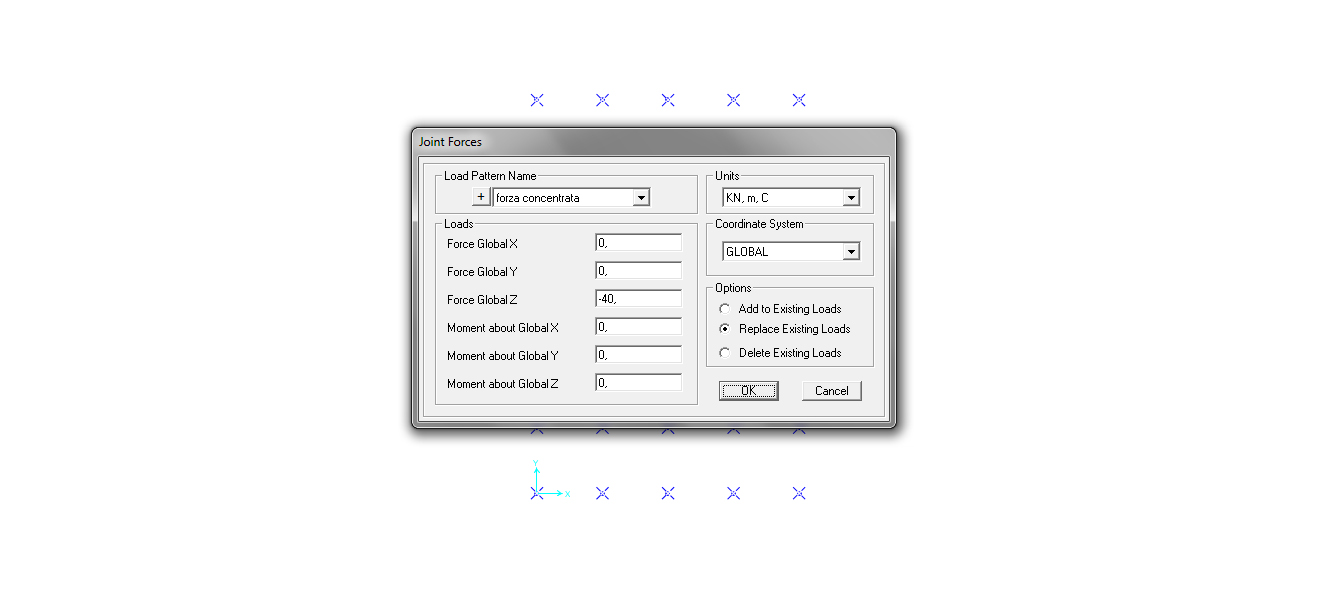
Assaign->joint loads->forces e inserisco un valore di -40 KN a “force global Z”.
11. ANALISI
Ora posso reimpostare le impostazioni di visualizzazione in modo tale che i nodi siano invisibili e le aste visibili e posso far partire l’analisi.
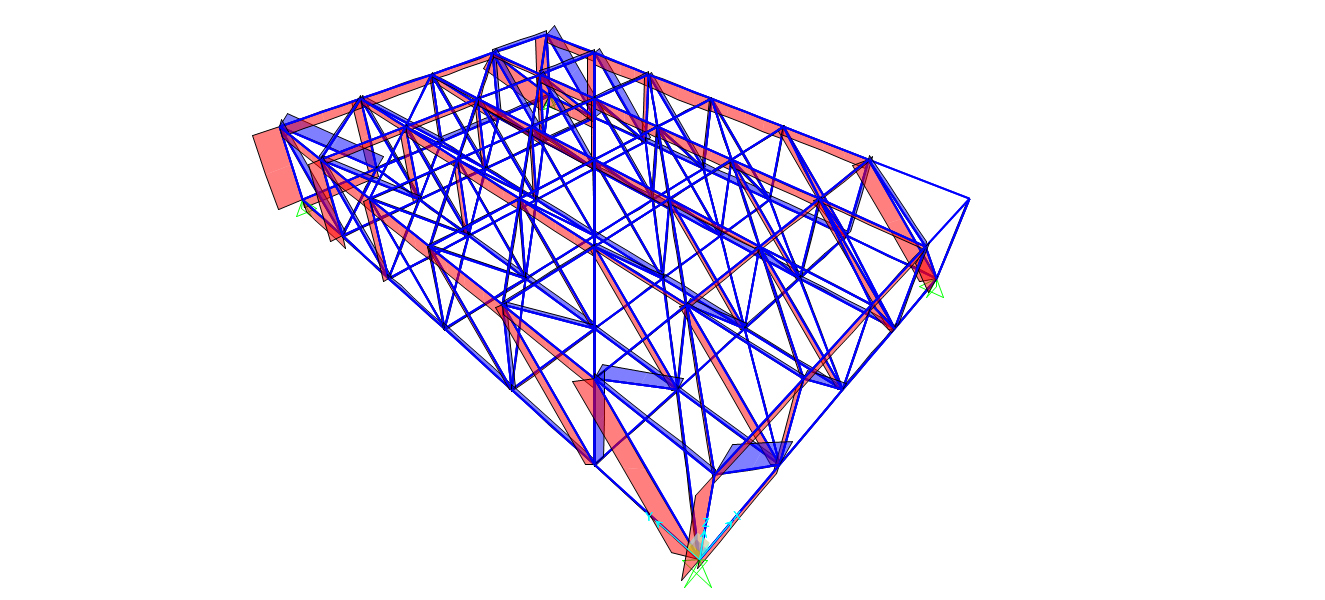
Dai diagrammi dello sforzo normale non si riesce ad avere una visione complessiva e chiara della situazione su tutte le aste ed è difficile individuare quali siano le aste più sollecitate; per questo possiamo andare su display->show tables e selezionare gli “analysis results”. In questo modo possiamo visualizzare le tabelle che sintetizzano i dati delle analisi della struttura e soprattutto aprendo la tabella “element forces-frames” possiamo visualizzare i valori di sforzo normale di tutte le aste ed individuare l’asta maggiormente tesa(220: N=258,934KN) e quella maggiormente compressa(12: N=-307,254KN).
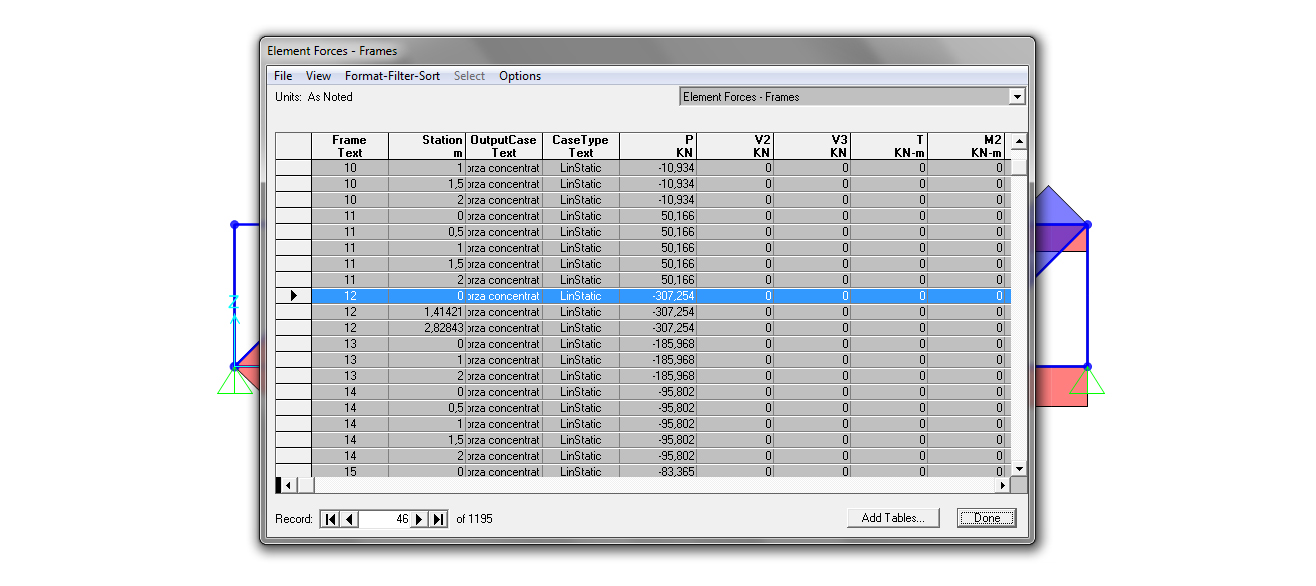
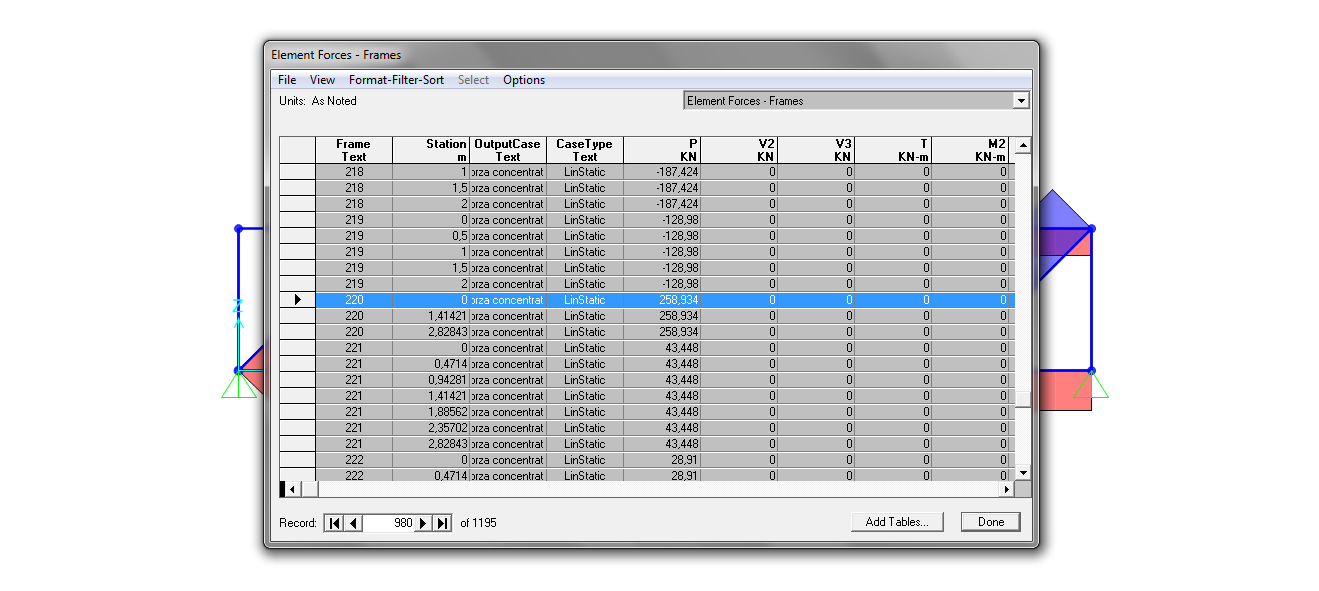
12. DIMENSIONAMENTO ASTA MAGGIORMENTE COMPRESSA: asta 12
Scelgo un acciaio abbastanza resistente Fe 510 S 355
Fd=N/A dove fd=fy/1.15=355/1.15=308.7 N/mmq
Quindi se N=-307,524 KN e fd=308.7N/mmq
A=N/fd=307524/308.7=996,19mmq=9,96cmq
Scelgo un profilato con sezione tubolare maggiore dalla minima appena calcolata A=10,70cmq=1070mmq
Verifichiamo che con l’area scelta N/A<fd 307524N/1070mmq=287,40N/mmq <fd ok!
12.1 VERIFICA ASTA MAGGIORMENTE COMPRESSA
Nel caso di aste sottoposte a compressione(ma anche di pilastri o setti strutturali compressi) non basta però verificare che il rapporto tra lo sforzo normale e l’area scelta sia minore della tensione di design perché l’elemento potrebbe incorrere nell’instabilità euleriana, cioè uno sbandamento della struttura dovuto a problemi di eccessiva snellezza dell’elemento.
La snellezza λ=l/ρmin non ha dimensione fisica e misura il rapporto tra la lunghezza e la larghezza del profilo
l=lunghezza dell’asta=2,82m
ρmin =giratore d’inerzia=√(J/A) in questo caso si tratta del raggio di inerzia i=3cm
λ=l/ρmin=282cm/3cm=94<200 valore di snellezza massimo per l’acciaio (dalle norme tecniche).
Ma occorre anche verificare che il carico di compressione di progetto Nd sia minore della resistenza all'instabilità Nbrd=A*X*fd minore del carico critico euleriano Ne=π2EJ/lo2.
Dove: E=modulo di elasticita 210.000Mpa
J=momento di inerzia minimo della sezione=96,30cm4=963000mm4
lo=lunghezza libera di inflessione che dipende dal tipo di vincolo, nel caso di cerniera/carrello
l= lo=2√2=2,82m (poiché l’asta maggiormente compressa è una diagonale del quadrato)
Ne=π2EJ/lo2=π2*210000N/mm2*963000mm4/7952400mm2=250730,2N~250,73KN
Nbrd=A*Χ*fd
Χ=1/[Φ+√( Φ2-λ2)]
Dove : Φ=0,5*[1+λ2+α(λ-0,2)]
α=0,49 fattore di imperfettibilità(dalle norme tecniche)
λ=√(A*fy)/Ne=1,52
quindi Φ=0,5*[1+λ2+α(λ-0,2)]=0,5*[1+2,29+(0,49*1,32)]=1,9684
Χ=1/[Φ+√( Φ2-λ2)]=1/[1,9684+√( 1,96842-1,522)]=1/3,227=0,31
Nbrd=A*Χ*fd=1070*0,31*308,7=218405 N=218,41KN
quindi Nbrd< Nd la sezione non è verificata!
Ripeto la verifica scegliendo di volta in volta sezioni con area maggiore. La sezione risulta verificata per un'area A=15,40cmq=1540mmq
Verifichiamo che con l’area scelta N/A<fd 307524N/1540mmq=199,69N/mmq <fd ok!
λ=l/ρmin=282cm/4.810cm=58.63<200 valore di snellezza massimo per l’acciaio (dalle norme tecniche)
Ne=π2EJ/lo2
Ne=π2EJ/lo2=π2*210000N/mm2*3570000mm4/7952400mm2=929498,2N~929,5KN
Nbrd=A*Χ*fd
Χ=1/[Φ+√( Φ2-λ2)]
Dove : Φ=0,5*[1+λ2+α(λ-0,2)]
α=0,49 fattore di imperfettibilità(dalle norme tecniche)
λ=√(A*fy)/Ne=0.77
quindi Φ=0,5*[1+λ2+α(λ-0,2)]=0,5*[1+0,59+(0,49*0,57)]=0,94
Χ=1/[Φ+√( Φ2-λ2)]=1/[0,94+√( 0,942-0,592)]=0,68
Nbrd=A*Χ*fd=1540*0,68*308,7=324662,92 N=324,67KN
quindi Nd<Nbrd e la sezione è verificata!
13 DIMENSIONAMENTO ASTA MAGGIORMENTE TESA: asta 220
Scelgo un acciaio abbastanza resistente Fe 510 S 355
Fd=N/A dove fd=fy/1.15=355/1.15=308.7 N/mmq
Quindi se N=258,934 KN e fd=308.7N/mmq
A=N/fd=258934/308.7=838,79mmq=8,39cmq
Scelgo un profilato con sezione tubolare maggiore dalla minima appena calcolata A=9,65cmq=965mmq
Verifichiamo che con l’area scelta N/A<fd:
258934N/965mmq=268,32N/mmq >fd non è verificata
Scelgo una sezione con area maggiore A=10,70cmq=1070mmq
258934N/1070mmq=241,994N/mmq <fd l’asta tesa è verificata!
RIPARTIZIONE DELLE FORZE SISMICHE
Una struttura ben progettata deve resistere bene sia alle forze e ai carichi verticali ma anche alle sollecitazioni orizzontali come per esempio l’azione del vento o le forze sismiche. Gli elementi strutturali chiamati a resistere alle sollecitazioni orizzontali sono i controventi.
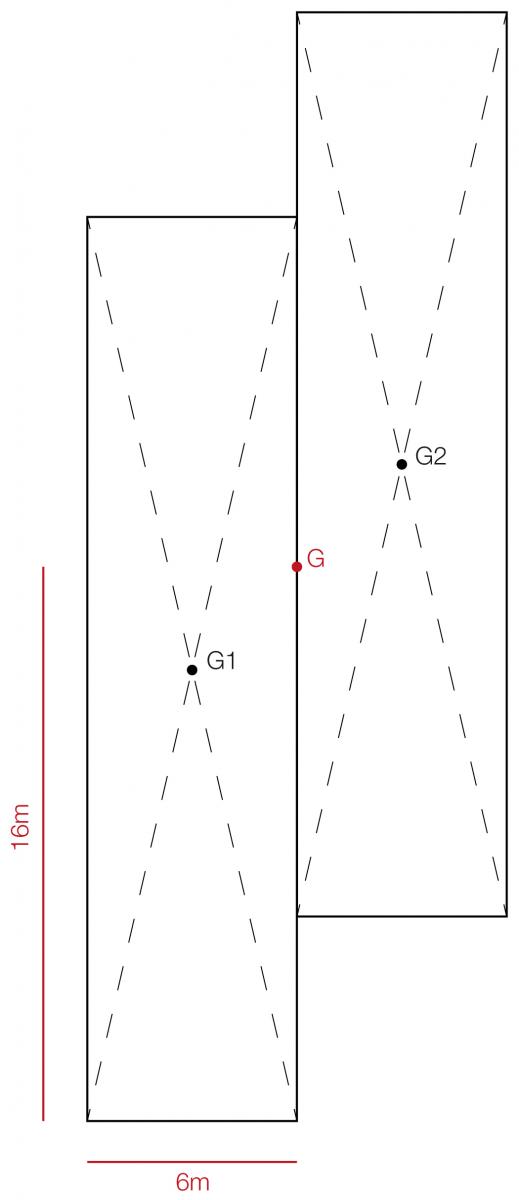
A seguito dell’aggiornamento della normativa sulla classificazione delle zone sismiche del 2008, in tutto il nostro paese è diventata obbligatoria la progettazione sismica. Ora vedremo come si ripartiscono le forze simiche su un impalcato di un edificio ad un piano in base alle rigidezze dei controventi. Nel caso studiato i controventi sono composti da una maglia di telai shear type, cioè telai che hanno la trave infinitamente rigida a flessione e accorciamento verticale dei pilastri trascurabile.
L’impalcato si comporta perciò come un corpo rigido e ha quindi solo 3 modi per muoversi: traslando verticalmente, traslando orizzontalmente o ruotando; i suoi vincoli sono proprio i controventi.
Se la struttura è isostatica posso risolverla facilmente ma se invece si tratta, come nel nostro caso, di una struttura iperstatica posso usare il metodo delle rigidezze per risolverla e considero i controventi come dei vincoli elastici e cioè dei vincoli che imprimono una forza per rispondere alla forza esterna applicata. La forza impressa dai vincoli nasce dalla deformazione del controvento che reagisce e si comporta come una molla elastica per la quale è valida la legge di Hooke.
f=k*δ dove k è la rigidezza della molla e δ lo spostamento elastico
La rigidezza traslante di ciascun telaio dipende dall’altezza dei pilastri, dal modulo elastico del materiale con cui sono costruiti e dal modulo di inerzia di ciascun pilastro che a sua volta dipende dalla forma e dalle dimensioni della sezione.
La distribuzione delle rigidezze in pianta è fondamentale quando entrano in gioco le sollecitazioni orizzontali perché, come abbiamo appena detto, per la legge di Hooke gli spostamenti dipendono sì dalla forza sismica ma anche e soprattutto dalla rigidezza. Per cui se la struttura è composta da controventi con rigidezze molto diverse(e che quindi si deformano anche in maniera molto diversa), il centro delle rigidezze non passerà per il centro delle masse e si verrà a creare un momento torcente con braccio pari alla distanza tra il centro delle rigidezze e il centro delle masse che farà ruotare l’intera struttura.
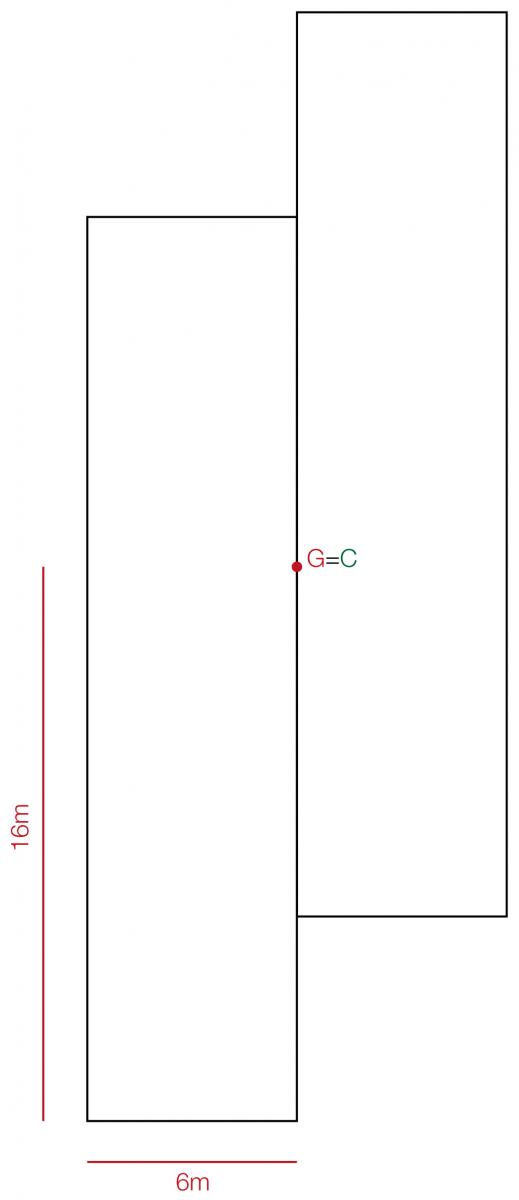
L’impalcato di studio è composto da 13 pilastri a sezione rettangolare di dimensioni 50x30cm e realizzati in cemento armato (con un modulo elastico E=21000N/mm2) che compongono 8 telai. La struttura si sviluppa su un piano solo e l’altezza dell’interpiano è pari a 3,50m.
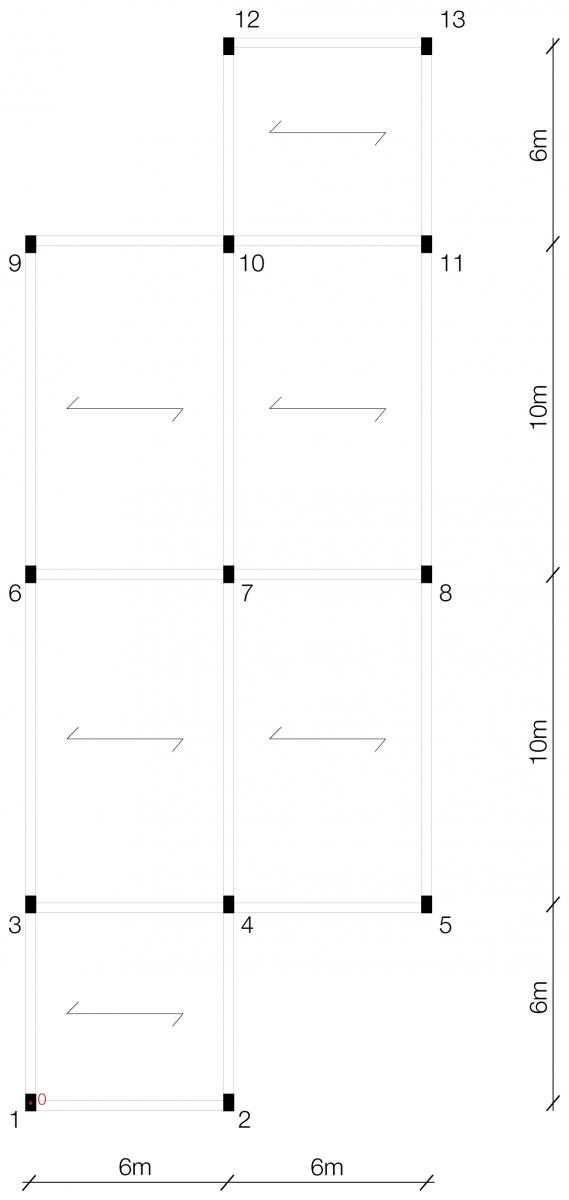
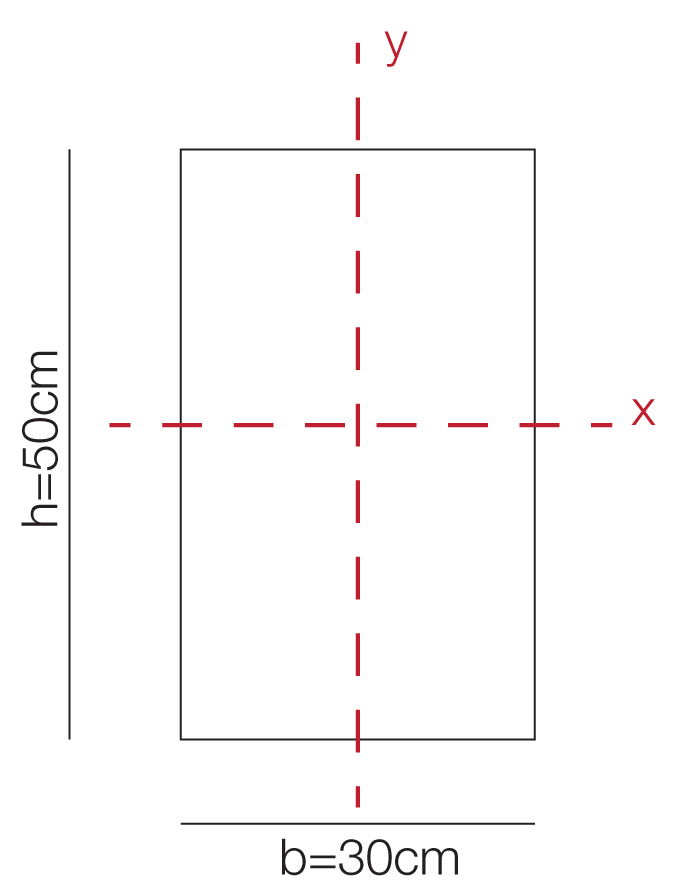
Visto che le sezioni rettangolari hanno due diversi momenti di inerzia, uno rispetto all’asse x e uno rispetto all’asse y, i pilastri devono essere disposti in base all’orditura e alla luce del solaio; nel caso studiato sono stati disposti tutti con lo stesso verso e perciò:
per i controventi orizzontali Iy=(hb3)/12=(50*303)/12=112500cm4
per i controventi verticali Ix=(bh3)/12=(30*503)/12=312500cm4.
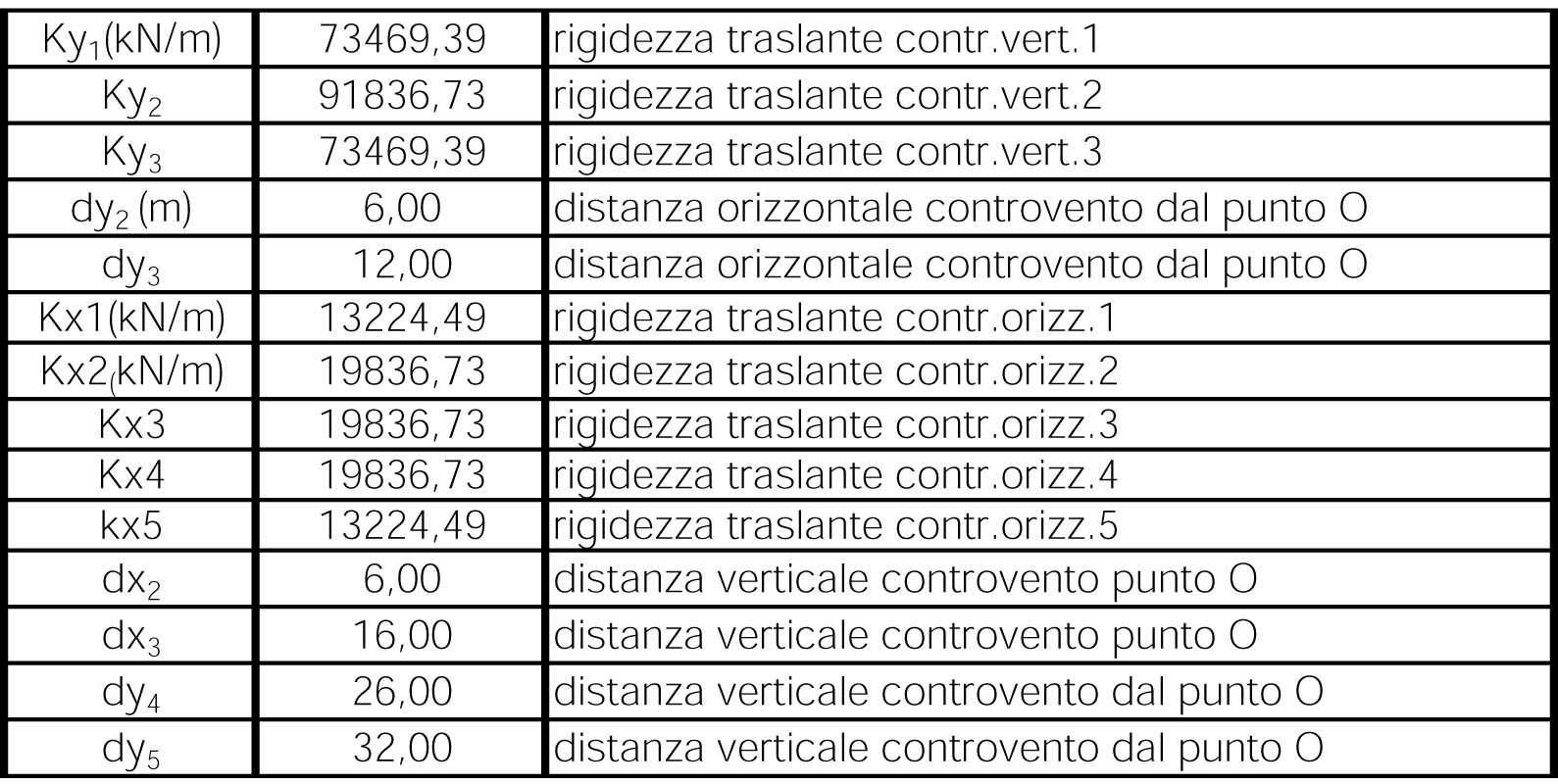
STEP 1 CALCOLO DELLE RIGIDEZZE TRASLANTI DEI CONTROVENTI DELL’EDIFICIO
Calcoliamo la rigidezza traslante per ciascuno degli 8 telai Kt=12E*(I1+I2+I3..)/h2.








STEP 2 TABELLA SINOTTICA RIGIDEZZE CONTROVENTI E DISTANZE
Riassiumiamo in una tabella sinottica le rigidezze dei telai e le distanze orizzontali e verticali di ciascun telaio dal punto di origine 0 del nostro sistema di riferimento.
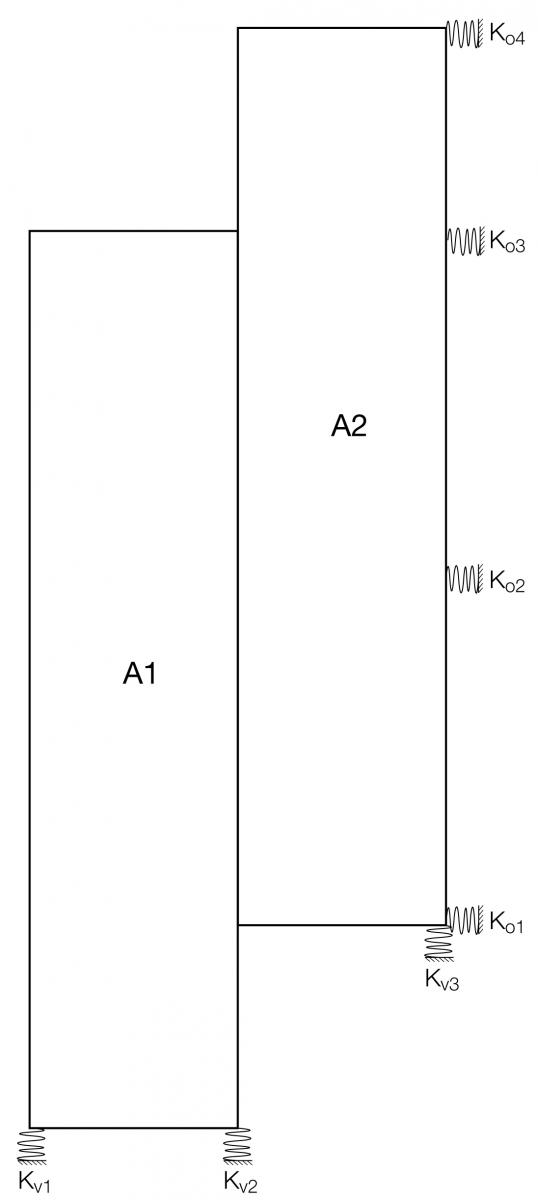
STEP 3 CALCOLO DEL CENTRO DI MASSA
Calcoliamo le coordinate del centro delle masse G:
XG=(A1*XG1+A2+*XG2)/(A1+A2)
YG=(A1*YG1+A2+*YG2)/(A1+A2)
Dove A1 e A2 sono le aree in cui abbiamo diviso l’impalcato e (XG1; YG1) e (XG2; YG2) sono rispettivamente le coordinate del baricentro di ciascuna delle due aree.

Ora possiamo perciò rappresentare l’impalcato attraverso le aree che lo compongono e le molle che rappresentano i controventi.
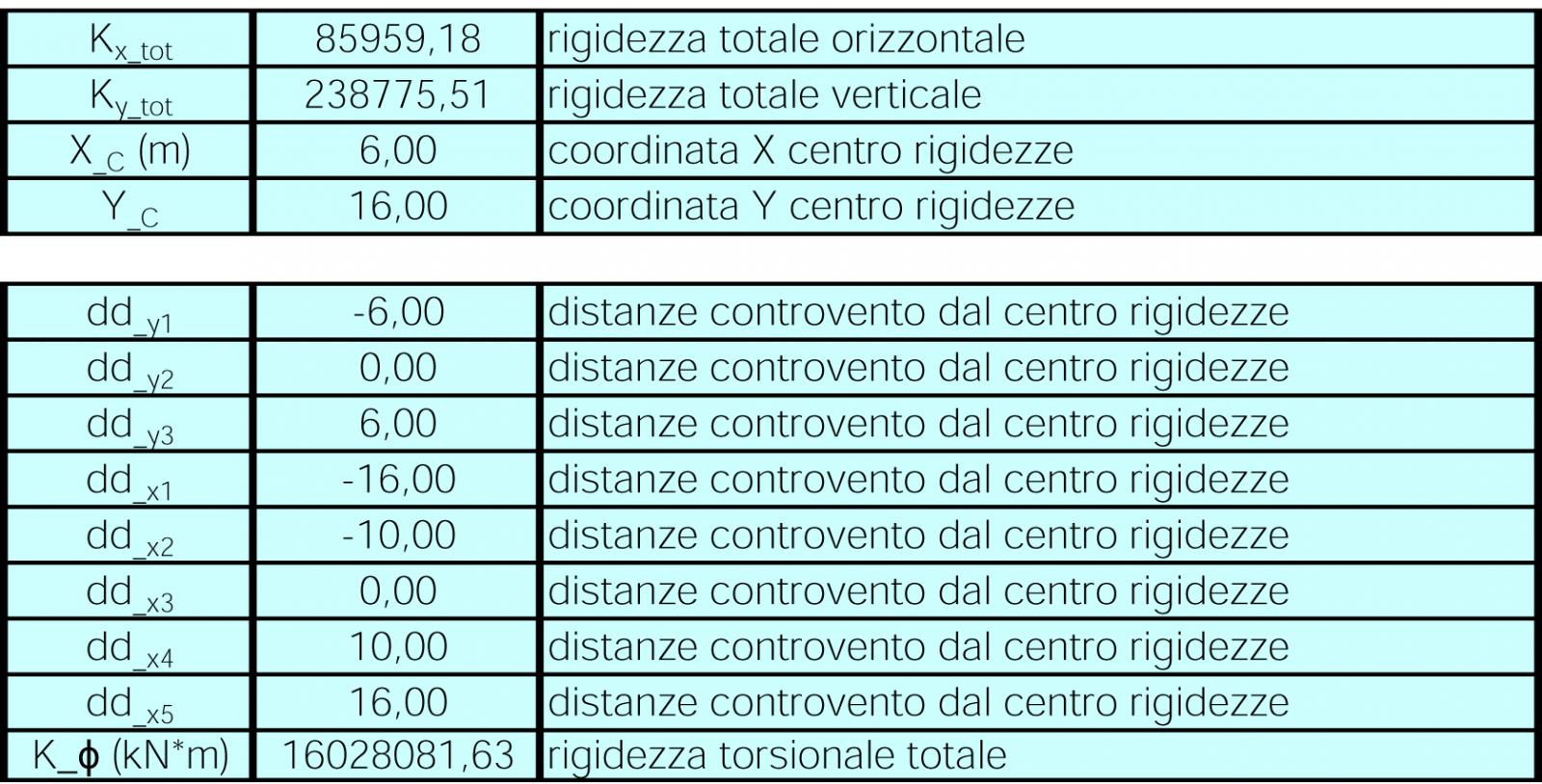
STEP 4 CALCOLO DEI CENTRO DELLE RIGIDEZZE E DELLE RIGIDEZZE GLOBALI
Calcoliamo le coordinate del centro delle rigidezze C
Xc = [Σi (Kvi*dvi)]/Kvtot
Yc = [Σi (Koi*doi)]/Kotot
e le distanze di ciascun controvento dal centro delle rigidezze e la rigidezza torsionale come Kφ=Σi(Ki*ddi2).
STEP 5 ANALISI DEI CARICHI SISMICI
La forza sismica è F=m*a dove a=c*g con c<1 (da normativa) quindi F=m*c*g ma m*g non è altro che il peso P della struttura quindi possiamo dire che la forza sismica è una “frazione del peso della struttura”.
c è il coefficiente di intensità sismica dato dalla normativa, per il nostro calcolo useremo c=0,20.
P = G+ψQ dove
G= (qs+qp)*Atot è il carico totale permanente dato dalla somma del carico strutturale e quello permante moltiplicata per l’area totale dell’impalcato
Q= qa*Atot è il carico totale accidentale dato dal carico accidentale moltiplicato per l’area totale dell’impalcato
Ψ=o,80 è il coefficiente di contemportaneità o di partecipazione che per normativa è <1
Quindi possiamo trovare la forza sismica come F=P*c.

STEP 6/7 RIPARTIZIONE FORZA SISMICA LUNGO x/y
In base alla normativa vigente, non potendo sapere se e con quale intensità e direzione arriverà il sisma, bisogna verificare la struttura per almeno due direzioni perpendicolari x,y e verificare che, per le due direzioni scelte, la struttura sopporti eventuali momenti torcenti nati dalla non coincidenza del centro delle masse (a cui è applicata la forza sismica)e del centro delle rigidezze.
Il momento torcente nelle due direzioni è Mx= F (XC - XG) e My= F (YC - YG) dove (XC-XG) e (YC-YG) sono i rispettivi bracci della forza sismica applicata lungo le due direzioni.
Una volta calcolati i momenti torcenti, la rotazione e le traslazioni orizzontali e verticali possiamo calcolare come la forza sismica si ripartisce su ogni controvento in entrambe le direzioni.
Lungo x:
per i controventi orizzontali Rio= Kio * (uo + ϕdio)
per i controventi verticali Riv= Kiv * ϕdiv
Lungo y:
per i controventi orizzontali Rio= Kio * ϕdio
per i controventi verticali Riv= Kiv * (uv + ϕdiv)

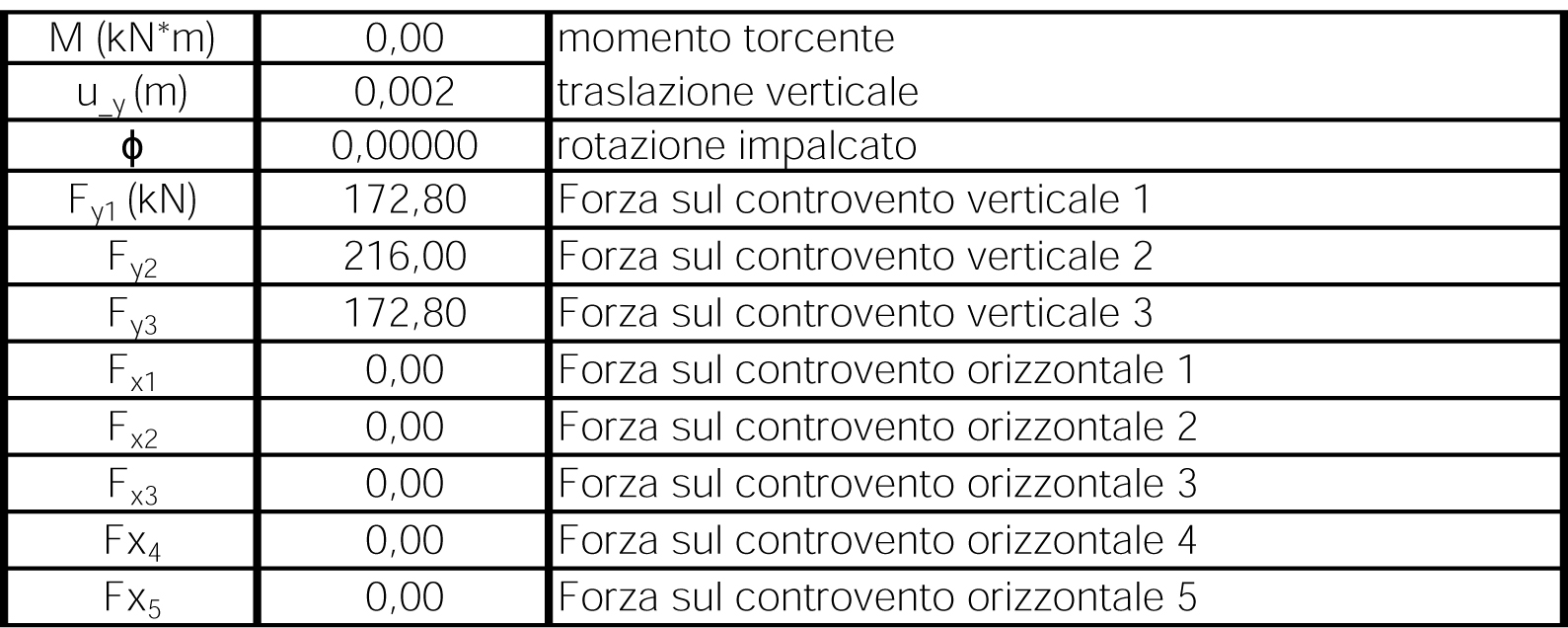
Nel caso studiato, la struttura è simmetrica sia per la disposizione degli elementi strutturali sia per la disposizione delle rigidezze per cui il centro delle rigidezze coincide con il centro delle masse e quindi in caso di sisma non si genererà né un momento torsionale né la conseguente rotazione, ma solo una leggera traslazione.
Commenti recenti