Esercizio sul dimensionamento di trave e pilastro più sollecitati all'interno di un telaio ingegnerizzato di un'abitazione civile nelle tipologie: cemento armato, acciaio e legno.
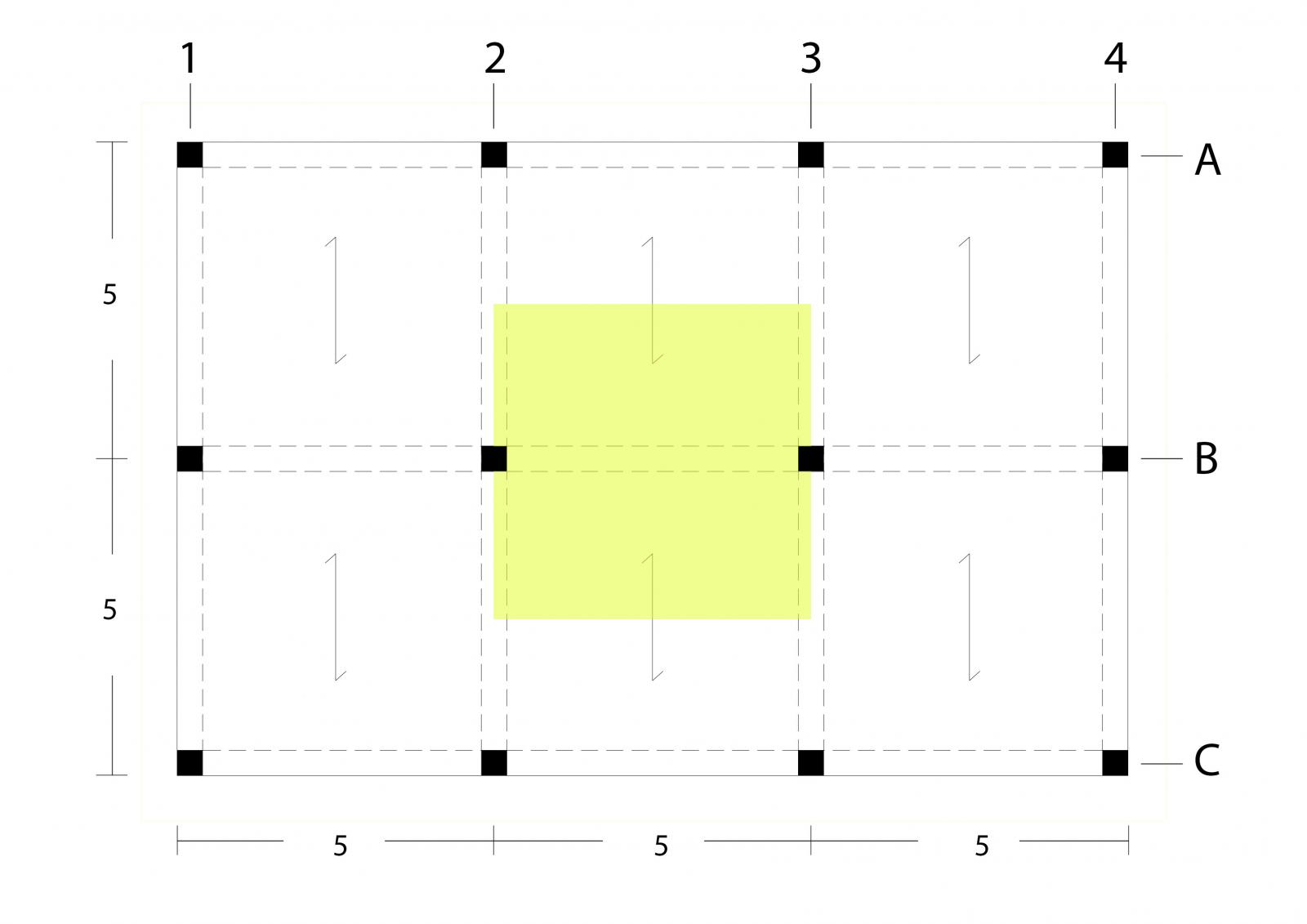
Il telaio studiato presenta una maglia strutturale regolare di 5 x 5 metri di interasse, si sviluppa su 4 piani ed ogni interpiano è di 3 metri --> Luce di 5 metri // Interasse di 5 metri // Interpiano di 3 metri // Area d'influenza pari a 25 mq
Sul solaio agiscono dei carichi: il CARICO STRUTTURALE Qs, dovuto dal peso degli elementi strutturali; il CARICO PERMANENTE Qp, dovuto a quei pesi che agiscono sulla struttura ma che non provengono da elementi strutturali ed il CARICO ACCIDENTALE Qa, il quale dipende dalla destinazione d'uso della costruzione.
La normativa propone combinazioni tipo di carico: per ottenere un CARICO TOTALE ˜Q moltiplichiamo i carichi Qs, Qp e Qa con dei coefficienti γ --> γs (1,3) x Qs + γp (1,5) x Qp + γa (1,5) x Qa = ˜Q (kN/mq)
Moltiplichiamo il valore ˜Q per l'interasse per ottenere un carico QU, ovvero il valore di carico che agisce direttamente sulla trave, la combinazione di carico di stato limite ultimo disposta dalla normativa.
TELAIO IN ACCIAIO

- TRAVE -
SOVRACCARICO STRUTTURALE QS :
• Soletta in cls alleggerito / Spessore di 10 cm / Peso Specifico di 1500 Kg/m^3
0,1 x 15 = 1,5 KN/m^2
• Lamiera grecata in acciaio / Spessore di 1,5 mm / Peso Specifico di 7860 Kg/M^3
0,015 x 7,86 = 0,1179 KN/m^2
SOVRACCARICO PERMANENTE QP:
• Pavimentazione in gres / Spessore di 2 cm / Peso Specifico di 0,40 Kg/m^3
0,02 x 0,40 = 0,008 KN/m^2
• Massetto / Spessore di 4 cm / Peso Specifico di 21000 Kg/m^3
0,04 x 21 = 0,84 KN/m^2
• Isolante in lana di roccia / Spessore di 2 cm / Peso Specifico di 30 Kg/m^3
0,03 x 0,3 = 0,006 KN/m^2
• Controsoffitto in cartongesso / Spessore di 1 cm / Peso Specifico di 1325 Kg/m^3
0,01 x 13,25 = 0,1325 KN/m^2
• Incidenza impianti = 0,5 KN/m^2
• Incidenza tramezzi = 1 KN/m^2
SOVRACCARICO ACCIDENTALE QA:
• Abitazione civile = 2 KN/m^2
QU = ( 1,3 x QS + 1,5 x QP + 1,5 x QA ) x 5 --> = 44,16135 KN/m
A questo punto, poichè la struttura si presenta come una trave doppiamente appoggiata di cui conosciamo il valore del diagramma del Momento, inseriamo il risultato ottenuto per QU e la luce L all'interno di questo e otteniamo:
Mmax = QU x L^2 / 8 --> Mmax = 138,0042 KN/m
Una volta scelta la tipologia di acciaio, in questo caso S235, inserisco il valore di snervamento Fyk all’interno del foglio excel. Trovo così la tensione di progetto Fd in quanto: Fd = Fyk / γs in cui γs è un coefficiente di sicurezza dell’acciaio pari a 1,05
Quindi Fd = 223,809 KN/mm^2
Nell’immagine in basso vediamo come ricavare il modulo di resistenza a flessione minimo Wx (cioè rispetto all’asse x), di nuovo grazie all’utilizzo del foglio di calcolo.
Wx,min = Mmax / Fd = 616,61 cm^3
Ottenuto il valore Wxmin scegliamo un profilato dalla tabella —> IPE 330 di Wx pari a 713,1 cm^3
Nella terza riga del foglio inseriamo il valore del sovraccarico strutturale QS della IPE 330 = 49,1 Kg/m ovvero 0,49 KN/m Ottengo così un nuovo valore QU che considera anche il peso del profilato e di conseguenza un nuovo Wxmin. Quest’ultimo verifica la sezione in quanto < di Wx della IPE
Dopo aver eseguito il calcolo su SAP e aver ottenuto il valore del Mmax pari a 53,09 KN/m la sezione è verificata!
- PILASTRO -
Per quanto riguarda il dimensionamento del pilastro più sollecitato abbiamo dovuto calcolare lo sforzo Normale su ogni piano tramite la formula:
N.1 piano = (A inf x Qu) + Peso Travi
in cui il Peso delle Travi è pari a = (A trave x La + A trave x Lb) x γ
Successivamente abbiamo moltiplicato lo sforzo Normale per ogni piano x il numero dei piani ed ottenuto, nel caso del telaio in acciaio, Nmax= 5609,03 KN
In un ulteriore foglio excel si è inserito come dato di partenza proprio lo sforzo Normale max pe ricavare il profilato adatto: nel nostro caso un profilo HEB 240

TELAIO IN CEMENTO ARMATO
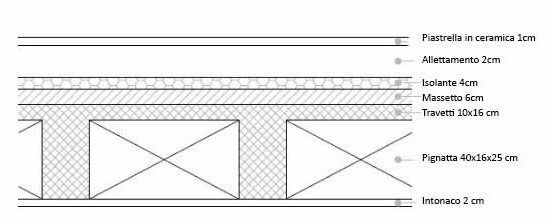
- TRAVE -
SOVRACCARICO STRUTTURALE QS:
• Soletta in cos / Spessore di 40 mm / Peso Specifico di 25 KN/m^3
0,04 x 25 = 1 KN/m^2
• Travetti / Spessore di 10x16 cm / Peso Specifico di 25 KN/m^3
(0,16 x 0.1) x 25 = 0,4 KN/m^2 —> x(2) = 0,8 KN/m^2
• Pignatte
x (2) = 0,16 KN/m^2
SOVRACCARICO PERMANENRE QP:
•Piastrelle in ceramica / Spessore di 1 cm / Peso Specifico di 0,2 KN/m^2
0,01 x 0,02 = 0,002 KN/m^2
• Massetto in cls / Spessore di 6 cm / Peso Specifico di 25 KN/m^3
0,06 x 25 = 1,5 KN/m^2
• Intonaco / Spessore di 2 cm / Peso Specifico di 16 KN/m^3
0,02 x 0,16 = 0,32 KN/m^2
• Incidenza impianti = 0,5 KN/m^2
• Incidenza tramezzi = 1 KN/m^2
SOVRACCARICO ACCIDENTALE QA:
• Abitazione civile = 2 KN/m^2
QU = ( 1,3 x QS + 1,5 x QP + 1,5 x QA ) x 5 --> = 55,95 KN/m
Stabiliamo il valore del Mmax = QU x L^2 / 8
Mmax = 174,85 KN/m
Inseriamo all’interno del foglio excel il valore di snervamento Fyk e ricaviamo la tensione di progetto Fyd, di nuovo grazie alla formula Fyd = Fyk / γs in cui γs è un coefficiente di sicurezza del calcestruzzo, in questo caso pari a 1,15.
Quindi Fyd = 391,30 KN/mm^2
Ineriamo adesso il valore della resistenza caratteristica fck, pari a 25 MPa
Ricaviamo la resistenza di progetto Fcd tramite la formula Fcd = αα x fck / γ in cui αα è un coefficiente riduttivo pari a 0,85
Otteniamo fcd = 14,16 N/mm^2
Attribuiamo alla base un valore, b = 40 cm che con i parametri β, fcd e ρ la utilizziamo per ricavare l’altezza utile Hu = 46,13 cm e per determinare l’altezza minima (anche con il parametro δ) Hmin = 51,13 cm
Ingegnerizziamo la trave ed otteniamo h = 50 cm

- PILASTRO -
Anche in questo caso si è iniziato un nuovo foglio excel partendo dallo sforzo Nmax
Nmax = 1509,327 KN/m
Tenendo conto che il valore σ < fcd, si è verificata la sezione scelta ovvero di b = 30 cm e h= 50 cm

TELAIO IN LEGNO
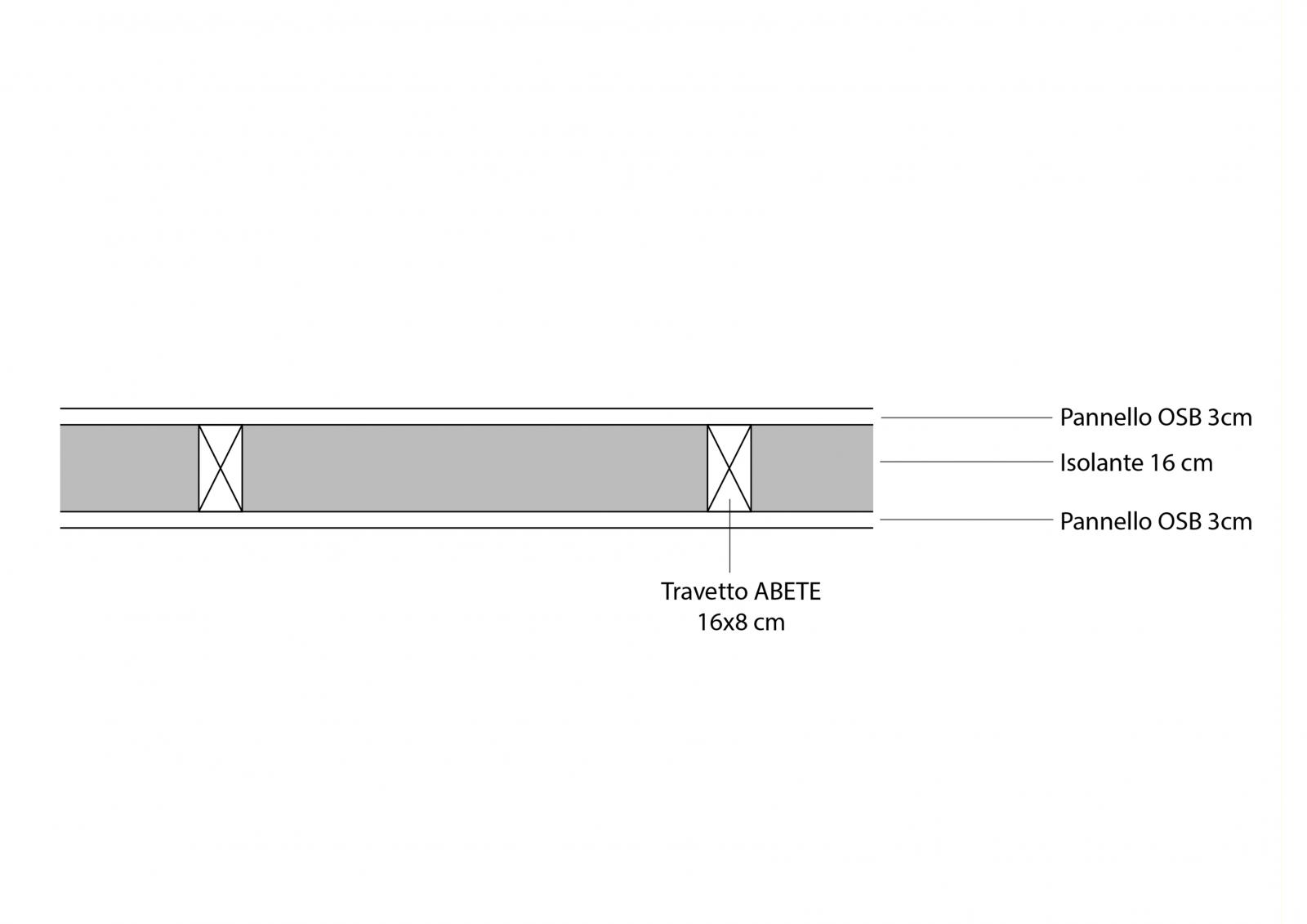
- TRAVE -
SOVRACCARICO STRUTTURALE QS:
• Due travetti in abete / Spessore di 8x16 cm ciascuno / Peso Specifico di 450 Kg/m^3
0,128 x 4,50 = 0,576 KN/m^2 —> x(2) = 1,152 KN/m^2
SOVRACCARICO PERMANENTE QP:
• Due pannelli in OSB / Spessore di 3 cm ciascuno / Peso Specifico di 650 Kg/m^3
0,03 x 6,5 = 0,195 KN/m^2 —> x(2) = 0,39 KN/m^2
• Isolante in polistirene estruso / Spessore di 16 cm / Peso Specifico di 15 Kg/m^3
0,15 x 0,16 = 0,024 KN/m^2
• Incidenza impianti = 0,5 KN/m^2
• Incidenza tramezzi = 1 KN/m^2
SOVRACCARICO ACCIDENTALE QA:
• Abitazione civile = 2 KN/m^2
QU = ( 1,3 x QS + 1,5 x QP + 1,5 x QA ) x 5 --> = 36,843 KN/m
Mmax = QU x L^2 / 8 --> Mmax = 115,1343 KN/m
Scelta la tipologia del legno, inseriamo sul foglio excel i valori:
fmk = 36 N/mm^2 valore caratteristico di resistenza
kmod = 0,7 coefficiente diminutivo
γ = 1,5 coefficiente di sicurezza
Tramite la formula fd = fmk x kmod / γm otteniamo fd = 16,8 N/mm^2
Imposto una base della trave b = 35 cm e tramite Hmin = √6 x Mmax / fmd x b ricavo il valore dell’altezza minima che dovrà avere la trave.
Quindi H > Hmin —> Hmin = 24,48 cm
H = 50 cm (ingegnerizzo la trave e la rendo più proporzionata)

- PILASTRO -
Come abbiamo fatto per i due materiali precedenti anche qui si è partiti dallo sforzo Normale max
N.1 piano = (A inf x Qu) + Peso Travi
formula in cui il Peso delle Travi è pari a = (A trave x La + A trave x Lb) x γ
Successivamente abbiamo moltiplicato lo sforzo Normale di ogni piano x il numero di piani ed ottenuto Nmax= 1784,81 KN
In un ulteriore foglio excel si è inserito come dato di partenza proprio lo sforzo Normale max per andare a ricavare le dimensioni della base e dell’altezza del pilastro in legno. In questo caso b = 35 cm e h = 50 cm

SAP 2000
Sul programma SAP 2000 abbiamo ricostruito i tre telai e verificato i valori numerici di Mmax e Nmax, i relativi diagrammi delle sollecitazioni di travi e pilastri ci hanno confermato quanto detto.
-CEMENTO ARMATO
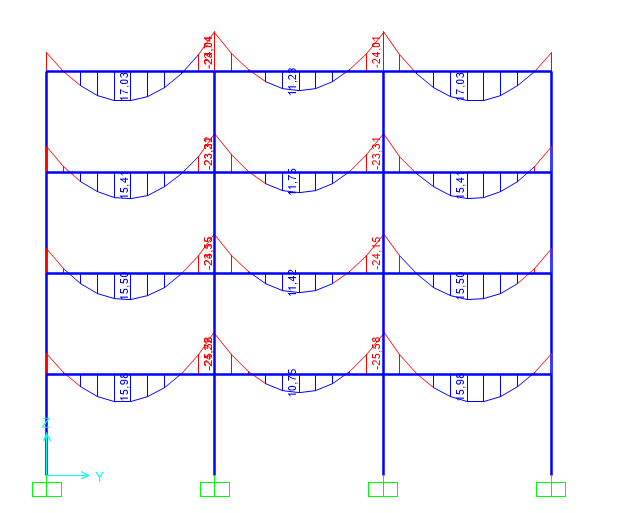
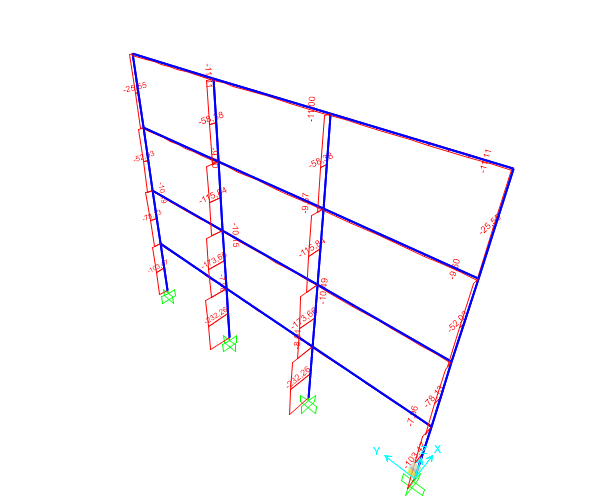
-LEGNO
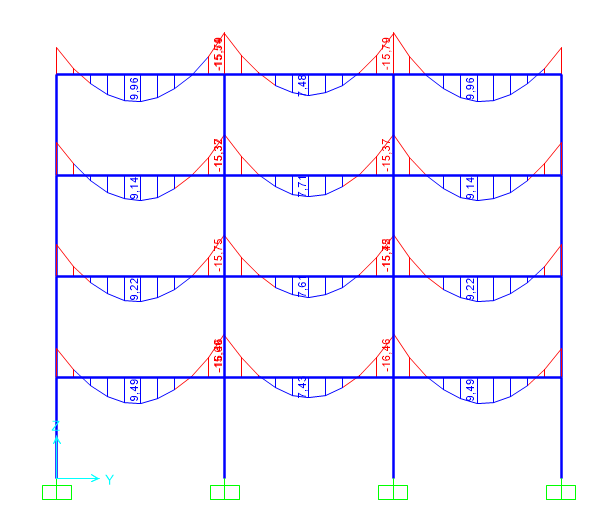
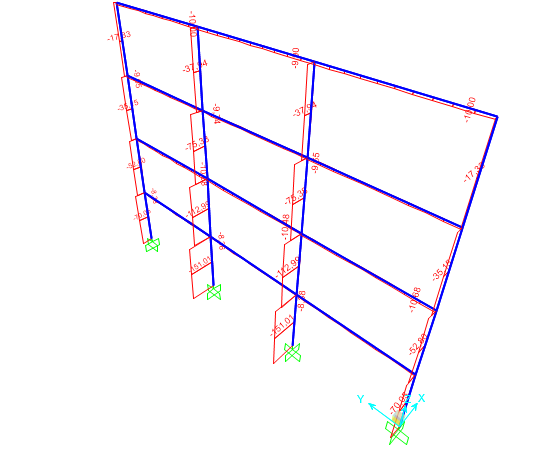
-ACCIAIO
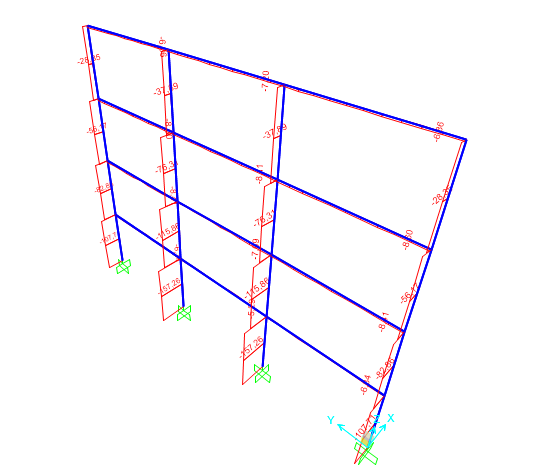
Esercitazione svolta in coppia con Serena Mariucci
Beatrice Taiariol
Commenti recenti