Travature reticolari
La travatura reticolare è formata da travi vincolate ai nodi attraverso cerniere in modo da costituire un elemento resistente e indeformabile. E' formata da due elementi continui chiamati correnti, aste verticali denominate montanti e inclinate chiamate diagonali. Attraverso i nodi vengono scambiate le forze assiali come uniche forze di contatto. A struttura completata le aste potranno risultare tese (forza assiale rivolta verso l'esterno dell'asta), compresse (forza assiale ricolta verso l'interno) o scariche.
Le travature reticolari sono strutture che possono essere risolte con il metodo delle sezioni o con il metodo dei nodi. Posterò qui di seguito i due esempi relativi alle prime due esercitazioni fatte.
Travatura reticolare simmetrica risolta con il metodo delle sezioni di Ritter

1) Il primo passo da eseguire in entrambi i casi è quello di verifcare l'isostaticità della struttura L=V
dove V=Ve+Vi e L=3(libertà)x11(numero delle aste)=33
la formula che permette di calcolare quanti gradi di libertà riesce a liberare una cerniera è 2(n-1) dove n è il nuemro dei corpi che la cerniera collega.
A e H: 2(2-1)=2
B e G: 2(3-1)=4
C, D ed E: 2(4-1)=6
Vi=2+2+4+4+6+6+6=30 Ve=3 V=Vi+Ve=33 V=L La struttura è isostatica
2) Reazioni vincolari
Rva= 30 KN Rvb=30 KN
3)Azioni di contatto
Applico delle sezioni che taglino tre aste non convergenti nello stesso nodo e vado cosi a determinare le azioni di contatto attraverso l'equilibrio alla traslazione orizzontale, verticale e l'equilibrio dei momenti rispetto ad un punto scelto.
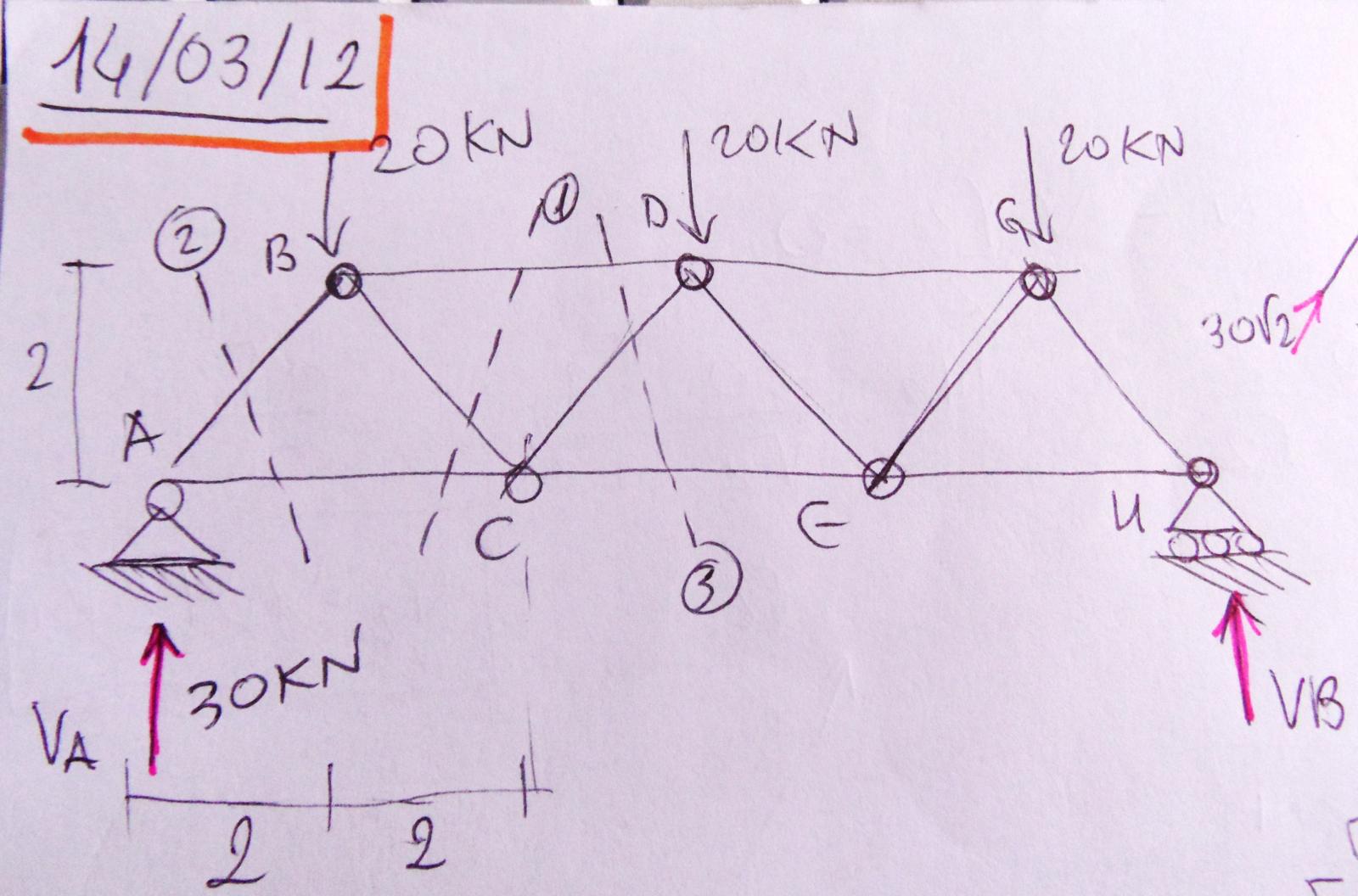
Faccio per prima la sezione 1 che passa per l'asta AC, BC e BD

Faccio l'equilibrio dei momenti attorno al punto C e ricavo N1 di compressione che vale 40 Kn, l'asta BD è quindi compressa. Con l'equilibrio dei momenti attorno al punto B trovo N3=30KN e l'asta AC è quindi tesa. Con l'equilibrio alla traslazione verticale trovo N2=10radice di 2 Kn e l'asta BC è quindi tesa.
Sezione 2 che passa per le aste AB e AC
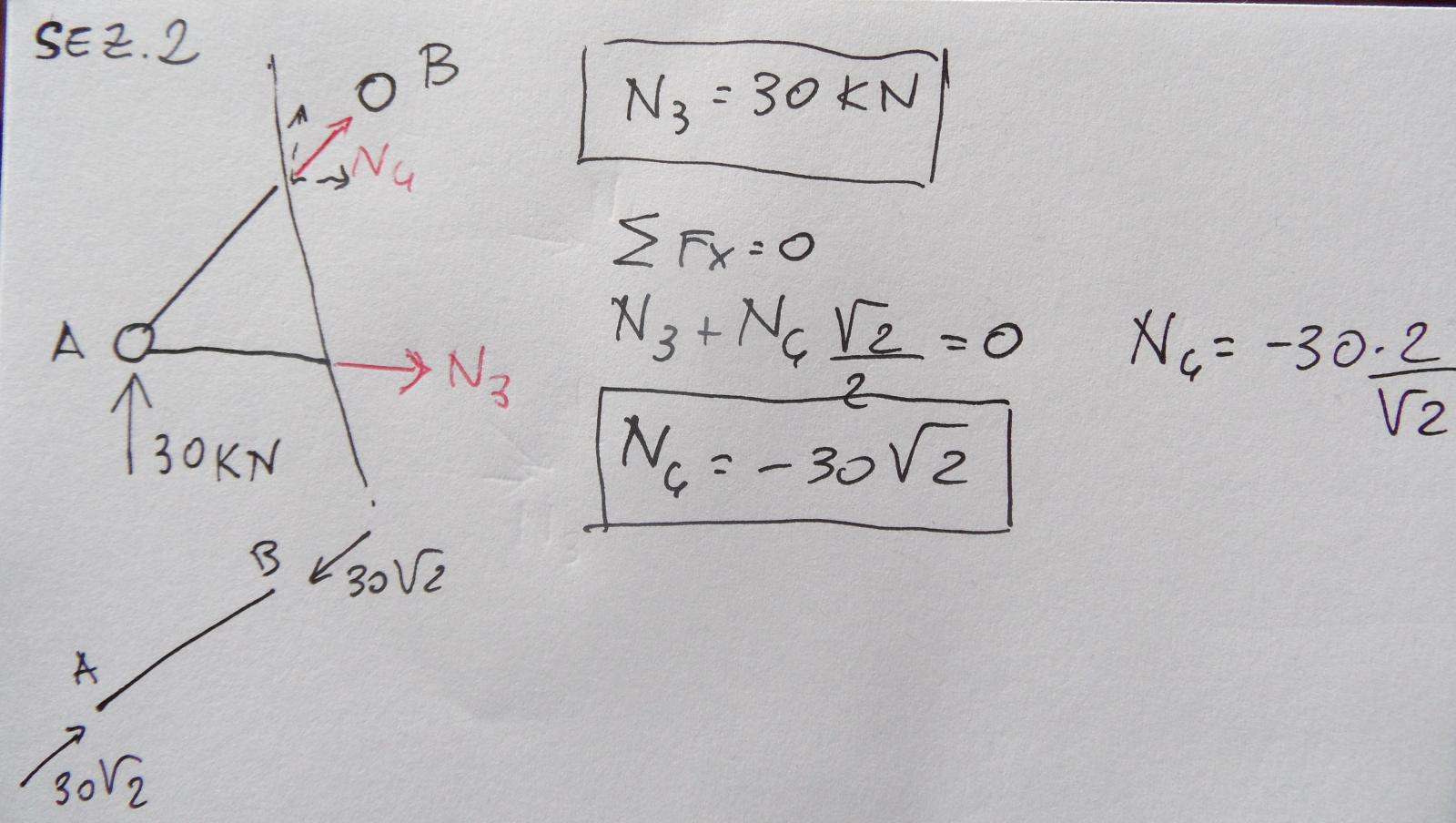
Avendo gia trovato N3 decido di fare l'equilibrio delle forze orizzontali. Scompongo la forza obliqua N4 nella componente orizzontale e verticale (N4 radice di 2/2). Trovo cosi la forza N4 di compressione che vale 30radice di 2.
Applico ora l'ultima sezione che passa per le aste BD, CD e CE.
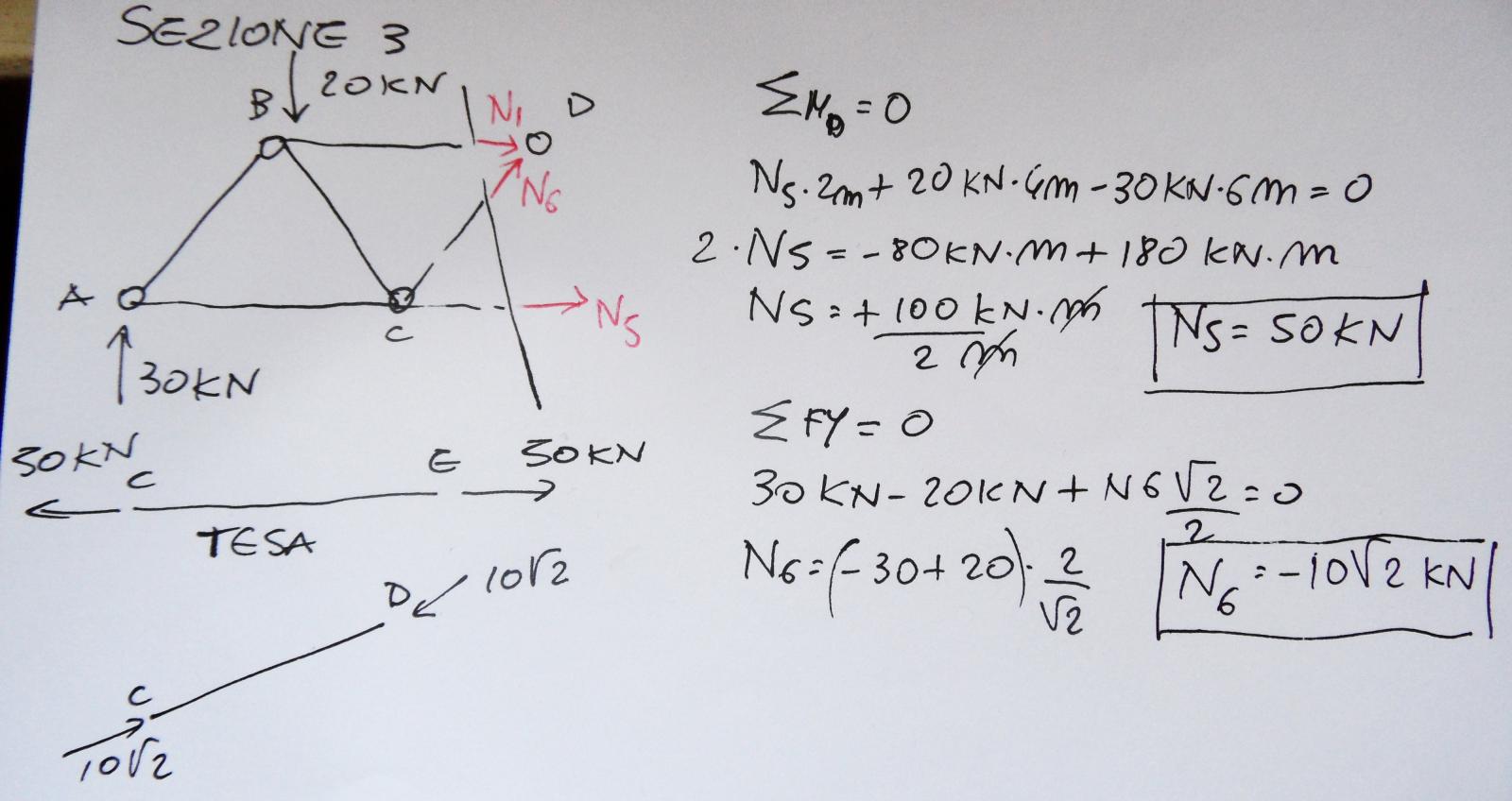
Con l'equilibrio alla rotazione in D ricavo la forza N5 di trazione che vale 50KN e con l'equilibrio alle traslazione verticale ricavo N6, forza di compressione che vale 10 radice di 2.
Lo schema delle aste tese e compresse è quindi il seguente.
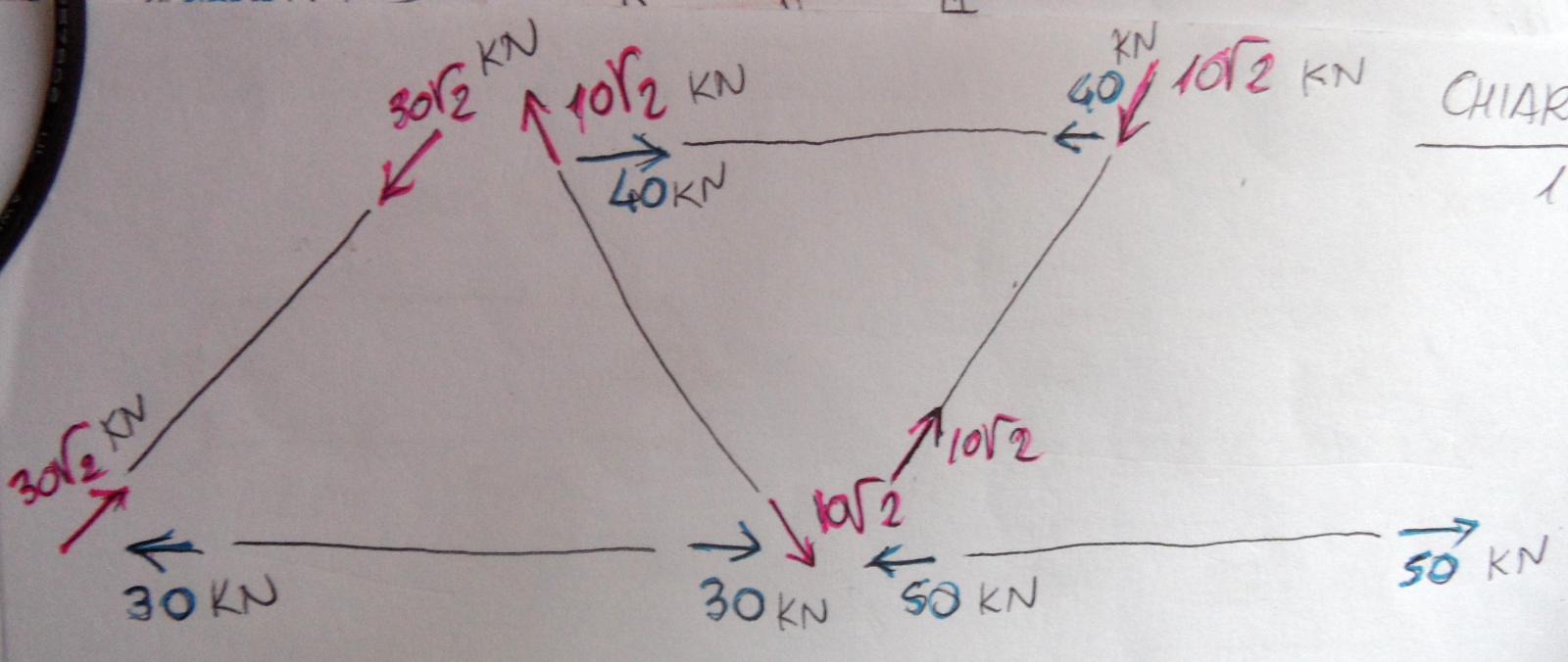
Essendo la struttura simmetrica sono succicienti tali sezioni. Il resto è identico.
Travatura reticolare asimmetrica risolta con il metodo dei nodi
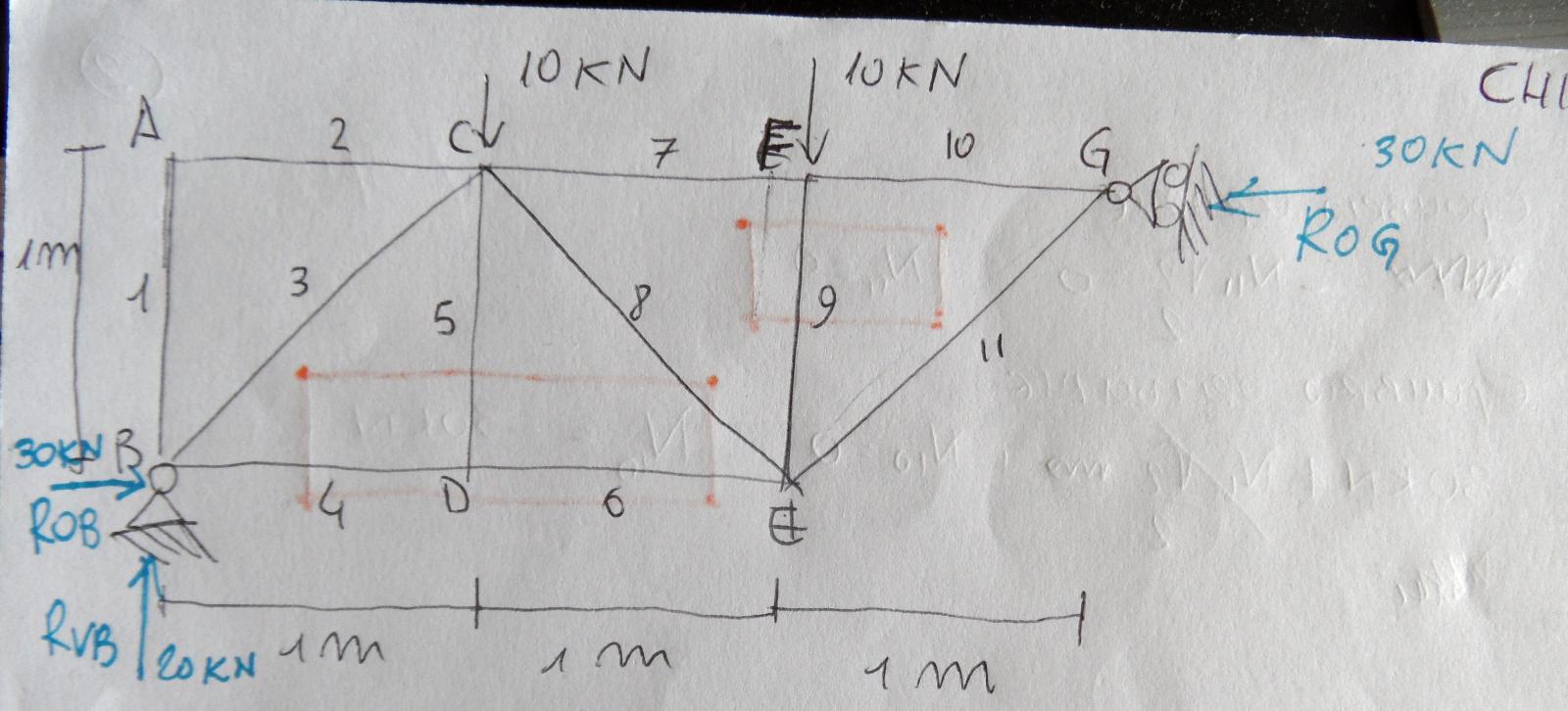
In questo caso si isolano i nodi e si calcolano le azioni di contatto attraverso gli equilibri alle traslazioni verticali e orizzontali.
1) Verifica isostaticità verificare che L=V
V=Ve+Vi Ve=3 (la cerniera toglie due gradi di libertà e il carrello 1)
Vi= A e G: (2-1)1=2
B, D e F: (3-1)2=4
C: (5-1)2=8
E: (4-1)2=6 Vi=2+2+4+4+4+8+6=30 Ve+Vi=3+30=33
L=3(libertà)x11(aste)=33 V=L=33
La struttura è isostatica.
2)Reazioni vincolari:

Con l'equilibrio alla traslazione verticale mi ricavo Rvb=20Kn
Con l'equilibrio alla traslazione orizzontale ricavo che Rog è uguale a Rob e con l'equilibrio alla rotazione in A ricavo che le due forze orizzontali valgono 30 Kn e sono di compressione.
3) Azioni di contatto attraverso il metodo dei nodi
Iniziamo isolando il punto G.

Anche questa volta avendo aste inclinate è necessario scomporre la forza obliqua nelle due componenti orizzontale e verticale per poter procedere con gli equilibri alla traslazione.
Attraverso l'equilibrio alla traslazione verticale ricavo che la mia forza assiale lungo l'asta 11 (N11), essendo l'unica forza verticale del nodo, è uguale a zero. Con l'equilibrio alla trasl. orizzontale (utilizzando come gia detto la componente orizzontale di N11) ricavo che N rispetto al nodo ha un valore di compressione e vale 30 KN (si oppone infatti alla forza del carrello che spinge anchessa verso il nodo.
Isoliamo ora il nodo F

Su di esso troviamo una forza concentrata di 10 KN e gia conosciamo N10 che è di compressione. Dobbiamo ricavare quindi N9 e e N7. Attraverso l'equilibrio alla traslazione verticale ci ricaviamo N9 forza di compressione che vale 10 KN e attraverso l'equilibrio alla traslazione orizzontale ricaviamo N7, anch'esso di compressione di valore 30 KN.
Passiamo ad isolare il nodo E
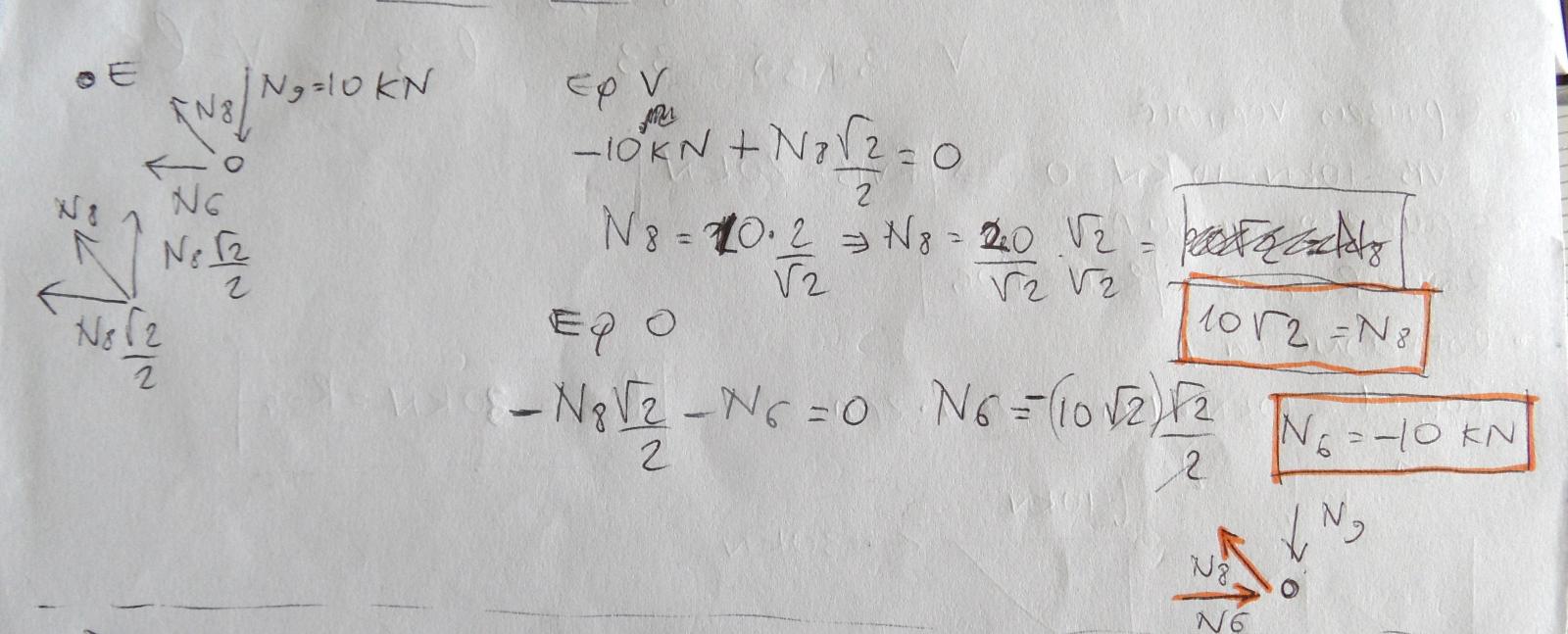
N9 già lo conosciamo e sappiamo che vale 10 Kn e che è una forza di compressione. Dobbiamo ricavare N8 ed N6. Con l'equilibrio alla traslazione verticale (scomponendo N8 nelle due componenti orizzontale e verticale) ricaviamo che la forza obliqua N8 è una forza di trazione e vale 10 radice di 2. Con l'equilibrio delle forze orizzontali ci ricaviamo N6 che è una forza di compressione e vale 10 KN.
Isoliamo ora il nodo D

N6 lo conosciamo e sappiamo che vale 10 Kn e che è forza di compressione. Facendo l'equilibrio delle forze orizzontali troviamo quindi che N4 è anch'esso forza di compressione e che vale 10 KN. Per ora non abbiamo abbastanza dati per calcolarci N5 quindi andiamo avanti.
Isoliamo il nodo B

Su questo nodo agiscono le forze del carrello, 30 Kn in orizzontale e 20 in verticale. Inoltre già conosciamo N4, forza di compressione di 10 Kn. Scomponiamo N3 obliqua nelle due componenti e con l'equilibrio alla traslazione verticale ricaviamo che N1 vale 0 (l'asta AB sarà quindi scarica). Con l'equilibrio alla traslazione orizzontale ricaviamo che N3 è una forza di compressione e che vale 20radice di 2 KN.
Isoliamo infine il nodo C
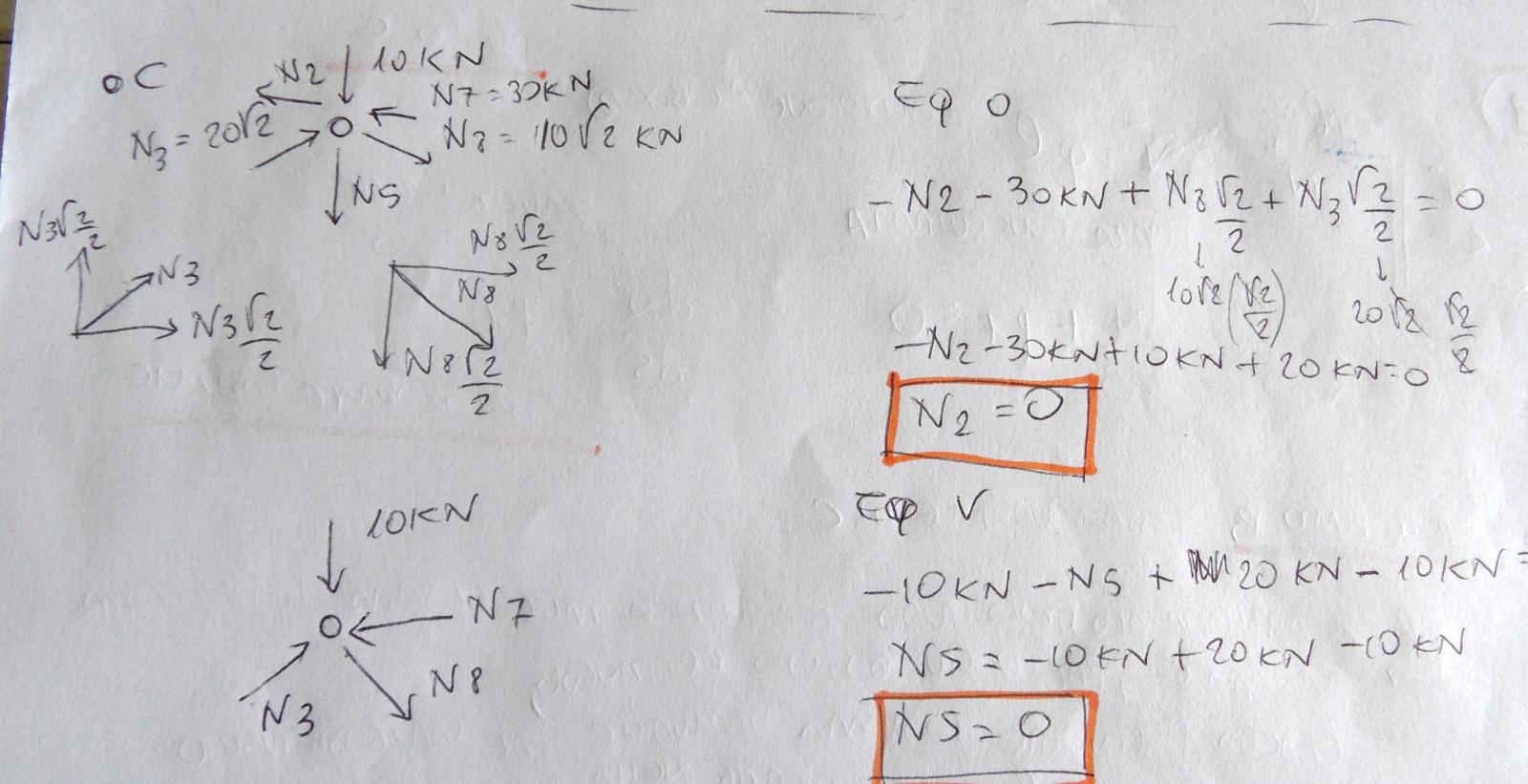
Su di esso agisce una forza esterna verticale verso il basso di valore 10 Kn, N3 N8 ed N7 sono noti. Con l'equilibrio alla traslazione orizzontale ricaviamo che N2 è uguale a 0 (l'asta AC è scarica). Con l'equilibrio alla traslazione verticale ricaviamo N5 che vale 0 (l'asta CD è scarica).
Dopo aver messo la struttura in SAP ho potuto osservare la deformata e i valori relativi allo sforzo normale, l'unico presente all'interno delle travature reticolari.
Deformata
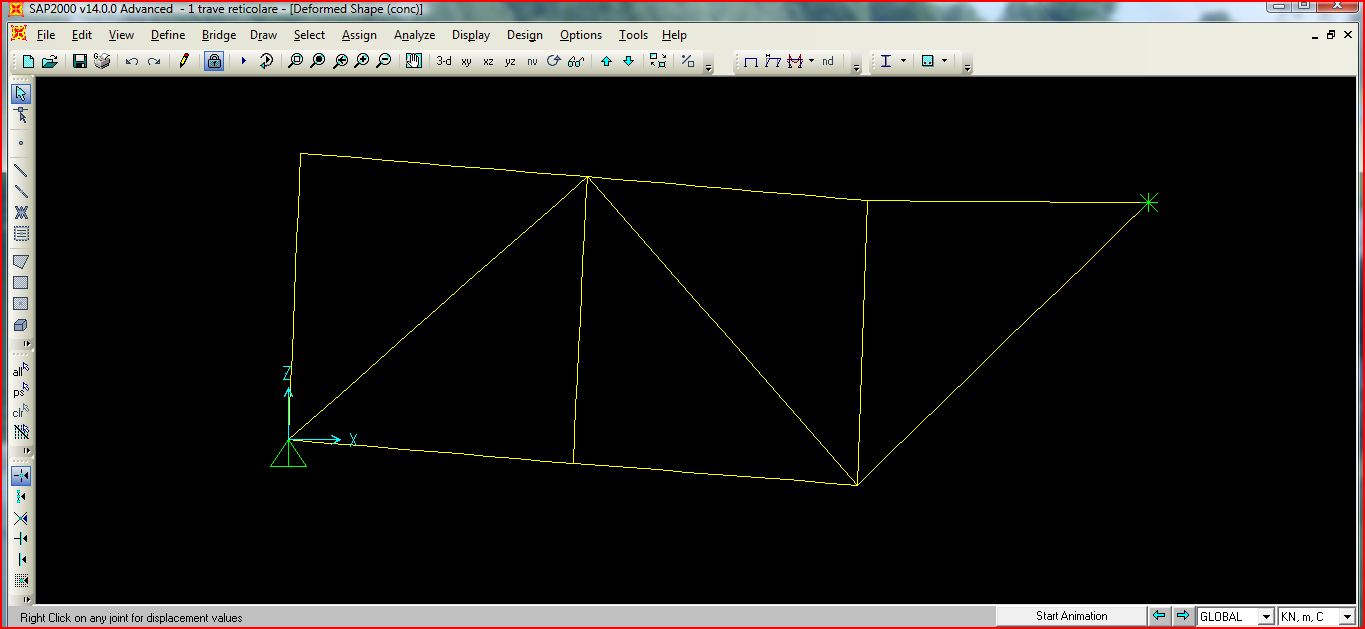
Diagramma dello sforzo normale

Dimensionamento trave (svolto con Manuel Lentini)
L’impalcato che abbiamo scelto è frutto di un primo ragionamento sulla struttura del nostro albergo (Prof. Cordeschi). Il sistema distributivo delle stanze prevede un corridoio di 2,40 m di larghezza e le stanze di 4 metri di interasse in larghezza e 6 m in profondità. Abbiamo scelto di dimensionare la trave 2-7 che copre una luce di 6,00 m e un interasse di 4,00 m. La sua area d’influenza è quindi pari a 6,00 x 4,00 = 24,00 mq.
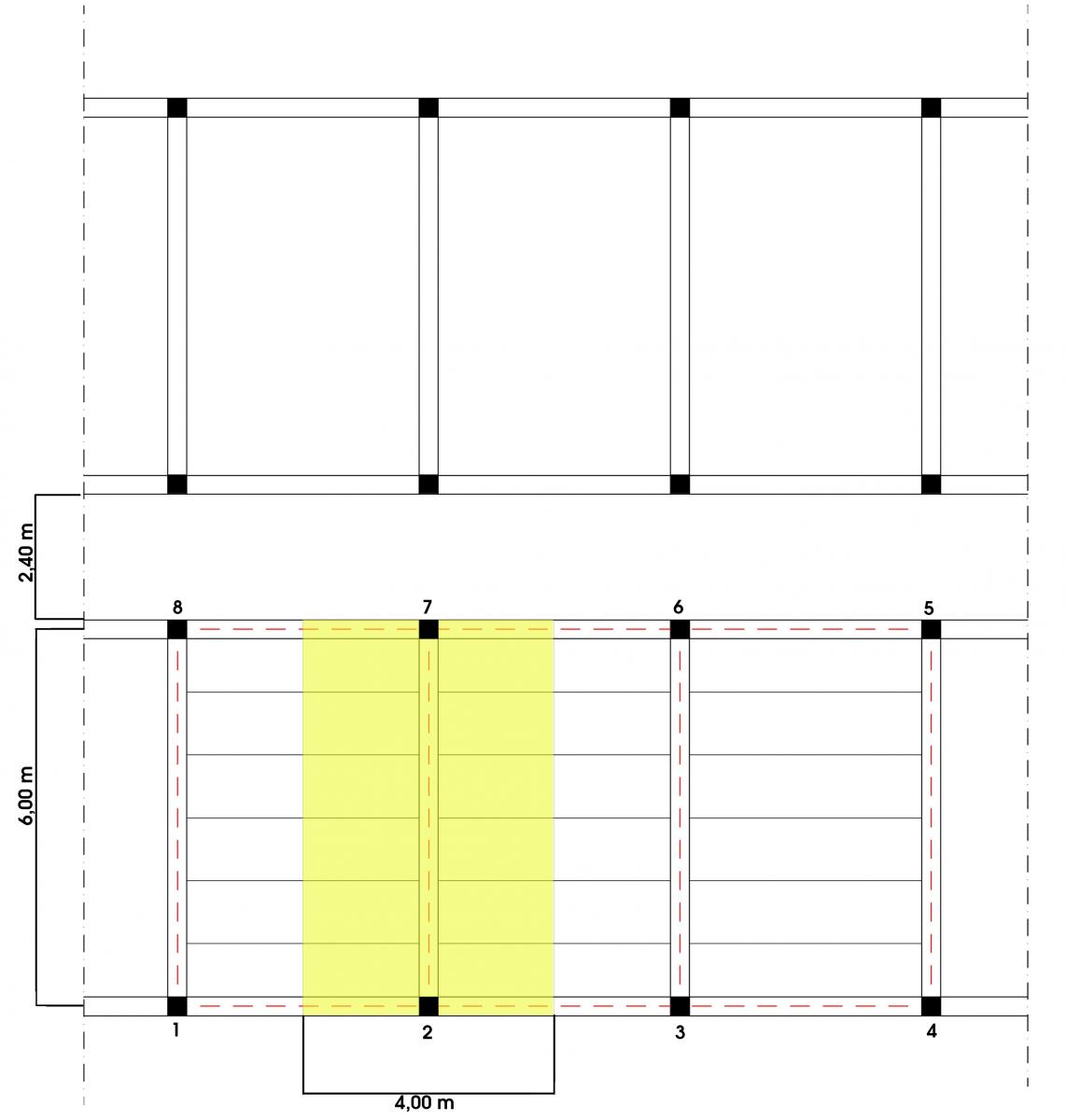
Per il dimensionamento corretto della trave è necessario calcolare Qs, Qp e Qa dove Qs (carico strutturale) indica il carico proprio della struttura; Qp (carico permanente) indica tutti quegli elementi non strutturali ma che permangono durante la vita della struttura e Qa indica il valore del carico accidentale dovuto ad esempio all’uso che si farà di quell’ambiente.
Trattandosi di stanze di un albergo abbiamo deciso di utilizzare come valore di carico accidentale quello relativo ai locali ad uso civile: 2,00 KN/Mq.
Ciascuno carico a mq è frutto della somma dei pesi (calcolati a mq) degli elementi che lo costituiscono:
P= V x γ / A dove V è il volume dell’elemento, γ è il peso specifico del materiale e A è l’area in questo caso relativa ad 1 mq di struttura.
Struttura in legno
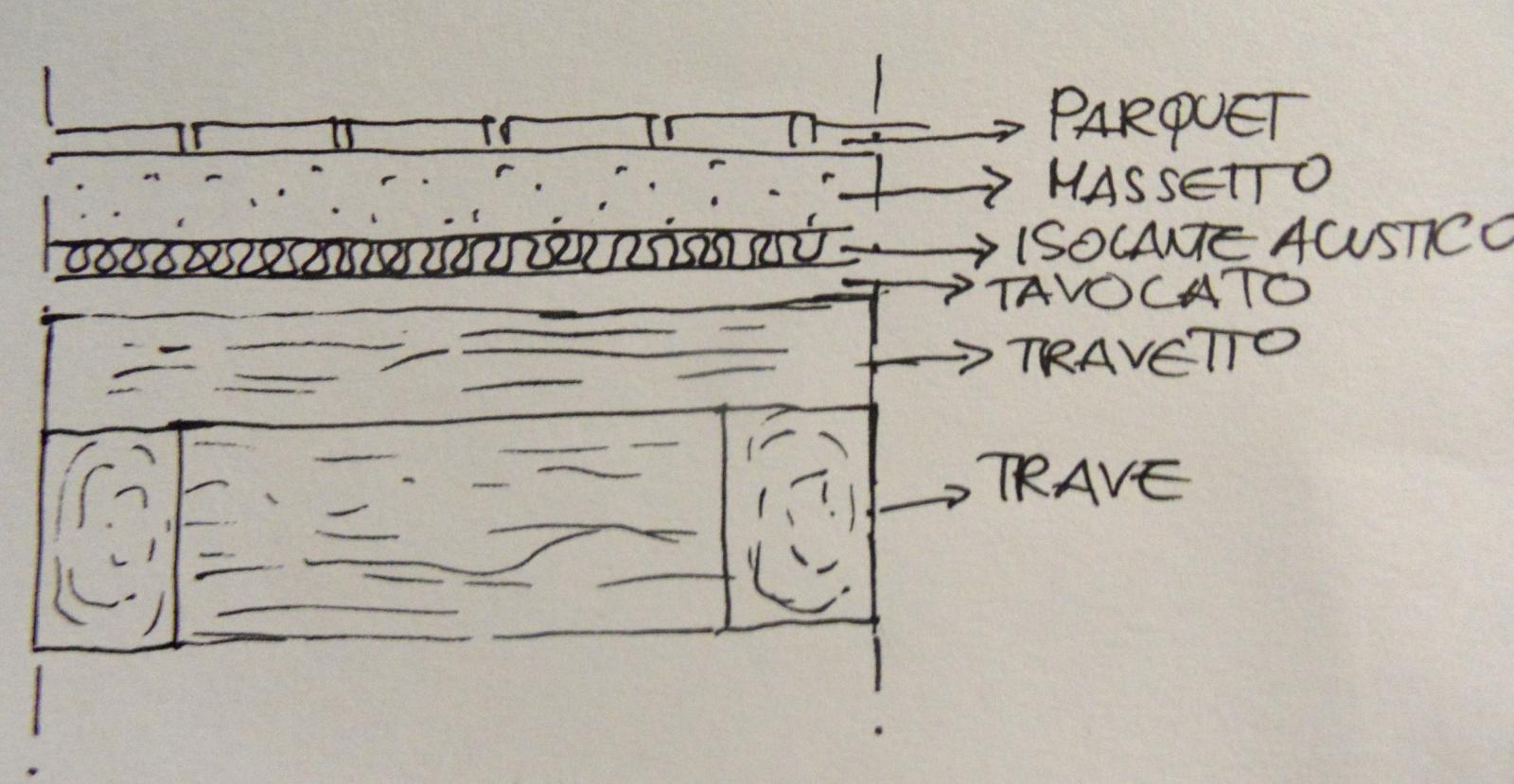
a) Dimensionamento del travetto (interasse 1m, luce 4m):
Partiamo con il dimensionamento del travetto prendendo come carico strutturale iniziale quello del tavolato.
Qs:
-Tavolato:
spessore : 0,045 m
peso specifico: 700 Kg/mc
Volume: 0,045 x 1 x 1 = 0,045 mc
Peso: 0,045 x 700 = 31,5 Kg 0,315 Kn
Peso a mq: 0,315 Kn/1 mq
Qp:
-Isolante acustico (Acustic system 7): http://www.termoisolanti.com/prodotti/isolanti-acustici/sistemi-fonoisolanti-e-antivibranti-per-solai-in-legno-laterocemento-e-c.a/acustic-system-7.php
Spessore : 0,007 m
Peso a mq: 3 Kg/mq 0,03 kn/mq (fornito dalla casa produttrice)
-Massetto in cls:
Spessore: 0,08 m
Peso specifico: 2000Kg/mc
Volume: 0,08 x 1 x 1 =0,08 mc
Peso: 0,08 x 2000 = 160 Kg 1,6 KN
Peso a mq: 1,6 kn/mq
-Parquet in ciliegio:
Spessore: 0,02 m
Peso specifico: 850 Kg/mc
Volume: 0,02 x 1 x 1= 0,02 mc
Peso: 0,02 x 850= 17 Kg 0,17 KN
Peso a mq: 0,17 KN/mq
-Incidenza impianti:
Peso a mq: 0,5 KN/mq
-Incidenza tramezzi:
Peso a mq: 1 Kn/mq
Qp tot: 0,03+1,6+0,17+0,5+1= 3,3 KN/mq
Qa:
-Civile abitazione: 2 KN/mq
Inseriamo i dati nella tabella excel (la formula presente nella tabella excel relativa al momento Ql^2/8 è in questo caso valida trattandosi di una trave doppiamente appoggiata. Se si fosse trattato di una trave a sbalzo l'espressione sarebbe stata Ql^2/2)

Dalla tabella possiamo leggere che con i carichi inseriti e assumendo una base per il travetto di 0,12m l’altezza deve essere non inferiore a 0,2201 m.
Abbiamo cosi scelto un travetto della casa produttrice Canducci GL24H 120x240 mm. (http//www.mmk-canducci.it/)
La classe di resistenza GL24H indica una resistenza a flessione 24N/mmq e dove Kmod è il coefficente moltiplicativo in funzione della durata del carico. Normalmente Kmod è compreso tra 0,5 e 1. In questo caso prendiamo un K mod ipotetico di 0,7 e lo inseriamo nella tabella excel.
Il passo successivo è stato quello di calcolare il peso a mq del travetto scelto e di inserirlo all’interno dei Qs nella nostra tabella excel.
Peso specifico: 550 Kg/mc
Volume: 0,12 x 0,24 x 1= 0,029 mc
Peso: 0,029 x 550= 15,95 Kg 0,1595 KN
Peso a mq: P x 1/ interasse 0,1595 x (1/1)= 0,1595 KN/mq
Qs tot: Tavolato più travetti 0,315 + 0,159 =0,474 KNmq

Inserendo il peso del travetto dalla tabella ci compare che assumendo di nuovo una base di 0,12 m l’altezza risulta essere di 0,2232 m. Il travetto da noi scelto era di 0,12 x 0,24 m. La sezione è quindi verificata.
b) Dimensionamento trave (luce 6 m, interasse 4m)
A questo punto possiamo inserire nella tabella la luce e l’interasse relativi alla trave (mantenendo gli stessi carichi).

Ne risulterà, assumendo come base 0,24 m, un’altezza di 0,4101 m.
Abbiamo proceduto con la scelta di una trave che soddisfacesse le misure richieste.
La trave scelta è una GL32H 240 x 440 mm.
Calcolo il peso della trave:
Volume: 0,24 x 0,44 x 1= 0,1056 mc
Peso specifico: 550 Kg
Peso: 0,1056 x 550= 50,08 Kg 0,5808 KN
Peso a mq: 0,5808 x 1/4= 0,1452 KN/mq (4 m = interasse trave)
A questo punto possiamo sommare il peso della trave agli altri valori in Qs:
Qstot: 0,474 + 0,1452 = 0,619 KN/mq
Abbiamo inserito il nuovo valore del carico strutturale all’interno della tabella excel e ciò che ne risulta è una trave di 24 x 41,52 cm, trave con dimensioni minori rispetto a quella scelta da noi.

La scelta della trave è quindi verificata.
Struttura in acciaio
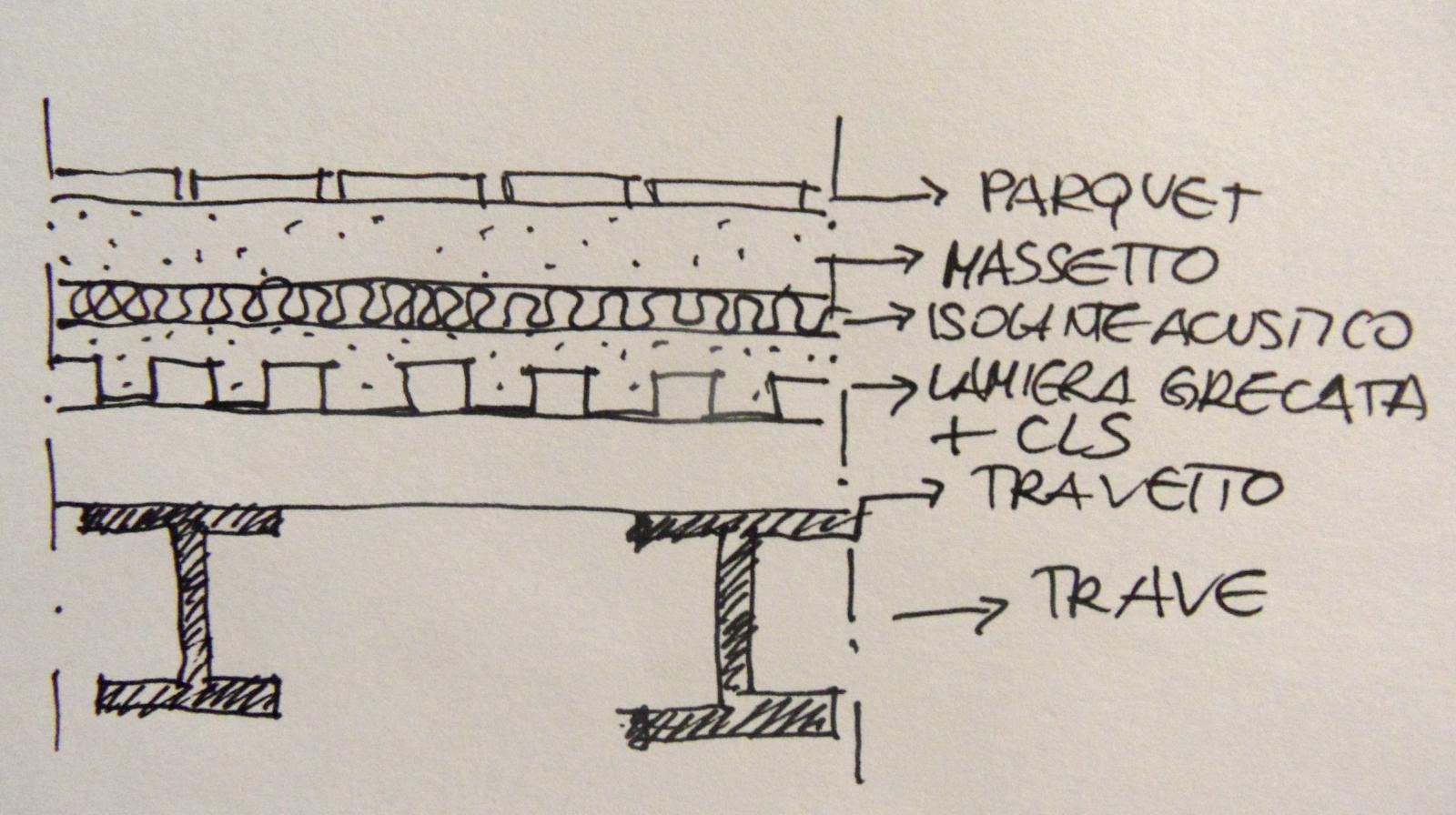
a) Dimensionamento del travetto (interasse 1m, luce 4m):
Partiamo con il dimensionamento del travetto prendendo come carico strutturale iniziale quello del tavolato.
Qs:
- Lamiera grecata più getto in cls:
Spessore: 0,1 m tipo: A55/P600
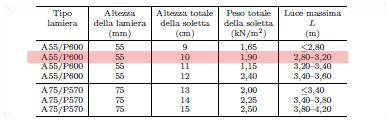
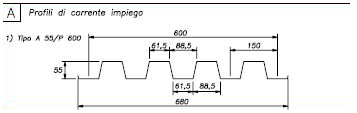
Come tabellato il peso a mq è 1,90 KN/mq
Qp:
-Isolante acustico (Acustic system 7):
Spessore : 0,007 m
Peso a mq: 3 Kg/mq 0,03 kn/mq (fornito dalla casa produttrice)
-Massetto in cls:
Spessore: 0,08 m
Peso specifico: 2000Kg/mc
Volume: 0,08 x 1 x 1 =0,08 mc
Peso: 0,08 x 2000 = 160 Kg 1,6 KN
Peso a mq: 1,6 kn/mq
-Parquet in ciliegio:
Spessore: 0,02 m
Peso specifico: 850 Kg/mc
Volume: 0,02 x 1 x 1= 0,02 mc
Peso: 0,02 x 850= 17 Kg 0,17 KN
Peso a mq: 0,17 KN/mq
-Incidenza impianti:
Peso a mq: 0,5 KN/mq
-Incidenza tramezzi:
Peso a mq: 1 Kn/mq
Qp tot: 0,03+1,6+0,17+0,5+1= 3,3 KN/mq
Qa:
-Civile abitazione: 2 KN/mq
Inseriamo i dati nella tabella excel

Scelgo un profilo IPE 140 con Wx= 77,3 cm^3 h=140 mm b= 73mm Area= 16,4 cmq
Peso specifico: 7800 kg/mc
Volume: 0,00164 x 1 =0,00164 mc
Peso: 0,00164 x 7800= 12,79 Kg 0,1279 KN
Peso mq: 0,1279x 1/1= 0,1279 KN/mq
Qstot: carico soletta più carico travetto 0,1279+1,9=2,027 KN/mq
A questo punto abbiamo inserito nella tabella il nuovo Qs comprendente anche il peso dei travetti.

Ne risulta una trave con Wx pari a 71,71 cm^3, valore inferiore a quello proprio del travetto da noi scelto.
Il travetto è quindi verificato.
b) Dimensionamento trave
A questo punto possiamo inserire nella tabella la luce e l’interasse relativi alla trave (mantenendo gli stessi carichi).

Abbiamo scelto una trave IPE 330 con Wx= 713cm^3 A=62,6 cmq
Peso specifico: 7800 Kg/mc
Volume: 0,00626 x 1= 0,00626 mc
Peso: 0,00626 x 7800 = 48,8 Kg 0,488 KN
Peso mq: 0,488 x 1/4 = 0,122 KN/mq
Abbiamo sommato il peso a Qs e aggiunto il nuovo valore alla tabella
Qs tot= 2,027 + 0,122 =2,149 KN/mq

Una volta inserito il peso della trave il nuovo Wx richiesto è di 656,15 cm^3, valore inferiore a quello relativo alla trave da noi scelta. Anche questa sezione è verificata.
Struttura in cemento armato
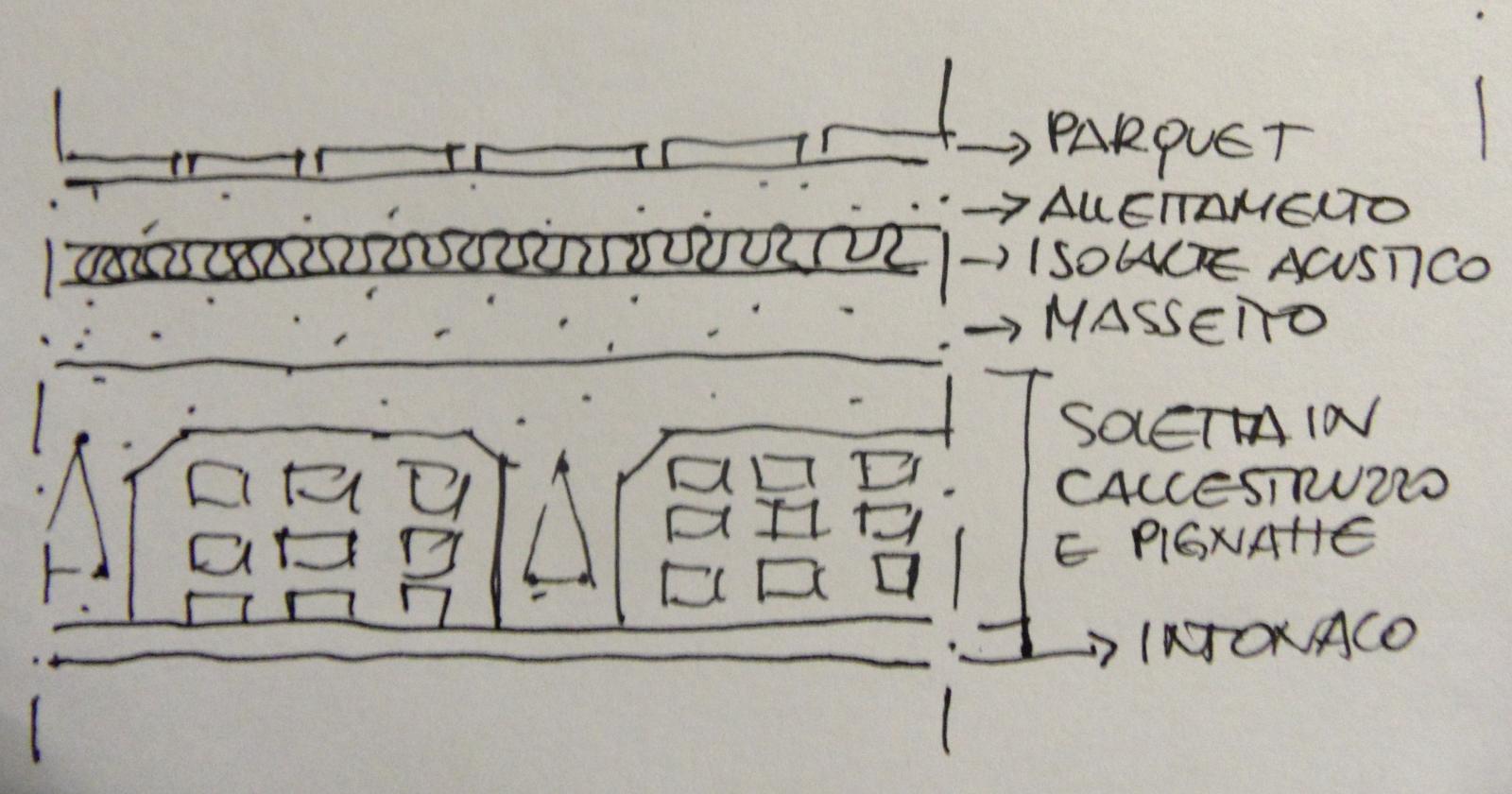
Qs:
-Pignatte:
Volume: 0,16 x 0,5 x 1= 0,08 mc
Peso specifico: 600 Kg/mc
Peso: 0,08 x 600= 48 Kg 0,48 KN
Peso mq: 0,48 KN/mq
-Travetti:
Volume: 0,1 x 0,16 x 1 = 0,016 mc
Peso specifico: 2500 Kg/mc
Peso: 0,016 x 2500 = 40 Kg 0,4 KN
Peso mq: 0,4 KN/mq
-Soletta:
Volume: 0,04 x 1 x 1= 0,04 mc
Peso specifico: 2500 Kg/mc
Peso: 0,04 x 2500= 100 Kg 1 KN
Peso mq: 1 KN/mq
Qs tot: 0,48 + 0,4 + 1 = 1,88 KN/mq
Qp:
-Massetto in cls:
Spessore: 0,04 m
Peso specific0: 2000 Kg/mc
Volume: 0,04 x 1 x 1= 0,04 mc
Peso: 0,04 x 2000 = 80 Kg 0.8 KN
Peso mq: 0,8 KN/mq
-Isolante acustico (Acustic system 7):
Spessore : 0,007 m
Peso a mq: 3 Kg/mq 0,03 kn/mq (fornito dalla casa produttrice)
-Allettamento in cls:
Spessore: 0,03 m
Peso specifico: 2000 Kg/mc
Volume: 0,03 x 1 x 1 =0,03 mc
Peso: 0,03 x 2000 = 60 Kg 0,6 KN
Peso a mq: 0,6 kn/mq
-Parquet in ciliegio:
Spessore: 0,02 m
Peso specifico: 850 Kg/mc
Volume: 0,02 x 1 x 1= 0,02 mc
Peso: 0,02 x 850= 17 Kg 0,17 KN
Peso a mq: 0,17 KN/mq
-Intonaco:
Spessore: 0,01 m
Peso specifico: 1200 Kg/mc
Volume: 0,01 x 1 x 1= 0,01 mc
Peso: 0,01 x 1200= 12 Kg 0,12 KN
Peso a mq: 0,12 KN/mq
-Incidenza impianti:
Peso a mq: 0,5 KN/mq
-Incidenza tramezzi:
Peso a mq: 1 Kn/mq
Qp tot: 0,8+0,03+0,6+0,17+1+0,5+ 0,12= 3,22 KN/mq
Qa:
-Civile abitazione: 2 KN/mq
Inseriamo i dati nella tabella excel

Dalla tabella si ricava che, data una base di 25 cm, l’altezza minima deve essere di 38,68cm. Prendiamo una trave 25x45 con classe di resistenza C40/50 (e acciaio B450C per zona sismica).
Aggiungiamo ai carici strutturali a mq il peso a mq della trave P: 2,42 x 1/interasse = 0,605 KN/mq
Qs tot= 1.88 + 0,605= 2,48 KN/mq
Inserendo il nuovo dato nella tabella si ricava che l'altezza necessaria è pari a 40,08 cm, inferiore all’altezza della trave scelta. La nostra sezione è quindi verificata.

Travatura reticolare 3D
Per eseguire questa esercitazione abbiamo utilizzato Autocad e Sap 2000.
In Autocad ho disegnato la travatura reticolare composta da 4x6 moduli collegati da aste inclinate sempre nella stessa direzione.

Ho successivamente importato il 3D in Sap.
Per prima cosa assegno le cerniere interne a tutto il corpo e applico i 4 vincoli (cerniere) alle estremità della base.
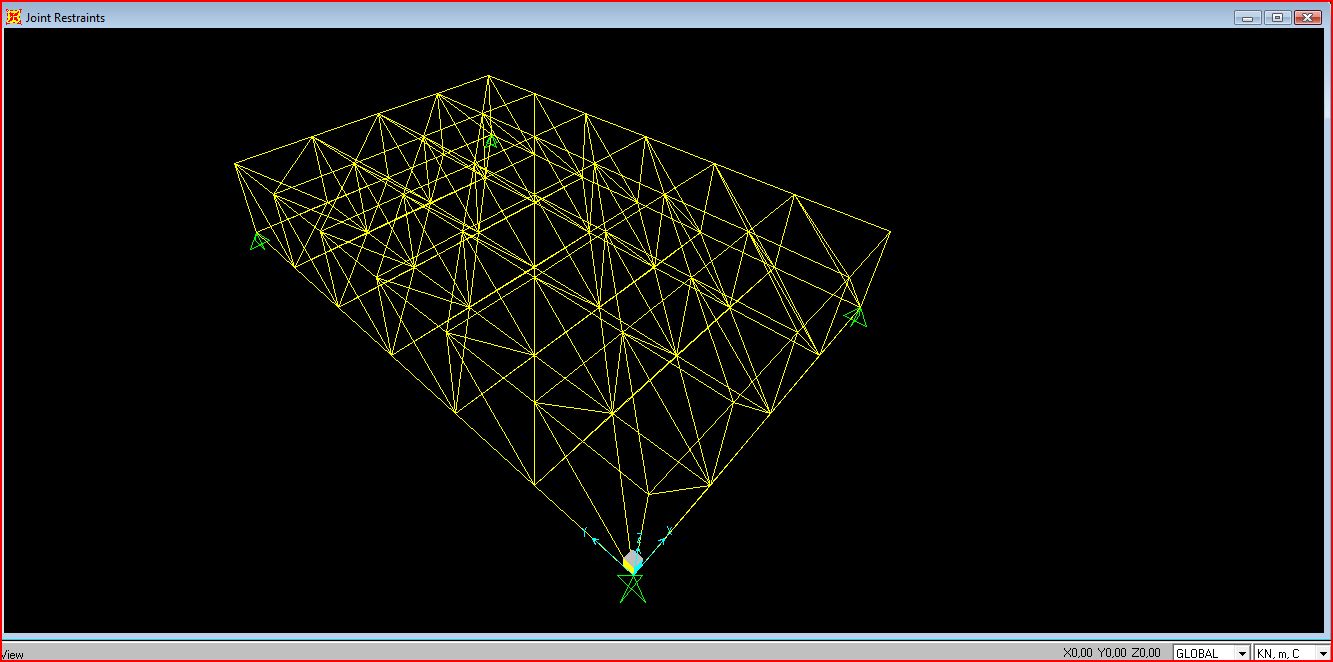

Ho in seguito definito il materiale e la sezione scegliendo una sezione tubolare in acciaio.
Definisco quindi un carico che chiamo “concentrato” di 40 KN verso il basso sull’asse Z e lo assegno ad ogni nodo della superficie superiore.

Dopo aver numerato le aste lascio analizzare la mia struttura dal sistema ottenendo così il diagramma dello sforzo normale.
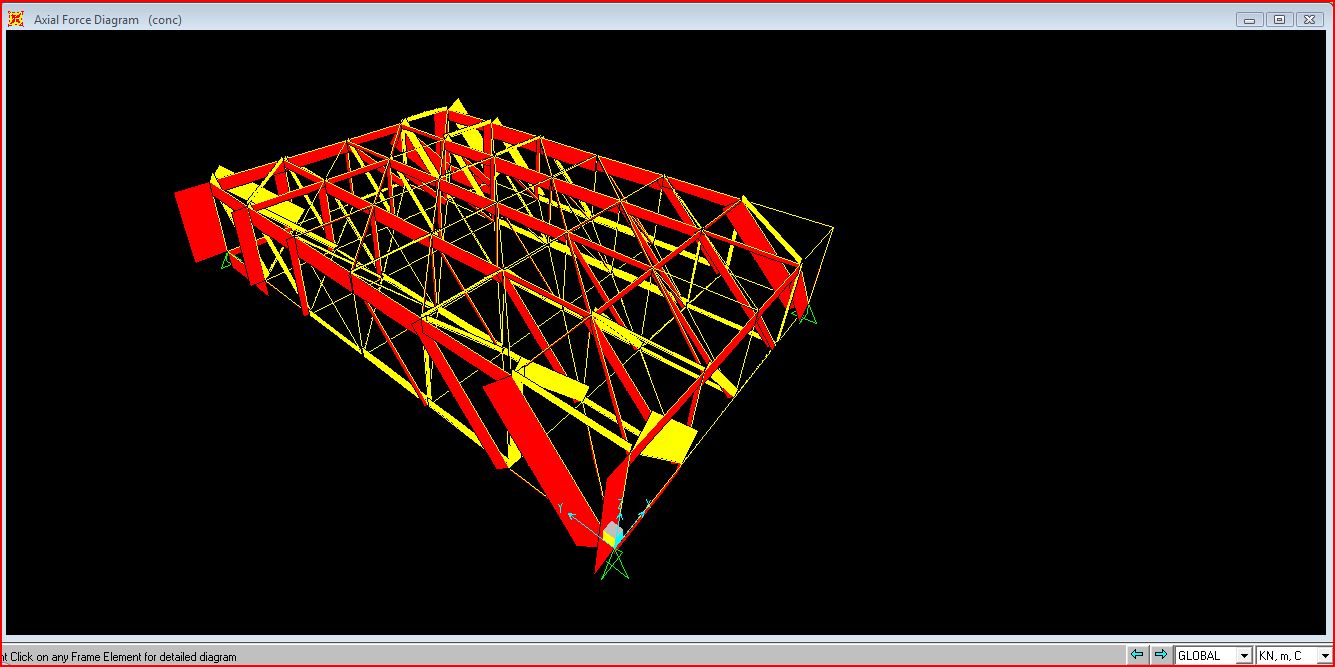
Esporto i dati nella tabella excel prendendo in considerazione solo quelli relativi alla lunghezza totale delle aste dritte (2m) e inclinate (2,8) essendo i dati relativi a sezioni eseguite in differenti punti della lunghezza totale.
Procedo riordinandomi i valori dello sforzo normale in ordine decrescente. Riesco così ad individuare immediatamente i valori massimi di trazione e di compressione.
PROGETTO E VERIFICA A COMPRESSIONE PER L'ASTA DI 2 M
L’asta sottoposta a maggior sforzo di compressione è l’asta n. 186 con sforzo normale pari a 296,438 Kn.

So che σ=N/A ≤ Fd. Per il progetto dell’asta ponendo σ= Fd=N/A ne risulta che, per trovare l’area della sezione, devo applicare la formula A=N/Fd dove Fd indica il valore di design che si calcola attraverso il rapporto tra Fy (valore della tensione di snervamento dell’acciaio) e γ (coefficiente di sicurezza che corrisponde a 1,05).
Scelgo un acciaio FE 510 S 355 che ha un Fy di 3550 Kg/cmq
Fd=3550/1,05=3380,96 Kg/cmq = 33,8096 Kn/cmq.
A= 296,438/33,8096= 8,8 cmq
Cerco sulla tabella dei profilati tubolari in acciaio (tratta dal sito www.oppo.it) la sezione subito maggiore che è quella di 9,650 cmq
Per eseguire la verifica della sezione scelta dovrà risultarmi una σ<Fd
σ= 296,438 Kn/9,65 cmq = 30,72 Kn/cmq Essendo 30,72 Kn/cmq< 33,8096Kn/cmq la sezione è verificata.
E’ ora necessario verificare che la sezione sia stata opportunamente dimensionata per evitare sbandamenti (instabilità Euleriana) e che resista quindi al carico critico Euleriano.
La formula per calcolare il peso critico è (π^2 x E x Jmin)/lo^2 dove E è modulo di elasticità che per l’acciaio è 210000 N/mmq, Jmin è il momento d’inerzia della sezione scelta e lo è la lunghezza libera di inflessione che si calcola moltiplicando la lunghezza dell’asta per un coefficiente relativo ai tipi di vincoli applicati all’asta (nel nostro caso il coeff. è 1 trattandosi di un’asta doppiamente incernierata.
P crit= (3,14^2 x 210000 N/mm^2 x 87,90 cm^4)/ 40000 cm= 455014,35 N = 455,01435 KN
Essendo il peso critico maggiore dello sforzo normale, 455,01435 > 296,438, l’asta progettata non andrà in instabilità euleriana.
PROGETTO E VERIFICA A COMPRESSIONE PER L'ASTA DI 2,8 M
L’asta sottoposta a maggior sforzo di compressione è l’asta n.7 con sforzo normale pari a 307,351 KN.

σ=N/A ≤ Fd Per il progetto dell’asta ponendo σ= Fd=N/A ne risulta che, per trovare l’area della sezione, devo applicare la formula A=N/Fd.
A=307,351Kn/ (338096 Kn/mq)= 9,091 Cmq
Scelgo una trave tubolare a sezione circolare con sezione metallica pari a 10,70 cmq.
Per eseguire la verifica della sezione scelta dovrà risultarmi una σ<Fd
σ= 307,351 Kn/10,7 cmq= 28,73 Kn/cmq 28,73 < 33,80 quindi la sezione è verificata.
Ora verificherò che anche questa sezione sia stata opportunamente dimensionata e che quindi non sia a rischio sbandamenti.
Ricordo che la formula per calcolare il peso critico è (π^2 x E x Jmin)/lo^2 e sostituisco i miei valori.
(9.86 x (210000 N/mm^2) x96,30cm^2)/78400cm = 254335,18N= 254,335Kn
Il peso critico risulta inferiore al nostro sforzo normale, la sezione non è quindi verificata.
Prendo una sezione più grande. La verifica a compressione non è necessaria perché essendo la sezione maggiore della precedente, verificata a compressione, sarà sicuramente verificata anch’essa.
Passo di nuovo a verificare che non sia sottoposta ad instabilità euleriana.
Peso critico= 9,86 x( 210000 N/mm^2) x 211 cm^4/78400cm= 557266,072 N= 557,267Kn
Questa volta il Peso critico è maggiore del nostro sforzo normale; La sezione è quindi verificata anche rispetto all’instabilità euleriana.
ORA PROCEDO CON IL PROGETTO E VERIFICA A TRAZIONE ma solamente sull’asta con valore di trazione maggiore, quella lunga 2,8 m.
La forza normale massima vale 256,572 Kn ed è applicata all'asta n.154

La verifica dell’instabilità euleriana non sarà effettuata perché riguarda solo le aste sottoposte a compressione.
Come nei casi precedenti per il progetto dell’asta, e quindi per la scelta della mia sezione utilizzo la formula σ=N/A ≤ Fd ; quindi ponendo σ= Fd=N/A ne risulta che, per trovare l’area della sezione, devo applicare la formula A=N/Fd.
A= 256,572 Kn/(338096 Kn/mq)= 0,00076 mq= 7,6 cmq
Scelgo quindi una trave tubolare con sezione metallica avente A=8,2 cmq e J=54cm^4
Ora verifico la mia sezione a trazione. Per la verifica dovrò avere la σ=N/A ≤ Fd
σ = 256,572 Kn /8,2 cmq= 31,29 Kn/cmq < 33,88 Kn/cmq (che è il mio Fd)
La sezione è quindi verificata a trazione.
Verificando l’asta lunga 2,8 m che è sottoposta al maggior valore di trazione non c’è bisogno di verificare la trazione massima dell’asta lunga 2 m, poiché il progetto viene fatto per resistere al valore maggiore in assoluto.
Commenti recenti