ESERCIZIO TRAVE RETICOLARE SIMMETRICA
INTRO
In questo esercizio ci troviamo di fronte ad una trave reticolare, ovvero una particolare tipologia strutturale in cui tutti gli elementi che compongono la struttura sono tratti lineari (puntoni o tiranti, sottoposti esclusivamente allo sforzo normale) collegati da due cerniere.
Il disegno della struttura è simmetrico per quanto riguarda la disposizione delle aste e la ripartizione dei carichi sui nodi, e questo ci sarà di aiuto perché basterà risolvere metà della struttura per poi estendere i risultati ottenuti al resto della nostra travatura.
STEP 1.
In primis dobbiamo verificare l’isostaticità della struttura (L=V, dove L sono i gradi di libertà e V corrisponde al numero di vincoli).
Per verificare che la struttura sia isostatica possiamo avvalerci di due metodi differenti:
metodo 1.
L=V (numero gradi di libertà = numero gradi di vincolo)
V = Ve + Vi = 3 + 30 = 33
L= 3 x numero corpi = 33
metodo 2.
Ve + a = 2 nodi (vincoli esterni+n. aste=n. nodi x 2)
3 + 11 = 2 x 7 à 14 = 14
Da queste uguaglianze possiamo dunque dire che la nostra struttura è isostatica.
STEP 2.
Adesso dobbiamo calcolare le reazioni vincolari.
Essendo una struttura simmetrica sottoposta a soli carichi verticali le reazioni vincolari (verticali) sono di uguale intensità e corrispondono a:
RVa = RVg = 60/2 = 30 Kn
STEP 3.
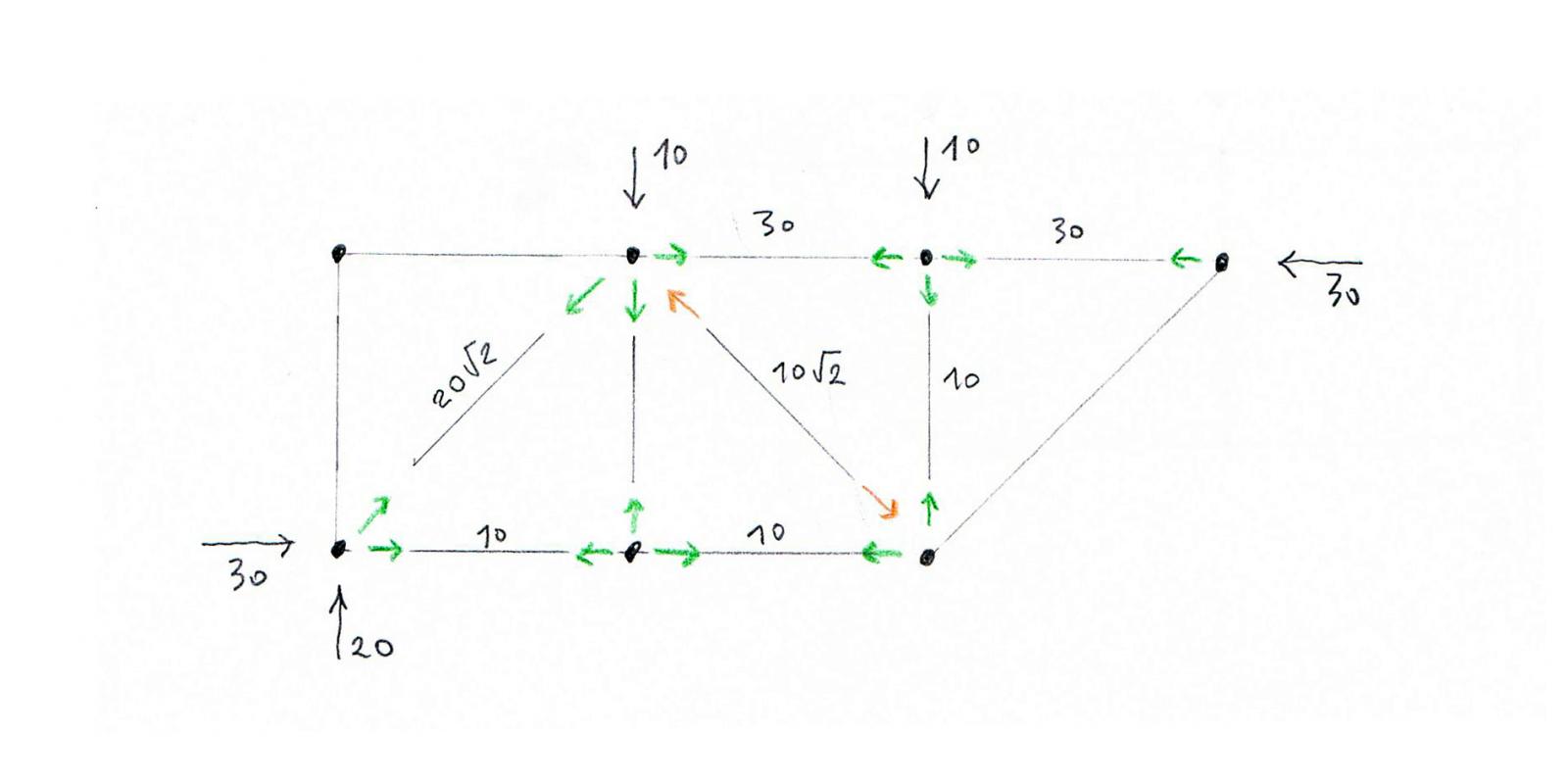
Risolviamo la struttura avvalendoci del metodo delle sezioni di Ritter ovvero andando a sezionare idealmente la trave in due parti, tagliando tre aste non convergenti nello stesso punto.
Quindi si procedere al taglio delle varie aste per trovare le azioni di contatto.
Sezione 1.
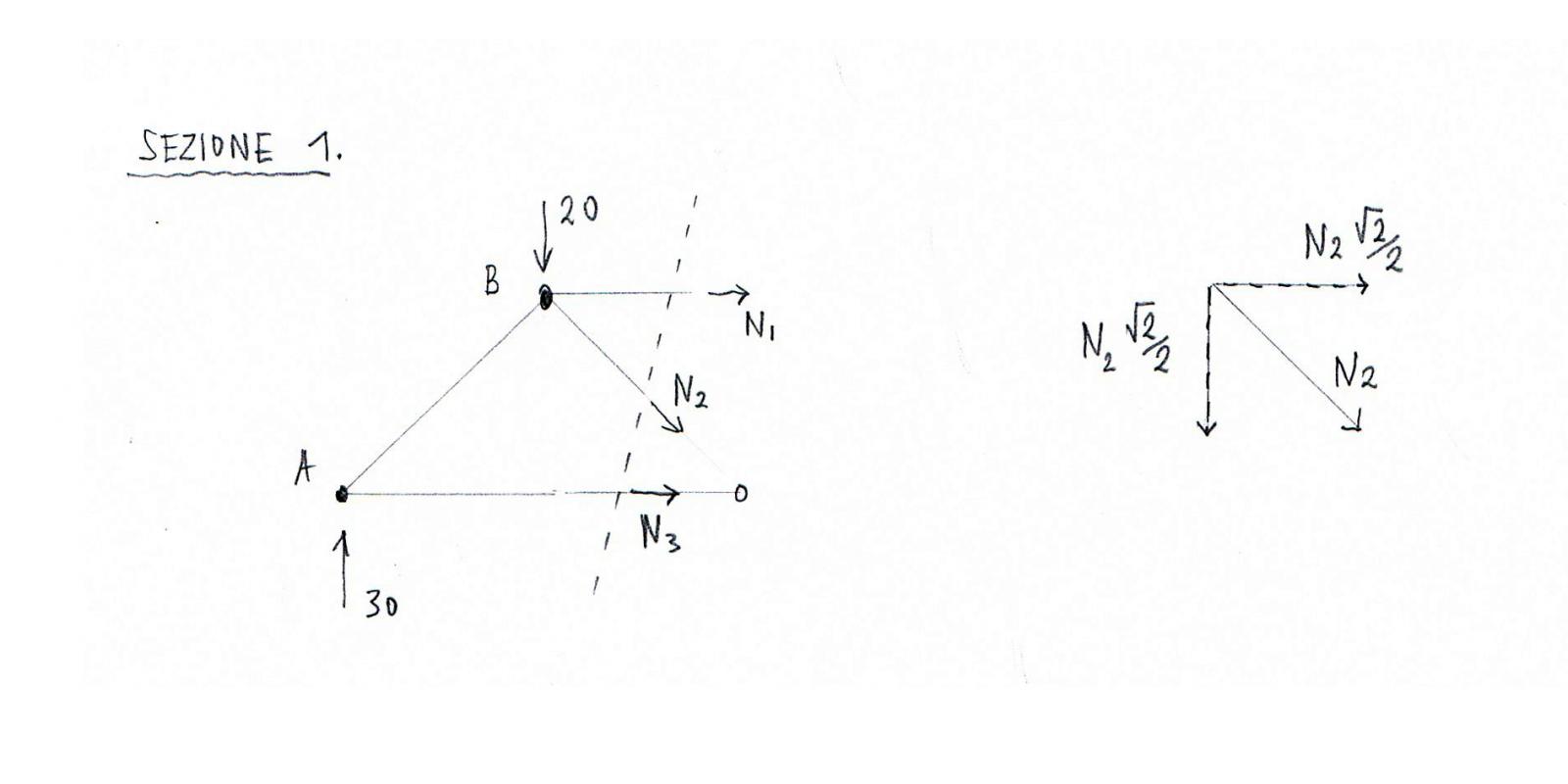Attraverso l’equilibrio dei momenti intorno al nodo C ricaviamo il valore di N1.
∑Mc=0 --> 30x4-20x2+N1=0 --> N1= -80/2 --> N1= -40 Kn --> asta compressa
Attraverso l’equilibrio dei momenti intorno al nodo B ricaviamo lo sforzo normale N3.
∑Mb=0 --> N3x2-30x2=0 --> N3=30 Kn --> asta tesa
Adesso dobbiamo fare attenzione! --> L’asta BC è inclinata di 45°e per calcolare il valore dello sforzo normale N2 sarà necessario scomporre la forza in una componente verticale ed una orizzontale.
Tramite l’equilibrio delle forze verticali calcolo N2.
∑Fy=0 --> 30-20-N2√2/2=0 --> N2 =102/√2= 20/√2 --> N2= 10√2 Kn --> asta tesa
Sezione 2.
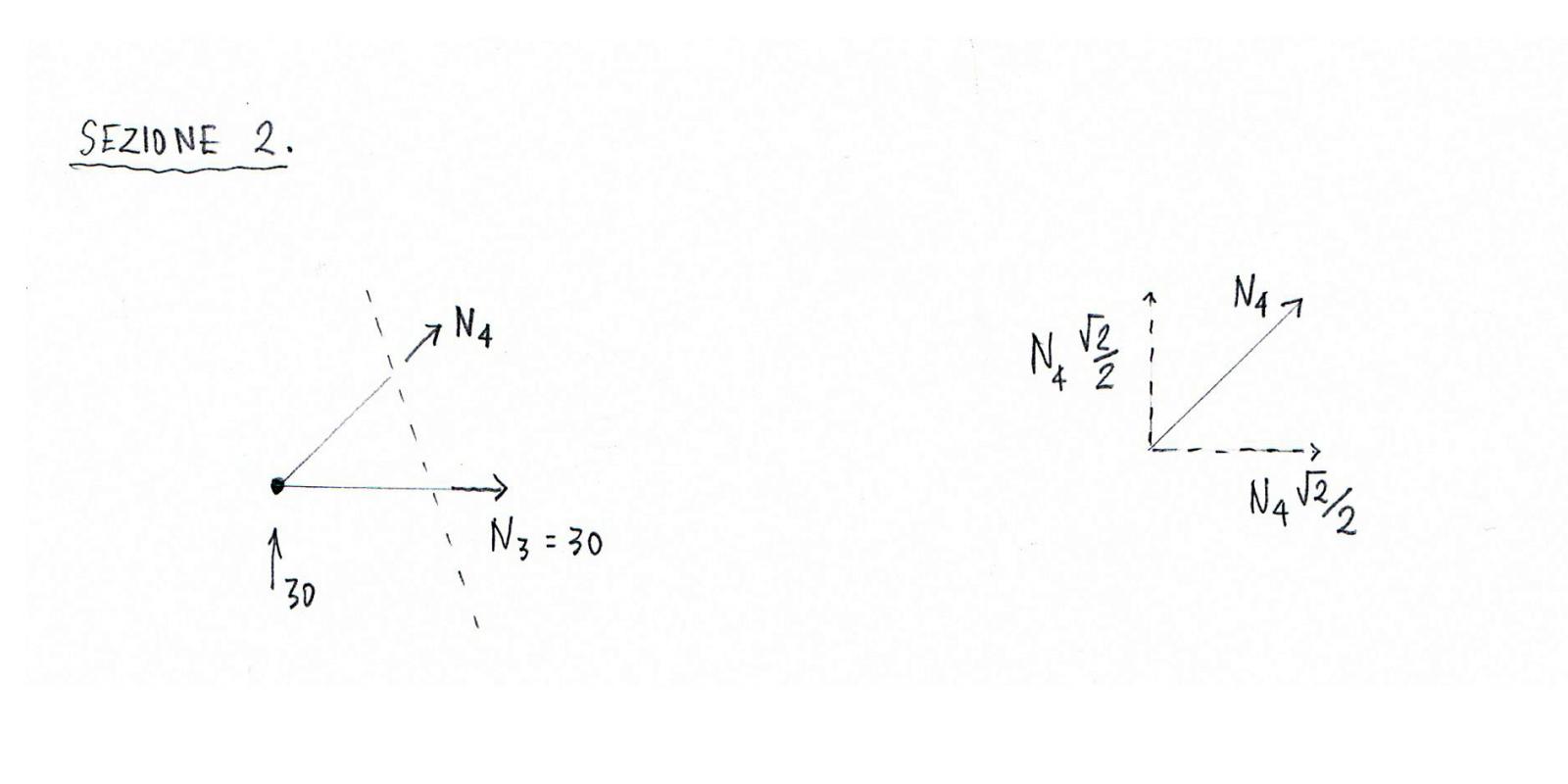Tramite l’equilibrio delle forze orizzontali calcolo N4.
∑Fx=0 --> 30+N4√2/2=0 --> N4√2/2+30=0 --> N4=-30√2 Kn --> asta compressa
Sezione 3.
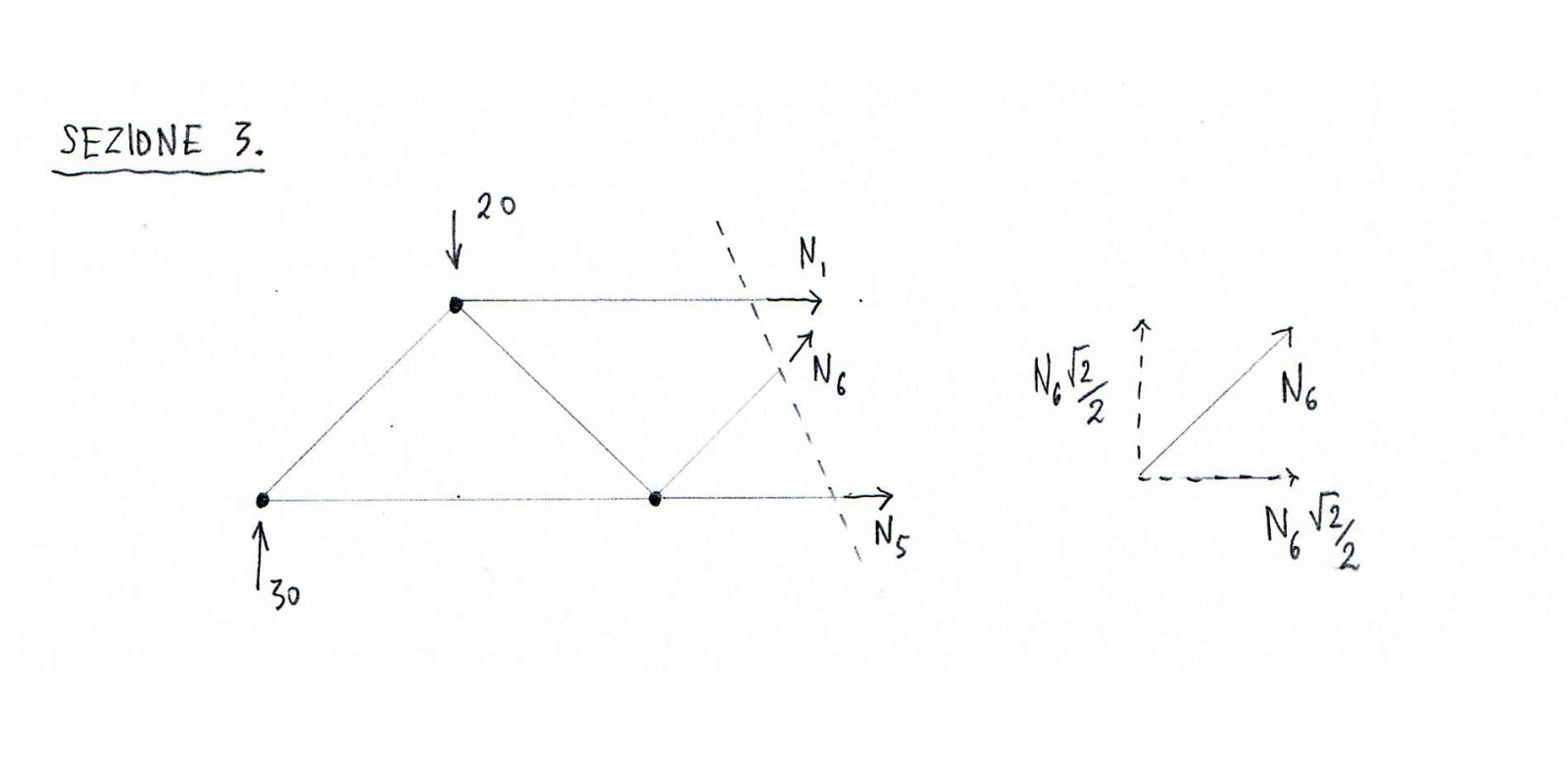Attraverso l’equilibrio dei momenti intorno al nodo D ricaviamo lo sforzo normale N5
∑Md=0 --> (N5x2)+(20x4)-(30x6)=0 --> 2N5+80-180=0 --> N5=50 Kn --> asta tesa
Tramite l’equilibrio delle forze verticali calcolo N6.
∑Fy=0 --> N6√2/2+30-20=0 --> N6= -10√2 Kn --> asta compressa
I risultati che abbiamo finora ottenuti possiamo estenderli all’altra metà della struttura perché, come abbiamo detto all’inizio, ci troviamo in una situazione di perfetta simmetria.
Infine, per avere conferma dei risultati ottenuti e dei grafici fatti a mano, ho disegnato la struttura con lo strumento di calcolo automatico SAP il quale mi ha dato anche una simulazione della deformata della trave reticolare.
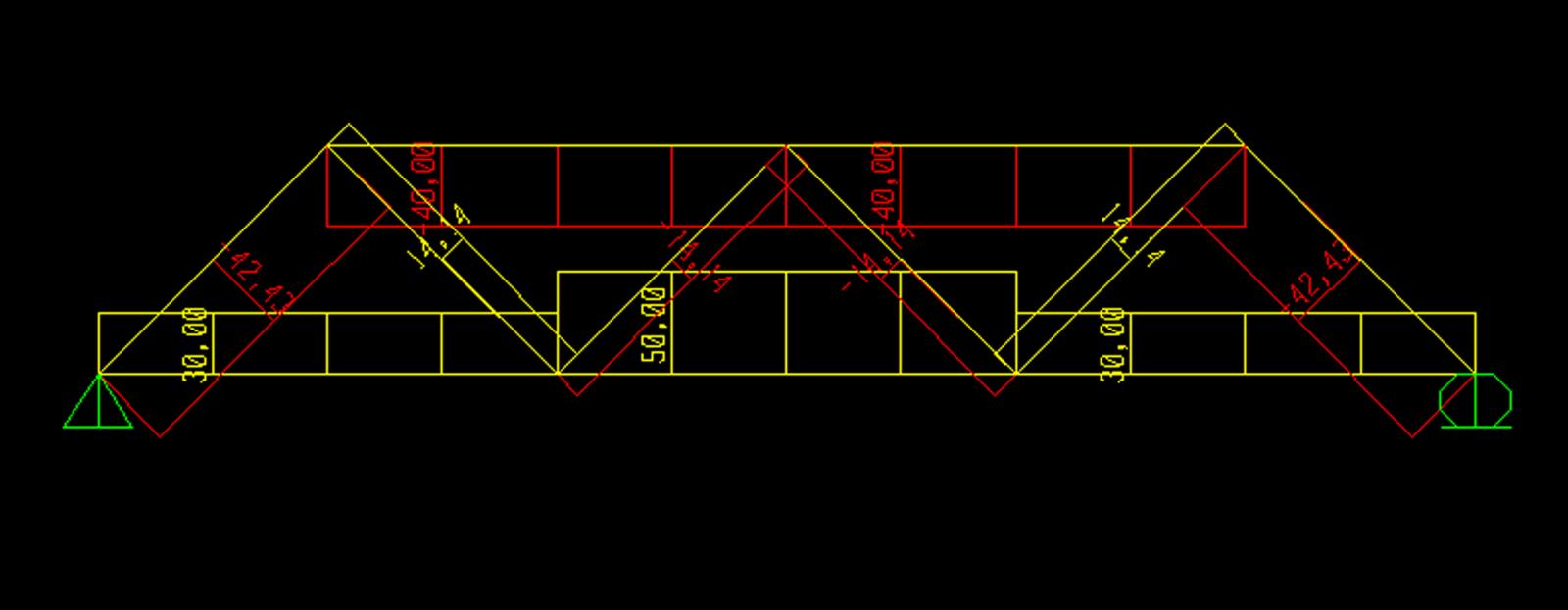
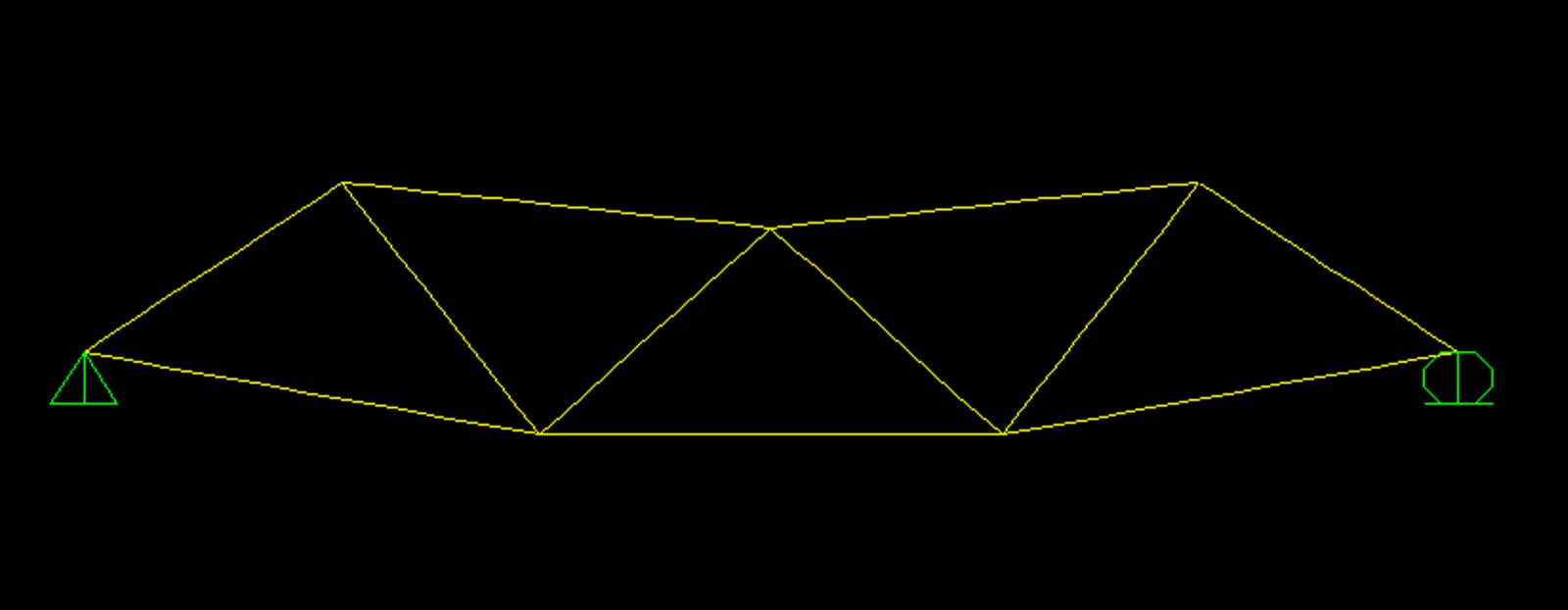
ESERCIZIO TRAVE RETICOLARE ASIMMETRICA
INTRO
Questa volta siamo alle prese con una struttura reticolare asimmetrica e quindi, non possiamo, come nel primo esercizio, avvalerci delle proprietà della simmetria.
STEP 1.
Verifichiamo subito se la trave reticolare asimmetrica data è isostatica:
gdl = gdv
gdl --> 11 x 3 = 33
gdv --> 3 + 2(n-1) = 33
33 = 33 c.v.d.
STEP 2.
Andiamo a calcolarci le reazioni vincolari.
∑Fy=0 --> Rvb-10-10=0 --> Rvb= 20 Kn
∑Fx=0
∑Mb=0 --> 10x1+10x2-Rhx1=0 --> Rh=30 Kn = Rob
STEP 3.
Questa volata per risolvere la struttura utilizziamo il metodo dei nodi.
Questo metodo prevede di isolare un nodo della struttura reticolare tagliando le aste che vi convergono. Poi si esplicitano gli sforzi normali trasmessi dalle aste al nodo e le eventuali forze esterne ed infine si scrivono le equazioni di equilibrio nodo per nodo.
Nodo A. e Nodo B.
Nodo A.
∑Fx=0 --> N1=0 --> asta scarica
∑Fy=0 --> N2=0 --> asta scarica
Nodo B.
∑Fy=0 --> 20+N3√2/2=0 --> N3= -20√2 Kn --> asta compressa
∑Fx=0 --> N3√2/2+N4+30=0 --> N4= -30 + 20= -10 Kn --> asta compressa
Nodo C.
∑Fy=0 --> N5=0 --> asta scarica
∑Fx=0 --> N6+10=0 --> N6= -10 Kn --> asta compressa
Nodo E. e Nodo G. e Nodo H.
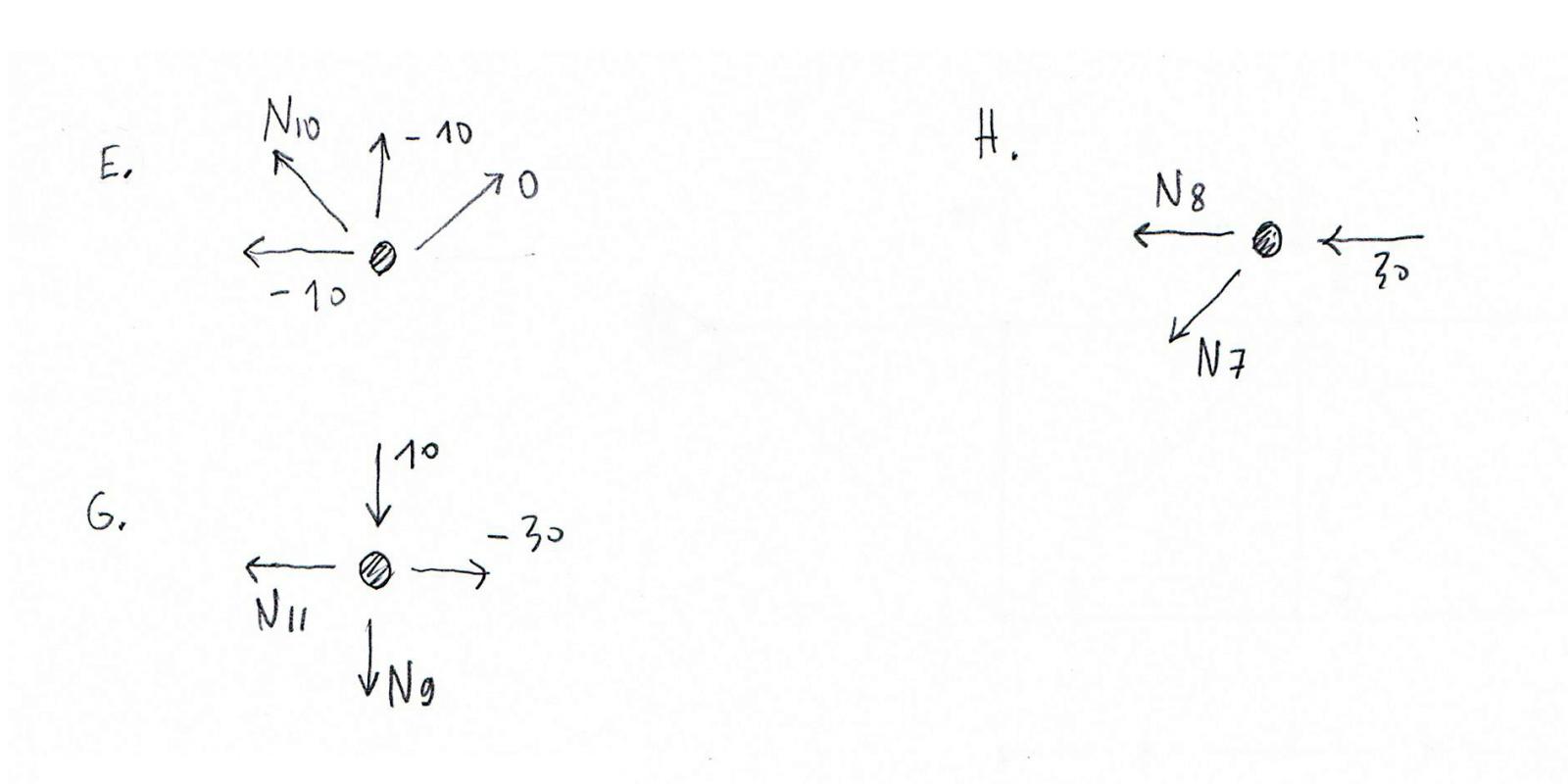
Nodo H.
∑Fy=0 --> N7=0 --> asta scarica
∑Fx=0 --> 30+N7√2/2+N8=0 --> N8= -30 Kn --> asta compressa
Nodo G.
∑Fy=0 --> N9+10= 0 --> N9= -10 Kn --> asta compressa
∑Fx=0 --> N11= -30 Kn --> asta compressa
Nodo E.
∑Fy=0 --> N10√2/2-10=0 --> N10= 10√2/2 --> 10√2 Kn --> asta tesa
Nodo D.
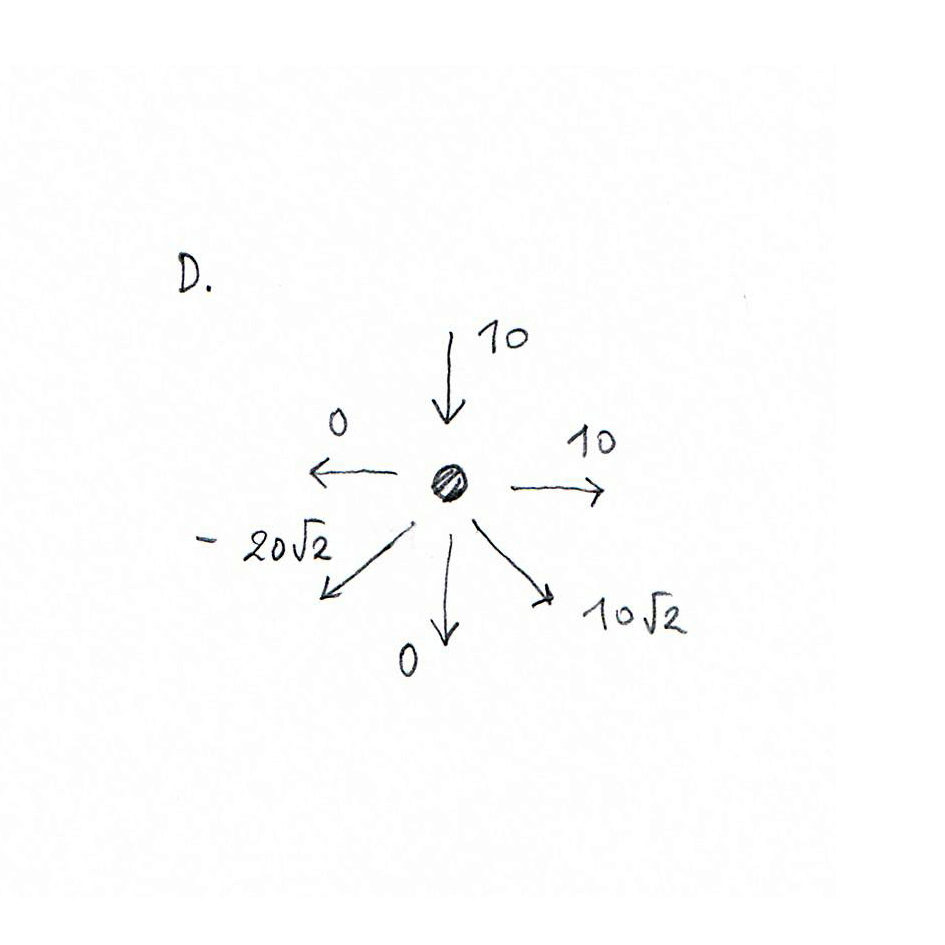
Infine, per avere conferma dei risultati ottenuti e dei grafici fatti a mano, ho disegnato la struttura con lo strumento di calcolo automatico SAP il quale mi ha dato anche una simulazione della deformata della trave reticolare.
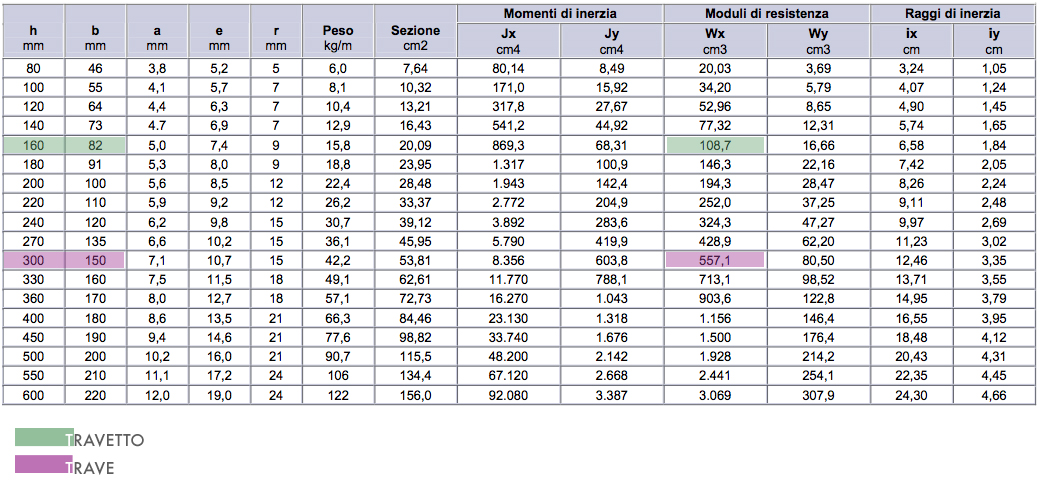
DIMENSIONAMENTO TRAVE
PIASTRA RETICOLARE SPAZIALE
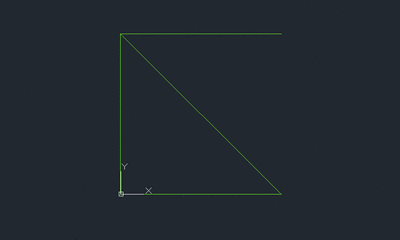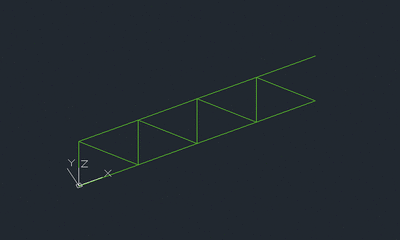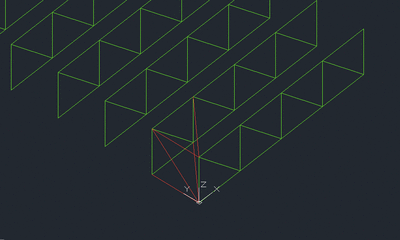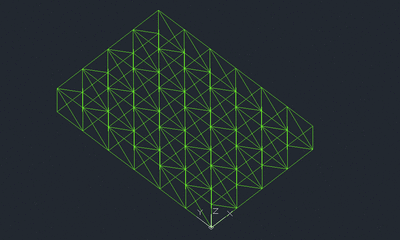
e adesso passo per passo!
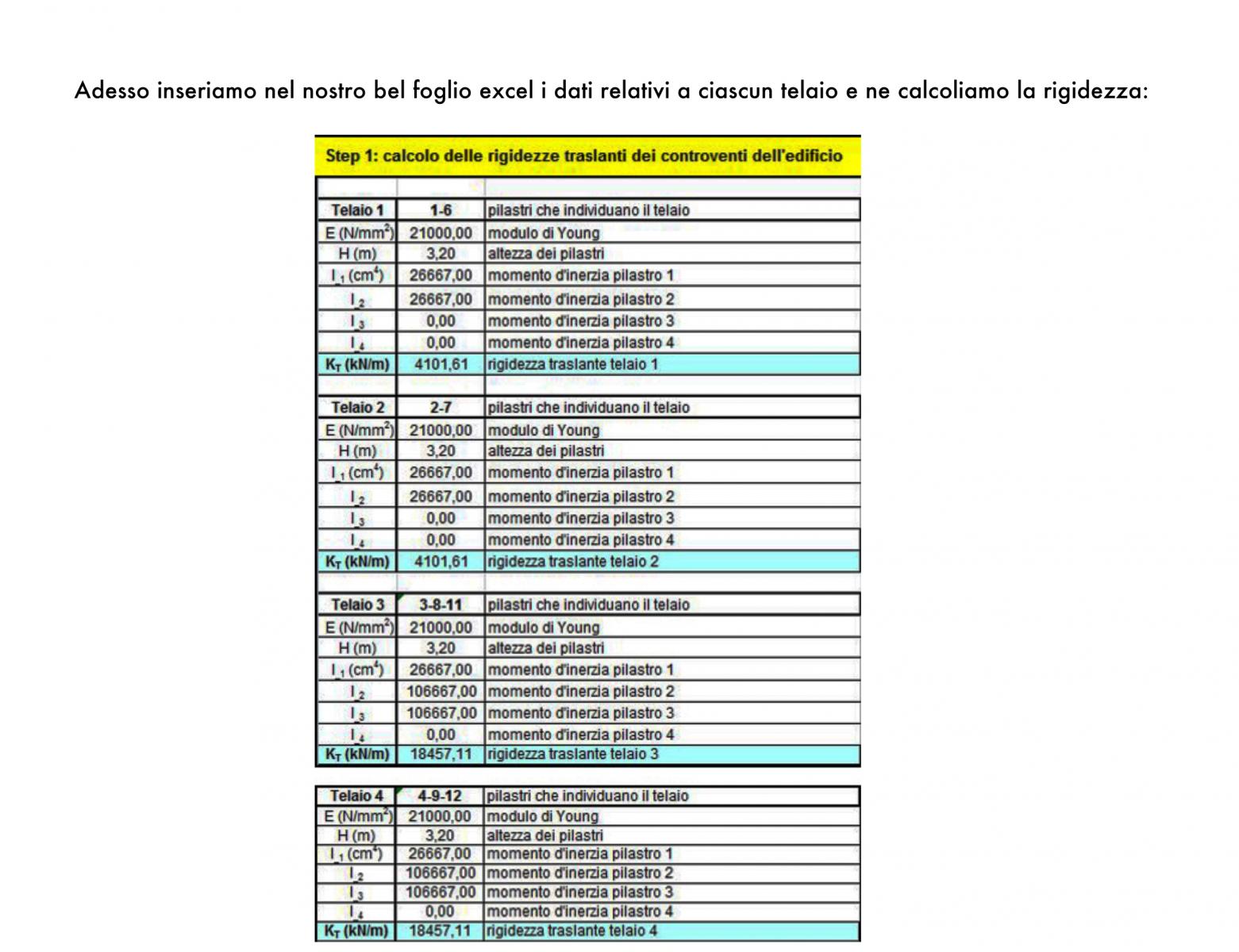
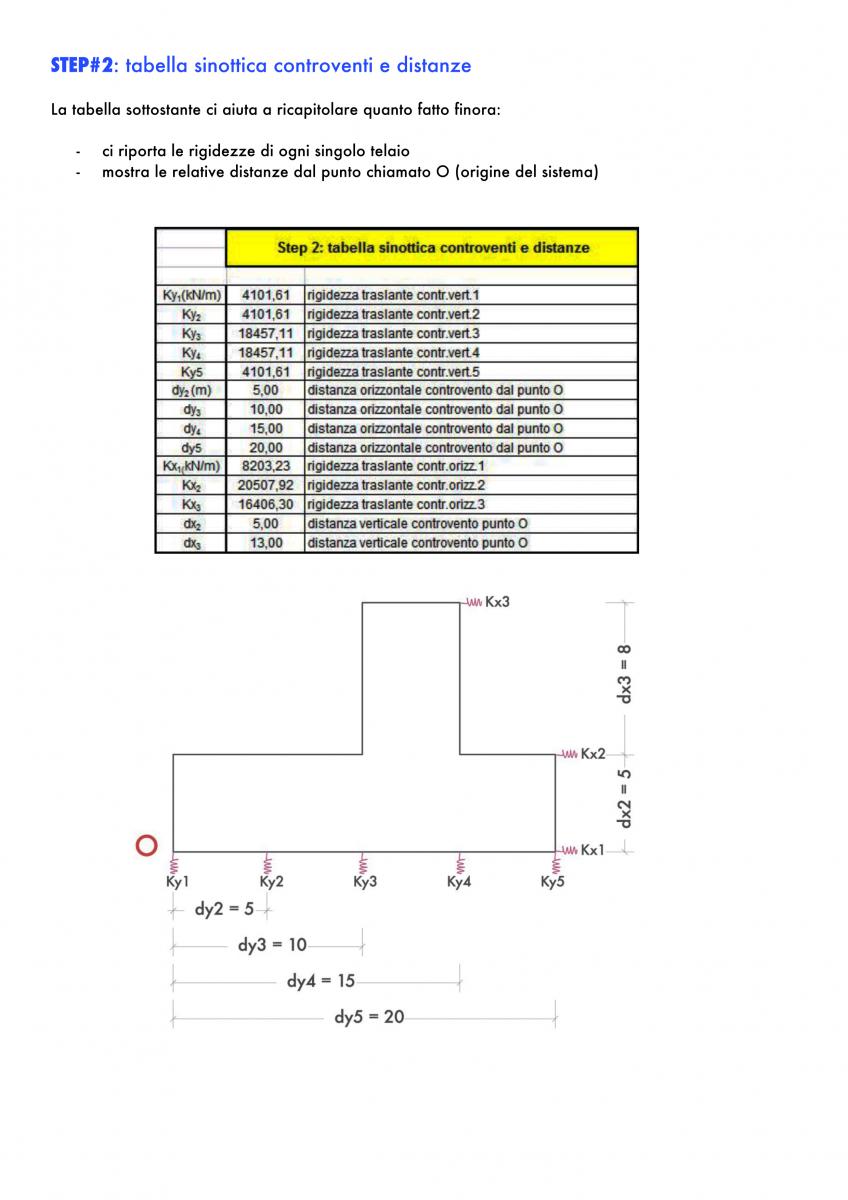
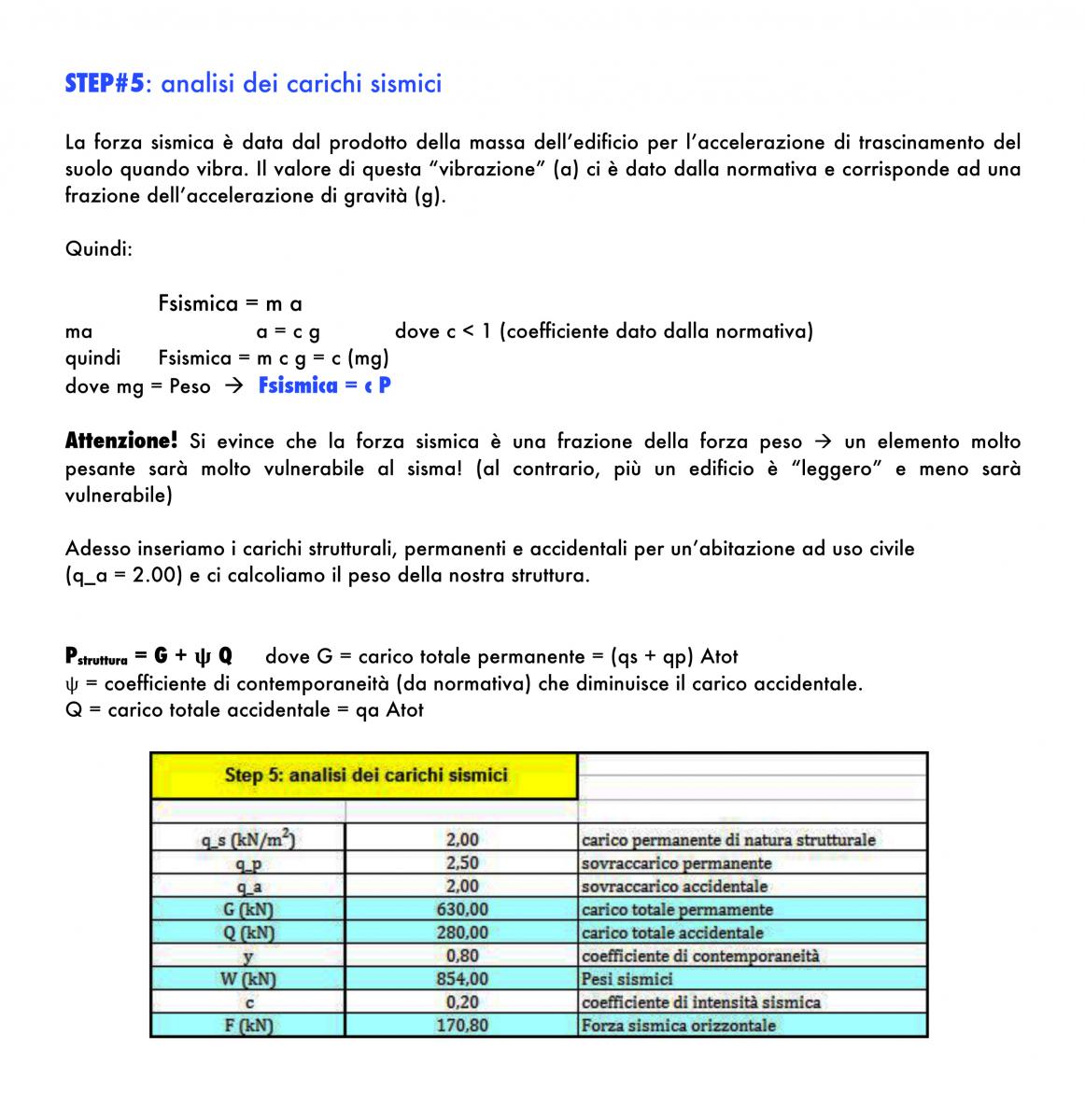
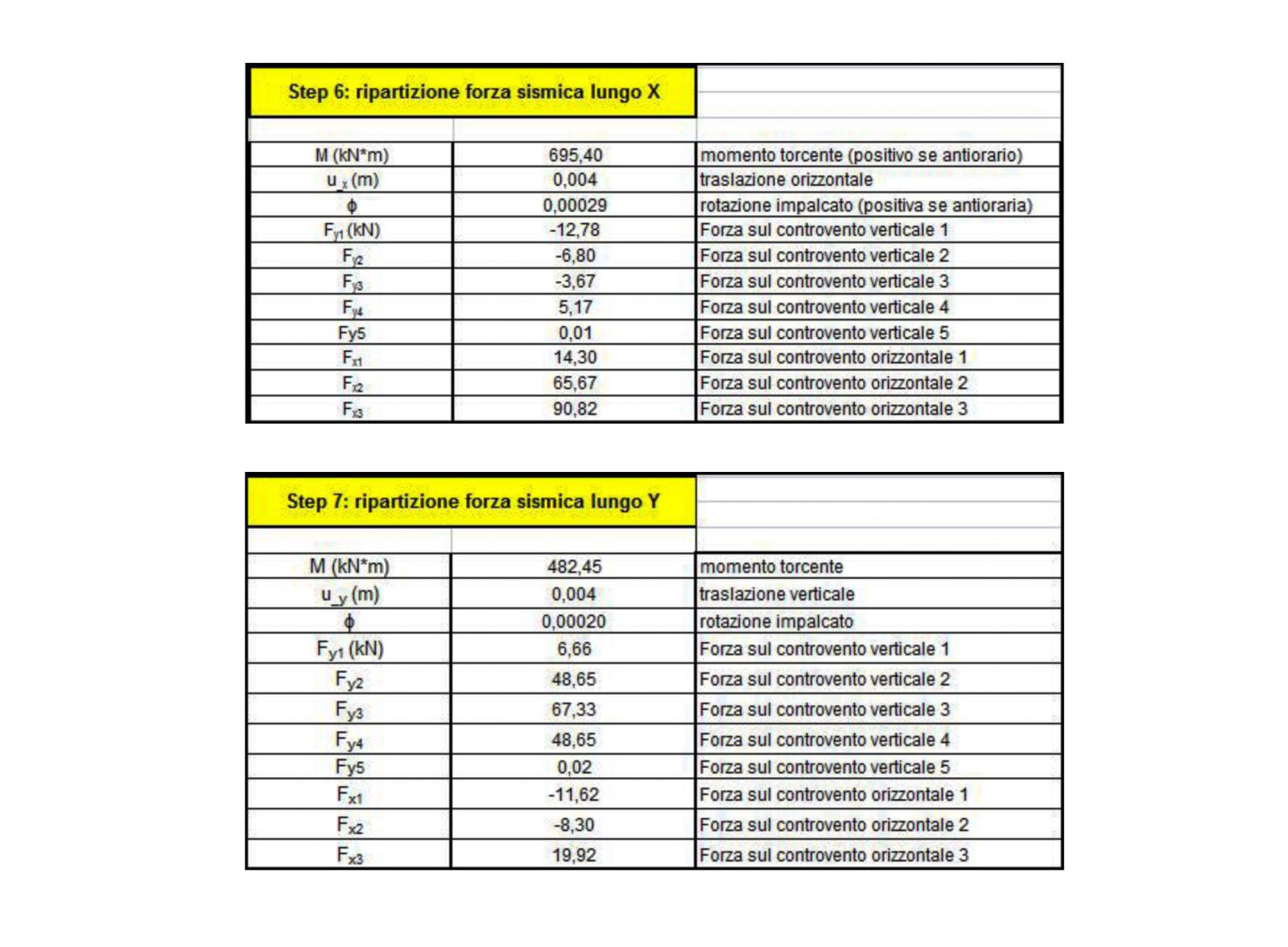
RIPARTIZIONE FORZE SISMICHE
Commenti recenti