Commenti recenti

  • Reply to: Calcolo Automatico delle strutture   11 anni 1 mese fa
    (Nessun oggetto)

  • Reply to: Analisi della curvatura Gaussiana e del fattore di scala di una superficie a forma libera   12 anni 8 mesi fa
    Passo indietro

    Quelle erano linee coordinate. Questa dovrebbe essere la nuvola di punti che identifica le linee di curvatura, sto cercando di capire come isolare una sola direzione perchè in questo modo non riesco a ricostruirle con precisione:

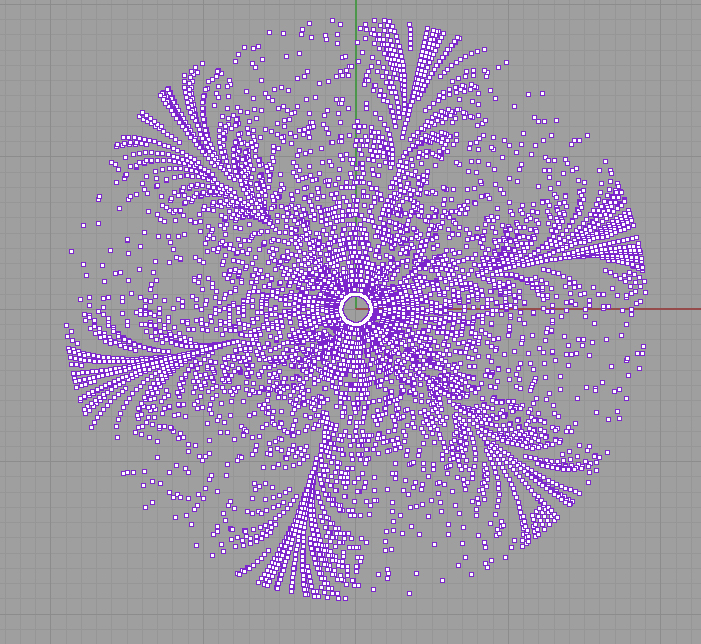
  • Reply to: Analisi della curvatura Gaussiana e del fattore di scala di una superficie a forma libera   12 anni 8 mesi fa
    Passi avanti

    Ho provato a calcolare le linee di curvatura del paraboloide ellittico. Ho rifatto i calcoli in Maple trovando i coeficienti fondamentali:

    Poi sono passata a RhinoScript ed ho provato a disegnare una sola linea di curvatura come una successione di punti, il risultato è il seguente:

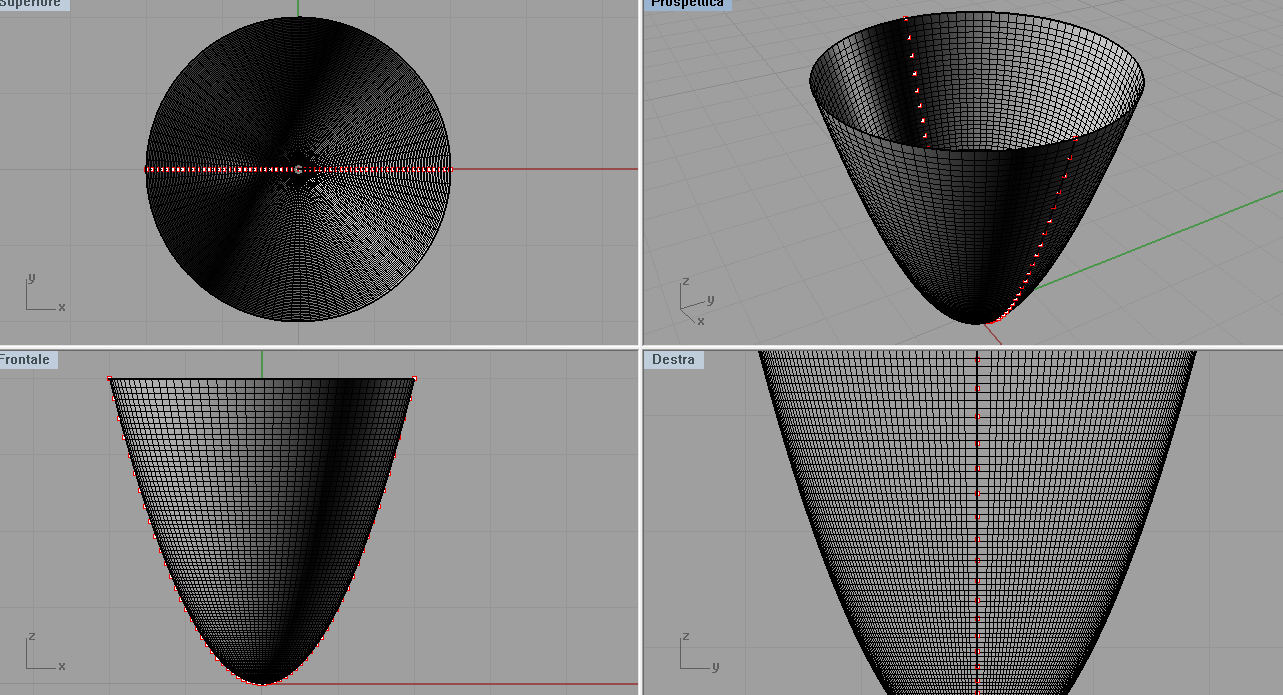
    I punti seguono effettivamente la linea di curvatura. Quindi ho ripreso in mano il file Maple del "fungo" ed ho ricontrollato ogni passaggio utilizzato per calcolare i coefficienti fondamentali, che risultano:

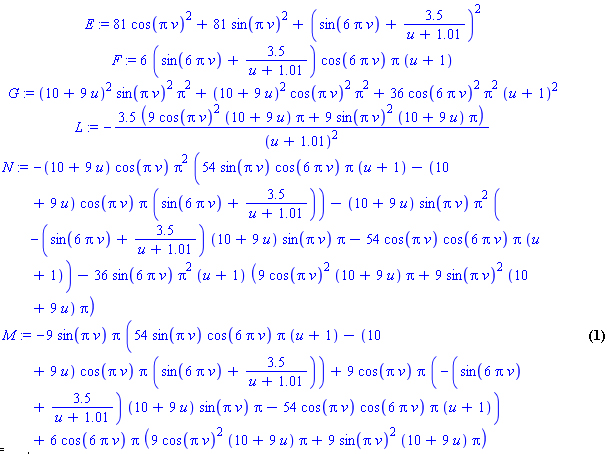
    Quindi sono tornata sullo script ed ho provato a disegnare le linee di curvatura, prima in una direzione e poi nell'altra:

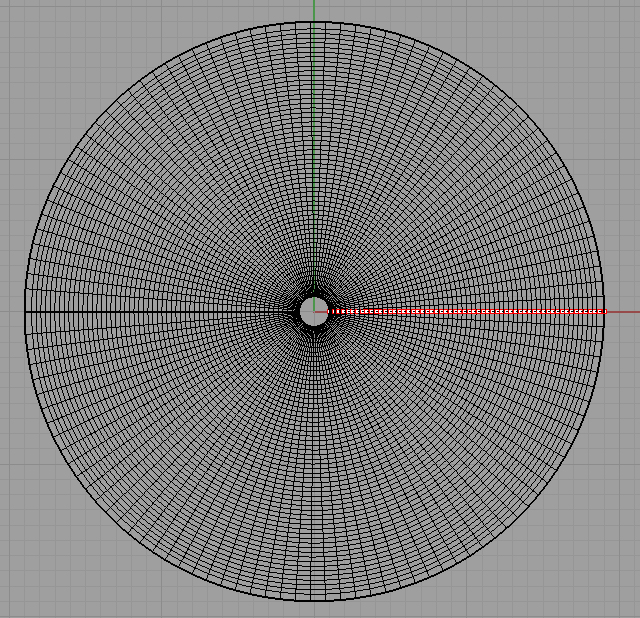
    Quelle che vengono fuori sono le linee coordinate, ma se questo procedimento è corretto non caisco perchè i coefficienti fondamentali F ed M non sono uguali a zero. Ho comunque costruito la grid-shell:

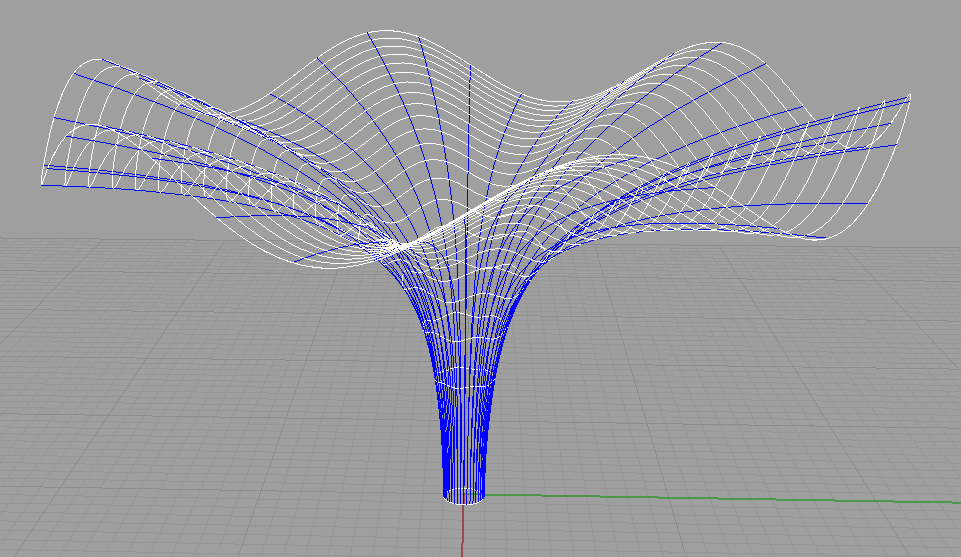
    L'unica spiegazione possibile è che nel generare la successione di punti nello script abbia reso un parametro costante. Se così fosse queste sarebbero le linee coordinate, non per forza linee di curvatura.

  • Reply to: Analisi della curvatura Gaussiana e del fattore di scala di una superficie a forma libera   12 anni 8 mesi fa
    Forma Libera

    Allego anche un'immagine che ho sempre dimenticato di postare di com'è diventata la forma libera a seguito di tutte le modifiche dovute al calcolo, ora dovrebbe funzionare:

  • Reply to: Analisi della curvatura Gaussiana e del fattore di scala di una superficie a forma libera   12 anni 8 mesi fa
    Perpendicolarità Direzioni Principali

    Allora, cito testualmente quanto riportato dal testo Schaum a pagina 185:

    "Teorema 9.9. Una direzione du:dv è una direzione principale in P se e solo se du e dv soddisfano la condizione:
     
    (EM - LF) du2 + (EN - LG) dudv + (FN - MG) dv2 = 0
     
    Si può dimostrare che in un punto non ombelicale questa equazone si fattorizza in due equazioni lineari della forma A du + B dv = 0 relativa alle due direzioni principlai, perpendicolari tra loro."
     
    Questo teorema si rifersca a carte locali arbitrarie e non a casi particolari, per cui le direzioni principali sono sempre ortogonali. A mio avviso abbiamo male interpretato il significato di "du:dv". Infatti più di una volta viene scritto che le linee coordinate si dispongono ortogonalmente una in direzione du=0,dv=1 ed una in direzione dv=0,du=1, qundi la direzione non viene indicata con il rapporto du/dv anche perchè, nel caso delle linee coordinate, una delle due direzioni risulterebbe uguale ad un numero diviso zero, che è impossibile.
     
    Sempre lo Schaum a pagina 186 dice:
     
    "Teorema  9.14. La direzione du:dv in un punto di una carta locale rappresenta una direzione principale se e solo se per un opportuno scalare k, dN = Nudu + Nvdv e dx = xudu + xvdv soddisfano la relazione:
     
    dN = - k dx
     
    In questo caso k è la curvatura principalenella direzione du:dv.
     
    La formula precedente, che caratterizza completamente le direzioni principali, viene detta formula di Rodrigues, e dovrebbe essere imparata a memoria."
     
     
leggi tutto