blog di Alessia Scavo

 

La progettazione strutturale è fondamentale per la buona formazione di ogni architetto. Essa permette ad un’espressione compositiva su un foglio di carta di diventare realtà. Questo passaggio non è così immediato perché bisogna tener conto di molti aspetti a partire dalla funzione della struttura che si sta progettando, alla sua forma, alla sua collocazione geografica, alle sue dimensioni, al materiale utilizzato e anche ai diversi carichi che possono gravare su di essa. Questa affascinante materia non deve essere né sottovalutata né tanto meno, quando possibile, affidata ad altre figure professionali, semplicemente per timore di non essere in grado di effettuare dei calcoli più complicati.

In questo blog cercherò di spiegare, spero in modo corretto, i passaggi per poter arrivare a progettare sia strutture semplici, come quelle isostatiche, che quelle un po’ più complesse come quelle più volte iperstatiche.

Prima di cominciare questo percorso sono necessari dei chiarimenti sulle tre grandezze fisiche fondamentali che affronteremo: la lunghezza [L] che ha come unità di misura il metro [m] , la forza [F] che ha come unità di misura il newton [N] e il tempo [T] che ha come unità di misura il secondo [sec].

Per esempio “ql” è una forza [F] [L] / [L] = [F] ; invece “ql²” è un momento [F] [L²] / [L] = [F][L] .

Ma cosa è il momento? Il momento è un ente che provoca la rotazione dei corpi ed è definito come il prodotto di una forza per un braccio ( M=F b).

STRUTTURE ISOSTATICHE

Una struttura è isostatica se il numero di gradi  di vincolo è pari al numero dei suoi gradi di libertà, ovvero se v=l=3.

Una trave doppiamente appoggiata, vista come corpo rigido, che ha per vincoli un carrello (v=1) e una cerniera (v=2) è isostatica.

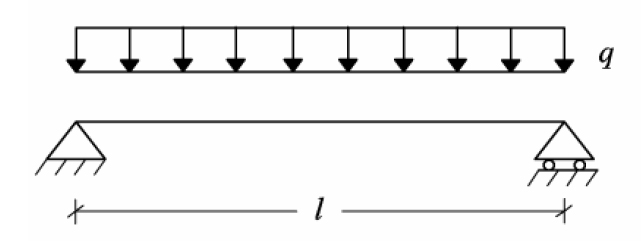
Per risolvere una struttura isostatica bisogna innanzitutto determinare le reazioni vincolari, per poi definire le caratteristiche di sollecitazione (N,T,M) disegnando i relativi diagrammi.

Ma quale è l’andamento delle sollecitazioni sulla trave? Per rispondere a questa domanda dobbiamo determinare le equazioni di bilancio della trave:

dN/ds + q1 = 0

dT/ds + q2 = 0       0<s<l

dM/ds + T + µ = 0

dove q1, q2 e µ sono densità di carichi distribuiti su una lunghezza.

Le equazioni di bilancio consentono di calcolare le reazioni vincolari e le azioni di contatto (forze interne alla trave e rappresentano l’interazione meccanica tra parti di trave che interagiscono attraverso le sezioni). 

Dalla prima equazione si nota un legame tra lo sforzo normale e il carico q1, per cui se q1 è zero la derivata della normale è costante; se q1 è costante (diverso da zero) lo sforzo normale è lineare.

Dalla seconda equazione ne deriva che in assenza di densità di carico, il valore del taglio è costante. Se il carico è diverso da zero il taglio è lineare.

La seconda e la terza equazione ci fanno notare come il taglio e il momento siano legati: il taglio è la derivata del momento.

Bisogna però chiarire che su una trave possono agire carichi esterni: una forza concentrata F e un carico distribuito q (le cui dimensioni fisiche sono diverse). In base al tipo di carico i diagrammi di N, T e M saranno differenti, infatti:

Se è presente un carico distribuito lo sforzo normale è costante, il taglio è lineare e il momento è parabolico.

Se è presente una forza concentrata lo sforzo normale è zero, il taglio è costante e il momento è lineare. Una forza concentrata genera discontinuità nell’andamento delle funzioni N, T e M. Il punto di applicazione della forza è un punto di non derivabilità (la derivata destra e sinistra in quel punto hanno un valore diverso) e questo produce un salto nel diagramma.  

Un metodo molto utile per risolvere questo tipo di strutture è il metodo qualitativo, che consiste nel determinare l’andamento delle funzioni N, T e M attraverso le equazioni di bilancio, significa quindi effettuare delle operazioni di integrazione per risalire dalle equazioni derivate a quelle primitive. L’analisi qualitativa termina con la determinazione delle condizioni al bordo sia di natura statica (N,T,M) che di natura cinematica (spostamenti in presenza dei vincoli).

In presenza di un carrello : condizioni cinematiche -->  v(s=0) = 0

                                       condizioni statiche  -->  N(0) =0    M(0) =0

In presenza di una cerniera : condizioni cinematiche --> u (s=0) = 0   v (s=0) = 0 

                                         condizioni statiche  --> M(0) =0

In presenza di un incastro : condizioni cinematiche -->  u (s=0) = 0   v (s=0) = 0  φ(s=0) = 0 

In presenza di un pendolo : condizioni cinematiche  --> u (s=0) = 0   φ(s=0) = 0

                                        condizioni statiche -->  T(0) =0

STRUTTURA RETICOLARE

  

Un esempio di struttura isostatica è quella reticolare. Una struttura reticolare è un insieme di aste vincolate attraverso cerniere interne. Le aste sono sottoposte a sforzo normale e possono essere compresse (puntoni) o tese (tiranti).  I carichi sono concentrati sui nodi, ovvero sulle cerniere interne. Questo tipo di travatura è impiegato per strutture sempre più leggere e di grandi luci.

Il maggior sviluppo si ebbe nell’ottocento quando si riuscì a produrre industrialmente i laminati diferro con caratteristiche meccaniche sufficientemente sicure, diffusamente utilizzati nellarealizzazione di ponti ferroviari. Contemporaneamente, il reticolo di travi si viene ad orientare versoschemi caratterizzati ciascuno da un preciso funzionamento statico.

Fra le diverse aste che compongono la struttura si distinguono i CORRENTI, costituiti dalle aste essenzialmente orientate nella direzione della dimensione maggiore della trave reticolare, e le DIAGONALI e MONTANTI, costituiti da aste orientate obliquamente o trasversalmente a tale direzione.

 

Esercizio 1

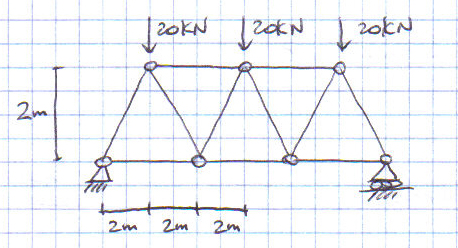
I metodi per calcolare le reazioni vincolari sono due: metodo dei nodi e metodo delle sezioni o di Ritter.

Prima di svolgere l’esercizio devo verificare che la struttura sia isostatica, ovvero che i gradi di vincolo (V) devono essere uguali ai gradi di libertà (L) :   V=L

In questo caso L= Nastex Nvincoli= 11 x 3 = 33

V=Ve+Vi  cioè la somma dei gradi di vincolo esterni e gradi di vincolo interni,

dove Ve = 3 e Vi = 2(n-1)  “n” è  il numero delle aste che convergono nella cerniera.

A, H: 2(2-1) = 2       n = 2

B, G: 2(3-1) = 4       n = 3

C, D, E: 2(4-1) = 6   n = 4

Vi = 2x2+2x4+3x6= 30 + 3= 33  Verificato!

Per velocizzare i calcoli posso usare un’altra formula: Ve+a=2n dove "a" è il numero delle aste e "n" il numero dei nodi.

Ora procedo con il calcolo delle reazioni vincolari:

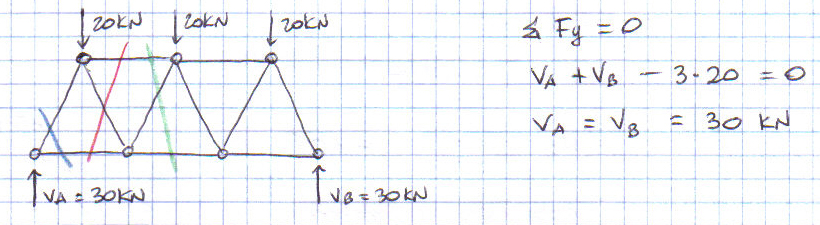
Calcolo delle azioni di contatto: Metodo delle sezioni o di Ritter

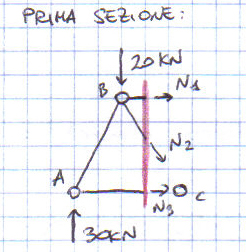
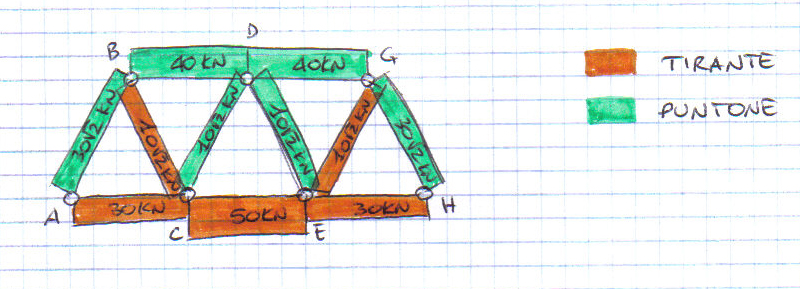
Con questo metodo posso tagliare la struttura effettuando una sezione ideale, che divida la struttura in due parti. Si sezionano tre aste che non concorrono nello stesso nodo. Lo sforzo in una delle tre aste viene calcolato attraverso un’equazione di equilibrio dei momenti intorno al polo in cui convergono le altre due. Si può notare che la struttura è simmetrica, quindi effettuerò il calcolo per metà struttura.

Effettuo tre sezioni: nella prima faccio polo nel nodo C e trovo che l’asta BD è compressa, poi faccio polo in B e trovo che l’asta AC è tesa. Successivamente effettuo l’equilibrio alla traslazione verticale e vedo che l’asta BC è tesa.

 

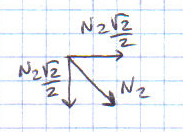
Nella seconda sezione trovo che l’asta AB è compressa e nella terza sezione che l’asta CE è tesa e quella CD è compressa.

 

 

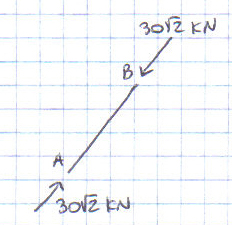
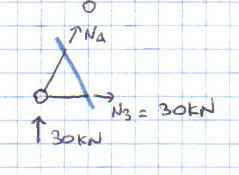
Di conseguenza riporto i risultati trovati sulla struttura (ovviamente essendo simmetrica i risultati si ripetono nella parte destra della struttura).

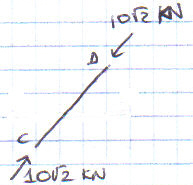
Secondo Esercizio

Questa struttura reticolare è invece asimmetrica, l’ho svolta con il metodo dei nodi.

Come prima cosa verifico che la struttura sia isostatica per procedere con il metodo sopra citato. Poi ho calcolato le reazioni vincolari.

 

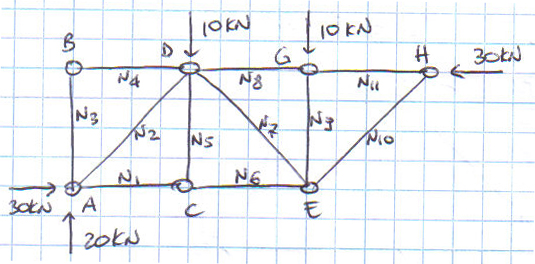
Per il metodo dei nodi conviene iniziare con un nodo semplice, per esempio in cui convergono due aste e risolverlo mediante le due equazioni di equilibrio del nodo stesso. Si isola un nodo della struttura reticolare tagliando le aste che vi convergono.

Parto dal nodo H e ne faccio l’equilibrio alla traslazione orizzontale e verticale. Sin da subito comprendo che l’asta N10 è scarica.

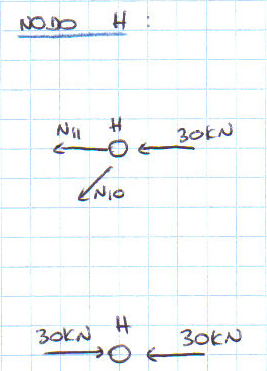
Procedo con il nodo G, poi E, C, A e D.

 

 

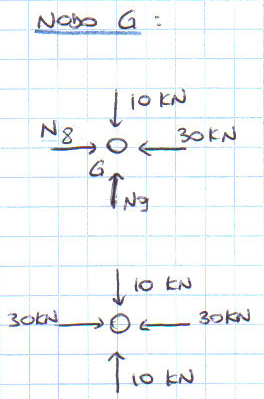
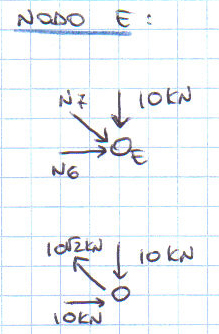
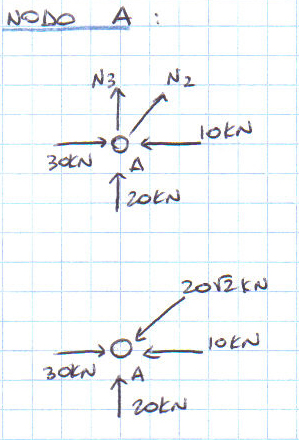
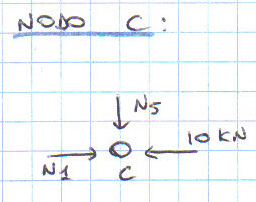
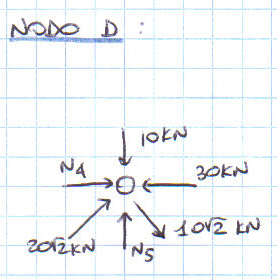
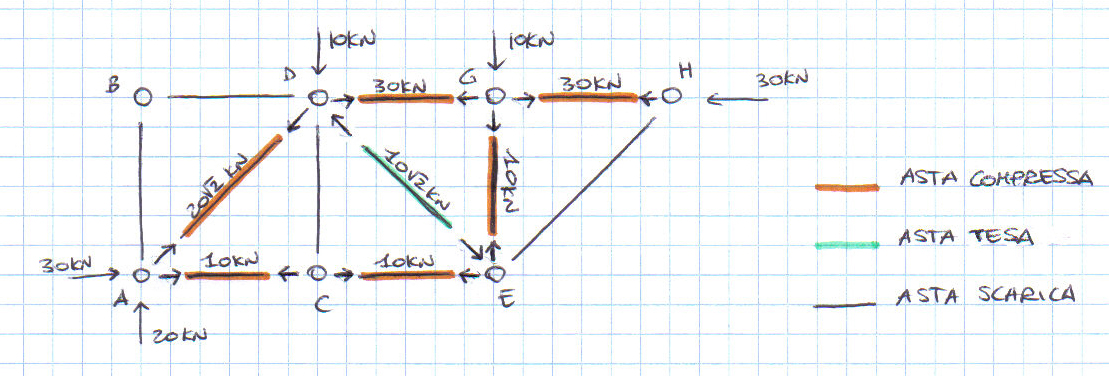
Le aste AB, BD, DC e HE sono scariche, mentre le aste AD, AC, CE, DG, GH e GE sono compresse e l’asta DE è tesa.

Riporto i valori trovati sulla struttura:

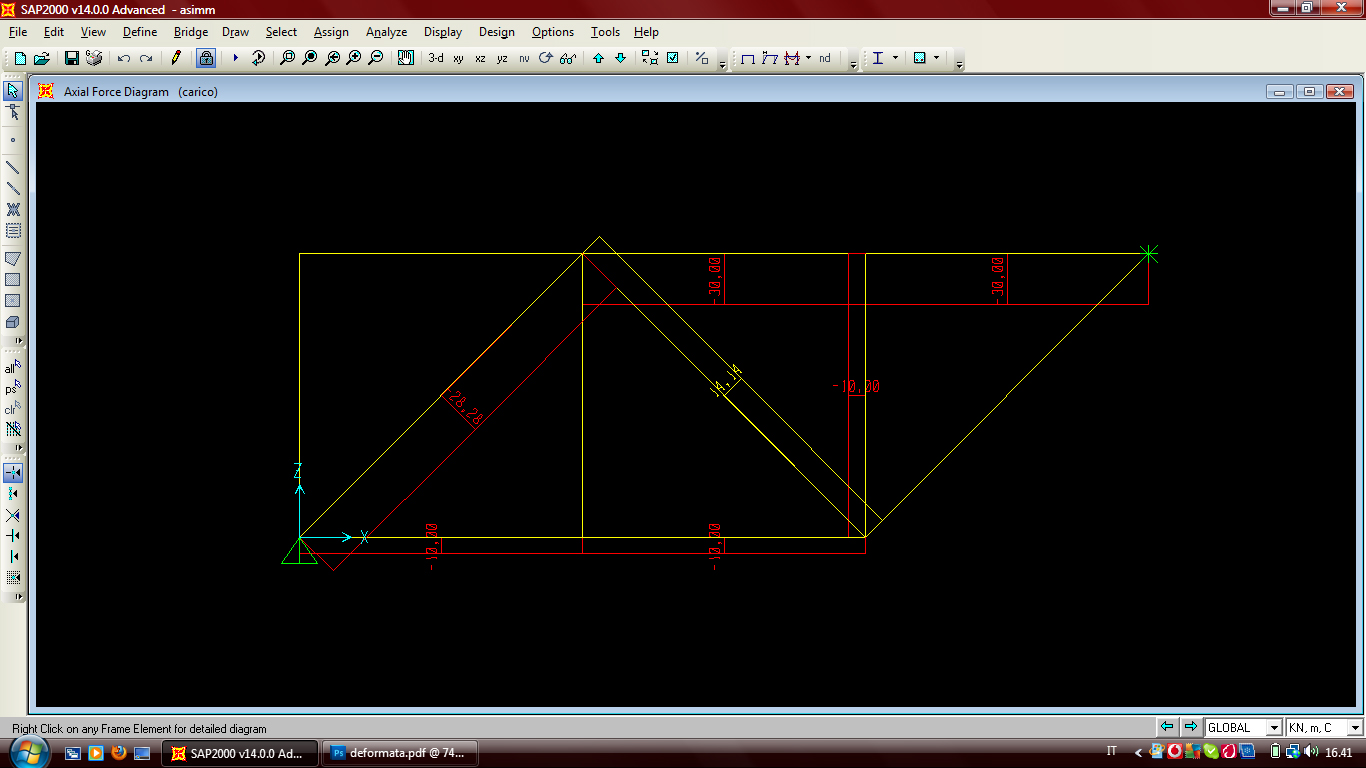
Successivamente ho verificato la struttura su SAP, riporto in seguito la deformata, le reazioni vincolari e i diagrammi.

 

Mensola

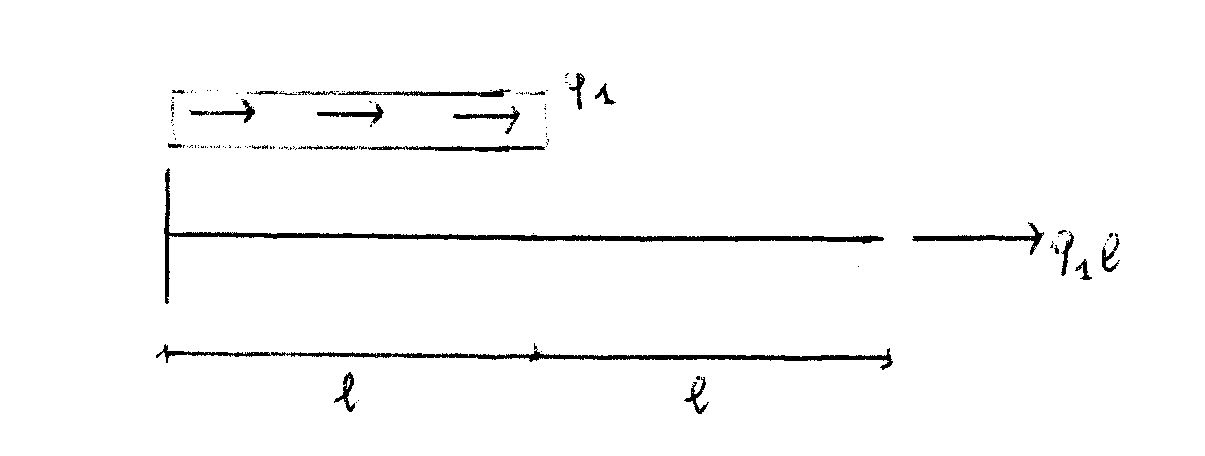
Su questa struttura è presente solo sforzo normale. Mentre sulla prima metà della struttura vi è il carico distribuito “q”, all’estremità dell’altra metà vi è una forza concentrata “ql”.

Questo è il diagramma della normale, che è positivo perché di trazione:

Trave

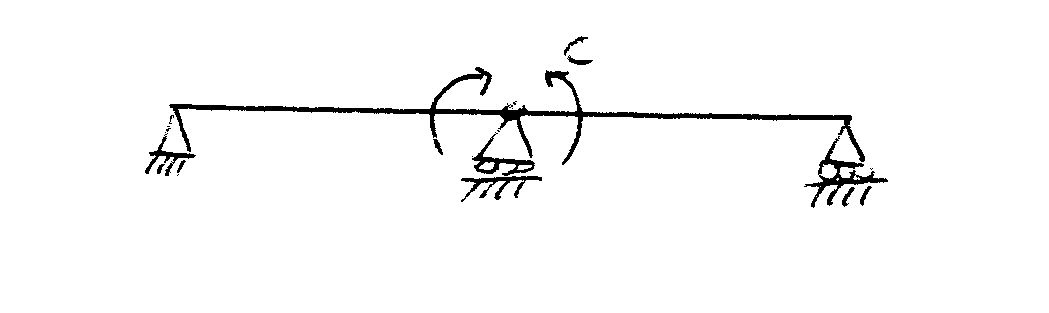
In questo esercizio vediamo una trave con cerniera e carrello alle estremità e al centro un ulteriore carrello con un momento concentrato. Divido la struttura in due parti:

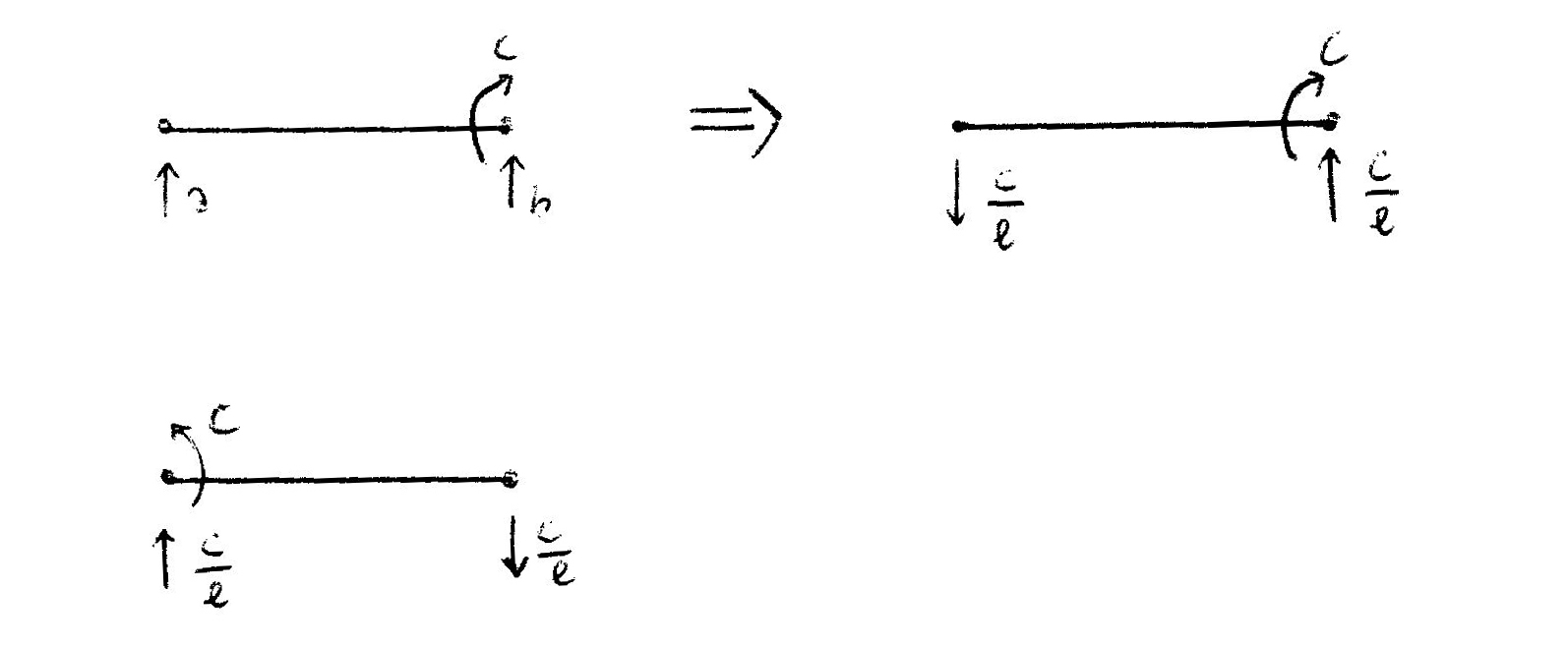
a+b= 0 --> a= -C/l

bl-C=0  --> b= C/l

Dobbiamo vedere la coppia C/l come bilancio del momento C (uguale ed opposto).

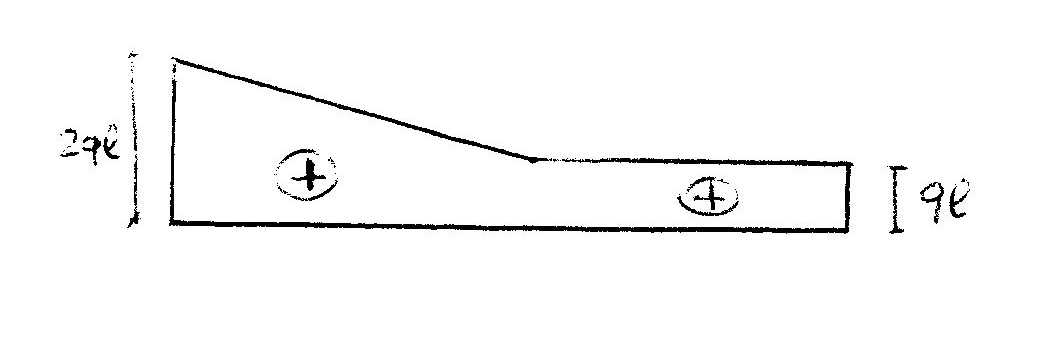
Questi sono i diagrammi del taglio e del momento (quello dello sforzo normale è zero!).

Arco a tre cerniere

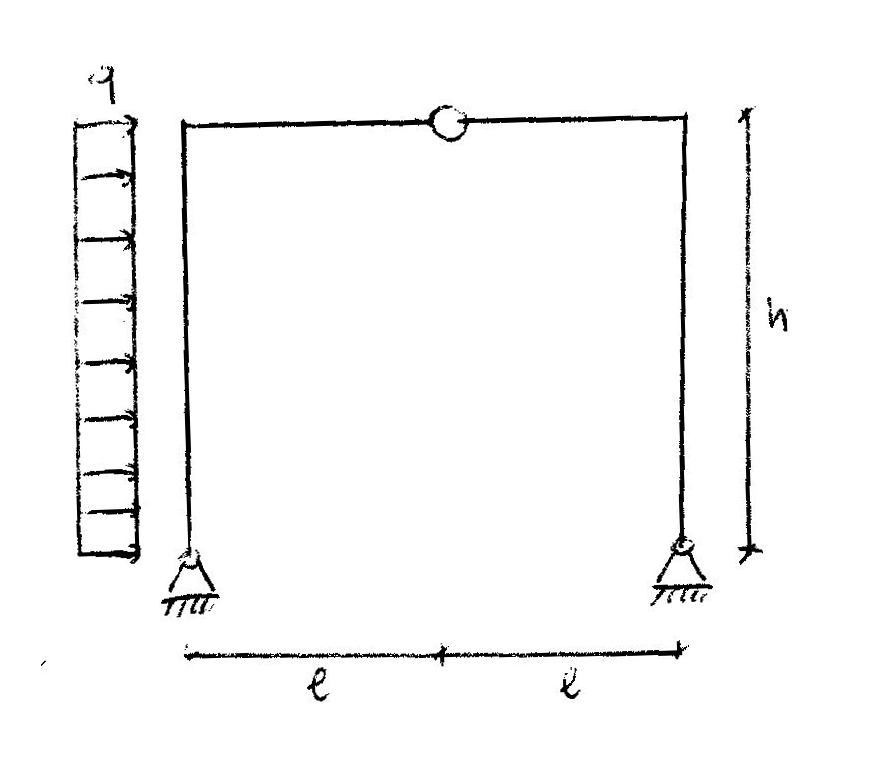
La prima struttura è un arco a tre cerniere che presenta un carico distribuito sul pilastro sinistro del valore “q”. Come prima cosa si sono trovate le reazioni vincolari: inizialmente ho considerato la struttura unica e facendo l’equilibrio alla traslazione verticale ho trovato le reazioni RvB e RvA che valgono entrambe qh²/4l. Per trovare le reazioni vincolari orizzontali ho diviso la struttura in due parti:

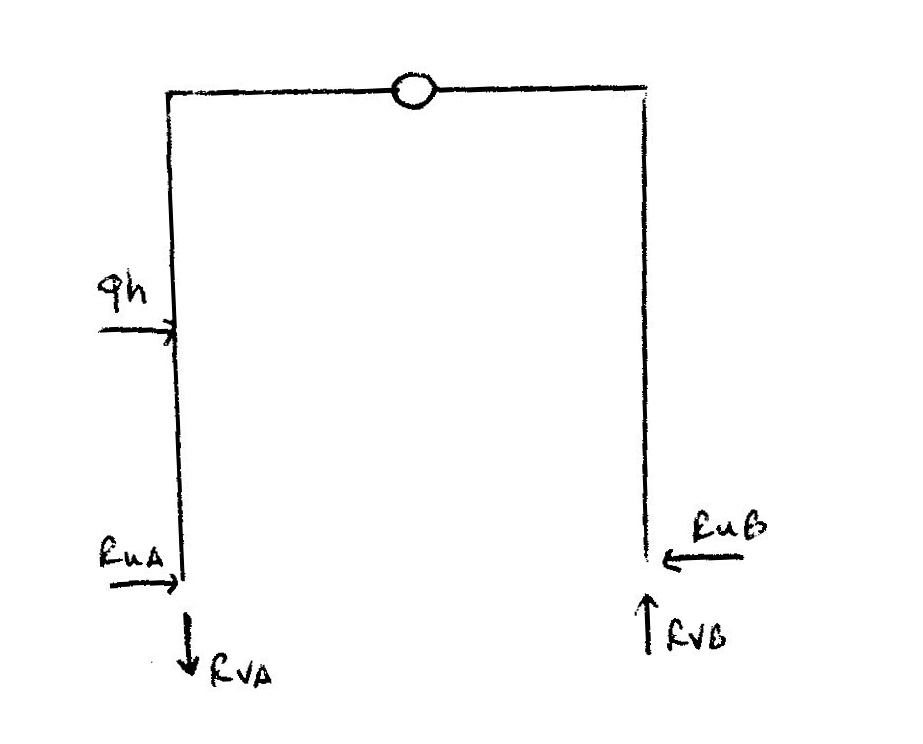
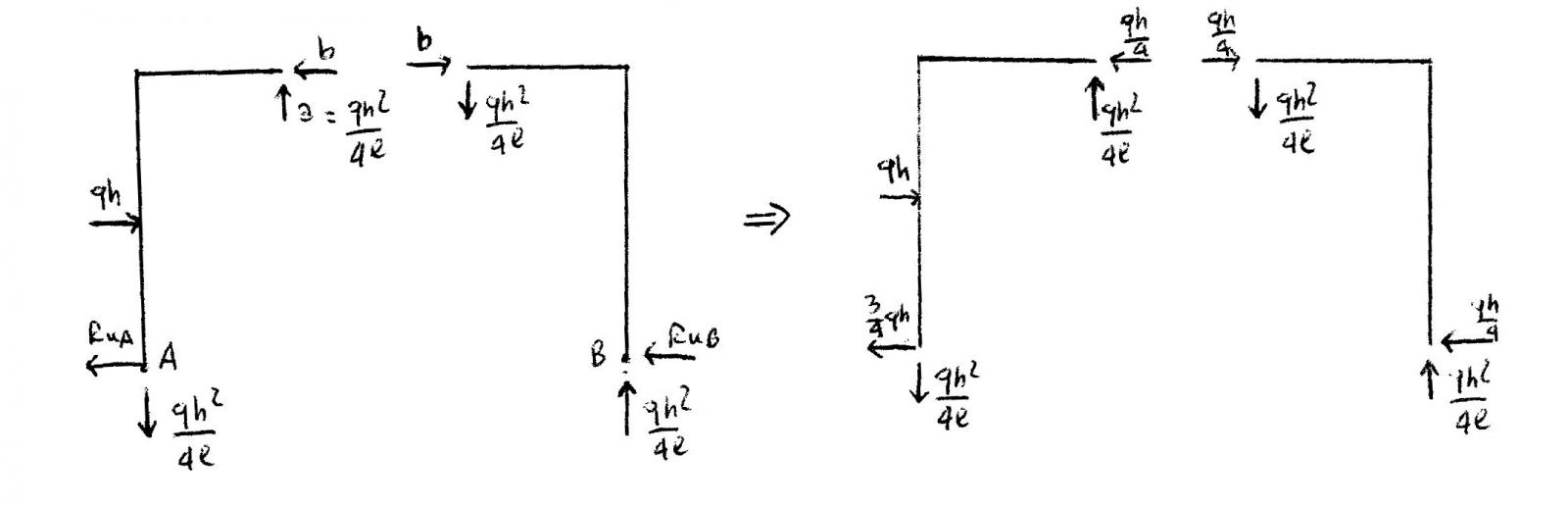
Rifacendo l’equilibrio alla traslazione verticale, l’equilibrio alla traslazione orizzontale e l’equilibrio dei momenti in A, ho trovato che RuA=3/4 qh , RuB=qh/4 e di conseguenza le reazioni vincolari nel nodo superiore saranno uguali e opposte e del valore di quelle orizzontali e verticali nelle cerniere inferiori.

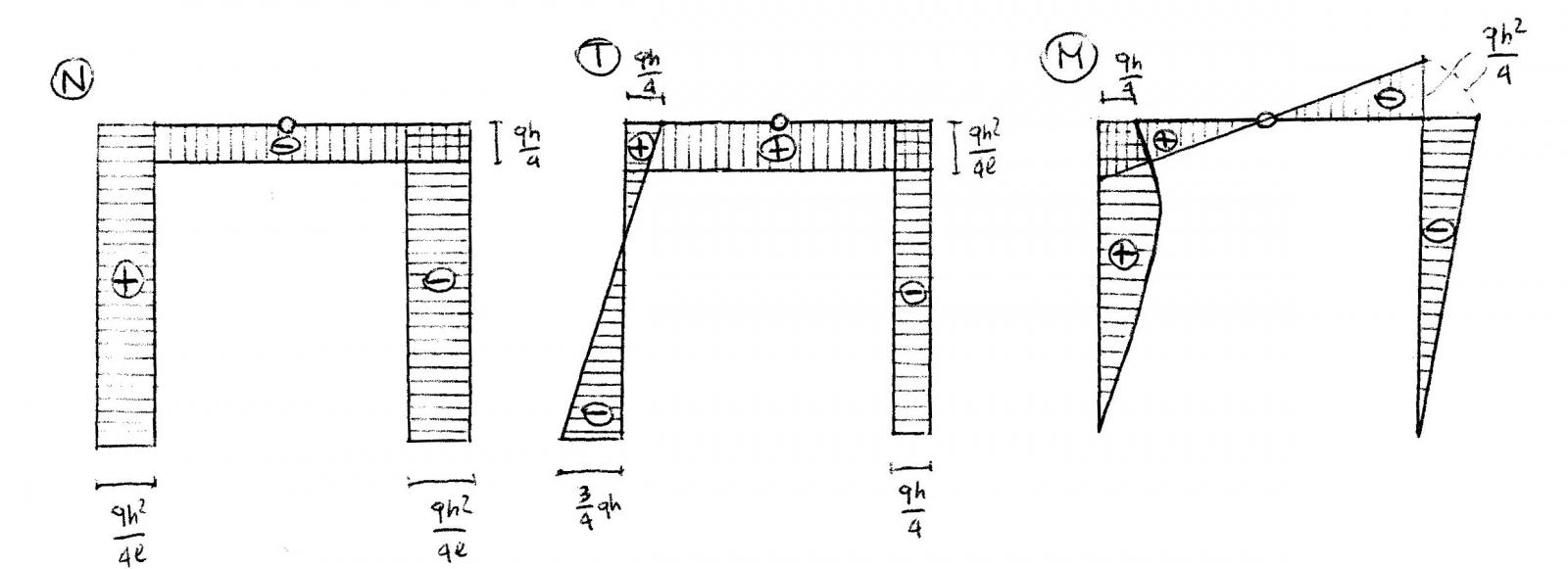
Dato che è assente un carico distribuito parallelo all’asse di ogni elemento, il diagramma dello sforzo normale è costante in ogni punto. Data la presenza del carico q, il diagramma del taglio sarà lineare nel pilastro sinistro, e costante in ogni altro punto poiché sono assenti altri carichi distribuiti nella struttura. Il diagramma dei momenti sarà invece parabolico nel tratto verticale sinistro (dove il taglio si annulla il momento ha un massimo), e nel resto della struttura sarà lineare (dato che nel taglio è costante).

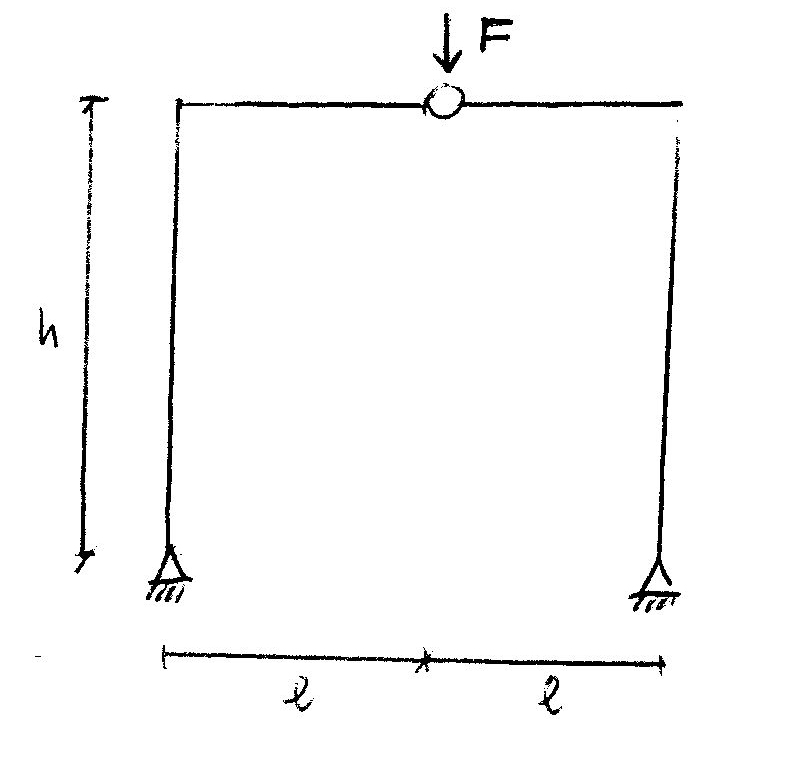
Il secondo esercizio sull’arco a tre cerniere è molto simile al primo, a parte il fatto che invece di avere il carico distribuito sul pilastro, in questo caso vi è una forza concentrata di valore “F” applicata sul nodo. Procedo col calcolare le reazioni vincolari: facendo l’equilibrio alla traslazione orizzontale, quello alla traslazione verticale  e quello dei momenti nel punto A, trovo che: RvA=F/2 e anche RvB=F/2.

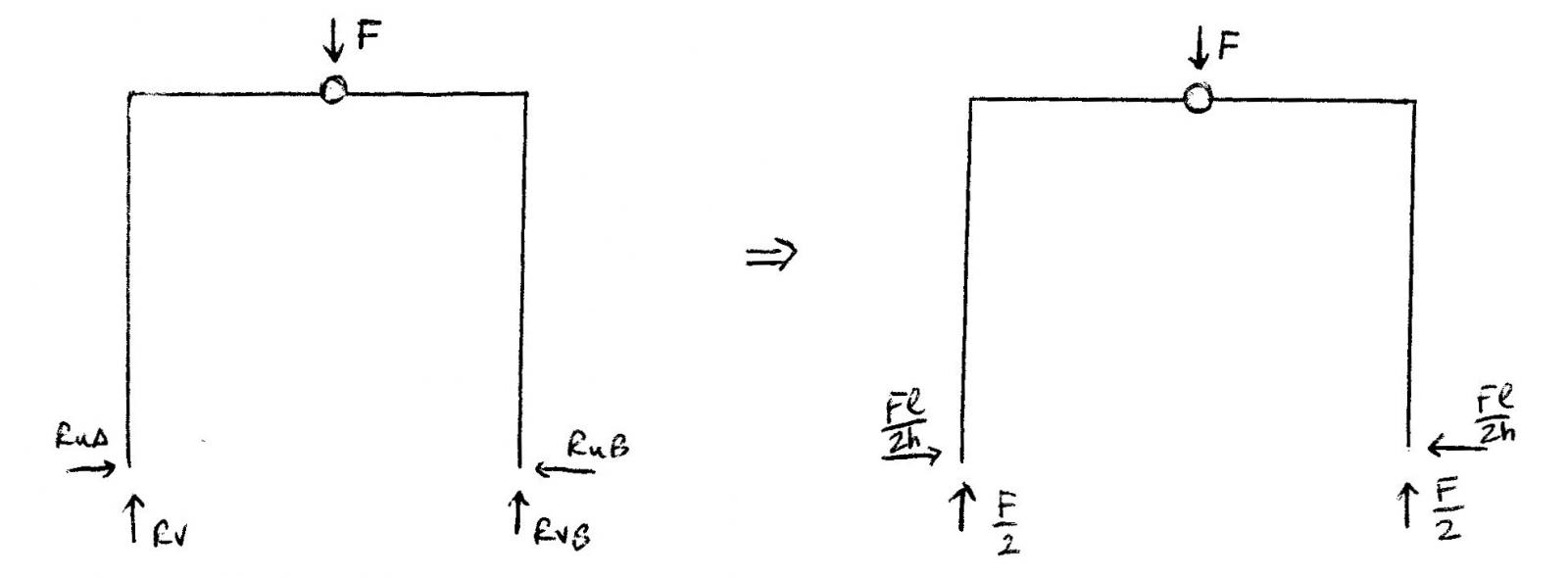
Diciamo che avendo la forza concetrata F sul nodo o comunque nell’asse di simmetria della struttura, era quasi scontato che le due reazioni che la bilanciassero valgono F/2 entrambe! Mentre le due reazioni vincolari orizzontali RuA e RuB sono uguali ed opposte alle reazioni vincolari orizzontali sul nodo e valgono Fl/2h. Riporto ora i diagrammi:

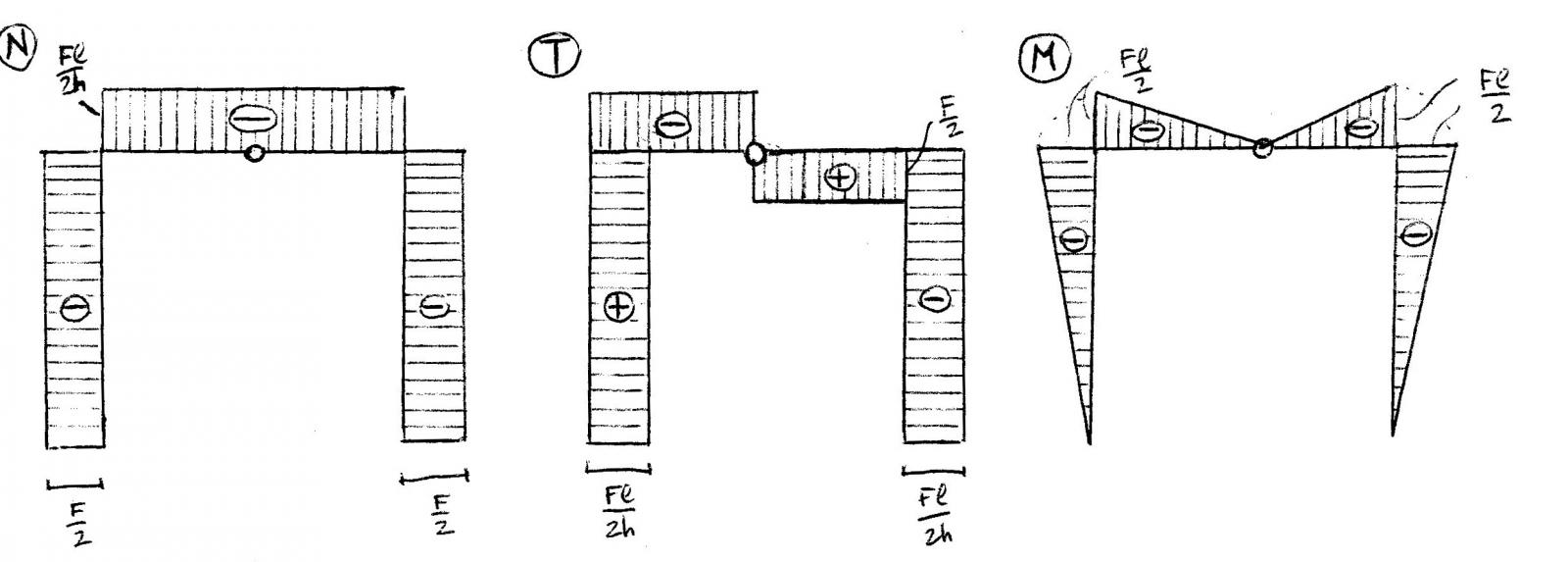
Dato che non è presente un carico distribuito parallelo all’asse di ogni elemento, il diagramma dello sforzo normale è costante in ogni punto. Il diagramma del taglio è costante in ogni punto per lo stesso motivo del diagramma della normale (poichè è assente un carico distribuito) . il diagramma effettua un “salto” nella cerniera a causa della presenza della forza concentrata F e corrispondente  proprio al valore della forza. Il diagramma dei momenti sarà quindi lineare in ogni punto e si annulla nelle cerniere.

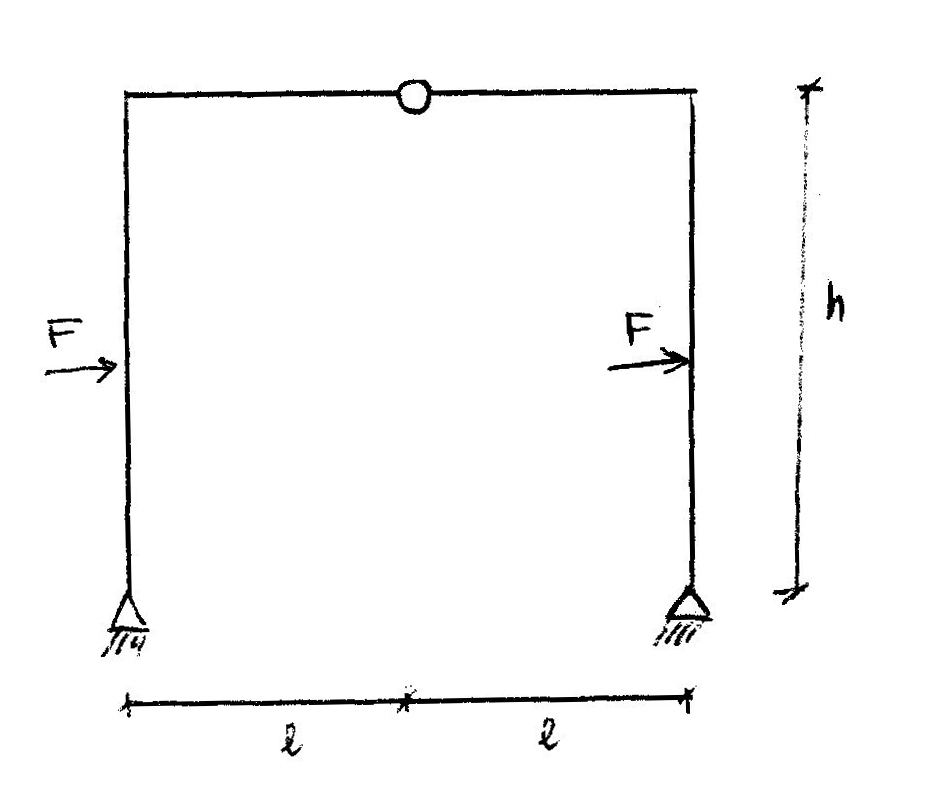
Per il terzo esercizio sull’arco a tre cerniere vediamo che la struttura è analoga, ma in questo caso vi sono due forze F concentrate e applicate a metà di ogni pilastro. Il procedimento eseguito è il medesimo degli altri due esercizi: ho calcolato le reazioni vincolari prima considerando la struttura unica e poi dividendola in due parti per facilitare i calcoli e trovare i valori di ogni reazione: RuA=RuB=F (ovviamente devono bilanciare le due forze F orizzontali), RvA=RvB= Fh/2l.

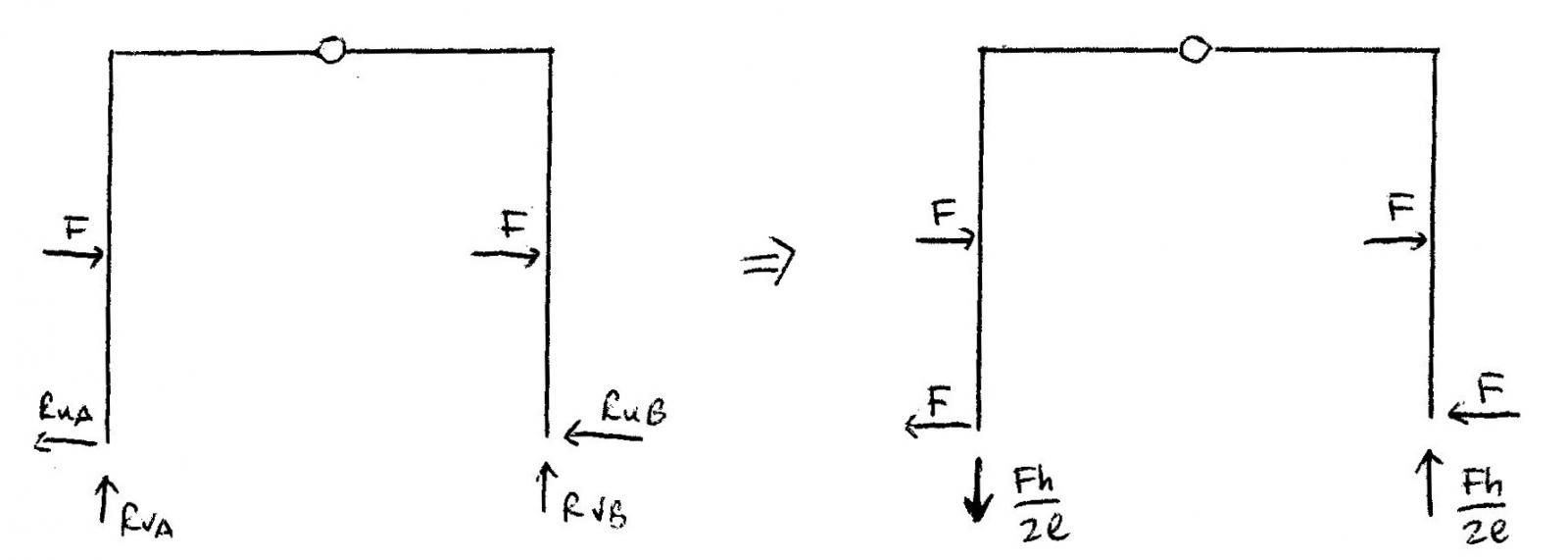
Riporto i diagrammi:

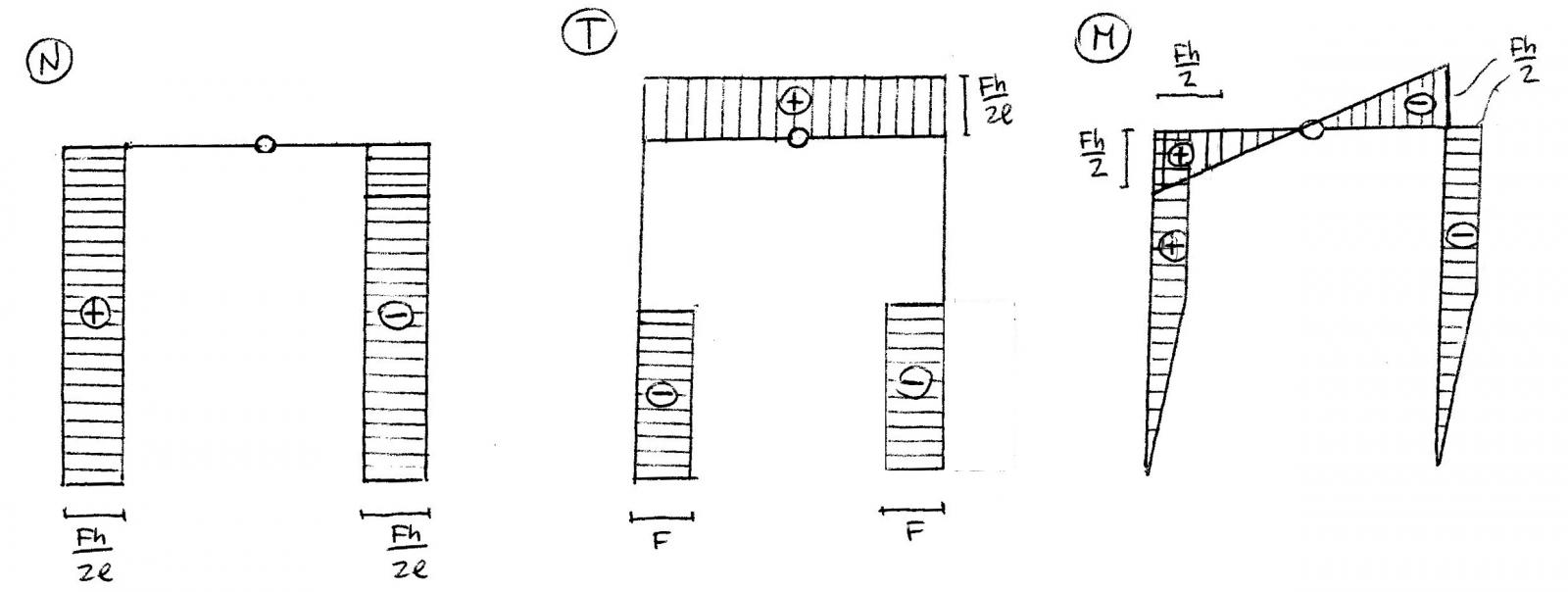
Il diagramma dello sforzo normale è costante in ogni punto, tranne sul tratto orizzontale in cui è pari a zero. Dato che è assente un carico distribuito perpendicolare all’asse di ogni elemento, il diagramma del taglio è costante in ogni punto.  Questo diagramma è caratterizzato dall’annullamento del taglio nella parte superiore dei pilastri, dovuto alla presenza di forze concentrate. Il diagramma dei momenti sarà quindi lineare in ogni punto e si annulla nelle cerniere.

Progetto della struttura:

Come ho già anticipato, progettare significa scegliere una forma, un materiale e delle dimensioni che rispondano alla portata e ai carichi. I materiali da costruzione hanno diverse caratteristiche e proprietà meccaniche.

Acciaio:

L’acciaio è una lega composta principalmente da ferro e carbonio. A seconda del contenuto di carbonio cambia la resistenza dell’acciaio. È un materiale omogeneo, ovvero che ha le medesime caratteristiche fisiche per ogni punto. Viene prodotto nelle fabbriche attraverso due lavorazioni, per laminazione (a caldo) e per trafilatura (a freddo). Esistono diversi tipi di acciaio che vanno dagli extra dolci, ai dolci,ai duri e ai semiduri. Di solito gli acciai da carpenteria sono di tipo dolce e sono sostanzialmente tre: Fe 360 S 235, Fe 430 S 275 e Fe 510 S 355 ( dove il primo numero che compare è la tensione di rottura in MPa e il secondo numero è la tensione di snervamento sempre in MPa).

L’acciaio inoltre è un materiale duttile ( proprietà fisica che indica la capacità di deformarsi plasticamente sotto carico prima di giungere a rottura, cioè la capacità di sopportare deformazioni plastiche) ed isotropo (ha la stessa direzione). L’acciaio resiste bene sia a compressione che a trazione.

Per determinare le caratteristiche del materiale, viene effettuata la prova di trazione ad un provino di acciaio. La macchina utilizzata per la prova di trazione fornisce direttamente un diagramma, detto diagramma tensione-deformazione, che mette in relazione i "carichi unitari" o "sforzi" (δ) in funzione degli "allungamenti unitari" o "deformazioni" (ε).

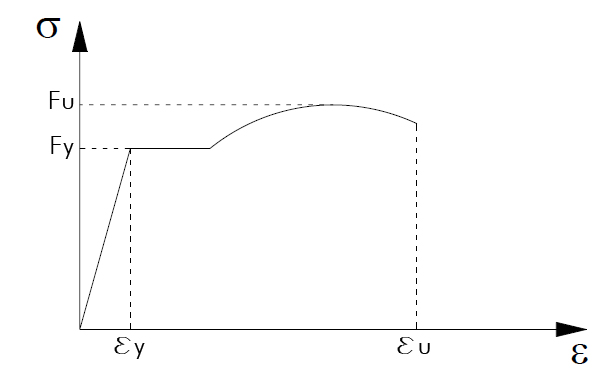
Dal punto di vista del comportamento meccanico, gli acciai da carpenteria sono caratterizzati da un legame costitutivo δ– ε simmetrico a trazione ed a compressione, in cui è possibile individuare tre fasi. Una prima fase elastica pressochè lineare fino al raggiungimento della tensione di snervamento Fy; una seconda fase plastica in cui la deformazione cresce a carico pressochè costante, una terza fase incrudente in cui il carico riprende a crescere fino  al raggiungimento del carico massimo Fu. Raggiunto il carico massimo la tensione inizia a diminuire fino al raggiungimento della deformazione ultima eu e quindi alla crisi del materiale per eccesso di deformazione portando alla rottura del provino di acciaio.

Per il nostro progetto bisogna prendere un valore più basso dello snervamento Fd, che indica la tensione di design.

Fd = Fy / γ   dove γ è il coefficiente di sicurezza.

Calcestruzzo:

Il calcestruzzo armato è un materiale non omogeneo ed è costituito da calcestruzzo (una miscela di cemento, acqua, sabbia e inerti, cioè elementi lapidei, come la ghiaia) e barre di acciaio (armatura) annegate al suo interno ed opportunamente sagomate ed interconnesse fra di loro.

Il cls ha una notevole resistenza a compressione, ma ha una scarsa resistenza a trazione, per questo viene utilizzato l’acciaio in barre che vengono annegate nel cls, garantendo così la resistenza a trazione. Le barre hanno diametro variabile e possono essere impiegate sia come armatura longitudinale, sia come "staffe", ovvero come barre che racchiudono altre barre (in genere di maggior diametro) a formare una sorta di "gabbie" opportunamente dimensionate secondo le necessità d'impiego.

La sinergia tra due materiali così eterogenei è spiegata tenendo presenti due punti fondamentali:

• Tra l'acciaio ed il calcestruzzo si manifesta un'aderenza che  trasmette le tensioni dal calcestruzzo all'acciaio in esso annegato.
• I coefficienti di dilatazione termica dei due materiali sono sostanzialmente uguali.

Per aumentare l'aderenza tra i due materiali da qualche decennio al posto delle barre lisce di acciaio vengono utilizzate barre ad aderenza migliorata, cioè barre sulle quali sono presenti delle filettature.

Nel calcolo elastico delle sezioni si ipotizza che i legami elastici siano rappresentati dalla Legge di Hooke:

  δc = Ec εc  e δs = Es εs 

Il calcestruzzo e l’acciaio hanno la stessa deformazione ma non la stessa tensione -->  εc=εs

Ne deriva che δc / Ec = δs / Es -->  δs = (Es/ Ec) δc = n δc

Dove “n” è il coefficiente di omogeneizzazione (spesso viene considerato n= 15 o almeno n=10). Dato che il cls non è un materiale omogeneo, per renderlo tale si utilizza questo coeff. di omogeneizzazione. Inoltre si nota che le tensioni si differenziano di una quantità pari al rapporto dei loro moduli elastici.

Classi di resistenza del calcestruzzo

Il calcestruzzo è classificato in classi di resistenza in base alla resistenza a compressione, tenendo conto della Resistenza cilindrica  (fck) e della Resistenza cubica (Rck), entrambe espresse in MPa.

La resistenza cubica  Rck viene determinata sulla base dei valori ottenuti da prove di compressione monoassiale su provini cubi di 150 mm di lato, maturati 28 giorni; la resistenza cilindrica  fck viene determinata invece utilizzando provini cilindrici di 150 mm di diametro e 300 mm di altezza.

Tra i due valori esiste la seguente relazione:    fck = 0,83 Rck

La differenza tra i due valori dipende fondamentalmente dal diverso stato tensionale che si genera nel provino a seguito delle prove di compressione, che dipende dal fatto che i provini cubici sono tozzi mentre quelli cilindrici sono snelli. Si va dalle classi  C8/10, C16/20, C50/60, C100/120 .

Le prime classi vengono utilizzate per le fondazioni e non sono armate. Quelle che si utilizzano maggiormente vanno da C20/25 a C70/75.

Per l’acciaio da calcestruzzo vengono utilizzati il B450A e il B450C (quest’ultimo utilizzato in zona sismica ).

Per il nostro progetto dobbiamo utilizzare la tensione massima δmax = Mx / Wx ovvero il rapporto tra il momento massimo e il modulo di resistenza a flessione. Si deve poi confrontare con Fd, e la verifica è soddisfatta se δmax < Fd.

Legno

Il legno è un materiale solido, naturale, organico e cellulare. Si tratta di un composto costituito da un complesso chimico di cellulosa, emicellulose, lignina ed estrattivi.

È un materiale anisotropo: le fibre sono orientate in una direzione preferenziale e perciò il materiale reagisce alle sollecitazioni in maniera diversa in ogni direzione. Il legno è più resistente se la direzione è parallela alle fibre.  In base alle proprietà meccaniche (durezza, resistenza a trazione, a compressione e a flessione)  i legnami si suddividono in legni duri (latifoglie) e legni teneri (conifere).

Il legno è dotato di molte e differenti caratteristiche: molte specie e diverse condizioni ambientali in cui crescono le stesse varietà, come il terreno più umido o più siccitoso, ricco o povero di sostanze nutrienti, con diversa struttura, temperatura, posizione, ecc.. Vi sono, tuttavia, alcune caratteristiche che accumunano tutti i legni, e sono:

Porosità,  Eterogeneità, Igroscopia (il legno è pronto a rilasciare nell’aria secca una parte dell’acqua che contiene, pronta a riassorbirla se l’ambiente che la circonda contiene più acqua di quella contenuta nel legno stesso), Anisotropia (il legno presenta una diversa resistenza meccanica a seconda della sollecitazione; sia alla trazione sia alla compressione è molto più resistente nel senso longitudinale del fusto e, molto meno, in quello trasversale), Biodegradabilità (è soggetto ad essere attaccato e demolito per effetto della vita animale, vegetale fungina o batterica).

Il legno, in quanto materiale da costruzione, ha ottime proprietà:

• ecologico
• genera benessere e confort abitativo
• ottimo rapporto peso/resistenza
• buon comportamento al fuoco
• ridottissima sensibilità agli sbalzi di temperatura
• durabilità e ridotta manutenzione
• inattaccabilità all’aggressione chimica ed ambientale
• ottime prestazioni termiche ed acustiche
• ottima resistenza a flessione, compressione e trazione
• facilità di lavorazione
• consente ottimizzazione nelle lavorazioni grazie all’elevato grado di prefabbricabilità
• ottimo in zone sismiche

Un aspetto fondamentale del legno è che sente il tempo e l’umidità. Il legno è costretto a lavorare ad un’umidità diversa da quella in cui è stagionato ( per diventare un materiale da costruzione il legno deve essere stagionato). Il legno assorbe o perde umidità in relazione all'umidità dell'ambiente che lo circonda. I movimenti, dimensionali e volumetrici, che ne derivano possono generare fenomeni indesiderati quali fessurazioni, torsioni, svergolamenti e imbarcature. Si deve conoscere quale sia il grado di umidità dell'ambiente in cui dovrà essere posizionato il legno.

Per quanto riguarda il progetto : Fd = ( Kmod Fk ) / γm   dove Kmod è un coefficiente moltiplicativo molto basso che tiene conto dello scorrere del tempo.

Anche il legno è diviso per classi di resistenza ( che si riferiscono al legno lamellare):

GL24h , GL28h , GL32h , GL36h  dove i numeri 24, 28, 32, 36 rappresentano la resistenza a flessione Fk. Mentre la resistenza a trazione è rispettivamente  16.5 , 19.5 , 22.5 , 26.

Esercitazione: Dimensionamento di una trave in tre tecnologie differenti

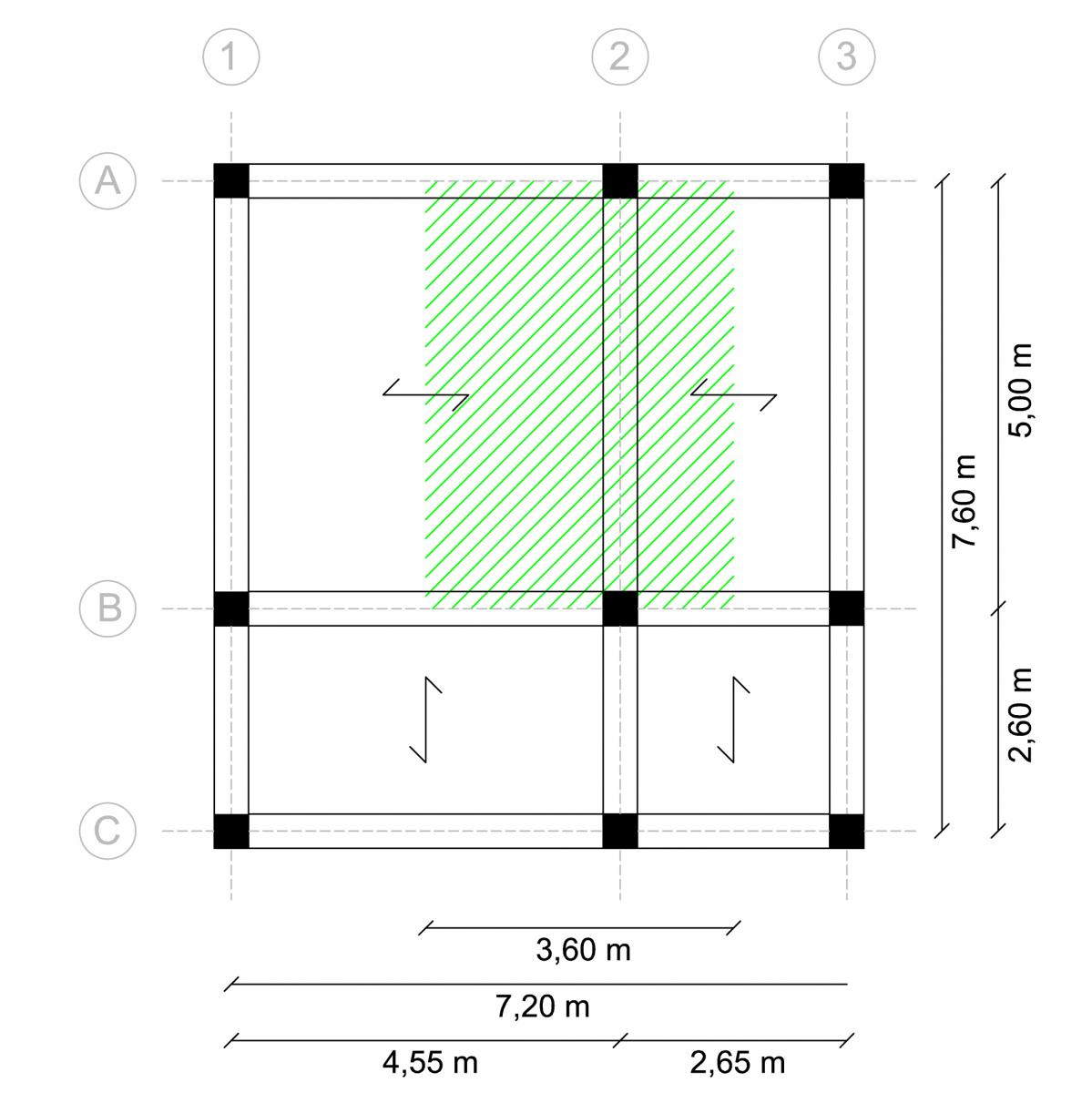
La pianta presa in esame per l’esercitazione è il piano terra di un’abitazione unifamiliare che ho progettato per l’esame di Costruzione dell’Architettura del primo anno della laurea triennale. Ho scelto di dimensionare la trave tra i pilastri A2 e B2, che ha una luce di 5,00 m e un’ interasse di 3,60 m. L’area di influenza della trave è quindi 5,00 x 3,60 = 18 m².

Ora per prima cosa bisogna trovare i valori dei carichi accidentali (Qa), strutturali (Qs) e permanenti (Qp).

 -Il carico Qa è legato alla funzione dell’edificio, nel mio caso è quello considerato per “Ambienti ad uso residenziale” che si trova sulla Normativa, e vale 2,00 KN/ m².

-Il carico Qs è il peso di tutti gli elementi strutturali.

-il carico Qp comprende i carichi non strutturali che si trovano permanentemente sulla struttura come gli impianti, gli intonaci, gli isolanti, i pavimenti, ecc. 

Ora procederò nel progettare la trave scelta in tre diversi materiali: in legno, in acciaio e in calcestruzzo armato.

LEGNO:

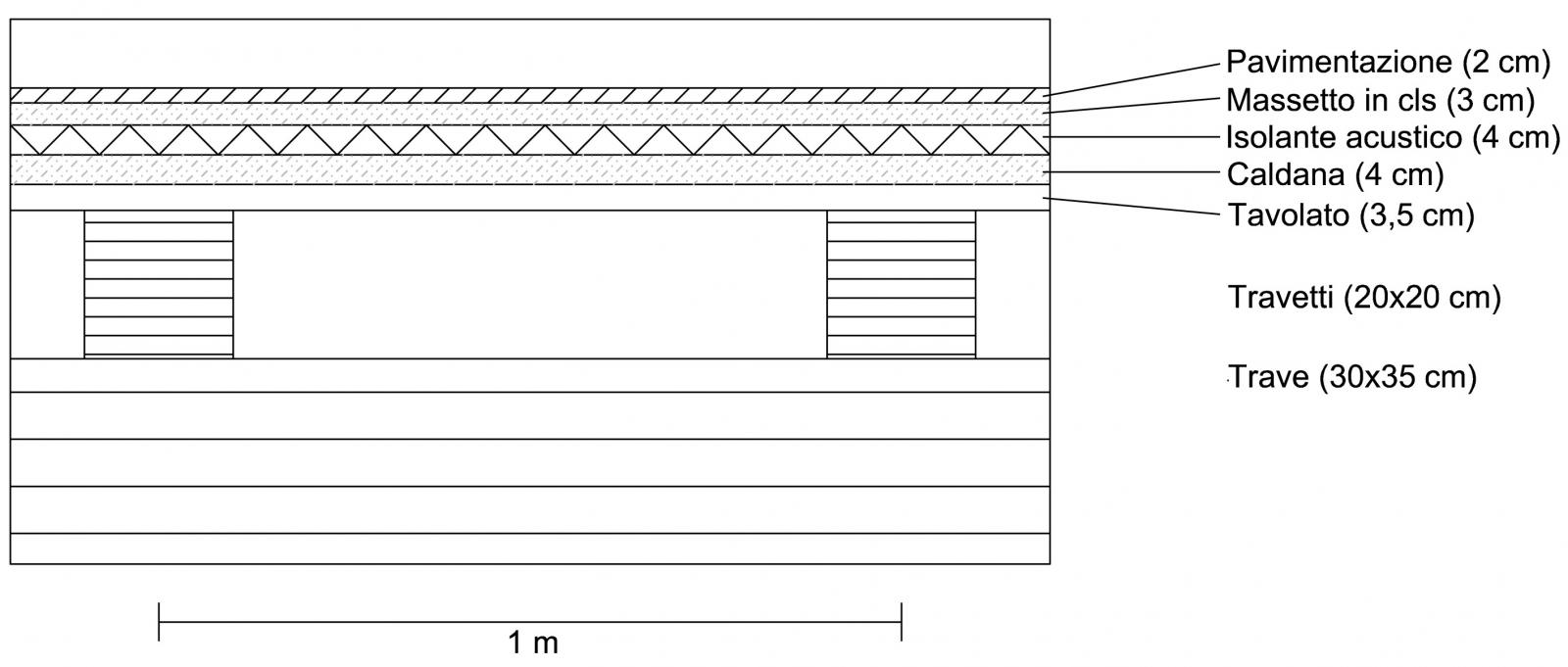
Travetto

L’interasse dei travetti è di 1 m e la luce è di 4.55 m.

Calcolo dei carichi:

-Sovraccarico accidentale Qa = 2 KN/m²

-Carico strutturale (Qs) = y x h = peso specifico x spessoreTavolato: 6 KN/m³ x 0,035 m = 0,21 KN/m²

• Tavolato: 6 KN/m³ x 0,035 m = 0,21 KN/m²

-Sovraccarico permanente (Qp)= y x h = peso specifico x spessore

• Pavimentazione in legno: spessore 2 cm --> 0,25 KN/m²
• Massetto: 24 KN/m³ x 0,03m = 0,72 KN/m²
•  Isolante acustico: 4 KN/m³ x 0,04m = 0,16 KN/m²
• Caldana: 10 KN/m³ x 0,04m = 0,4 KN/m²
• Ipotesi d'incidenza impianti e tramezzi: 0,50 KN/m²+ 1,00 KN/m²= 1,50 KN/m²

Qp= 0,25+0,72+0,16+0,4+1,5= 3,03  KN/m²

Ora vado a sostituire I valori trovati nel foglio excel e quindi procedo con il dimensionamento dei travetti. Inserisco i valori dei tre diversi carichi e il valore dell’interasse (I). Per trovare il carico totale al metro lineare bisogna moltiplicare la somma dei carichi per l’interasse:

Qtot=(Qs+Qp+Qa)x I = 0,21+3,03+2) x 1 = 5,24 KN/m

Successivamente imposto la luce del travetto (4,55 m) e mi trovo il valore del momento. In questo caso si tratta di una trave doppiamente appoggiata, quindi il valore del momento è ql²/8 :

M= (5,24 x 4,55²)/8 = 13,56 KNm

Ora per calcolare le dimensioni della sezione del travetto devo calcolare fD ovvero la tensione di design che si trova:

fD= Kmod x fk/γm

dove Kmod è un coefficiente che indica il degrado che la trave in legno subisce in funzione del tempo (vale 0,5), fk è la tensione di snervamento e va impostata a seconda della classe di legno che viene scelta (in questo caso ho scelto la classe GL36h), il valore γm è il coefficiente di sicurezza che varia a seconda del materiale (in questo caso 1,45). Sia Kmod che γm tendono a diminuire la resistenza di progetto.

fD= 0,5 x 36/1,45 = 12,41 N/mm²

Ora, impostando la dimensione della base del travetto (20 cm), posso trovare la sua altezza:

h= (6 x M x 1000 / b x fD) ^ 0,5 = (6 x 13,56 x 1000 / 20 x 12,41)^ 0,5 = 18,10 cm

Approssimando per eccesso i valori ottenuti ottengo un travetto di dimensioni 20x20 cm.

Per verificare il risultato ottenuto effettuo di nuovo i calcoli con il foglio excell sommando al carico strutturale il carico dei travetti:

Qtr al metro lineare = A x γ= 0,1 m x 0,20 m x 6 KN/m³= 0,12 KN/m

Qtr al metro quadro = Qtr / interasse = 0,12 KN/m / 1 m = 0,12 KN/m²

Qs = 0,21 KN/m² + 0,12 KN/m² = 0,33 KN/m²

Ottengo un’altezza pari a 18,31 cm quindi il dimensionamento risulta corretto. 

Travetto in legno GL36h 20x20cm

Trave

L’interasse della trave è di 3,60 m e la luce è di 5,00 m. Per il calcolo della trave utilizzo lo stesso procedimento del dimensionamento dei travetti.

Calcolo dei carichi:

-Sovraccarico accidentale Qa = 2 KN/m²

-Carico strutturale (Qs) = y x h = peso specifico x spessore

• Tavolato: 6 KN/m³ x 0,035 m = 0,21 KN/m²
• Travetti : 6 KN/m³ x 0,02 m = 0,12 KN/m²

Qs = 0,21 + 0,12 =0,33 KN/m²

-Sovraccarico permanente (Qp)= y x h = peso specifico x spessore

• Pavimentazione in legno: spessore 2 cm --> 0,25 KN/m²
• Massetto: 24 KN/m³ x 0,03m = 0,72 KN/m²
• Isolante acustico: 4 KN/m³ x 0,04m = 0,16 KN/m²
• Caldana: 10 KN/m³ x 0,04m = 0,4 KN/m²
• Ipotesi d'incidenza impianti e tramezzi: 0,50 KN/m²+ 1,00 KN/m²= 1,50 KN/m²

Qp= 0,25+0,72+0,16+0,4+1,5= 3,03  KN/m²

Qtot=(Qs+Qp+Qa)x I = 0,33+3,03+2) x 3,60 = 19,296 KN/m

M= (19,296 x 5,00²)/8 = 60,3 KNm

fD= 0,5 x 36/1,45 = 12,41 N/mm²

h= (6 x M x 1000 / b x fD) ^ 0,5 = (6 x 60,3 x 1000 / 30 x 12,41)^ 0,5 = 31,17 cm

Ipotizzando la base 30 cm e approssimando per eccesso, l’altezza è pari a 35 cm --> Trave 30x35 cm. Ora verifico il risultato ottenuto:

Qtr al metro lineare = A x γ= 0,30 m x 0,35 m x 6 KN/m³= 0,63 KN/m

Qtr al metro quadro = Qtr / interasse = 0,63 KN/m / 3,6 m = 0,175 KN/m²

Qs = 0,33 KN/m² + 0,175 KN/m² = 0,505 KN/m²

Ottengo un’altezza pari a 31,67 cm quindi il dimensionamento risulta corretto. 

Trave in legno GL36h 30x35 cm

ACCIAIO:

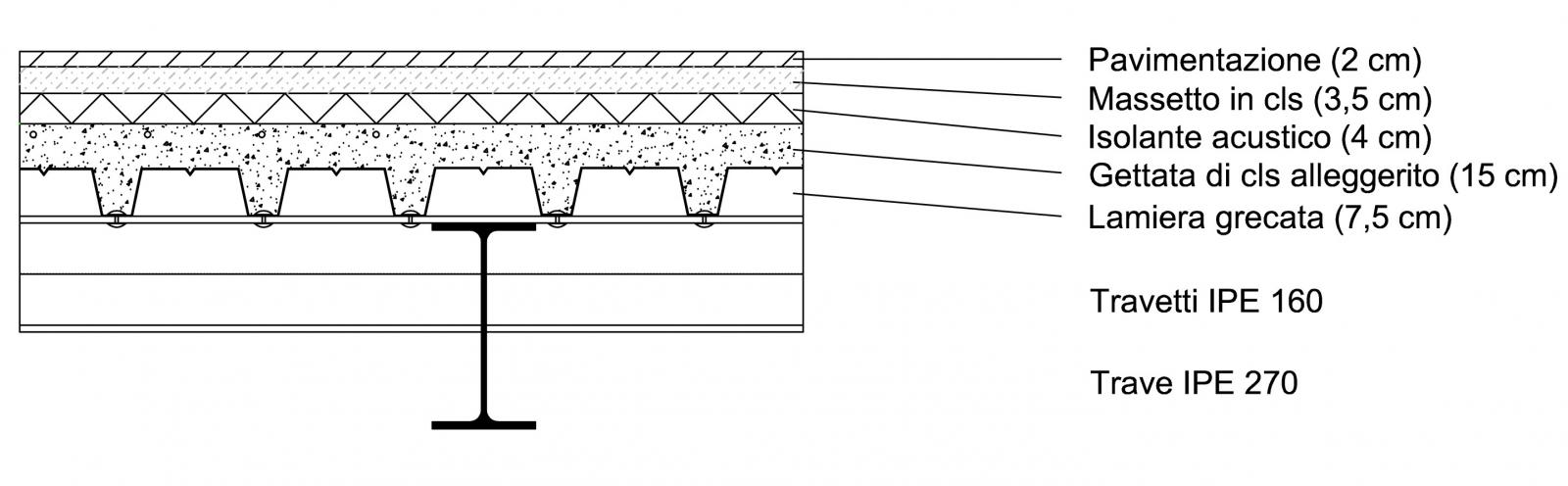
Travetti

Applico il medesimo procedimento per calcolare i travetti. L’interasse è di 1 m e la luce è di 4,55 m.

Calcolo dei carichi:

-Sovraccarico accidentale Qa = 2 KN/m²

-Carico strutturale: carico soletta in lamiera grecata e getto di calcestruzzo di 15 cm = 2,50 KN/m²

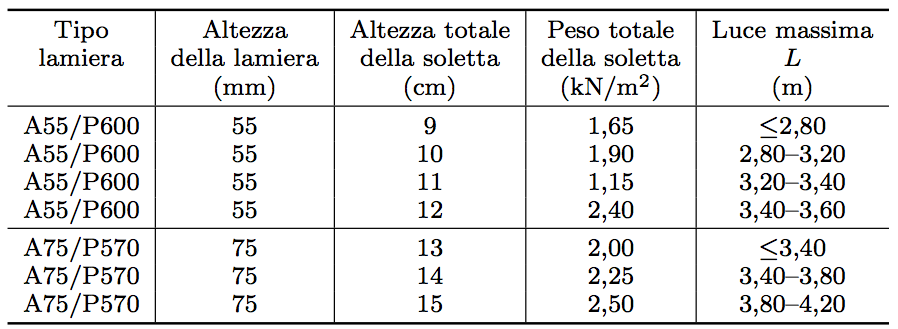
Qs = 2,50 KN/m²

-Sovraccarico permanente (Qp)= y x h = peso specifico x spessore

• Pavimentazione in ceramica: spessore 2 cm --> 0,4 KN/m²
• Massetto: 24 KN/m³ x 0,03 m= 0,72 KN/m²
• Isolante acustico: 4 KN/m³ x 0,04 m = 0,16 KN/m²
• Ipotesi d'incidenza impianti e tramezzi: 0,50 KN/m²+ 1,00 KN/m²= 1,50 KN/m²

Qp= 0,4+0,72+0,16+1,5= 2,78KN/m²

Qtot=(Qs+Qp+Qa)x I = 2,50+2,78+2) x 1 = 7,28 KN/m

M= (7,28 x 4,55²)/8 = 18,83 KNm

fD= fyk / 1,05 = 235 / 1,05 = 223,81 N/mm²

Ora calcolo il modulo di resistenza Wx = M/fD = 18,83 KNm / 223,81 N/mm²x1000 = 84,18 cm³

Per dimensionare la trave cerco sul profilario il valore di Wx, definendo così le dimensioni della sezione.

IPE 160 con Wx = 109 cm³

Verifico quindi le dimensioni aggiungendo il peso della trave:

Qtr al metro lineare = 0,158 KN/m (valore tabellato)

Qtr al metro quadro = Qtr / interasse = 0,158 KN/m / 1 m = 0,158 KN/m²

Qs = 2,50 KN/m² + 0,158 KN/m² = 2,658 KN/m²

Ottengo un Wx pari a 86,00 cm³quindi il dimensionamento risulta corretto. 

Travetto in acciaio S235 IPE 160

Trave

L’interasse della trave è di 3,60 m e la luce è di 5,00 m.

Calcolo dei carichi:

-Sovraccarico accidentale Qa = 2 KN/m²

-Carico strutturale  Qs = carico soletta + carico travetto = 2,5 KN/m² + 0,158KN/m² =2,658 KN/m²

-Sovraccarico permanente Qp = 0,4+0,72+0,16+1,5= 2,78 KN/m²

Qtot=(Qs+Qp+Qa)x I = 2,658+2,78+2) x 3,60 = 26,77 KN/m

M= (26,77 x 5,00²)/8 = 83,67 KNm

fD= fyk / 1,05 = 235 / 1,05 = 223,81 N/mm²

 

Wx= M/fD = 83,67 KNm / 223,81 N/mm²x1000 = 373,88 cm³

IPE 270 con Wx = 429 cm³

Verifico quindi le dimensioni aggiungendo il peso della trave:

Qtr al metro lineare = 0,361 KN/m (valore tabellato)

Qtr al metro quadro = Qtr / interasse = 0,361 KN/m / 3,60 m = 0,10 KN/m²

Qs = 2,658 KN/m² + 0,10 KN/m² = 2,758 KN/m²

Ottengo un Wx pari a 378,90 cm³quindi il dimensionamento risulta corretto. 

Trave in acciaio S235 IPE 270

 

CALCESTRUZZO ARMATO:

Trave

L’interasse della trave è di 3,60 m e la luce è di 5,00 m.

Calcolo dei carichi:

-Sovraccarico accidentale Qa = 2 KN/m²

-Carico strutturale: solaio in laterocemento con travetti armati, altezza totale di 25 cm

Qs = 2,65 KN/m²

-Sovraccarico permanente (Qp)= y x h = peso specifico x spessore

• Pavimentazione in ceramica: spessore 2 cm --> 0,4 KN/m²
• Massetto: 24 KN/m³ x 0,04 m= 0,96 KN/m²
• Isolante acustico: 4 KN/m³ x 0,04 m = 0,16 KN/m²
• Intonaco:  spessore 1,5 cm --> 0,3 KN/m²
• Ipotesi d'incidenza impianti e tramezzi: 0,50 KN/m²+ 1,00 KN/m²= 1,50 KN/m²

• Qp= 0,4+0,96+0,16+0,3+1,5= 3,32KN/m²

Qtot=(Qs+Qp+Qa)x I = 2,65+3,32+2) x 3,60 = 28,69 KN/m

M= (28,69 x 5,00²)/8 = 89,66 KNm

Ipotizzando la base della trave b=30cm, ottengo il valore dell’altezza utile h = 25,75 cm. Siccome bisogna aggiungere 5 cm di copriferro, la mia altezza utile diventa 30,75 cm. Per eccesso prendo una sezione più grande, e variando le dimensioni delle sezioni di cls armato di 5 cm alla volta, la sezione diventerà di 30 x 35 cm.

La classe di resistenza presa in considerazione è C40/50 e acciaio B450C (normativa per zona sismica).

Dal foglio excell si ottiene il peso proprio lineare che è pari a 2,31 KN/m. Sommando questo peso al carico totale: 28,69 + 2,31 = 31 KN/m , H risulta uguale a 31,77 cm. Il dimensionamento è verificato!

Esercitazione: Analisi e dimensionamento Struttura Reticolare Spaziale

In questa esercitazione realizzerò una struttura reticolare spaziale utilizzando due programmi: Autocad 2010 e Sap2000.

Prima di tutto bisogna creare la struttura su Autocad disegnando il modulo base attraverso la polilinea dando una dimensione alle aste di 2 metri ciascuna.

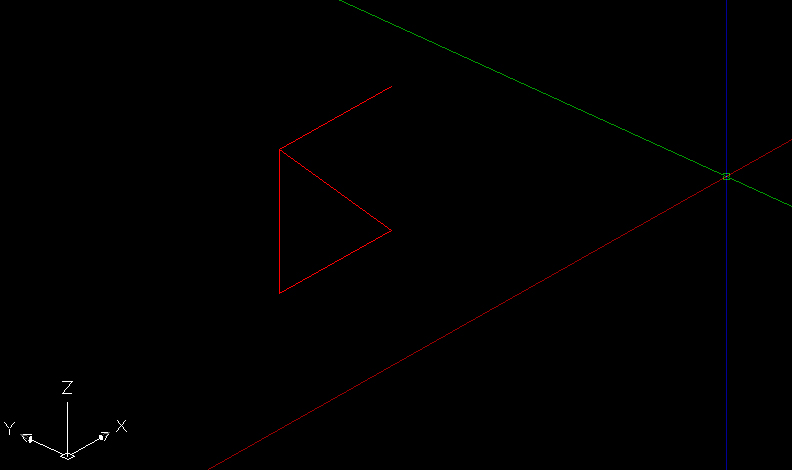
Successivamente passiamo alla vista tridimensionale (premendo shift+rotellina del mouse) e ruotiamo questo modulo sul piano ZX. Ora dobbiamo realizzare una serie, utilizzando proprio il comando “serie” (o array) lungo la direzione X, creando 4 colonne di distanza 2 m (la lunghezza delle aste!).

Ora chiudiamo la struttura e disegnamo le altre aste (due orizzontali e una obliqua) in direzione Y.

Quindi ripetiamo il comando “serie” in direzione X, creando 5 colonne sempre alla distanza di 2 m.

In seguito disegnamo le aste oblique superiori e inferiori che completano la prima campata.

Utilizziamo nuovamente il comando “serie” in direzione Y per disegnare l’intera struttura, creando 7 colonne sempre a distanza 2 m. Ne ho realizzata una in più perché poi si dovranno eliminare le aste per chiudere la struttura in modo corretto. 

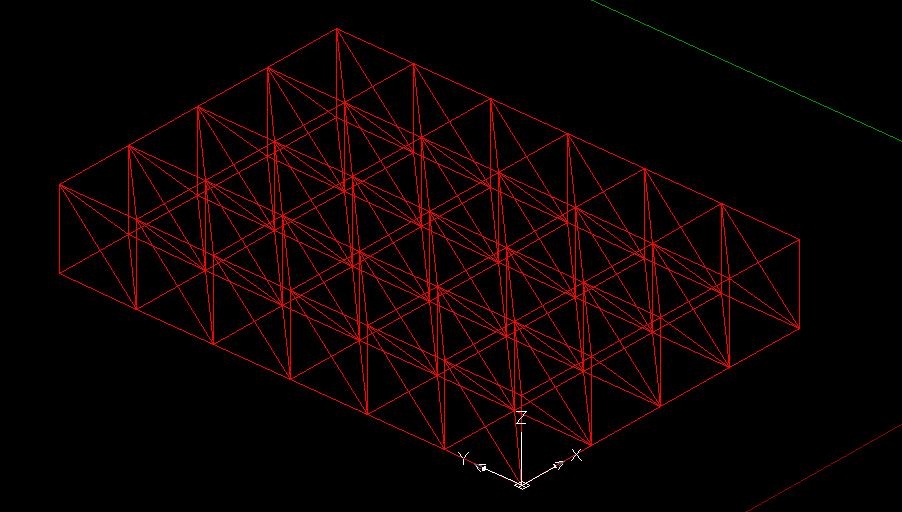
Ho quindi realizzato una struttura di 4x6 campate! Con il cad i procedimenti sono finiti, bisogna salvare il file in dxf per poi importarlo su Sap.

Importiamo quindi la struttura su Sap, impostando l’unità di misura (KN,m,C°). Come prima cosa assegnamo ai quattro vertici esterni le cerniere (“assign_joint_restraint”).

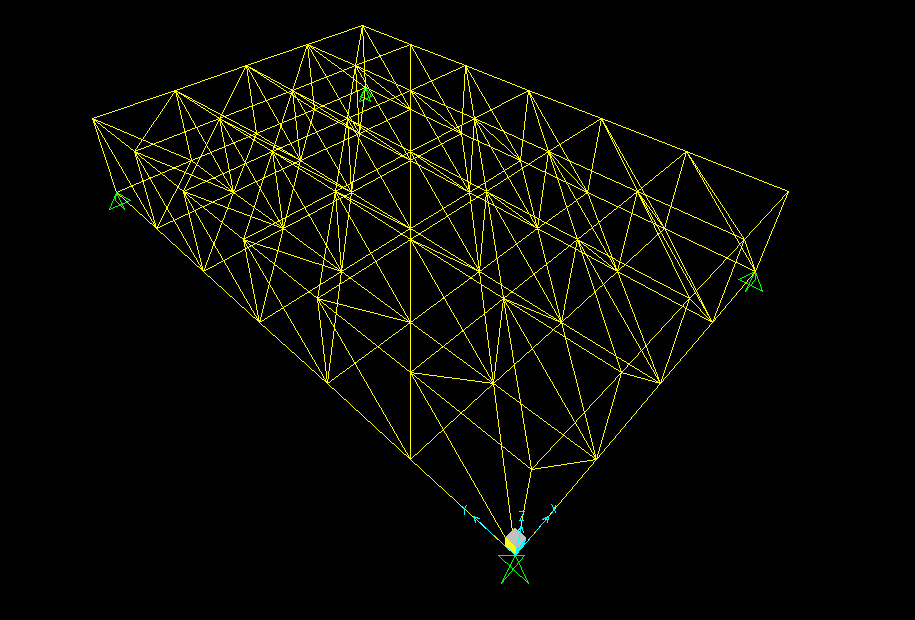
Bisogna selezionare tutte le aste rilasciano il “momento 22 e 33” (0 sia all’inizio che alla fine) in modo che le aste siano sollecitate solo assialmente.

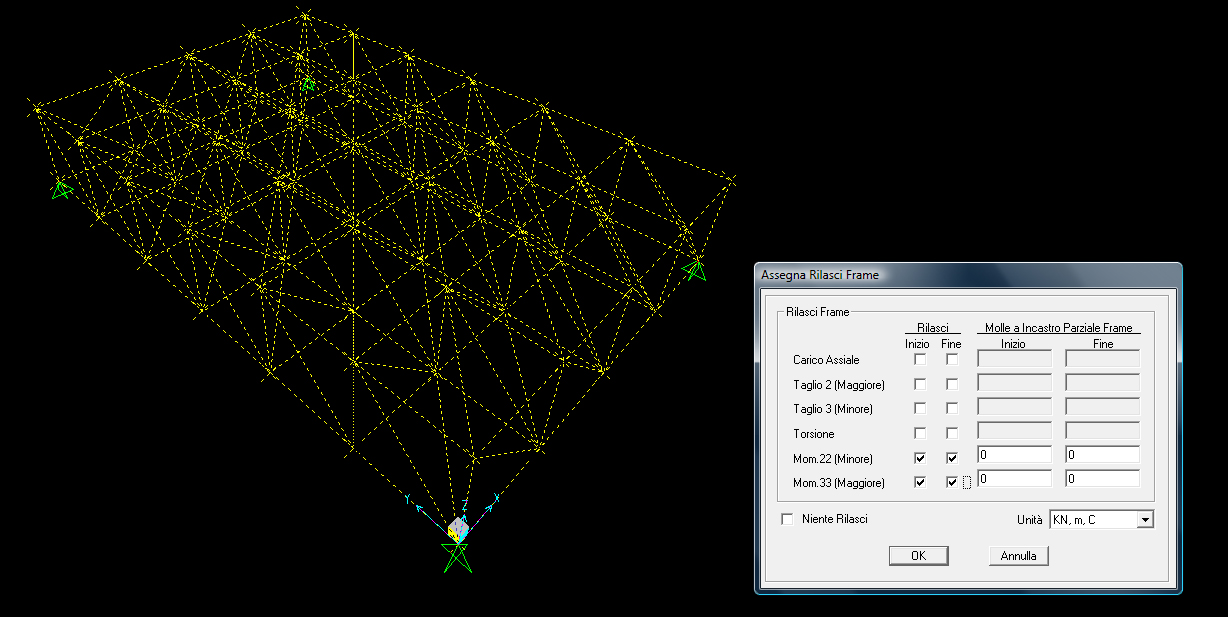
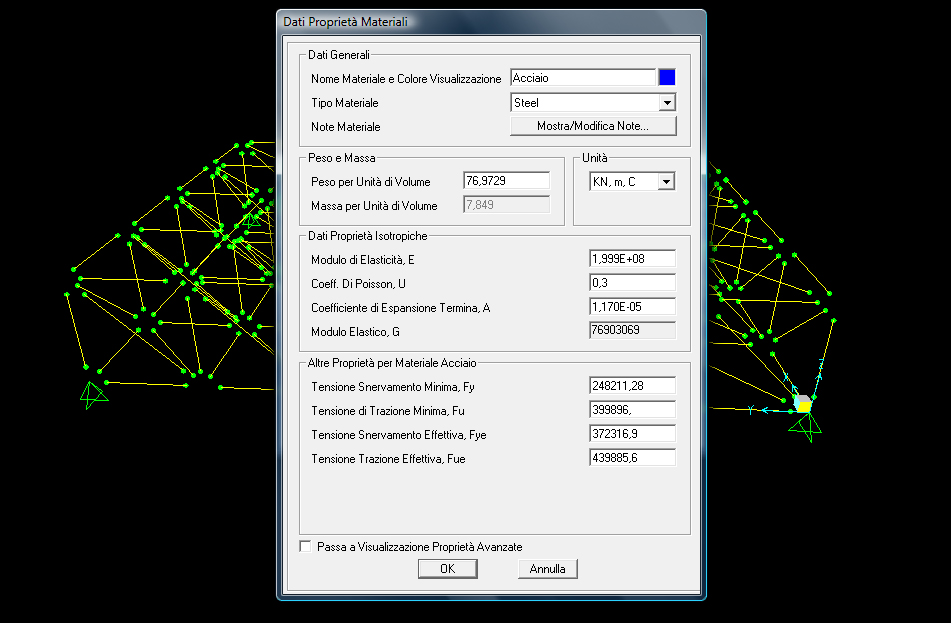
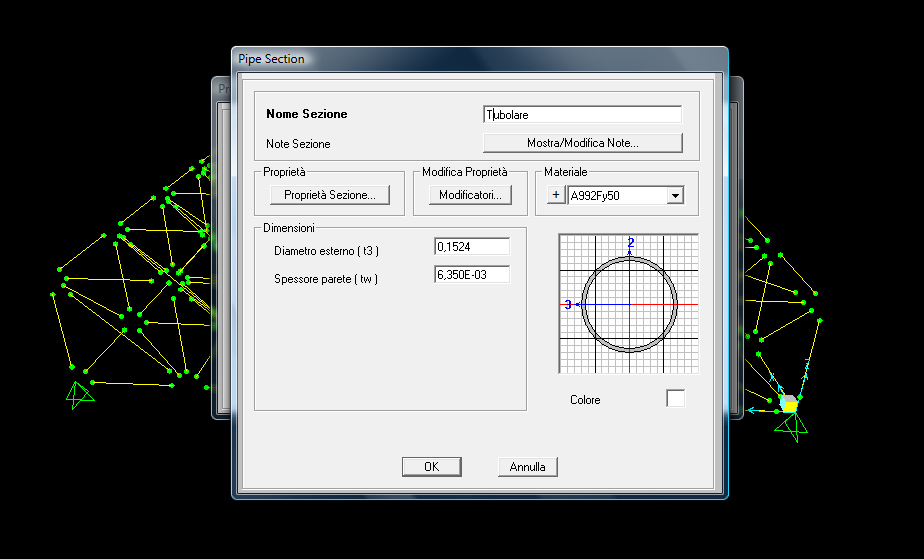
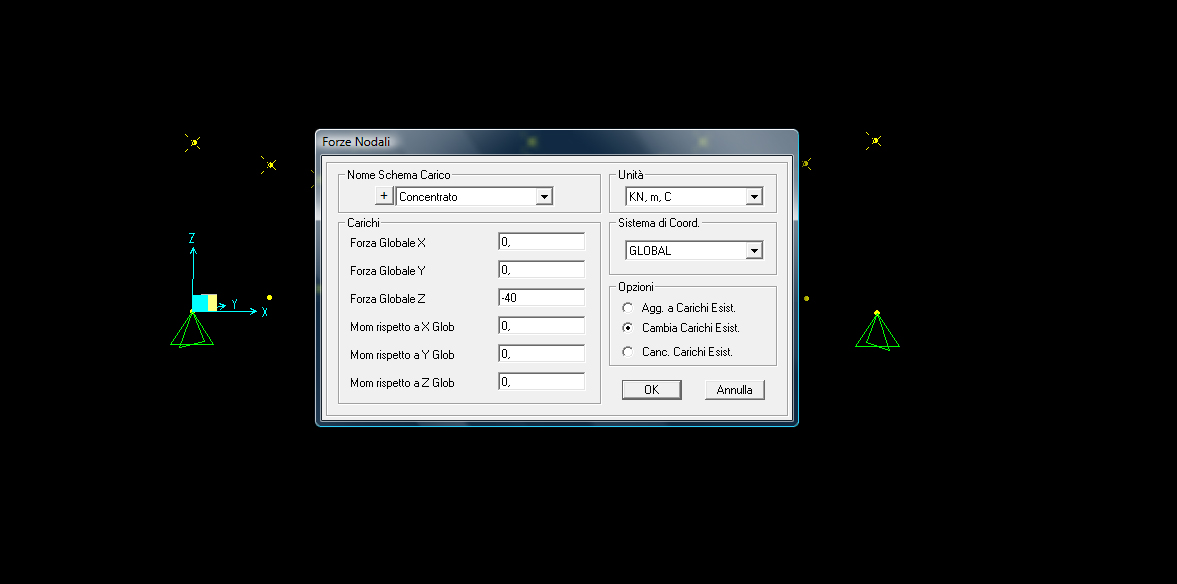
Definiamo il materiale (acciaio) con “define_material”, la sezione (tubolare o pipe) con “define_section proprieties_section frame”, e il carico con “define_load pattern” (carico concentrato) dandogli il valore di -40 KN. 

Il carico va assegnato solo ai nodi superiori! 

Ora salviamo e analizziamo la struttura premendo “run”. Ci apparirà la deformata della struttura.

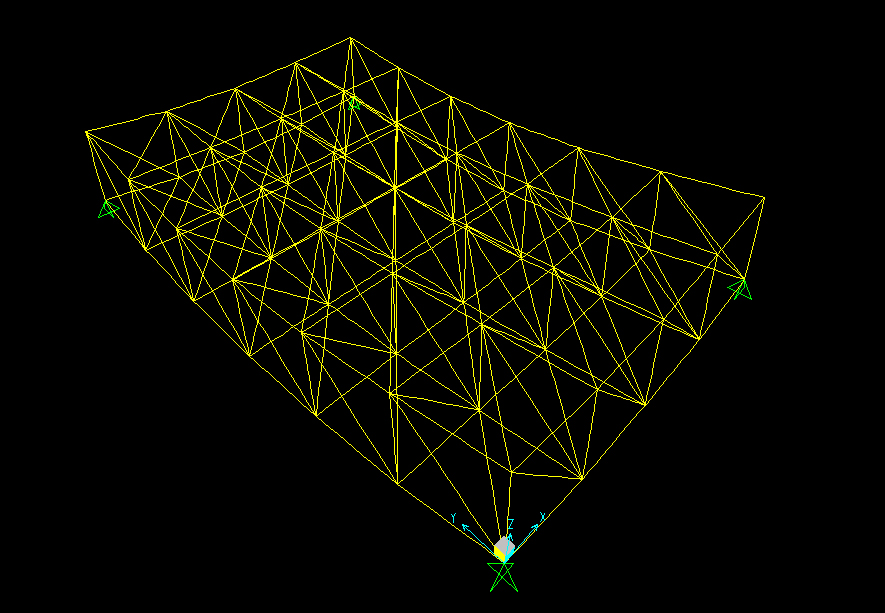
È possibile notare che nei diagrammi del momento e del taglio non si vede nulla, mentre quello dello sforzo normale ovviamente è l’unico visibile.

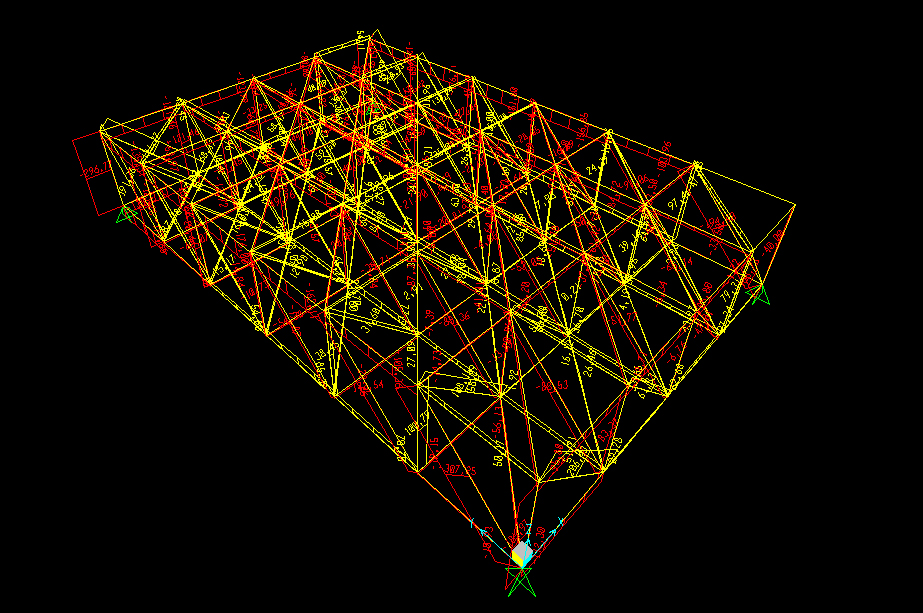
Infine con il comando “set display options_frames/cables/tendons” spuntando “labels” le aste verranno numerate, e aprendo una tabella da “display_show tables”, è possibile identificare l’asta maggiormente sollecitata in compressione e in trazione.

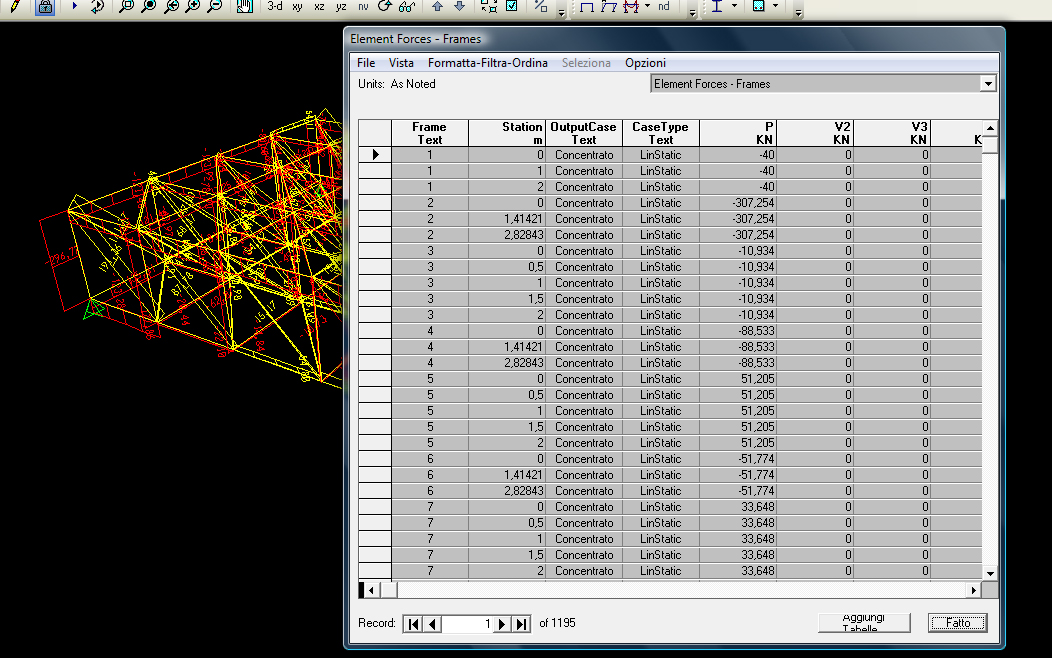
Questa tabella può essere esportata su excell, ordinando la colonna degli sforzi normali dal valore più basso a quello più alto.

Per procedere con il dimensionamento bisogna avere il valore dell’asta più compressa e dell’asta più tesa. Questi sono rispettivamente il valore più basso (negativo) e quello  più alto (positivo) della tabella.

Dopo aver progettato (in collaborazione con Marco Trimaldi) una tabella su excel  capace di “fare i calcoli al posto nostro”, inseriamo i valori di sforzo normale per fare il progetto a resistenza e trovarci un’area minima per l’asta. Questo, per quanto riguarda le aste tese, può bastare, mentre per le aste compresse bisogna procedere con 2 verifiche: quella a snellezza e quella a stabilità.

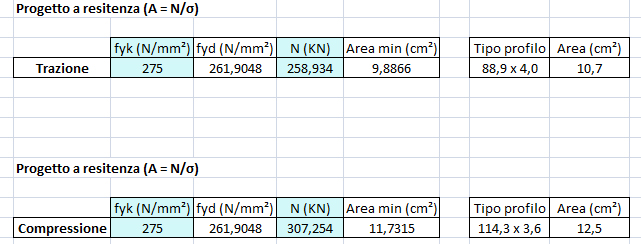
(NTC, Capitolo 4.2.4.1.3)

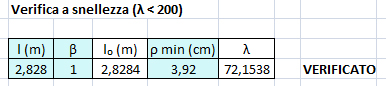
Limitazioni della snellezza

Si definisce lunghezza d’inflessione la lunghezza  l₀ = β l  da sostituire nel calcolo del carico critico elastico Ncr  alla lunghezza l dell’asta quale risulta dallo schema strutturale. Il coefficiente β deve essere valutato tenendo conto delle effettive condizioni di vincolo dell’asta nel piano di inflessione considerato.

Si definisce snellezza di un’asta nel piano di verifica considerato il rapporto

λ = l₀ /ρ

dove  l₀ è la lunghezza d’inflessione nel piano considerato,

         ρ è il raggio d’inerzia relativo.

È opportuno limitare la snellezza λ al valore di 200 per le membrature principali ed a 250 per le membrature secondarie.

Stabilità delle membrature

La verifica di stabilità di un’asta si effettua nell’ipotesi che la sezione trasversale sia uniformemente compressa. Deve essere Nd ≤ Nbrd

dove   Nd è l’azione di compressione di calcolo,

          Nbrd è la resistenza all’instabilità nell’asta compressa, data da

                                                                    

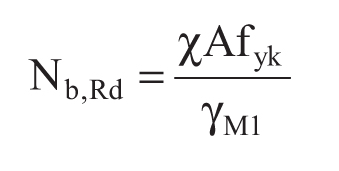
Il coefficiente χ dipende dal tipo di sezione e dal tipo di acciaio impiegato; esso si desume, in funzione di appropriati valori della snellezza adimensionale λ , dalla seguente formula

                                                           

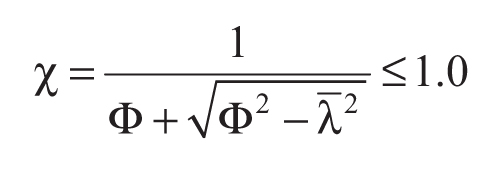
dove φ = 0.5[1+ α (λ - 0.2) + λ² ], α è il fattore di imperfezione, ricavato dalla Tabella 4.2.VI, e la snellezza adimensionale λ è pari a

                                                                 

 

 

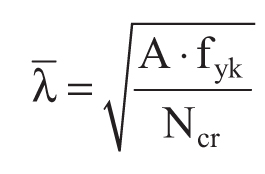
Cenni sull’instabilità delle strutture snelle: Carico Critico Euleriano

Tutti i materiali reagiscono in modo diverso allo sforzo normale, si deve effettuare quindi un’analisi materiale per materiale. Per lo sforzo normale centrale (passa nel centro geometrico della sezione) la tensione è costante e pari a δ = N/A .

In zona sismica può succedere che il sisma stesso cambia il segno della tensione, ovvero un elemento progettato per resistere a trazione in seguito resiste a compressione.

Un esempio è l’asta di Eulero, che si comporta in maniera diversa in trazione e in compressione. Un asta può essere snella (lunga e stretta) oppure tozza (bassa e larga). Dalla formula di Eulero si arriva ad un valore preciso della snellezza. Questa formula detta anche del carico critico euleriano dà il valore di P critico, tale che se il carico P>Pcrit  l’asta è instabile; se P<Pcrit l’asta è stabile.

Pcrit = ( π² E Jmin ) / lo²

Dove “E” è il modulo di elasticità, “Jmin” è il momento d’inerzia e “lo” è la lunghezza libera di inflessione.

Calcolo degli spostamenti per strutture isostatiche

Il metodo degli spostamenti è un metodo che risolve il problema dell’equilibrio sia per strutture isostatiche, sia per strutture iperstatiche. Infatti consente di individuare le reazioni vincolari, i diagrammi delle sollecitazioni, gli spostamenti e le deformazioni, a partire dai tre gruppi di equazioni del modello di trave di Bernoulli.

Equazioni di bilancio:

dN/ds + q1 = 0

dT/ds + q2 = 0      

dM/ds + T + µ = 0

Equazioni del Legame Costitutivo:

N=EAε

M=EJχ

Equazioni di deformazione:

ε=u’

φ=v’

χ=φ’ --> χ=v’’ ( non è un caso che la derivata seconda che misura la concavità è legata proprio alla curvatura!)

Queste sono equazioni differenziali e per risolverle bisogna integrare. Esse necessitano sempre di condizioni al bordo.

Per calcolarci gli spostamenti e le rotazioni di una struttura sottoposta a dei carichi agenti dobbiamo procedere in questo modo:

1)    Determinare la funzione momento M(s)

2)    Determinare la funzione curvatura χ(s)=M(s)/ EI

3)    Trovare la funzione rotazione integrando la funzione curvatura φ(s)= ∫χ(s) ds

4)    Trovare la funzione spostamento integrando la funzione rotazione v(s)= ∫φ(s) ds

5)    Imporre le condizioni al bordo di natura cinematica.

Ora riporto degli esempi di strutture isostatiche:

Trave incastrata con la forza F applicata all’estremo destro:

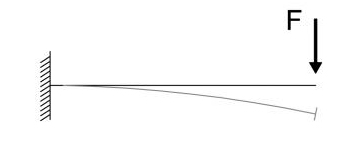
φmax(s=l) = - FL² /2EI

vmax(s=l) = - FL³ / 3EI

Trave incastrata con momento applicato all'estremo destro:

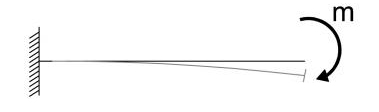
φmax(s=l) = - mL/EI

vmax(s=l) = - mL² / 2EI

Trave incastrata con carico distribuito:

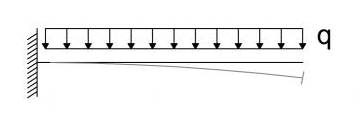
φmax(s=l) = - qL³ /6EI

vmax(s=l) = - qL⁴ / 8EI

Trave incastrata con la forza F applicata in mezzeria:

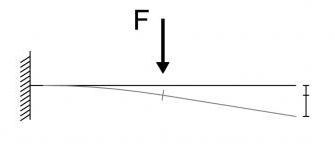
φ(l/2) = - FL³ / 8EI

v(l/2) = - FL³ / 24EI

v(l) = - 5FL³ / 48EI

Trave doppiamente appoggiata con carico distribuito:

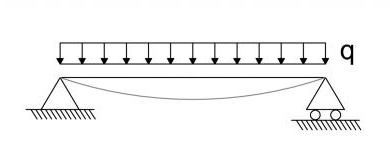
φ(s=0) = - qL³ /24EI

φmax(s=l) = qL³ /24EI

v(l/2) = - 5qL⁴ / 384EI

Trave doppiamente appoggiata con momento applicato:

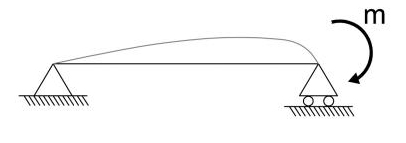
φ(s=0)= mL/6EI

φ(s=l)= - mL/3EI

Trave doppiamente appoggiata con forza applicata in mezzeria:

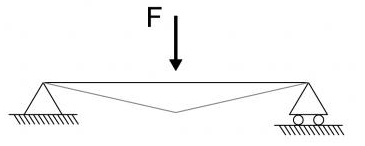
φ(0) = - FL^₂ / 16EI

φ(l) =   FL^₂ / 16EI

v(l/2) = - FL³ / 48EI

In questo caso ci sono due funzioni momento, perchè la forza al centro crea un punto di discontinuità, quindi il valore del momento da destra e da sinistra sono differenti. Di conseguenza avrò due curvature, due rotazioni, due spostamenti e 4 costanti di integrazione.

METODO DELLE FORZE

Il metodo delle forze si utilizza per risolvere strutture iperstatiche, ovvero quelle strutture in cui il numero dei gradi di vincolo è superiore al numero dei suoi gradi di libertà. Questo metodo si adatta a comprendere il gioco delle deformazioni e delle reazioni vincolari, ovvero delle equazioni di congruenza.

Il metodo delle forze consiste nel porre come incognite del problema alcune reazioni vincolari il cui numero è pari al grado di iperstaticità della struttura presa in considerazione. Successivamente si procede utilizzando il principio di sovrapposizione degli effetti, determinando le equazioni di compatibilità cinematica che ci permetteranno di trovare le incognite.

Per cui in primis bisogna individuare una struttura isostatica di riferimento e determinare le incognite iperstatiche,  in seguito scrivere le equazioni di compatibilità cinematica che sostituiscono i vincoli cinematici che abbiamo trasformato in forza (X). Dobbiamo quindi risolvere il sistema di equazioni per determinare le incognite iperstatiche. Infine applichiamo il principio di sovrapposizione degli effetti per determinare le azioni di contatto. 

Ad un’unica struttura iperstatica possono corrispondere vari modelli isostatici di riferimento. La scelta del modello da utilizzare non influenza il risultato finale.

RIGIDEZZA E METODO DELLE RIGIDEZZE

Per capire cosa è la rigidezza prendo come esempio la trave doppiamente appoggiata con il momento applicato che abbiamo visto precedentemente. Abbiamo visto che la rotazione nel punto in cui è applicato il momento è φ= ml/3EI. Se isoliamo il momento diventa: m= (3EI φ) / L

Se ho una rotazione pari a 1 --> m = 3EI / L dove 3EI / L = K_φ che è proprio la rigidezza.

Quindi la rigidezza non è altro che la forza necessaria a produrre uno spostamento unitario.

m= K_φ φ

Il metodo delle rigidezze viene utilizzato per risolvere strutture iperstatiche e isostatiche specialmente di strutture intelaiate, sfruttando la rigidezza Dato che il metodo delle forze ha un utilizzo limitato, viene impiegato il metodo delle rigidezze in quanto è applicabile ad ogni tipo di struttura. Esso utilizza il metodo degli spostamenti sfruttando il calcolo della rigidezza di ogni elemento della struttura. In una struttura il carico si ripartisce in funzione della rigidezza, infatti meno una sezione è rigida e meno prende carico. Inoltre la rigidezza dipende dalle caratteristiche della trave: dalla luce, dal modulo di elasticità e dal momento di inerzia.

Riporto la tabella sinottica delle rigidezze a rotazione:

Trave doppiamente appoggiata con momento applicato:

Kφ = 3EI / L

Trave con cerniera e glifo con momento applicato:

Kφ = EI / L

Trave incastrata con cerniera con momento applicato:

Kφ = 4EI / L

Riporto la tabella sinottica delle rigidezze a traslazione:

Trave incastrata con glifo e forza concetrata sul glifo:

Kφ = 12EI / L³

Trave con cerniera e glifo e forza concetrata sul glifo:

Kφ = 3EI / L³

TELAI SHEAR-TYPE

Un telaio shear-type è una tipologia di telaio che possiede tutti i nodi ad incastro e la trave è considerata infinitamente rigida flessionalmente rispetto ai pilastri.

Nella trave è impedita la rotazione, infatti può solo traslare. I pilastri non si accorciano e non si allungano, si deformano in modo trascurabile. Piuttosto si deformano a flessione.

I telai shear-type sono dei tipi di controvento, ovvero dei vincoli che impediscono alla struttura di effettuare uno spostamento o una rotazione dovuta ad una forza orizzontale.

 

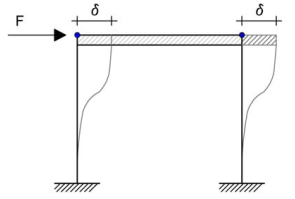
In questo tipo di telaio la rigidezza totale non è altro che la somma delle rigidezze di ogni elemento:

Rigidezza di ogni telaio --> F = (12EI / L³) δ

Rigidezza totale --> F = (12EI / L³) δ+ (12EI / L³) δ= (24EI / L³) δ

Anche per un telaio multipiano il procedimento è il medesimo. F= K_T δ

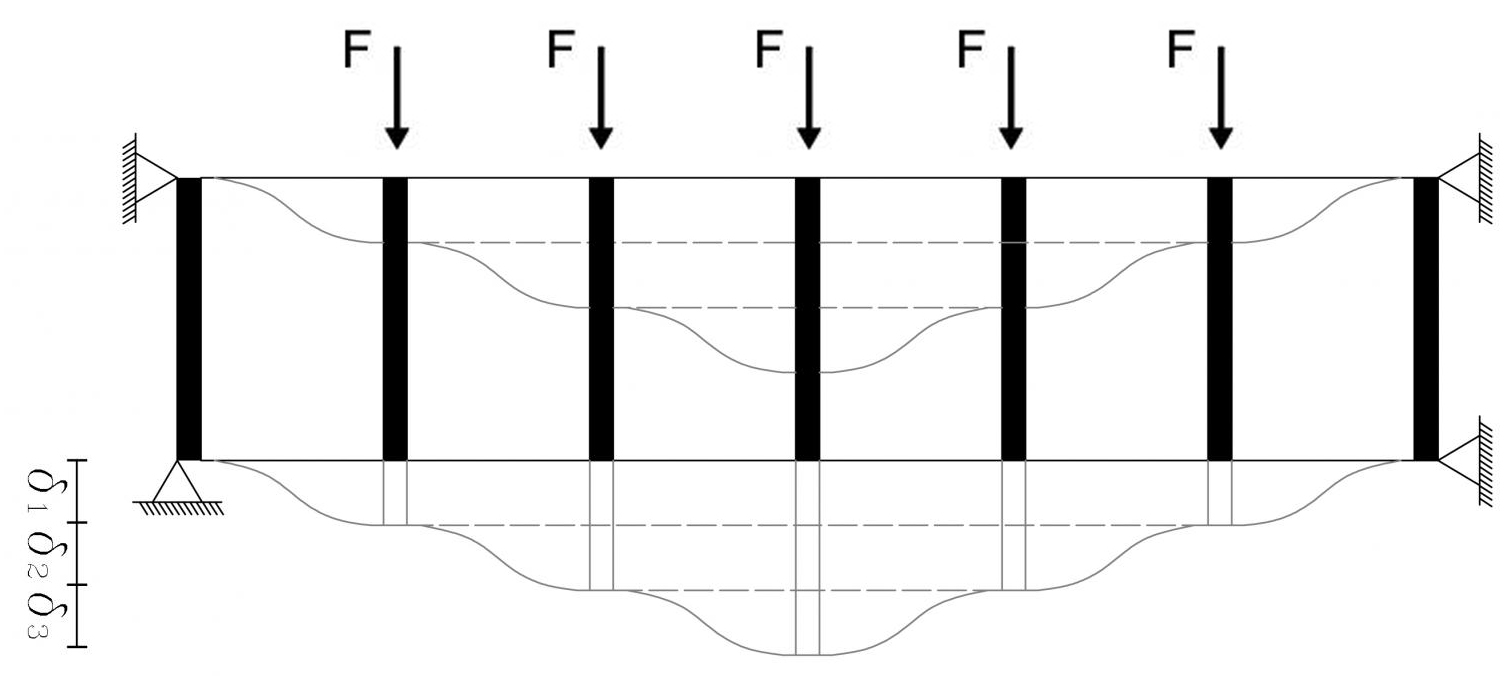
TRAVI VIERENDEEL

La trave Vierendeel è una tipologia di trave inflessa piana risolta senza diagonali. Fu denominata in questo modo dall'ingegnere belga Arthur Vierendeel che la brevettò. Questa trave è prevalentemente utilizzata in strutture miste nelle quali c'è interazione tra costruzioni in acciaio e in cemento armato.

A causa delle diagonali mancanti, nelle travi Vierendeel i nodi si devono progettare in modo da trasmettere momenti flettenti mentre negli altri tipi di capriata i nodi sono considerati delle cerniere. Infatti la maglia triangolare è nel suo insieme indeformabile anche se sono ammesse rotazioni nei nodi mentre quella rettangolare non lo è e quindi l'indeformabilità viene garantita con giunzioni in grado di impedire la rotazione reciproca tra le aste. I momenti flettenti presenti nei montanti e nei correnti, oltre che nei nodi, sono localmente molto elevati e determinano in modo essenziale le dimensioni delle sezioni.

Un'altra caratteristica della trave Vierendeel è che, grazie alla forma regolare delle maglie, può essere tamponata con finestre nel caso sia utilizzata come trave-parete.

 

Esercitazione 3: Ripartizione Forze Sismiche (Svolto con Marco Trimaldi)

Una struttura, soprattutto nel nostro paese che è considerato quasi del tutto zona sismica, necessita di una progettazione che tiene conto non solo delle forze e dei carichi verticali, ma anche di sollecitazioni orizzontali. Per contrastare questo tipo di spinte si devono opportunamente disporre all’interno della struttura dei particolari vincoli detti controventi.

In questa esercitazione vedremo come si ripartiscono le forze sismiche all’interno di una struttura ad un piano. La prima ipotesi da fare è che questa struttura abbia dei telai shear-type, ovvero un telaio con tutti nodi ad incastro e con la trave considerata infinitamente rigida flessionalmente rispetto ai pilastri. La seconda ipotesi è che i pilastri non si deformano né a compressione né a trazione, o comunque si deformano in maniera trascurabile.

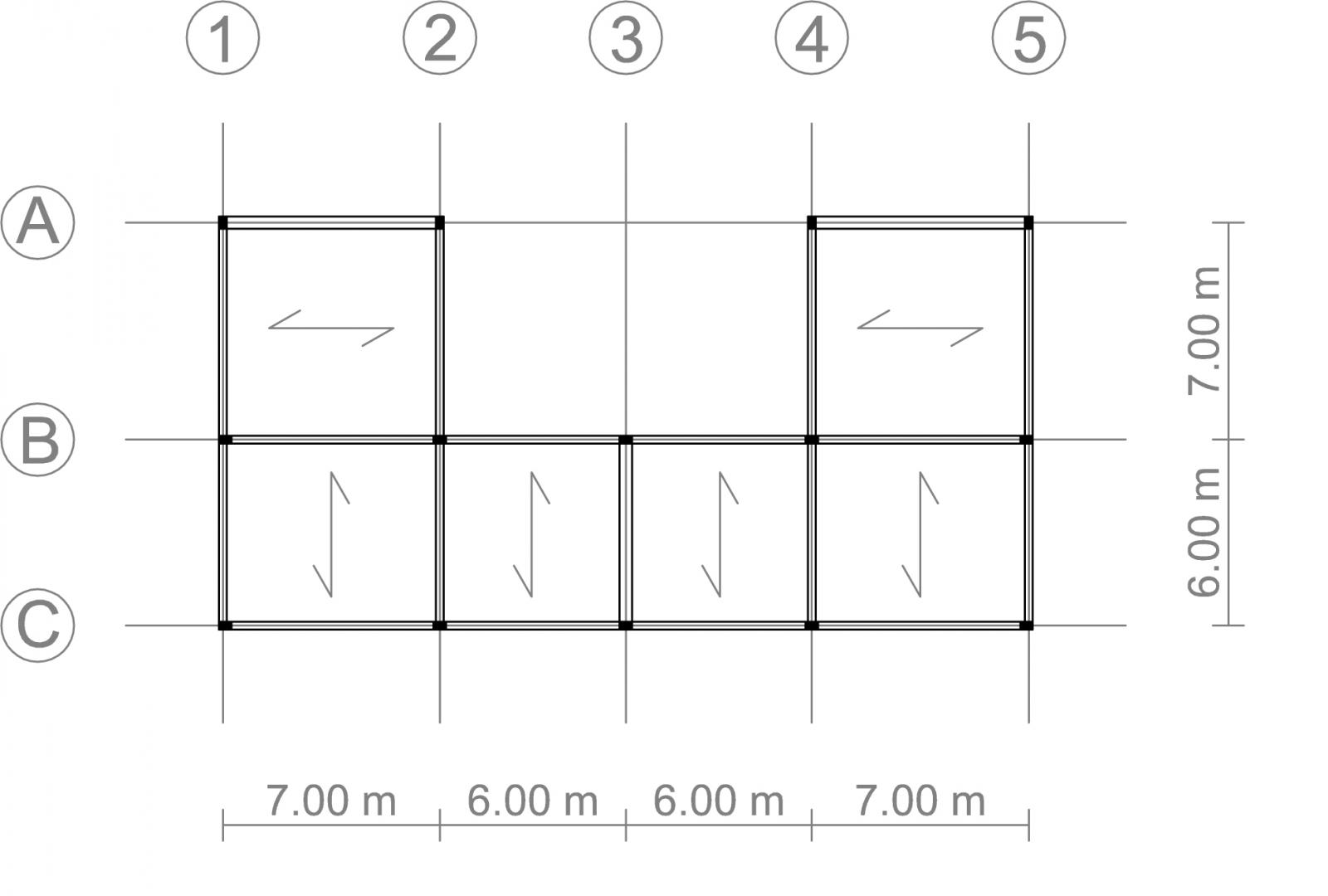
L’impalcato preso in esame è in calcestruzzo armato (quindi con modulo elastico E=21000 N/mm²) ed è composto da 14 pilastri aventi sezione rettangolare e dimensioni 25x40 cm. Dato che una sezione rettangolare ha due momenti d’inerzia, uno lungo l’asse x e l’altro lungo l’asse y, i pilastri sono stati disposti in base alla tessitura del solaio.

Infatti    Ix= bh³/12 --> 133333,33 cm⁴

            Iy= hb³/12 --> 52083,33 cm⁴

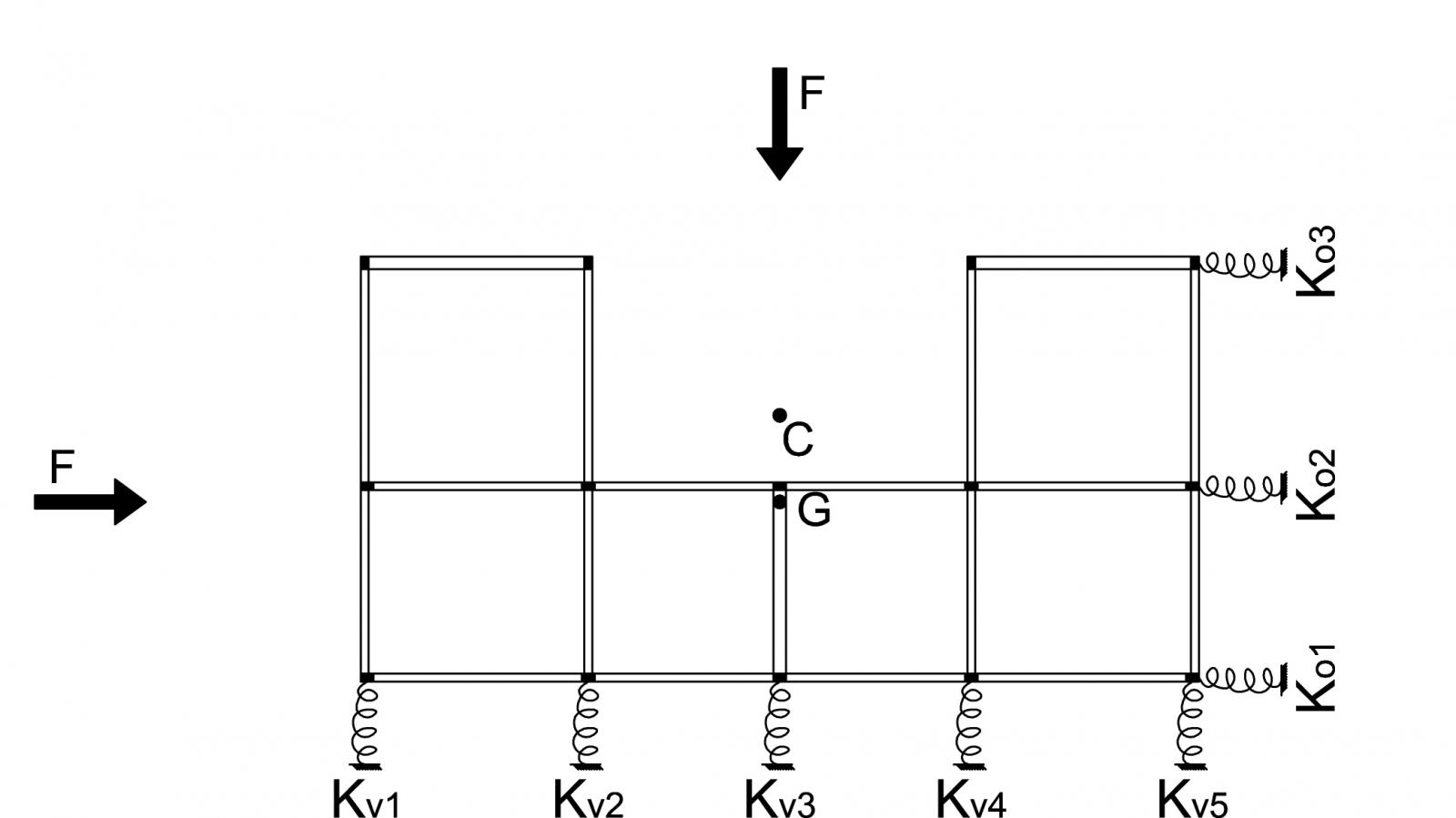
I nostri controventi sono costituiti da pilastri disposti su uno stesso asse e sono collegati rigidamente in sommità dal solaio shear-type. Essendo i controventi degli elementi con comportamento elastico, essi possono essere semplificati come delle vere e proprie molle, seguendo quindi la legge di Hooke: F=K x s (costante elastica per lo spostamento). Applicata al nostro caso: F=Kt x δ , dove Kt è la rigidezza del controvento e δ è la traslazione del telaio. Ogni pilastro contribuisce sul proprio controvento con una rigidezza Kt = 12EI/h³ .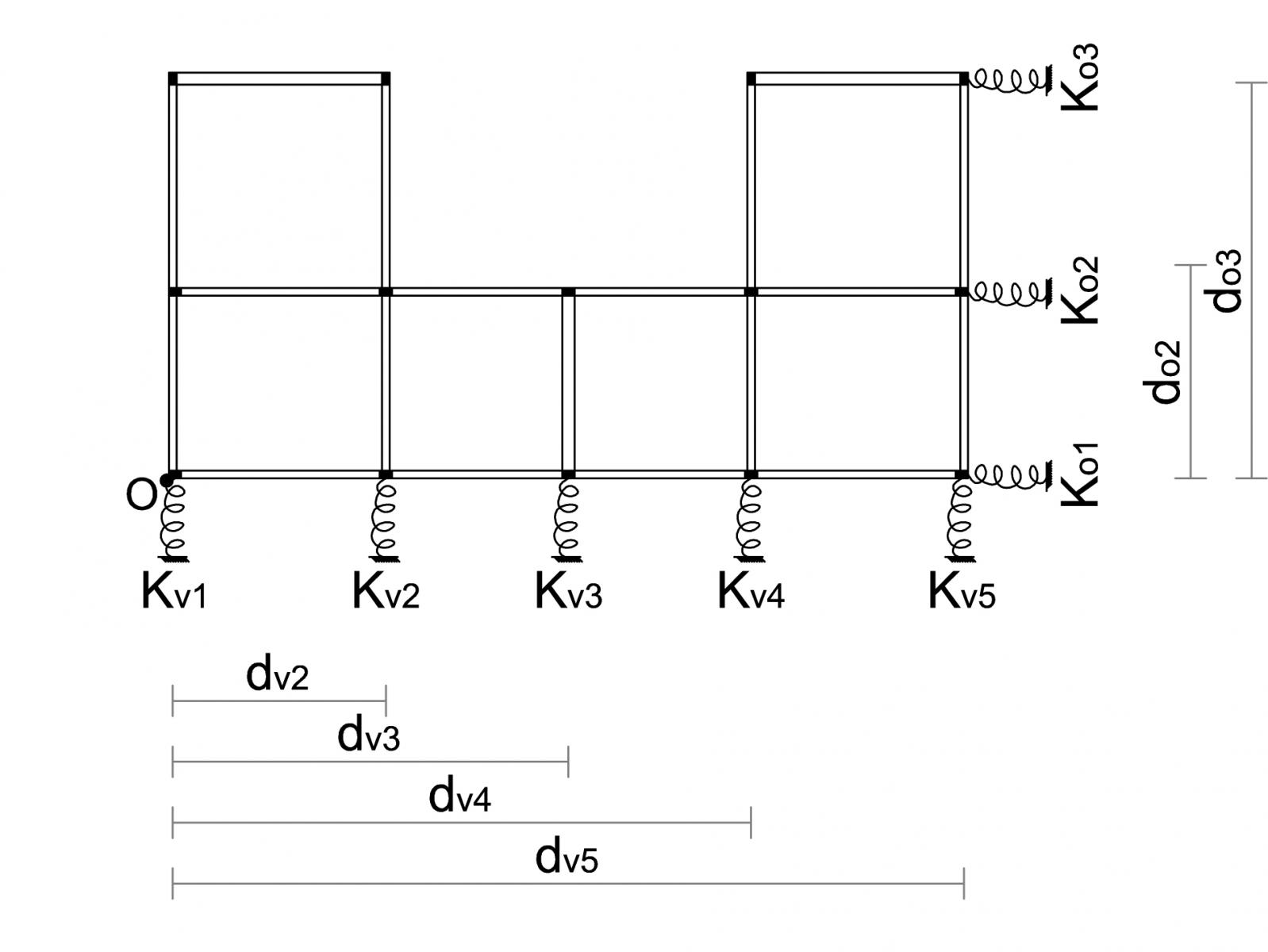

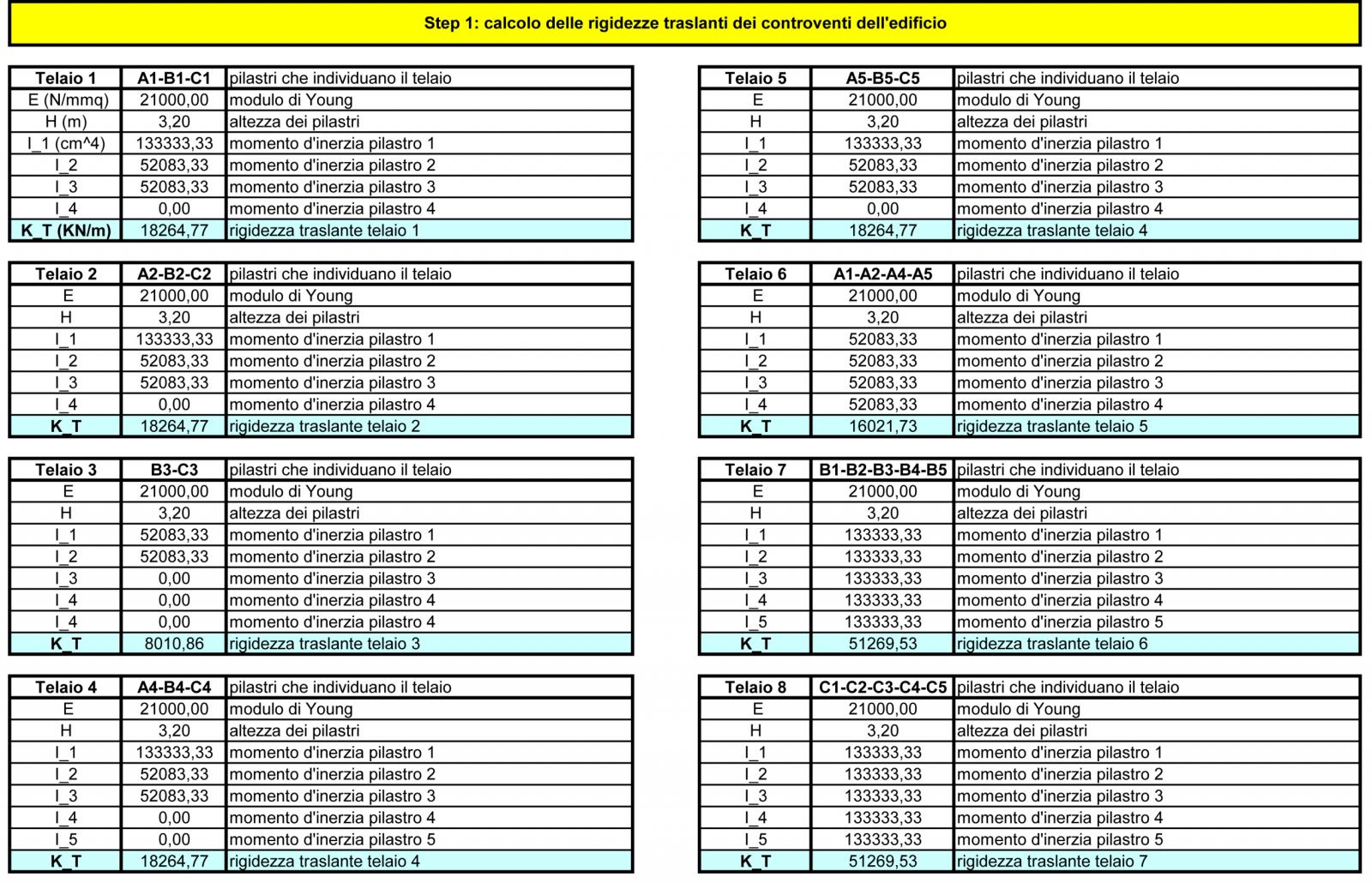
STEP 1: Calcolo delle rigidezze traslanti dei controventi dell'edificio

Si procede ora al calcolo della rigidezza traslante di ogni controvento, quindi tenendo conto del Modulo di Young (E), dell’altezza dei pilastri (h) e del momento d’inerzia di ogni pilastro (I). Seguono le tabelle:

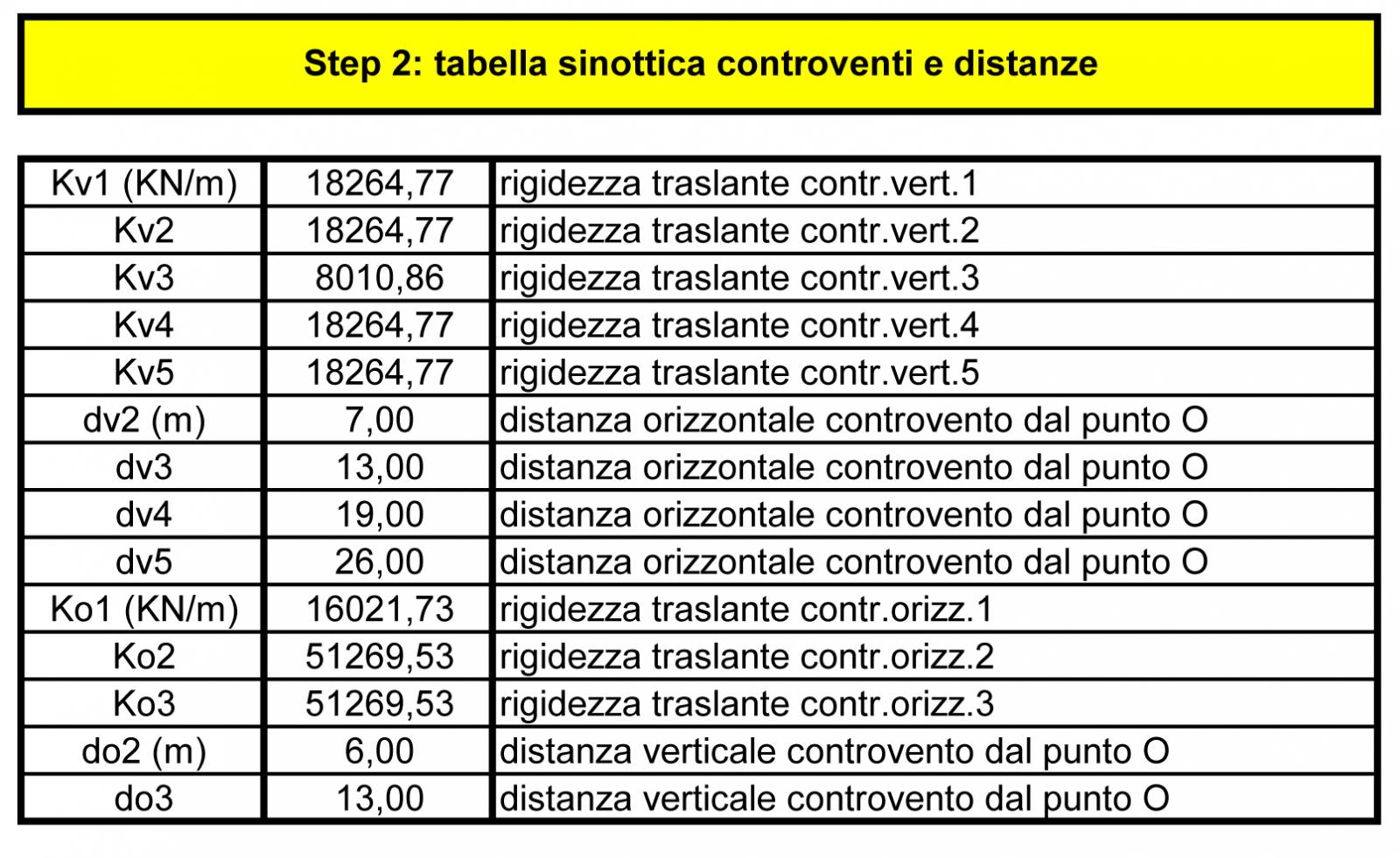
STEP 2: Tabella sinottica controventi e distanze

Ora si calcolano le distanze verticali (dv) e orizzontali (do) del controvento dal punto O, che è l’origine del nostro sistema di riferimento.

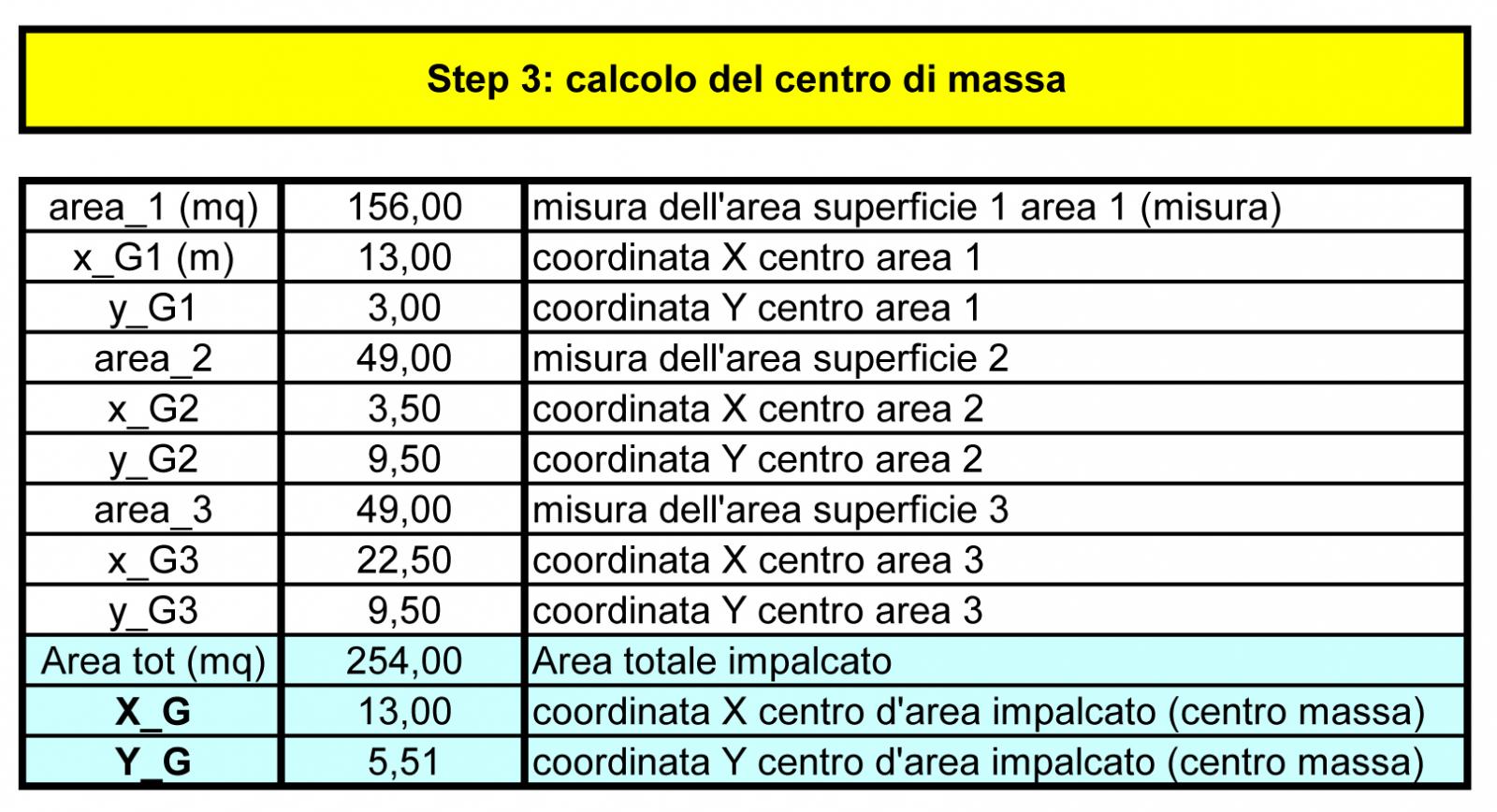
STEP 3: Calcolo del centro di massa

 

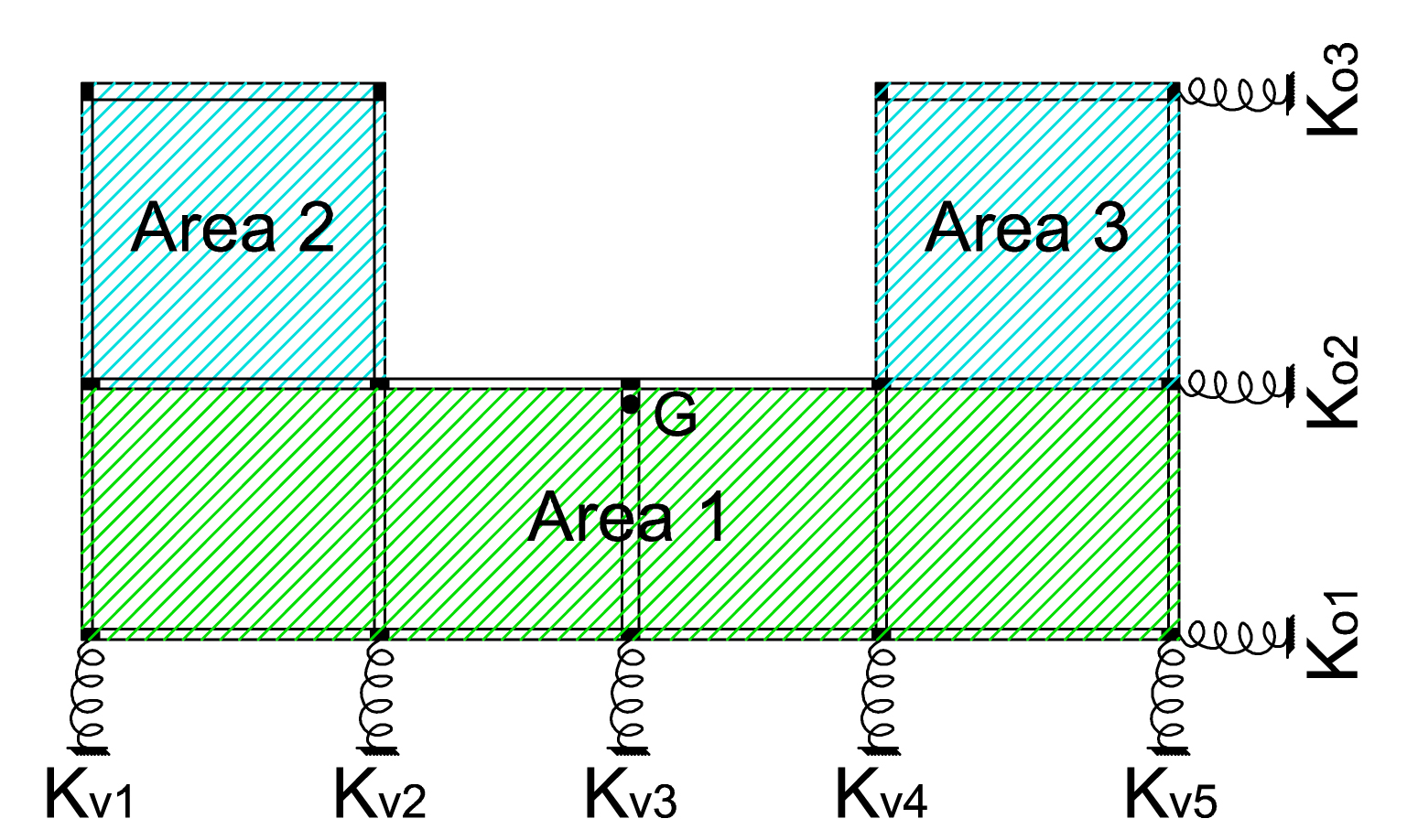
Per calcolare il centro di massa G, abbiamo diviso la struttura in tre aree, la più grande di 156 m² e le due più piccole ed uguali di 49 m². Successivamente abbiamo inserito nella tabella la misura di ogni superficie e le coordinate dei relativi baricentri, tenendo sempre contro dell’origine O come riferimento.

Le coordinate del centro di massa G (Xg, Yg) vengono calcolate in questo modo:
Xg =( A1 x Xg1+ A2 x Xg2 + A3 x Xg3) / (A1+ A2 + A3) --> 13 m
Yg  =( A1 x Yg1+ A2 x Yg2 + A3 x Yg3) / (A1+ A2 + A3) --> 5,51 m

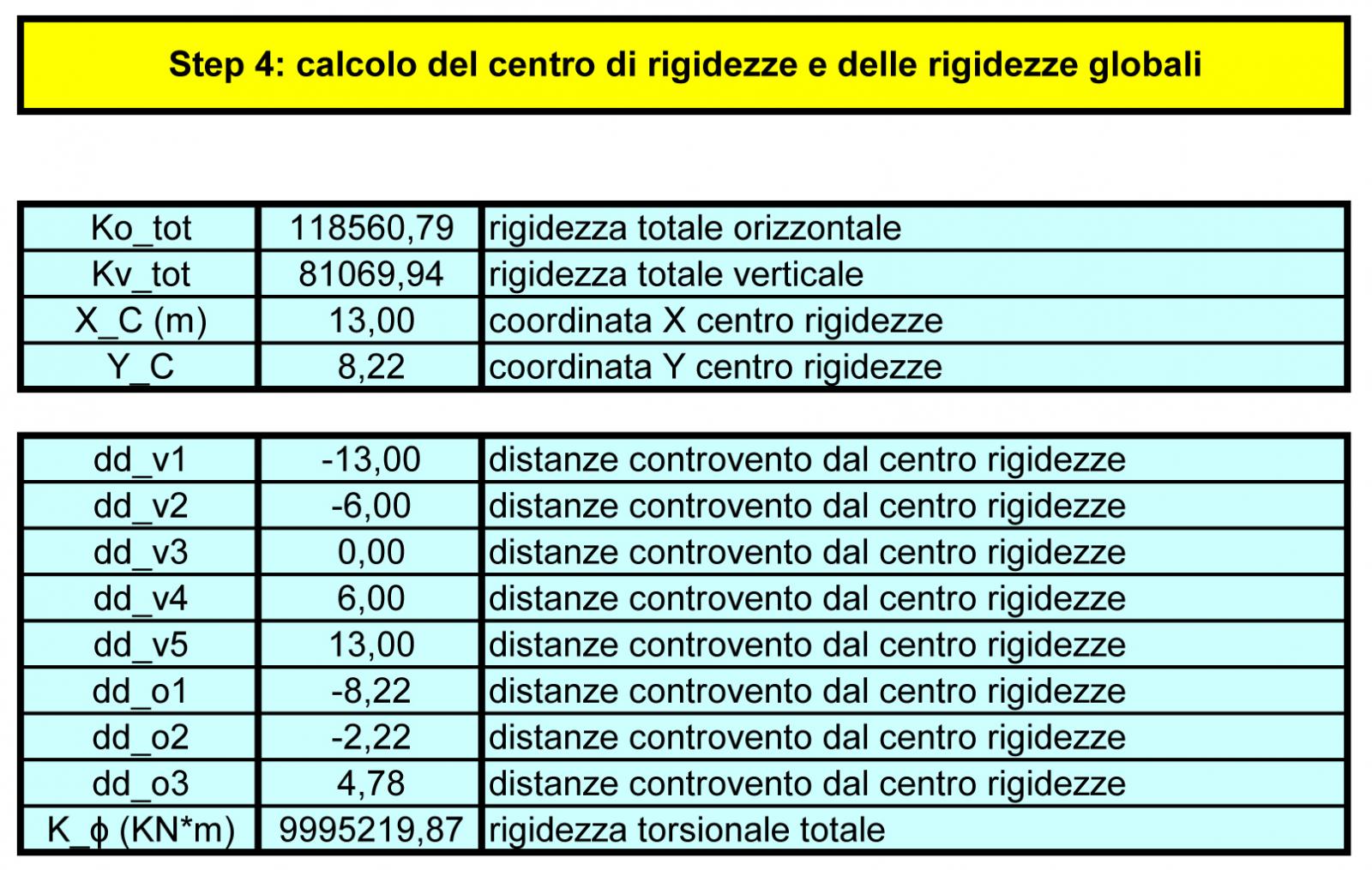
STEP 4: Calcolo del centro di rigidezze e delle rigidezze globali

A questo punto la tabella trova il centro delle rigidezze C, ovvero il punto in cui ruota la struttura se nasce un momento, grazie a queste equazioni:
Xc = Σi Kv x dv / Kv tot.
Yc =  Σi Ko x do / Ko tot.
Bisogna calcolare il centro di massa perché la forza sismica è proprio applicata in questo punto!
In seguito vengono calcolate le distanze di ogni controvento dal centro delle rigidezze e infine la rigidezza torsionale totale eseguendo la sommatoria di ogni rigidezza moltiplicata per la distanza al quadrato dal centro delle rigidezze: kΦ = Σi Ki x ddi² .

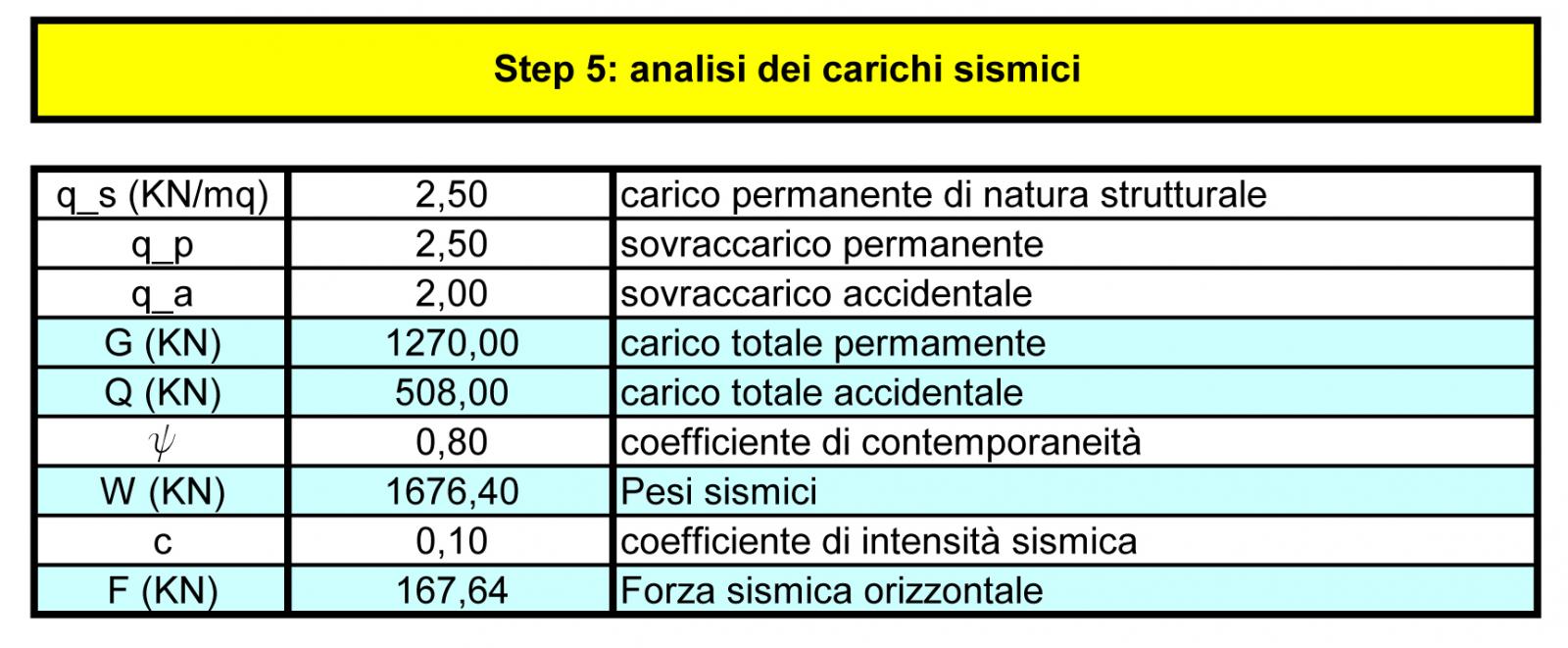
STEP 5: Analisi dei carichi sismici

 

 

Per calcolare la forza sismica bisogna fare il prodotto della massa dell’edificio per l’accelerazione di trascinamento del suolo:

F=m x a.
a= c x g (dove "c" è il coefficiente di intensità sismica (minore di 1, da normativa) e "g" è l’accelerazione gravitazionale pari a 9,81 m/sec² ).
Quindi F=m x c x g = c x (mg) = c x P   (dove P è il peso della struttura).

P ( o W) si trova sommando il peso proprio della struttura più il sovraccarico permanente più il sovraccarico accidentale (legato alla funzione) moltiplicato per un coefficiente di contemporaneità ψ (generalmente pari a 0,80).
Ora, attraverso l’individuazione di questi valori che sono obbligatori da normativa, si procede con il calcolo della Forza Sismica Orizzontale, che nella nostra struttura è pari a 167, 64 KN.

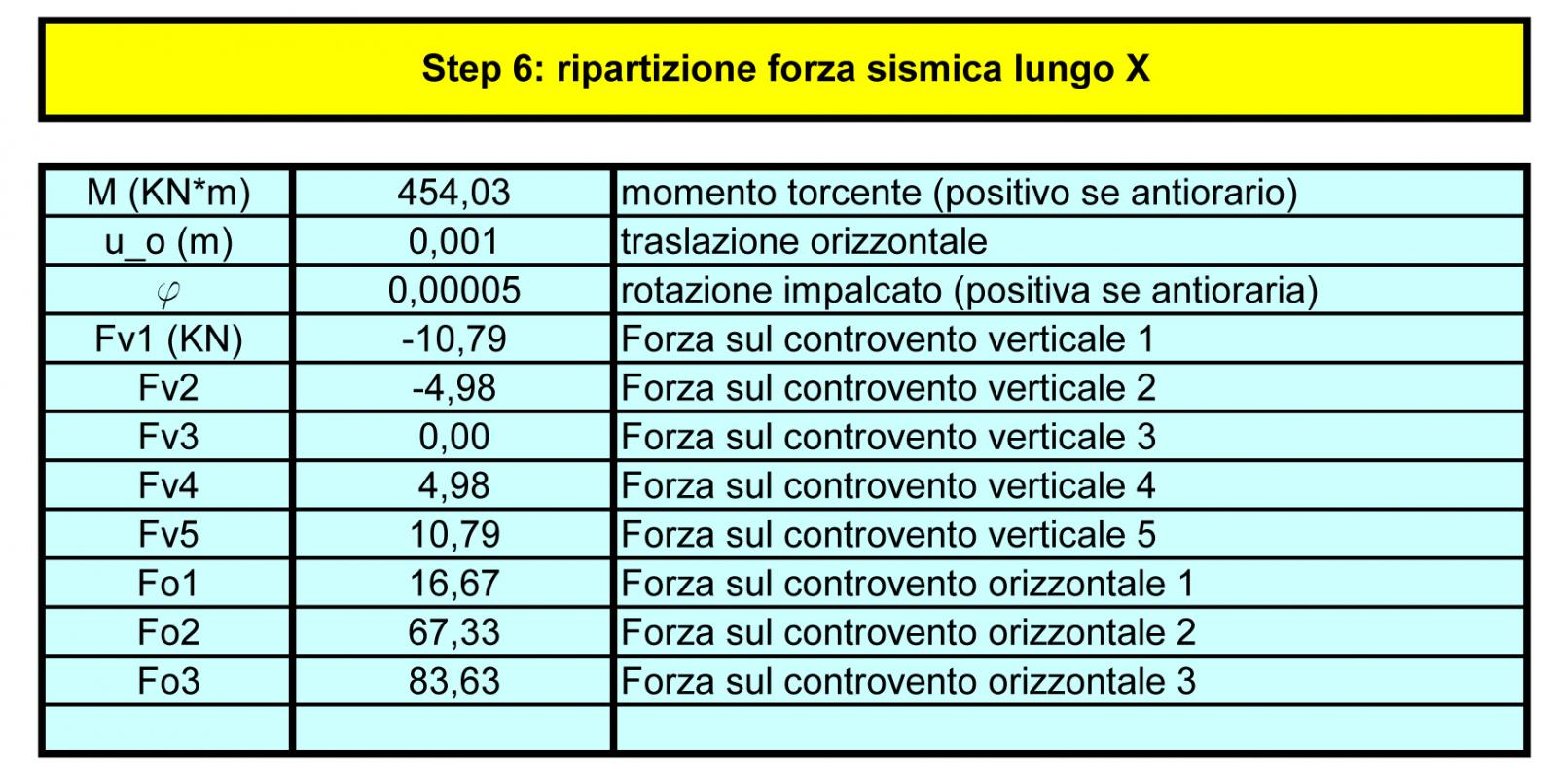
STEP6 – STEP7: Ripartizione della forza sismica lungo x e lungo y
Essendo il sisma un evento aleatorio, bisogna verificare la struttura almeno su due direzioni verticale e orizzontale che sono perpendicolari tra loro. La forza sismica inoltre è applicata nel centro di massa G, che molto spesso non coincide con il centro delle rigidezze C. Questo provoca una torsione della struttura in quanto si genera un braccio tra i punti G e C. Maggiore sarà il braccio e maggiore sarà la rotazione dell’impalcato.
Per quanto riguarda il nostro impalcato i punti C e G si trovano lungo lo stesso asse verticale: quindi per l’azione di una forza verticale non si genera alcuna rotazione ma solo una traslazione. Invece per l’azione di una forza orizzontale, dato che i punti C e G non coincidono ma hanno una distanza di 2,71 m, provocheranno una rotazione antioraria della struttura.
La tabelle 6 e 7 calcolano il momento torcente della struttura, le traslazioni e le rotazioni secondo le due direzioni perpendicolari.
La traslazione (sia verticale che orizzontale) si calcola così:  F/ K tot
La rotazione ϕ sarà uguale a  Fb / Kϕ tot
Dopo aver verificato i precedenti valori, è possibile calcolare come la forza sismica si ripartisce su ogni controvento in entrambe le direzioni.
Controventi orizzontali:  Ri^o= Ki^o x (uo+ϕdi^o)
Controventi verticali:  Ri^v= Ki^v x (ϕdi^v)

Se volessimo progettare la stessa struttura in acciaio dovremmo sostituire il modulo di elasticità E= 210000 N/mm²  e modificare i momenti d’inerzia in base ai profili scelti.

IL COMPORTAMENTO AD ARCO

L’arco è un’invenzione molto antica risalente già dagli Etruschi e messa a punto successivamente dagli antichi Romani. L’arco è una struttura che trasforma i carichi prevalentemente in sforzo normale, le sollecitazioni dovute allo sforzo di taglio e al momento sono minime. Gli archi sopportano i carichi esterni per opera della loro forma geometrica (lo stesso vale per la struttura reticolare).

Come disse Leonardo da Vinci : “l’arco è la somma di due debolezze”.

Mettendolo a confronto con un trave, essa è prevalentemente inflessa, mentre l’arco è prevalentemente compresso.

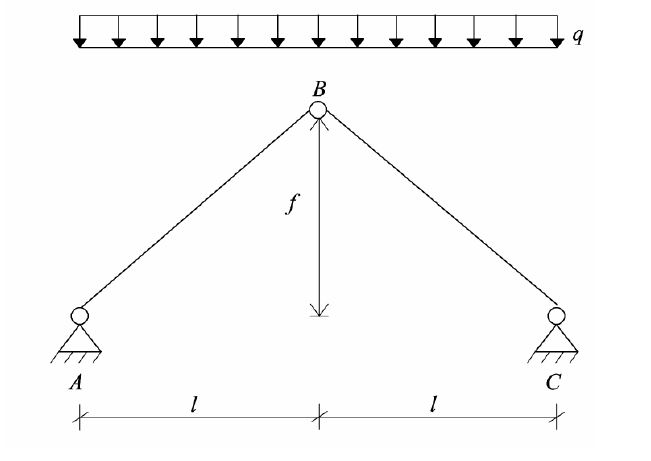
L’arco è una struttura isostatica, quindi siamo in grado di determinare le reazioni vincolari. L’arco è caratterizzato principalmente da due parametri:

• la freccia, cioè la distanza tra la chiave di volta e l’imposta dell’arco stesso
• la spinta, cioè la forza uguale e contraria alla reazione del vincolo che si trova all’imposta dell’arco

   

La spinta è inversamente proporzionale alla freccia, quindi se una diminuisce l’altra aumenta.

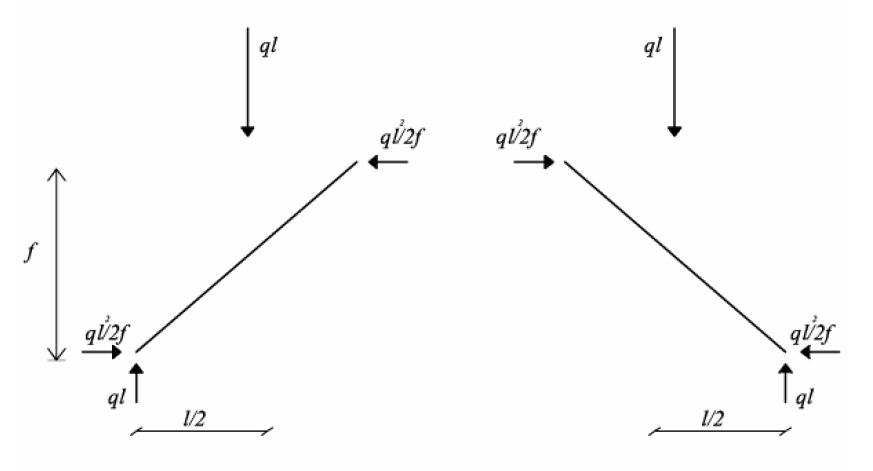
H = qL² / 2f

Esistono diversi tipi di archi che hanno comportamenti differenti: a parità di carico, è possibile notare come l’arco a tutto sesto (esattamente metà circonferenza) abbia una spinta che è la metà di quella di un arco ribassato. La forma dell’arco influenza il suo comportamento, quindi più un arco è ribassato e maggiore è la spinta che genera.

  

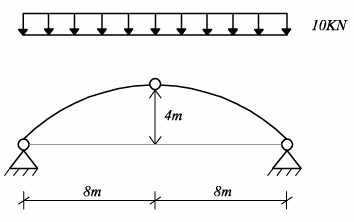
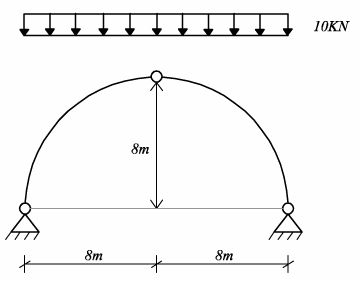
Un arco puro è quello in cui lo sforzo di taglio e il momento flettente sono pari a zero ed è presente solo sforzo normale: parliamo dell’arco parabolico.

   

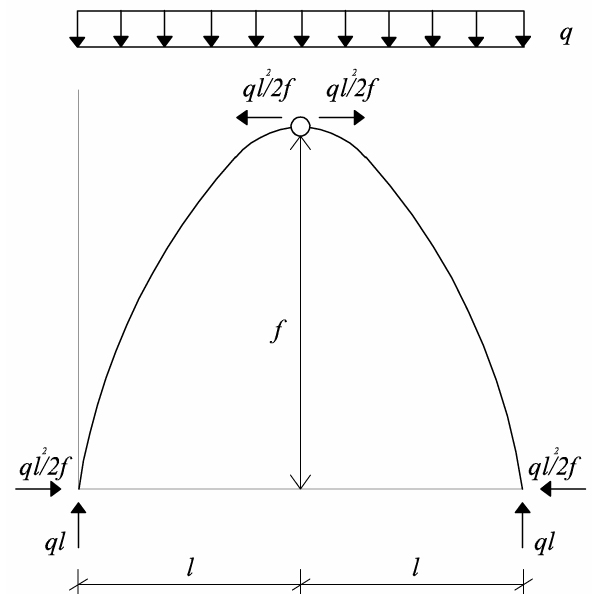
Per la progettazione di un arco un problema che bisogna tener conto è proprio la spinta, quindi bisogna saper affrontare il metodo di eliminazione della spinta.

L’arco trasmette ai supporti (i piedritti) una forza verticale diretta verso il basso ed una spinta orizzontale rivolta verso l’esterno. Quest’ultima tende a ribaltare i supporti che sorreggono l’arco.

Determinando l’equilibrio a rotazione nel punto A, otteniamo due momenti: il momento ribaltante e il momento stabilizzante.

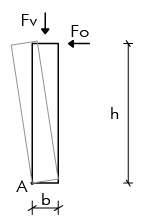           M_R = Fo h        M_S = Fv b/2

 

 

Il supporto si ribalta se M_R > M_S  -->  Fo h > Fv b/2

Per far si che non si ribalti bisognerebbe aumentare il valore del momento stabilizzante, quindi amplificare la forza Fv o aumentare la base del supporto, oppure effettuare entrambe le cose.

Si è cercato di eliminare la spinta attraverso una sequenza di archi, come gli acquedotti romani, facendo rimanere il problema solo agli archi posti alle estremità.

Un altro modo per risolvere il problema è l’utilizzo del tirante posto tra le due sezioni dell’imposta, si crea una situazione simile alla travatura reticolare. In questo modo la spinta viene assorbita proprio dalla catena, che diventa una reazione vincolare interna.

Un ulteriore risoluzione è quella di prevedere delle mensole disposte alle estremità dell’arco, che fanno si che le reazioni verticali nel colmo e nell’imposta siano pari a zero, quindi la spinta dell’arco diminuisce.