Blog di Marco Trimaldi
Progettare significa scegliere una forma, un materiale e delle dimensioni
È nella concezione generale che l’architetto debba pensare solo alla composizione di una magnifica opera e che l’ingegnere debba risolvere i calcoli per farla reggere. In alcuni casi questo può anche essere vero, ma a mio parere un bravo architetto è uno che, grazie alle sue conoscenze, riesca a prevedere già in fase di progettazione alcune accortezze di carattere strutturale. Molto spesso capita che, data l’assurdità del concept iniziale, si arrivi a costruire un’opera del tutto diversa da come era stata pensata dall’architetto. Questo perché, subentrati gli ingegneri, sono stati inseriti nel progetto dei vincoli.
A questo punto mi chiedo, non sarebbe stato meglio iniziare la progettazione tenendo già conto di questi vincoli anziché affrontarli a progetto iniziato?
Strutture Isostatiche
Esercizio 1. Calcolare le reazioni vincolari della struttura reticolare e trovare i valori della normale in ogni asta.
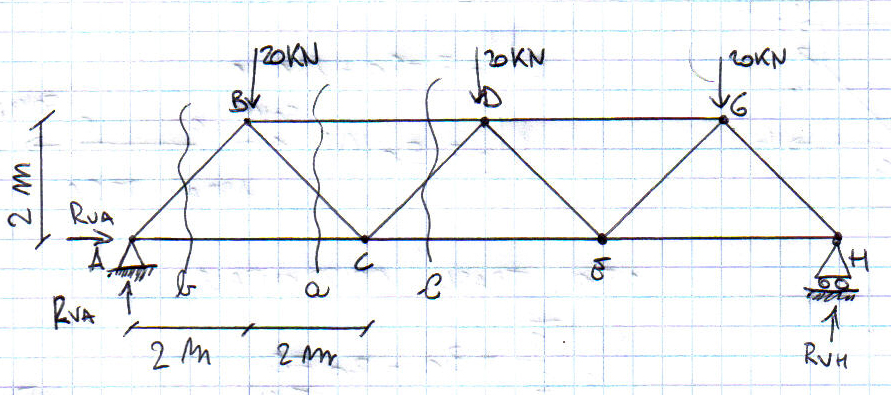
La struttura, essendo simmetrica sia nella sua forma che nella disposizione dei carichi, ha il valore delle due reazioni vincolari verticali (RVA e RVH) pari ognuna alla metà della somma delle 3 forze.
RVA=RVH=30 KN
RUA è nulla a causa dell'inesistenza di forze orizzontali.
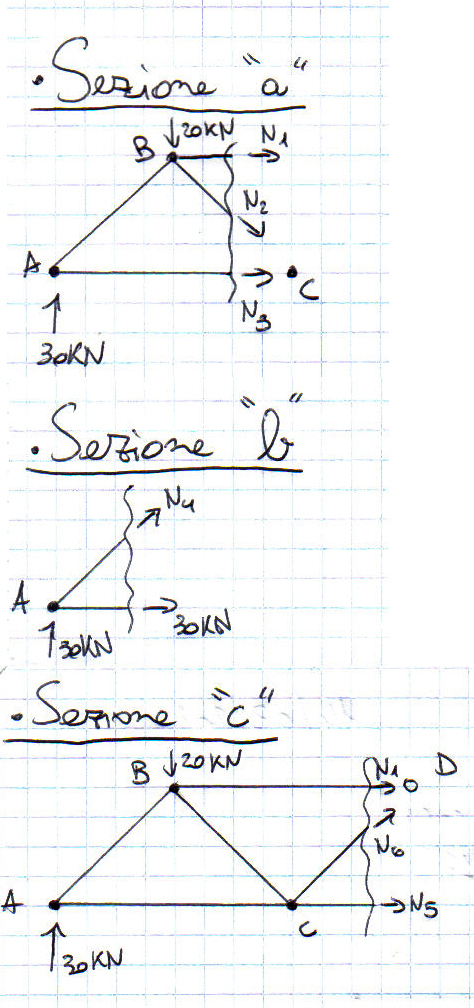
Dopo aver trovato le reazioni vincolari si procede con il metodo delle sezioni. Si effettua un taglio su 3 aste ipotizzando un verso qualsiasi per lo sforzo normale di ogni asta.
La sezione "a" passa per le aste 1, 2 e 3. Tutte le aste sono state ipotizzate tese.
- N1 si trova facendo l'equilibrio dei momenti nel nodo C. Il valore è di 40 KN di compressione.
- N3 si trova facendo l'equilibrio dei momenti nel nodo B. Il valore è di 30 KN di trazione.
- N2 si trova scomponendo lo sforzo normale ed effettuando l'equilibrio alla traslazione verticale dell'intera sezione "a" con la componente verticale di N2. Il valore è di 10√2 kN di trazione.
La sezione "b" passa per le aste 4 e 3 (di cui già sappiamo il valore pari a 30 KN di tensione). L'aste è stata ipotizzata tesa.
- N4 si trova scomponendo lo sforzo normale ed effettuando l'equilibrio alla traslazione orizzontale dell'intera sezione "b" con la componente orizzontale di N4. Il valore è di 30√2 kN di compressione.
La sezione "c" passa per le aste 5, 6 e 1 (di cui già sappiamo il valore pari a 40 KN di compressione). Le altre aste sono state ipotizzate tese.
- N5 si trova facendo l'equilibrio dei momenti nel nodo D. Il valore è di 50 KN di trazione.
- N6 si trova scomponendo lo sforzo normale ed effettuando l'equilibrio alla traslazione orizzontale dell'intera sezione "c" con la componente orizzontale di N6. Il valore è di 10√2 kN di compressione.
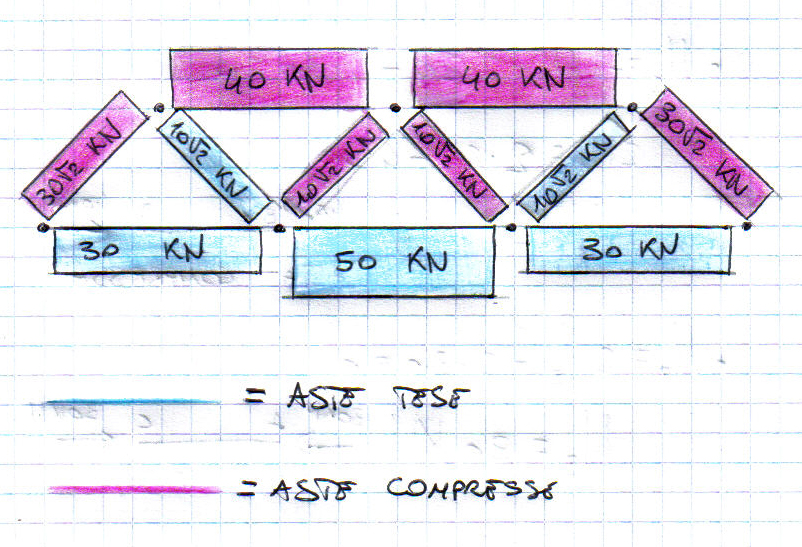
In seguito è riportato il diagramma degli sforzi normali (di compressione e di trazione) e i relativi valori per ogni asta.
Esercizio 2. Verificare che la struttura reticolare sia isostatica, calcolare le reazioni vincolari e trovare i valori della normale in ogni asta.
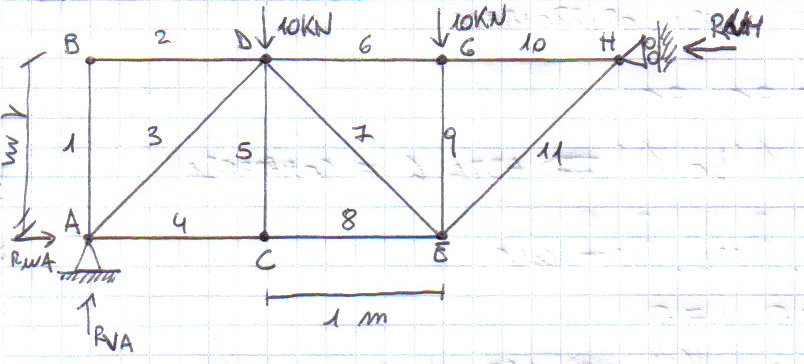
Per verificare che la struttura sia isostatica bisogna eguagliare "l" (numero di aste * grado di vincoli esterni) con "V" (grado di vincoli esterni + grado di vincoli interni):
l = 11 x 3 = 33
Vi = 2 (numero di aste che arrivano in ogni cerniera - 1) ===> [A=4 + B=2 + C=4 + D=8 + E=6 + G=4 + H=2]= 30
V = 3 + 30 = 33
l = V ===> la struttura è isostatica (verificato)
La reazione vincolare RVA essendo l'unica a contrastare le due forze applicate sui nodi D e G avrà un valore pari a 20 KN.
Di RUA ed RUH sappiamo che, essendo le uniche forze orizzontali, dovranno essere uguali, ma per trovare il valore si deve fare l'equilibrio dei momenti in un punto dove una delle due abbia braccio uguale a zero, come ad esempio nel nodo A. RUH = 30 KN = RUA.
Si procede ora con il metodo dei nodi per trovare gli sforzi assiali di ogni asta. Questo metodo si basa esculsivamente sulle equazioni di equilibrio orizzontali e verticali poichè prendendo in analisi una cerniera (considerata come un punto) tutte le forze che vi convergono hanno braccio, e quindi momento, uguale a zero.
Come nel metodo delle sezioni, anche qui si ipotizza un verso qualsiasi per gli sforzi normali, avendo l'unica accortenza nel considerare che le direzioni degli sforzi assiali (teso/compresso) hanno una convenzione opposta rispetto al metodo delle sezioni.
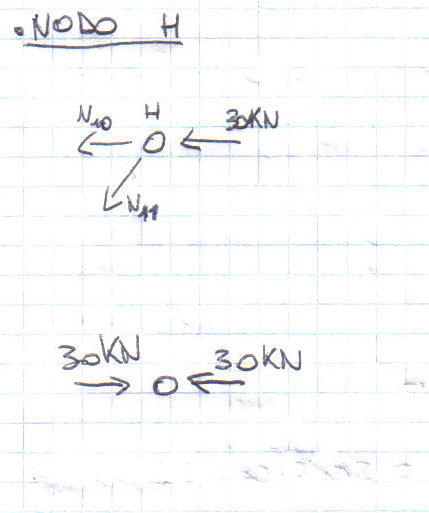
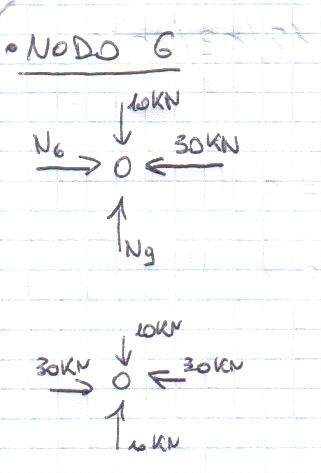
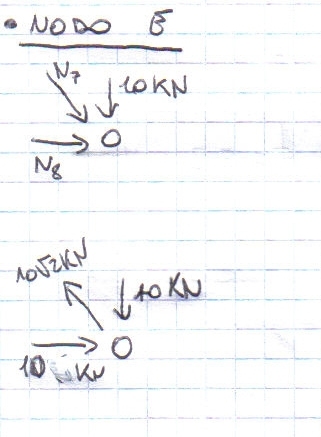
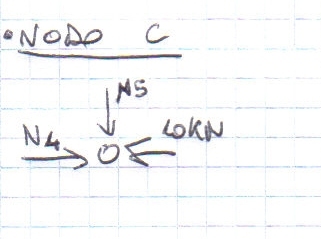
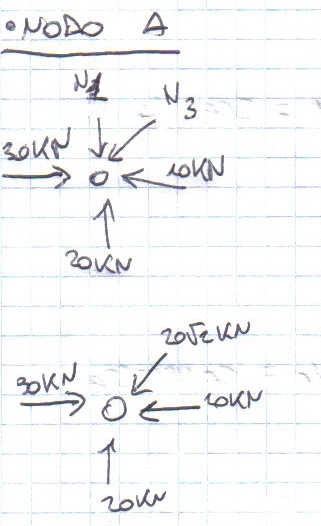
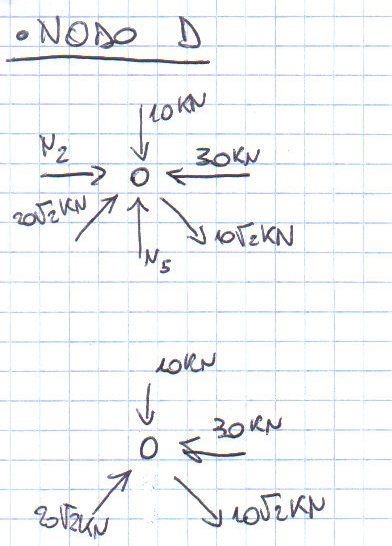
Dopo aver analizzato i nodi tramite le equalizioni di equilibrio verticali e orizzontali si sono trovati i seguenti valori:
Asta 11 = scarica;
Asta 10 = compressa (30 KN);
Asta 6 = compressa (30 KN);
Asta 9 = compressa (10 KN);
Asta 7 = tesa (10√2 KN);
Asta 8 = compressa (10 KN);
Asta 4 = compressa (10 KN);
Asta 3 = compressa (20√2 KN);
Asta 1 = scarica;
Asta 2 = scarica;
Asta 5 = scarica;
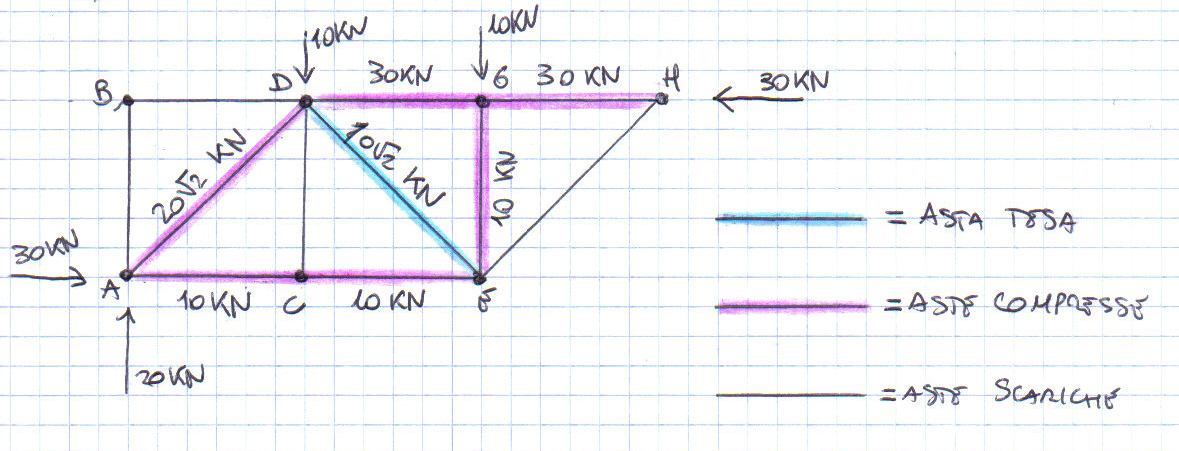
In seguito è riportato il diagramma degli sforzi normali (di compressione e di trazione) e i relativi valori per ogni asta.
Bridge Constructor
Qualche giorno fa, cercando un gioco carino sull'apple store, mi imbatto in Bridge Constructor. Incuriosito lo scarico e inizio a giocare:
"A seguito di un forte terremoto tutti i ponti del paese sono crollati, tocca a te ricostruirli..."
Incominciamo dal primo livello... come materiale ho solo il legno e ho un budget di 5000 $!
Essendo il primo ponte ho le linee guida da seguire per la costruzione. Una volta terminato lo verifico facendo passare sopra delle macchine o dei camion (quest'ultimi danno più punti).
Il secondo ponte è diverso, ha la possibiltà di poggiare su due piloni intermedi:
il materiale è sempre il legno.
Una volta costruito procedo con la solita "verifica a camion" e ora capisco perchè il ponte diventa verde: ogni elemento si colora in base al suo sforzo su una scala cromatica da verde a rosso, dove il verde sta per "poco carico" e il rosso sta per "quasi in rottura".
Terzo ponte: luce più ampia, elementi in legno.
Decido di creare un ponte reticolare ma che non intralciasse il passaggio delle vetture:
I correnti inferiori risultano essere i più sollecitati.
Quarto ponte: luce ancora più ampia, elementi in legno.
Questa volta sono costretto a creare un ponte reticolare verso l'alto a causa dell'acqua sottostante ma succede qualcosa di inaspettato:
L'elemento superiore centrale si rompe a causa di una compressione troppo elevata. Provo a cambiare forma:
Quinto ponte: luce molto grande, legno e tiranti in acciaio (quindi da inserire solo come elementi tesi).
Realizzo una travatura reticolare a maglia quadrata con tirante diagonale in acciaio.
Dopo vari tentativi il più valido risulta essere questo, nonostante questo tipo di ponte non passi la "verifica a camion" ma solo la "verifica ad automobile".
Sesto ponte: possibilità di creare un pilone in cemento armato sul quale appoggiare il ponte.
Anche questo ponto è stato verificato. Purtroppo la versione gratuita di questo gioco finisce qui, ma guardando su internet le cose che si possono creare con questa applicazione sono quasi infinite.
Esercizio 3. Calcolare le reazioni vincolari dei seguenti "portali" (archi a 3 cerniere) e trovare i valori dei diagrammi.
1)
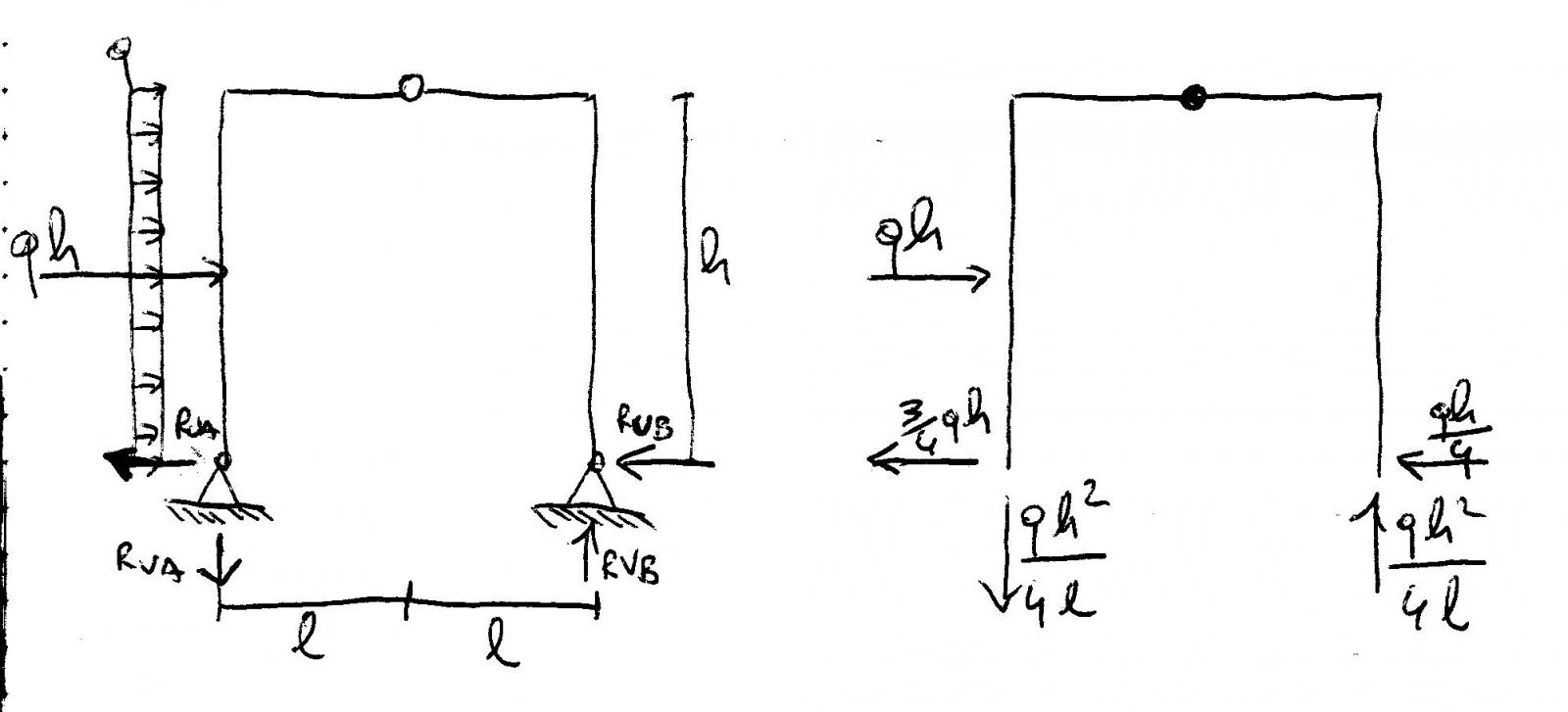
Questa struttura ha un carico distribuito "q" sull'elemento verticale sinistro. Ciò implica che le due reazioni orizzontali (RUA e RUB) vadano entrambe a contrastare la risultante del carico pari a qh, e che, mancando delle forze verticali sulla struttura, le due reazioni verticali (RVA e RVB) abbiano lo stesso valore ma verso opposto.
Svolgendo le equazioni di equilibrio alla traslazione orizzontale, alla traslazione verticale e dei momenti, si trovano i valori e i versi delle reazioni vincolari come disegnato in figura.
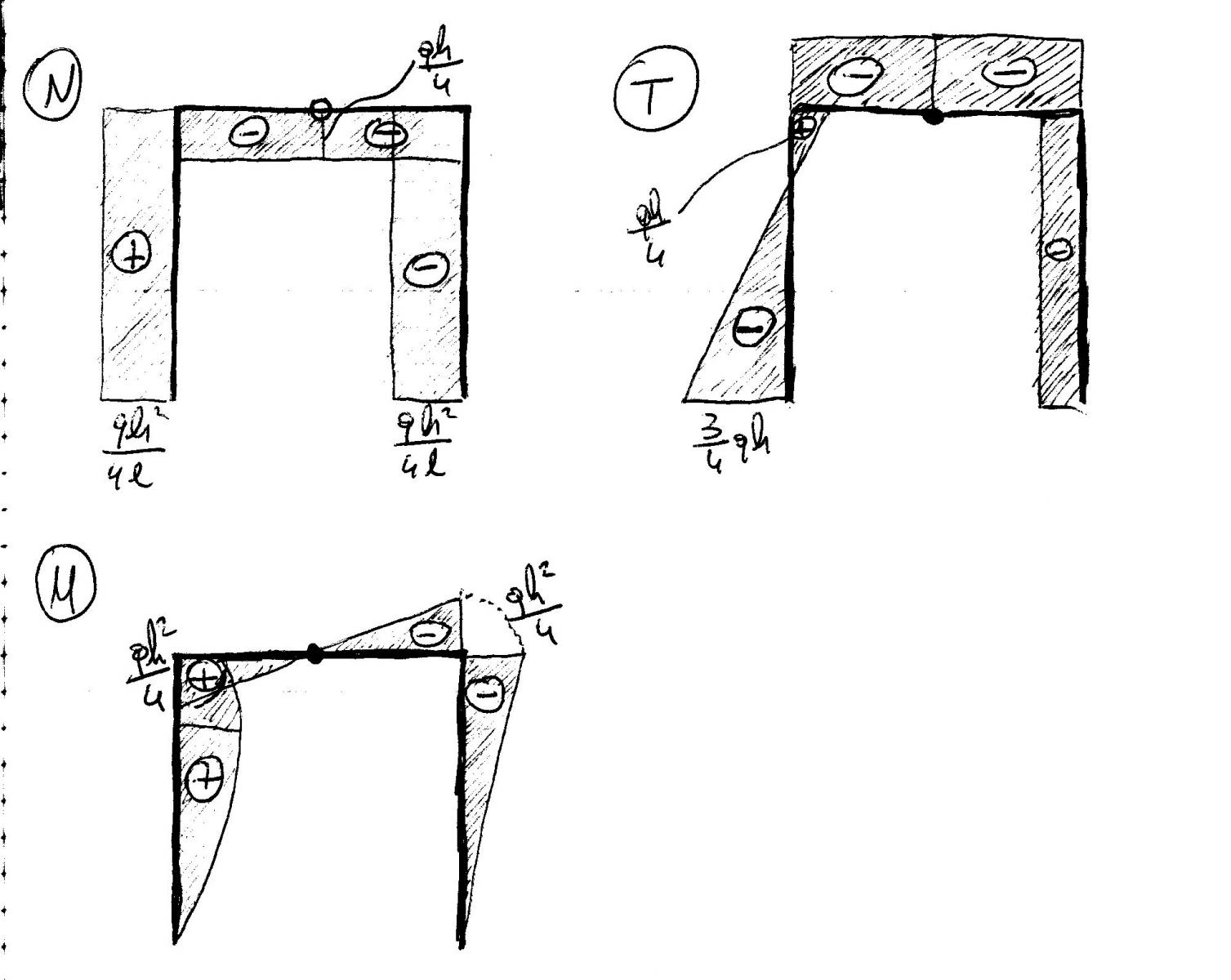
Il diagramma dello sforzo normale ha un andamento costante in ogni punto poichè è assente un carico distribuito parallelo all'asse di qualsiasi elemento.
Il diagramma dello sforzo di taglio ha nel tratto verticale sinistro un andamento lineare, visto la presenza del carico q, e un andamento costante in ogni altro punto poichè nel resto della struttura sono assenti carichi distribuiti perpendicolari all'asse degli elementi.
Il diagramma dei momenti quindi avrà un andamento parabolico nel tratto verticale sinistro, con un massimo nel punto in cui il taglio si annulla, mentre per il resto della struttura seguirà un andamento lineare visto che nei medesimi tratti il taglio è costrante.
2)
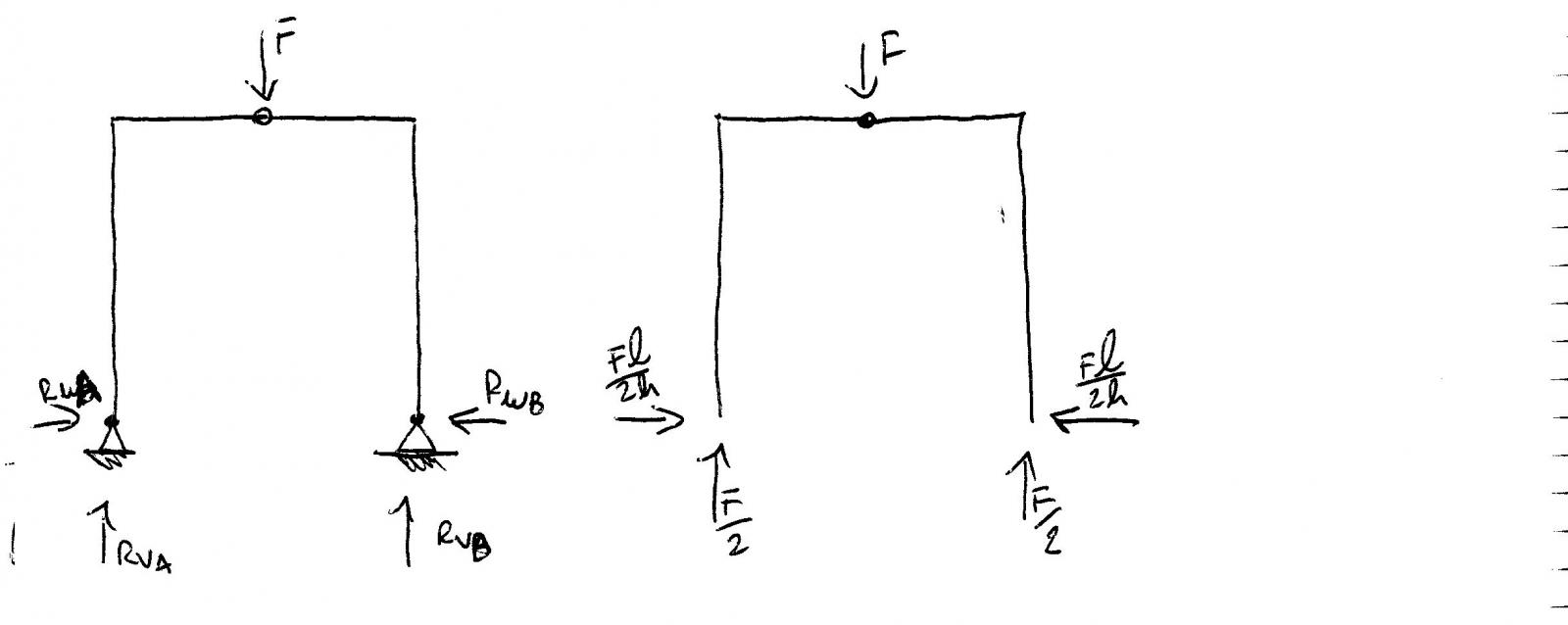
Quest'altro "portale" presenta una forza concentrata sulla cerniera interna. Data la simmetria della struttura, e la forza applicata esattamente sull'asse di simmetria, si può dedurre che le reazioni vincolari verticali siano uguali tra di loro nel verso e nel modulo (ognuna pari alla metà della forza concentrata), mentre quelle orizzontali siano uguali nel modulo e opposte nel verso.
Svolgendo le equazioni di equilibrio dei momenti, si trovano i valori e i versi delle reazioni vincolari come disegnato in figura.
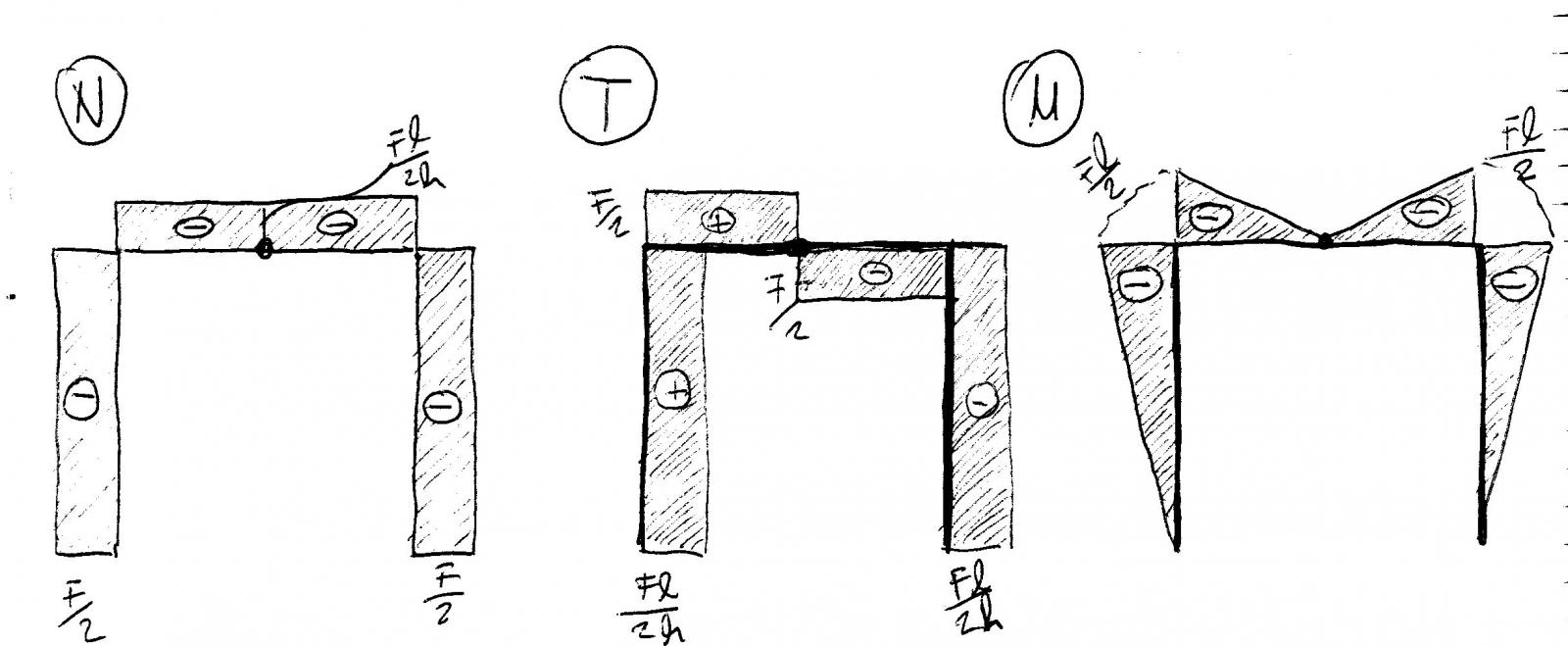
Il diagramma dello sforzo normale ha un andamento costante in ogni punto poichè è assente un carico distribuito parallelo all'asse di qualsiasi elemento.
Il diagramma dello sforzo di taglio ha un andamento costante in ogni punto poichè è assente un carico distribuito perpendicolare all'asse di qualsiasi elemento. Nella cerniera però il diagramma effettua un taglio dovuto alla presenza della forza concentrata pari proprio al valore della forza.
Il diagramma dei momenti quindi avrà un andamento lineare in ogni punto, annullandosi ovviamente nelle cerniere.
3)
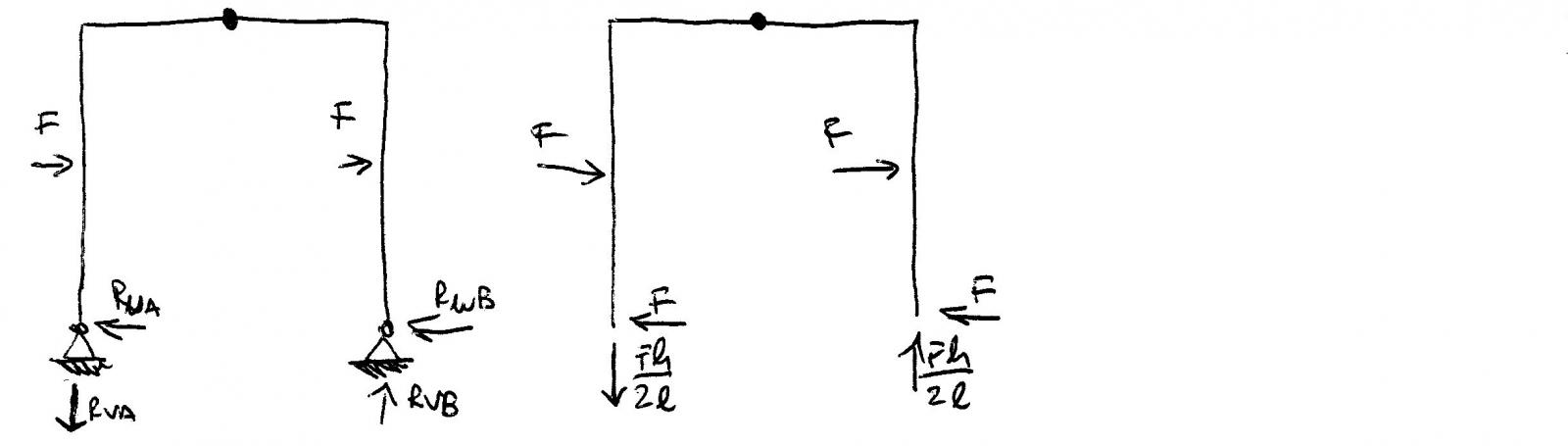
Il terzo portale ha due forze concentrate orizzontali ognuna applicata nelle mezzerie di entrambi i tratti verticali. Entrambe le forze hanno modulo e verso uguale, quindi anche le due reazioni vincolari orizzontali (RUA e RUB) hanno le stesse caratteristiche, ma ovviamente il loro verso si oppone a quello delle due forze. Vista l'assenza di forze verticali, le altre due reazioni, quelle appunto verticali (RVA e RVB), avranno verso opposto ma uguale modulo.
Svolgendo le equazioni di equilibrio dei momenti, si trovano i valori e i versi delle reazioni vincolari come disegnato in figura.
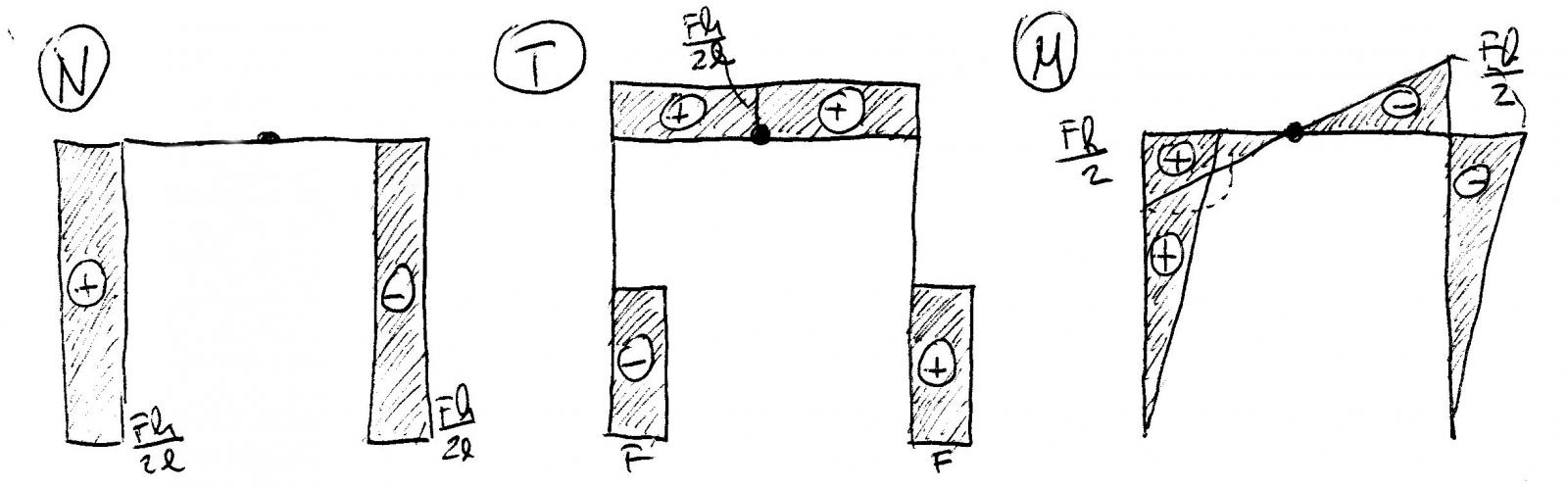
Il diagramma dello sforzo normale ha un andamento costante in ogni punto poichè è assente un carico distribuito parallelo all'asse di qualsiasi elemento.
Il diagramma dello sforzo di taglio ha un andamento costante in ogni punto poichè è assente un carico distribuito perpendicolare all'asse di qualsiasi elemento. La particolarità di questo diagramma sta nel fatto che nella parte superiore degli elementi verticali il taglio si annulla a causa delle forze concentrate. L'annullamento è dovuto proprio al medesimo valore delle reazioni orizzontali con le forze.
Il diagramma dei momenti quindi avrà un andamento lineare in ogni punto, annullandosi nelle cerniere.
Meccanica dei materiali
·Il calcestruzzo armato
Il calcestruzzo armato è un materiale composto da calcestruzzo e barre di acciaio annegate al suo interno. Questa combinazione è possibile poiché questi due materiali hanno lo stesso coefficiente di dilatazione termica.
A seconda degli utilizzi ci sono diversi tipi di calcestruzzo:
· calcestruzzo non strutturale: C8/10 - C12/15
· calcestruzzo ordinario (NSC - Normal Strength Concrete): C16/20 - C20/25 - C25/30 - C28/35 - C30/37 - C32/40 - C35/45 - C40/50 - C45/55
· calcestruzzo ad alte prestazioni (HPC - High Performance Concrete): C50/60 - C55/67- C60/75
· calcestruzzo ad alta resistenza (HSC - High Strength Concrete): C70/85 - C80/95 - C90/105- C100/120
Per ogni classe di resistenza, il primo dei valori rappresenta fck (resistenza cilindrica) ed il secondo Rck (resistenza cubica), ambedue espressi N/mm2 (o MPa).
I calcestruzzi non strutturali vengono usati per i magroni sotto le fondazioni, il calcestruzzo ordinario e quello ad alte prestazioni sono usati per la normale edilizia, mentre per i calcestruzzi ad alta resistenza (che sono resistenti quasi come l’acciaio) hanno bisogno dell’autorizzazione del ministero dei lavori pubblici.
Per quanto riguarda i tondini di acciaio, che sono filettati in modo tale da migliorare l’aderenza al calcestruzzo, sono classificati in B450A e B450C. I B450C data la loro maggiore duttilità sono da usare obbligatoriamente in zona sismica (quindi nella quasi totalità del nostro paese).
Affinché il principio della conservazione delle sezioni piane persista, il cls e l’acciaio si devono deformare ugualmente durante uno sforzo. Per rendere possibile ciò, entra in campo l’omogeneizzazione della sezione che, attraverso il coefficiente di omogeneizzazione “n”, fa si che i due materiali vicini abbiano la stessa deformazione, nonostante le loro tensioni siano completamente diverse, a seconda delle loro capacità meccaniche (il rapporto tra i loro moduli elastici è maggiore di 10, circa 15).
εc = εf
σc/Ec = σf/Ef
σf = (Ef/Ec) σc n= (Ef/Ec)
σf = n σc

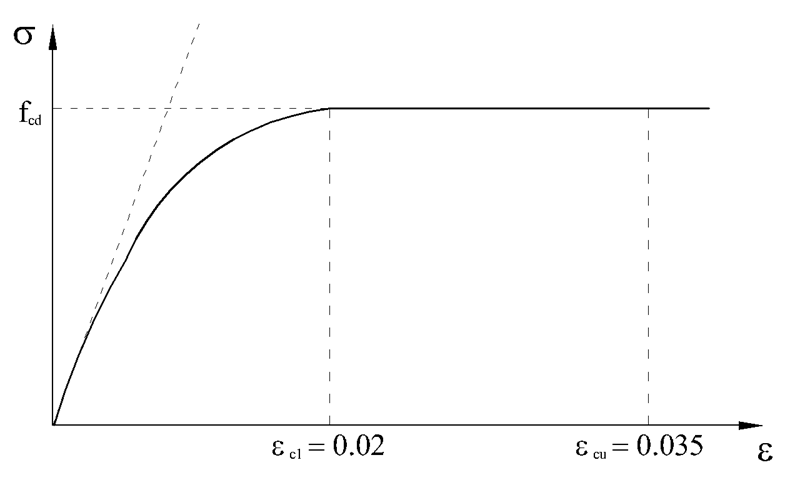
Test a compressione del cls Diagramma Tensione-Deformazione del cls
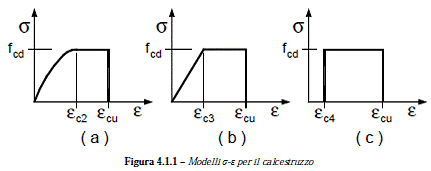
Calcolo dello stress-block
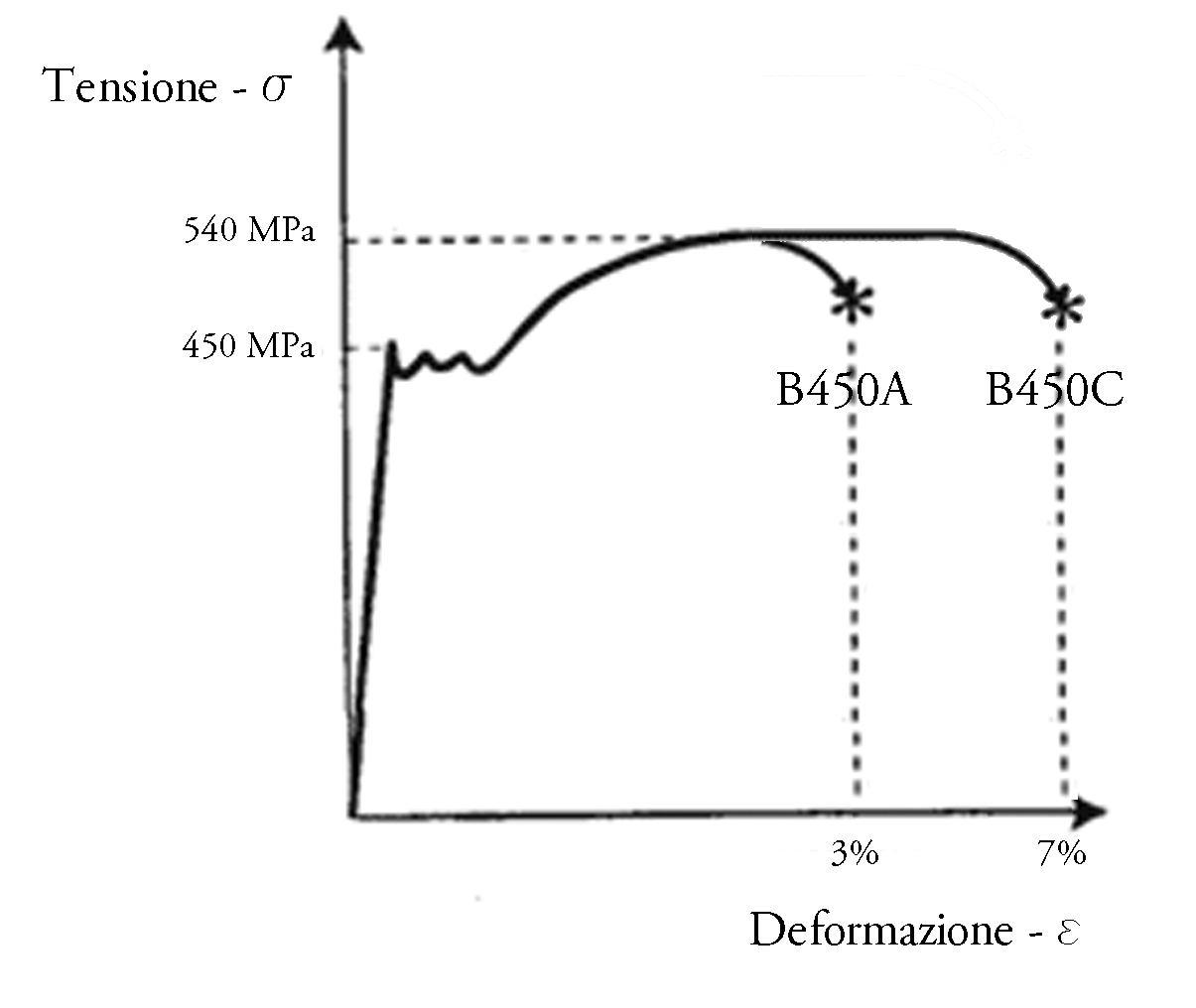
Diagramma Tensione-Deformazione dei tondini di acciaio
·Acciaio da carpenteria
Gli acciai di uso generale (laminati a caldo, in profilati, barre, larghi piatti, lamiere, ecc…) utilizzati nelle costruzioni metalliche possono essere divisi in 3 classi di resistenza:
· Fe 360/S235
· Fe 430/S275
· Fe 510/S355
Dove il primo numero indica la tensione a rottura caratteristica e il secondo la tensione di snervamento caratteristica, ambedue espressi N/mm2 (o MPa).
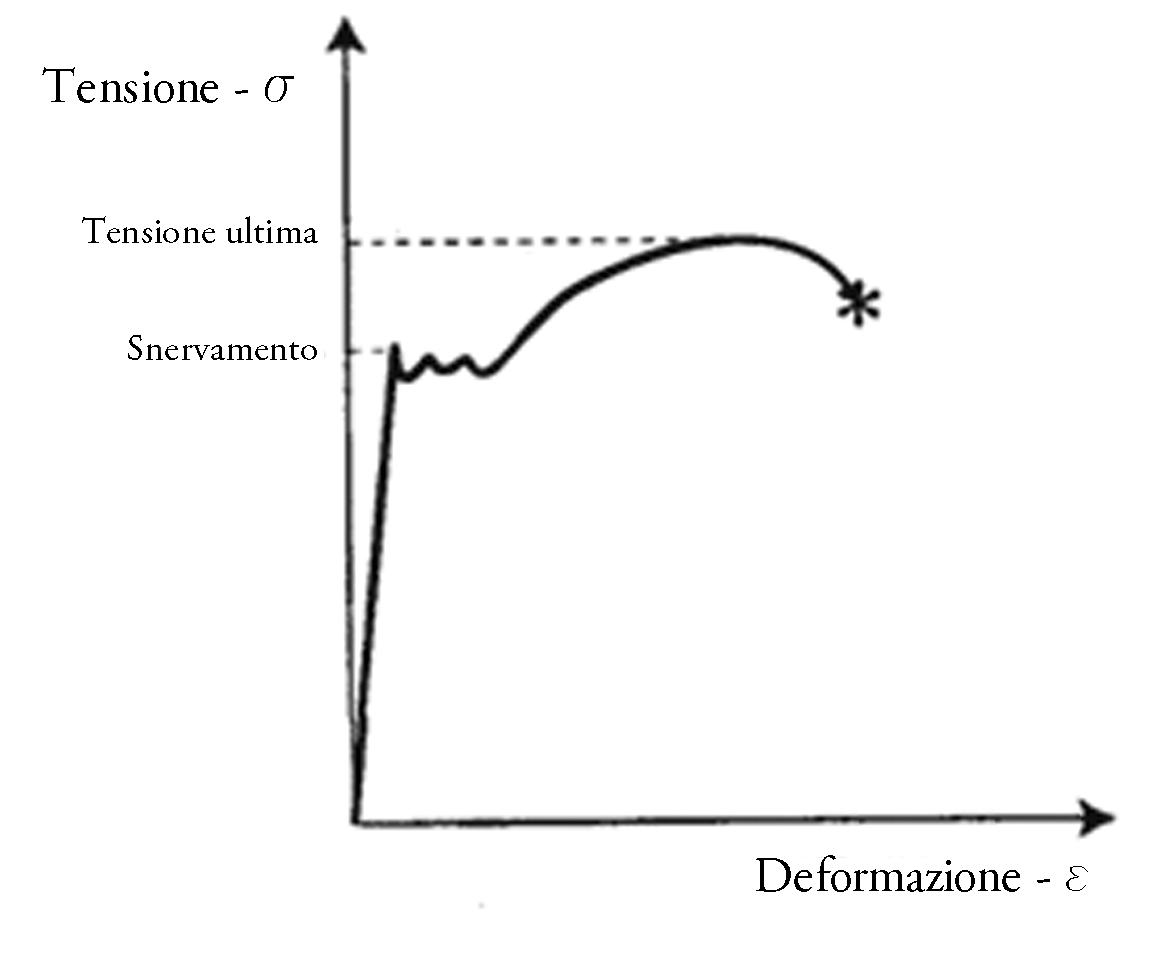
Diagramma Tensione-Deformazione dell'acciaio
·Legno Lamellare
Il legno sente il tempo e l’umidità (materiale viscoso), modificandone le sue caratteristiche meccaniche. L’umidità però rappresenta un problema solo se l’umidità del luogo dove lavora è molto diversa da quella del luogo dove è stato stagionato. (luogo umido --> stagionatura umida)
Una problematica del legno è che più tempo deve resistere a sforzi e più diminuisce la sua resistenza meccanica. Per questo motivo, nella formula per passare da resistenza caratteristica a resistenza di design, va applicato un coefficiente (Kmod) che può essere anche molto basso se il tempo di applicazione del carico è molto lungo.
Il legno è un materiale ortotropo, a differenza di acciaio e calcestruzzo, ciò vuol dire che si comporta in maniera differente a seconda della sua disposizione: maggiore nel verso parallelo alle fibre, minore nella direzione perpendicolare.
Le classi del legno sono quattro:
· GL24h --> Resistenza a flessione 24 Mpa
Resistenza a trazione (parallela alle fibre) 16.5 Mpa
Resistenza a compressione (parallela alle fibre) 24 Mpa
· GL28h --> Resistenza a flessione 28 Mpa
Resistenza a trazione (parallela alle fibre) 19.5 Mpa
Resistenza a compressione (parallela alle fibre) 26.5 Mpa
· GL32h --> Resistenza a flessione 32 Mpa
Resistenza a trazione (parallela alle fibre) 22.5 Mpa
Resistenza a compressione (parallela alle fibre) 29 Mpa
· GL36h --> Resistenza a flessione 36 Mpa
Resistenza a trazione (parallela alle fibre) 26 Mpa
Resistenza a compressione (parallela alle fibre) 31 Mpa
Carichi
· Permanenti (qs) --> Peso proprio strutturale + sovraccarichi (pavimenti, impianti, intonaco, muri, ecc…)
· Variabili (qp)--> Carichi legati all’imprevedibilità (neve, vento, acqua, ecc…)
· Accidentali (qa) --> Carichi legati alla funzione (persone, mobili, libri, ecc…)
2 KN/m2 Edificio di civile abitazione
3 KN/m2 Uffici
4 KN/m2 Edifici soggetti a carico di folla
5 KN/m2 Biblioteche
DIMENSIONAMENTO DI UNA TRAVE PER TRE TIPOLOGIE DI STRUTTURE DIVERSE (Legno, acciaio, calcestruzzo armato).
Per l’esercitazione sul dimensionamento di una trave ho deciso di riprendere la struttura della mensa progettata al secondo anno della laurea triennale nel Laboratorio di Progettazione 2.
Dell’intera struttura prendiamo in considerazione la trave tra i pilastri I1 e I2, avente una luce di 8.00 m. Situata tra il piano terra e il primo piano, la trave sorregge un solaio che prevede una sala mensa priva, almeno in quel tratto, di tramezzature.
L’interasse tra le file di pilastri H, I ed I, L sono uguali tra di loro e pari a 4.20 m. Ciò vuol dire che l’area di solaio, che la trave presa in considerazione deve sorreggere, è di 33.6 m2 (4.20 m x 8.00 m).
Dopo questi dati dimensionali vanno trovate le caratteristiche di peso, degli elementi strutturali e non strutturali, a seconda della tipologia di solaio da progettare.
Data la sua destinazione d’uso abita a mensa, l’edificio è sottoposto in alcuni momenti della giornata ad un affollamento molto elevato, per questo in ogni tipologia di solaio si utilizzerà un carico d’esercizio di 4 KN/m2.
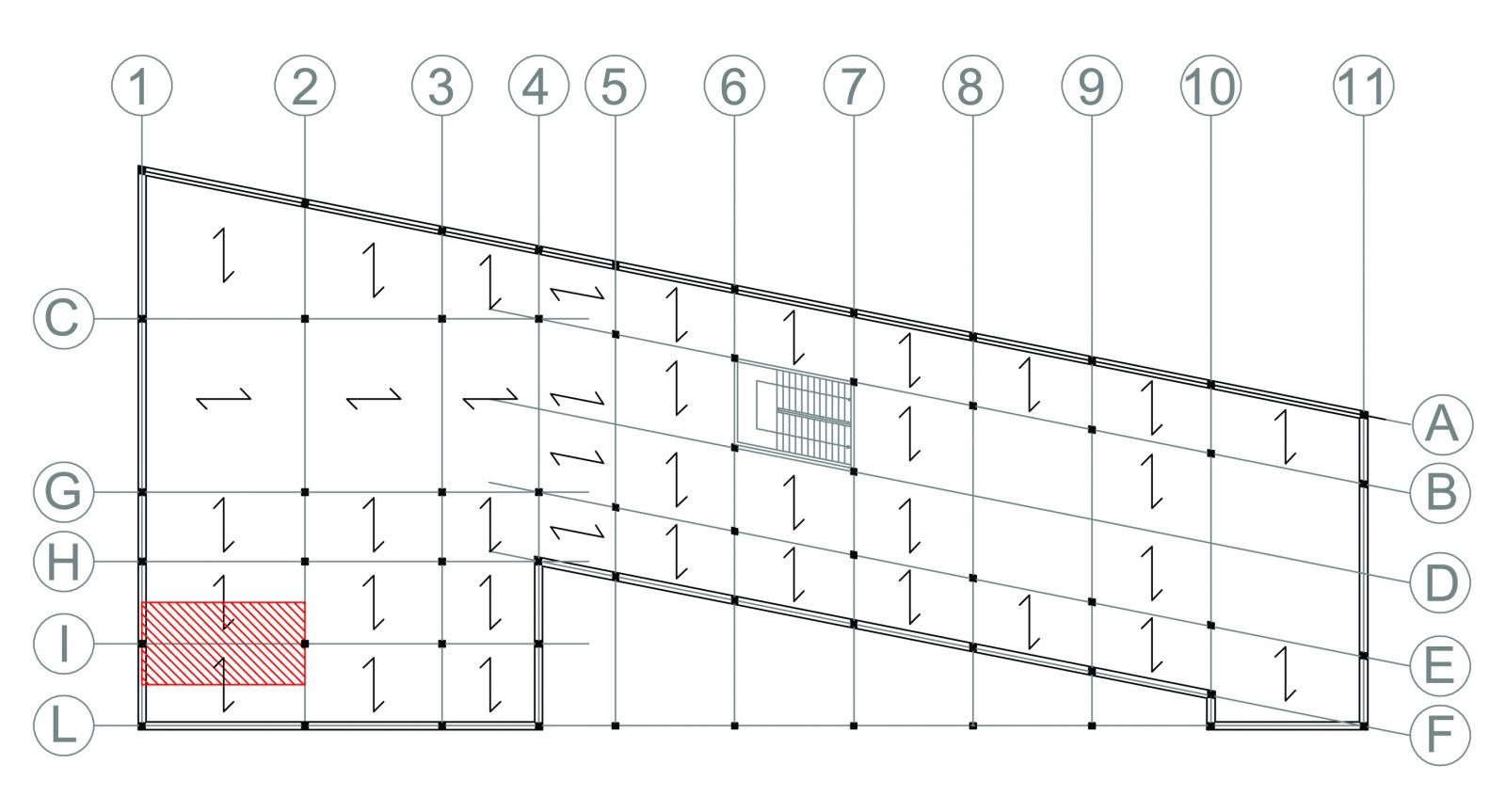
LEGNO
Travetti (interasse 1 m, luce 4.20 m)
Carico strutturale (0.24 KN/m2)
· Tavolato in legno (6 KN/m3) --> Spessore 4 cm --> 0.24 KN/m2
Carico non strutturale (2.63 KN/m2)
· Gettata di cls alleggerito (24 KN/m3) --> Spessore 4 cm --> 0.96 KN/m2
· Isolante (4 KN/m3) --> Spessore 3 cm --> 0.12 KN/m2
· Massetto (20 KN/m3) --> Spessore 4 cm --> 0.8 KN/m2
· Pavimentazione in legno --> Spessore 2 cm --> 0.25 KN/m2
· Impianti --> 0.5 KN/m2
Trovati i valori per i differenti tipi di carico, inserisco nel foglio excell i risultati, la luce della trave e il suo interasse. Avendo deciso di utilizzare un legno GL36h, inserisco il suo valore caratteristico a rottura che equivale a 36 N/mm2. A questo punto l’altezza minima del travetto, avendo ipotizzato una base di 20 cm, è di 19.13 cm. Per facilità vengono adottati dei travetti 20 x 20 cm. Ora che si ha la geometria dei travetti si procede con la verifica a peso proprio:
Peso proprio di un travetto 1.35 KN
Peso al m2 dei travetti (1.35 KN /4.20 m / 1 m) = 0.32 KN/m2
Altezza = 19.57 cm --> VERIFICATO
Trave
Carico strutturale (0.56 KN/m2)
· Travetti 20 x 20 cm (8 KN/m3) --> 0.32 KN/m2
· Tavolato (6 KN/m3) --> Spessore 4 cm --> 0.24 KN/m2
Carico non strutturale (2.63 KN/m2)
· Gettata di cls alleggerito (24 KN/m3) --> Spessore 4 cm --> 0.96 KN/m2
· Isolante (4 KN/m3) --> Spessore 3 cm --> 0.12 KN/m2
· Massetto (20 KN/m3) --> Spessore 4 cm --> 0.8 KN/m2
· Pavimentazione in legno --> Spessore 2 cm --> 0.25 KN/m2
· Impianti --> 0.5 KN/m2
Eseguo lo stesso procedimento dei travetti. Qui l’altezza minima della trave, avendo ipotizzato una base di 40 cm, è di 54.03 cm. Per facilità viene adottata una trave 40 x 55 cm. Ora che si ha la geometria della trave si procede con la verifica a peso proprio:
Peso proprio della trave 14.08 KN
Peso al m2 della trave (14.08 KN / 8 m /4.20 m) = 0.42 KN/m2
Altezza = 55.58 cm --> NON VERIFICATA va adottata una trave più alta
Trave 40 x 60 cm
Peso proprio di un trave 15.36 KN
Peso al m2 della trave (15.36 KN / 8 m /4.20 m) = 0.46 KN/m2
Altezza = 55.73 cm --> VERIFICATA

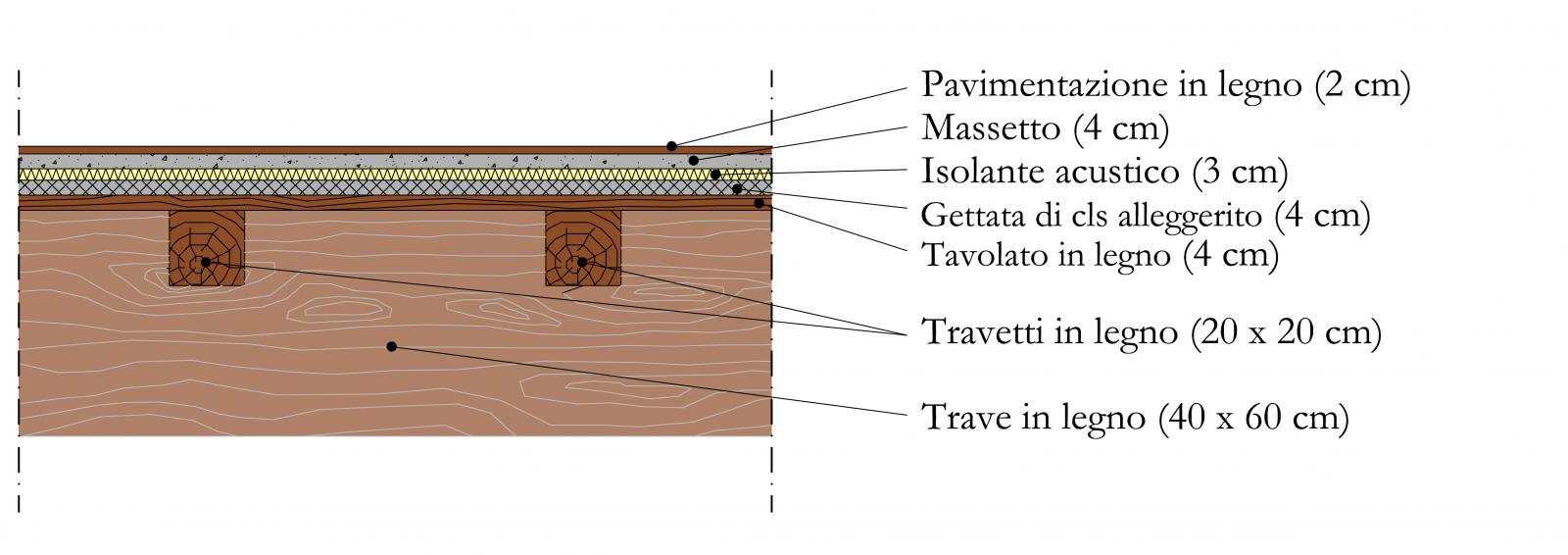
ACCIAIO
Travetti (interasse 1 m, luce 4.20 m)
Carico strutturale (2.5 KN/m2)
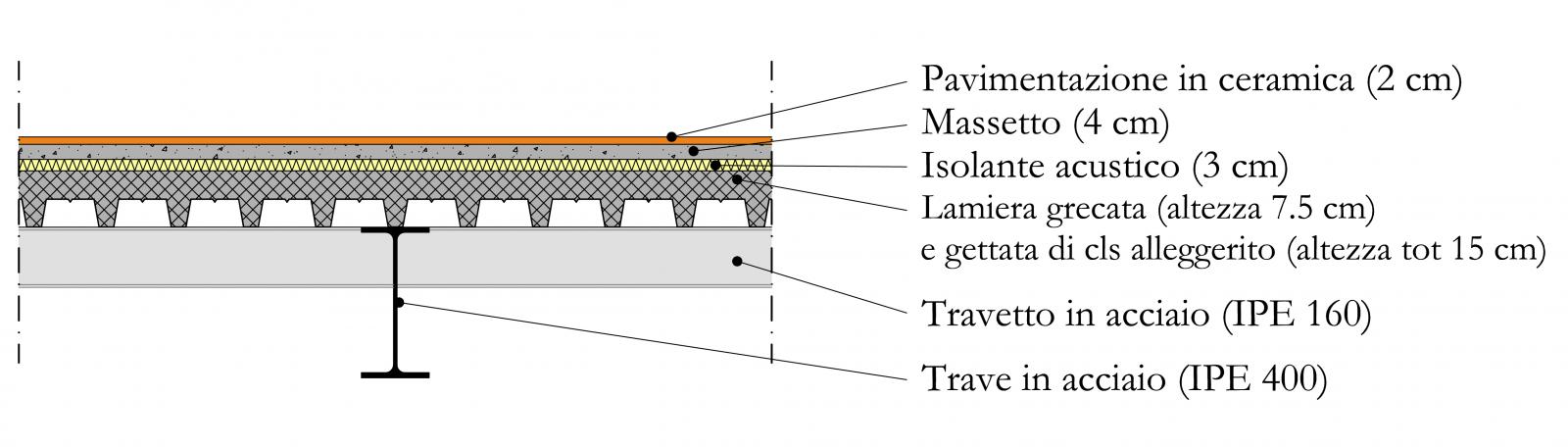
· Lamiera grecata (altezza 7.5 cm) e gettata di cls alleggerito --> Altezza totale 15 cm --> 2.5 KN/m2
Carico non strutturale (2.12 KN/m2)
· Isolante (4 KN/m3) --> Spessore 3 cm --> 0.12 KN/m2
· Massetto (20 KN/m3) --> Spessore 4 cm --> 0.8 KN/m2
· Pavimentazione in ceramica --> Spessore 2 cm --> 0.4 KN/m2
· Impianti --> 0.5 KN/m2
· Controsoffitto --> 0.3 KN/m2
Trovati i valori per i differenti tipi di carico, inserisco nel foglio excell i risultati, la luce della trave e il suo interasse. Avendo deciso di utilizzare un acciaio Fe360/S235, inserisco il suo valore caratteristico a snervamento che equivale a 235 N/mm2. Il modulo di resistenza minimo per i travetti è di 84.93 cm3. Quindi vengono adottate delle IPE 160 (W = 109 cm3). Si procede con la verifica a peso proprio che da profilario è di 0,158 KN/m:
Peso al m2 dei travetti (0.158 KN / 1 m) = 0.158 KN/m2
W = 86.48 cm3 --> VERIFICATO
Trave
Carico strutturale ( 2.658 KN/m2)
· Travetti IPE 160 --> 0.158 KN/m2
· Lamiera grecata (altezza 7.5 cm) e gettata di cls alleggerito --> Altezza totale 15 cm --> 2,5 KN/m2
Carico non strutturale (2.12 KN/m2)
· Isolante (4 KN/m3) --> Spessore 3 cm --> 0.12 KN/m2
· Massetto (20 KN/m3) --> Spessore 4 cm --> 0.8 KN/m2
· Pavimentazione in ceramica --> Spessore 2 cm --> 0.4 KN/m2
· Impianti --> 0.5 KN/m2
· Controsoffitto --> 0.3 KN/m2
Trovati i valori per i differenti tipi di carico, inserisco nel foglio excell i risultati, la luce della trave e il suo interasse. Avendo deciso di utilizzare un acciaio Fe430/S275, inserisco il suo valore caratteristico a snervamento che equivale a 275 N/mm2. Il modulo di resistenza minimo per la trave è di 1126.14 cm3. Quindi vengono adottate delle IPE 400 (W = 1160 cm3). Si procede con la verifica a peso proprio che da profilario è di 0,663 KN/m:
Peso al m2 della trave (0.663 KN / 4.2 m) = 0.158 KN/m2
W = 1146.41 cm3 --> VERIFICATO (il valore è verificato, anche se visto la prossimità dei due moduli di resistenza converrebbe adottare una IPE 450)

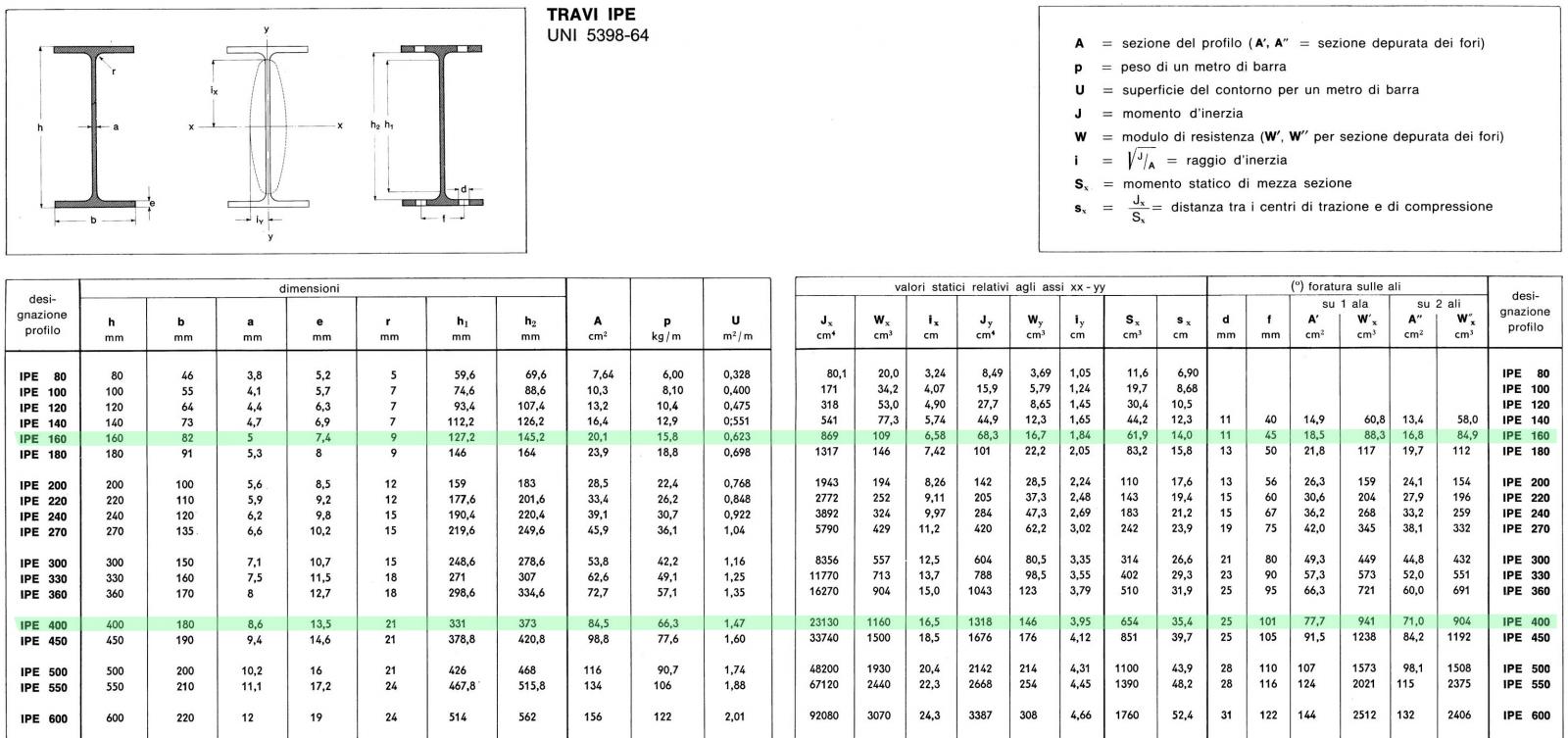
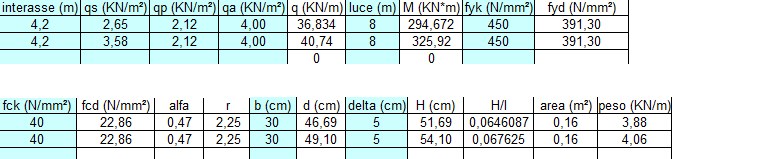
CALCESTRUZZO ARMATO
Trave
Carico strutturale (2,65 KN/m2)
· Solaio in laterocemento con travetti armati --> Altezza totale 25 cm --> 2,65 KN/m2
Carico non strutturale (2,12 KN/m2)
· Isolante (4 KN/m3) --> Spessore 3 cm --> 0.12 KN/m2
· Massetto (20 KN/m3) --> Spessore 4 cm --> 0.8 KN/m2
· Pavimentazione in ceramica --> Spessore 2 cm --> 0.4 KN/m2
· Impianti --> 0.5 KN/m2
· Intonaco --> Spessore 1.5 cm --> 0.3 KN/m2
Trovati i valori per i differenti tipi di carico, inserisco nel foglio excell i risultati, la luce della trave e il suo interasse. Utilizzando delle barre d’acciaio B450C e un calcestruzzo C40/50, inserisco loro valori di resistenze meccaniche nella tabella. L’altezza utile d per questa trave è di 46.69 cm. Dovendo aggiungere 5 cm di copriferro e dato che le sezioni standard in calcestruzzo armato hanno dimensioni che variano di 5 cm alla volta, sono obbligato a scegliere una sezione di 30 x 55 cm. Si procede con la verifica a peso proprio:
Peso al m lineare della trave = 3.88 KN/m
Peso al m2 della trave = 0.93 KN/m2
Altezza utile trave = 49.10 cm
Altezza totale trave = 54.10 cm --> VERIFICATO
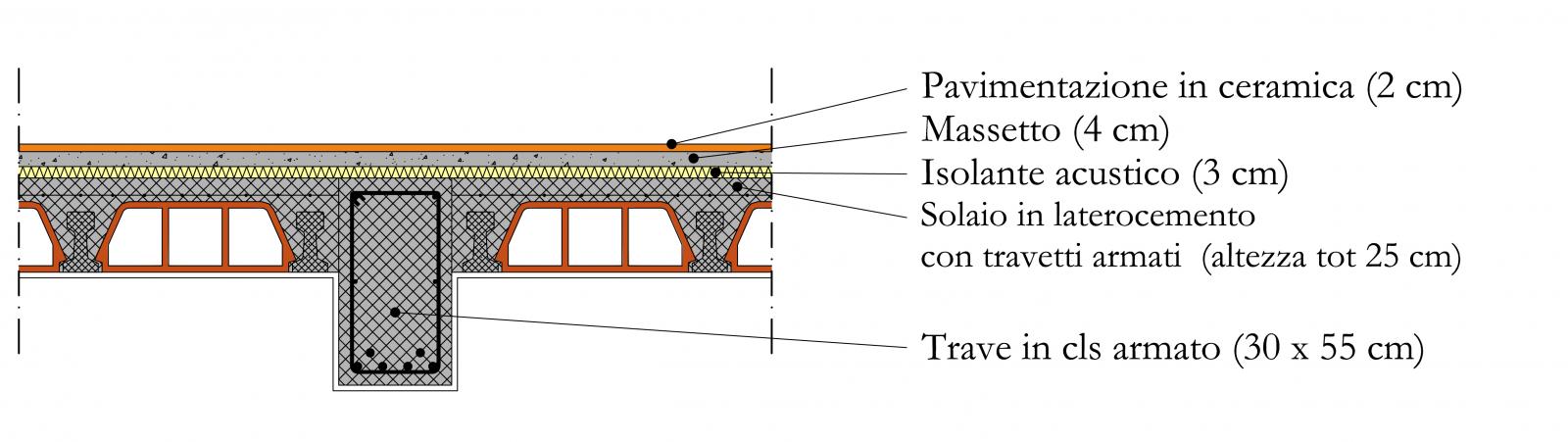
Si è svolto inoltre un dimensionamento e la successiva verifica dell’armatura longitudinale del calcestruzzo. Dopo aver creato una nuova tabella, avendo inserito nelle celle le formule adottate nel corso di Tecnica delle Costruzioni, mi basta inserire il numero di barre e il loro diametro per vedere se il momento resistente della trave è maggiore di quello di progetto, utilizzando l’equilibrio alla traslazione e l’equilibrio alla rotazione.
Utilizzo 6 barre con diametro “Φ” 22 mm --> VERIFICATO

DISEGNO, ANALISI E DIMENSIONAMENTO DEGLI ELEMENTI DELLA STRUTTURA RETICOLARE SPAZIALE.
Per progettare una struttura reticolare spaziale si parte con il disegno su autocad di un modulo base che verrà ripetuto nelle tre dimensioni grazie al comando “serie” (o “Array”). In figura si può capire come procedere per la riproduzione del modulo base, facendo attenzione a non sovrapporre più linee durante la copia (questo può provocare problemi nel calcolo di Sap2000).
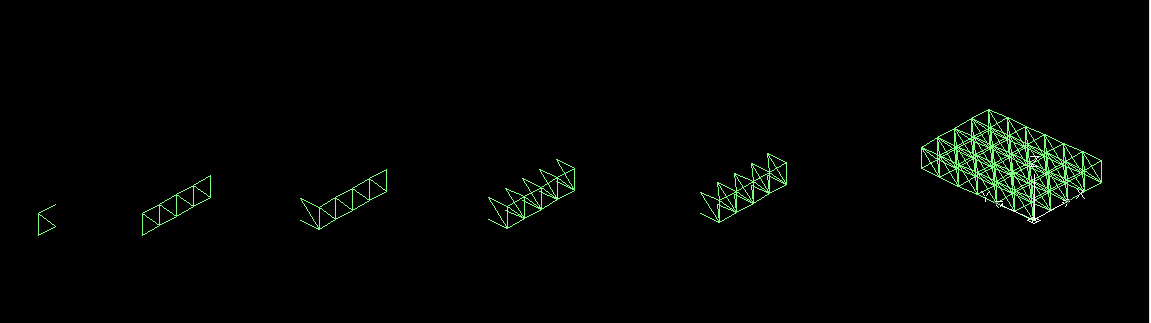
Una volta ottenuta la “piastra” reticolare delle dimensioni e campate desiderate si salva il file autocad in formato dxf 2000 e si importa su Sap, ricordando di assegnare alla voce “frame” (o “telai”) il nome del layer di autocad attribuito alla struttura disegnata precedentemente. Effettuata quest’operazione si ha una struttura che “galleggia” nello spazio e che quindi necessita di essere vincolata. A tal proposito vengono assegnate 4 cerniere nei rispettivi 4 vertici del rettangolo di base.
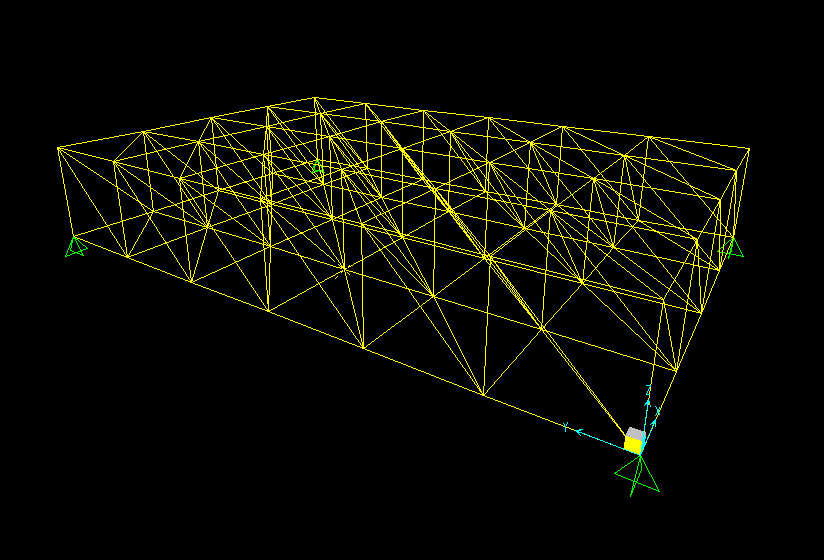
Ora, visto che Sap considera tutte le aste come incastrate tra di loro, dobbiamo assegnare all’inizio e alla fine di ogni asta un momento uguale a zero. Questo perché, essendo una struttura reticolare, tutte gli elementi sono incernierati tra di loro, provocando solo sforzi normali e non di taglio o momento.
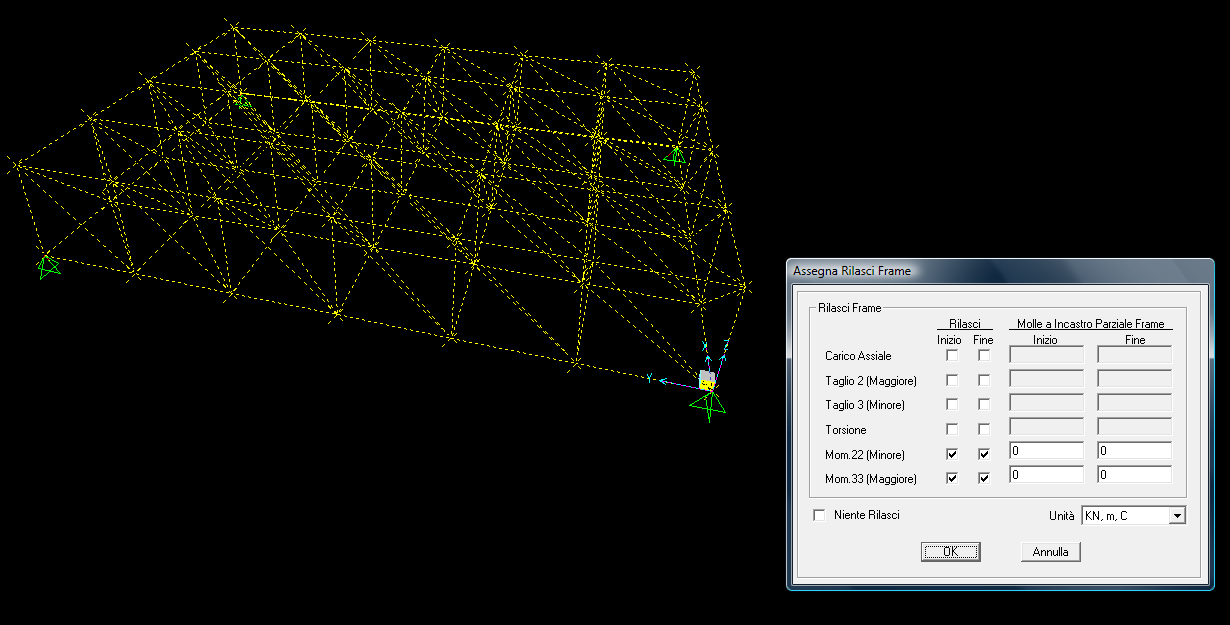
Per un calcolo di questo tipo, affinché il risultato ottenuto sia più veritiero, è meglio assegnare alle aste un materiale (acciaio – steel) e una sezione (tubo – pipe).
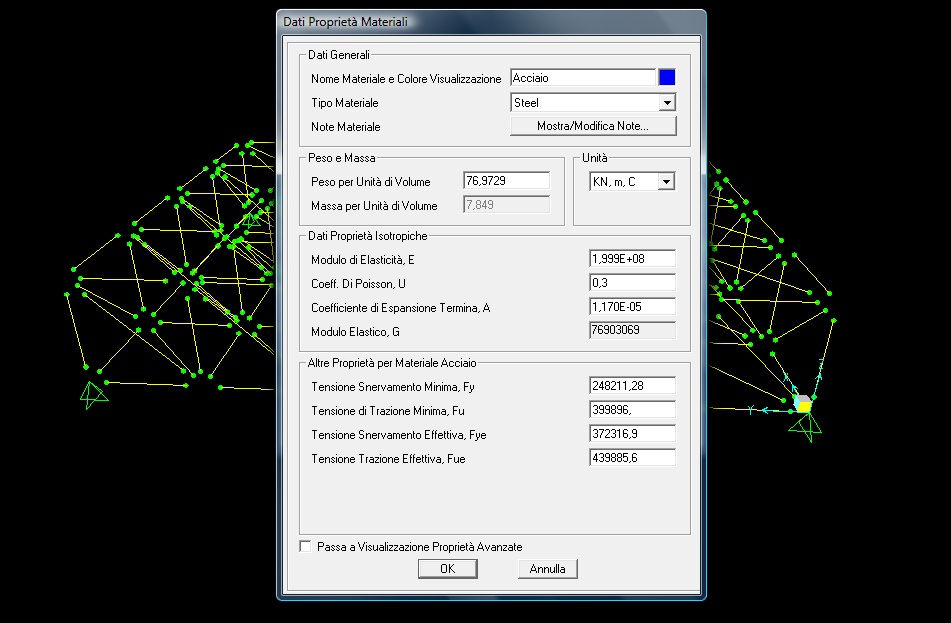
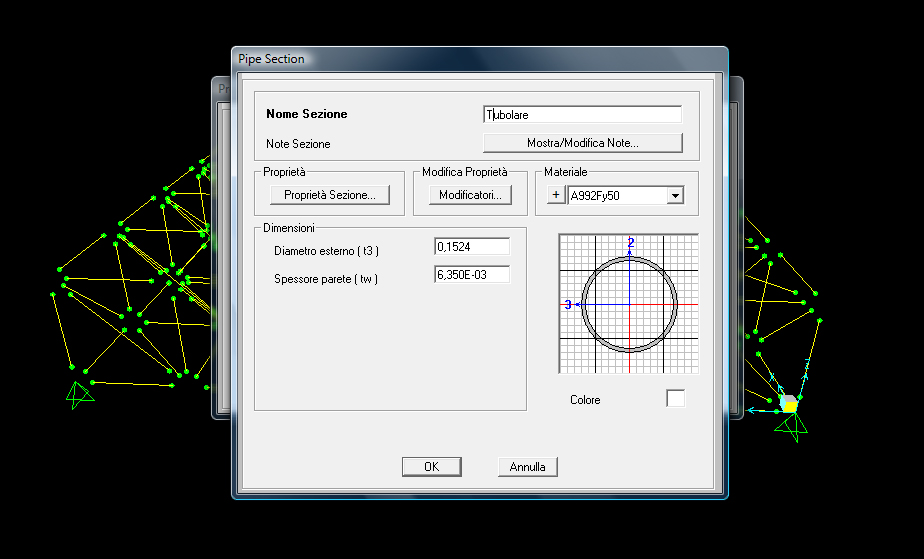
Viene definito un carico concentrato e, sempre perché la struttura sia sollecitata solo a sforzo normale, viene applicato direttamente sui nodi. In questo caso il valore della forza viene fissato di 40 KN verso il basso e applicato su tutti i nodi della parte superiore.
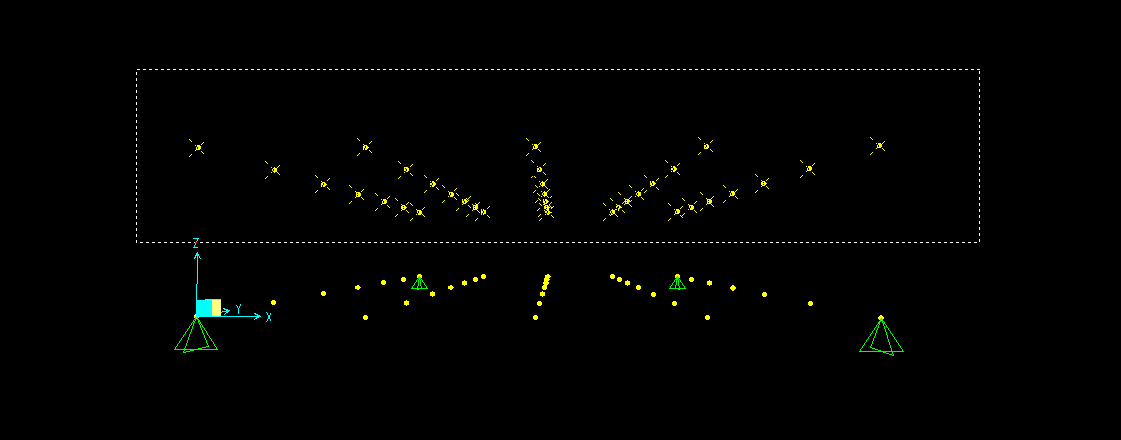
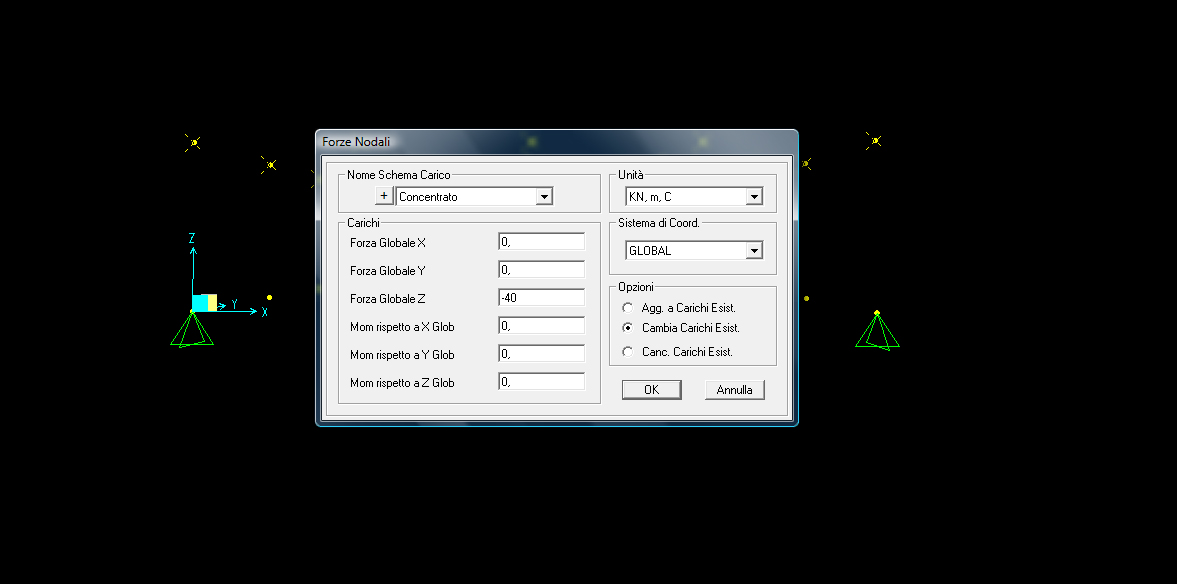
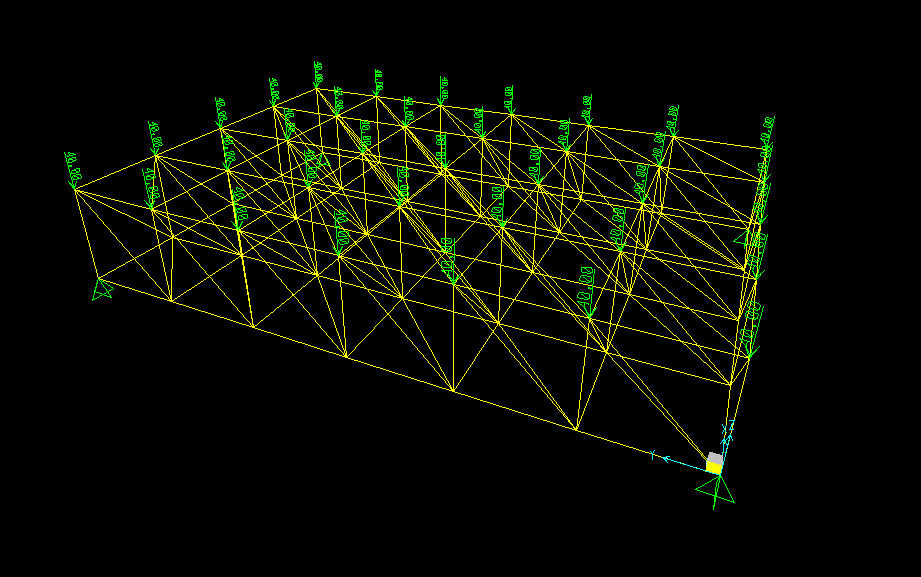
Ora si passa all’analisi degli effetti di queste forze sulla struttura. La deformazione è concentrata per lo più nella parte centrale della struttura mentre gli sforzi normali più alti si trovano in prossimità dei vincoli.

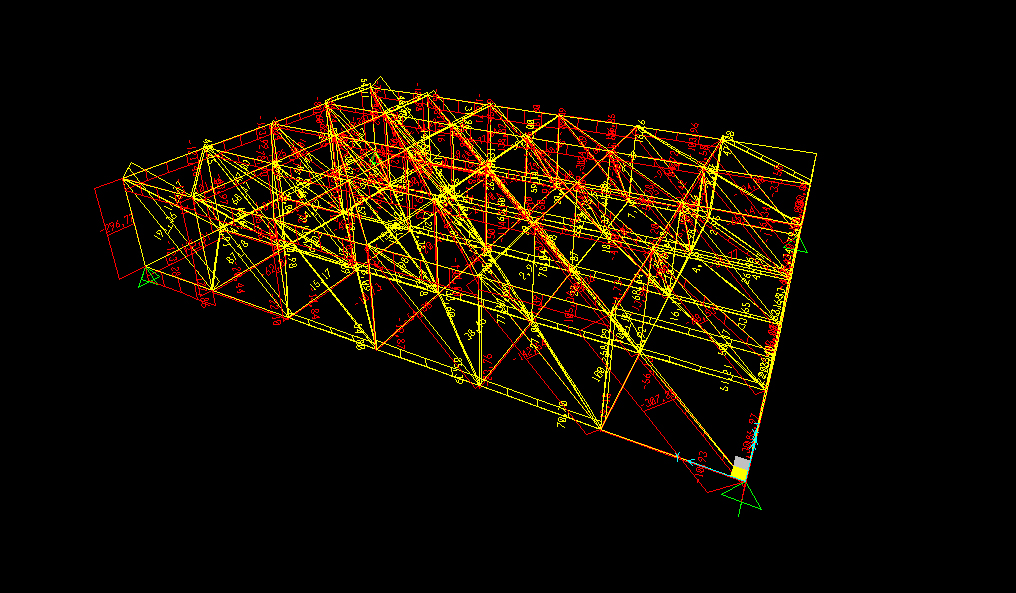
Conclusa la fase di analisi Sap permette di aprire una tabella che indica tutti i valori di sforzo delle aste. Questa tabella può essere esportata su excel dove è possibile ordinarla, secondo la colonna degli sforzi normali, dal valore più basso a quello più alto. Per procedere con il dimensionamento serve avere il valore dell’asta più compressa e dell’asta più tesa. Questi sono rispettivamente il valore più basso (negativo) e quello più alto (positivo) della tabella.
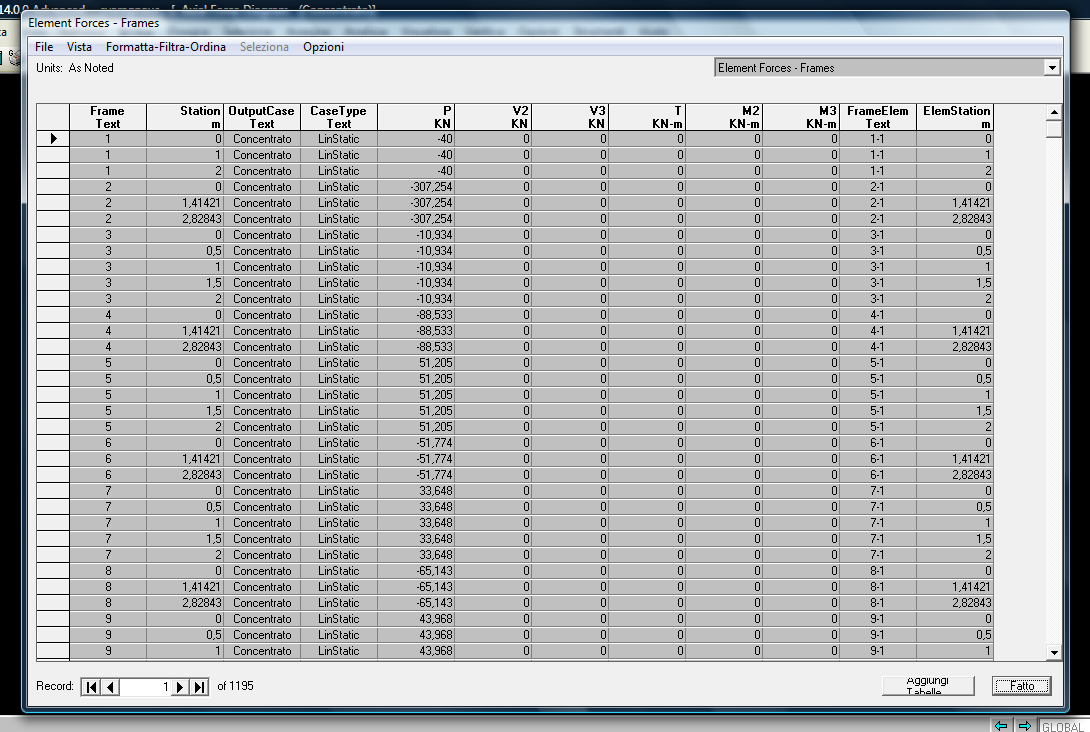
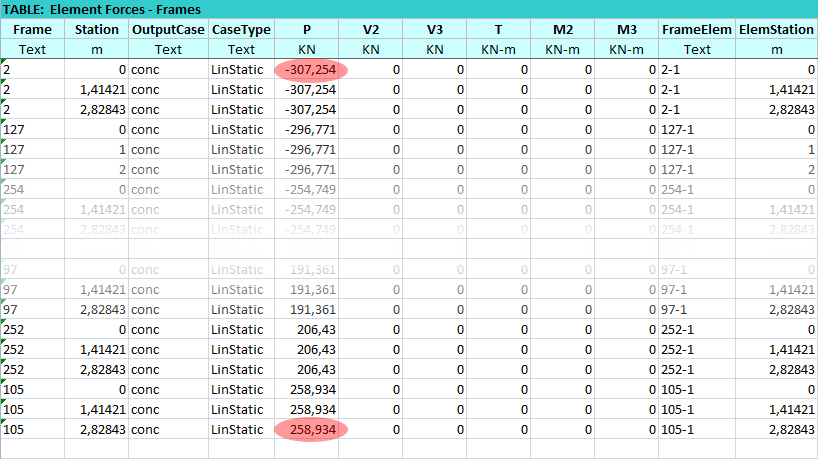
Dopo aver progettato (in collaborazione con Alessia Scavo) una tabella su excel capace di “fare i calcoli al posto nostro”, inseriamo i valori di sforzo normale per fare il progetto a resistenza e trovarci un’area minima per l’asta.
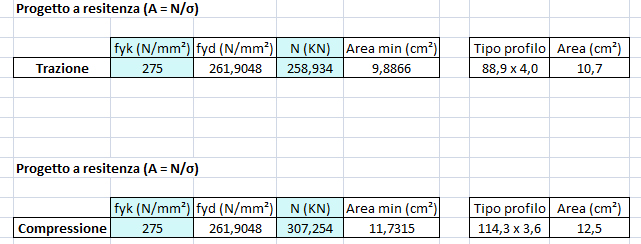
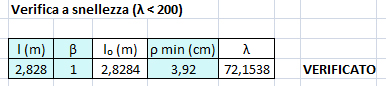
Questo, per quanto riguarda le aste tese, può bastare, mentre per le aste compresse bisogna procedere con 2 verifiche: quella a snellezza e quella a stabilità.
(NTC, Capitolo 4.2.4.1.3)
Limitazioni della snellezza
Si definisce lunghezza d’inflessione la lunghezza l0 = β l da sostituire nel calcolo del carico critico elastico Ncr alla lunghezza l dell’asta quale risulta dallo schema strutturale. Il coefficiente β deve essere valutato tenendo conto delle effettive condizioni di vincolo dell’asta nel piano di inflessione considerato. Si definisce snellezza di un’asta nel piano di verifica considerato il rapporto:
λ = l0 /ρ
dove
l0 è la lunghezza d’inflessione nel piano considerato,
ρ è il raggio d’inerzia relativo.
È opportuno limitare la snellezza λ al valore di 200 per le membrature principali ed a 250 per le membrature secondarie.
Stabilità delle membrature
La verifica di stabilità di un’asta si effettua nell’ipotesi che la sezione trasversale sia uniformemente compressa. Deve essere
Nd ≤ Nbrd
dove
Nd è l’azione di compressione di calcolo,
Nbrd è la resistenza all’instabilità nell’asta compressa, data da:
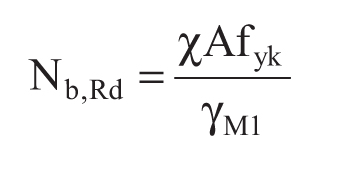
Il coefficiente χ dipende dal tipo di sezione e dal tipo di acciaio impiegato; esso si desume, in funzione di appropriati valori della snellezza adimensionale λ , dalla seguente formula
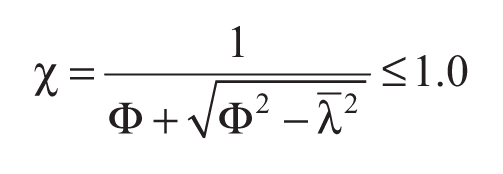
dove φ = 0.5[1+ α (λ - 0.2) + λ2 ], α è il fattore di imperfezione, ricavato dalla Tabella 4.2.VI, e la snellezza adimensionale λ è pari a
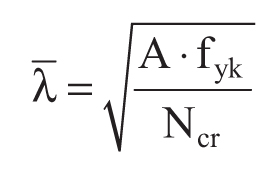

Calcolo degli spostamenti e delle rotazioni delle sezioni
Procedimenti:
1) Determinare la funzione momento
2) Determinare la funzione curvatura (χs)= Ms/EI
3) Integrare per trovare la rotazione (φs)
4) Integrare una seconda volta per trovare lo spostamento (vs)
5) Imporre le condizioni al bordo di natura cinematica (B.C.)
6) Determinare rotazione e spostamento massimo
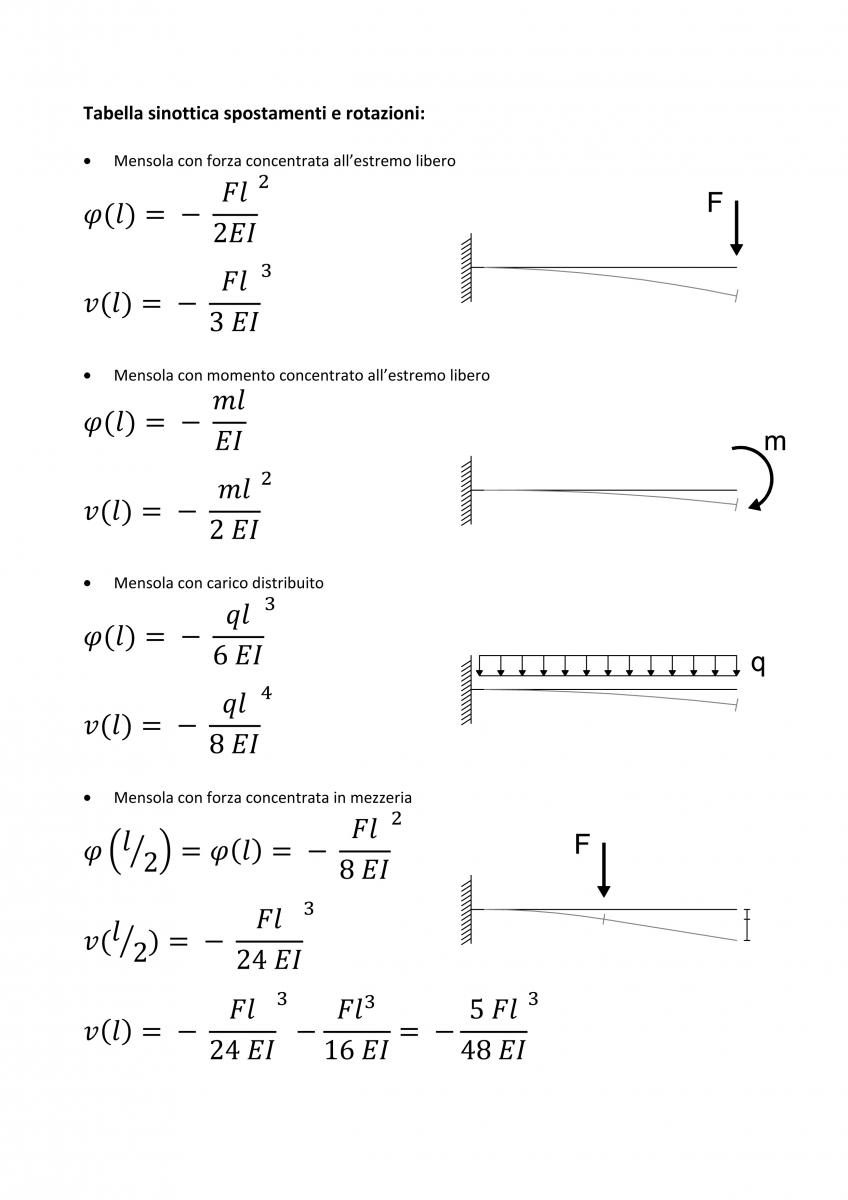
Segue una tabella sinottica con gli spostamenti e le rotazioni massimi di alcuni casi noti:
· Mensola con forza concentrata all’estremo libero
· Mensola con momento concentrato all’estremo libero
· Mensola con carico distribuito
· Mensola con forza concentrata in mezzeria
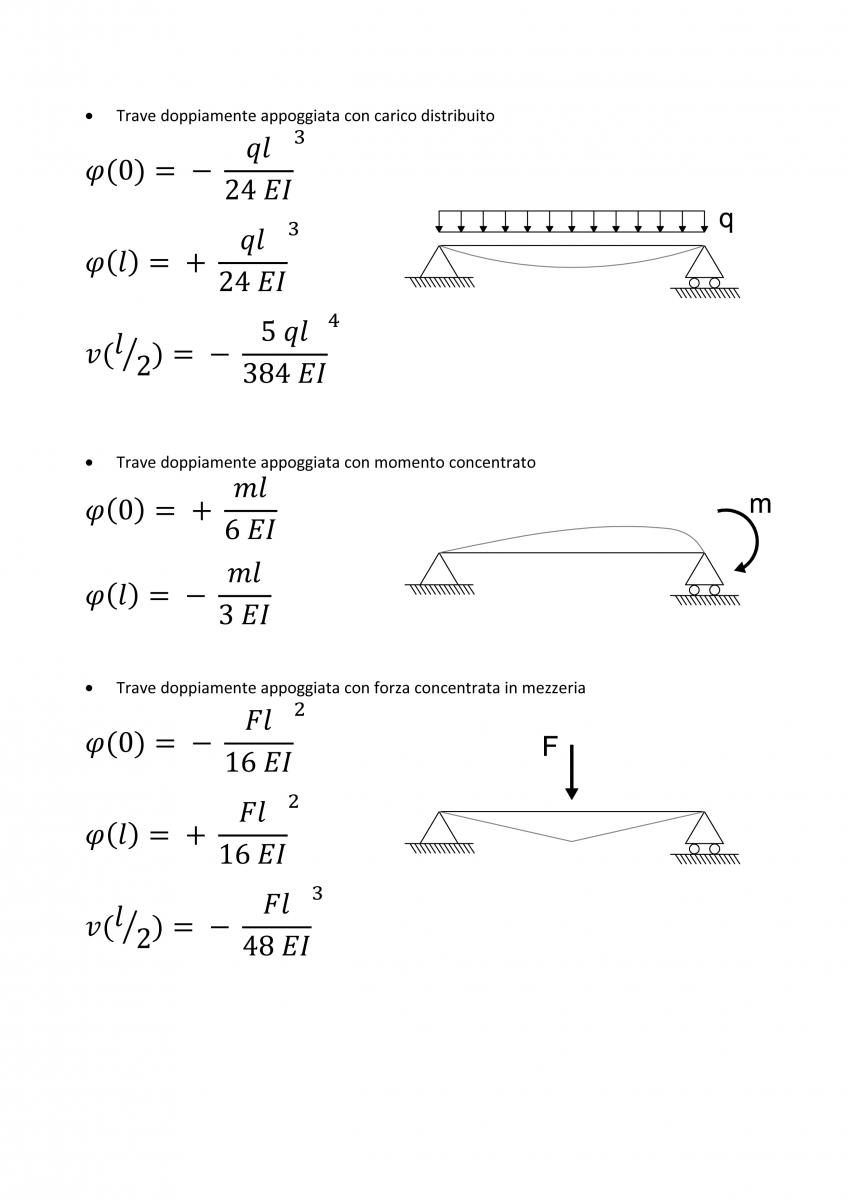
· Trave doppiamente appoggiata con carico distribuito
· Trave doppiamente appoggiata con momento concentrato
· Trave doppiamente appoggiata con forza concentrata in mezzeria
Metodo delle forze
Il metodo delle forze viene usato per risolvere i sistemi iperstatici sfruttando gli spostamenti e le rotazioni delle strutture isostatiche. Questo metodo scompone il sistema iperstatico in due isostatici che grazie al principio di sovrapposizione possono essere ricondotti di nuovo ad un sistema unico. Il procedimento impone di risolvere prima il sistema come se fosse isostatico e poi ci si aggiunge l’incognita che lo renderebbe iperstatico dopo averla calcolata in un sistema a parte.
L’incognita iperstatica si trova sommando (o sottraendo) gli spostamenti o le rotazioni dei due sistemi.
Spostamento estremo libero con carico distribuito --> v(l)= -ql4/8EI
Spostamento estremo libero con forza concentrata --> v(l)= +Xl3/3EI
-ql4/8EI + Xl3/3EI = 0 --------> X= (3/8) ql
Trovata l'incognita iperstatica si risolve il problema come se fosse un sistema isostatico.
Questo metodo è molto utile per risolvere problemi che sono la somma di due sistemi noti, invece per quanto riguarda problemi tipo travi continue su molti appoggi non conviene più utilizzarlo poiché bisognerebbe trovare un caso per ogni numero di appoggi della trave.
Metodo delle rigidezze
Il metodo delle rigidezze sfrutta gli spostamenti e le rotazioni delle strutture isostatiche per risolvere i sistemi iperstatici e non, ma in modo diverso rispetto al metodo delle forze. Questo metodo si presta bene per risolvere l’iperstaticità di un telaio poiché sfrutta il contributo di rigidezza di ogni elemento, da cui poi è possibile calcolare gli sforzi su ognuno di loro e infine dimensionarli opportunamente.
La rigidezza di un elemento dipende innanzi tutto dalla sua condizione di vincolo ma ovviamente entrano in campo fattori come la luce e il modulo elastico del materiale.
Segue una tabella sinottica con le rigidezze di alcuni casi noti:
· Trave doppiamente appoggiata con momento concentrato
· Trave con cerniera e glifo con momento concentrato
· Mensola con carrello con momento concentrato
· Trave con incastro e glifo con forza concentrata sul glifo
· Trave con cerniera e glifo con forza concentrata sul glifo

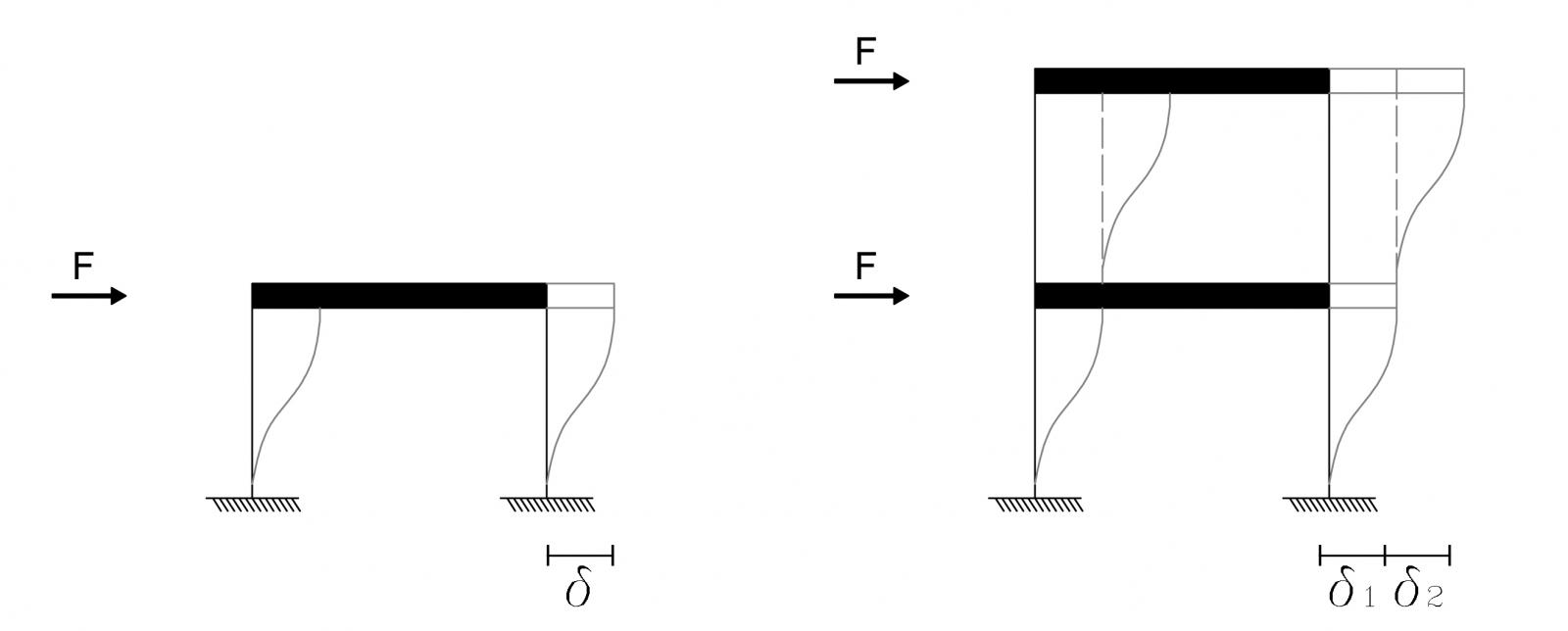
Telai Shear-Type
Un telaio shear-type è un impalcato con due fondamentali ipotesi:
1) La trave è infinitamente resistente a flessione (momento di inerzia molto alto)
2) I pilastri non si deformano se sottoposti ad un qualsiasi sforzo normale
Questo tipo di telaio assume come rigidezza totale la somma di tutte le rigidezze dei suoi pilastri.
F = Kδtot * δ ----------> δ = F / Kδtot
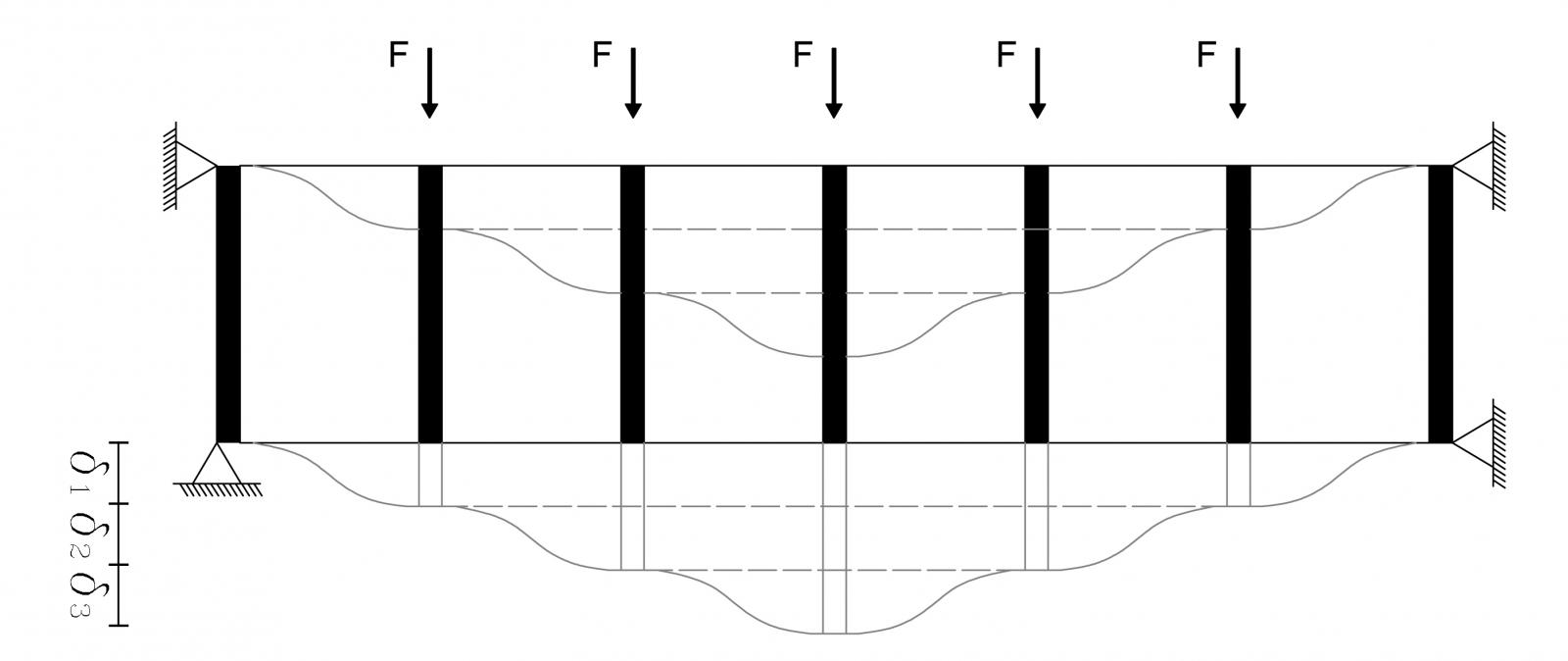
Travi Vierendeel
Una trave Vierendeel non è altro che un telaio shear-type ruotato di 90° rispetto alla posizione che noi siamo abituati a vedere. Proprio per questo, qui, sono i pilastri ad essere infinitamente resistenti a flessione e le travi non deformabili a sforzo normale. In più, per progettare una corretta trave Vierendeel, ogni campata deve essere uguale alle altre e si necessita di una struttura di supporto a normale.
Controventi
Ogni impalcato è composto da una maglia di telai, tessuti più o meno parallelamente e/o perpendicolarmente a seconda della “fantasia” del progettista. Questi telai (ipotizzando che siano shear-type) costituiscono dei controventi per l’intera struttura. I controventi sono dei vincoli che impediscono alla struttura di effettuare uno spostamento o una rotazione dovuta da una forza orizzontale. Essi, avendo comportamento elastico e per facilità di un calcolo isostatico, vengono rappresentati come delle molle dove la rigidezza di ognuna di esse rappresenta proprio la rigidezza di ogni telaio. Nel caso di una sollecitazione orizzontale (sisma, vento) la forza è applicata nel centro di massa (baricentro) della struttura. Per questo motivo quando si progetta una struttura bisogna pensare alla posizione di tutti i controventi (e alla rigidezza di ognuno) e a far coincidere il più possibile il centro di massa con il centro delle rigidezze (punto attorno al quale la struttura ruota) per diminuire il braccio della forza orizzontale e quindi il momento dovuto ad essa.
Ripartizione forze sismiche (esercitazione svolta con Alessia Scavo)
Una struttura, soprattutto nel nostro paese che è considerato quasi del tutto zona sismica, necessita di una progettazione che tiene conto non solo delle forze e dei carichi verticali, ma anche di sollecitazioni orizzontali. Per contrastare questo tipo di spinte si devono opportunamente disporre all’interno della struttura dei particolari vincoli detti controventi.
In questa esercitazione vedremo come si ripartiscono le forze sismiche all’interno di una struttura ad un piano. La prima ipotesi da fare è che questa struttura abbia dei telai shear-type, ovvero un telaio con tutti nodi ad incastro e con la trave considerata infinitamente rigida flessionalmente rispetto ai pilastri. La seconda ipotesi è che i pilastri non si deformano né a compressione né a trazione, o comunque si deformano in maniera trascurabile.
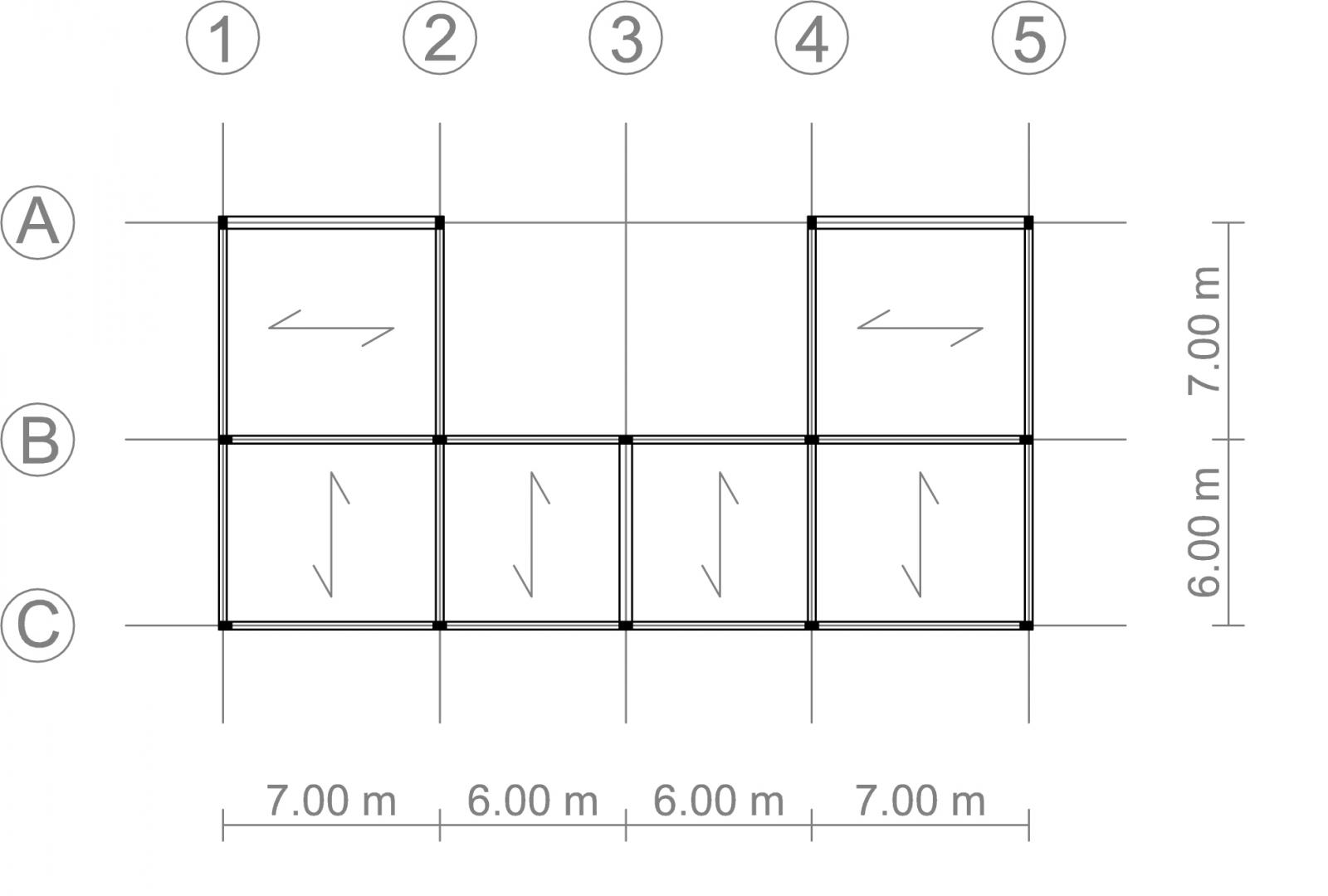
L’impalcato preso in esame è in calcestruzzo armato (quindi con modulo elastico E=21000 N/mm2) ed è composto da 14 pilastri aventi sezione rettangolare e dimensioni 25x40 cm. Dato che una sezione rettangolare ha due momenti d’inerzia, uno lungo l’asse x e l’altro lungo l’asse y, i pilastri sono stati disposti in base alla tessitura del solaio.
Infatti:
Ix= bh3/12 = 133333,33 cm4
Iy= hb3/12 = 52083,33 cm4
I nostri controventi sono costituiti da pilastri disposti su uno stesso asse e sono collegati rigidamente in sommità dal solaio shear-type. Essendo i controventi degli elementi con comportamento elastico, essi possono essere semplificati come delle vere e proprie molle, seguendo quindi la legge di Hooke: F=K x s (costante elastica per lo spostamento). Applicata al nostro caso: F = Kt x σ, dove Kt è la rigidezza del controvento e dè la traslazione del telaio. Ogni pilastro contribuisce sul proprio controvento con una rigidezza Kt= 12EI/h3.
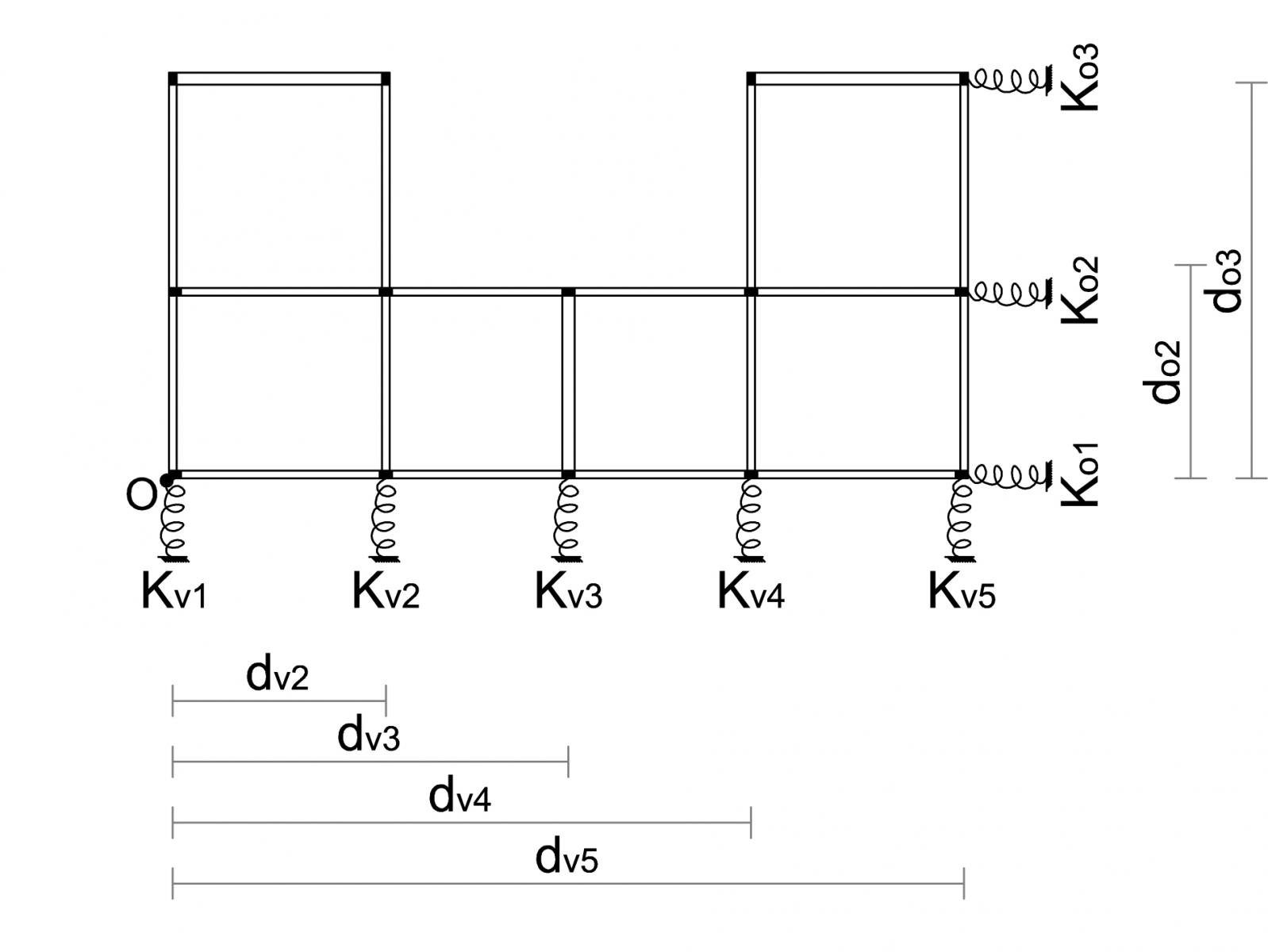
STEP 1: Calcolo delle rigidezze traslanti dei controventi dell'edificio
Si procede ora al calcolo della rigidezza traslante di ogni controvento, quindi tenendo conto del Modulo di Young (E), dell’altezza dei pilastri (h) e del momento d’inerzia di ogni pilastro (I). Seguono le tabelle:
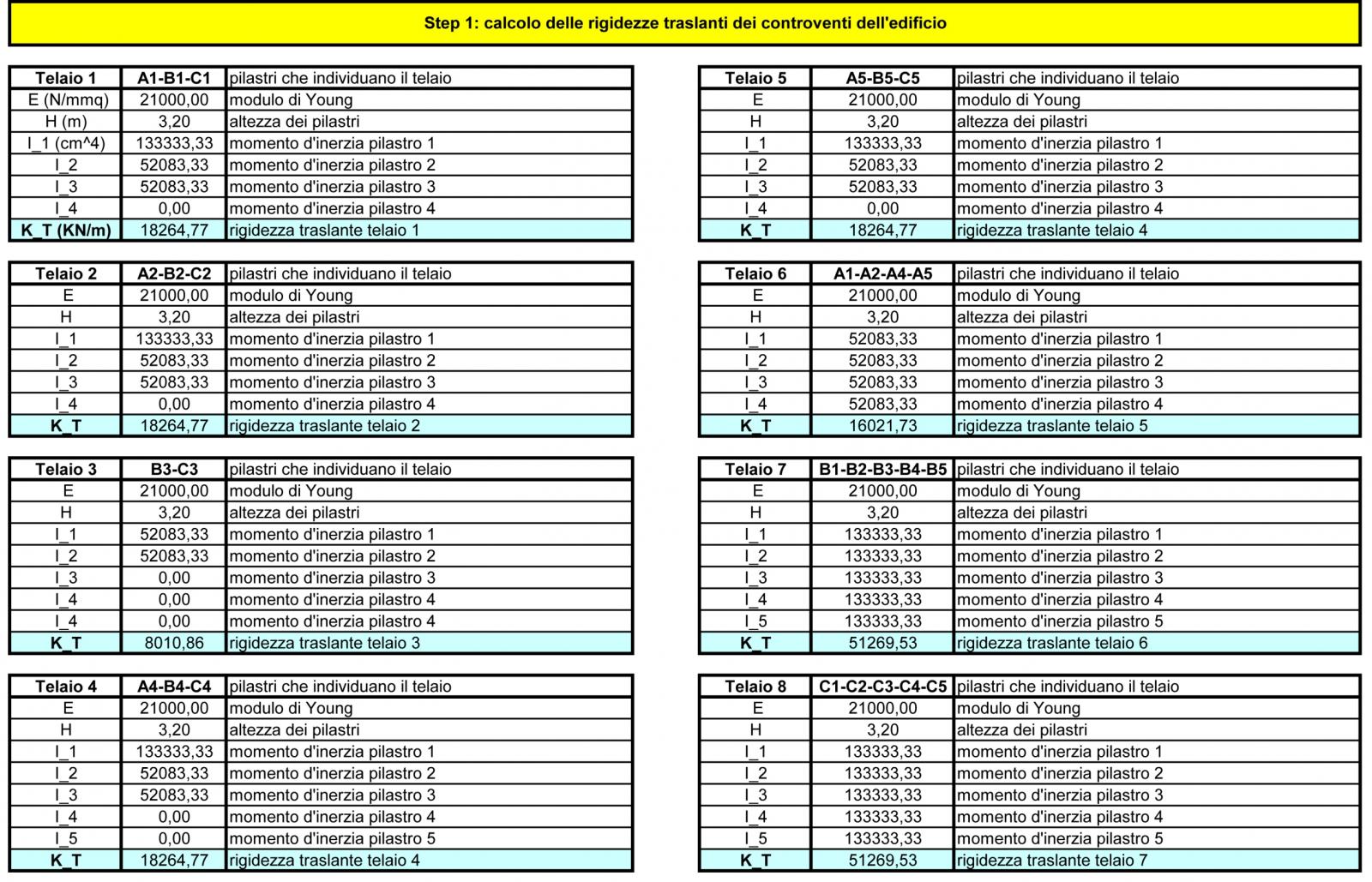
STEP 2: Tabella sinottica controventi e distanze
Ora si calcolano le distanze verticali (dv) e orizzontali (do) del controvento dal punto O, che è l’origine del nostro sistema di riferimento.
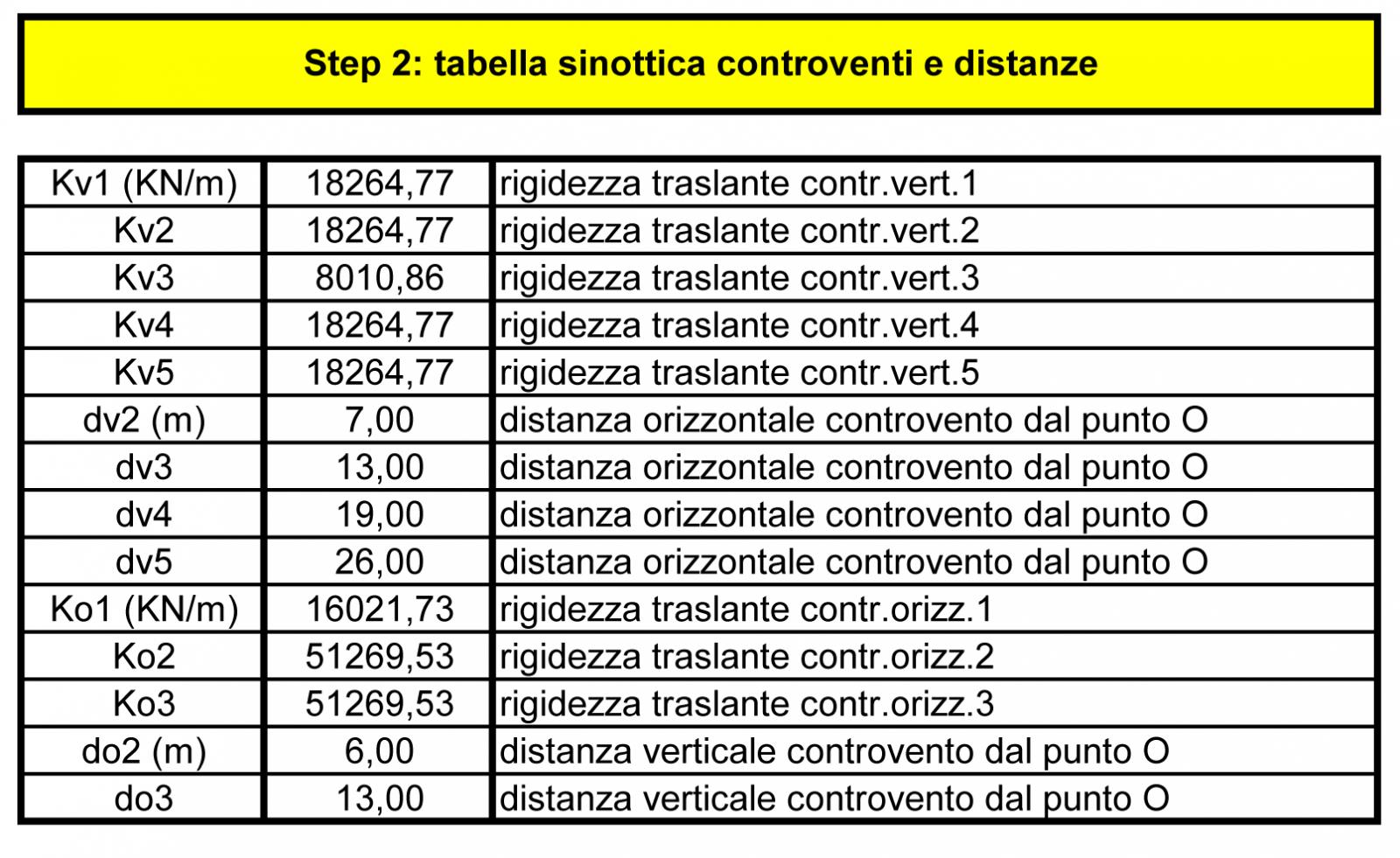
STEP 3: Calcolo del centro di massa
Per calcolare il centro di massa G, abbiamo diviso la struttura in tre aree, la più grande di 156 m2 e le due più piccole ed uguali di 49 m2. Successivamente abbiamo inserito nella tabella la misura di ogni superficie e le coordinate dei relativi baricentri, tenendo sempre contro dell’origine O come riferimento.
Le coordinate del centro di massa G (Xg, Yg) vengono calcolate in questo modo:
Xg = (A1 x Xg1+ A2 x Xg2 + A3 x Xg3) / (A1 + A2 + A3)
Yg = (A1 x Yg1+ A2 x Yg2 + A3 x Yg3) / (A1 + A2 + A3)
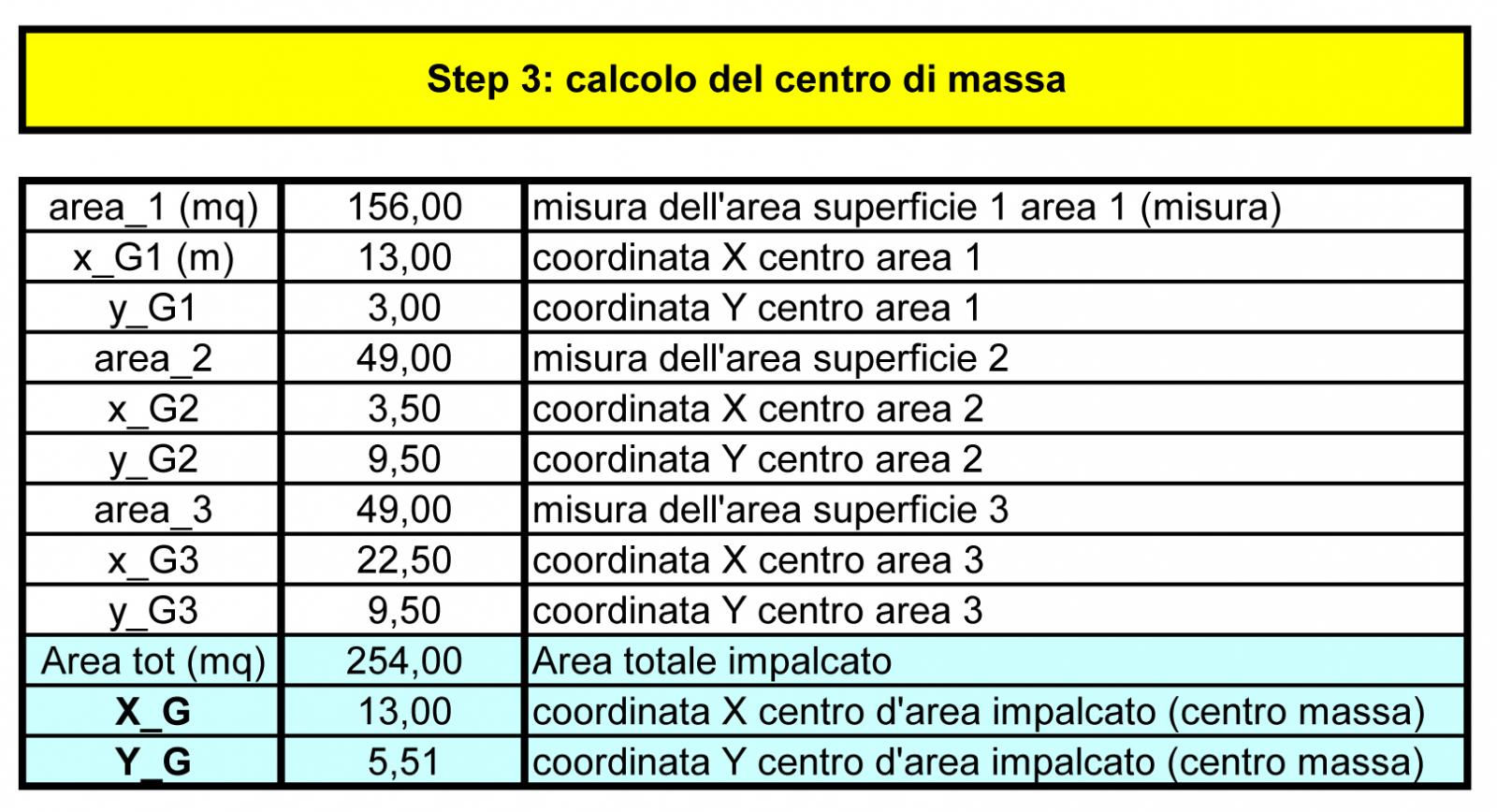
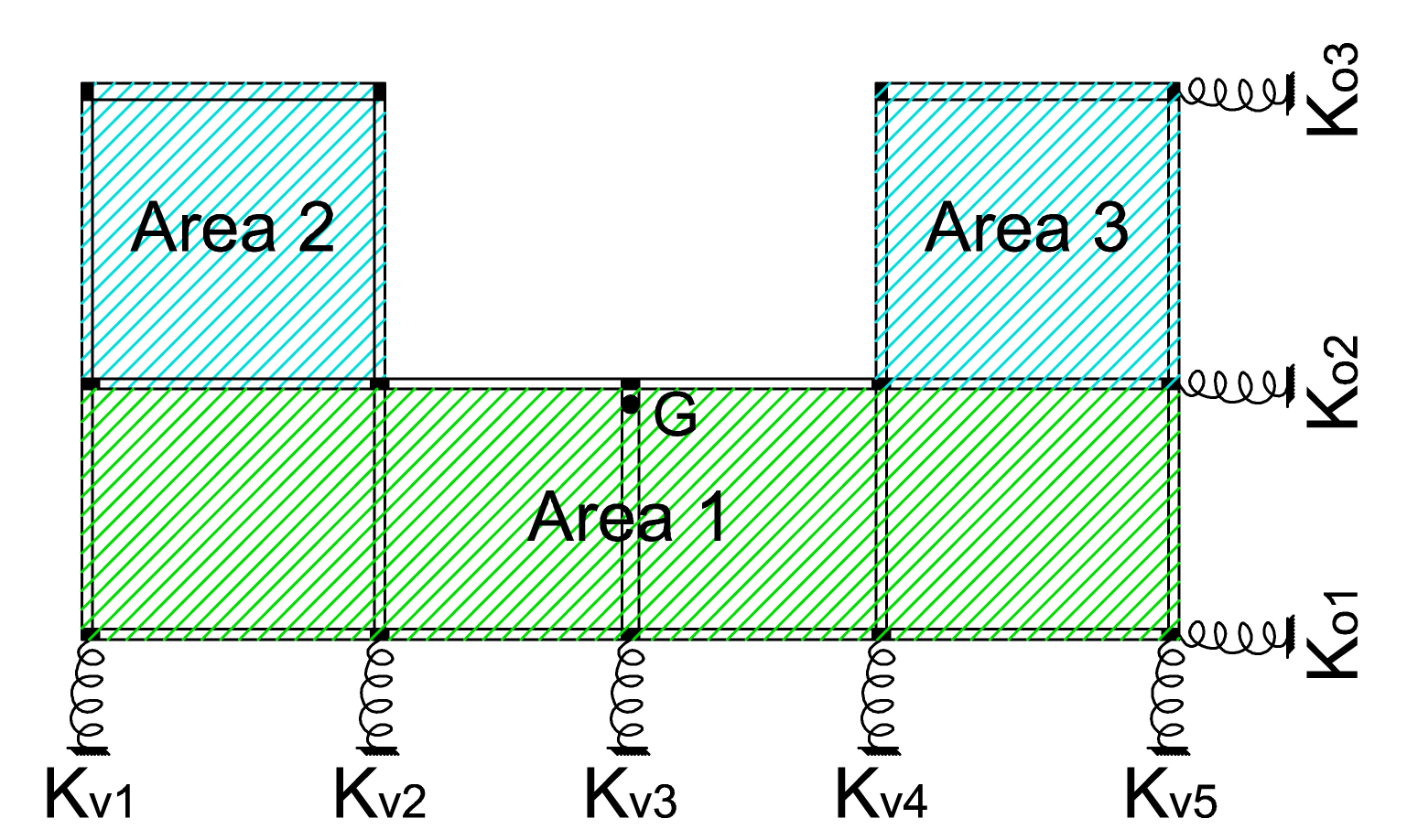
STEP 4: Calcolo del centro di rigidezze e delle rigidezze globali
A questo punto la tabella trova il centro delle rigidezze C, ovvero il punto in cui ruota la struttura se nasce un momento, grazie a queste equazioni:
Xc = Σi Kv x dv / Kv tot
Yc = Σi Ko x do / Ko tot
Bisogna calcolare il centro di massa perché la forza sismica è proprio applicata in questo punto!
In seguito vengono calcolate le distanze di ogni controvento dal centro delle rigidezze e infine la rigidezza torsionale totale eseguendo la sommatoria di ogni rigidezza moltiplicata per la distanza al quadrato dal centro delle rigidezze: KΦ= Σi Ki x ddi2.
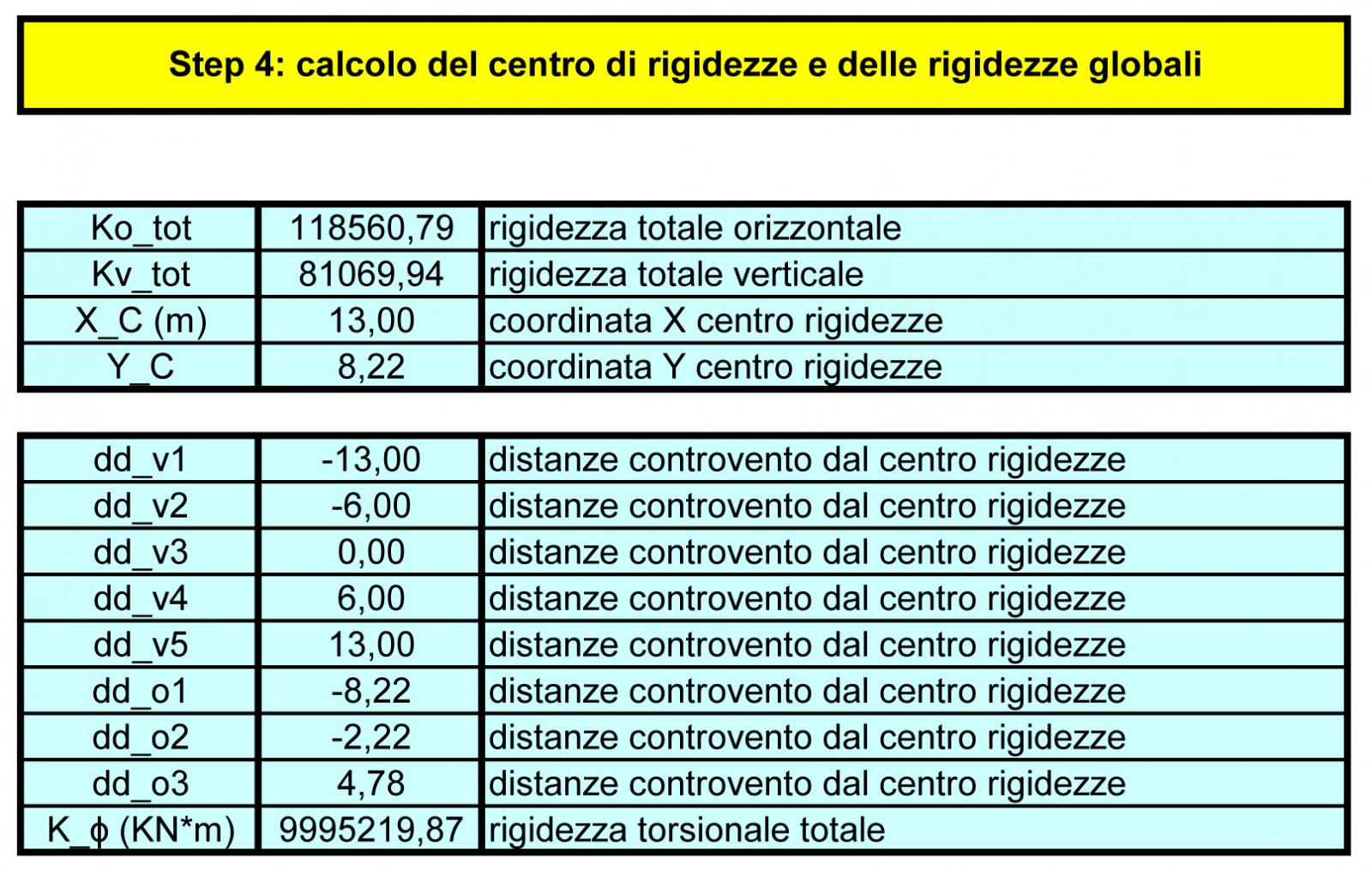
STEP 5: Analisi dei carichi sismici
Per calcolare la forza sismica bisogna fare il prodotto della massa dell’edificio per l’accelerazione di trascinamento del suolo: F = m x a.
a = c x g (dove c è il coefficiente di intensità sismica (minore di 1, da normativa) e g è l’accelerazione gravitazionale pari a 9,81 m/sec2 ).
Quindi F = m x c x g = c x (mg) = c x P (dove P è il peso della struttura)
P (o W) si trova sommando il peso proprio della struttura più il sovraccarico permanente più il sovraccarico accidentale (legato alla funzione) moltiplicato per un coefficiente di contemporaneità Ψ (generalmente pari a 0,80).
Ora, attraverso l’individuazione di questi valori che sono obbligatori da normativa, si procede con il calcolo della Forza Sismica Orizzontale, che nella nostra struttura è pari a 167, 64 KN.
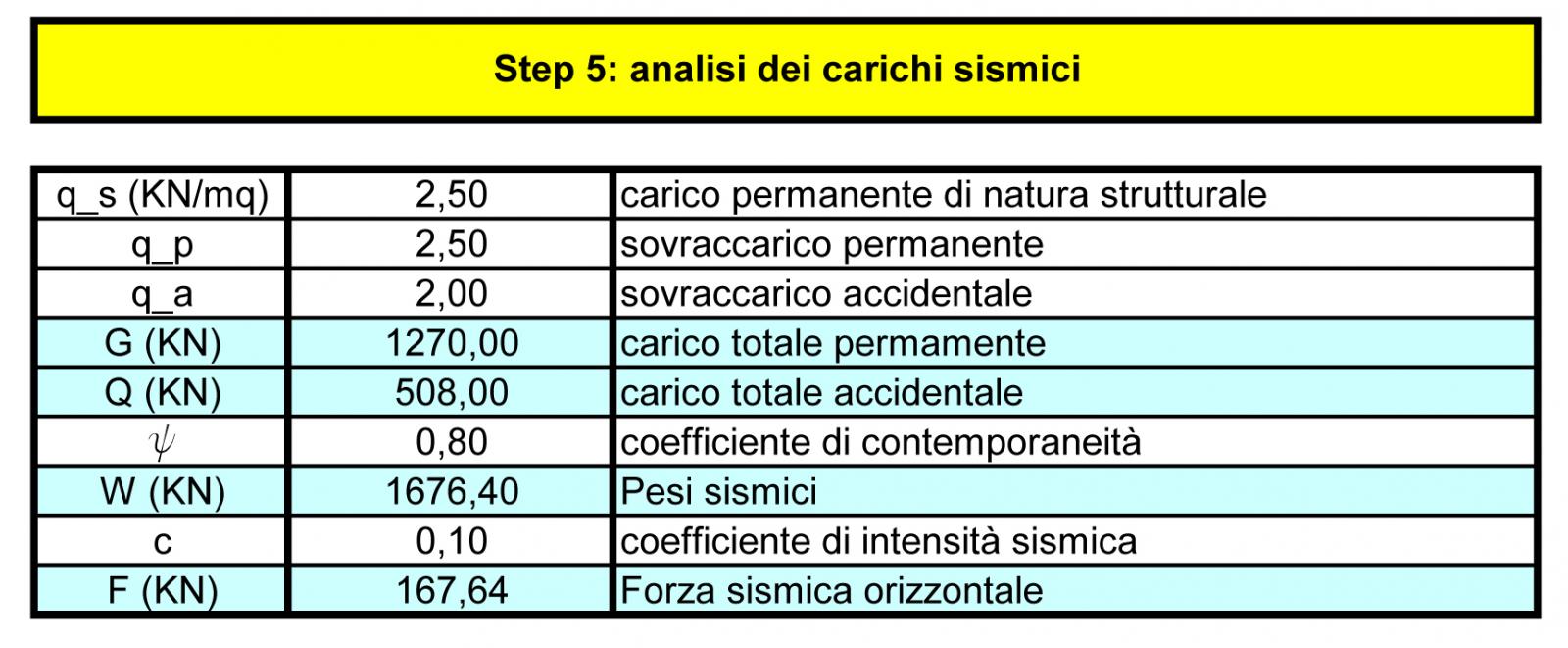
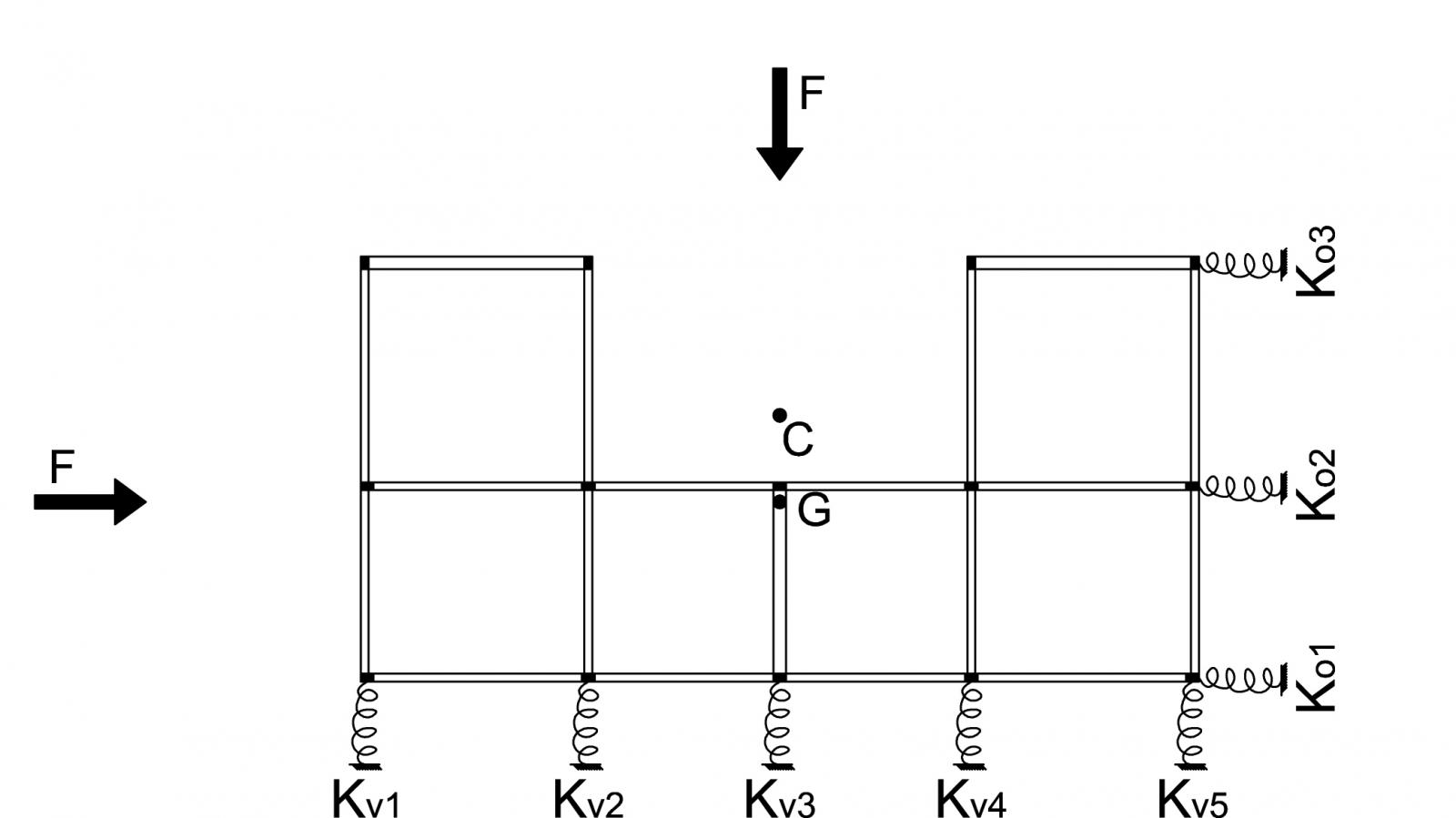
STEP6 – STEP7: Ripartizione della forza sismica lungo x e lungo y
Essendo il sisma un evento aleatorio, bisogna verificare la struttura almeno su due direzioni verticale e orizzontale che sono perpendicolari tra loro. La forza sismica inoltre è applicata nel centro di massa G, che molto spesso non coincide con il centro delle rigidezze C. Questo provoca una torsione della struttura in quanto si genera un braccio tra i punti G e C. Maggiore sarà il braccio e maggiore sarà la rotazione dell’impalcato.
Per quanto riguarda il nostro impalcato i punti C e G si trovano lungo lo stesso asse verticale: quindi per l’azione di una forza verticale non si genera alcuna rotazione ma solo una traslazione. Invece per l’azione di una forza orizzontale, dato che i punti C e G non coincidono ma hanno una distanza di 2,71 m, provocheranno una rotazione antioraria della struttura.
La tabelle 6 e 7 calcolano il momento torcente della struttura, le traslazioni e le rotazioni secondo le due direzioni perpendicolari.
La traslazione (sia verticale che orizzontale) si calcola così: F/ K tot
La rotazione ϕ sarà uguale a Fb / Kϕtot
Dopo aver verificato i precedenti valori, è possibile calcolare come la forza sismica si ripartisce su ogni controvento in entrambe le direzioni.
Controventi orizzontali: Rio= Kio x (uo + ϕdio)
Controventi verticali: Riv= Kiv x (ϕdiv)
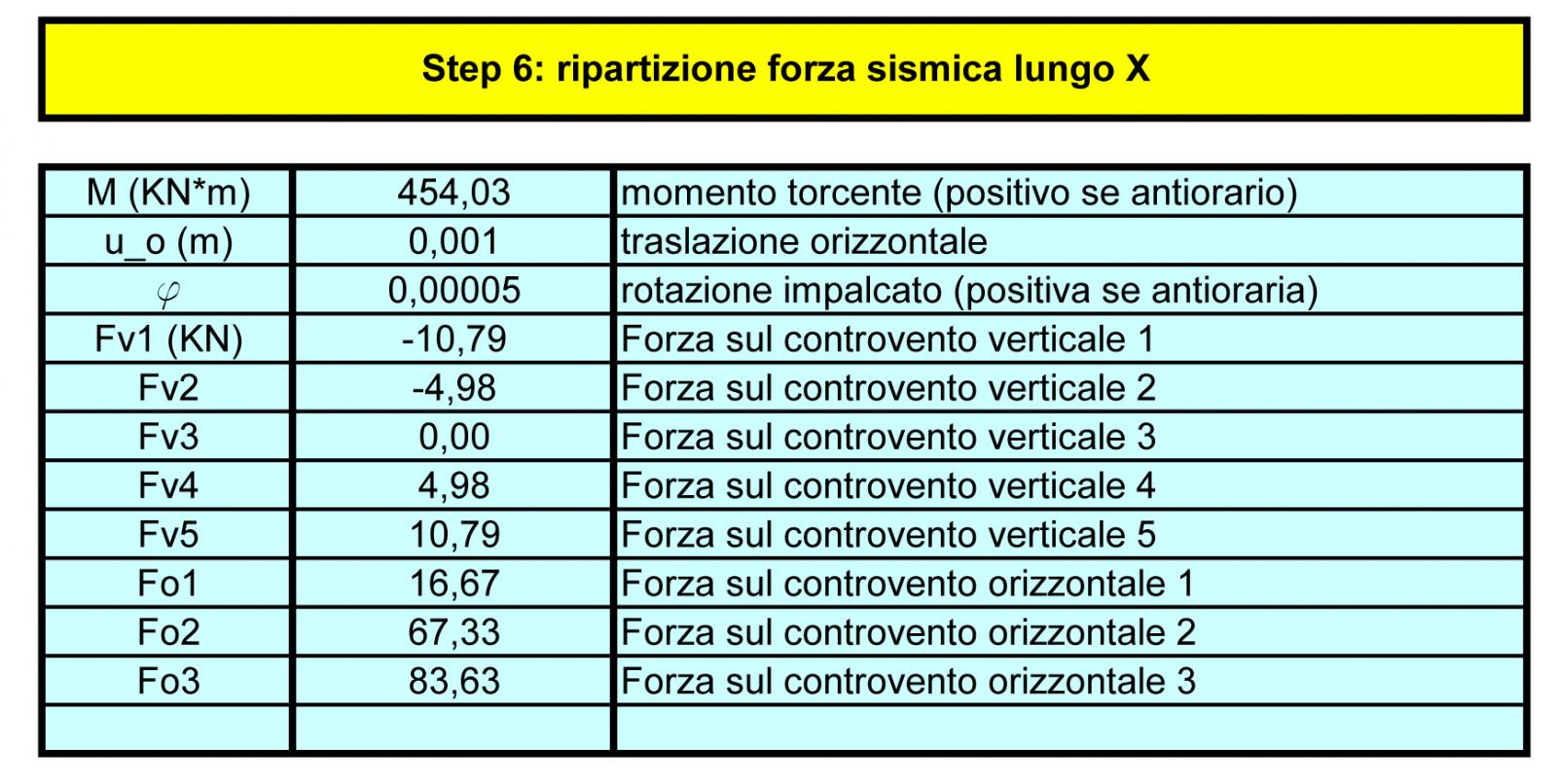
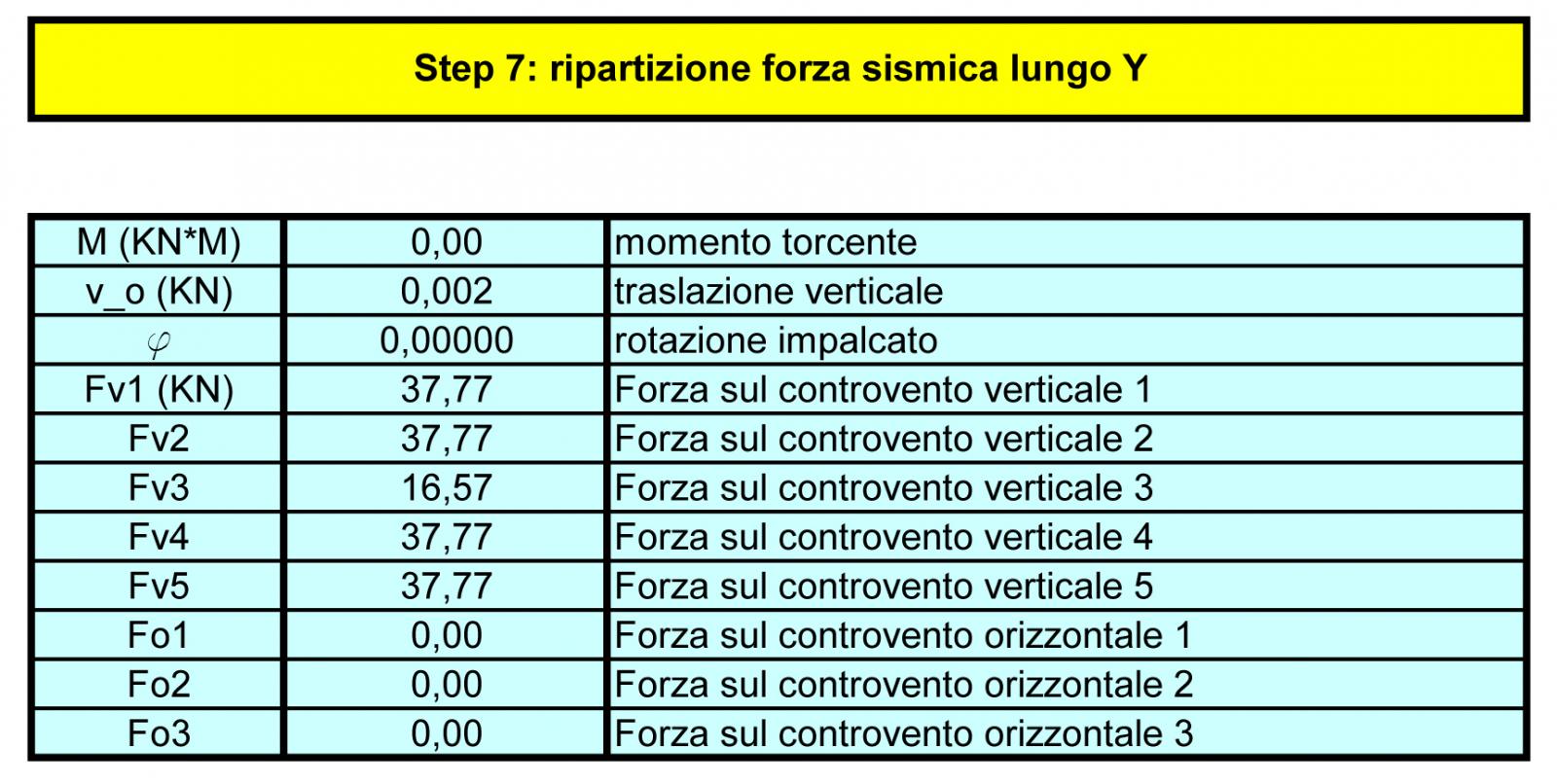
Se volessimo progettare la stessa struttura in acciaio dovremmo sostituire il modulo di elasticità E= 210000 N/mm2 e modificare i momenti d’inerzia in base ai profili scelti.
Il comportamento ad arco
“L’arco è la somma di due debolezze” (cit. Leonardo Da Vinci)
L’arco è un tipo di struttura che reagisce per forma alle sollecitazioni. Questo tipo di strutture (come il reticolare) tendono a lavorare per lo più a sforzo normale centrato, ciò permette loro di reagire con sezioni ottimizzate dal punto di vista del materiale.
L’arco trasforma i carichi prevalentemente in sforzo normale o addirittura solo in sforzo normale. Di solito il taglio e il momento flettente sono presenti in minima parte.
Il comportamento di un arco cambia a seconda della sua freccia (f), ovvero la distanza tra l’imposta dell’arco e la chiave di volta: più un arco è ribassato e maggiore sarà la sua spinta (H) sul terreno o sul suo appoggio. Da ciò si deduce che più un arco ha una freccia minore e più si comporta come un vero arco, cioè prevalentemente a sforzo normale.
Detto questo, l’arco perfetto è quello che trasforma tutto il carico in sforzo normale, ovvero l’arco parabolico. Effettivamente la parabola è proprio la forma che prendono le catene sulle quali vengono distribuiti uniformemente dei pesi (teoria dell’arco catenario).
La spinta dell’arco talvolta rappresenta un problema per l’intera struttura. Sin dall’antichità si sono cercati dei metodi per eliminare questo problema:
· Prevedere dei contrafforti;
· Aumentare il peso in corrispondenza dell’imposta dell’arco comporta un aumento del momento stabilizzante (Ms) in contrapposizione con il momento ribaltante (Mr);
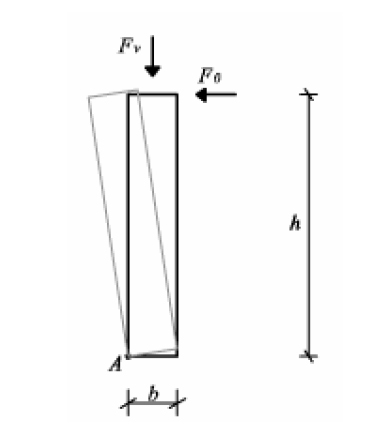 Ms= Fv * b/2 Mr= Fo*h
Ms= Fv * b/2 Mr= Fo*h
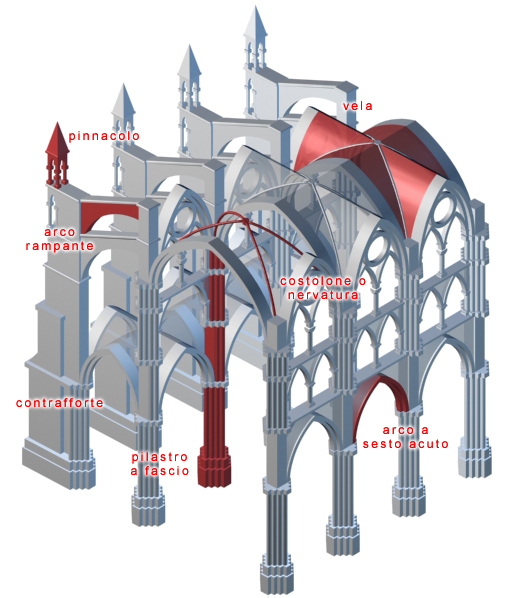

Schema di funzionamento di una cattedrale gotica Palazzo dello sport, Roma - Pierluigi Nervi
· Accostare più archi uno dopo l’altro in modo tale da compensare le spinte, anche se il problema si porrà poi nei supporti posti alle estremità;

Acquedotto di Vanvitelli, Maddaloni
· Costruire degli archi con catene che collegano le due imposte (archi a spinta eliminata);
Portico di San Giacomo, Bologna
· Prevedere delle mensole in prossimità degli appoggi che contribuiscano con il loro momento di incastro;
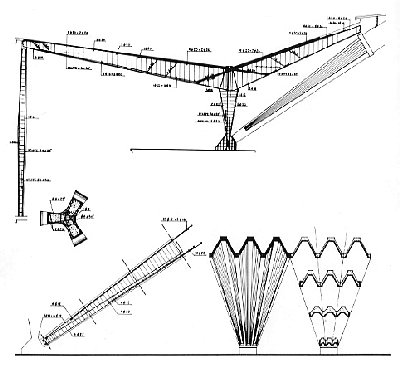
Palazzo dello sport, Roma - Pierluigi Nervi


Commenti recenti