Calcolo struttura reticolare simmetrica con il metodo delle sezioni di Ritter
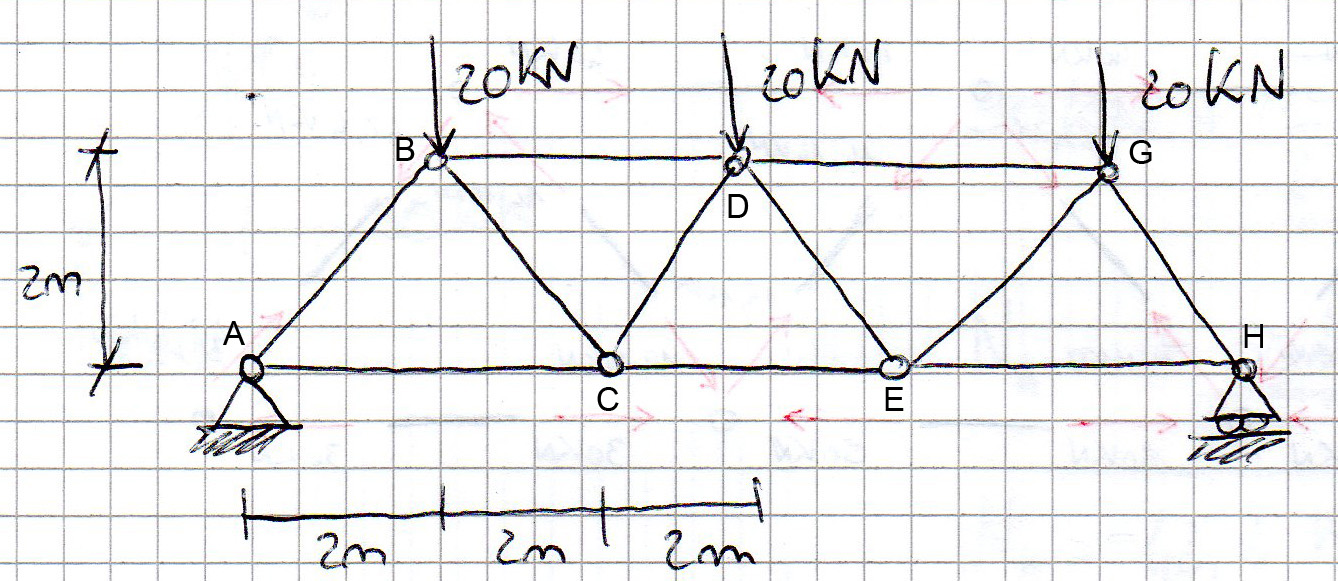
Ci troviamo di fronte ad una struttura reticolare, una struttura formata da elementi lineari, collegati da cerniere, soggetti a solo sforzo normale.
Passo 1
Per prima cosa dobbiamo verificare se la struttura è isostatica. Per fare ciò dobbiamo vedere se il numero dei vincoli è uguale al numero dei gradi di libertà della struttura.
Il numero di gradi di libertà è dato dal numero di aste presenti nella struttura moltiplicato per il numero di gradi di libertà di ogni elemento.
l = 11 (aste) x3 (gradi di libertà) =33
Il numero dei vincoli è dato dalla somma dei vincoli interni e esterni.
V = Ve + Vi
I vincoli esterni sono 3: la cerniera blocca 2 gradi di libertà, il carrello blocca la traslazione verticale perciò un grado di libertà.
Per calcolare i vincoli interni utilizziamo la formula: Vi = 2*(n -1) dove n è il numero di aste che arrivano alla cerniera interna. Calcoliamo perciò il contributo di ogni cerniera:
A-H --> 2*(2-1) = 2
B-G --> 2*(3-1) = 4
C-D-E --> 2*(4-1) = 6
La sommatoria dei vincoli interni sarà perciò: Vi = 2+2+4+4+6+6+6 = 30, che sommata ai vincoli esterni Ve = 3 dà V = 33
Perciò: V(33) = l(33) VERIFICATO!
Bene, ora abbiamo verificato l' isostaticità della struttura, passiamo al calcolo delle reazioni vincolari:
Passo 2
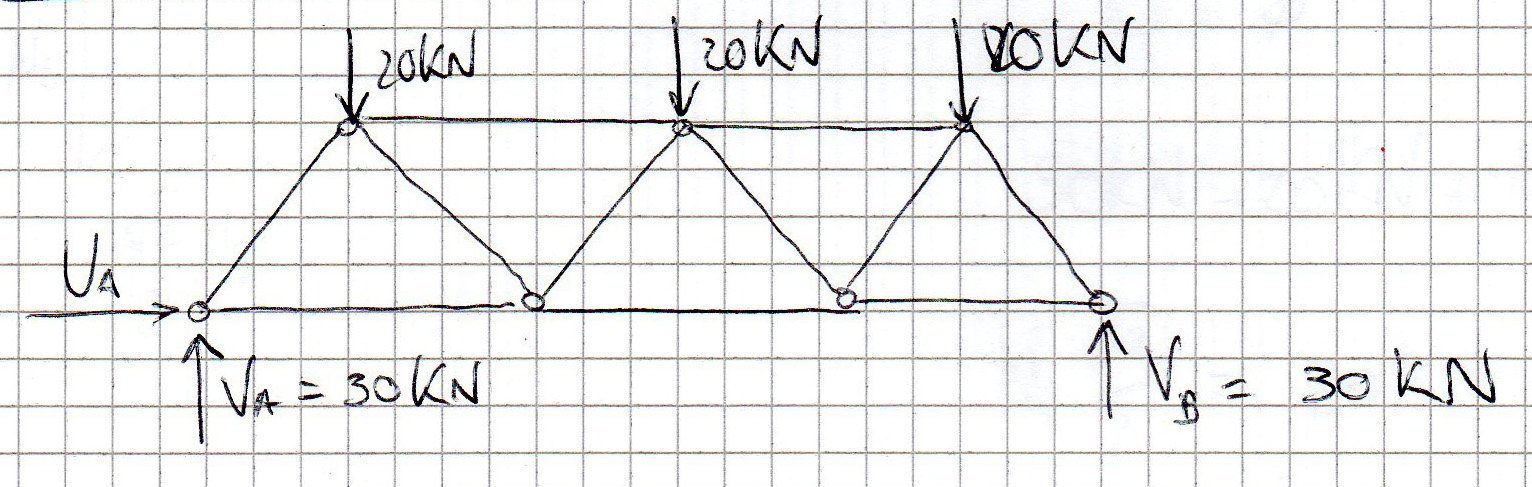
Equilibrio alla traslazione orizzontale: UA = 0
Equilibrio alla traslazione verticale: VA + VB - 60 kN = 0
Essendo simmetrica la struttura: VA = VB = 30 kN
Passo 3: Metodo delle sezioni di Ritter
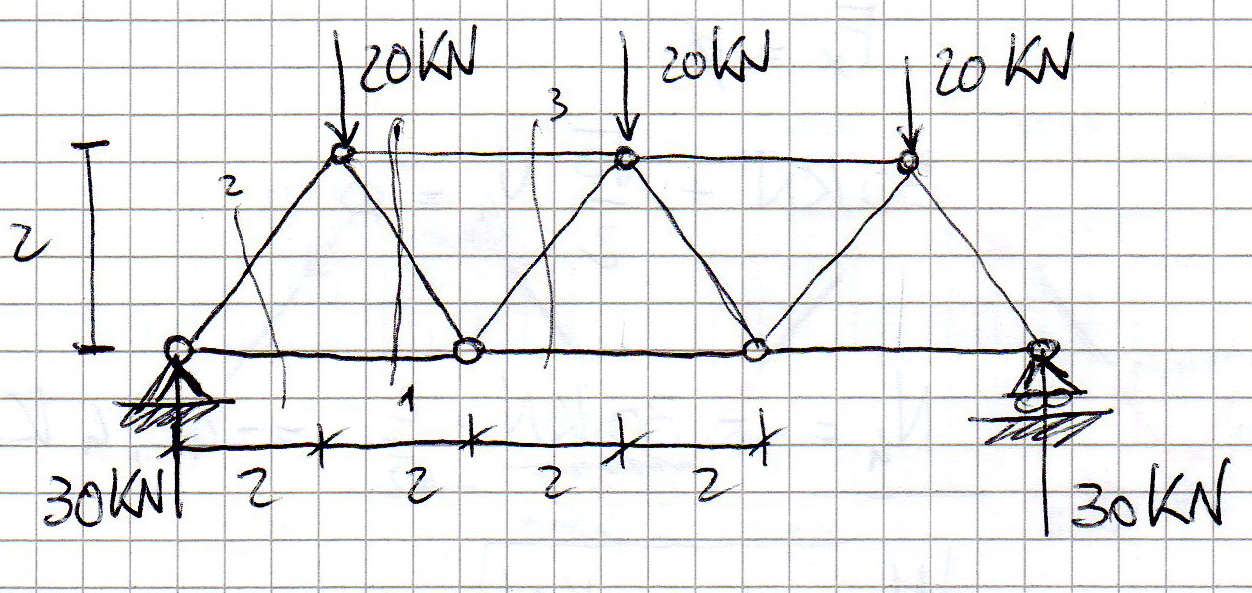
A questo punto utilizzando il metodo delle sezioni di Ritter calcoliamo gli sforzi assiali nelle singole aste.
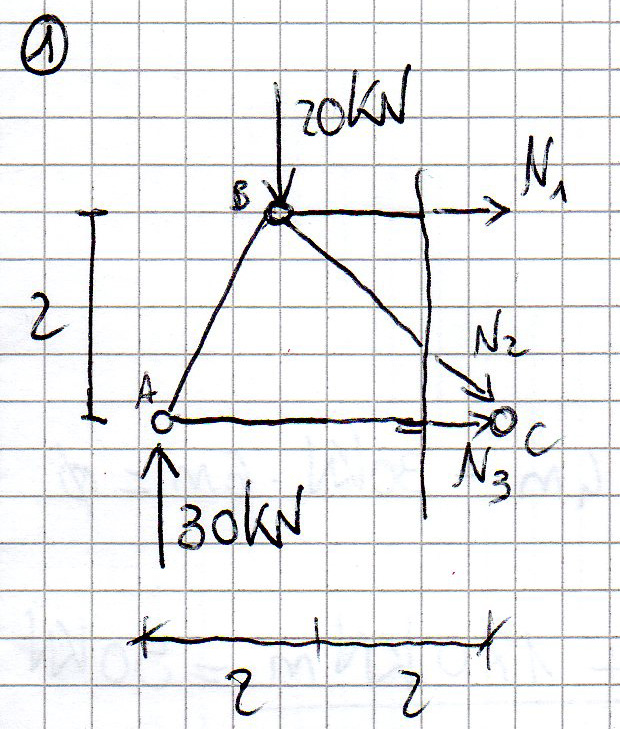
Faccio l' equilibrio alla rotazione nel nodo C: -120 kNm + 40 kNm - 2N1 = 0 ----> N1 = -40 kN
Equilibrio alla rotazione in B: -30 kN * 2 m + 2m * N3 = 0 ----> N3 = 30 kN
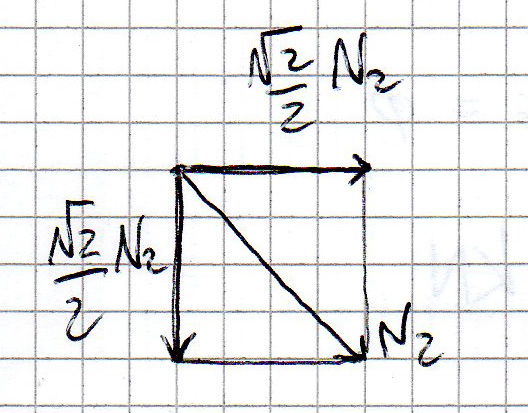
Per calcolare N2 faccio l' equilibrio alla traslazione verticale considerando la componente verticale di N2:
30 kN - 20 kN - N2 * radice2/2 = 0 -----> N2 = 14,14 kN
Passiamo ora alla sezione n° 2:
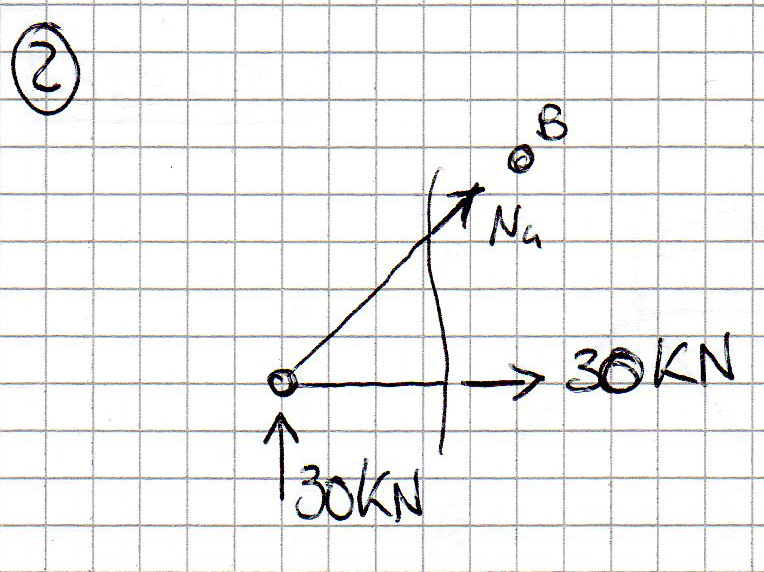
Faccio l' equilibrio alla traslazione orizzontale per calcolare N4:
30 kN + radice2/2 N4 = 0 ----> N4 = -42,4 kN

Faccio l' equilibrio alla rotazione in D: N5*2m + 20 kN*4m - 30 kN*6m = 0 -----> N5 = 50 kN
Faccio ora l' equilibrio alla traslazione verticale per calcolare la reazione restante N6:
30 kN - 20 kN + radice2/2*N6 = 0 ----> N6 = - 14,14 kN
Sfruttando le proprietà della simmetria riesco a disegnare tutte le reazioni nelle aste:

A questo punto posso verificare i risultati trovati tramite il software SAP2000:
- disegno la struttura
- assegno i carichi
- avvio l' analisi della struttura
Diagramma dello sforzo assiale:
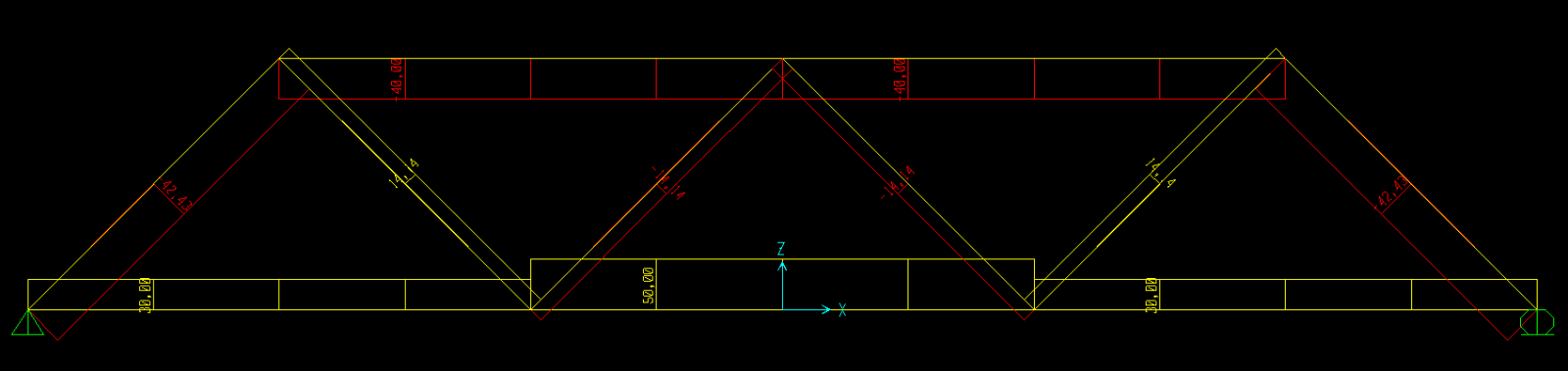

Commenti recenti