Questa esercitazione viene svolta con l’obiettivo di individuare il metodo di ripartizione di una forza orizzontale, come quella sismica e del vento, sui diversi telai che costituiscono una struttura, applicando il metodo delle rigidezze.
Si prende in considerazione un edificio generico ad un solo piano, in cui struttura è composta da telai piani che, oltre a trasmettere i carichi verticali alla fondazione, possono costituire dei controventi per le azioni orizzontali. In particolare, i telai piani che compongono tale struttura sono realizzati sul modello del telaio Shear-type. I telai Shear-Type sono un modello teorico che hanno la capacità di possedere travi infinitamente rigide, questo fa si che le estremità dei pilastri non possono ruotare. La rotazione impedita porta a deformare i pilastri stessi come travi doppiamente incastrate. In questo caso la deformata si avvicina alla deformata di una trave deformabile per solo taglio.
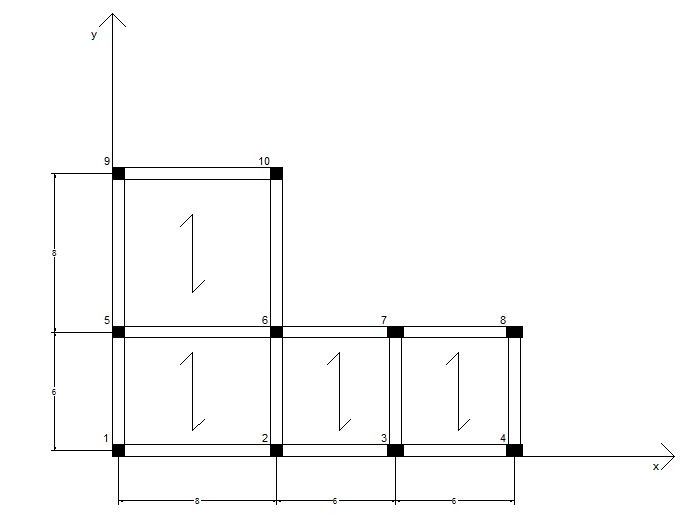
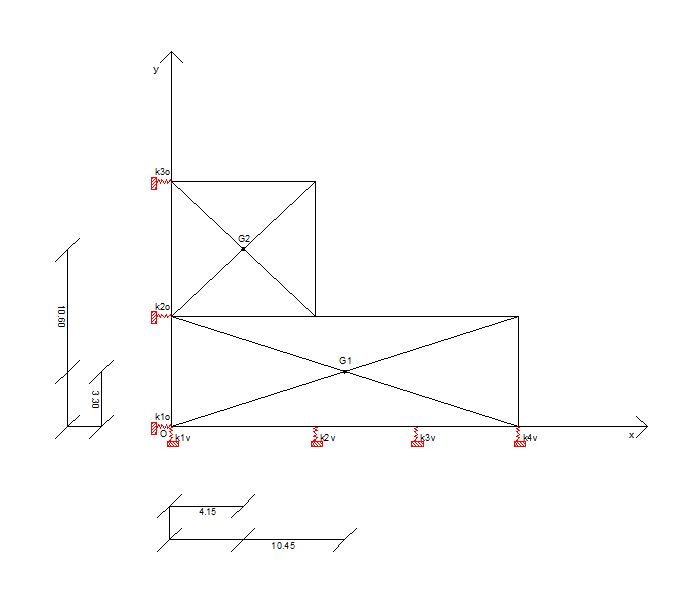
Nell’ impalcato in figura si individuano 7 telai, 3 paralleli all’asse x e quattro paralleli all’asse y.
- Telaio 1 verticale: pilastri 1-5-9
- Telaio 2 verticale: pilastri 2-6-10
- Telaio 3 verticale: pilastri 3-7
- Telaio 4 verticale: pilastri 4-8
- Telaio 1 orizzontale: pilastri 1-2-3-4
- Telaio 2 orizzontale: pilastri 5-6-7-8
- Telaio 3 orizzontale: pilastri 9-10
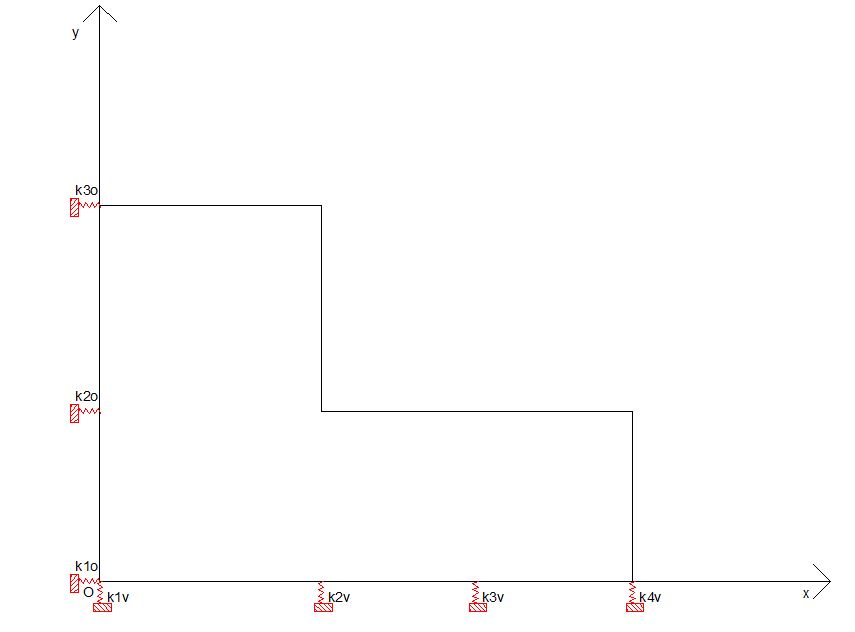
I controventi, che per il solaio rappresentano vincoli cedevoli elasticamente, possono essere schematizzati nel piano dell’impalcato come molle.
In tutta la struttura sono presenti due tipologie di pilastro, uno rettangolare di dimensioni 50x30 cm e uno quadrato di dimensioni 30x30 cm. Pertanto otterremo tre momenti di inerzia distinti (bh³/12), due per il pilastro rettangolare, uno rispetto ad x e l’altro rispetto ad y, e uno per il pilastro quadrato.
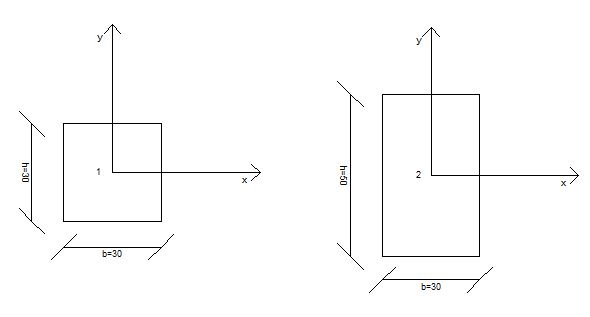
I₁xy= bh³/12= 67.500 cm⁴ I₂x= bh³/12= 31.2500 cm⁴ I₂y= b³h/12= 11.2500 cm⁴
Tramite la tabella excel, dopo aver inserito tutti i valori trovati dei diversi momenti d’inerzia, calcoliamo la rigidezza traslante associata a tutti i controventi, inserendo per ognuno di essi l’inerzia dei pilastri che lo compongono. Si parla di telai Shear type, pertanto, per trovare la rigidezza traslante di un telaio composto da n pilastri utilizziamo la formula:
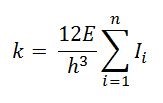
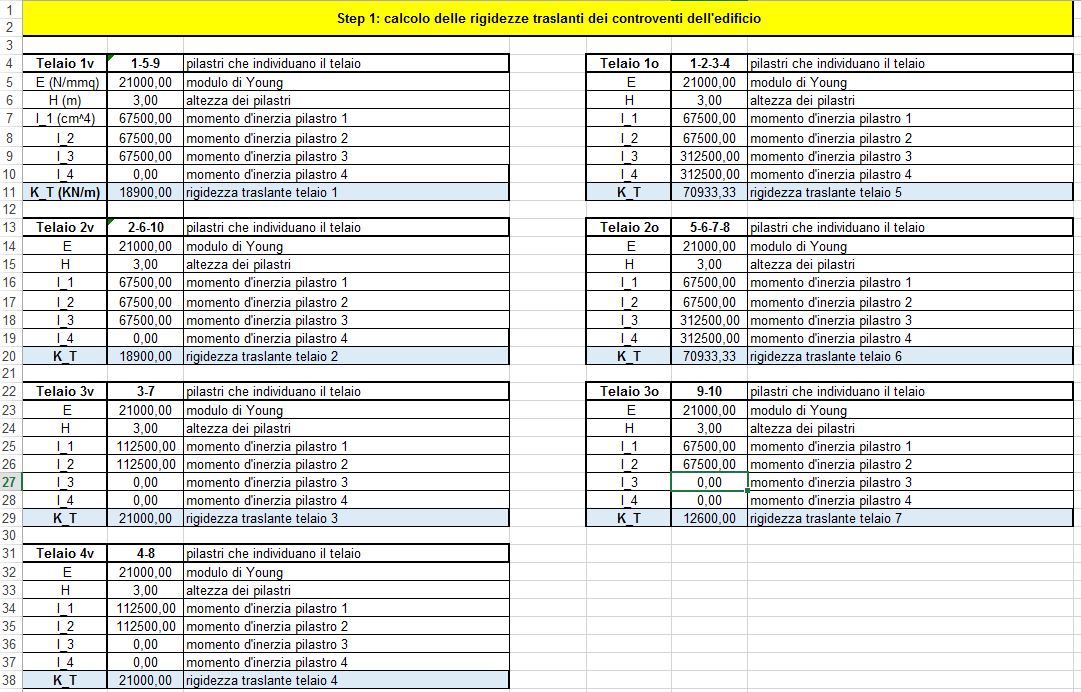
Si ottiene anche una tabella riassuntiva in cui vengono riportate le rigidezze di tutti i controventi calcolati precedentemente. Nella stessa tabella, si devono inserire le distanze di ogni controvento, calcolate da un’origine O arbitraria, che per comodità collochiamo nell’angolo in basso a sinistra dell’impalcato.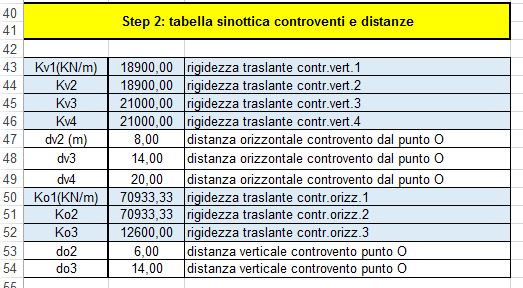
Si calcola ora il centro di massa dell’edificio, che corrisponde al centro delle aree dato che si considera l’impalcato con densità di massa uniforme, suddividendo la struttura in tre figure elementari di cui conosciamo il centro in modo intuitivo.
Per farlo utilizziamo la formula derivata da quella per ottenere le coordinate del centro di un sistema di vettori paralleli:
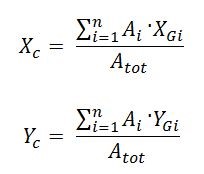
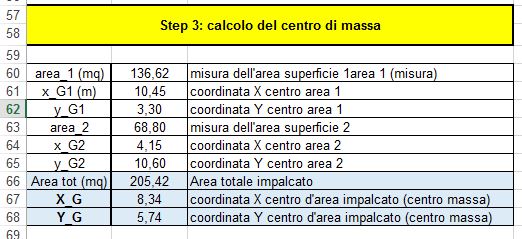
Giunti a questo punto, si calcola la rigidezza totale orizzontale, data dalla somma delle singole rigidezze dei controventi orizzontali, e la rigidezza totale verticale, data dalla somma delle singole rigidezze dei controventi verticali. Così sarà possibile calcolare il centro delle rigidezze riadattando la formula precedentemente utilizzata per il centro di massa, e la rigidezza torsionale totale.
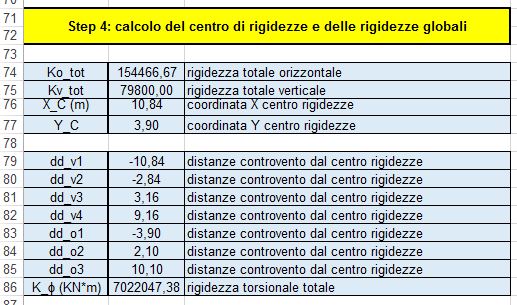
Si riesce così ad individuare sia il centro di massa G sia il centro delle rigidezze C, dell’intero impalcato.
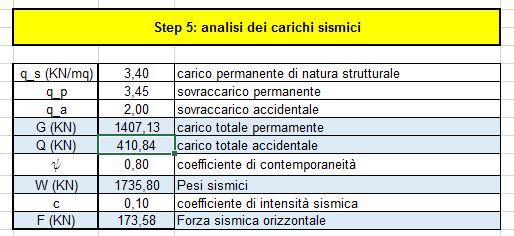
Si effettua l’analisi dei carichi sismici per ricavare la forza che agisce nel centro di massa. Si calcola il carico totale permanente (G) e accidentale (Q) del solaio, partendo dal valore dei carichi per unità di superficie [kN/mq] e utilizzando le seguenti formule:
G = (qs + qu) Atot Q = qa Atot
In accordo con la normativa tecnica si utilizza la combinazione sismica per calcolare i pesi sismici:
W = G + ψ2j · Q in cui ψ rappresenta il coefficiente di contemporaneità indicato dalla normativa.
F = W c moltiplicando W, ossia il peso sismico, per un coefficiente di intensità sismica c che tiene conto della sismicità del luogo di progettazione dell’edificio, si ottiene F, la forza sismica da applicare al centro di massa.
Ora si considera l’azione della forza sismica lungo x e poi lungo y. Si trova lo spostamento orizzontale, verticale e la rotazione tramite le seguenti formule:
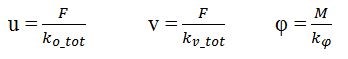
Ora che abbiamo tale forza la andiamo ad applicare nel centro d’area creando 2 casi:
- forza applicata in direzione x, che comporterà ad possibile rotazione e traslazione orizzontale dell’impalcato
- forza applicata in direzione y, che comporterà ad possibile rotazione e traslazione verticale dell’impalcato

Commenti recenti