Con l’intenzione di ideare una struttura che si applicasse allo schizzo volumetrico, ho pensato di modellare una struttura reticolare a piramide rovesciata. Il modello simula la struttura di un edificio a due piani, nella quale il volume superiore scarichi sui nodi del volume inferiore. Per sfruttare al meglio la travatura reticolare, infatti, facendo in modo che le aste siano soggette solo a sforzo normale, è necessario che ne siano caricati solo i nodi.
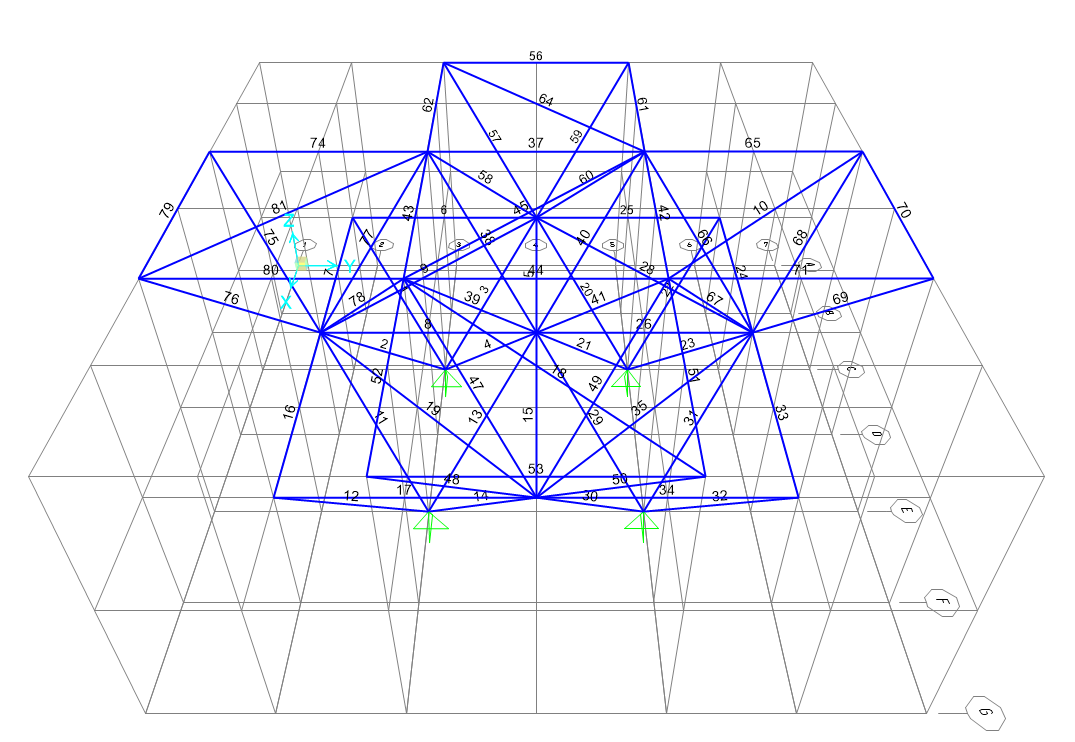
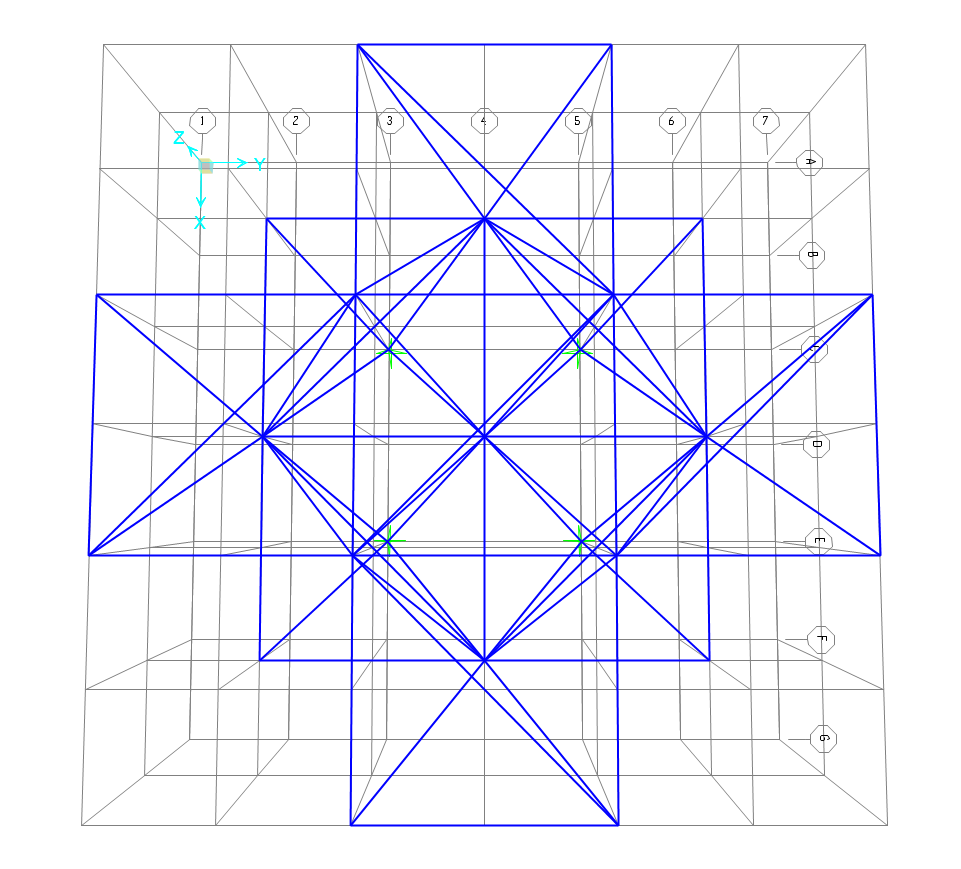
Per cominciare, ho modellato la struttura su una griglia di 7x7x3, con interassi orizzontali (x,y) di 3m e interasse interpiano (z) di 4m. In aggiunta alle aste che disegnano gli spigoli della piramide, ho aggiunto un’asta di controventamento alla base, per far sì che ne risultasse una struttura isostatica, non labile, composta da un sistema di triangoli.
Una volta modellata la struttura, ho assegnato agli appoggi inferiori una cerniera sferica.
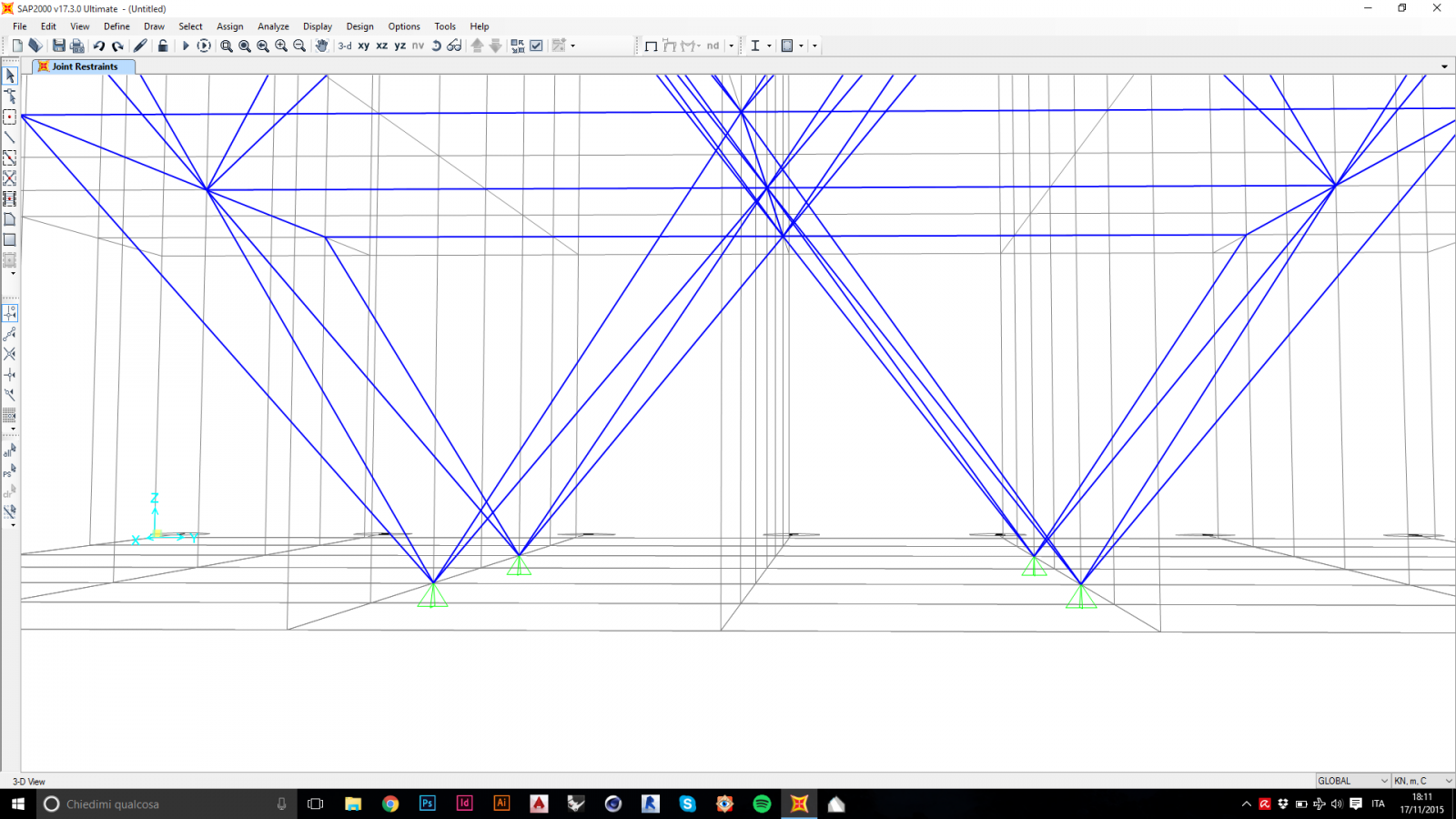
Sempre perché ne risultasse una struttura reticolare, è necessario che le cerniere interne che collegano le aste non trasmettano momento, ma solo sforzi assiali. Di conseguenza ho assegnato a tutte le aste un rilascio dei momenti ad entrambi gli estremi delle aste.
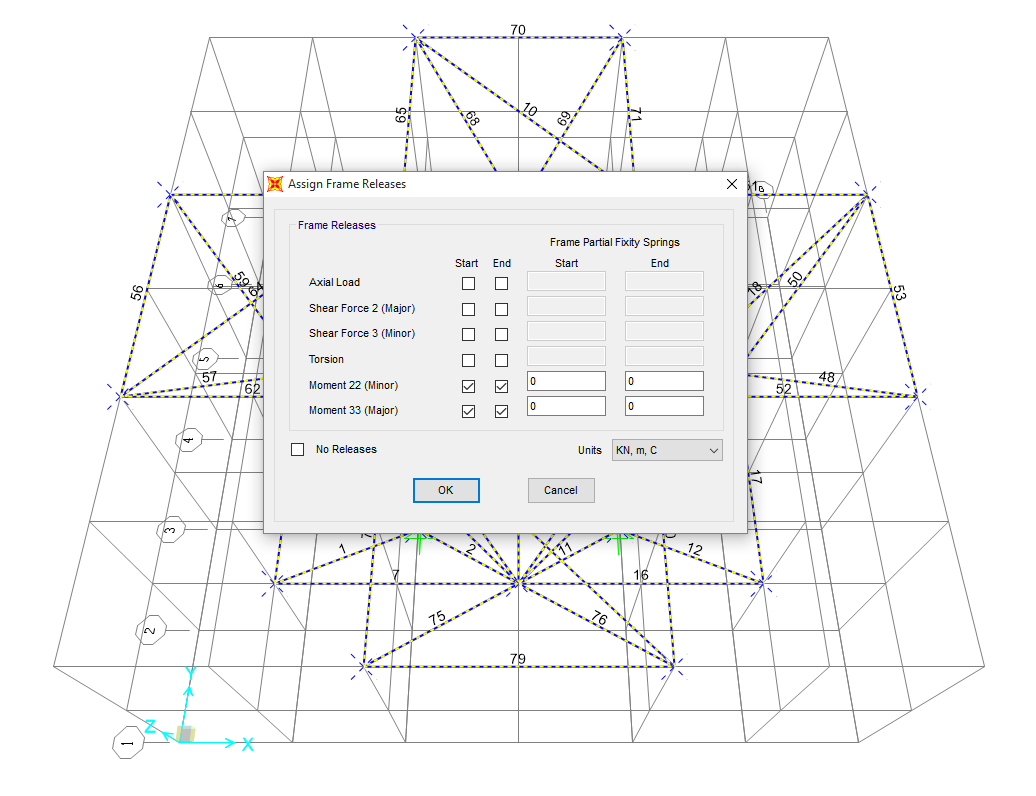
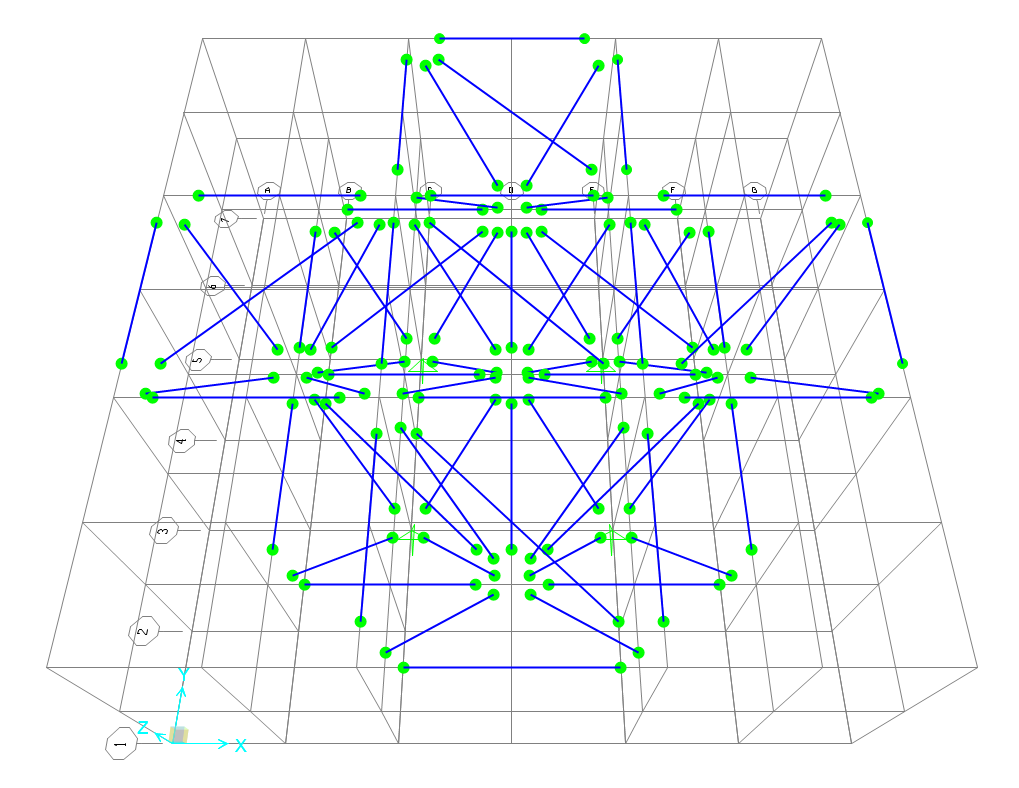
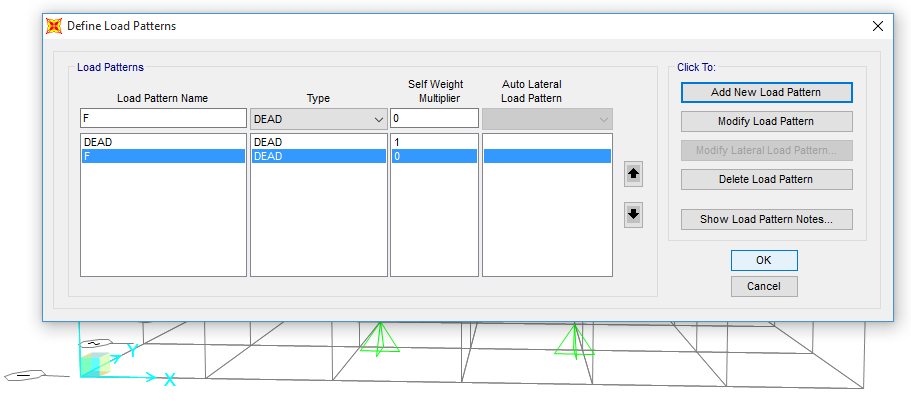
Per l’assegnazione dei carichi, nella riduzione dei vari carichi distribuiti sul solaio e del solaio stesso a forze concentrate, ho fatto una semplice stima proporzionale senza una effettiva corrispondenza dei valori: sulla base dell’analisi delle aree di influenza dei singoli nodi, ho assegnato carichi di 25,50,75 e 100 KN, dopo aver definito un load pattern (F) che non consideri il peso proprio della struttura.
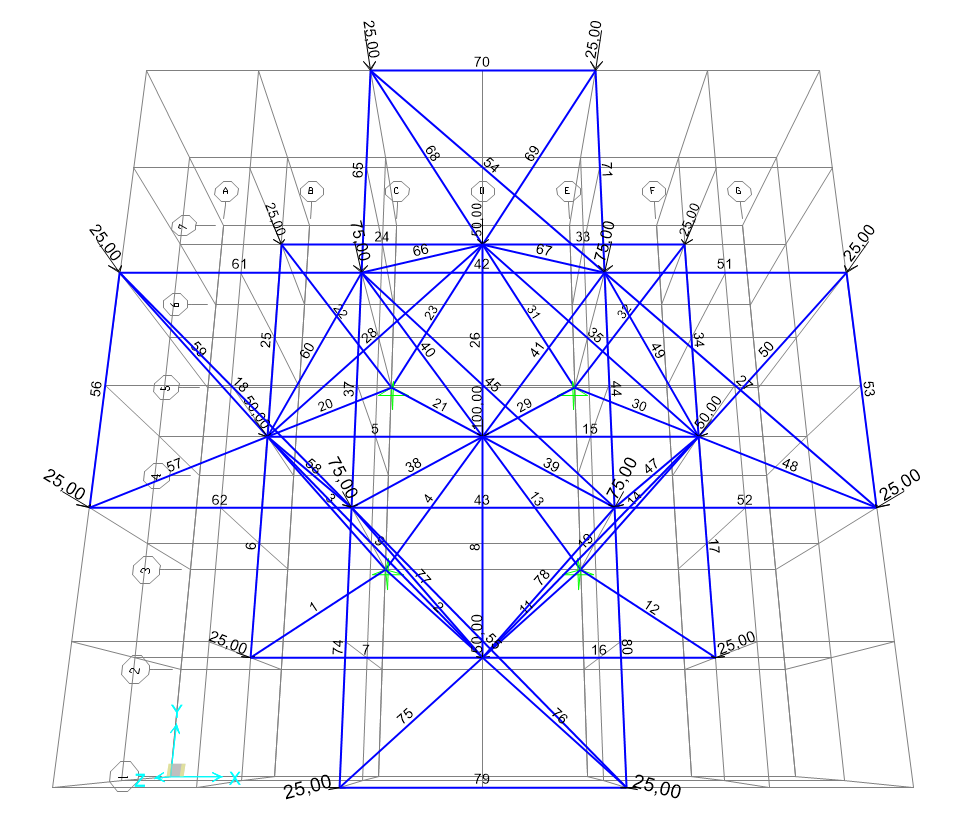
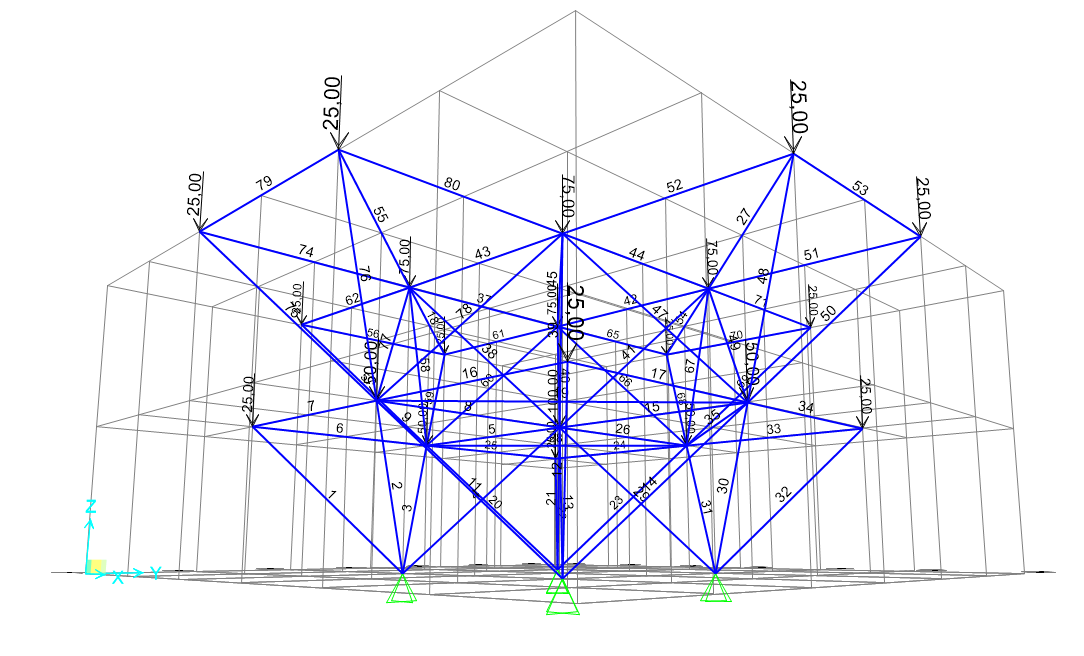
Definita la geometria della struttura, i vincoli e i carichi, è il momento di passare all’analisi delle sollecitazioni; a questo fine, ho escluso dall’analisi il carico statico che tiene conto del peso proprio della struttura e il carico modale, considerando solo il load pattern da me definito.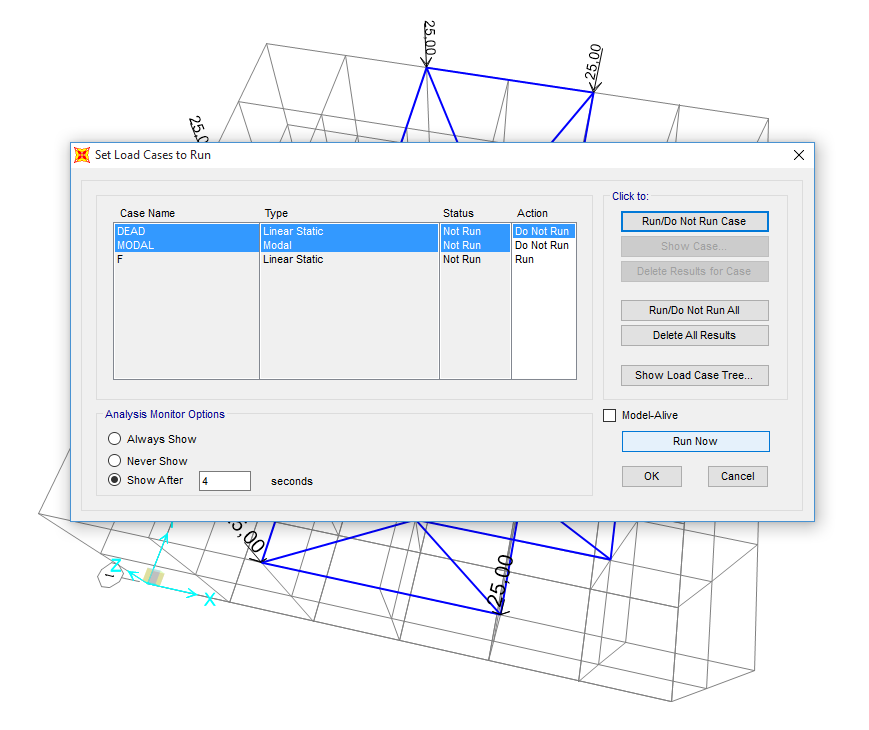
Come primo output, l’analisi restituisce la deformata, che per ora non ci interessa, non avendo ancora definito né materiale né profilato.
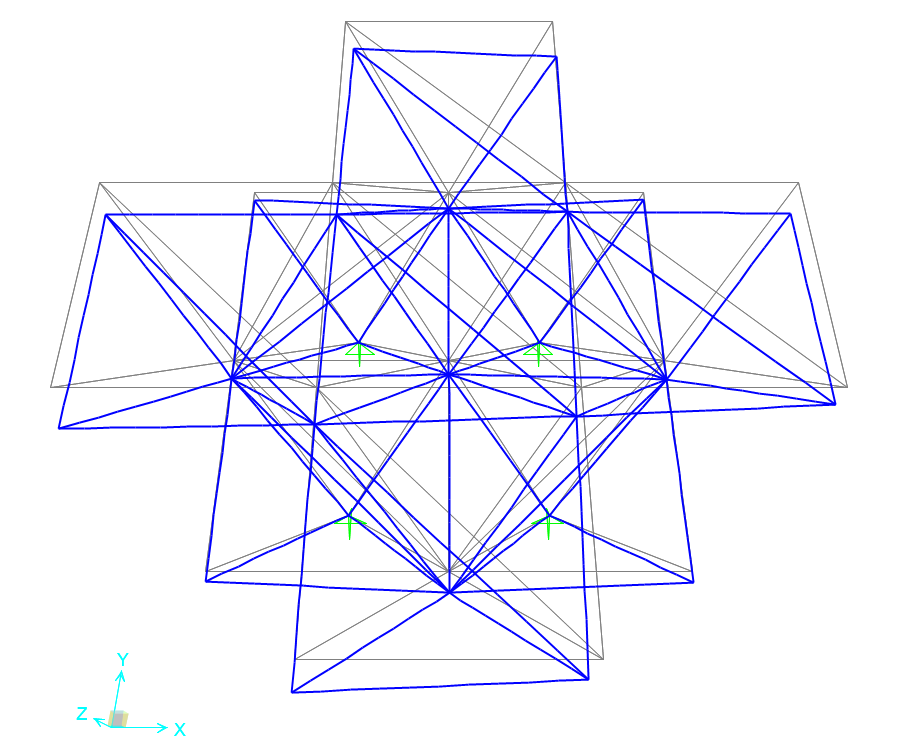
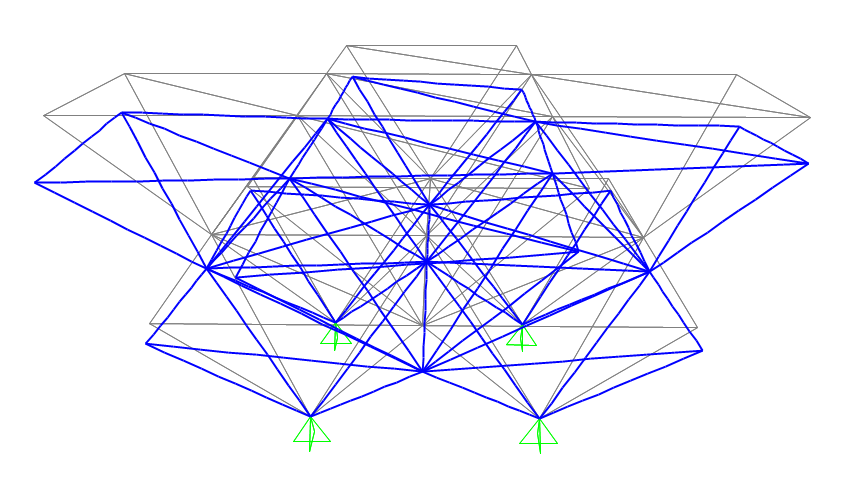
Dopo aver verificato che lo sforzo flessionale è nullo su tutte le aste, impostando la visualizzazione dello sforzo assiale, possiamo vedere come tutte le aste inclinate che compongono gli spigoli verticali delle piramidi risultino compresse, mentre le aste che ne compongono la base siano tese.
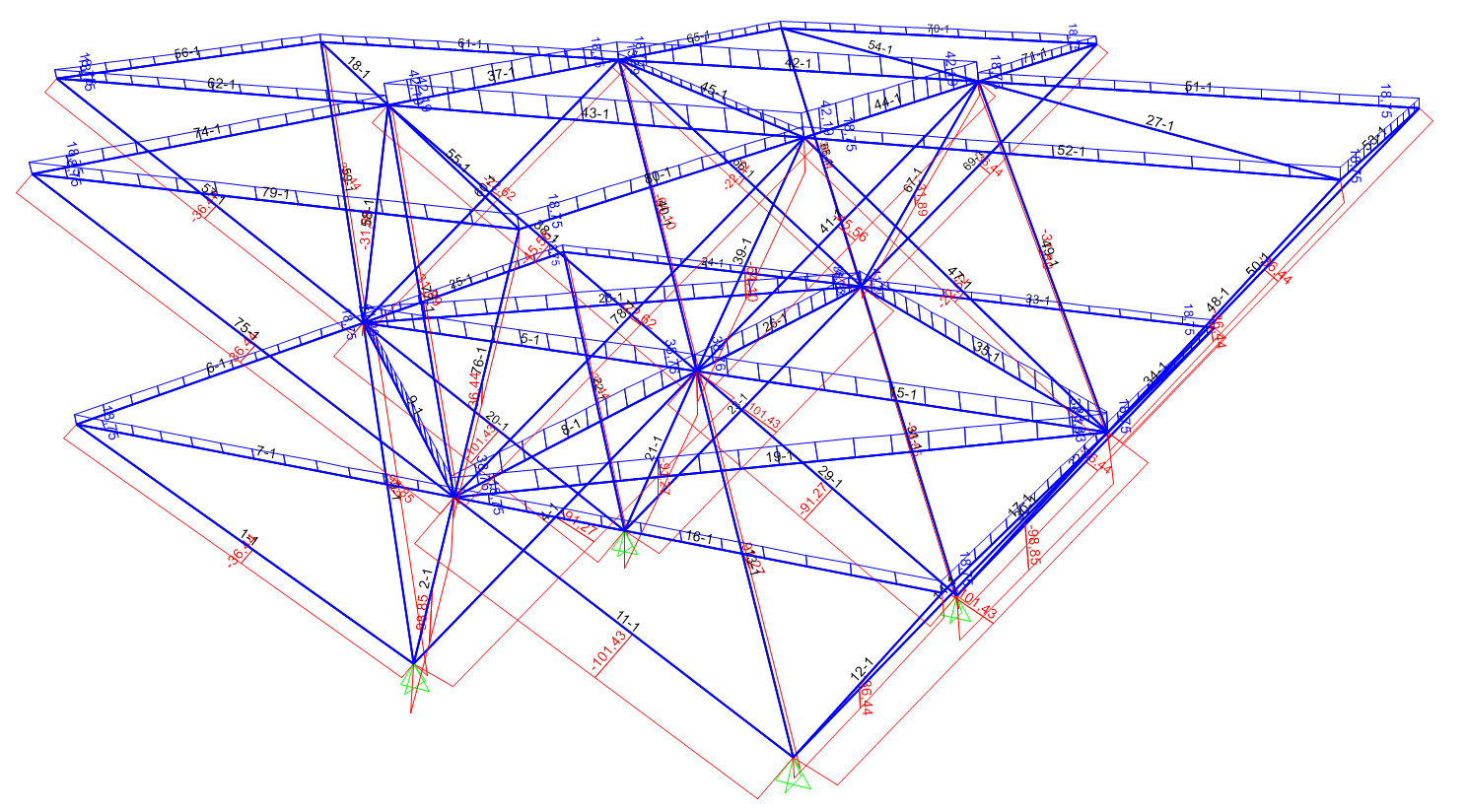
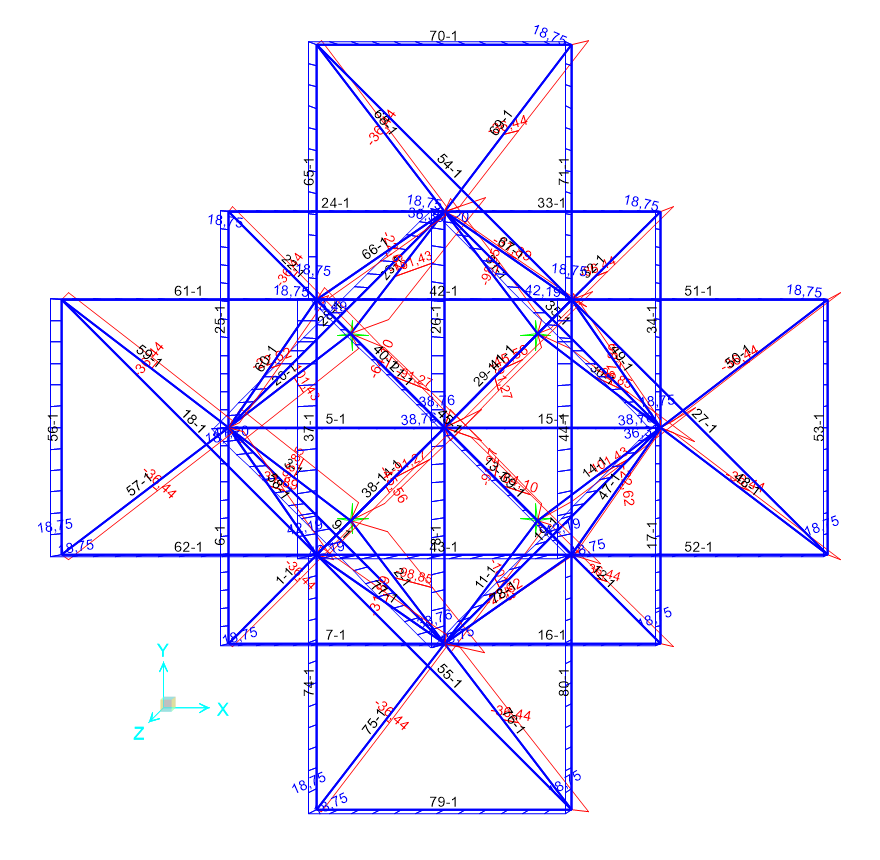
A questo punto, ho mostrato la tabella relativa agli output dei singoli elementi della struttura (display>show table>analysis results>element output), selezionando solo il load pattern che mi interessava (F), per poi esportarla in formato Excel.
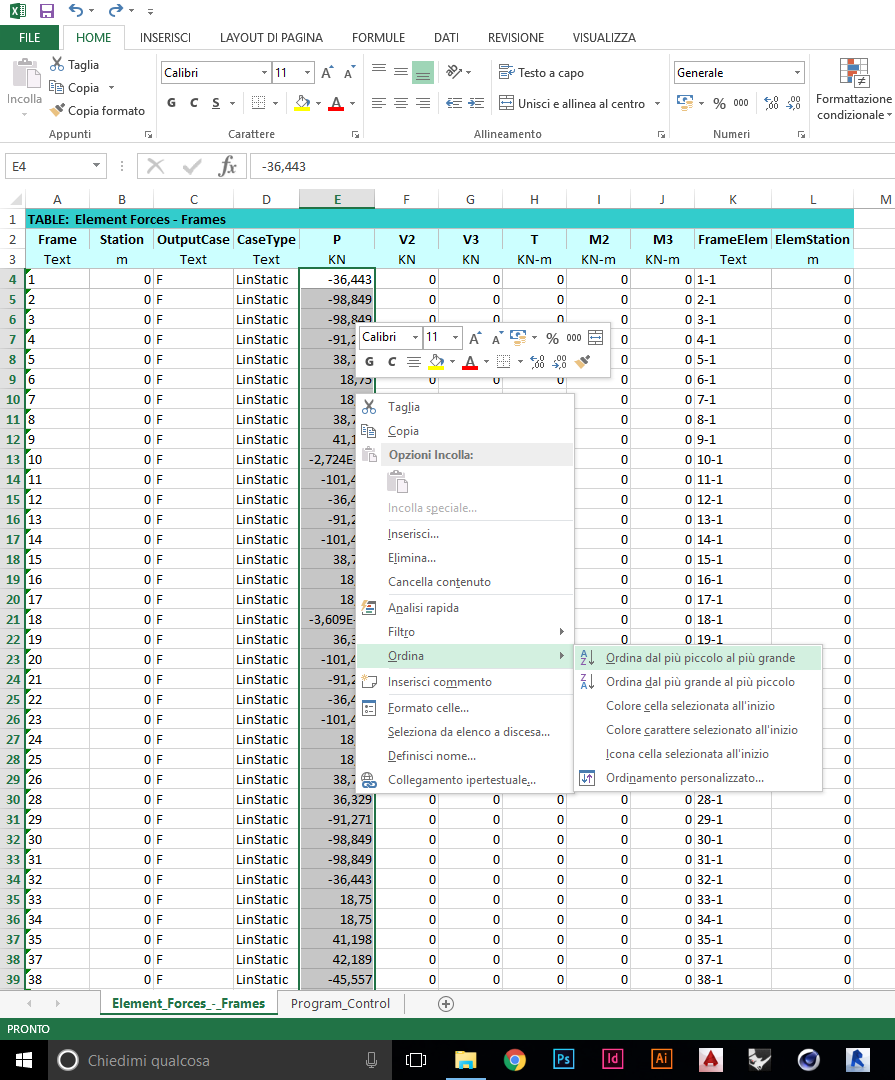
Per ogni frame, SAP fornisce i dati relativi a diverse ‘station’; tuttavia, poiché con carichi concentrati lo sforzo assiale delle aste di una reticolare risulta costante su tutto il tratto, possiamo considerare solo l’estremo finale di ogni asta, in modo, inoltre, da mantenere come dato la lunghezza delle stesse, per il successivo dimensionamento. Per farlo, usiamo lo strumento ‘ordina’ di Excel.
Eliminati i dati superflui, ho potuto ordinare le aste sulla base della sollecitazione assiale, in ordine crescente, e successivamente dividerle tra aste compresse (blu) e aste tese (rosse).
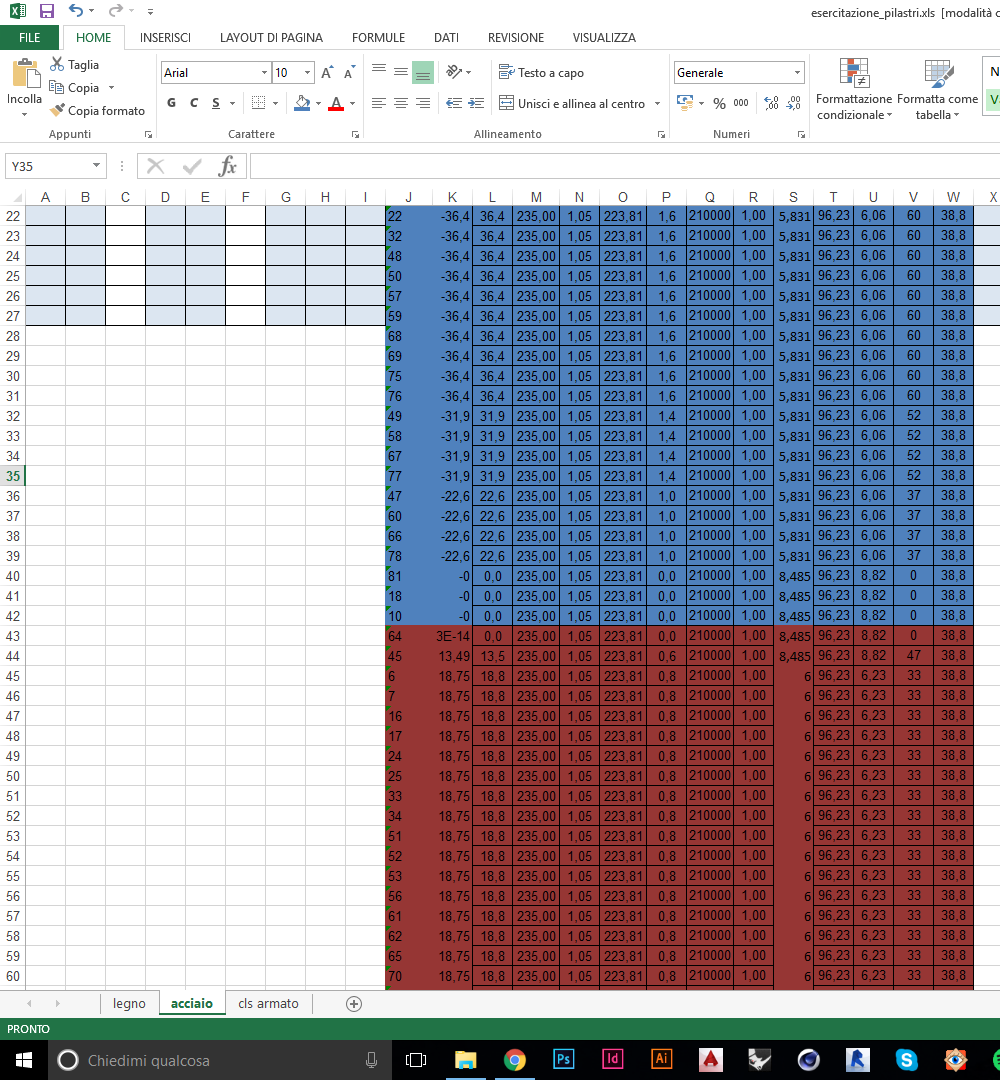
Per quanto riguarda le aste tese, il dimensionamento si limita al calcolo dell’area minima della sezione, sulla base della formula di Navier (s=N/A): la sollecitazione di progetto relativa ad ogni singola asta è già data e, una volta scelto l’acciaio (S235), i soli dati di cui ho bisogno sono la tensione caratteristica dell’acciaio (fyk=235 MPa) e il coefficiente di sicurezza (Y=1,05), grazie ai quali posso calcolare la tensione di progetto (fyd=223,81 MPa). L’area minima quindi non è che il rapporto tra la sollecitazione e la tensione di progetto.
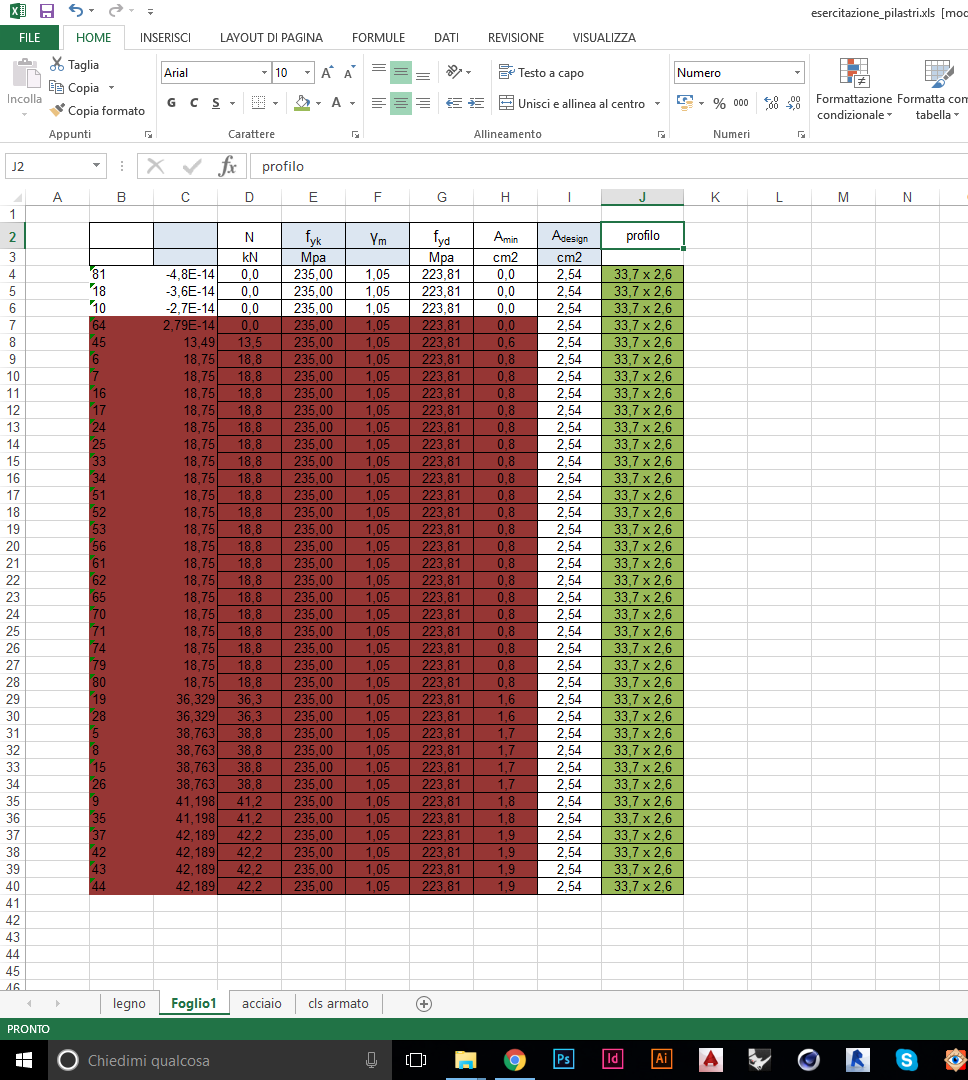
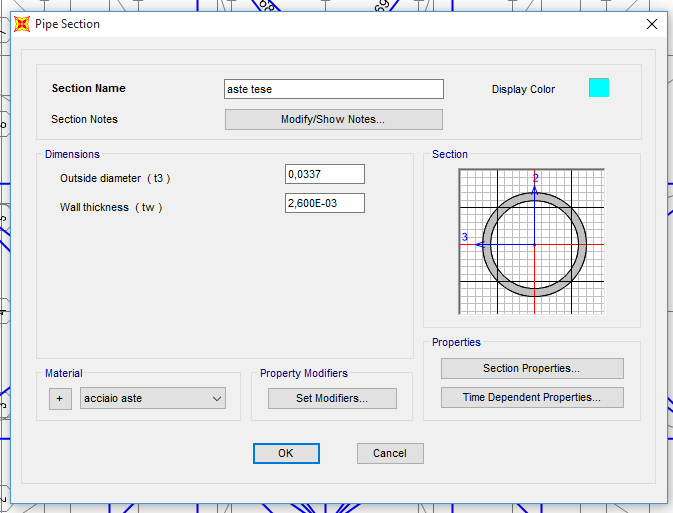
Dal foglio Excel risulta che l’area minima non supera mai gli 1,9 cm^2, per cui si può scegliere per tutte un unico profilato: 33,7mm x 2,6mm, con area 2,54 cm^2.
Quando le aste risultano, invece compresse, è necessario effettuare un’ulteriore e più restrittiva verifica di stabilità, per verificare che lo sforzo assiale di progetto non provochi tensioni superiori non solo alla tensione ammissibile, ma anche alla tensione critica eureliana, per la quale è possibile che si verifichino episodi di instabilità globale (‘svergolamento’).
Posta la lunghezza libera di inflessione uguale alla lunghezza effettiva delle aste (b=1), poiché si tratta di tutte aste incernierate, posso verificare che la snellezza sia inferiore alla snellezza critica, derivata a partire dalla formula sviluppata da Eulero per il calcolo della tensione critica (l<lcr; lcr = π (E/fyd)1/2). Sulla base della snellezza critica, posso calcolare il giratore di inerzia e il momento di inerzia minimi affinché non si raggiunga lo stato di instabilità:
ρmin= l0 / λ*
Imin= Amin ρ2min
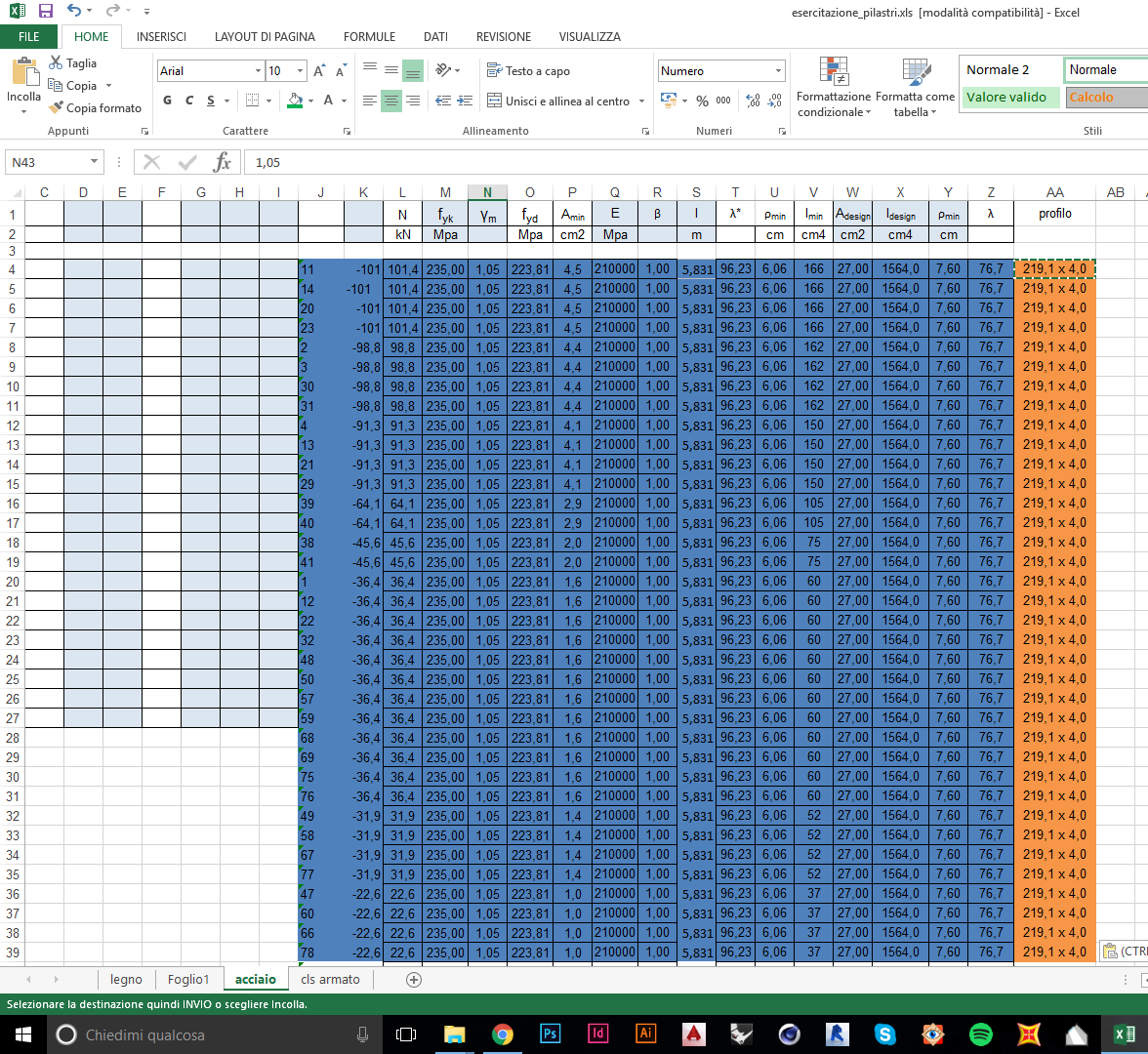
Nella scelta del profilato, è molto rilevante anche il valore della snellezza, che deve risultare inferiore alla snellezza critica, che dipende dall’acciaio scelto. Essendo le aste compresse molto lunghe, la dimensione geometrica più restrittiva risulta essere il giratore di inerzia, da cui dipende la snellezza.
λ=l/ρmin
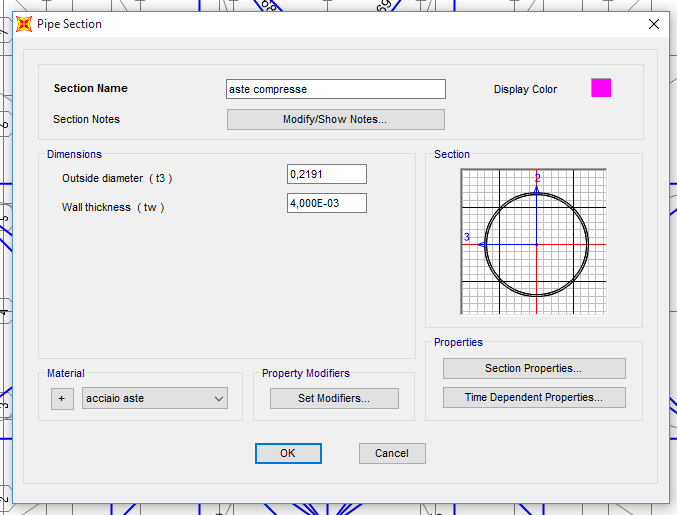
Poiché le aste compresse hanno una lunghezza quasi costante, tutte le aste risultano avere lo stesso profilato: 219,1 x 4,0, con area 27 cm^2.
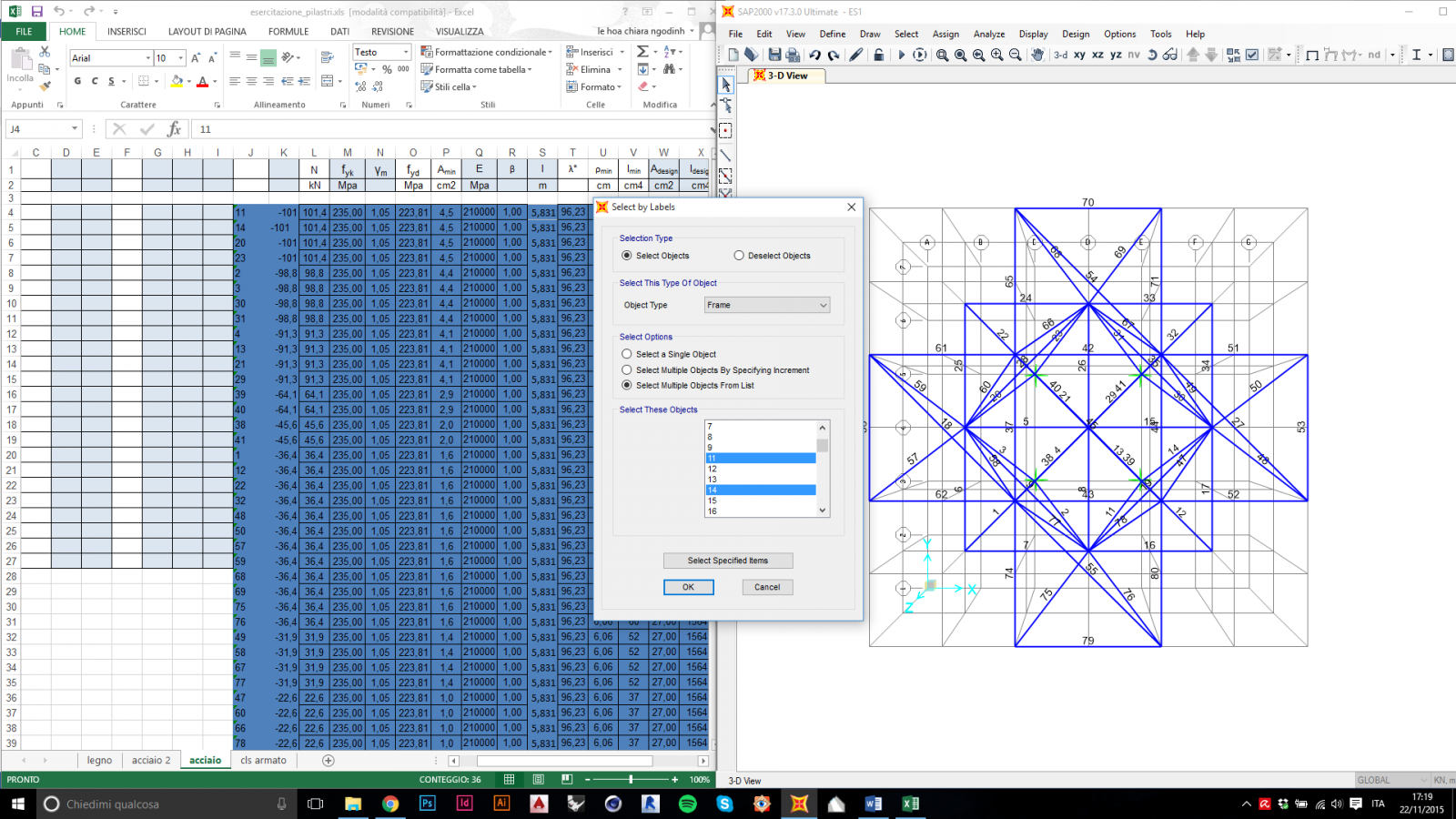
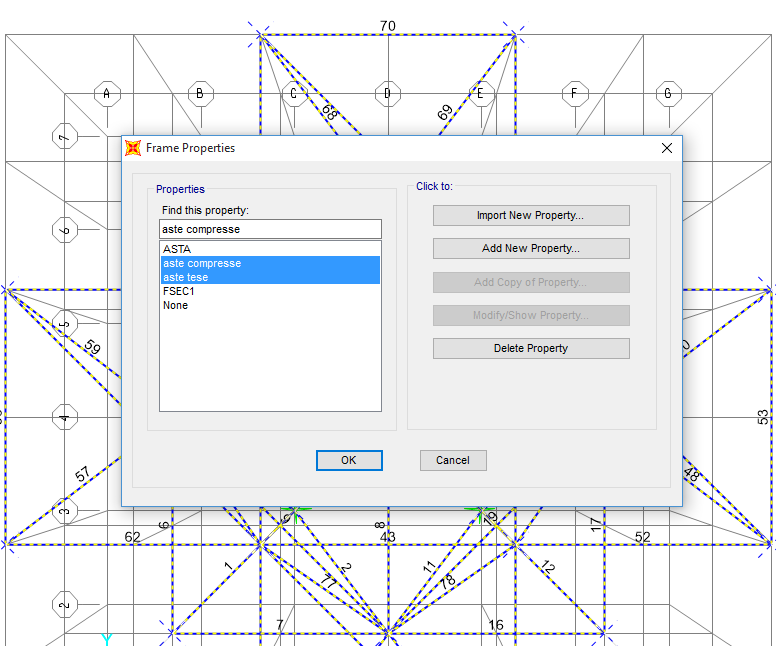
Una volta dimensionate tutte le aste, definendo il materiale scelto e due nuove sezioni, una per le aste tese e una per quelle compresse, queste possono essere assegnate ai giusti frame, grazie alla loro classificazione sul foglio Excel e allo strumento select>labels di SAP.
Commenti recenti