ES.1 STRUTTURA RETICOLARE SIMMETRICA_METODO DELLE SEZIONI DI RITTER
Per la risoluzione di questa struttura reticolare mi sono servita del metodo delle sezioni di Ritter al fine di calcolare gli sforzi normali ai quali sono sottoposte le aste. Per prima cosa bisogna verificare che la struttura sia esternamente ISOSTATICA (numero dei gradi di libertà deve essere uguale al numero dei gradi di vincolo).

Una volta verificata la condizione di isostaticità della struttura, posso calcolare le REAZIONI VINCOLARI tramite le EQUAZIONI DI BILANCIO (equilibrio esterno).
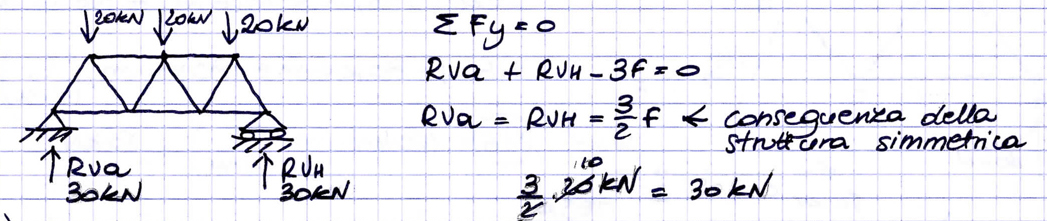
Uso il METODO DELLE SEZIONI DI RITTER per calcolare le AZIONI DI CONTATTO. Quando seziono le aste, metto in evidenza gli sforzi normali e faccio un ipotesi a priori sostenendo che siano tutte tese. Applico l'equilibrio alla rotazione prendendo come poli i punti dove si incontrano tutte le aste tranne una. Se il segno dello sforzo normale che ho calcolato è negativo, allora l'asta è compressa e dovrò cambiarle il verso.
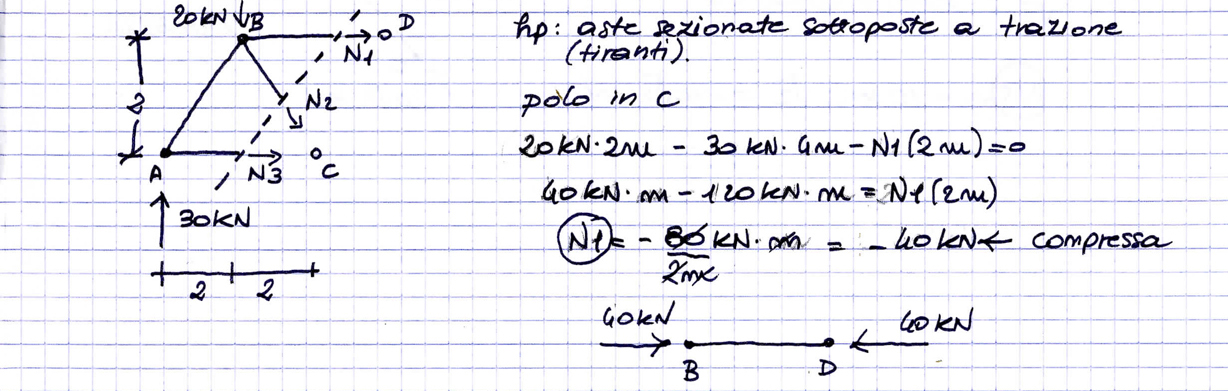
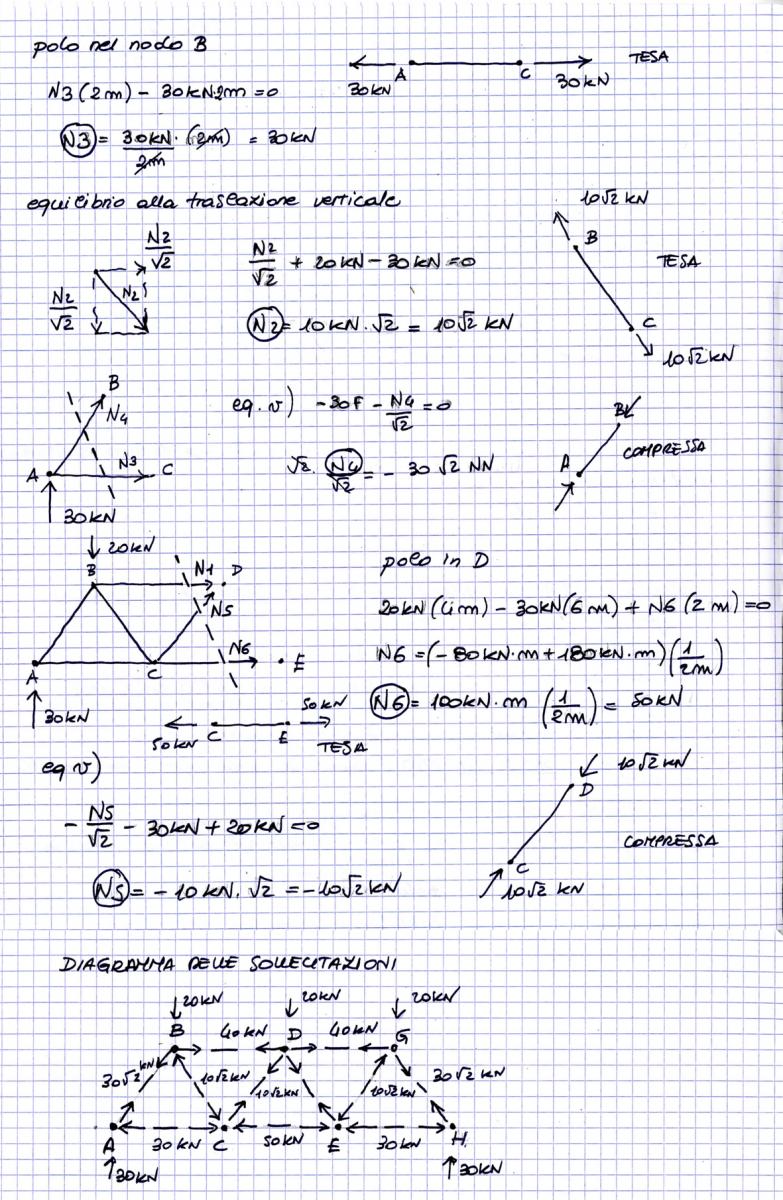
Sfruttando la simmetricità della struttura e delle forze applicate su di essa si può risolvere metà della struttura in quanto gli sforzi normali saranno anch'essi simmetrici.
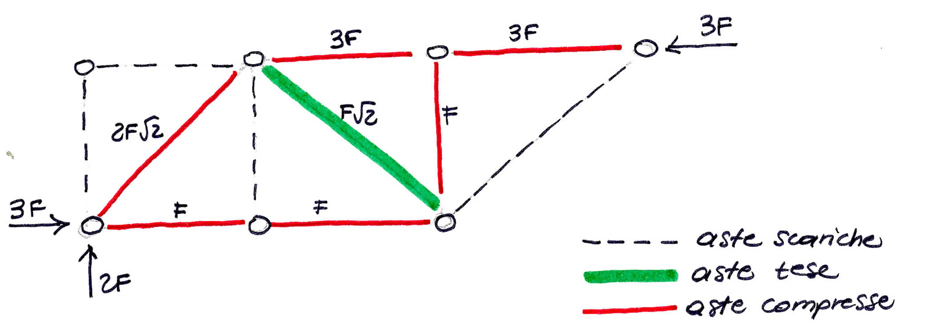
Il diagramma di sollecitazione mostra i correnti superiori compressi e quelli inferiori tesi. (tipico delle STRUTTURE RETICOLARI APPOGGIATE).
ES.2 STRUTTURA RETICOLARE ASIMMETRICA_METODO DEI NODI
Dopo aver verificato l'isostaticità della struttura e calcolato le reazioni vincolari, calcolo le azioni di contatto delle forze normali alle quali è sottoposta ogni asta.
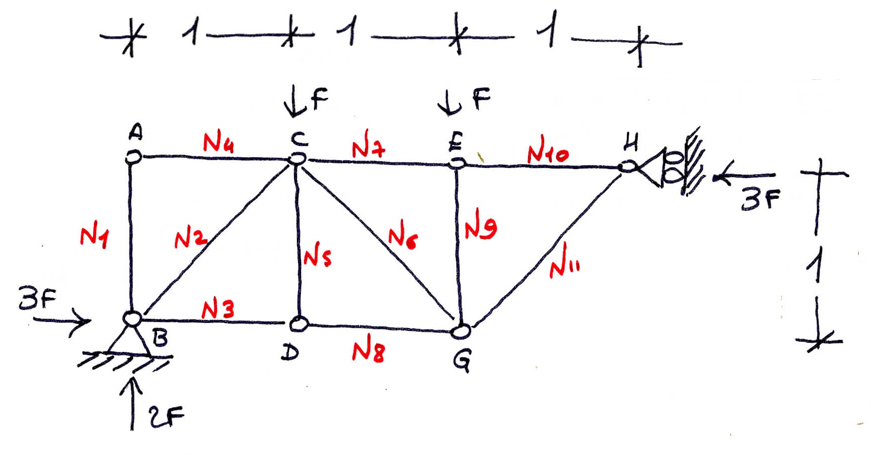
Come per il metodo delle sezioni, anche per quello dei nodi bisogna fare un'ipotesi sul comportamento delle aste (tese o compresse). Di seguito sono riportati alcuni esempi:
- nel nodo A abbiamo il caso in cui entrambe le aste sono scariche.
- nel nodo E ipotizzo che l'asta 9 sia un puntone. Facendo l'equilibrio alla traslazione verticale si ottiene che N9=F. Dato che il segno della normale risulta positivo, allora l'ipotesi iniziale è corretta.
- viceversa nel nodo B, l'ipotesi che l'asta 2 sia un tirante è errata e ciò perché il segno della normale risulta essere negativo.
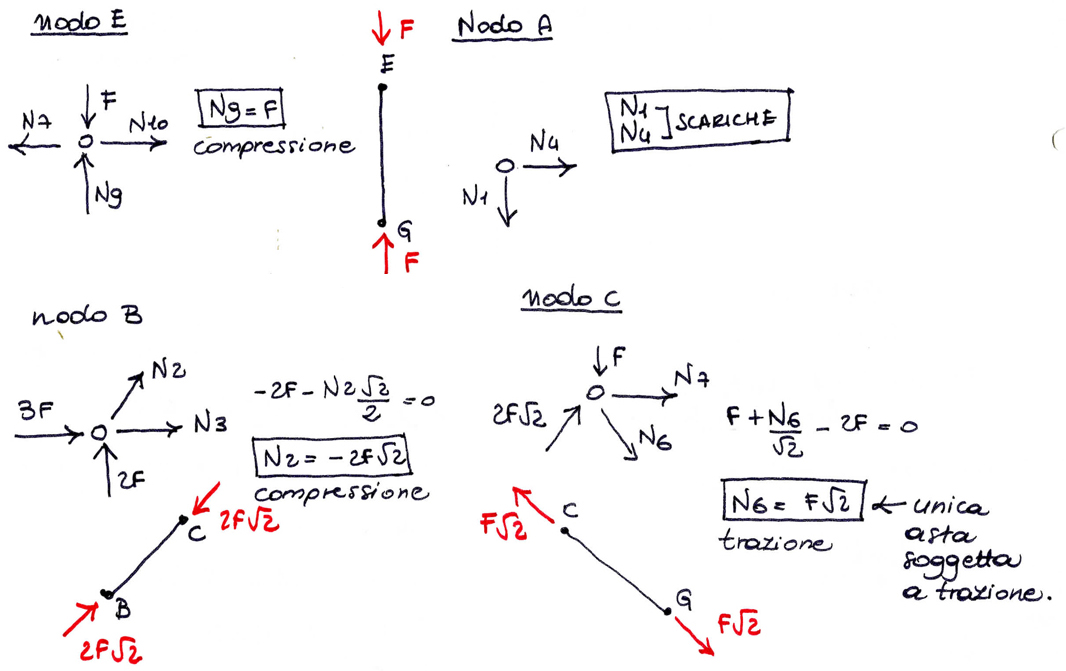
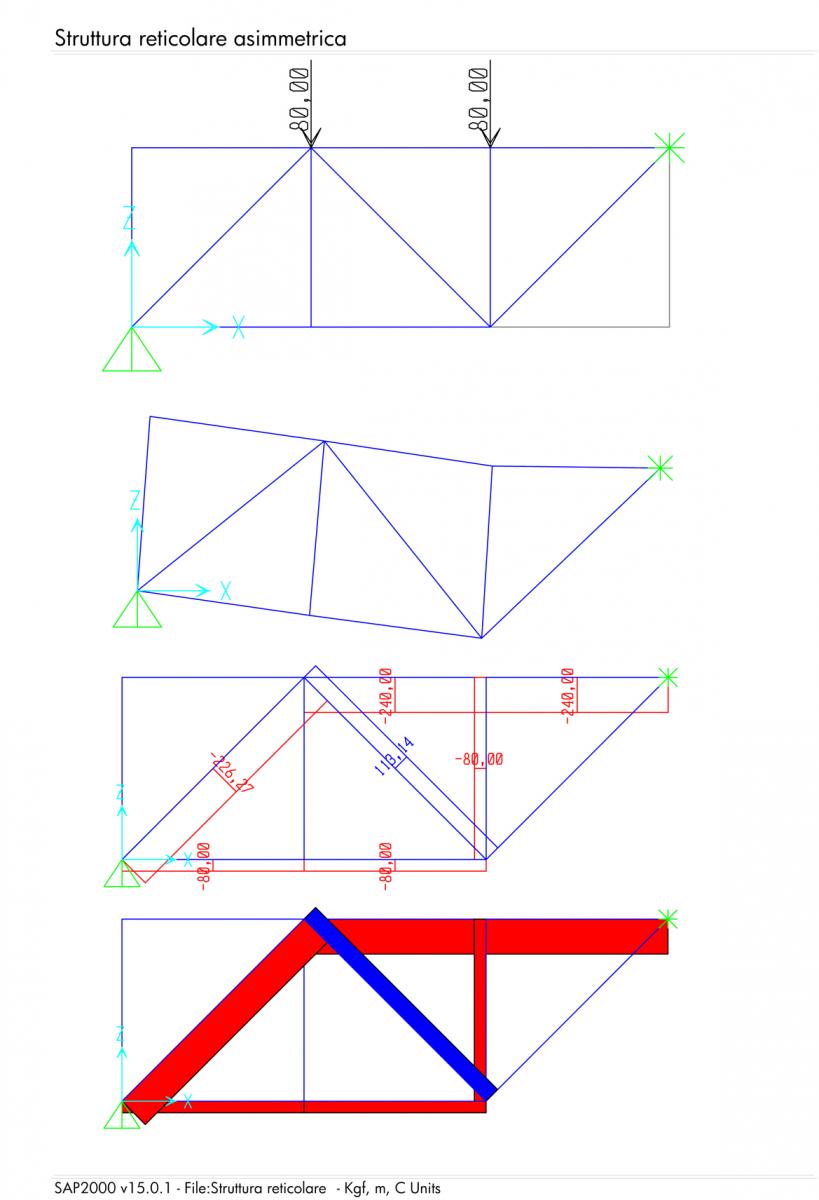
Di seguito è riportata l'analisi globale delle sollecitazioni a cui sono sottoposte le aste e la verifica fatta con SAP2000 applicando alle forze dei valori numerici.
__________________________________________________________________
DIMENSIONAMENTO TRAVI (LEGNO, ACCIAIO E CLS ARMATO)
PROGETTO DI UNA TRAVE DI UN IMPALCATO DI UN HOTEL
In questa esercitazione viene simulato il processo di progetto di una trave relativa al solaio di un albergo, con tre diversi materiali: acciaio, legno e calcestruzzo armato.
Mediante l'immissione di alcuni dati nel foglio elettronico excel verranno calcolate, attraverso apposite equazioni, le tre incognite relative ai tre materiali utilizzati: nel caso del legno l'incognita sarà l'altezza della trave, nell'acciaio il più piccolo modulo di resistenza (Wx) e per quanto riguarda il calcestruzzo l'altezza utile della trave stessa.
Di seguito è riportato uno schema dell'impalcato con evidenziata la trave da progettare, il relativo interasse (larghezza del solaio portato dalla trave), la luce e l'orditura del solaio.
La porzione di solaio sorretta dai pilastri è relativa alle stanze dell'albergo, mentre quella a sbalzo corrisponde ai ballatoi.
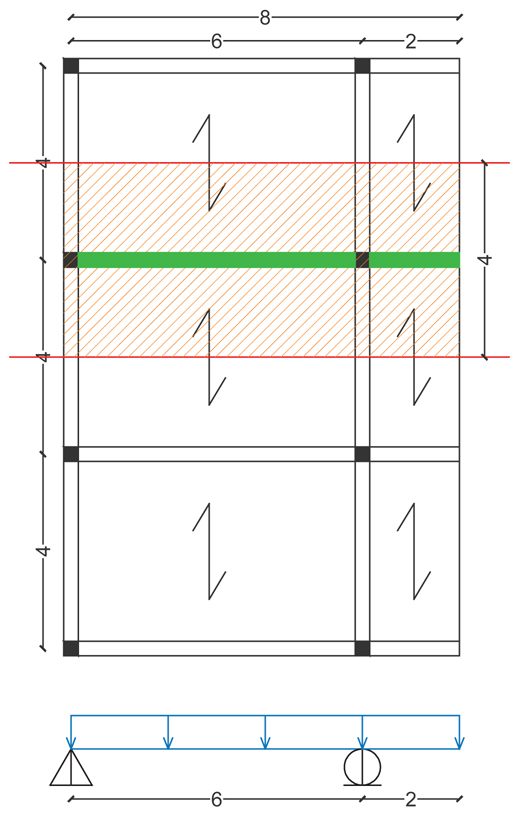
TRAVE: Area di influenza= 32,60 mq | Interasse= 4m | Luce= 8m
Per prima cosa risolvo la struttura isostatica per ricavare la formula del momento che andrò ad inserire nel foglio excel per il dimensionamento di massima della trave.
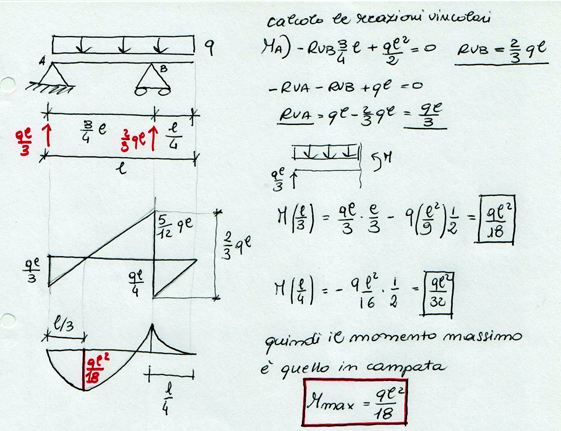
Definisco i CARICHI agenti sul solaio:
- il carico strutturale qs, (ipotesi provvisoria di massima che si andrà a verificare)
legno: 1KN/mq
acciaio: 2KN/mq
cls armato: 3KN/mq
- i sovraccarichi permanenti non strutturali qp, comuni ai tre tipi di solaio (legno, acciaio e cls)
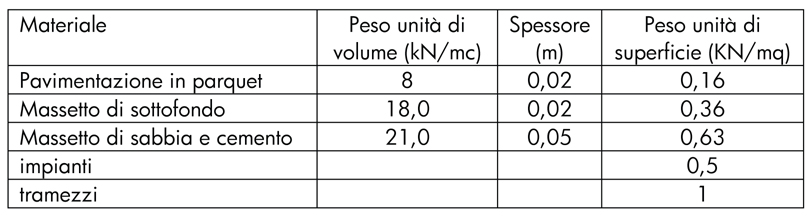
qp=2,65KN/mq
Valori presi dalle schede tecniche delle aziende (http://www.artechint.com/prezziario/solai.html) e dalle Nuove Norme Tecniche per le Costruzioni.
- carichi accidentali qa legati alla funzione dell'edificio, trai quali i carichi variabili e quelli di natura aleatoria (es. neve, sisma). Si deve fare riferimento alleNuove Norme Tecniche per le Costruzioni (DM 14 gennaio 2008, pubblicato sulla Gazzetta Ufficiale n. 29 del 4 febbraio 2008- Suppl. Ordinario n. 30).
qa: 2KN/mq
PROGETTO DI UNA TRAVE IN LEGNO
Solaio in legno a doppia orditura, composto da travi (interasse di 4 m), travetti (interasse 0,50 m), tavolato, massetto con relativi impianti e pavimentazione in parquet. Si vuole progettare una delle travi portanti di tale solaio.
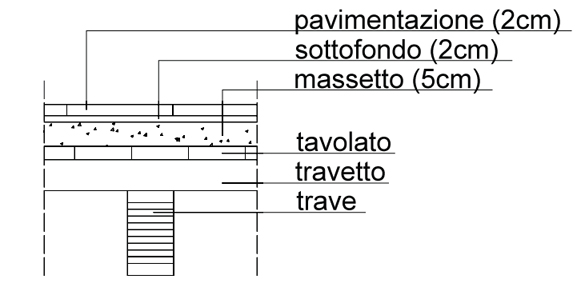
Stima provvisoria dei carichi agenti sul solaio:
- Carico strutturale (trave, travetti, tavolato) - valore ipotetico che si andrà a verificare.
qs: 1KN/mq(carico standard in un solaio in legno)
- Sovraccarico accidentale
qa: 2KN/mq
- Carico permanente non strutturale
qp: 2,65KN/mq
carichi agenti totali: qs+qa+qp= : 1KN/mq+ 2KN/mq + 2,65KN/mq = 5,65KN/mq
carico a metro lineare: 5,65 kN/mq*4m=22,56 KN/m
Una volta ottenuto il carico a metro lineare ipotetico (22,56 KN/m) vado a consultare le tabelle utili per i dimensionamenti di travi e travetti dell'azienda Tecsol. http://www.tecsol.it/prodotti_tecsol_travi_legno_lamellare.htm.
TRAVE (luce 8m, interasse 4m, M=ql2/18)
Scelgo una trave in legno lamellare con sezione 16x56cm
Area sezione trave A= 0,16 m x 0,56m = 0,089mq
Volume in 1m di trave V = 0,89 mq * 1 m = 0, 089 mc
Peso in un metro di trave P= Volume*p.specifico = (0,089mc * 500Kg/mc)/m = 44,5 kg/m= 0,45KN/m
Peso trave in 1 mq= 1/interasse*P = 1/4* 0,45KN = 0,11KN/mq
TRAVETTI (luce 4m, interasse di 0,50 m, M=ql2/8)
Carico a metro lineare= (qtot-qtrave)*interasse=(5,65kN/mq-0,11 kN/mq)*0,50m= 2,77KN/m
Consulto le tabelle dell'azienda Tecsol e scelgo il travetto10x20cm
A= 0,10m *0,20 m = 0,020 mq
V= 0,020 mq *1m = 0,020 mc
P(peso in un metro di travetto)= 0,020 * 500 =10 kg/m = 0,10 kN/m
Travetti in 1m2= 1/0.50*0,10 kN= 0,20KN/mq
TAVOLATO (spessore 0,03cm)
P = 0,15KN/mq
Qs tot= 0,11 KN/mq +0,20 KN/mq +0,15 kN/mq= 0,46 KN/mq
Carichi agenti totali: qs+qa+qp= : 0,46KN/mq+ 2KN/mq + 2,65 KN/mq= 5,11 KN/mq
Carico a metro lineare: q=5,11 KN/mq*4= 20,44KN/m
Inserisco nel foglio excel i valori dei carichi, l'interasse e la luce di travi e travetti, inoltre per quanto riguarda il momento relativo alla trave nella formula metterò M=ql2/18 (trave appoggiata con sbalzo), mentre per i travetti metterò la formula del momento pari a M=M=ql2/8.
Per quanto riguarda l'fm, scelgo il valore 24 che identifica la classe legno e nello specifico la resistenza a trazione durante la flessione.
fD=fm*Kmod/γm=24*0,6/1,45
Il Kmod è un coefficiente moltiplicativo che viene assegnato in base alla durata del carico (più il tempo è lungo e più il coefficiente si abbassa), mentre il valore γm è stato preso dalle Nuove Norme Tecniche per le Costruzioni.

Per quanto riguarda il dimensionamento di travi e travetti si può osservare che il valore dell'altezza h è minore rispetto a quello che ho ipotizzato di progettare, quindi sono entrambi verificati. Consultando le tabelle della ditta posso scegliere una trave con base 16 e un'altezza h che si avvicina al valore ricavato dal foglio excel (37,04). Posso dunque scegliere una trave con sezione 16x52cm, invece di quella ipotizzata all'inizio di 16x56cm.
trave 16x52 | 52>39,29
travetto 10x20 | 20>17,57
PROGETTO DI UNA TRAVE IN ACCIAIO
Dello stesso impalcato considerato in precedenza, progetto una trave in acciaio che sorregge un solaio in lamiera grecata. Di seguito è riportanta una sezione schematica per individuare gli elementi che copongono l'impalcato:
Faccio innanzitutto una stima provvisoria dei carichi del solaio:
- Carico strutturale (trave e travetti Ipe, rete elettrosaldata, lamiera grecata, getto in cls) - valore ipotetico che si andrà a verificare.
qs: 2KN/mq(carico standard in un solaio in acciaio)
- Sovraccarico accidentale
qa: 2KN/mq
-Carico permanente non strutturale
qp=2,95KN/mq
carichi agenti totali
qs+qa+qp= 2KN/mq+ 2KN/mq + 2,95KN/mq = 6,95KN/mq
q=6,95kN/mq *interasse=27,8 KN/m
TRAVE (luce 8m, interasse 4m, M=ql^2/18)
TRAVETTO (luce 4m, interasse 1m, M=ql^2/8)
TRAVE (luce 8m, interasse 4m, M=ql^2/18)
TRAVETTO (luce 8m, interasse 1m, M=ql^2/8)
Inserisco nel foglio excel i valori dei carichi, l'interasse e la luce di travi e travetti.
fy,D=fy,k/γm= 235/1,05
Il γm è stato preso dalle Nuove Norme Tecniche per le Costruzioni.
Bisogna sottolineare che il qs che viene inserito nel foglio di calcolo è un valore provvisorio, che successivamente verrà sostituito con il qs effettivo.
Quello che ottengo dai calcoli del foglio excel sono i valori dei moduli di resistenza a flessione (Wx) rispettivamente di trave e travetti. Dopodiché consulto le tabelle relative ai profilati metallici IPE e scelgo due profilati che hanno un valore di resistenza simile, approssimato per eccesso. (
http://www.oppo.it/tabelle/profilati_ipe.htm)

Scelgo i profilati:
TRAVE
Scelgo l'IPE 300, con base 15cm e altezza 30cm.
Trave in 1 mq= 1/interasse*P = 1/4* 0,422 kN = 0,10 KN/mq
TRAVETTI
Scelgo l'IPE 140
Travetti in 1 mq= 1/interasse*P = 1/1* 0,129KN = 0,129 KN/mq
Avendo scelto i profilati di progetto, verifico che siano ben dimensionati andando a calcolare il carico strutturale effettivo (qs):
SOLETTA ARMATA(rete elettrosaldata e getto di riempimento)

qs soletta=1,23 KN/mq
LAMIERA GRECATA
Per quanto riguarda la scelta della lamiera grecata devo calcolare i carichi agenti su di essa e poi consultare i valori dell'azienda produttrice per scegliere il prodotto più opportuno. (
http://www.edilpanel.it/xprodotti.htm)
carico agente sulla lamiera grecata:
qa+qp=2 KN/mq + 2,95 KN/mq = 4,95 KN/mq = 495 Kg/mq
P= 7,16 Kg/mq= 0,07KN/mq
qs tot= 0,07KN/mq+0,129 KN/mq+1,23KN/mq+0,10KN/mq=1,52 KN/mq
Avendo trovato il qs reale vado a inserire nuovamente i dati in tabella.

Sia la trave che il travetto risultano ben dimensionati, in quanto il valore effettivo del modulo di resistenza calcolato risulta essere minore rispetto a quello dei profilati scelti:
TRAVE IPE 300 Wx=557,1cm3>4441,146cm3
TRAVETTI IPE 140 Wx=77,32cm3>57,82cm3
TRAVE IN CALCESTRUZZO ARMATO
Considerando lo stesso impalcato si vuole progettare una trave in cls armato che sorregge un solaio in latero-cemento.
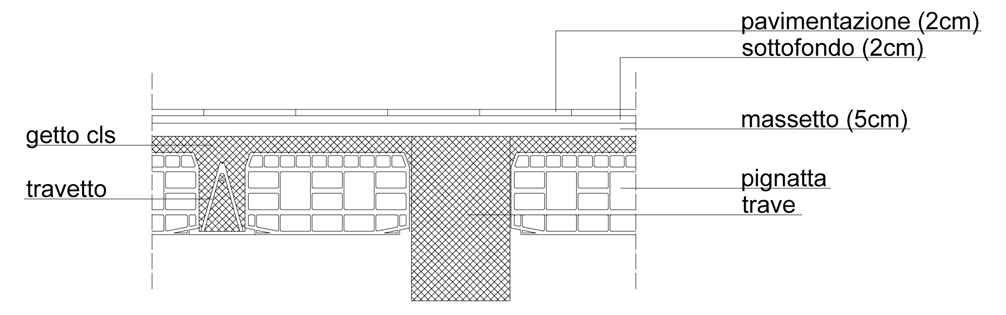
Così come per il legno e l'acciaio, per prima cosa vanno calcolati i carichi strutturali, accidentali e permanenti non strutturali:
-carichi permanenti non strutturali qp:
qp=2,95KN/mq
-carico strutturale qs (trave, travetti, pignatte, getto di cls), valore ipotetico che si andrà a verificare.
qs= 3 KN/mq
- Sovraccarico accidentale
qa=2 KN/mq
Inserisco i valori in tabella (Classe del cemento armato non precompressoC40/50 con Rck=40 (cls ordinario)
Carico totale: qtot= qa+qp+qs=7,95 KN/mq
carico al metro lineare= 7,95 KN/mq*4=
31,8 KN/m
Una volta ottenuta l'altezza utile della trave in cls posso calolare il reale carico strutturale del solaio:
trave: 25x40 cm | area sezione: 0,10 mq | peso: 2,09 KN/m
porzione di trave in 1mq=1/interasse=1/4m
Peso specifico in 1mq =1/4*2,09=0,52KN/mq
pignatte: 0,16x0,38m | p= 2(0,16*0,38*1)*6 KN/m=0,72KN/mq
(2 pignatte in un mq)
travetti in cls armato: 0,16x0,10m | p= 2(0,16*0,10)*25 KN/m=0,8KN/mq
(2 travetti in un mq)
getto di cls spessore=0,04m - Peso unità di volume (KN/mc)=20 | Peso unità di superficie (KN/mq)=0,8KN/mq
qs tot=0,52KN/mq+0,72 KN/mq+0,8 KN/mq+0,8 KN/mq=2,84 KN/mq
Inserendo nel foglio excel il reale valore del carico strutturale qs, ottengo un'altezza utile della trave pari a 33,12cm, dunque la trave ipotizzata all'inizio, avente sezione 25x35 risulta essere ben dimensionata.
_______________________________________________________________________
COSTRUZIONE E PROGETTO DI UNA STRUTTURA RETICOLARE A SCHEMA CUBICO
In questa esercitazione verrà illustrata dapprima la realizzazione di una struttura reticolare di quattro per sei campate, con il software Rhinoceros e in seguito il progetto delle aste maggiormente sollecitate (a trazione e compressione), con l'aiuto di SAP 2000.
COSTRUZIONE DELLA STRUTTURA RETICOLARE A SCHEMA CUBICO
Di seguito sono illustrati i quattro passaggi "chiave", utili per la costruzione della struttura reticolare. E' bene sottolineare che il software di modellazione 3d (Rhinoceros) è utile per disegnare solamente le aste, mentre i nodi, i vincoli e i carichi agenti verranno definiti successivamente tramite il software di calcolo SAP2000.
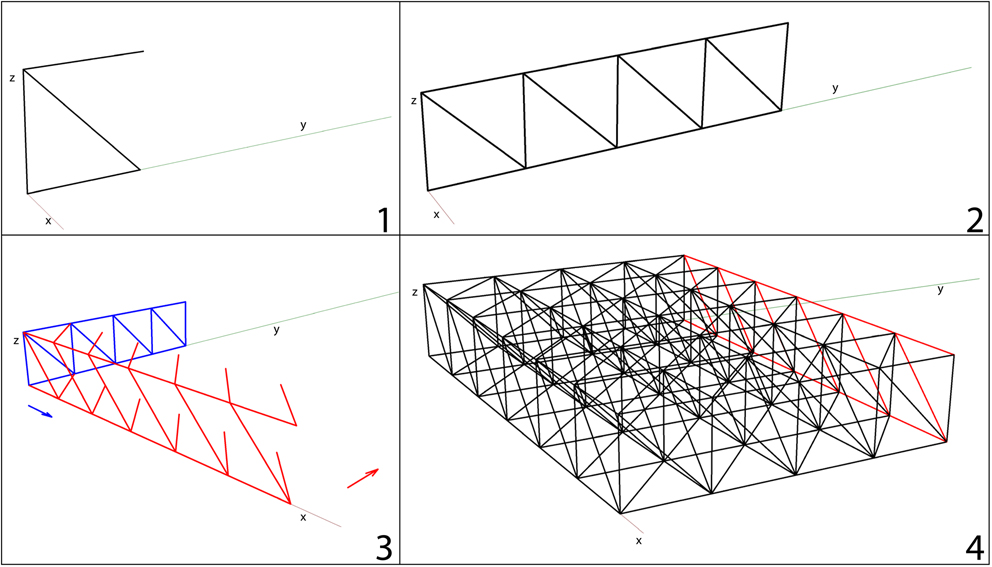
1_Disegno il primo modulo base composto da quattro aste reticolari: quelle parallele agli assi con lunghezza 2m e quella obliqua 2√2m.
2_Il passo successivo consiste nel copiare il modulo precedentemente realizzato grazie al comando "copia in serie" lungo l'asse y. Va completata l'ultima campata tramite il posizionamento di un'asta verticale.
3_Affinché non si sovrappongano le aste, per non compromettere il calcolo con SAP, è opportuno fare attenzione a copiare i moduli minimi che andranno a comporre la struttura reticolare spaziale. A tale scopo sono evidenziate in figura con il colore rosso le aste che verranno copiate serialmente lungo l'asse y e in blu quelle che verranno copiate lungo l'asse x.
4_L'ultimo passo per la costruzione della struttura reticolare sarà quello di "chiudere" le ultime campate attraverso il posizionamento di tre aste per ogni campata (due parallele all'asse x e una obliqua).
PROGETTO ASTE MAGGIORMENTE SOLLECITATE
L'obiettivo finale di questa esercitazione è il progetto delle aste maggiormente sollecitate a trazione e a compressione.
Per il caso della trazione lo sforzo massimo positivo potrà interessare sia un'asta lineare che un'asta obliqua indifferentemente, quindi basterà progettare quella più sollecitata.
Per quanto riguarda lo sforzo massimo negativo, ovvero quello a compressione, la lunghezza dell'asta non va sottovalutata, in quanto le aste lineari e oblique hanno due carichi critici diversi, quindi bisogna progettarle e verificarle entrambe.
E' bene sottolineare che alla resistenza a trazione concorre solo il materiale che compone l'asta, mentre per quella a compressione svolge un ruolo importante il carico di punta e ciò significa che una sezione potrebbe perdere l'equilibrio in campo elastico.
Dopo aver importato la struttura precedentemente realizzata, impostiamo i vincoli, cioè quattro cerniere sui quattro spigoli della struttura stessa e in seguito definiamo il materiale e il tipo d sezione delle aste, ovvero dei tubolari in acciaio.
Per ultima cosa assegniamo ad ogni nodo della struttura una forza pari a 40KN.
Di seguito è riportato uno schema della deformata che scaturisce dall'analisi fatta con SAP.
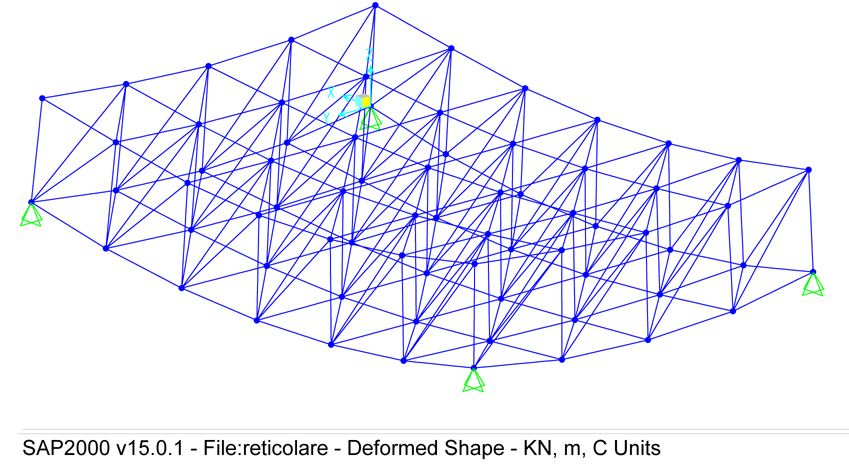
Consultando le tabelle di analisi degli sforzi normali di ogni asta, attraverso il menu "show tabels", riusciamo ad individuare le tre aste maggiormente sollecitate (grazie all'esportazione nel foglio excel che permette di ordinare dalla maggiore sollecitazione alla minore).
Nella tabella seguente sono riportate le aste che andrò a progettare:
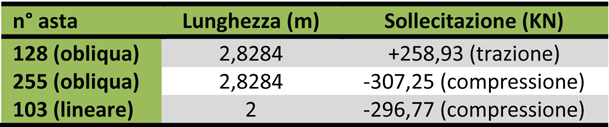
A questo punto, conoscendo i valori massimi di compressione e trazione, possiamo progettare le aste.
PROGETTO TIRANTE MAGGIORMENTE SOLLECITATO
Dopo aver individuato il valore dell'asta maggiormente sollecitata a trazione, con N=258,93KN, posso effettuare il progetto dell'asta, andando a scegliere un profilato metallico opportunamente dimensionato.
Scelgo l'acciaio da carpenteria Fe430S275 e calcolo la tensione di progetto fD, che è pari alla tensione di snervamento (fy), diviso il coefficiente di sicurezza (γm), pari a 1,05.
fD= fy/γm=275/1,05= 261,90N/mm2
N=258,93KN=258930N
Posso dunque calcolare il valore dell'area della sezione del profilato:
A=N/fD=258930/261,90=988,65mm2=9,88cm2
A questo punto scelgo di utilizzare un profilato metallico in acciaio a sezione circolare, avente un'area simile, approssimata per eccesso:
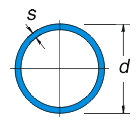
PROGETTO PUNTONI MAGGIORMENTE SOLLECITATI
Per quanto riguarda il progetto delle aste maggiormente sollecitate a compressione, è opportuno, dopo aver calcolato l'area della sezione minima che evita di arrivare alla "crisi", verificare che le aste in esame non siano soggette al carico di punta.
Siccome la lunghezza libera di inflessione l0 dipende, oltre che dal tipo di vincolo, dalla lunghezza dell'asta, nel caso della compressione, bisogna verificare sia l'asta lineare (lunga 2m), che quella obliqua (lunga 2,8284m).
PROGETTO ASTA LINEARE
Partiamo dal progetto dell'asta lineare n°103, lunga 2m e soggetta una compressione pari a -296,77KN.
fD= fy/γm=275/1,05= 261,90N/mm2 (calcolato in precedenza)
N=-296,77KN=-296770N
Posso dunque calcolare il valore dell'area della sezione del profilato:
A=N/fD=296770/261,90=1133,14mm2=11,33cm2
Consulto le tabelle del profilato metallico a sezione circolare e scelgo un profilato con un'area simile approssimata per eccesso. Di seguito è riportata la tabella con le caratteristiche della sezione del profilato scelto:

VERIFICA DELLA STABILITA' DELL'ASTA
Una volta progettata l'asta devo verificare che lo sforzo normale a compressione alla quale è sottoposta è minore rispetto al carico critico Euleriano(P.critico).
Calcolo quindi il CARICO CRITICO EULERIANO:
P.crit.= π2EJmin / l02
dove:
Eè il modulo di Young, che per Fe430 è pari a 200.000KN/mm2
Jminè il momento di inerzia minimo della sezione: 192,0cm4=1.920.000mm2 (valore preso dalle tabelle del profilato metallico)
l02è la lunghezza massima di inflessione, che in questo caso, essendoci due cerniere alle estremità delle aste, è pari alla lunghezza dell'asta stessa (come dimostra lo schema sottostante). Quindi l02=2m=2000mm2
P.crit= (3,14)2(200.000)(1.920.000)/(2000)2=945.600N= 945,6KN
296,77KN<945,6KN
N<P.crit.quindi non si innesca il fenomeno di instabilità euleriana, dunque l'asta è verificata e stabile.
PROGETTO ASTA OBLIQUA
Progetto l'asta obliqua n°255, lunga 2,8284m e soggetta una compressione pari a -307,25KN.
fD= fy/γm=275/1,05= 261,90N/mm2 (calcolato in precedenza)
N=-307,25KN=-307250N
Posso dunque calcolare il valore dell'area della sezione del profilato:
A=N/fD=307250/261,90=1173,15mm2=11,73cm2
Consulto le tabelle del profilato metallico a sezione circolare e scelgo un profilato con un'area simile approssimata per eccesso. Di seguito è riportata la tabella con le caratteristiche della sezione del profilato scelto.
VERIFICA DELLA STABILITA' DELL'ASTA
Una volta progettata l'asta devo verificare che lo sforzo normale a compressione alla quale è sottoposta è minore rispetto al carico critico Euleriano (P.critico).
Calcolo quindi il CARICO CRITICO EULERIANO:
P.crit.= π2EJmin/ l02
P.crit= (3,14)2(200.000)(2.110.000)/(2828,4)2=519597,46N= 519,59KN
307,25KN<519,59KN
N<P.crit.quindi non si innesca il fenomeno di instabilità euleriana, dunque l'asta è verificata e stabile.
__________________________________________________
RIPARTIZIONE DELLE FORZE SISMICHE
L’obiettivo di questa esercitazione è quello di vedere in che modo si ripartiscono le forze sismiche su una struttura costituita da otto controventi.
Ipotizziamo che la tecnologia che caratterizza l’intero impalcato sia la stessa (calcestruzzo), così da poter evidenziare l’importanza “relativa” di ciascun controvento.
Di seguito è riportato lo schema dell’impalcato, costituito da 13 piastri (30x40cm), opportunamente disposti e orientati, in modo tale da avere il momento di inerzia maggiore della sezione del pilastro in asse con la trave che ha una luce maggiore e di conseguenza un momento più grande.
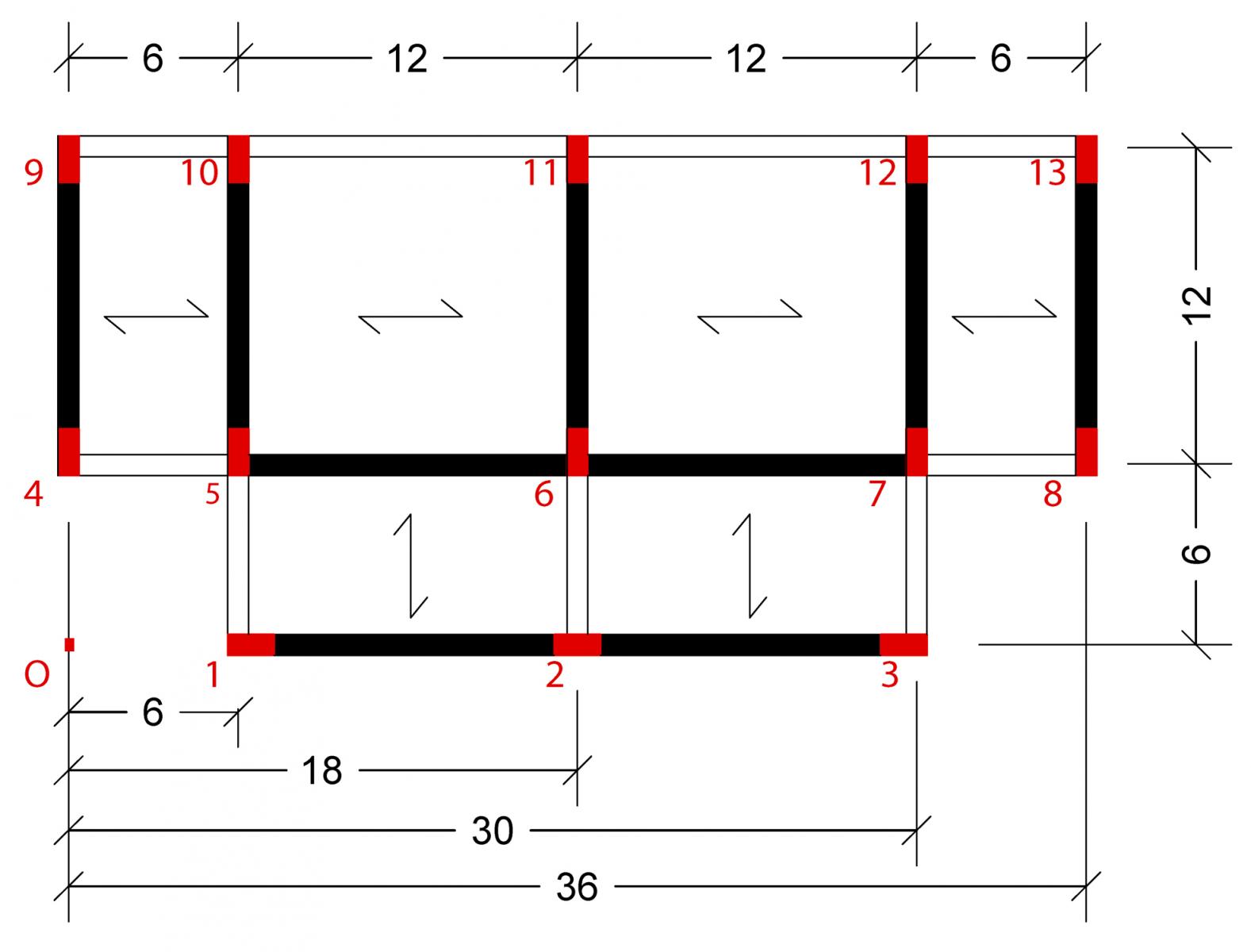
Step_1: calcolo delle rigidezze traslanti dei controventi dell’edificio
È possibile calcolare le rigidezze di ciascun controvento, inserendo nel foglio excel i valori di:
- modulo di Young (E), pari a 21000N/mmq
- altezza dei pilastri (H),
- momento di inerzia di ciascun pilastro. (J=bh3/12)
La rigidezza flessionale totale (KT) è data dalla seguente formula:
KT=12E(J1+J2+J3)/h3
I pilastri che compongono lo stesso controvento possono avere momenti di inerzia diversi rispetto ad un’asse, come ad esempio nel controvento n°3, costituito dai pilastri 2, 6, 11.
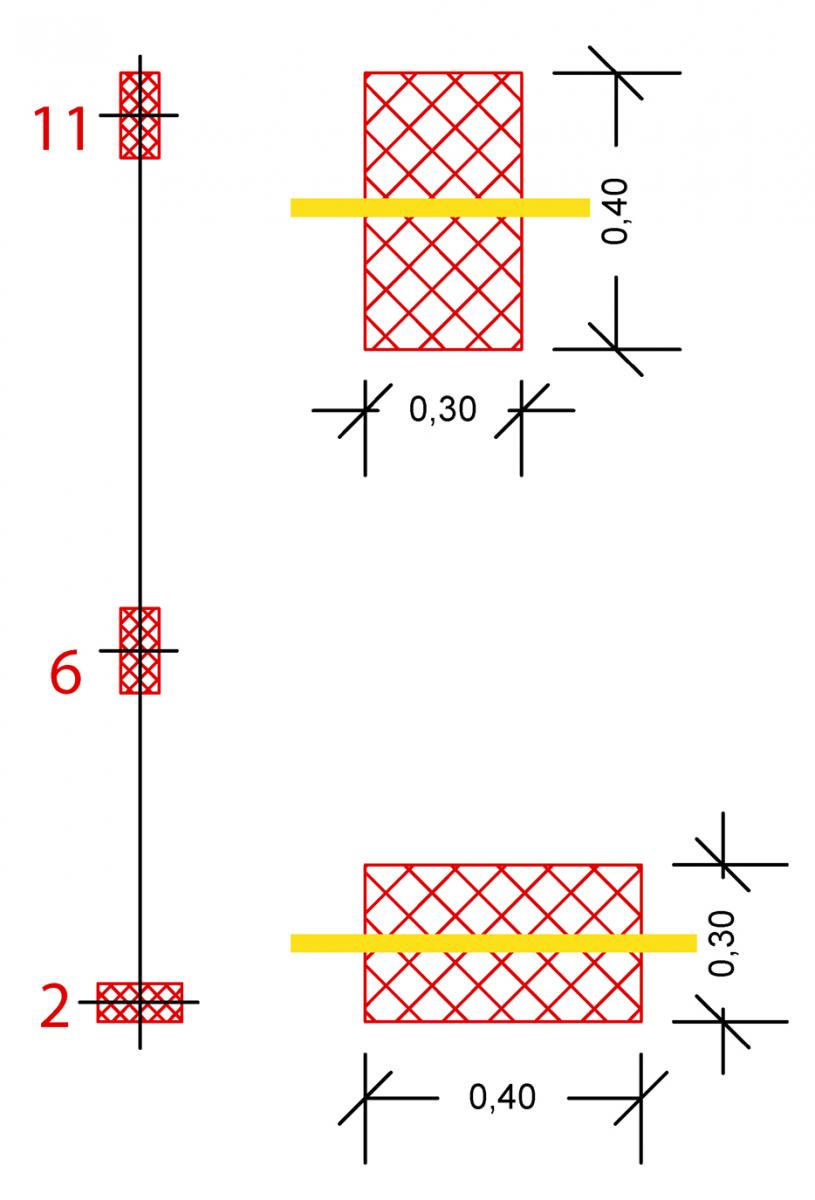
Pilastro 2 | J=(40x303)/12=90.000cm4
Pilastri 6-11 | J=(30x403)/12=160.000cm4
In questo caso la rigidezza flessionale totale è:
KT= 12*21000(160.000+160.000+90.000)/(3,5)3=2409,80kN/m
Di seguito sono riportate le tabelle utili per il calcolo delle rigidezze di ogni controvento:
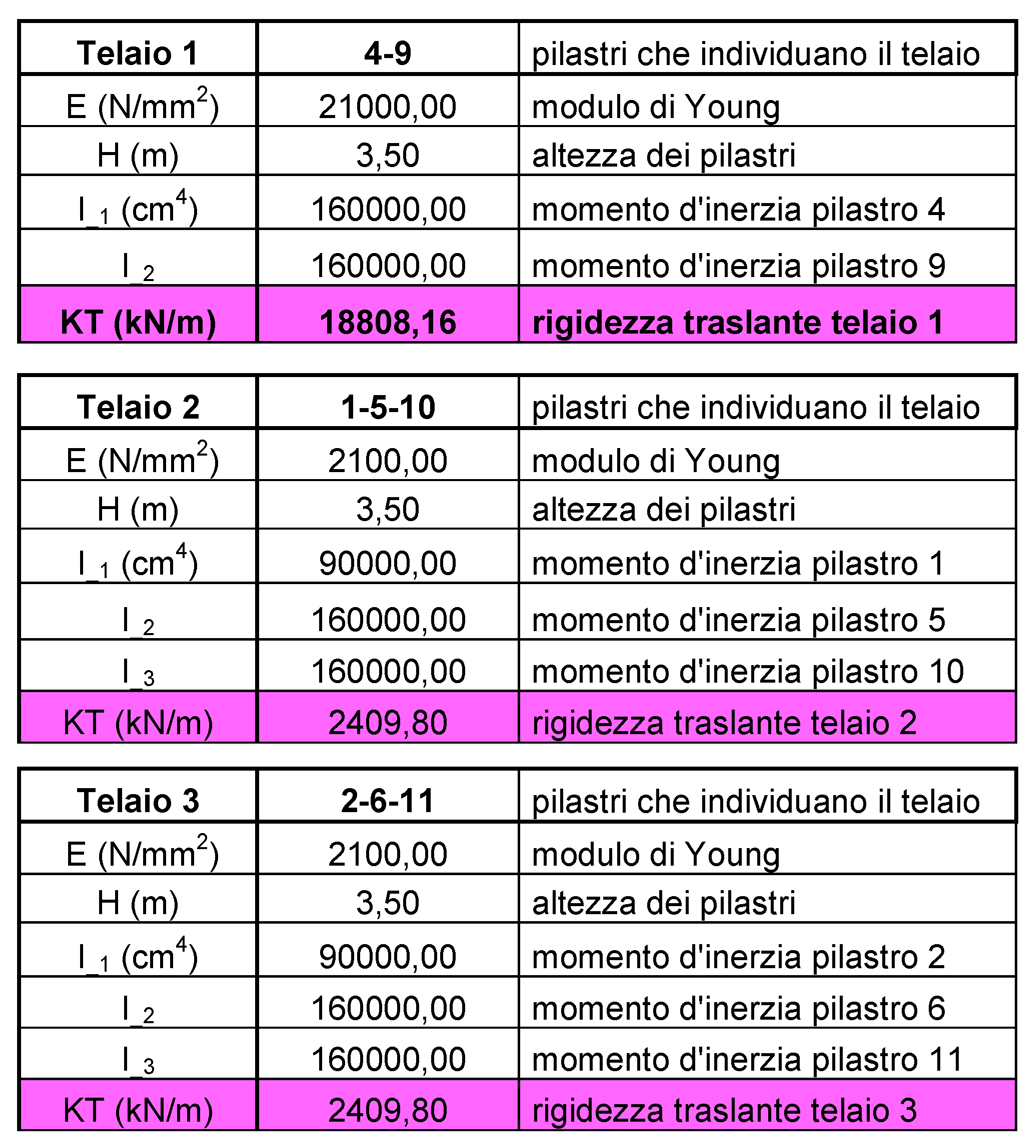
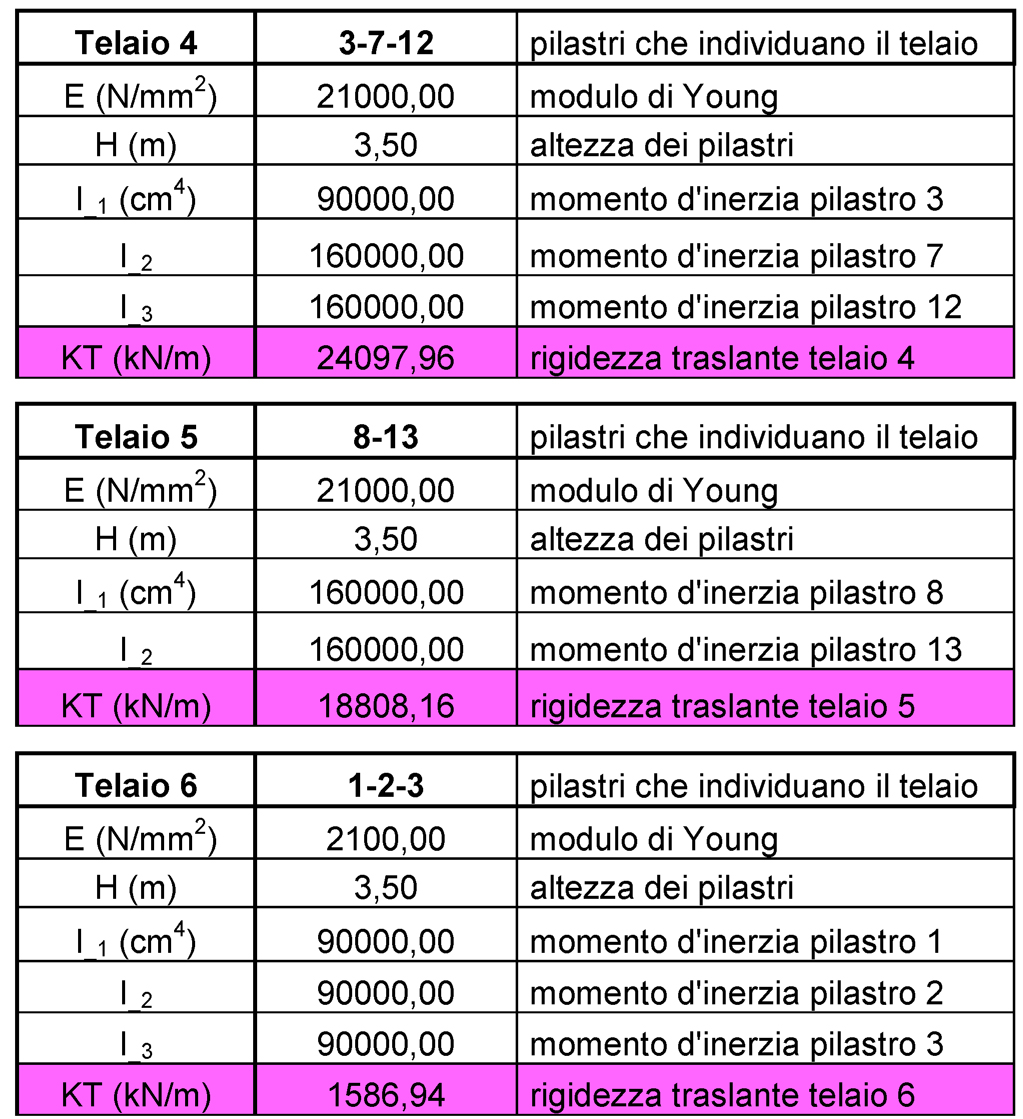
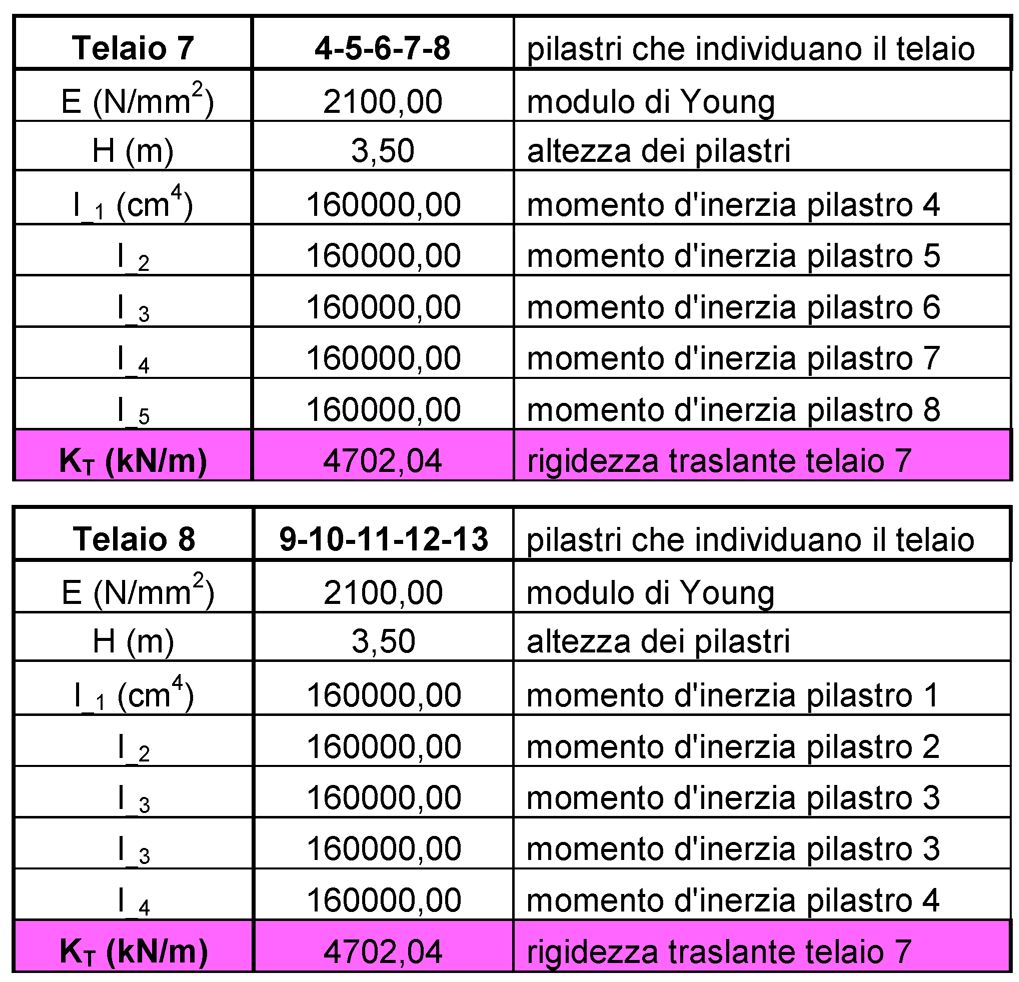
Step_2: Controventi e distanze (tabella sinottica)
Nella seguente tabella riassuntiva sono riportati i valori delle rigidezze di ogni controvento calcolate in precedenza e i valori delle distanze di ciascuno di essi dall'origine (O).
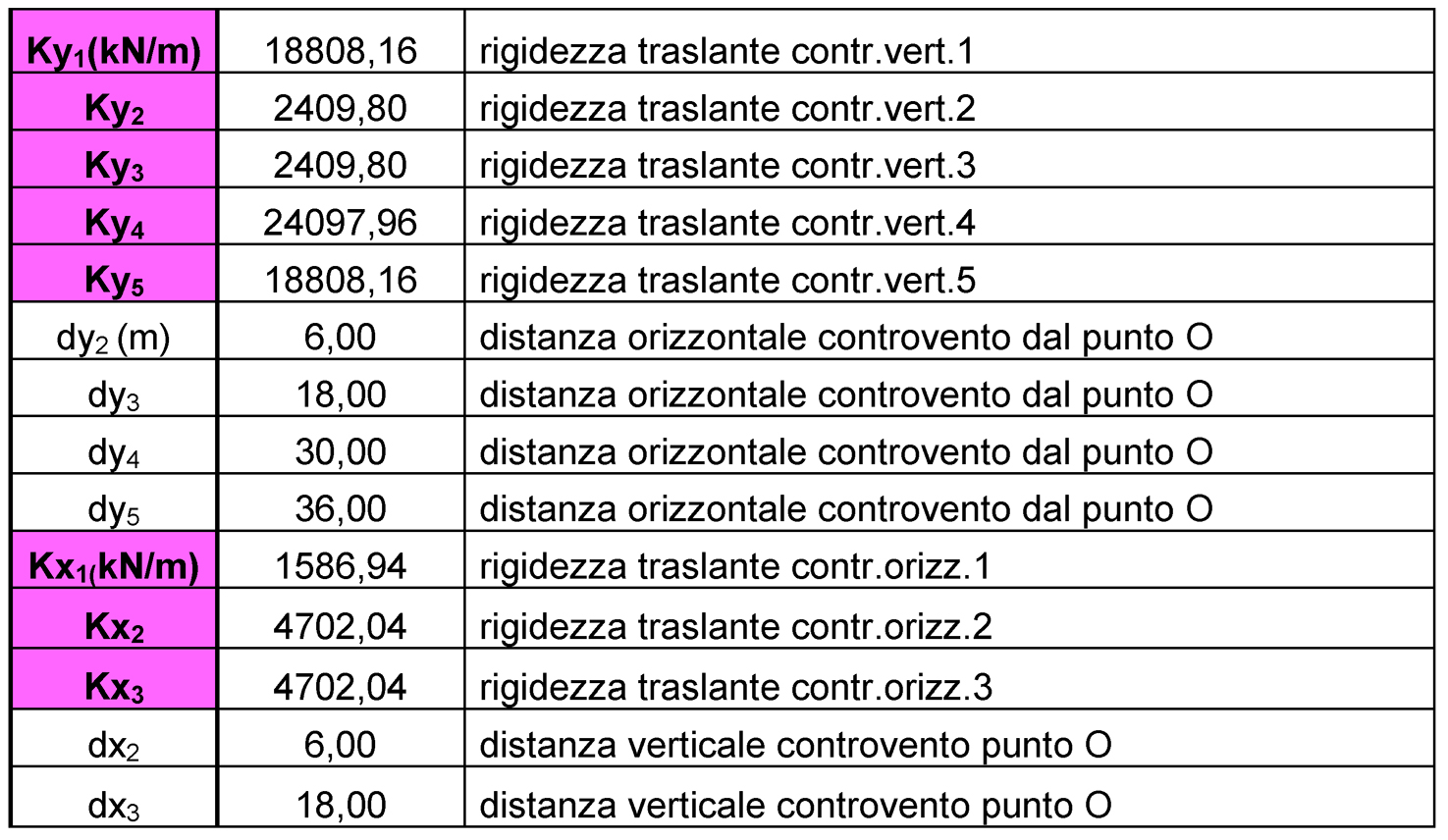
Kx_tot=10991,02kN/m | Ky_tot=66533,88kN/m
Step_3: Calcolo del Centro di Massa
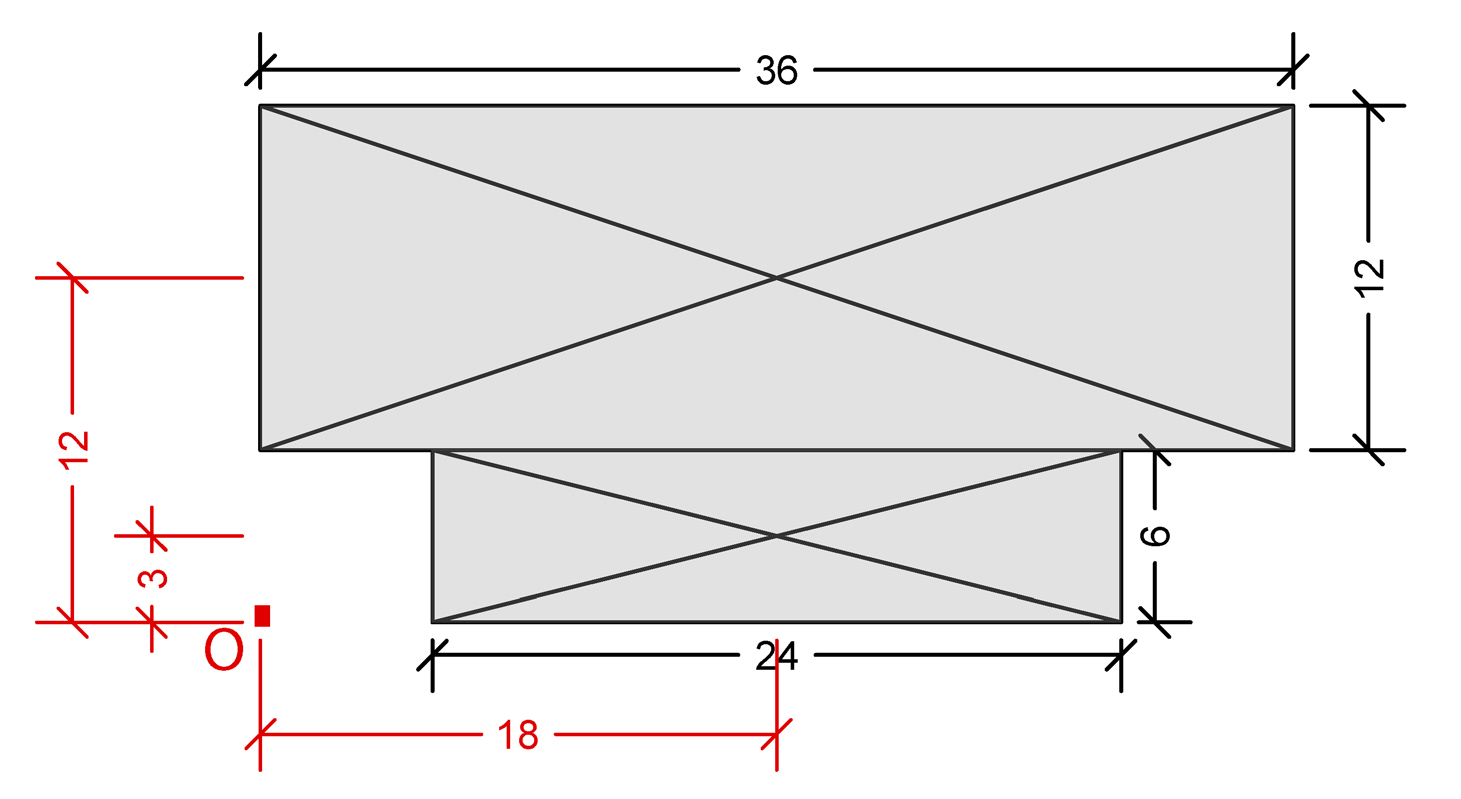
Il passo successivo è il calcolo del centro di massa, che si trova al centro delle aree. Per prima cosa calcoliamo le aree dei due rettangoli che individuano l'impalcato:
A1=24x6=144m | A2=12x36=432m | Atot=144+432=576mq
Coordinate del centro delle aree:
CA1= (18;3) | CA2= (18;12)
Possiamo quindi definire il centro di massa secondo le sue coordinate:
XG= (A1XG1+A2XG2)/Atot
YG= (A1YG1+A2YG2)/Atot

Step_4: calcolo del centro di rigidezze e delle rigidezze globali
Sappiamo che è importante vincolare la struttura a forze orizzontali, ed è per questo che è opportuno introdurre i controventi. Questi ultimi sviluppano delle forze ed i pilastri "reagiscono" con la loro rigidezza.
Una struttura è ben vincolata se ha almeno tre controventi ben dimensionati e ben disposti in pianta (non paralleli). Risulta altrettanto indispensabile individuare il centro delle rigidezze (centro di rotazione che rimane fermo, situato sull'asse centrale delle rigidezze dei controventi).
Il calcolo delle coordinate del centro delle rigidezze è il seguente:
Xc=K2yd2y+ K3yd3y+ K4yd4y/Ky_tot
Yc= K2xd2x+ K3xd3x+ K4xd4x/Kx_tot
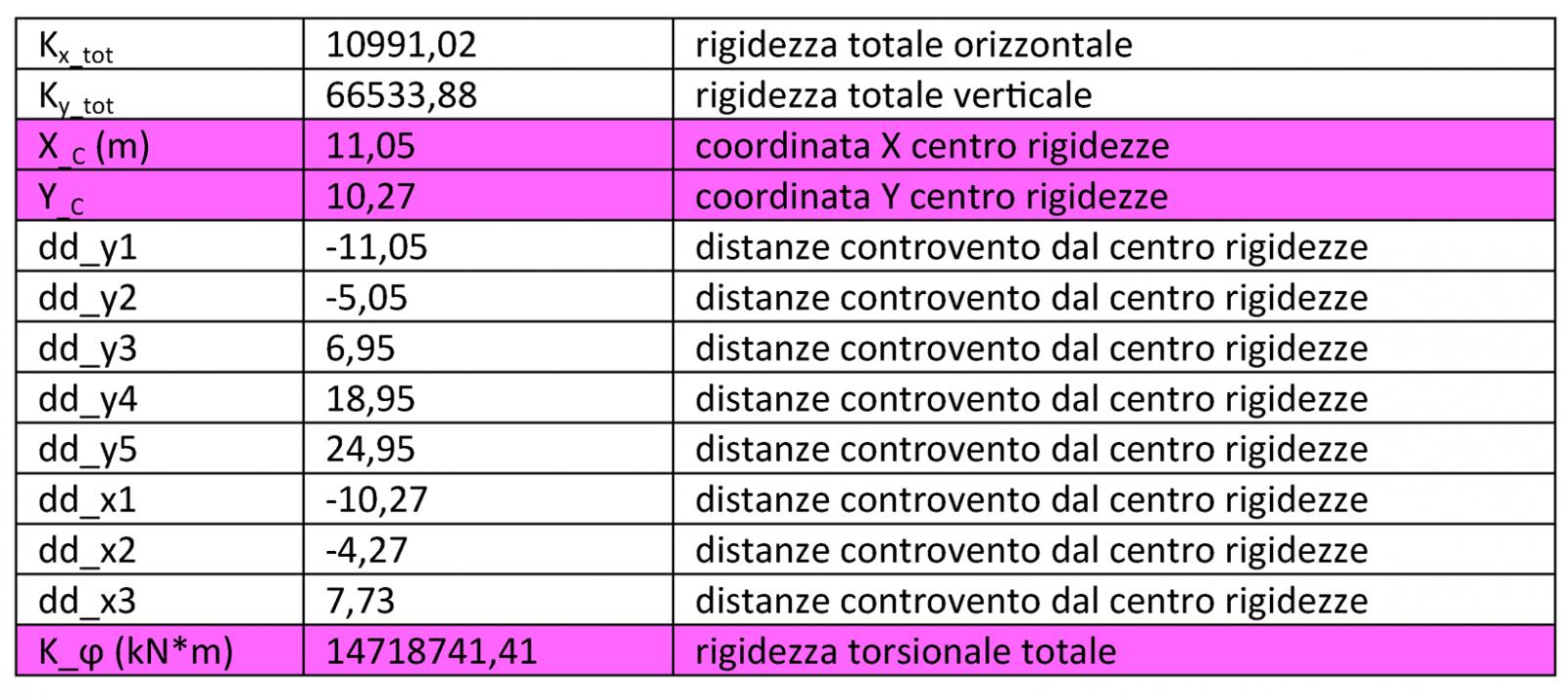
Il valore della rigidezza torsionale è:
Kϕ= ΣiKiddi2
Step_5: analisi dei carichi sismici
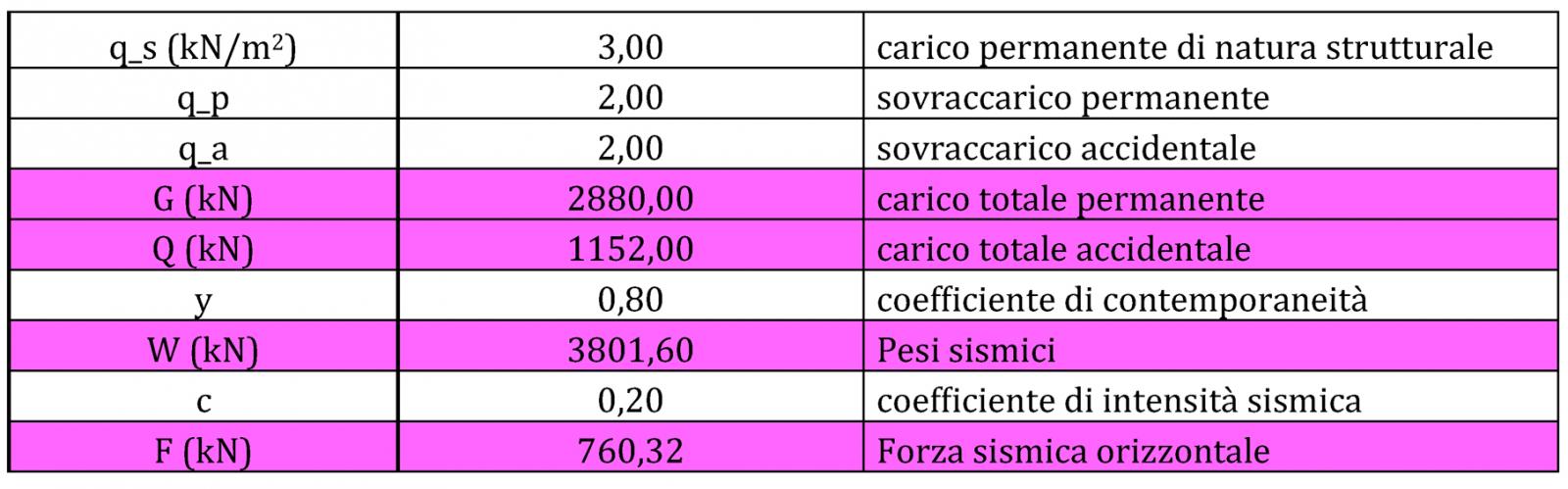
Avendo definito i carichi strutturali, permanenti e accidentali della struttura, è possibile calcolare con il foglio excel il peso sismico grazie alla seguente formula:
W=G+yQ
dove
G: (qs+qp)Atot
Q: qa Atot
y: coefficiente di partecipazione (o contemporaneità) dovuto al fatto che i carichi accidentali possono anche non esserci durante il sisma.
Avendo calcolato il peso sismico è possibile ricavare la FORZA SISMICA ORIZZONTALE. Si tratta di una forza d'inerzia dovuta al movimento del suolo che può essere definita come il prodotto tra la massa del corpo e l'accelerazione di trascinamento.
F=ma a=cg dove c è il coefficiente di intensità sismica
F=c (mg) dove mg è il peso della struttura quindi la forza sismica è una porzione di tale peso.
F=Wc
Step_6 | 7: ripartizione della forza sismica (lungo x e y)
I fenomeni sismici sono azioni aleatorie e di conseguenza è incerta la direzione lungo la quale si verificano. La normativa impone dunque di verificare le ripartizione delle forze sismiche almeno in due direzioni ortogonali fra loro.
La rotazione della struttura può avvenire per due motivi:
- la forza non passa per il centro delle rigidezze;
- i controventi non hanno la stessa rigidezza.
Sappiamo che quasi la totalità delle azioni sismiche non è diretta lungo l'asse delle rigidezze (quando il centro di massa e il centro delle rigidezze non coincidono). Avviene perciò una rotazione della struttura e si sviluppa un Momento torcente:
M= F(Yc-YG)
dove:
F è la forza sismica
Yc-YG è il braccio (differenza tra la coordinata del centro delle rigidezze e il quella del centro di massa)
Le ultime due tabelle sul foglio excel ricavano dapprima la traslazione orizzontale(ux), verticale (uy) e la rotazione (ϕ), dopodiché permettono di vedere in che modo la forza sismica si ripartisce su ciascun controvento grazie alle formule:
FxO= KxO(ux+ ϕdxO) per i CONTROVENTI ORIZZONTALI
FyO= KyO(uy+ ϕdyO) per i CONTROVENTI VERTICALI
Da queste formule si evince che se non ci fosse la rotazione ogni controvento prenderebbe la forza in base alla sua rigidezza.
Commenti recenti