Prima esercitazione - trave reticolare simmetrica
1) Per prima cosa si verifica l'isostaticità della trave, ovvero si calcola se il numero dei gradi di libertà sia pari al numero dei gradi di vincolo.
l=V ( n° gradi di libertà= n° gradi di vincolo)
l=3 x11 (3 x numero di corpi)
V= Ve +Vi (vincoli esterni + vincoli interni)
Ve= 3 Vi= 2(n-1)
A=H=2 B=G=4 C=D=E=6
Vi=4+8+18=30
V=3+30=33 l=33
2) Successivamente si calcolano le reazioni vincolari.
∑Fy=0
Va +Vh - 3F=0
Va +Vh - 60KN=0
Va +Vh =60KN ------> Va = Vh =30KN
La reazione vincolare nel nodo A è uguale a 0 perchè non vi sono altre forze orizzontali che la bilanciano.
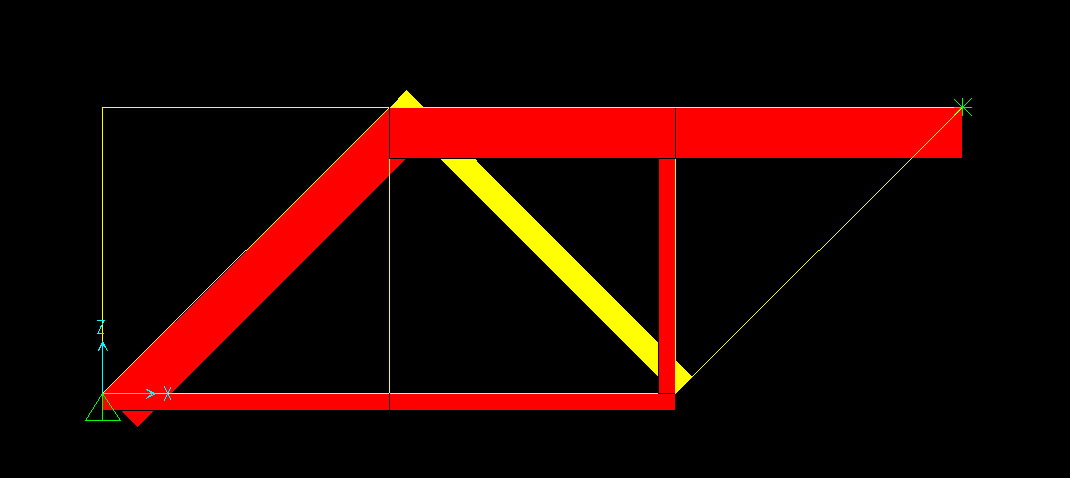
3) Adesso bisogna calcolare le azioni di contatto. Il metodo scelto in questo caso è stato il metodo di Ritter o metodo delle sezioni, in cui si sceglie di sezionare la trave in un punto tale che tagli tre aste non convergenti nello stesso punto.
------> 
Per ricavare lo sforzo normale N1 è stato fatto l'equilibrio dei momenti rispetto al punto C.
∑Mc=0
-30KNx4m + 20KNx2m - N1x2m =0 ----> N1= -40KN
Il verso ipotizzato per lo sforzo normale è sbagliato, l'asta BD risulta perciò compressa
Per ricavare lo sforzo normale N3 è stato fatto l'equilibrio dei momenti rispetto al punto B.
∑Mb=0
-30KNx2m + N3x2m =0 ----> N3= 30KN L'asta AC è tesa
Per ricavare lo sforzo normale N2 è stato fatto l'equilibro delle forze verticali scomponendo N2 per ricavare la sua componente verticale, poichè l'asta BC è inclinata a 45°. (N2 √2/2)
∑Fy=0
30KN - 20KN - N2 √2/2 = 0 ----> N2 = 10√2 KN L'asta BC è tesa
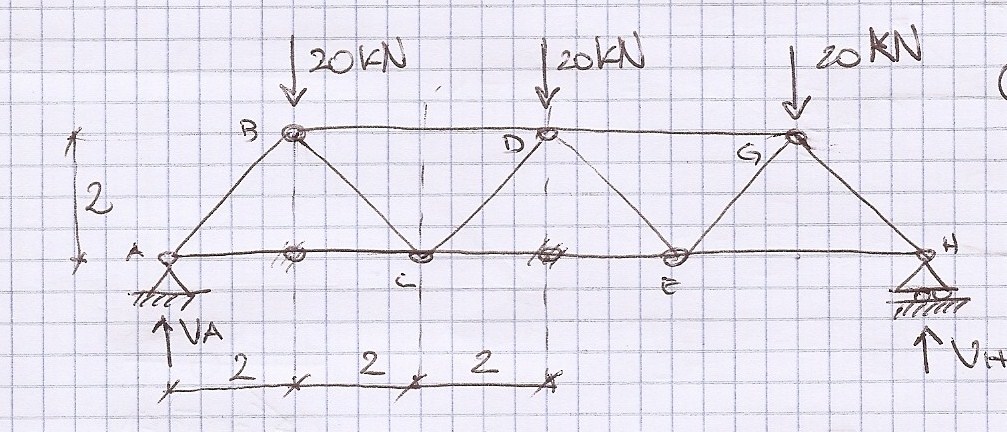
Anche l'asta AB è inclinata a 45° e per trovare lo sforzo a cui è sottoposta si fa una sezione che tagli le aste convergenti nel nodo A in modo da sezionare così l'asta incognita e una già calcolata (AC), potendo così fare l'equilibrio delle forze orizzontali.
-------> 
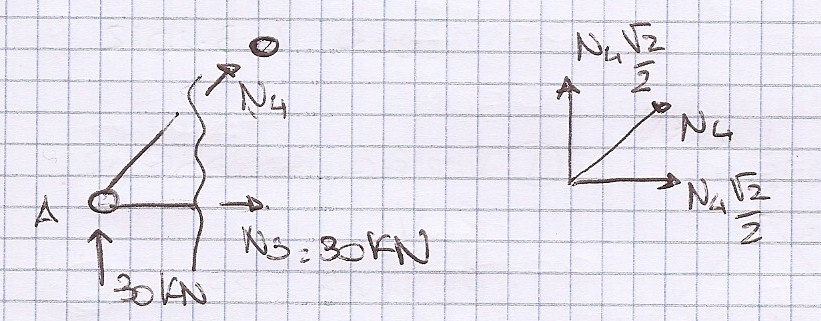∑Fx=0
30KN + N4 √2/2 = 0 ----> N4 = -30√2 KN
Il verso ipotizzato per lo sforzo normale N4 risulta sbagliato, perciò l'asta AB è compressa
Sezionando dopo il nodo C si tagliano le due aste di cui ancora si è calcolato lo sforzo normale, l'asta CE e l'asta CD
----> 
Facendo l'equilibrio dei momenti rispetto al nodo D si ottiene lo sforzo normale N5
∑Md=0
-30KNx6m + 20KNx4m + N5x2m =0 ----> N5= 50KN L'asta CE è tesa
Infine sfruttando l'equilibrio delle forze verticali si ottiene il valore dello sforzo N6
∑Fy=0
N6 √2/2 + 30KN -20KN = 0 ----> N6 = -10√2 NK ----> L'asta CD è compressa
Poichè la trave è di tipo simmetrico sia nella ripartizione dei carichi che nella disposizione delle aste, per capire se le aste mancanti sono puntoni o tiranti e ricavare il valore dello sforzo normale basta riportare in modo simmetrico i dati ottenuti dal calcolo della prima metà della trave.
Verifica con sap2000:
Per riprodurre la struttura su Sap2000 sono partita dal modello di una trave reticolare che ha di default gli stessi vincoli dell'esercizio, ho definito il numero e la dimensione delle campate, ho posto il momento all'inizio e alla fine di ogni asta uguale a 0, ho definito il carico e applicato le forze puntuali in corrispondenza dei nodi B, D e G ed ho avviato l'analisi:
Ottengo così l'immagine della deformata:
E i diagrammi con i valori dello sforzo assiale (rosso=aste copresse, giallo =aste tese):
Seconda esercitazione - trave reticolare asimmetrica
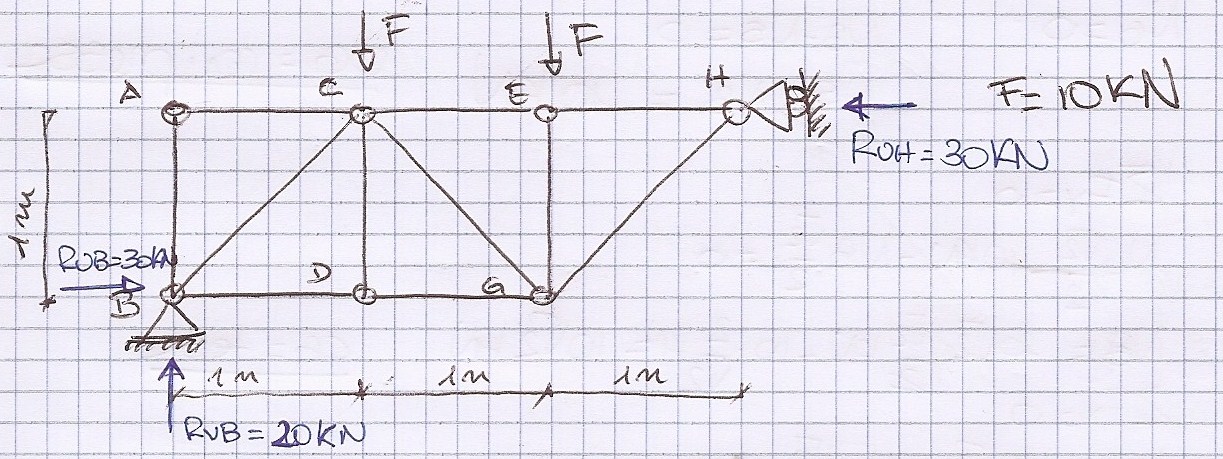
1) La prima cosa da fare è la verifica dell'isostaticità della trave, calcolando il numero dei gradi di libertè e il numero dei gradi di vincolo.
l=V ( n° gradi di libertà= n° gradi di vincolo)
l=3 x11 (3 x numero di corpi)
V= Ve +Vi (vincoli esterni + vincoli interni)
Ve= 3 Vi= 2(n-1)
A=H=2 B=D=E=4 C=8 G=6
Vi=4+12+8+6=30
V=3+30=33 l=33 ---> la struttura è isostatica
2) Il secondo passo è quello di trovare le reazioni vincolari facendo l'equilibrio delle forze verticali per ricavare la reazione verticale, e l'equilibrio dei momenti rispetto al nodo A per ricavare le reazioni orizzontali che riuslteranno uguali ed opposte esserndo le uniche presenti.
∑Fy=0
VB - 10KN -10KN =0 ----> VB=20KN
∑MA=0
UBx1m - 10KNX1m - 10KNx2m =0 ---> UB =30KN = UH
3) Le azioni di contatto sono state trovate utilizzando questa volta il metodo dei nodi, facendo cioè solamente l'equilibro delle forze verticali ed orizzontali per ottenere lo sforzo assiale che arriva sulla cerniera, isolando di volta in volta ogni nodo, In queso caso, non essendo una struttura simmetrica, è necessarico svolgere il procedimento per ogni nodo.
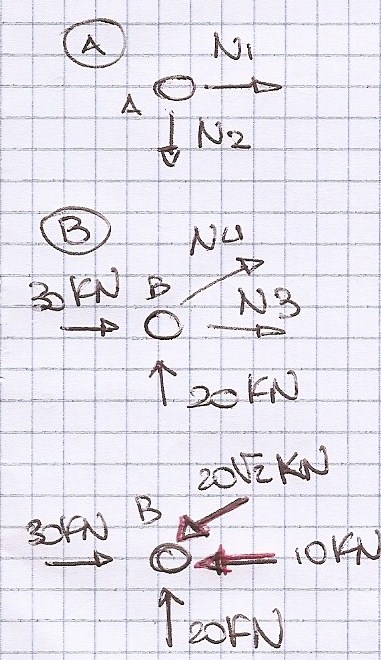
Partendo dal nodo A si nota subito che le due aste AC e AB sono scariche
Dall'equilibrio delle forze verticali del nodo B, scomponendo la forza poichè l'asta BC è a 45°, si ottiene lo sforzo assiale N4 = -20√2 KN, il verso ipotizzato è perciò sbagliato e l'asta BC risulta compressa
Dall'equilibrio delle forze verticali si ottiene incece N3 = -10KN e anche in questo caso il verso ipotizzato è sbagliato e l'asta BD è compressa
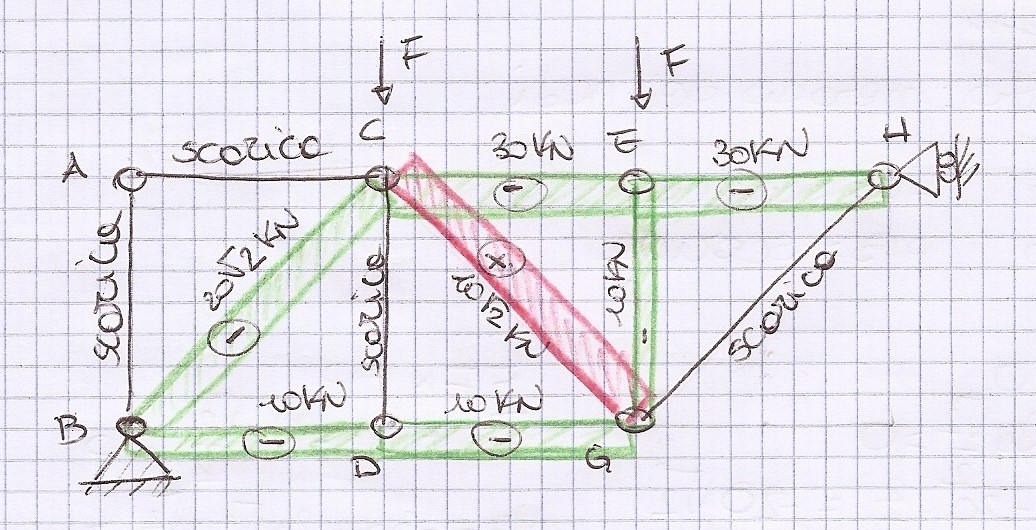
Lo stesso procedimento è stato utilizzato per i nodi restanti, in particolare l'asta DC e l'asta GH risultano scariche poichè nel nodo D N6=0 perchè non vi sono altre forze verticali che la equilibrano e nel nodo G N11=0
Tutte le aste sono compresse fatta eccezione per l'asta CG che è tesa con sforzo normale di trazione N8 =10√2 KN
N5=N3= 10KN DG asta compressa
N7= 30KN EC asta compressa
N10= 10KN EG asta compressa
N9= 30KN EH asta compressa
Nel nodo H facendo l'equilibrio alle forze orizzontali si verifica il valore dello sforzo di compressione dell'asta EH
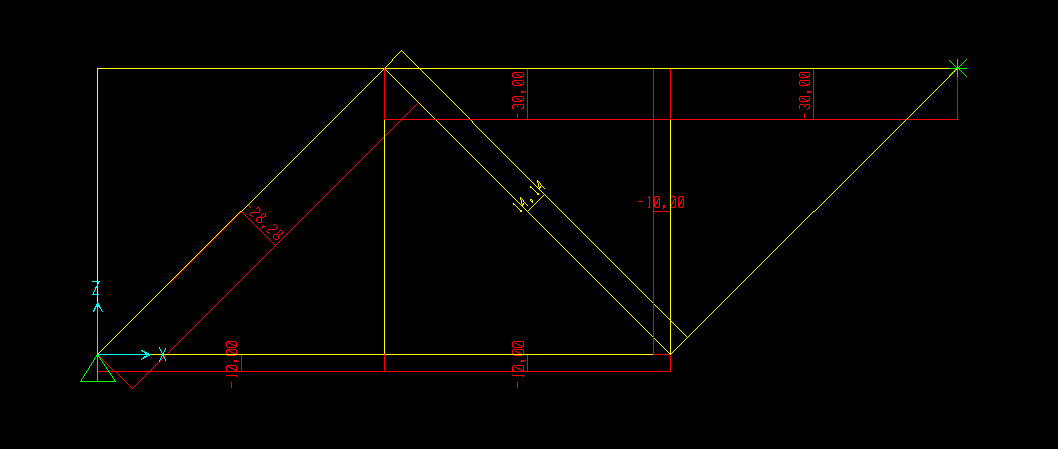
Verifica con sap2000:
Per riprodurre la trave su Sap2000 in questo caso ho utilizzato il modello della griglia, definedo numero e dimensione delle campate, disegnando poi le singole aste e applicando i vincoli nei nodi B ed H assegnando però al carrellino nel nodo H la sola traslazione verticale essendo posizionato verticalmente nell'essercizio. Ho poi posto il momento all'inizio e alla fine di ogni asta unguale a 0, ho definito e applicato i carichi puntuali nei nodi C ed E ed ho avviato l'analisi:
Si ottiene così l'immagine della deformata:
E i diagrammi con i valori dello sforzo assiale (rosso=aste copresse, giallo =aste tese):
Terza esercitazione - dimensionamento travi (svolto con Francesca Perusini)
Il solaio analizzato è quello di una casa a schiera progettata nel corso del Laboratorio di Progettazione1.
Essendo un edificio di civile abitazione il sovraccarico accidentale, legato alla funzione, sarà di 2 KN/m2. La trave da progettare sarà una trave doppiamente appoggiata in cui il momento massimo è ql2/8. L'esercitazione prevede il calcolo del solaio con tre diverse teconologie: acciaio, legno e calcestruzzo armato.
STRUTTURA IN ACCIAIO:
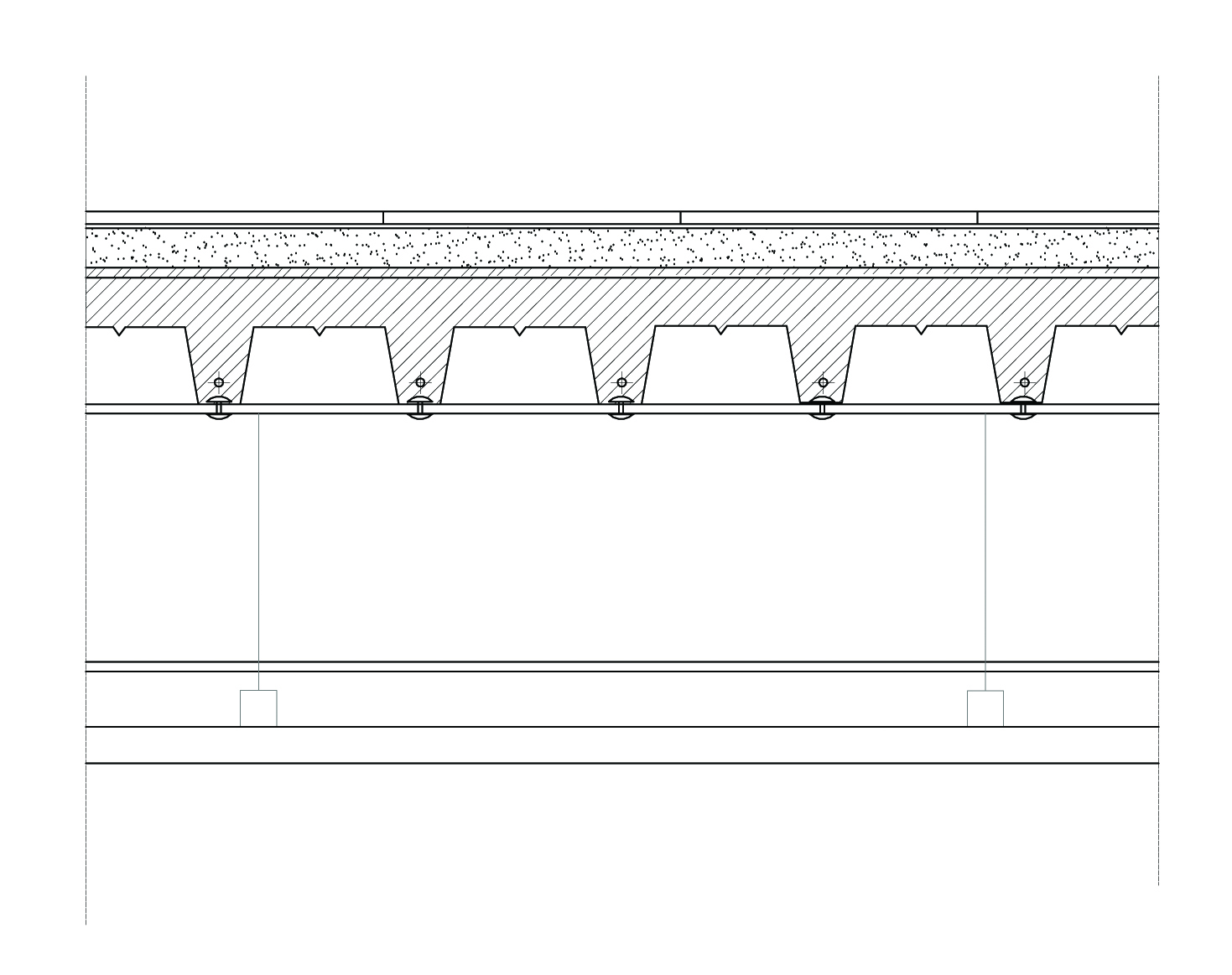
Dimensionamento della trave IPE:
Carico accidentale qa: 2KN/m2
Carico strutturale qs:
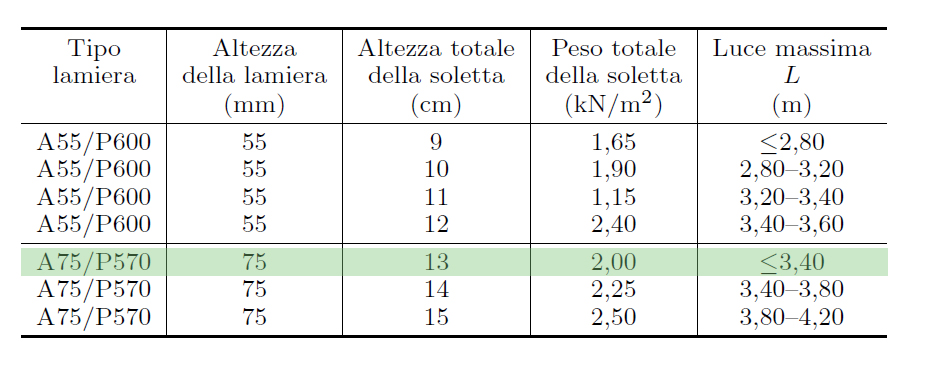
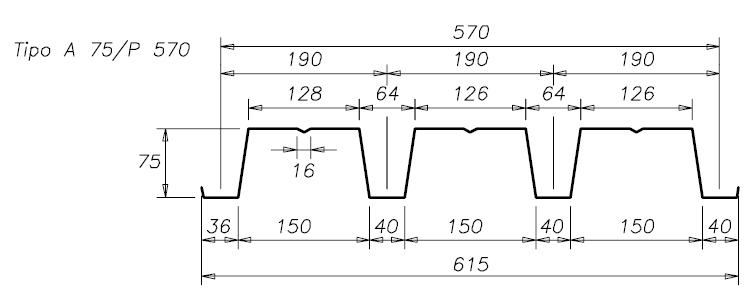
lamiera grecata tipo A75/P570: 2KN/m2
Sovraccarico permanente qp:
Isolante termoacustico: 360 Kg/m3 x 0,01 m = 3,6 Kg/m2 ------> 0,036 KN/m2
Massetto: 2000 Kg/m3 x 0,04 m = 80 Kg/m2 ------> 0,8 KN/m2
Piastrelle in Gres Porcellanato: 1540 Kg/m3 x0,013 m = 20 Kg/m2 -------> 0,2 KN/m2
Controsoffitto: 800 Kg/m3 x 0,03 m = 24 Kg/m2 ------> 0,24 KN/m2
Incidenza tramezzi : 1KN/m2
Incidenza impianti : 0,5 KN/m2
qp TOT = 0,036 KN/m2 + 0,8 KN/m2 + 0,2 KN/m2 + 1KN/m2 + 0,5 KN/m2 = 2, 536 KN/m2
Inserendo questi valori nel foglio di calcolo excel si ottiene il valore della resistenza Wx= 350,51 cm3
E' stata scelta perciò da profilario una trave IPE 270 il cui valore Wx = 429 cm3
STRUTTURA IN LEGNO:
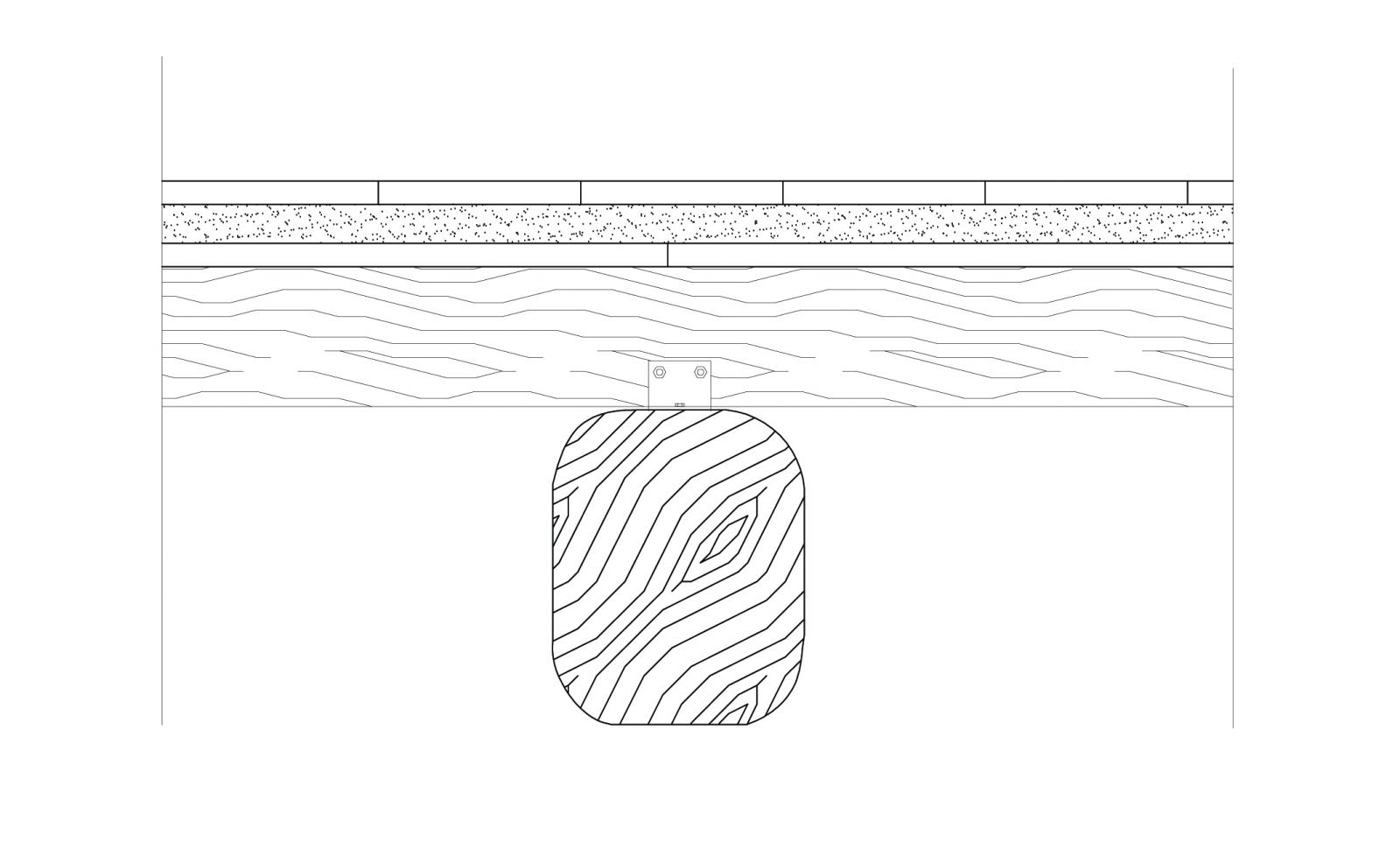
Dimensionamento travetto in legno:
Carico accidentale qa: 2KN/m2
Carico strutturale qs:
Tavolato in castagno 840 Kg/m3(Peso specifico ) x 0,03 m (Spessore) = 25,2 Kg/m2 -------> 0,25 KN/m2
Sovraccarico permanente qp:
Massetto: 2000 Kg/m3 x 0,05 m = 100 Kg/m2 -------> 1 KN/m2
Parquet in rovere: 720 Kg/m3x 0,02 m = 14,4 Kg/m2 --------> 0,144 KN/m2
Incidenza tramezzi: 1KN/m2
Incidenza impianti: 0,5 KN/m2
qp TOT= 1 KN/m2 + 0,144 KN/m2 + 1KN/m2 + 0,5 KN/m2 = 2,644 KN/m2
Dati:
Legno GL28h fk = 28 MPa
Interasse = 0,9 m
Luce = 3 m
b = 0,1 m
Inserendo questi dati nel foglio di calcolo excel si ottiene l'altezza del travetto:
E' stato perciò scelto un travetto di sezione 10cm x 20cm, poichè l'altezza minima necessaria risulta di 17, 65 cm
Dimensionamento trave in legno:
Carico accidentale qa: 2KN/m2
Carico strutturale qs:
Travetti in legno: 500 Kg/m3 x 0,1 x 1 = 50 Kg/m2 ------> 0,5 KN/m2
Tavolato in castagno: 0,25 KN/m2
qs TOT= 0,5 KN/m2 + 0,25 Kn/m2 = 0,75 KN/m2
Sovraccarico permanente qp: 2,644 KN/m2
Dati:
Legno GL28h fk = 28 MPa
Interasse = 3 m
Luce = 6 m
b = 0,2 m
Modificando i valori dell'interasse, luce, qp e b nel foglio excel, tenendo conto perciò anche del peso strutturale dei travetti, si ottiene l'altezza della trave:
La trave scelta ha una sezione di 20m x 50cm, essendo il valore minimo dell'altezza di 47,81 cm.
STRUTTURA IN CALCESTRUZZO ARMATO:
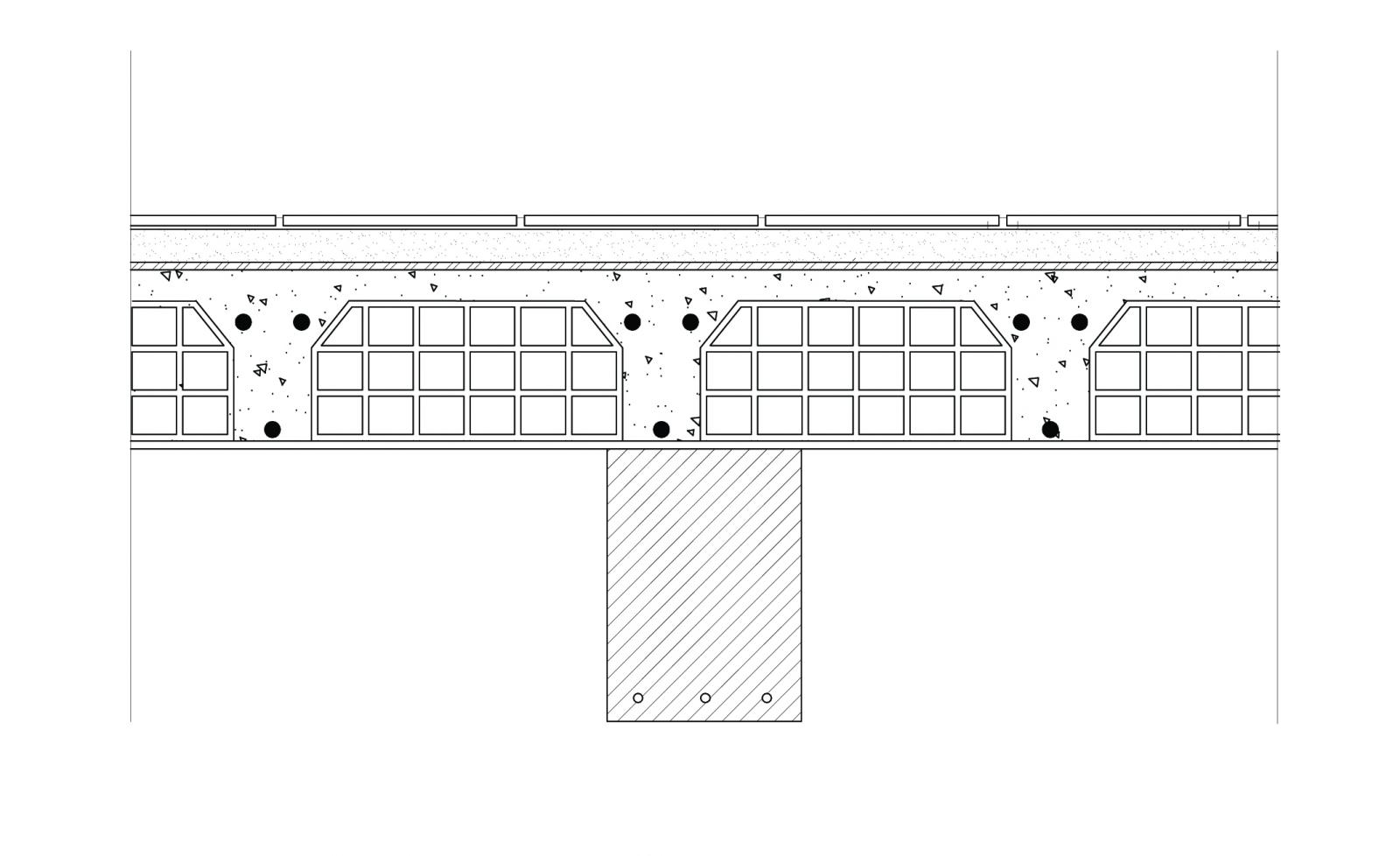
Dimensionamento trave:
Carico accidentale qa: 2KN/m2
Carico strutturale qs:
Travetti: 2500 Kg/m3 x 0,18 m x 0,1 m = 45 Kg -----> 0,45 KN x 2 (n° travetti in 1 m2)= 0,9 KN/m2
Pignatte: 550 Kg/m3 x 0,18 m x 0,4 m = 40 Kg ------> 0,4 KN x 2 (n° pignatte in 1 m2) = 0,8 KN/m2
Caldana: 2500 Kg/m3 x 0,04 m = 1 KN/m2
qs TOT= 0,9 KN/m2 + 0,8 KN/m2 + 1 KN/m2 = 2,7 KN/m2
Sovraccarico permanente qp:
Massetto: 2000 Kg/m3 x 0,04 m = 80 Kg/m2 -----> 0,8 KN/m2
Isolante termoacustico: 360 Kg/m3 x 0,01 m = 3,6 Kg/m2 ------> 0,036 KN/m2
Piastrelle in Gres Porcellanato: 1540 Kg/m3 x0,013 m = 20 Kg/m2 -------> 0,2 KN/m2
Intonaco: 200 Kg/m3 x 0,01 m =2 Kg/m2 -------> 0,02 KN/m2
qp TOT= 0,8 KN/m2 + 0,036 KN/m2 + 0,2 KN/m2 + 0,02 KN/m2 = 1,056 KN/m2
Dati :
Calcestruzzo C 25/30 fck = 30 MPa
base = 25 cm
copri ferro = 3 cm
Inserendo questi dati nel foglio di calcolo excel si ottiene l'altezza della trave:
Il valore minimo dell'altezza risulta essere 31,38 cm, la trave scelta ha perciò una sezione di 25cm x 35cm.
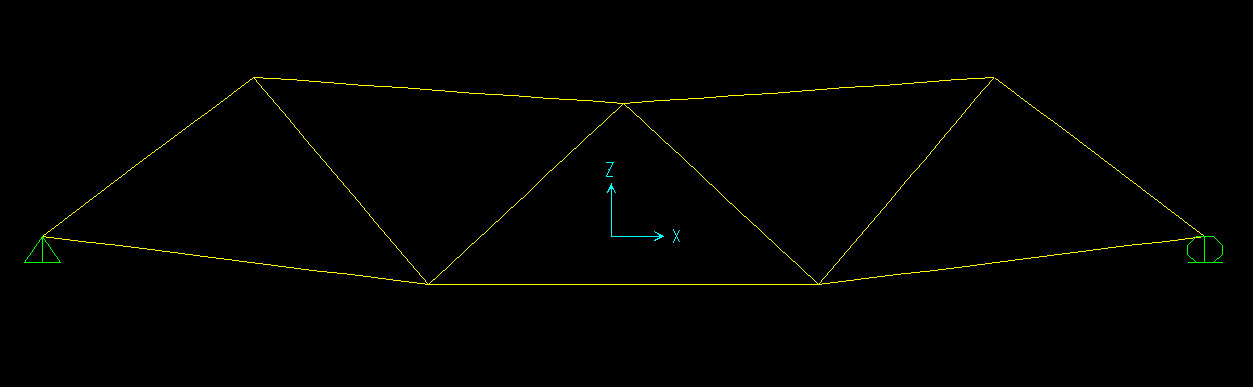
Quarta esercitazione - piastra reticolare spaziale
Disegno di una struttura reticolare spaziale su AutoCAD per poi importarla su Sap2000 in modo da poterla analizzare.
Disegno con AutoCad :
Si parte dal disegno di un modulo quadrato 2m x 2m costituito da tiranti, puntoni e diagonali in modo tale da poterlo riprodurre in serie.Si inizia a disegnare partendo dall’origine degli assi 0,0,0 utilizzando una polilinea per rappresentare le 3 aste e la diagonale, non chiudendo il quadrato in modo da non avere aste ripetute e sovrapposte dopo aver utilizzato la riproduzione in serie. Questo perchè il programma Sap2000 in cui si importerà il disegno non riconosce le aste sovrapposte.
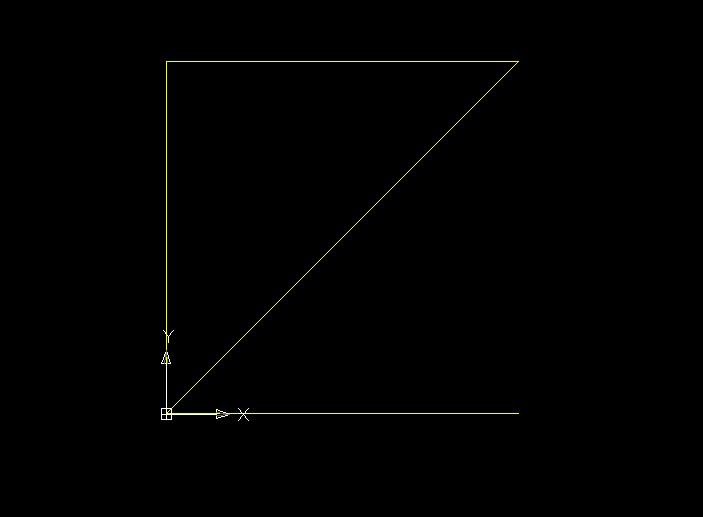
A questo punto è necessario passare dal piano 2D allo spazio 3D in modo da poter rappresentare gli elementi mancanti del modulo cubico (2m x2m x2m) da riprodurre in serie.
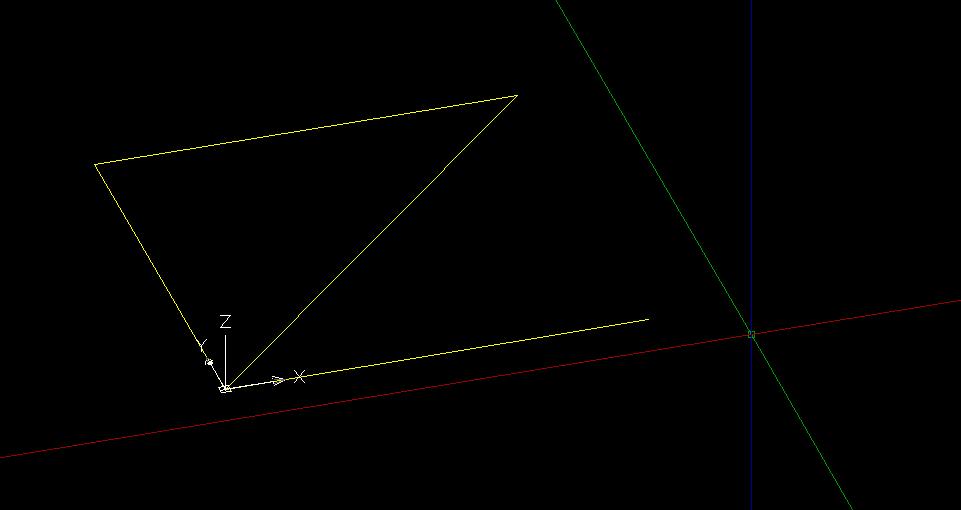
Prima di utilizzare il comando “serie” il disegno va ruotato nuovamente.
Fatto questo si selezionano le 4 aste e utilizzando il comando serie (array) ,che permette di fare copie in serie rettangolari, si fa la prima asta reticolare definendo una serie di 4 colonne con distanza l’una dall’altra di 2 m.
Alla reticolare così ottenuta va disegnata l’asta verticale finale assente nel modulo di base.
Ora si disegna il modulo base delle 3 aste e diagonale anche nella direzione dell’asse y e si riproduce in serie nello stesso modo usato precedentemente( con il comando serie/array). E’ necessario cambiare l’UCS, mettendo l’asse X lungo la direzione del nuovo array (UCS > invio > seleziona origine > seleziona direzione asse x > seleziona direzione asse y).
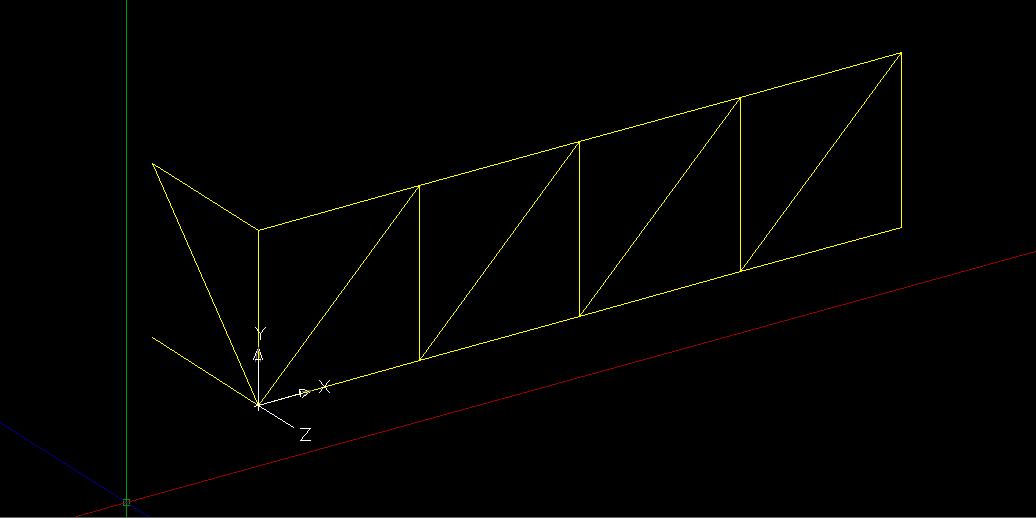
Si completa poi la prima campata disegnando le aste oblique superiori ed inferiori del primo modulo e duplicandole sempre con il comando serie/array, dopo aver opportunamente cambiato UCS.
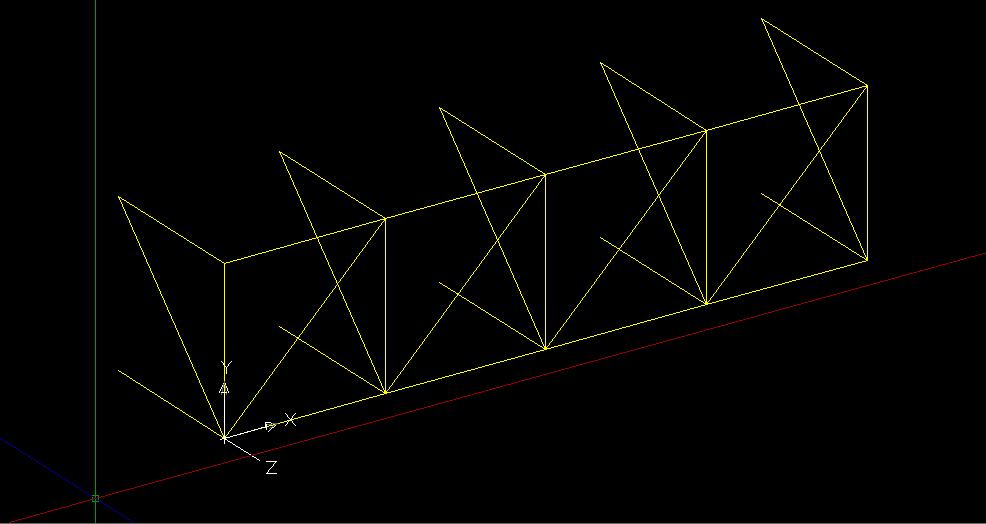
A questo punto si cambia nuovamente UCS (l’asse x deve essere sempre nella direzione della serie) e tutta la prima “riga” (modulo definitivo) viene selezionata e riprodotta con il comando serie/array con una serie di 7 colonne distanziate sempre di 2 m (dimensione del modulo base).
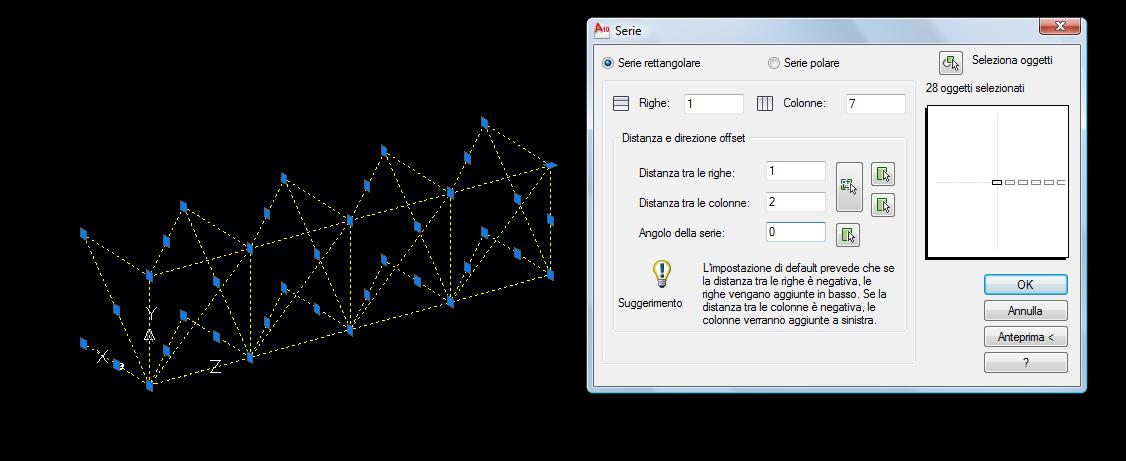
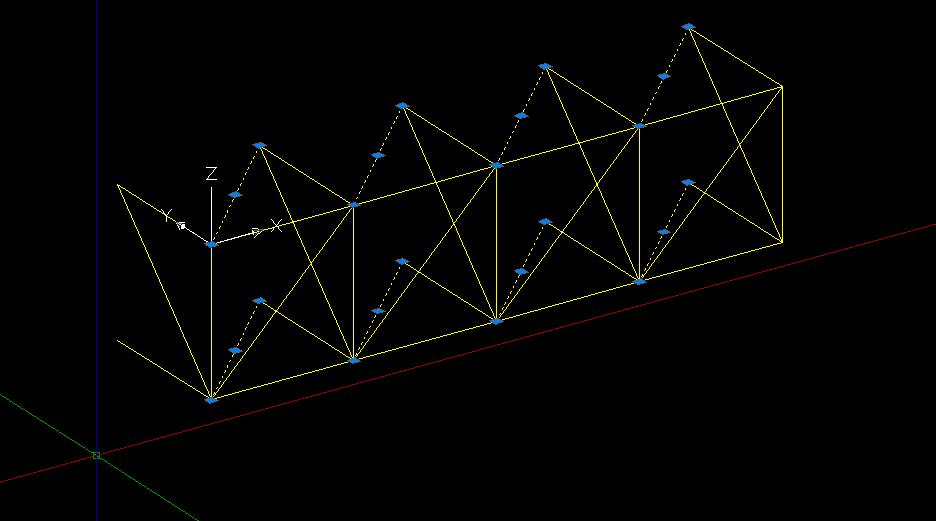
Si ottiene così una struttura reticolare spaziale con 4 capate lungo l’asse z e 7 lungo l’asse x. Dovendo quest’ultime essere 6, si cancellano le aste in eccesso; questo procedimento risulta più semplice rispetto alla riproduzione in serie del modulo solo per 6 colonne, dovendo poi disegnare tutte le aste di chiusura mancanti.
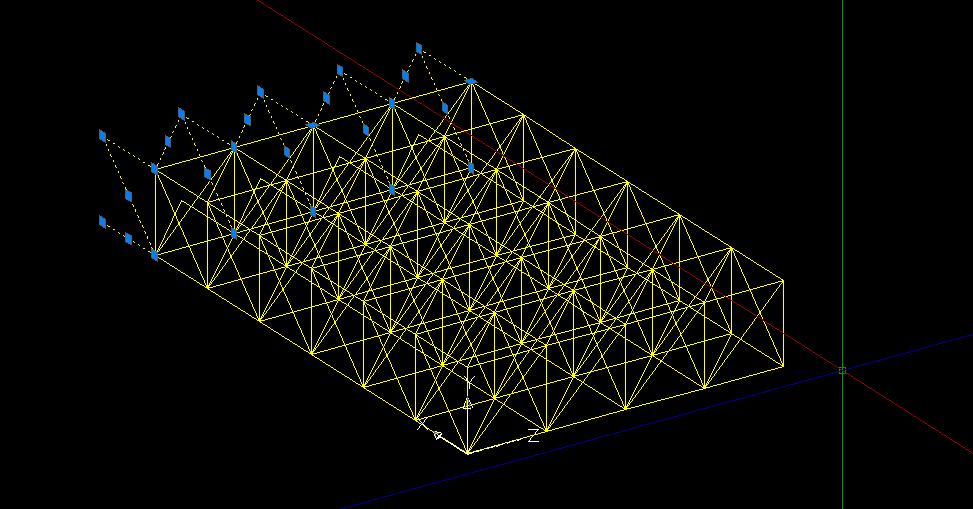
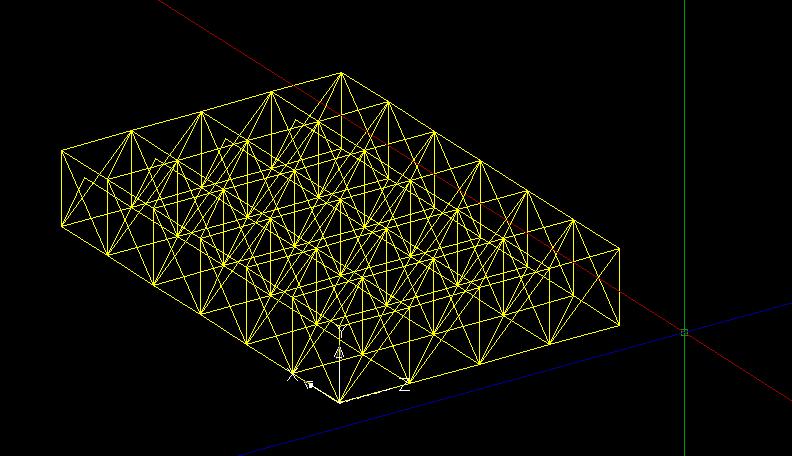
Prima di importare il disegno su Sap2000 si separano le polilinee con il comando “esplodi”.
Analisi su Sap2000:
Per importare il file, è necessario un salvataggio in formato .dxf2000. Una volta importato il file su Sap, sulla finestra che si aprirà automaticamente, bisogna selezionare alla voce “Frame” il layer usato su AutoCad per le aste (in questo caso il layer “aste”).
Successivamente si selezionano i 4 vertici della struttura per assegnare i vincoli (Assign > Join > Restraints ).
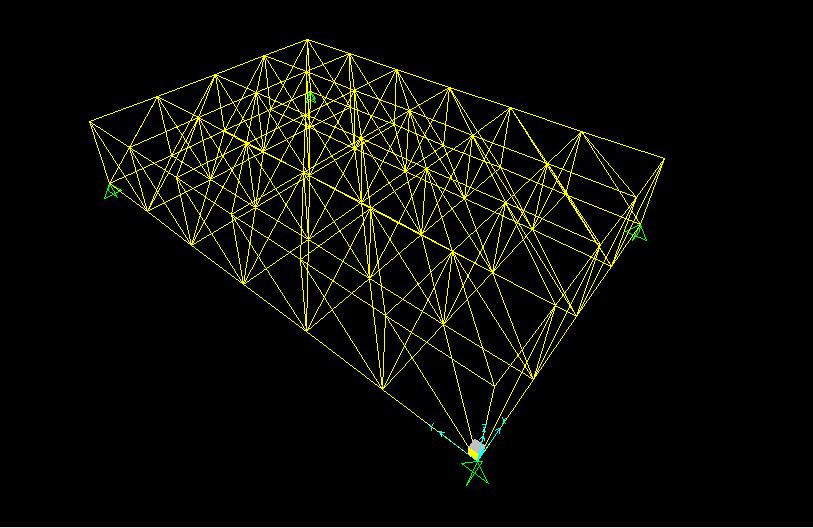
E’ poi necessario rilasciare i momenti nei nodi, in quanto cerniere interne, per assicurarsi che le aste siano sollecitate solo assialmente. Per fare questo, dopo aver selezionato tutto, si rilasciano i momenti all’inizio e alla fine di ciascun’asta (Assign > Frame> Partial Fixity).
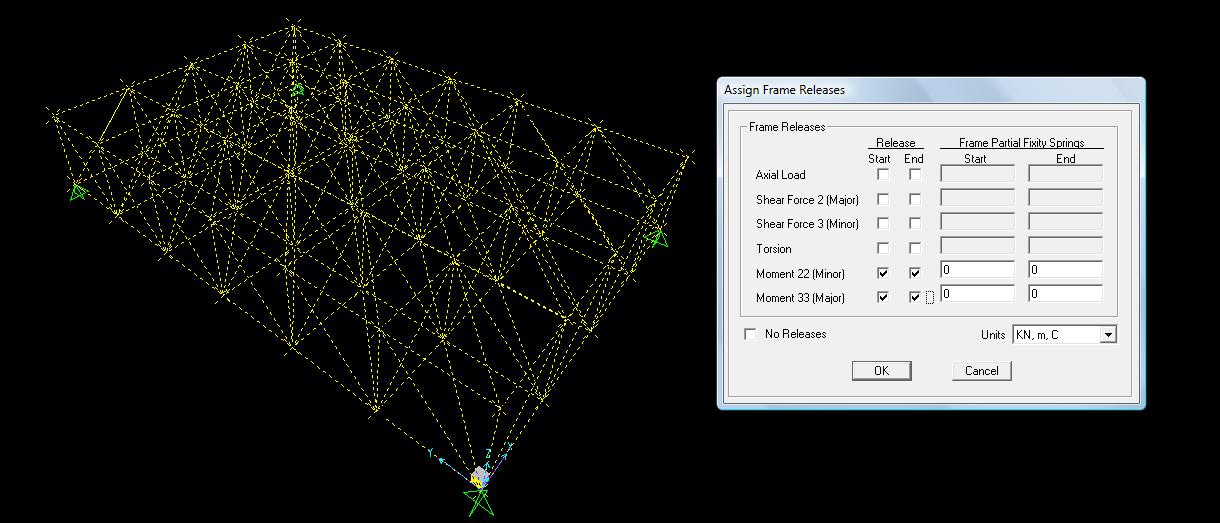
Prima di procedere con l’analisi della struttura è fondamentale definire il materiale e la sezione delle aste.
Define > Materials > Add New > “Steel”
Define > Section Proprieties > Frame Section > Add new > “Tubolare”(Pipe)---àMaterials > “Steel”
Definito questo si assegna alla struttura la sezione scelta con il relativo materiale (Assign > Frame > Frame Section > “Tubolare”).
Anche il carico deve essere prima definito e poi assegnato. A questo punto perciò si definisce un carico concentrato gravitazionale da applicare poi solamente nei nodi superiori opportunamente selezionati. Il carico verrà applicato sull’asse z con un valore di - 40 KN.
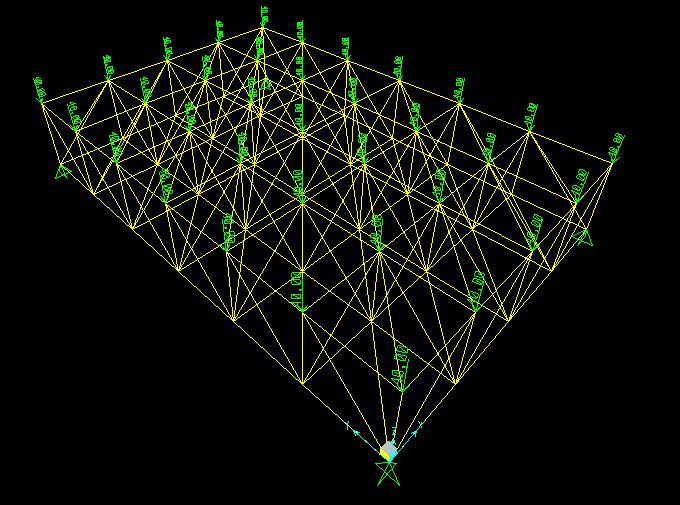
Fatto questo si può avviare l’analisi.
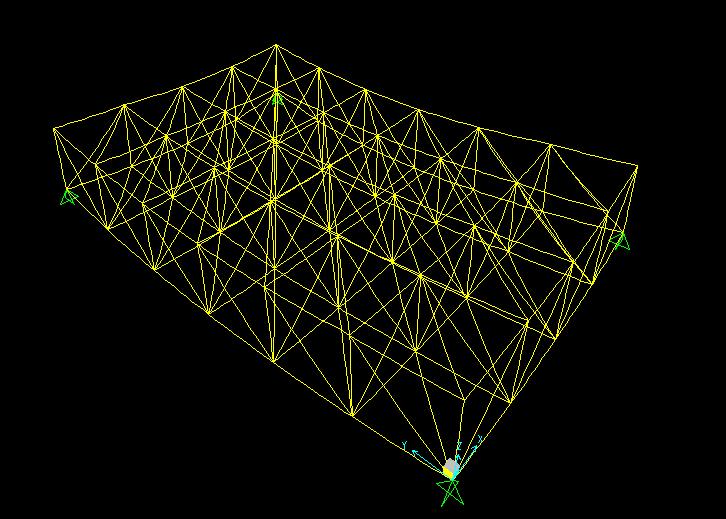
Poiché taglio e momento devono essere nulli, visto che le aste lavorano solamente a sforzo assiale, si ottengono solamente i diagrammi dello sforzo normale.
Diagramma sforzo assiale sul piano zx:
Diagramma sforzo assiale sul piano zy:
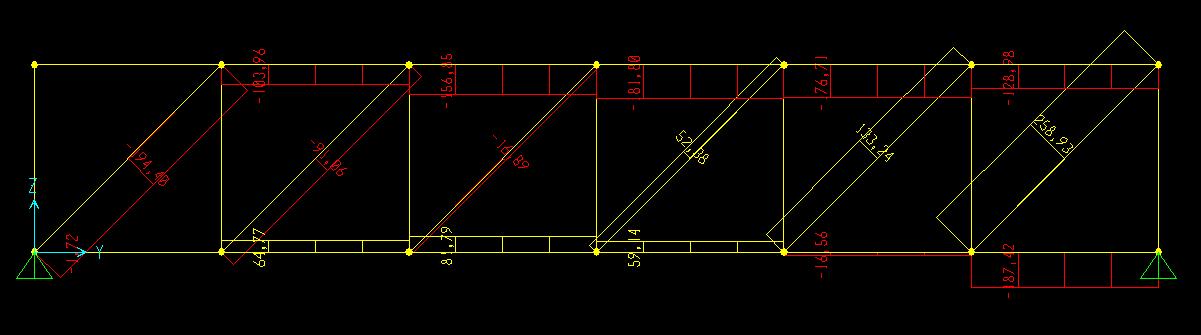
Spuntando la voce “Label”, nella tabella che si aprirà da set display options,tutte le aste verranno numerate; da display > show tables selezionando poi element output si aprirà una tabella con i dati di tutte le aste numerate. Per ciascuna asta sono presenti 3 valori che corrispondono alle sollecitazioni alle due estremità e nel mezzo. Alcune aste sono lunghe 2m ed avranno i 3 valori sotto la voce “station” di 0-1-2m, mentre altre(quelle diagonali) sono lunghe 2√2m ed avranno come misure 0-1,41-2,83m. I valori dello sforzo di taglio e momento come previsto risultano nulli.
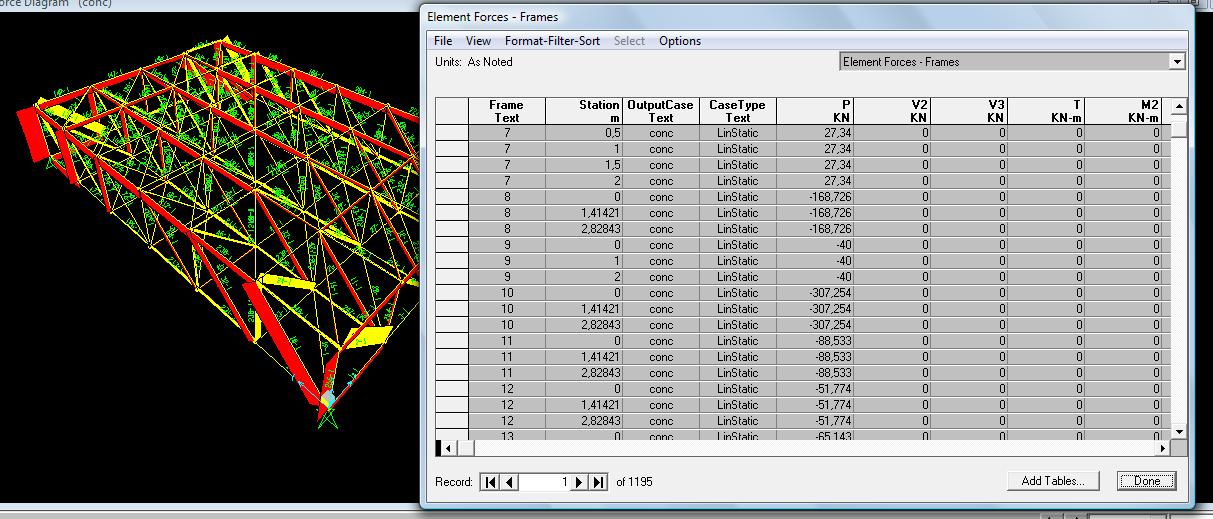
Esportando la tabella su Excel sarà più facile ordinare le aste in base a quelle soggette a maggiore sforzo normale sia di trazione (positivo) che di compressione (negativo). Dopo aver individuato queste due, si passa al progetto e verifica delle aste.
Progetto asta tesa:
Scelgo l’asta maggiormente tesa in modo da mantenermi in sicurezza; questa risulta essere la n°124 con un valore N=258,93KN.
Utilizzando la formula di Navier posso dimensionare l’asta.
Sapendo quindi che fd = N / A
A=N/fd dove fd= fyk/γm
fyk = resistenza a snervamento
γm=1,05 = coefficiente di sicurezza
Scelgo un acciaio Fe360 S235 e trovo un valore dell’area minima per poter resistere pari a:
A=258934 N/ (235 MPa/1.05) = 1157mm2 = 11,57cm2
Nel profilario dei tubi in acciaio a sezione circolare cerco un profilo che abbia un’area superiore a quella ottenuta.
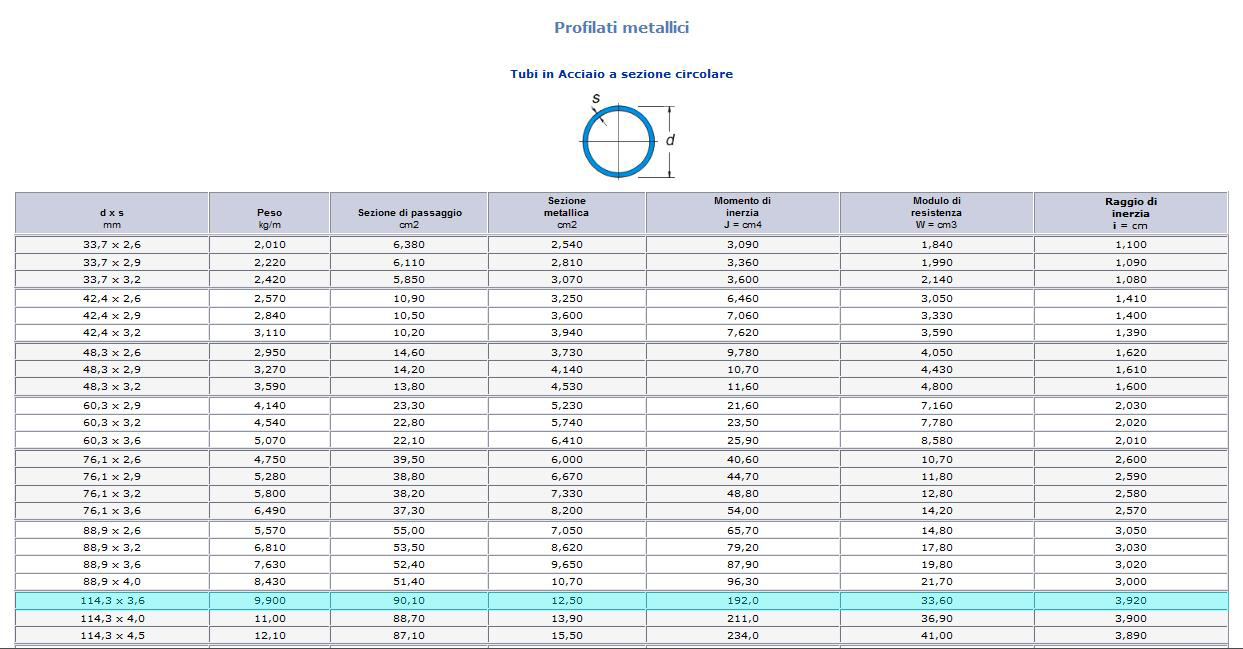
Scelgo perciò il profilo: d x s = 114,3x3,6 mm
A’= 12,50 cm2 > 11,57cm2.
Verifica a resistenza:
(N/A’)< fd
258934 N/1250 mm2= 207,14 MPa < 223,81 MPa
Asta verificata a resistenza.
Progetto asta compressa:
Lo stesso procedimento applicato all’asta maggiormente tesa, viene utilizzato per il progetto dell’asta compressa.
Le aste compresse possono però essere anche soggette a carico critico euleriano che le porta ad un’inflessione dell’asta fino al collasso. Questa è strettamente legata alla snellezza, ovvero quando il rapporto tra l’altezza e la lunghezza dell’elemento è molto grande.
Sono perciò necessarie anche verifiche a snellezza e a stabilità.
Scelgo l’asta maggiormente tesa in modo da mantenermi in sicurezza; questa risulta essere la n°10 con un valore N= -307,25KN.
Scelgo un acciaio Fe430 S275 e trovo un valore dell’area minima per poter resistere pari a:
A=N/fd
A=307254 N/ (275 MPa/1.05) = 1173mm2 = 11,73cm2
Nel profilario dei tubi in acciaio a sezione circolare cerco un profilo che abbia un’area superiore a quella ottenuta.
Scelgo perciò il profilo: d x s = 114,3x3,6 mm
A’= 12,50cm2 > 11,73cm2
Verifica a resistenza:
(N/A’)< fd
307254 N/1250 mm2= 245,80 MPa < 261,90 MPa
Asta verificata a resistenza.
Verifica a snellezza:
λ<200 λ =lo/ρ
lo = luce libera di inflessione che dipende dal tipo di vincolo dell’asta.
In questo caso abbiamo un’asta doppiamente incernierata
b=1
l=283 cm (asta diagonale)
lo=b*l=1*l;
ρ =raggio d’inerzia = 3,92cm (da tabella)
λ =283/3,92=7 2,19 < 200
Asta verificata a snellezza.
Verifica a stabilità:
Devo trovare il carico critico euleriano Ncr e verificare che lo sforzo assiale Nd sia minore della resistenza a stabilità Nd<Nbdr
Ncr = π2 x E x Jmin / l02
Dove: E = modulo elastico a compressione = 210000 N/mm2
Jmin= momento di inerzia minimo della sezione (da profilario) = 192 cm4 = 1920000 mm4
l0 = luce libera di inflessione, ovvero quanto è larga l'onda sinusoidale che definisce lo sbandamento,che dipende dai vincoli. In questo caso i i vincoli sono cerniere perciò l0 = l. l = √2 m = 2,83 m (asta diagonale).
Ncr = π2x 210000 N/mm2 x 1920000 mm4 / (2830 mm)2=
= 9,86x 210000 N/mm2 x 1920000 mm4 / 8008900 mm2= 496371,6 N = 496,37 KN
Nd < Nbdr
dove Nbdr = resistenza all'instabilità = χ* A* fyk / γm
χ = 1 / (φ + √φ2-λ2) < 1
φ = 0,5 (1 + α (λ_ - 0.2) + λ_2)
α = fattore di imperfezione = 0,21
λ_= √(A * fyk / Ncr)
Inserendo queste formule in un foglio Excel il calcolo sarà più immediato
Le caselle in bianco sono quelle in cui i dati vanno inseriti, quelle in azzurro sono quelle in cui il valore viene calcolato.
Ottengo Nbrd = 254,31 KN > Nd =307,25 KN
Asta non verificata a stabilità.
Scelgo perciò una sezione maggiore e ricalcolo il valore di Ncr inserendo il relativo momento d'inerzia. Utilizzando il foglio di calcolo excel è possibile vare rapidamente più prove fino ad arrivare al profilo che soddisfi la verifica a stabilità.
Secondo tentativo: asta non verificata
Terzo tentativo: asta verificata
Profilo scelto: d x s = 114,3x4,5 mm
A’= 15,50cm2
Ncr = π2x 210000 N/mm2 x 2430000 mm4 / (2830 mm)2=
= 9,86x 210000 N/mm2 x 1920000 mm4 / 8008900 mm2= 604952,9 N = 604,95 KN
Nd < Nbdr
Ottengo Nbrd = 313,57 KN > Nd =307,25 KN
Asta verificata a stabilità.
Quinta esercitazione - RIPARTIZIONE DELLE FORZE SISMICHE (svolto con Francesca Perusini)
La forza sismica è una forza d’inerzia che arriva alla struttura per effetto di un’accelerazione di trascinamento. Dipende dal prodotto della massa della struttura per l’accelerazione massima che la struttura riceve quando viene scossa dal terreno; infatti maggiore sarà la massa dell’edificio, maggiore sarà la forza sismica agente su di esso.
F = m*a
a è una frazione dell’accelerazione di gravità:
a = c g dove c < 1 è coefficiente di intensità sismica
La forza sismica è perciò:
F = m*cg = c (mg) dove mg = forza peso P ----> F = cP.
Per contrastare la forza sismica è necessario prevedere nella struttura dell’edificio dei controventi che permettano di resiste anche alle sollecitazioni orizzontali.
Per analizzare l’azione della forza sismica si considera che il solaio in esame si comporti come un corpo rigido e perciò possa subire una traslazione verticale, traslazione orizzontale e rotazione. I telai inoltre si comportano come dei corpi elastici (delle molle) che ricevono la forza sismica e la restituiscono come forza di richiamo.
La forza sismica agisce sul centro di massa e determina una traslazione del corpo rigido.
E’ molto importante la distribuzione delle rigidezze in pianta perché la struttura può subire anche una rotazione intorno al centro delle rigidezze sempre dovuta all’effetto della forza orizzontale. Questo accade nel caso in cui il centro delle rigidezze non coincide con il centro di massa; in questa situazione si crea un momento dato dalla forza sismica per il braccio, ovvero per la distanza tra il centro di massa e il centro delle rigidezze.
La struttura analizzata è in acciaio ed è composta da 5 controventi verticali e 4 controventi orizzontali.
La sezione dei pilastri è una HE 160 con valori di momento d’inerzia:
Ix = 1673 cm4
Iy = 616 cm4
I pilastri sono disposti in pianta con l’anima parallela alla trave principale, con le ali perpendicolari alla trave principale poiché devono anche portare il solaio; per questo motivo i due pilastri centrali dell’impalcato (3,5) sono posizionati diversamente rispetto agli altri. Bisogna tenere conto di questo nella scelta del momento d’inerzia da inserire nelle tabelle per il calcolo delle rigidezze in quanto si sceglierà quello rispetto all’asse y per tutti i pilastri ad eccezione di dei pilastri centrali per i quali si utilizzerà il momento d’inerzia rispetto all’asse x.
Step 1 : CALCOLO DELLE RIGIDEZZE TRASLANTI DEI CONTROVENTI DEL’EDIFICIO
Utilizzando il foglio di calcolo excel si trovano i valori delle rigidezze traslanti dei 9 telai della struttura, inserendo opportunamente i diversi momenti d’inerzia, come sopra descritto.
La rigidezza totale si trova:
KT =( 12E *Σi Ii ) / h3
E = modulo di Young = 210000 N/mm2 per l’acciaio
h = altezza dei pilastri
Σi Ii = sommatoria dei momenti di inerzia di tutti i pilastri della struttura.
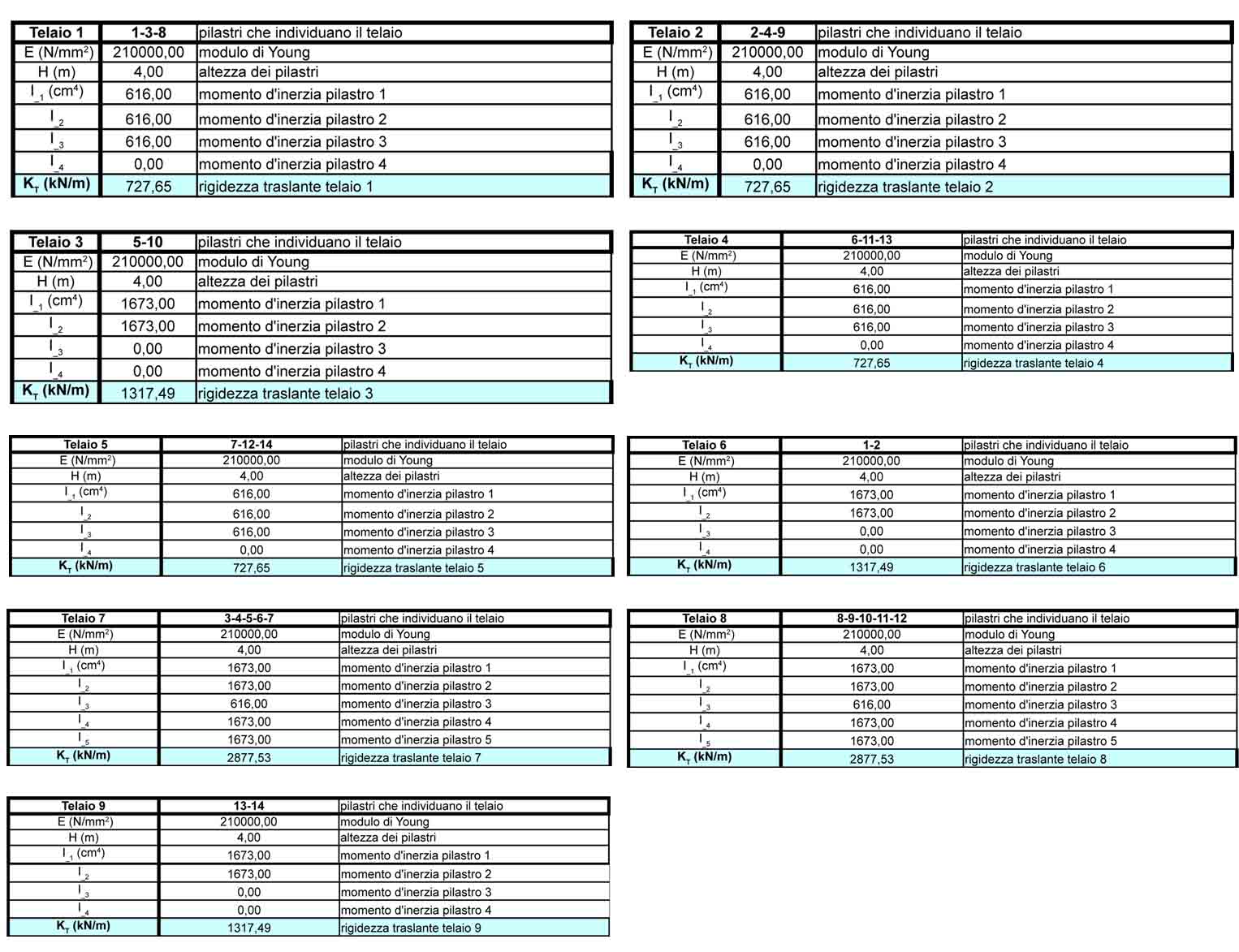
Step 2 : TABELLA SINOTTICA CONTROVENTI E DISTANZE
Nella tabella sono riportati i valori delle rigidezze calcolate precedentemente e le relative distanze dal punto O.
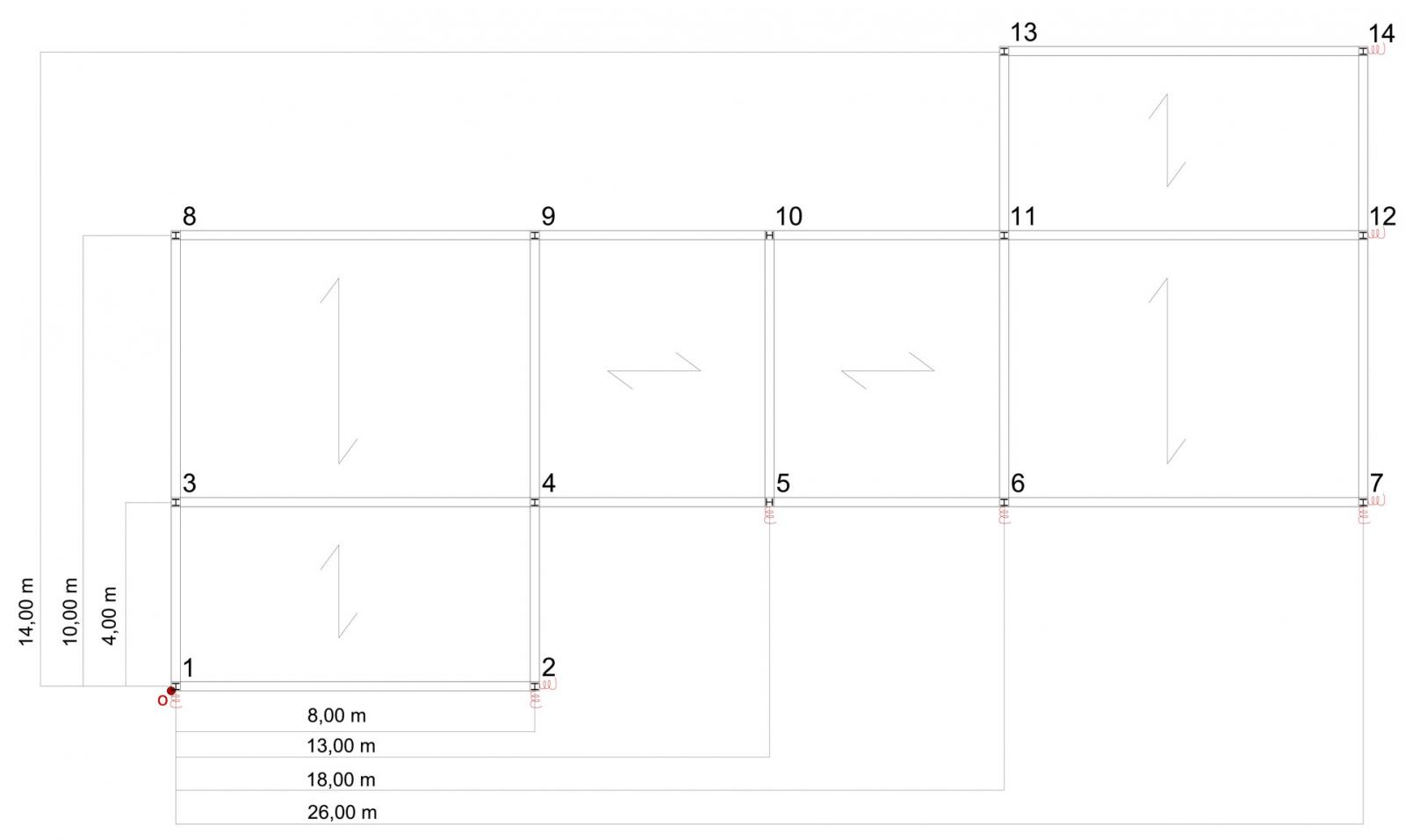
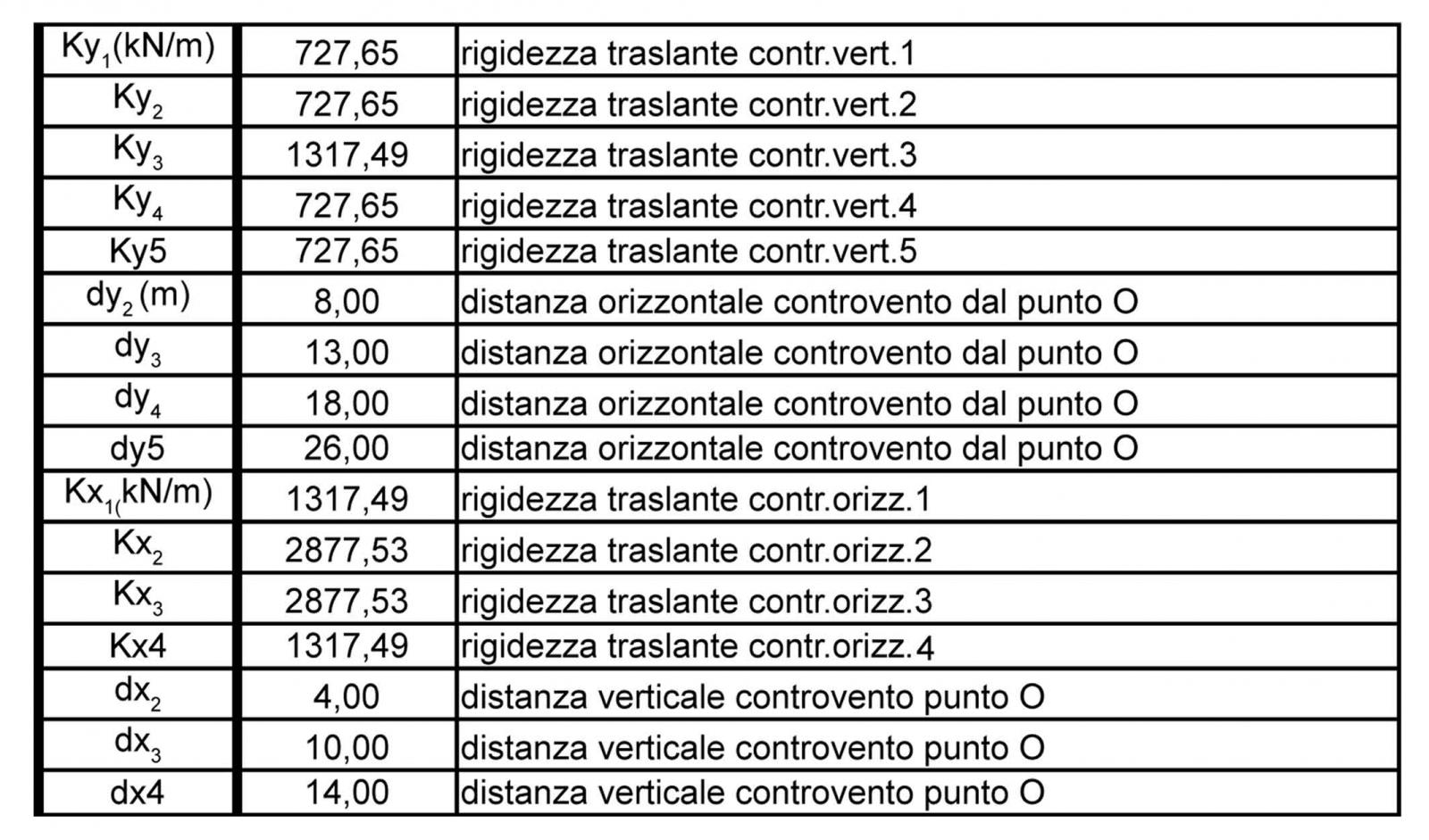
Step 3 : CALCOLO DEL CENTRO DI MASSA
La forza sismica viene applicata nel centro di massa. Si calcola perciò il valore delle tre aree in cui abbiamo diviso l’impalcato e le coordinate dei rispettivi centri di massa (XG,,YG). Per trovare il centro di massa dell’area totale dell’impalcato so sommano i prodotti delle tre aree per le rispettive coordinate x e y e si divide per l’area totale.
XG = (A1 xG1 + A2 xG2 + A3 xG3) / (A1 + A2 + A3) = ΣiAi*xi/ Atot
YG = (A1 yG1 + A2 yG2 + A3 yG3) / (A1 + A2 + A3) = ΣiAi*yi/ Atot
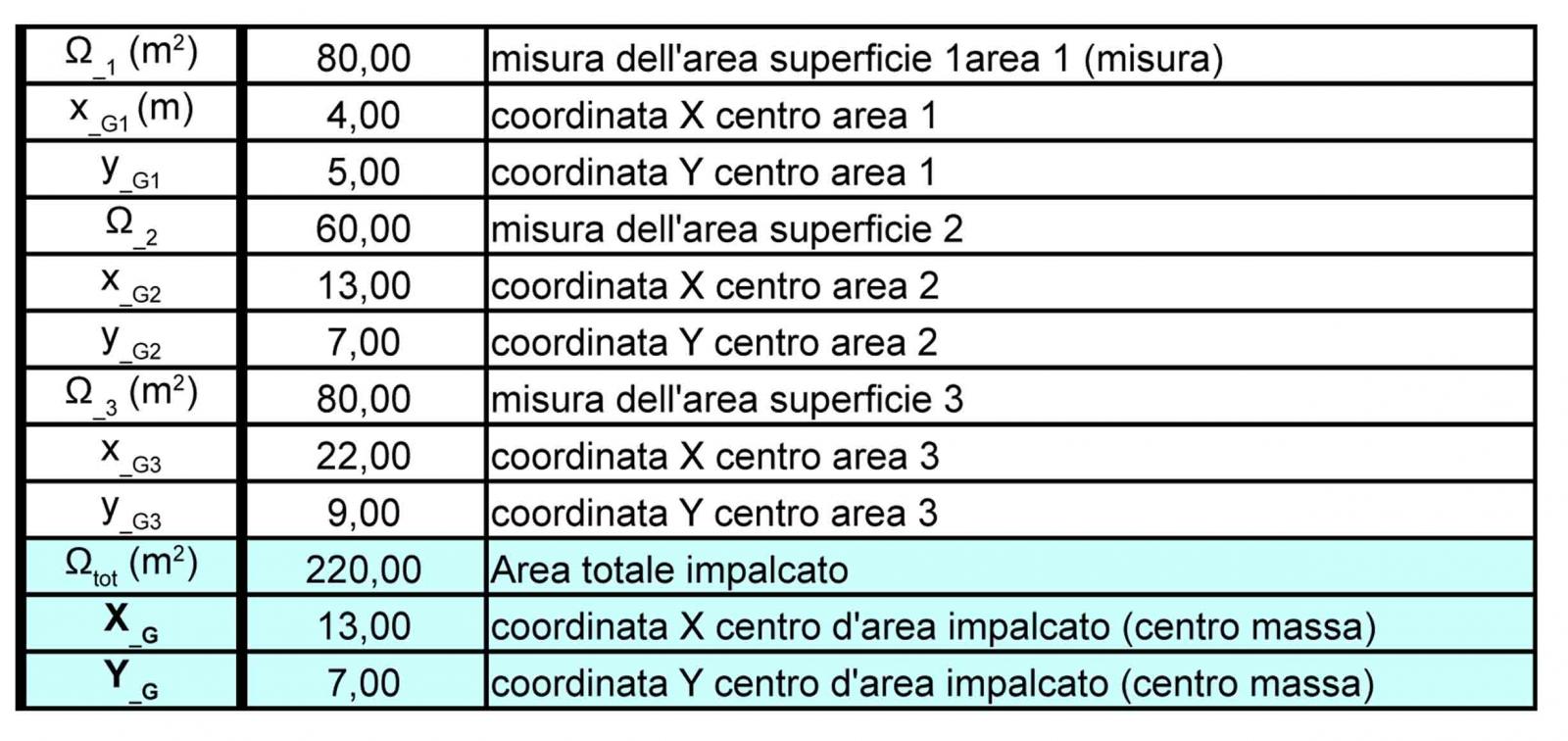
Step 4 : CALCOLO DEL CENTRO DELLE RIGIDEZZE E DELLE RIGIDEZZE GLOBALI
A questo punto tramite il foglio excel si calcolano le rigidezze totali verticali ed orizzontali e le relative coordinate del centro delle rigidezze (Xc , Yc):
ΣiKxi = rigidezza totale orizzontale (Kx tot)
ΣiKyi = rigidezza totale verticale (Ky tot)
Xc = ΣiKxi*dyi/ kyitot. sommatoria delle rigidezze dei controventi orizzontali per le relative distanze verticali dal punto 0
Yc = ΣiKyi*dxi / kxitot. sommatoria delle rigidezze dei controventi verticali per le relative distanze orizzontali dal punto 0
Il centro delle rigidezze è il punto attorno a cui l’impalcato ruota ne caso in cui la forza esterna (sismica) non passi per ques’ultimo.
Si calcola ora la rigidezza torsionale totale :
Kφtot = ΣiKyi*ddyi2 + ΣiKxi*ddxi2
dove ddy e ddx sono le distanze dei controventi dal centro delle rigidezze ed hanno segno positivo o negativo in base alla rotazione positiva o negativa che subiscono (molle si allungano o si accorciano per effetto della rotazione).
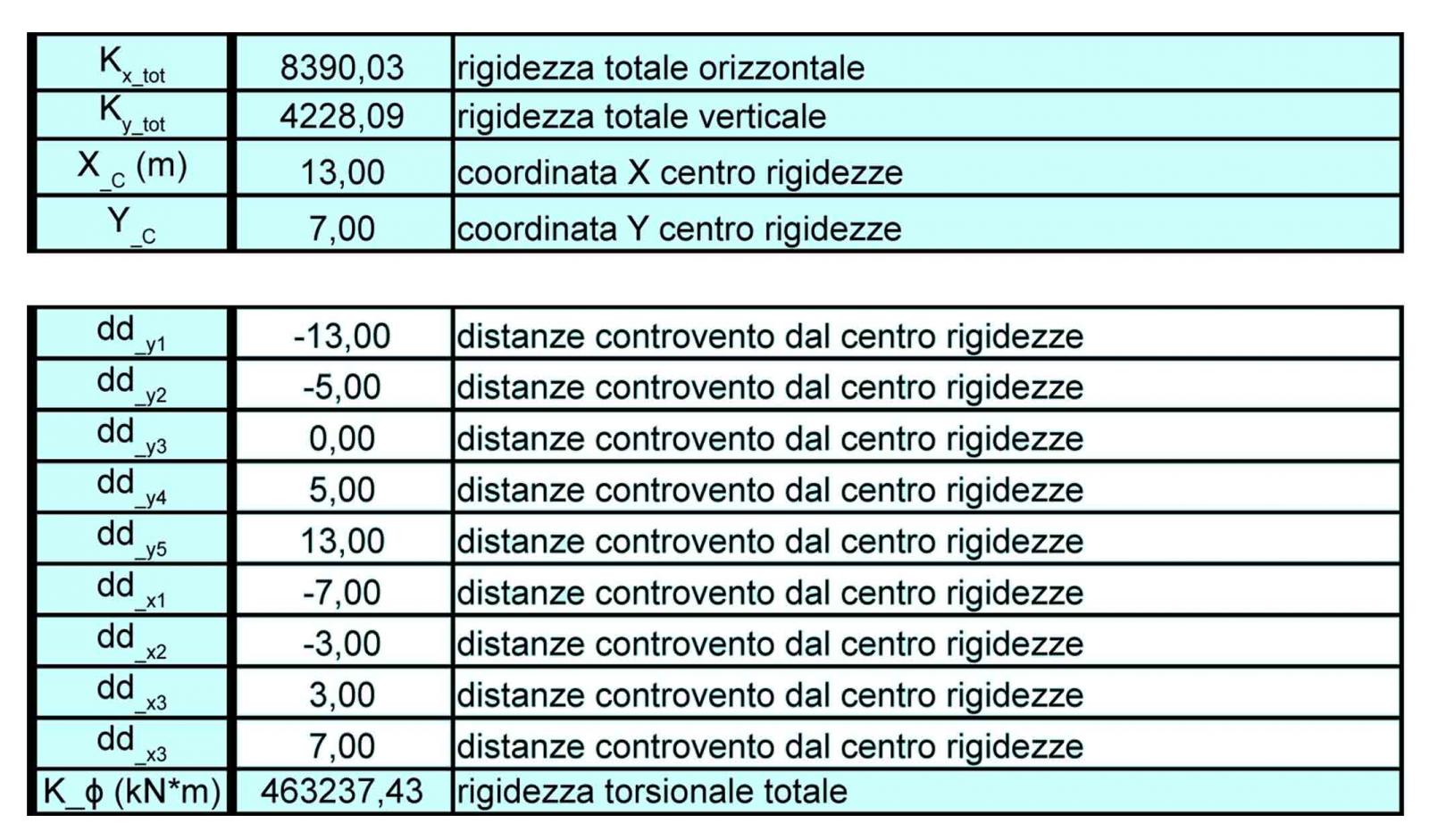
Step 5 : ANALISI DEI CARICHI SISMICI
La forza sismica, come già detto, è data dalla forza peso per il coeff. d’intensità sismica:
F = cP
E’ perciò una frazione della forza peso (poiché c < 1).
Per calcolare la forza sismica è necessario perciò calcolare il peso della struttura (P), definendo carichi strutturali, sovraccarico permanente e carico accidentale (qs , qp, qa).
P = G + ψ Q
G = carico totale permanente = (qs + qp) *Atot
Q = carico totale accidentale = qa *Atot
ψ = coefficiente di contemporaneità, dato dalla normativa, che diminuisce il carico accidentale (ψ=0,80).
Adesso si può calcolare il valore di F assumendo c=0,20
Step 6_7 : RIPARTIZIONE DELLA FORZA SISMICA LUNGO X E LUNGO Y
A questo punto si analizza la ripartizione della forza sismica sia lungo x che lungo y; questo perché l’azione del sisma è incerto e non possiamo sapere a priori in quale direzione si svilupperà.
Il foglio di calcolo excel riporta il calcolo di:
-Momento torcente: M = F (XC - XG)
M = F (YC - YG)
dove (XC - XG) è il braccio della forza, ovvero la distanza tra la coordinata Y del centro delle rigidezze e quella del centro di massa, nel caso in cui il centro di massa non coincida con il centro delle rigidezze.
-Traslazione: ux = F/Kx tot
uy = F/Ky tot
-Rotazione rigida: φ = F*b / Kφtot (Momento torcente/rigidezza totale)
Ora si può calcolare come la forza sismica si ripartisce su ogni controvento in relazione alle loro rigidezze:
Rxi = Kxi (ux + φ ddxi) controventi orizzontali
Ryi = Kyi (uy + φ ddyi) controventi verticali
Ripartizione della forza sismica lungo x:
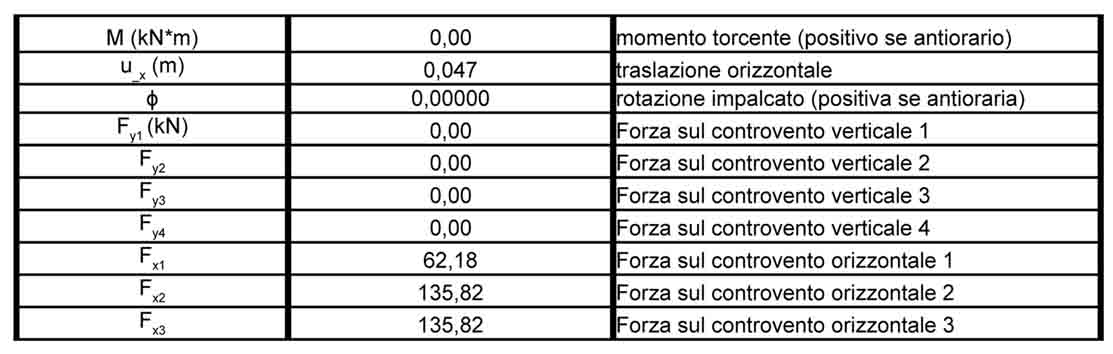
Ripartizione della forza sismica lungo y:
In questo caso la rotazione risulta nulla. Questo è dovuto al fatto che l’impalcato scelto è simmetrico perciò il centro di massa (punto di applicazione della forza sismica) coincide con il centro delle rigidezze e di conseguenza il braccio della forza sismica , responsabile della rotazione sarà nullo.
Commenti recenti