blog di Marika.Prete

TRAVI RETICOLARI

Le travi reticolari sono strutture composte da aste che possono essere solo tese (tiranti) o solo compresse (puntoni), collegate tra di loro tramite cerniere interne. Trascurando il peso delle aste e in presenza di forze concentrate, la struttura è così soggetta ai soli sforzi assiali.

1.      Risolvere la travatura reticolare asimmetrica col metodo dei nodi

1.   Verifica dell’isostaticità della struttura

·         La struttura è isostatica se il numero dei gradi di vincolo è pari al numero dei gradi di libertà della struttura: n°gdv=n°gdl

n°gdl Si calcola moltiplicando il numero degli elementi per 3 che è il numero dei gradi di libertà nel piano di ciascun corpo.                     Quindi abbiamo:      n°gdl= 11 (n° delle aste)*3=33.

n°gdv Si calcola sommando i vincoli esterni ai vincoli interni. n°gdv=Ve+Vi

La struttura presenta 3 vincoli esterni : Ve=3  (2 gradi di libertà bloccati dalla cerniera e 1 grado di libertà bloccato dal carrello)

Il numero dei vincoli interni della struttura si calcola applicando, per ogni nodo,  Vi=2*(n-1) dove n rappresenta il numero di aste che convergono nel nodo.

Vi A-G           n=2       2*(2-1)=2

Vi B-D-E        n=3       2* (3-1)=4

Vi F                n=4        2*(4-1)=6

Vi C                n=5        2*(5-1)=8

Vi= 2*2 + 4*3 + 6 + 8= 30

n°gdv= Ve+Vi= 3+30=33= n°gdl  quindi l’isostaticità è verificata

·         Un altro metodo consiste nel verificare che Ve + a = 2*n°nodi         dove a è il numero delle aste.

Per cui abbiamo 3+11 = 2*7

         14=14       Anche in questo modo l’isostaticità è verificata

 

2.   Calcolo delle reazioni vincolari

Imponendo l’equazione di bilancio alla traslazione verticale ottengo che V(B)= 20kN.

Attraverso l’equazione di bilancio ai momenti M(B) ottengo che U(G)= 30kN

Imponendo l’equazione di bilancio alla traslazione orizzontale ottengo che U(G)= U(B) =30kN

 

 

3.   Calcolo delle azioni di contatto

A questo punto vado a calcolare le forze lungo le aste mediante il metodo dei nodi. Questo metodo si basa sull’assunto che il modello tramite cui studiamo le travature reticolari considera le forze concentrate sui nodi; sapendo questo, e sapendo che le aste sono soggette al solo forzo normale, possiamo andare a studiare il sistema in 2modi

·         Attraverso l’equilibrio al nodo, scomponendo le forze che agiscono su ogni nodo e applicando le equazioni di bilancio alla traslazione orizzontale e verticale (in quanto le cerniere sono soggette solo a sforzi assiali, per cui tutte le forze che vi convergono hanno braccio nullo producendo, quindi, azioni di momento nulle)

·         semplicemente secondo il metodo geometrico utilizzando la regola del parallelogramma per la scomposizione delle forze

Utilizzare entrambe le procedure può essere anche uno strumento di verifica.

NODO A

Poste le incognite N1 e N2 (decido arbitrariamente se  le aste sono soggette a trazione o compressione e cambio il verso se il risultato è negativo), osserviamo subito come le aste 1 e 2 siano scariche.

NODO B

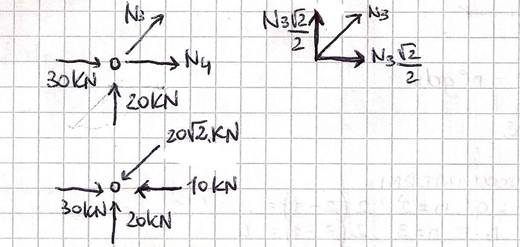
Scomponendo N3 nelle sue componenti e imponendo l’equilibrio alla traslazione orizzontale e verticale ottengo che le aste 3 e 4 sono compresse.

Andiamo a studiare lo stesso nodo tramite il metodo geometrico: questo metodo consiste nello scomporre tutte le forze che agiscono sul nodo tramite la regola del parallelogramma (sempre seguendo l’inclinazione delle aste della trave delle quali sto cercando i contributi), una alla volta, e sommare quelli che risulteranno essere i contributi di diverse forze agenti lungo la stessa retta d’azione. Scompongo così la forza verticale pari a 20 kN lungo la direzione delle aste 3 e 4 e trovo velocemente i contributi di queste aste verificando il risultato precedentemente trovato.

NODO D

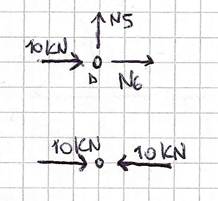
Notiamo subito come l’asta 5 sia scarica e l’asta 6 debba dare un contributo opposto a quello imposto, ossia debba essere compressa.

NODO C

 

Scompongo i contributi delle aste 5 e 7. Ottengo che l’asta 7 è tesa, mentre l’asta 8 è compressa. Verifico i risultati mediante il metodo geometrico.

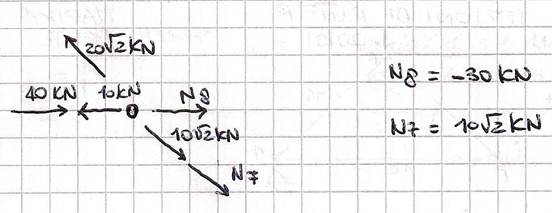
NODO F

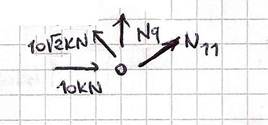
Risolvo il nodo F applicando direttamente il metodo geometrico. Ottengo che l’asta 11 è scarica mentre l’asta 9 è compressa.

NODO G

Essendo scarica l’asta 11, l’unico contributo incognito nel nodo in questione è quello dell’asta 10 che risulta essere compressa.

A questo punto posso disegnare l’intera struttura e vederla nel suo complesso.

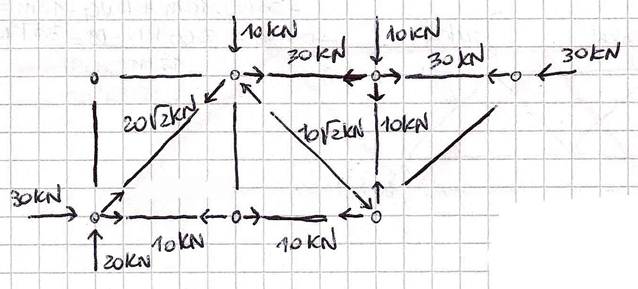
4.   Verifica della struttura con SAP2000

Disegno la struttura mediante una griglia. Annullati i momenti all’inizio e alla fine di ogni asta, assegno i vincoli esterni. Dopo aver assegnato una sezione tubolare alle aste e definito il materiale, in questo caso l’acciaio, creo un carico concentrato (in Load Patterns) e lo assegno ai nodi C ed E. Mando infine l’analisi.

 

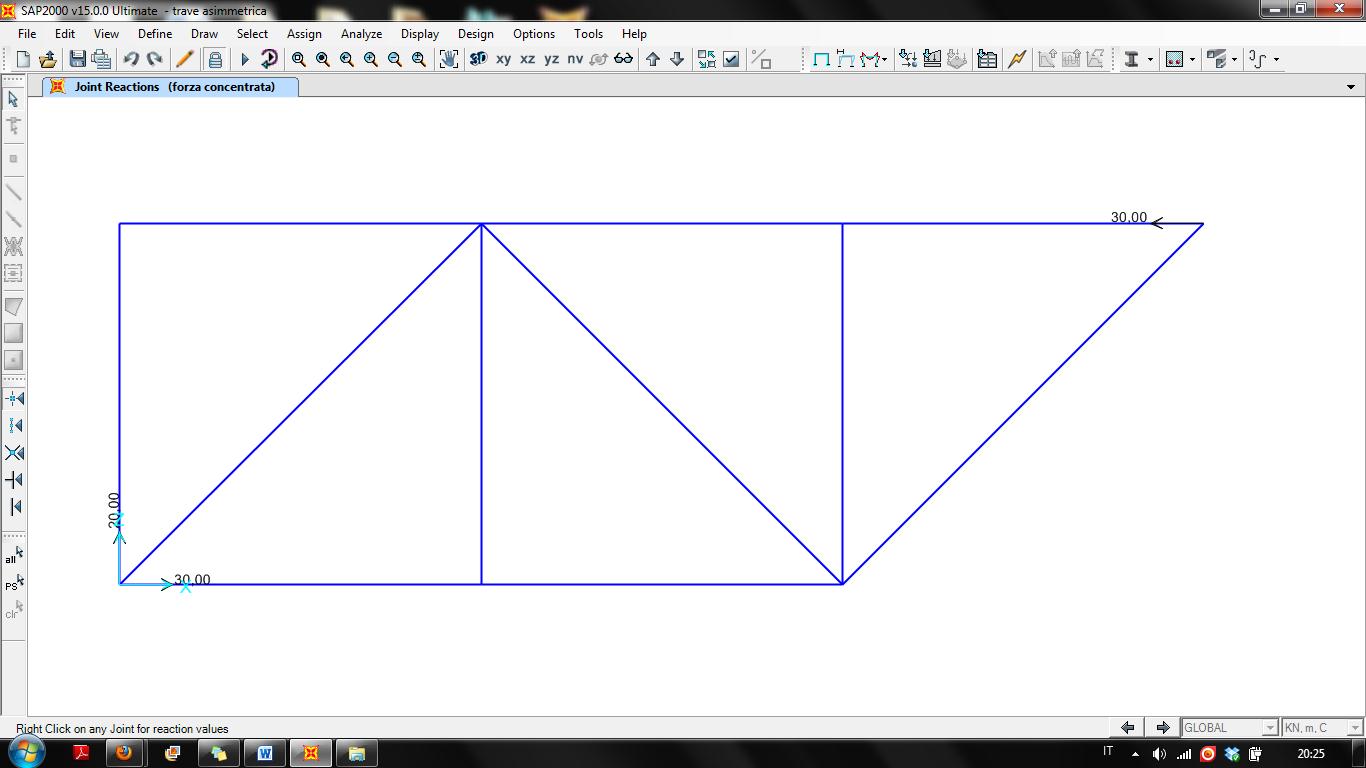
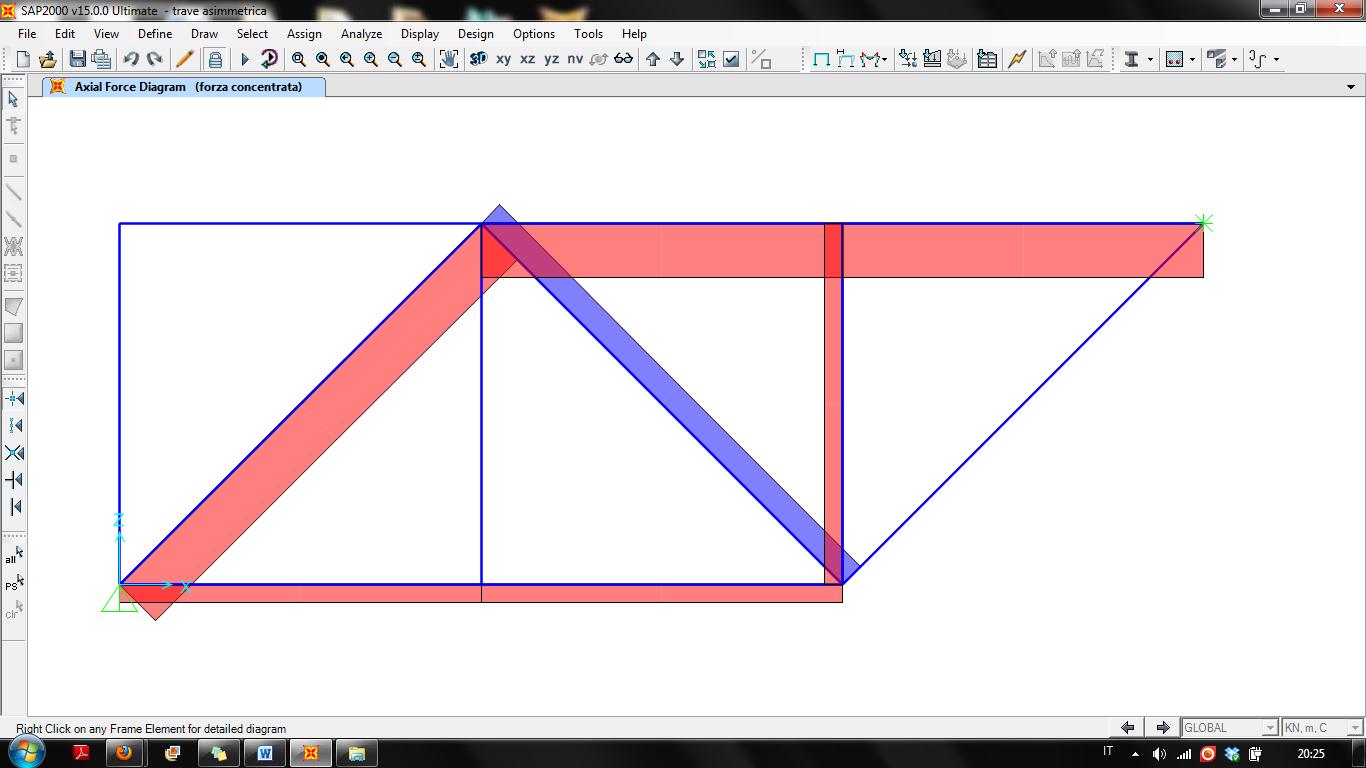
2. Risolvere la travatura reticolare simmetrica col metodo delle sezioni

1.   Verifica dell’isostaticità della struttura

Come già visto al punto 1 dell’esercizio 1 verifichiamo l’isostaticità della struttura.

n°gdv=n°gdl

n°gdl = 11 (n° delle aste)*3=33

n°gdv=Ve+Vi

Vi B-G                       n=2   2*(2-1)=2

Vi A-F                        n=3   2*(3-1)=4

Vi C-D-E                    n=4      2*(4-1)=6

Vi= 2*2 + 4*2 + 6*3= 30

n°gdv= Ve+Vi= 3+30=33= n°gdl  quindi l’isostaticità è verificata

 

2.   Calcolo delle reazioni vincolari

In questo caso le reazioni vincolari in (B) ed in (G) dovute alla cerniera ed il carrello, si calcolano semplicemente imponendo l’equilibrio alla traslazione verticale (come nel caso di una trave appoggiata) e data la simmetria del sistema i vincoli si ripartiscono equamente la reazione ai carichi applicati (60kN).

RU(A) è nulla non dovendo bilanciare nessun’altra forza orizzontale.

 

 

3.   Calcolo delle azioni di contatto

Per mettere in evidenza le azioni di contatto (che in questo caso sono gli sforzi normali nelle aste) dobbiamo effettuare un taglio virtuale della struttura in due parti tramite una sezione di Ritter. Dicesi sezione di Ritter una sezione che divide in due la struttura tagliando tre aste non convergenti nello stesso nodo.

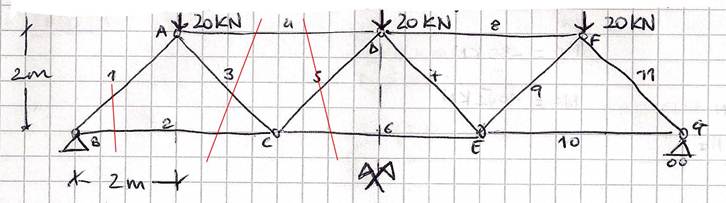
SEZIONE 1

Una volta effettuato il taglio virtuale, si mettono in evidenza gli sforzi normali agenti sulle sezioni delle aste tagliate. Disegnare le forze (N1), (N2) ed (N3) uscenti dalla sezione vuol dire considerare in prima ipotesi che le aste sezionate siano sottoposte a trazione (tiranti). Posso scegliere arbitrariamente il verso di queste forze, in quanto sarà il risultato delle equazioni di equilibrio che confermerà il verso delle azioni di contatto o deciderà che il verso è opposto: in tal caso l'asta risulterà in compressione (puntone). A questo punto, per determinare i valori di (N1), (N2) ed (N3), userò l'assioma di bilancio che sancisce - per una struttura deformabile - l'equilibrio di tutte le forze agenti sulla generica parte.

Le incognite sono tre e tre sono le equazioni di bilancio a nostra disposizione. Quindi il problema è risolvibile.

La regola che viene suggerita è quella di scrivere tre equazioni di equilibrio a rotazione, cambiando ogni volta il polo, che viene scelto nel punto di incontro di due delle tre aste tagliate.

Per esempio: nel nodo (C) convergono due delle tre aste sezionate; ciò implica che nell'equazione di equilibrio del momento rispetto a (C), rimarrebbe una sola forza incognita, ossia l'azione di contatto dell'asta che non converge in C. Otteniamo così che N4 = -40 kN , è un risultato negativo, per cui ne concludiamo che l’asta 4è un puntone. Allo stesso modo, mediante l’equilibrio dei momenti rispetto ad A, trovo il contributo dell’asta 2 pari a 30 kN, che risulta essere uno sforzo di trazione. Per calcolare (N3) potrei imporre l’equilibrio a momento intorno al nodo (B) o più comodamente l’equilibrio alla traslazione verticale dell’intera sezione (che si può anche interpretare come l’equilibrio a momento rispetto ad un punto che si trova all’infinito).

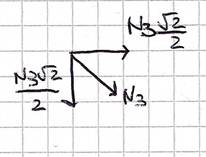
Scomponendo la forza nelle sue componenti orizzontale e verticale imponendo le equazioni di equilibrio alla traslazione otteniamo che N3 è una forza di trazione, quindi l’asta 3 è un tirante

SEZIONE 2

Della prima parte di trave che stiamo studiando l’unica asta di cui non conosciamo il comportamento è l’asta 1, che non era stata sezionata. Andiamo a fare una seconda sezione di Ritter:

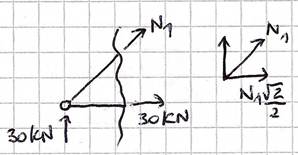
Conoscendo il valore di (N2), possiamo scrivere sia l’equilibrio alla traslazione verticale che l’equilibrio alla traslazione orizzontale, i cui risultati non potranno differire tra di loro. Dall'equilibrio alla traslazione orizzontale, otterremo

che N1 è uno sforzo assiale di compressione.

SEZIONE3

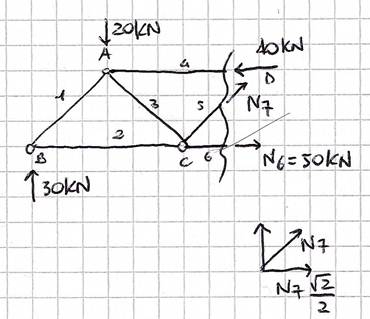
Mediante l’equilibrio ai momenti rispetto a D, troviamo il contributo dell’asta 6, che risulta essere un tirante. Mediante l’equilibrio alla traslazione orizzontale troviamo invece la forza N7, che è una forza di compressione.

 

Ovviamente la struttura è simmetrica, nonché caricata simmetricamente, per cui tutti i valori finora trovati li possiamo riportare sulla parte di trave che per ora non abbiamo considerato, ottenendo

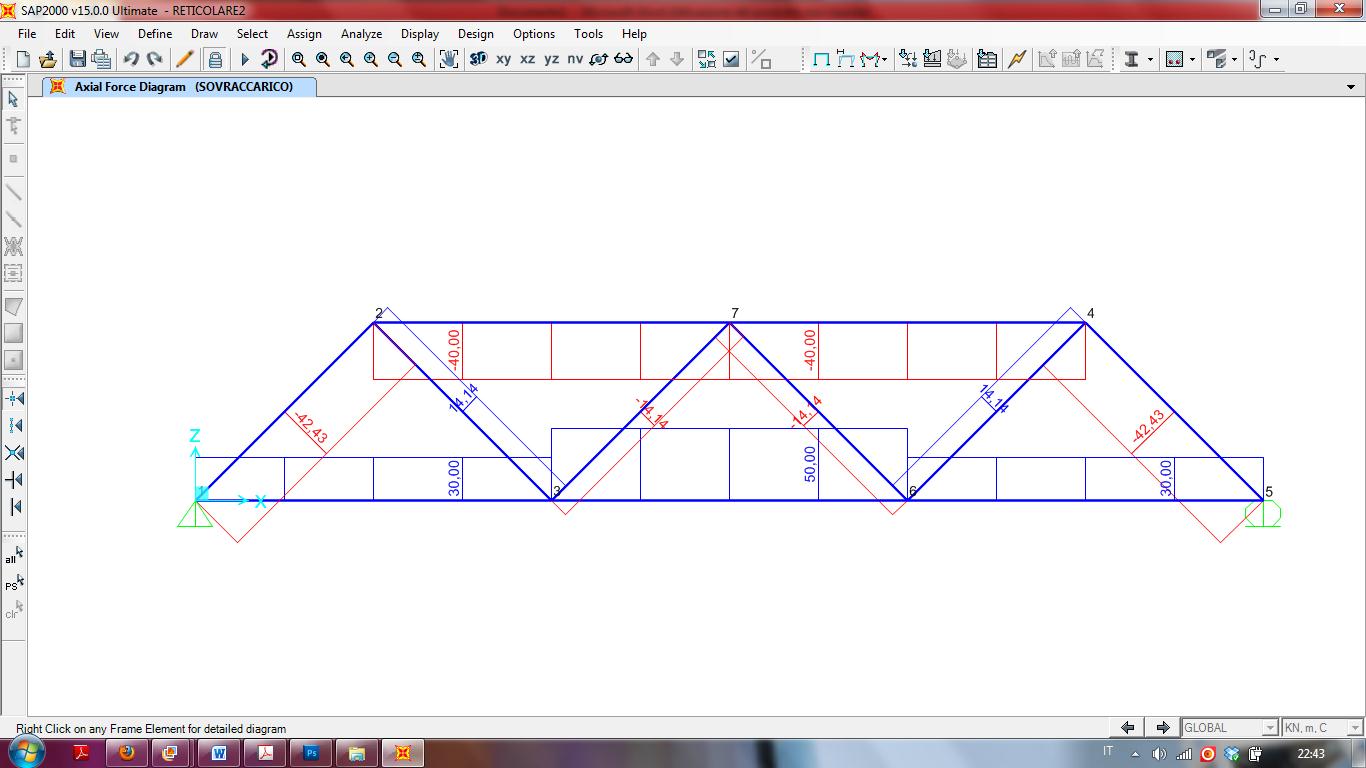
4.   Verifica della struttura con SAP2000

Come già visto nel punto 4 dell’es. 1, verifico la correttezza dell’esercizio svolto con SAP2000.

Parliamo, come nell’es.1 di strutture isostatiche e quindi teoricamente risolvibili medianti le condizioni di equilibrio (senza le informazioni riguardanti la geometria della sezione e il materiale); tuttavia occorre dare queste informazioni sulla travatura reticolare al SAP  in quanto  quest’ultimo utilizza il metodo degli spostamenti (la maggior parte delle strutture sono iperstatiche e questo metodo ne permette la risoluzione).

 

 

 

 

ESERCITAZIONE_DIMENSIONAMENTO DI UNA TRAVE A FLESSIONE 

Prendo in analisi l’ impalcato di un solaio ad orditura semplice oggetto di un esercitazione all’interno del Laboratorio di Costruzione 1C.

La trave più sollecitata è quella AB lungo il filo 2 ed è soggetta a un carico la cui area di influenza (tratteggiata in rosso) è pari a

A= L x i = 4,70 x 3,375 = 15,86 mq

dove L= luce

         i= interasse

 

 

 

 

 

Prima di passare al dimensionamento della trave occorre calcolare il carico totale del solaio per unità di lunghezza gravante sulla trave, carico necessario per dimensionare la trave stessa. Esso è dato dalla somma dei 3 tipi di carico caratterizzanti l’area di influenza e misurati in KN/mq (carico esercitato da un’unità di superficie) moltiplicati per l’interasse dell’area di influenza.

 

• Il peso proprio (Qs) della struttura è ovviamene il carico che il peso della struttura stessa esercita su se stessa. Dipende quindi dal volume dell’elemento strutturale e dal materiale con cui è realizzata, in particolare dal suo peso specifico.

• Il carico permanente (Qp) è il carico esercitato sull’elemento strutturale dagli elementi costruttivi fissi che esso deve sorreggere. Esso quindi dipende dal numero di elementi fissi che la struttura deve reggere e dal materiale con cui essi sono realizzati.

• Il carico accidentale (Qa) è il carico relativo all’utilizzo a cui è sottoposta la struttura: essi possono essere o meno presenti ed attivi sulla struttura stessa ( ad esempio gli spettatori in una sala cinematografica, una colonna di tir su un viadotto) nonché i carichi di origine ambientale a cui essa potrebbe essere soggetta (come il carico da neve nel caso di una struttura a capriata portante di una copertura). Si tratta di un valore tabellato che varia in base alle varie categorie di edifici. Di seguito alcuni valori.

Ambienti ad uso residenziale                                                                                  2KN/mq

Uffici                                                                                                                        2÷3 KN/mq

Ambienti suscettibili di affollamento                                                                        3÷5 KN/mq

Ambienti ad uso commerciale                                                                                 4÷5 KN/mq

Biblioteche, archivi, magazzini, depositi, laboratori manifatturieri                          ≥6 KN/mq

 

Nel calcolo del carichi strutturali e permanenti (come già detto espressi in mq) sommeremo il carico di ogni elemento del nostro pacchetto di solaio (differente in base alla tecnologia scelta) , considerando che Q= ps (peso specifico del materiale espresso in kg/m3 ) x h (altezza elemento).

Ad esempio prendendo ad esempio in considerazione una lastra di calcestruzzo da 1m x 1m e sp. 0,05 m

Si ha che P = V x γ = volume x peso specifico (espresso in kg)  P= 1m x 1m x 0,05 m x 2500 kg/mc = 125  kg

Sappiamo che 1kg è circa uguale a 10 N per cui  Q= 1,25 kN

Vogliamo sapere il carico della lastra per unità di superficie = Q/A = 1,25 KN / 1 mq = 1,25 KN/mq

È per questo motivo che più rapidamente, per calcolare il carico  si moltiplica il peso specifico per l’altezza dell’elemento e si effettua la trasformazione da kg a kN.

Nel calcolare il volume dell'elemento strutturale si considera quindi lo spessore dell'elemento e l'area di 1 mq.

Se si dispone già del peso per unità di superficie, spesso fornito dalle ditte produttrici in quanto riferito ad altezze standard dei materiali si inserirà direttamente il valore nella sommatoria dei carichi.

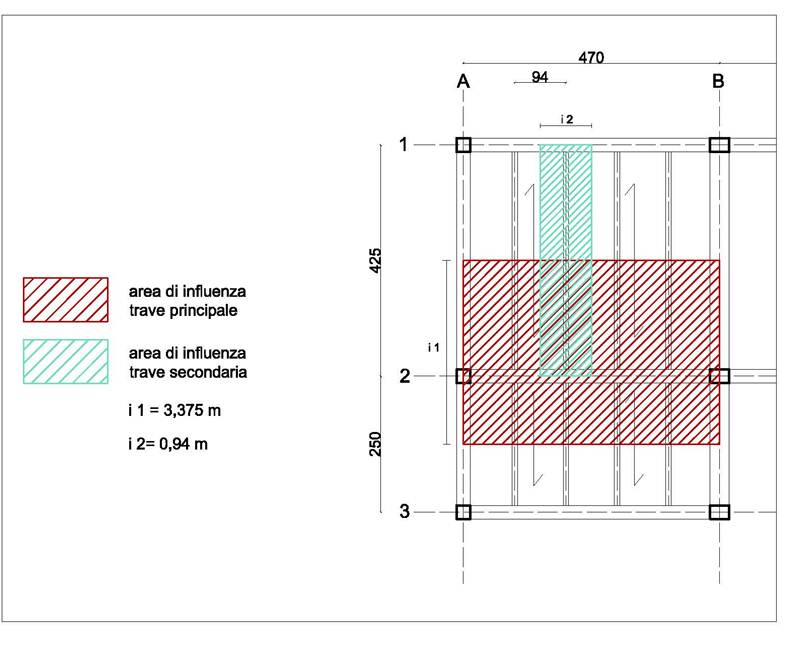
Nel calcolo del carico totale di un solaio composto da travi principali e travi secondarie, occorre sapere, all’interno dei carichi strutturali, il peso proprio della trave secondaria.

Andremo quindi a progettare a flessione anche la trave secondaria, verificando la sezione aggiungendo alla sommatoria dei carichi il peso proprio della trave stessa.

Col carico totale ( comprensivo quindi del peso strutturale dei travetti) dimensiono in questo modo la sezione della trave principale, andando a verificare anche qui che la sezione sia in grado di portare il suo peso proprio.

 

 

 

 

 

 

DIMENSIONAMENTO TRAVE IN LEGNO

Supponiamo di prendere in considerazione il solaio in legno rappresentato.

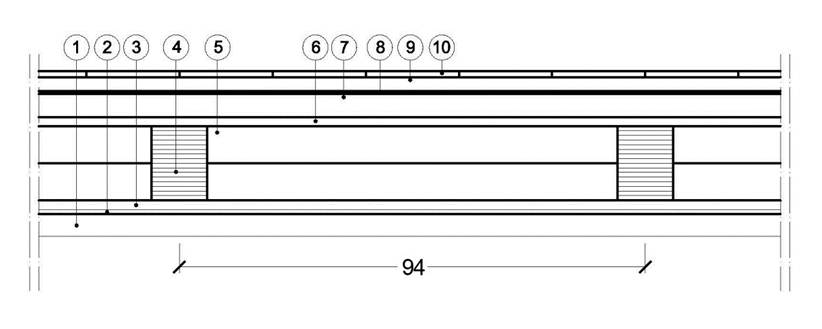
1. Trave principale in legno lamellare di abete ps= 400 kg/mc

2. Controsoffitto in gesso rivestito accop
piato con micro lamina di alluminio (barriera al vapore) sp. 9,5 mm P= 8,2 Kg/mq

3. Tavole di supporto al controsoffitto in legno d’abete sp 20 mm ps 0,75 kg/dmc

4. trave secondaria in legno lamellare di abete ps= 400 kg/mc

5. Pannello per isolamento termico in lana di roccia sp.80 mm ps 90 kg/m3

6.Piano di masonite sp 1,9 cm 950 kg/mc

7. Massetto in calcestruzzo alleggerito 350kg/mc sp 5 cm

8. Strato isolante fono assorbente in polietilene espanso reticolato con interposta lamina di piombo(barriera al vapore) sp 6 mm 4,05 kg/mq

9. Sottofondo pavimento 1800kg/mc 3cm

10. Pavimento in cotto 13 mm 28 kg/mq

 

DIMENSIONAMENTO DEL TRAVETTO    (maggiormente sollecitato, di luce 4,25 m)                        

Analisi dei carichi

Peso strutturale:        6.  Piano di masonite:  P = 950 kg/mc x 0,019 m =  18,05 kg/mq ≈ 0,18 kN/mq

Peso permanente:

2.Controsoffitto in gesso rivestito accoppiato con micro lamina di alluminio (barriera al vapore): P= 8,2 Kg/mq ≈ 0,08 kN/mq

3.Tavole di supporto al controsoffitto in legno d’abete P= 0,02 m x 0,75 kg/0,001mc = 15 kg/mq ≈ 0,15 kN/mq

5.Pannello per isolamento termico in lana di roccia P = 0,08m x 90 kg/mc = 7,2 kg/mq ≈ 0,07 kN/mq

7.Massetto in calcestruzzo alleggerito P= 350kg/mc x 0,05 m =17,5 kg/mq ≈ 0,17 kN/mq

8.Strato isolante fono assorbente P= 4,05 kg/mq ≈ 0,04 kN/mq

            9. Sottofondo pavimento P= 1800kg/mc x 0,03m = 54 kg/mq ≈ 0,54 kN/mq

10. Pavimento in cotto P= 28 kg/mq ≈ 0,28 kN/mq

 

Incidenza impianti Q= 0,5 kN/mq

Incidenza tramezzi Q= 1 kN /mq

 

Carico accidentale:         2kN/mq (per ambiente ad uso residenziale)

Carico totale per unità di superficie: 5,01 kN/mq

A questo punto conosciamo anche il carico espresso in densità lineare:

 q= 5,01 kN/mq x 0,94m = 4,70 kN/m

Considerando che la trave è appoggiata siamo anche in grado di trovare il momento massimo che agisce sulla sezione, sapendo che si trova in mezzeria ed è pari a ql^2/8. Ora è quindi possibile dimensionare la sezione stessa. La nostra incognita è proprio l’altezza della sezione.

Dimensionamento della sezione del travetto

Sappiamo che Wx= Mx/fD dove Mx è il momento massimo appena trovato (fissate nel progetto la luce e il materiale) ed fD è la tensione di progetto ( dato che deriva dall’abbattimento del valore della resistenza del materiale) vogliamo trovare il più piccolo modulo di resistenza della sezione affinché la formula sia verificata e la sezione abbia dimensioni adeguate per mantenerci distanti dalla crisi.

Supponiamo che il travetto analizzato abbia una resistenza a flessione pari a 28 N/mmq.

Mentre per il legno ci interessa la distanza dal valore di rottura , così come per il calcestruzzo, per l’acciaio ci interessa la distanza dallo snervamento essendo un materiale duttile.

 

 

 

 

 

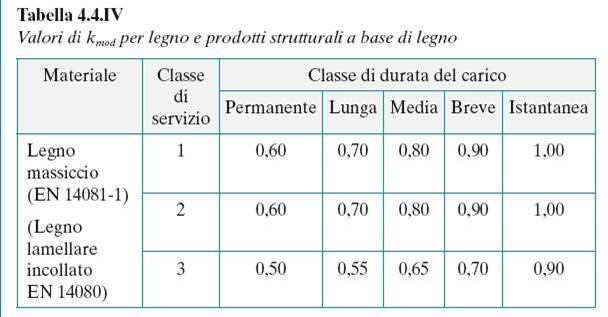
La resistenza del legno viene abbattuta due volte, in quanto oltre al coefficiente di sicurezza γm, influsce un altro fattore moltiplicativo molto basso (k mod) che tiene conto della durata del carico e di fattori  legati all’umidità ambientale. Complessivamente il legno ha quindi il fattore di sicurezza più alto rispetto agli altri materiali. 

 

fD= kmod x fk / γm = 0,6 x 28 N/mmq / 1,45 = 11,59 N/mmq

 

 

Trovata la tensione di design, sappiamo innanzitutto che la sezione rettangolare resiste meglio data la sua inerzia, la quale è una caratteristica geometrica della sezione che varia in base alla distanza dell’area dal centro. Dalla formula di Navier, infatti, σ= Mx/Ix x ymax (come ricordiamo esprime l’andamento della tensioni normale nella sezione della trave inflessa) vediamo che per abbattere la tensione del materiale ci vogliono grandi momenti di inerzia.  Di conseguenza il modulo di resistenza è un valore fondamentale essendo W=Ix/ymax. Osservando anche σ= Mx/Wx vediamo anche qui come grandi Wx abbattano la tensione.

Mettendo ora a sistema Wx= Mx/fd e Wx=bh^2/6 (il modulo di resistenza di una sezione rettangolare), otteniamo che Mx/fD = bh^2/6. Scrivendo l’equazione in funzione dell’altezza e fissando il valore alla base siamo così in grado di trovare la nostra incognita.

Il foglio elettronico ci permette molto rapidamente di effettuare questi calcoli.

 

 

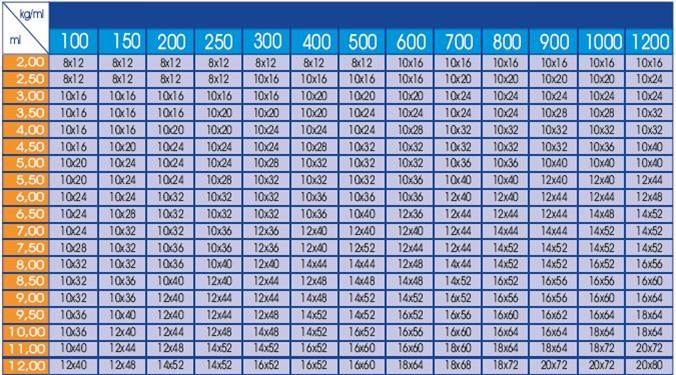
Fissato il valore della base pari a 10 cm, otteniamo il valore minimo dell’altezza che ci consente di mantenerci distanti dalla crisi. Dalla tabella relativa alle sezioni standard per travature in legno lamellare scelgo la sezione del travetto affinché l’altezza sia almeno pari o superiore a quella trovata. In questo caso scelgo un TRAVETTO GL28 DI SEZIONE 10X24 CM

 

 

 

 

 

 

 

 

 

 

 

Verifico peso proprio travetto

A questo punto verifico che la sezione sia in grado di portare oltre i carichi del solaio sopra calcolati anche il suo peso proprio che andrà aggiunto ai carichi strutturali.

Carico per unità di lunghezza = ps x A sezione

Carico per unità di superficie= carico per unità di lunghezza x 1/interasse

P= 400 kg/mc x 0,10 x 0,24 m x 1/0,94m =  10,21 kg/mq ≈ 0,1 kN/mq    

 

 

Il dimensionamento è corretto.

È possibile osservare come cambiando la resistenza del materiale cambi la sezione, scegliendo infatti un legno GL24 e imponendo lo stesso valore della base imposto nei calcoli precedenti (10 cm) vediamo come l’altezza della sezione aumenti (h minima 25, 35cm contro i 23,47 cm trovati sopra).

DIMENSIONAMENTO DELLA SEZIONE DELLA TRAVE (maggiormente sollecitata di luce 4,70 m)

Ora, con lo stesso metodo, sono in grado di calcolare la sezione della trave.

Conosco l’interasse, i carichi che gravano su di essa (escluso il peso proprio che andrà poi verificato come fatto per il travetto), la luce e di conseguenza la massima sollecitazione a flessione (in mezzeria anche qui considerando la trave appoggiata).

 

 

Anche in questo caso abbatto la resistenza del materiale trovando la tensione di design e sono così in grado di definire l’altezza.

 

 

Scelgo una TRAVE GL 28 DI SEZIONE 20X40

Verifico peso proprio trave

A questo punto verifico che la sezione sia in grado di portare oltre i carichi del solaio sopra calcolati anche il suo peso proprio che andrà aggiunto ai carichi strutturali.

P= 400 kg/mc x 0,20m x 0,40 m x 1/3,375 m =  9,48 kg/mq ≈ 0,09 kN/mq

 

 

Il dimensionamento è corretto.

 

DIMENSIONAMENTO TRAVE IN CLS

Nel corso del laboratorio di costruzione si chiedeva di dimensionare le travi dell’impalcato in base a formule empiriche che mettevano in rapporto l’altezza della trave con la sua luce, ad esempio nel caso del calcestruzzo, secondo la relazione h= 1/10 L

Prendiamo in esempio la trave più sollecitata otteniamo che la sua altezza si aggira intorno ai 47 cm.

Questa relazione è data dal fatto che se possiamo esprimere l’altezza come

h= √6Mx/fD b       >         h= √6qL^2/8 fD b            >             h= L √3q/4 b fD                >             h= Χ L

Vediamo come L sia la grandezza importante che influisce sul dimensionamento.    

Voglio ora dimensionare la trave in maniera precisa utilizzando anche il foglio elettronico come strumento di verifica.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Pacchetto del solaio analizzato:

 

 

 

 

 

 

 

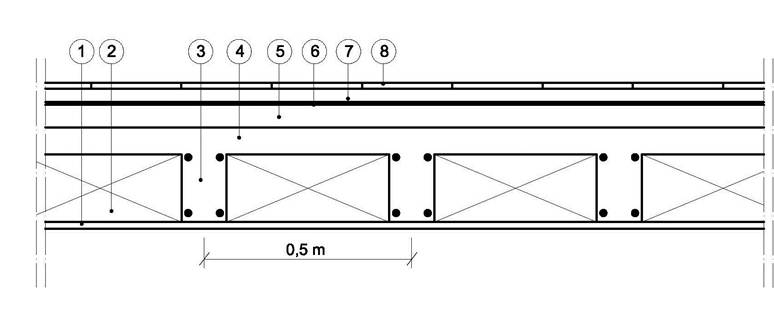
DIMENSIONAMENTO TRAVETTO

Analisi dei carichi

Peso strutturale:

      2.       Pignatte                              P= 5 kN/mc x 0,15m x 0,36 m x 1/0,5 m =  0,54 kN/mq

      4.       Getto in calcestruzzo    P= 2500kg/mc x 0,06 m = 150 kg/mq ≈ 1,5 kN/mq

Peso permanente:

1.Intonaco P= 800 kg/mc    x 0,015 m = 12kg/mq≈ 0,12 kN/mq

5.Massetto in calcestruzzo alleggerito P= 350kg/mc x 0,05 m =17,5 kg/mq ≈ 0,17 kN/mq

      6. Strato isolante fono assorbente P= 4,05 kg/mq ≈ 0,04 kN/mq

      7.Sottofondo pavimento P= 1800kg/mc x 0,03m = 54 kg/mq ≈ 0,54 kN/mq

      8. Pavimento in cotto P= 28 kg/mq ≈ 0,28 kN/mq

 

Incidenza impianti Q= 0,5 kN/mq

Incidenza tramezzi Q= 1 kN /mq

 

Carico accidentale:  2kN/mq(per ambiente ad uso residenziale)

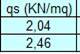
Carico totale: 6,69 kN/mq

A questo punto conosciamo anche il carico espresso in densità lineare:

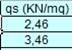
 q= 6,69 kN/mq x 0,5m = 3,345 kN/m

Considerando che la trave è appoggiata siamo anche in grado di trovare il momento massimo che agisce sulla sezione, sapendo che si trova in mezzeria ed è pari a ql^2/8. Ora è quindi possibile dimensionare la sezione stessa. La nostra incognita è proprio l’altezza utile della sezione.

 

 

Dimensionamento della sezione del travetto

Anche nel caso del calcestruzzo il foglio elettronico mette in relazione formule in cui compaiono la luce dell’elemento strutturale, i carichi che vi gravano e il materiale da cui è costituito.

Si procede ora con la scelta del calcestruzzo, il quale sarà caratterizzato da una classe di resistenza. Le classi sono circa 15 e vanno dalle prime che riguardano il calcestruzzo non strutturale (non armato) utilizzato per magroni e fondazioni a quelli estremamente performanti.

Quelli più usati nei sistemi costruttivi vanno dalla C20/25 a C60/65.   In questo caso scelgo un cls C25/30 in cui  il primo dei valori rappresenta f_ck  (resistenza cilindrica) e il secondo R_ck   (resistenza cubica) ambedue espressi N/mm², che dipendono dalla geometria dell’elemento sottoposto alla prova di compressione.

Prendiamo così la distanza dal valore corrispondente alla rottura del materiale mediante i coefficienti di sicurezza.

fD= fckx α α    / γ                                           con y= 1,6 e α α = 0,85 (coefficiente correttivo che tiene conto delle imperfezioni del calcestruzzo)

Èimportante sapere inoltre anche la resistenza dell’acciaio delle armature, in quanto il cls non è un materiale omogeneo. Scelgo un acciaio B450C (unico ammesso in zona sismica) con fyk = 450 MPa

Nella formula legata all’altezza utile hu= r √M/b , sappiamo che nel fattore r compaiano sia la resistenza del calcestruzzo che la resistenza delle barre (fattore α)  , nonché il fattore n, che permette di omogeneizzare la sezione, ossia di dire che la tensione dell’acciaio è n volte quella del calcestruzzo (σf= n σc). Osserviamo come anche qui sia importante la resistenza del materiale,  e ben più importante la luce dell’elemento strutturale.

 

Una volta scelto il materiale siamo in grado di calcolare sia

n= Ef/Ec      >      210000MPa/21000MPa = 10

e di conseguenza α = fc/fc+ff/n                              >             20MPa/20MPa+450MPa/10 = 0,31

Il foglio elettronico ci consente così di calcolare r e di conseguenza la nostra altezza utile. Fissando la base, ad es. 14 cm, otteniamo che l’altezza totale è 23,54 cm comprensiva dell’altezza del copriferro.

 

Potrei scegliere un travetto di dimensioni 14 cm x 24 cm e ridimensionare la pignatta in base all’altezza del travetto trovata. In questo caso potrei utilizzare una pignatta di 36 cm x 24 cm, in modo tale che l’interasse tra i travetti rimanga di 50 cm. Verifico tuttavia il travetto al peso strutturale della nuova pignatta e al peso proprio del travetto stesso.

Pignatta                              P= 5 kN/mc x 0,24m x 0,36 m x 1/0,5 m =  0,8 kN/mq

Travetto                              P= 25 kN/mc x 0,14m x 0,24 m x 1/0,5 m =  0,16 kN/mq

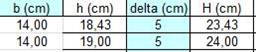
Il dimensionamento del travetto risulta corretto

 

DIMENSIONAMENTO TRAVE

Con lo stesso procedimento calcolo la sezione della trave principale, tenendo conto che la luce e l’interasse dell’area di influenza cambia.

Fissata la base, ad esempio 30 cm, scelgo una trave di altezza totale pari a 45 cm.

A questo punto verifico la trave al suo peso proprio.

Trave                    P= 25 kN/mc x 0,30m x 0,45 m x 1/3,375 m =  1 kN/mq

Il dimensionamento risulta corretto

 

 

DIMENSIONAMENTO TRAVE IN ACCIAIO

Come fatto per il legno, considero un impalcato costituito da un’orditura primaria con area di influenza L=4,70 e i =3,375 e un’orditura secondaria con area di influenza di L=4,25 e i= 0,94.

 

 

 

 

 

 

 

Analisi dei carichi

·         Carico strutturale

Soletta (Lamiera grecata sp 1,5 mm + getto in calcestruzzo) P = 172 kg/mq ≈ 1,72 kN

 

 

 

 

 

·         Carico permanente

 Massetto in calcestruzzo alleggerito P= 350kg/mc x 0,05 m =17,5 kg/mq ≈ 0,17 kN/mq

       Strato isolante fono assorbente P= 4,05 kg/mq ≈ 0,04 kN/mq

       sottofondo pavimento P= 1800kg/mc x 0,03m = 54 kg/mq ≈ 0,54 kN/mq

       Pavimento in cotto P= 28 kg/mq ≈ 0,28 kN/mq

 Controsoffitto in gesso rivestito accoppiato con micro lamina di alluminio (barriera al vapore) sp. 9,5 mm  P= 8,2 Kg/mq ≈ 0,08 kN/mq

 

Incidenza impianti Q= 0,5 kN/mq

Incidenza tramezzi Q= 1 kN /mq

 

·         Carico accidentale  2 KN/mq

Dimensionamento del travetto

La nostra incognita è Wx, il modulo di resistenza flessionale della sezione. Sapendo che Wx= Mx/fD , avendo come dati del problema sia Mx che fD (dati dall’imposizione della luce e della scelta del materiale) siamo in grado di trovare il più piccolo modulo di resistenza affinché l’equazione sia verificata e la sezione sia così in grado di resistere alla sollecitazione massima. Ovviamente, per questioni di sicurezza è opportuno scegliere una trave che abbia un Wx superiore a quello trovato. È il sagomario che ci permette di trovare , dal modulo di resistenza scelto,  la trave corrispondente. Mentre nel caso del legno dal modulo di resistenza si otteneva facilmente l’altezza dell’elemento strutturale dato che W di una sezione rettangolare è uguale a bh^2/6, in questo caso è opportuno avere un sagomario che metta queste grandezze in relazione dato che i profili di acciaio non hanno una sezione rettangolare.

Scelgo un acciaio S275 in cui 275 rappresenta il valore da cui vogliamo prendere le distanze per progettare la sezione.

Nel caso dell’acciaio occorre prendere le distanza non dalla rottura del materiale ma dal suo snervamento, in quanto il materiale ha un comportamento meccanico molto diverso rispetto al legno e al calcestruzzo per cui prima di arrivare a rottura si crea strizione nel provino. Arrivato il punto di snervamento il materiale inizia a deformarsi irreversibilmente fino ad arrivare alla deformazione ultima di rottura. Questo intervallo può essere più o meno ampio a seconda della duttilità dell’acciaio scelto.  Anche qui fD= fyk/γ     con γ=1,05

 

IPE 120 con Wx = 53  e P=10,4 kg/m

Verifico al peso proprio

Dal sagomario abbiamo il peso espresso al metro lineare; voglio esprimerlo come densità superficiale per cui  P= 10,4 kg/m x i = 9,776 kg ≈ 0,09  kN                                                                i=0,94 m

Q/A= 0,09 KN / 1 mq = 0,09 KN/mq

 

Il dimensionamento risulta corretto.

Dimensionamento della sezione della trave principale

in questo caso

 

scelgo una IPE 220 con Wx= 252 cm3 e peso = 26,2 kg/m

Verificandola al peso proprio ottengo che il dimensionamento non risulta corretto

P=  26,2 kg/m x i = 88,425 kg/m ≈ 0,88 kN

Q/A= 0,88 KN / 1 mq = 0,88 KN/mq

 

Scelgo quindi una ipe con un modulo di resistenza maggiore, ossia una IPE 240 con Wx= 324cm3 e verifico facilmente che la sezione è correttamente dimensionata.

 

RIASSUMENDO

Acciaio =               trave secondaria                             IPE 120   

                 trave principale                               IPE 240

Legno =                GL28 DI SEZIONE                            10cm X 24cm

                             GL 28 DI SEZIONE                           20cmX  40cm

Cls=                      travetto                                          14 cm x 24 cm   

                             trave                                               30 cm x 45 cm

Abbiamo visto come a parità di luce la resistenza elevata dell’acciaio permette di ottenere un’altezza della trave contenuta rispetto a quelle in cls e legno, che risultano comparabili.          

 

 

 

COSTRUZIONE DI UNA PIASTRA RETICOLARE SPAZIALE

1.       Disegno in AUTOCAD

 

 

 

 

Vogliamo disegnare una piastra reticolare spaziale che abbia il seguente schema cubico di lati 2m x 2m x 2m e di dimensione totale pari a 6 moduli x 4 moduli.

 

 

 

Creo un nuovo layer che chiamerò ASTE.

 

Disegno una faccia del modulo nella vista in pianta, facendo attenzione a non chiuderlo. Per comodità disegno nel punto di origine del mio sistema di riferimento (Polilinea – 0,0,0) in modo che sarà più facile ritrovare il disegno nello spazio di autocad o di sap (una volta importato).

 

 

 

 

 

Mi sposto nella vista assonometrica

 

 

 

 

 

E ruoto il mio disegno di 90° intorno all’asta inferiore impostando il mio sistema di riferimento nel modo seguente verificando che l’asse x sia la direzione nella quale effettuerò la copia in serie del modulo col commando Array.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

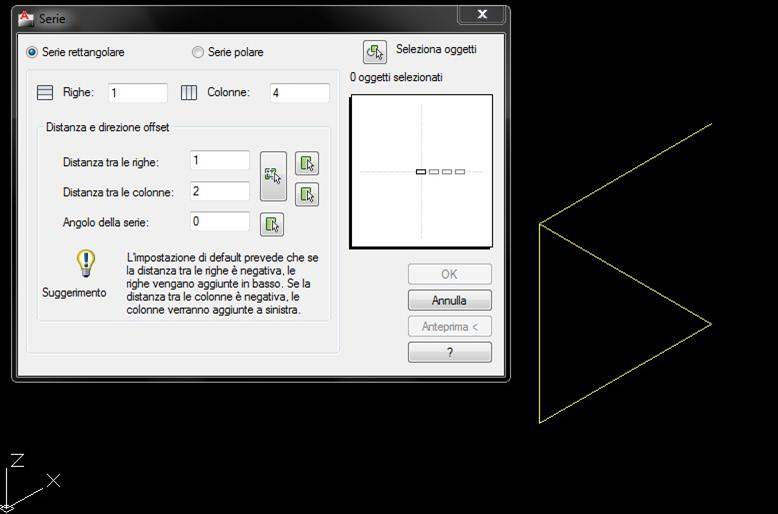
Chiamo il comando array, imposto a i valori della serie  (1 riga, 4 colonne e 2 la distanza tra le colonne) e seleziono gli oggetti.

Chiudo la serie disegnando l’ultima asta.

 

 

 

 

 

 

 

 

Disegno le altre aste con una polilinea 3d (oppure sposto l’ucs, come visibile nell’immagine ruotandolo di 90 intorno all’asse x, così sono sicura che con i comandi linea o polilinea 2D andrò a disegnare le altre aste su un piano perpendicolare a quello precedente).

 

 

 

 

 

 

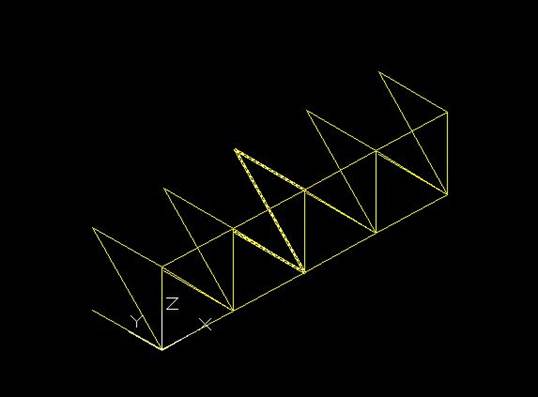
Con l’ucs impostato nella direzione dell’array, chiamo nuovamente il comando per realizzare la serie, questa volta realizzando 5 colonne.

 

 

 

 

 

 

 

 

 

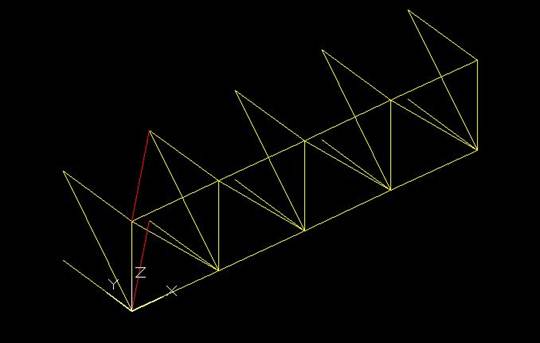
Disegno le diagonali superiore e inferiore (avendo cura di disegnare sul piano xy) del primo modulo e richiamo il comando Serie (4 colonne).

 

 

 

 

 

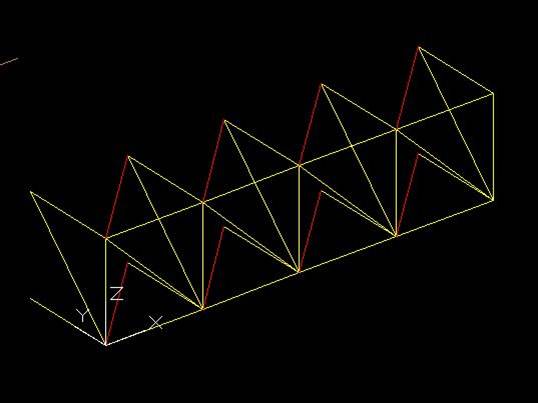
Cambio l’ucs, ruotando l’asse x intorno a z di 90° ed effettuo l’ultima Serie lungo x. Per evitare di chiudere a mano un disegno 3d, realizzo 7 colonne (poi cancellerò le aste che non mi servono).

 

 

 

 

 

 

 

 

 

 

 

Prima di cancellare le aste, seleziono tutti gli oggetti e chiamo il comando Esplodi, in modo da avere aste separate nel caso in cui abbia disegnato delle polilinee.

Ora cancello le aste che non mi servono. Ottengo così la piastra reticolare.

 

Posso procedere ora con il salvataggio nel formato dxf 2000.

 

 

 

 

 

 

 

 

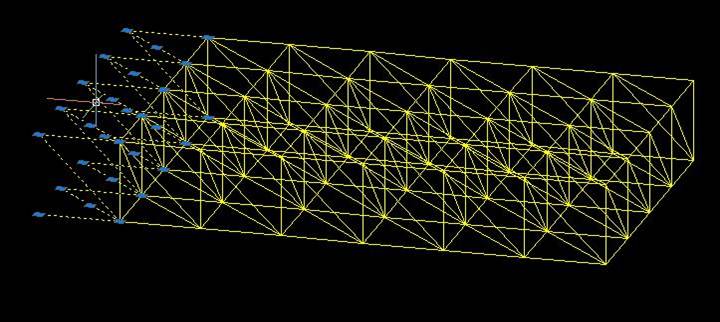
2.       Analisi in SAP2000

Importo ora il file salvato precedentemente mediante Import/Autocad DxF File. Nelle informazioni d’importazione controllo che le unità di misura siano kN, m, C.

 

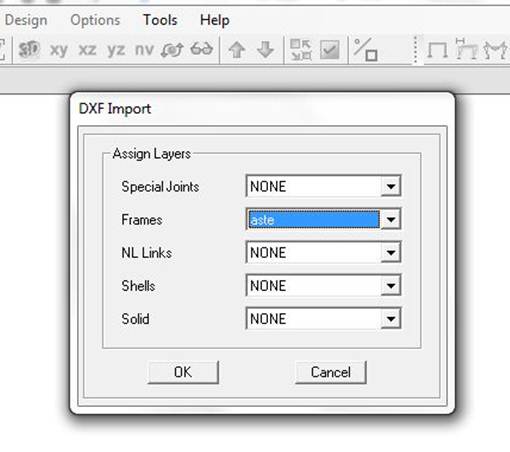
Nella finestra DXF Import devo invece dire che il layer ASTE utilizzato in Autocad deve diventare ora la struttura da analizzare in SAP, quindi in corrispondenza di Frames seleziono ASTE; tutto il layer diventa così Frames.

 

 

 

 

 

 

 

Innanzitutto si assegnano i vincoli; supponiamo che ci siano siano 4 pilastri alle estremità della piastra. Seleziono i 4 punti e vado su Assign/Joint/Restraints selezionando il vincolo d’appoggio.

 

 

 

 

 

 

 

 

 

 

 

 

 

Seleziono  tutte le aste e impongo il rilascio dei momenti (poiché le aste sono incernierate) con Assign/Frame/Releases Partial Fixity  mettendo il segno di spunta sul momento - all’inizio e alla fine di ogni asta – sia in 2 che 3 dimensioni.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Per i sistemi più complicati SAP vuole conoscere le informazioni riguardo il materiale e le sezioni della struttura.

Definisco il materiale con Define/Materials/Add New Material e su Material name scrivo “acciaio”.

Definisco la sezione con Define/Section Properties/Frame Sections/Add New Property scelgo la sezione tubolare “Pipe” e su Section Name scrivo “tubolare” e su Material imposto “acciaio” (il materiale precedentemente creato).

A questo punto assegno la sezione tubolare in acciaio creata alla mia struttura, selezionando tutto e andando su  Assign/Frame/Frame Section e selezionando “tubolare”.

Ora devo definire e assegnare i carichi. Per assegnare più comodamente le forze sui nodi, tramite il comando Set Disply Options, rendo visibili soltanto i nodi nascondendo momentaneamente le aste.

 

 

 

 

 

 

 

 

 

Ora voglio assegnare le forze solo ai nodi superiori. View/Set 2D view/ seleziono il piano xy e scrivo Z=2 (dico in questo modo che voglio lavorare su quel piano).

Dopo aver creato il carico in Define/Load Patterns – lo chiamo “concentrato” , do 0 al moltiplicatore e lo aggiungo alla lista dei carichi mediante Add New Load Pattern – lo vado ad assegnare: seleziono tutti i nodi che ho nella vista in pianta (verranno selezionati solo quelli corrispondenti al piano Z=2) e vado su Assign/Joint Loads/Forces e su Load Patterns Name seleziono il carico che avevo creato, in questo caso “concentrato” e in Force Global Z assegno un valore di – 40 kN (forza concentrata verso il basso).

A questo punto posso lanciare l’analisi ricordandomi di non far girare i carichi DEAD e MODAL (andranno impostati su Do Not Run).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

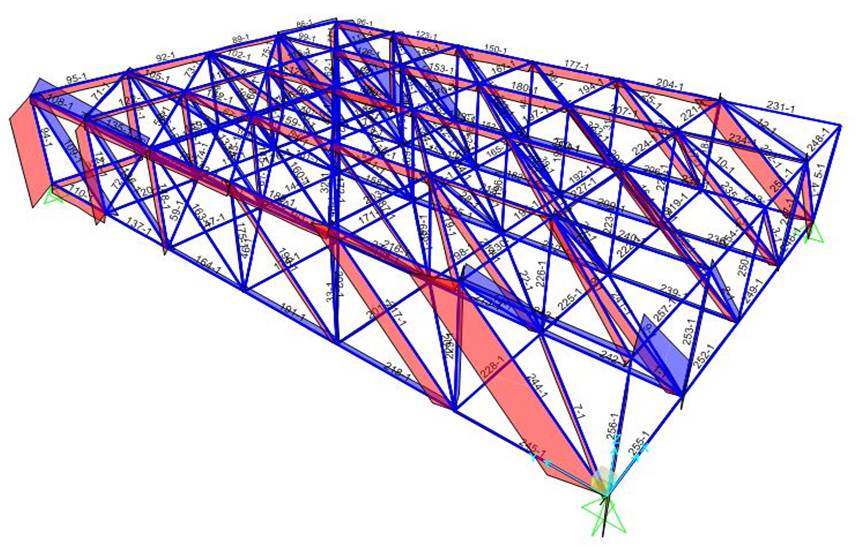
Con Show Forces-Stresses/Frames-Cables-Tendons e selezionando Axial Forces posso osservare le azioni di contatto.

Su Set Display Options, nella sezione Frames, spunto Labels, in modo da visualizzare le aste numerate.

 

Ricordiamo che trascurando il peso proprio e in presenza di forze concentrate , le travature reticolari sono soggette ai soli sforzi assiali. Possiamo verificare che i valori di taglio e momento siano nulli selezionando Shear 3-3 o Moment 3-3. In questo modo sappiamo se la struttura è stata disegnata e analizzata correttamente.

Per trovare i massimi sforzi di trazione e compressione ed individuare le aste più sollecitate vado su Show Tables e nella sezione Analysis Results spunto Element Output. Esporto poi le tabelle in Excel :    Export current table-To excel.

A questo punto, utilizzando la funzione Max e Min individuo facilmente le sollecitazioni massime e le aste più sollecitate.

 

 

 

 

 

 

 

 

 

 

 

 

 

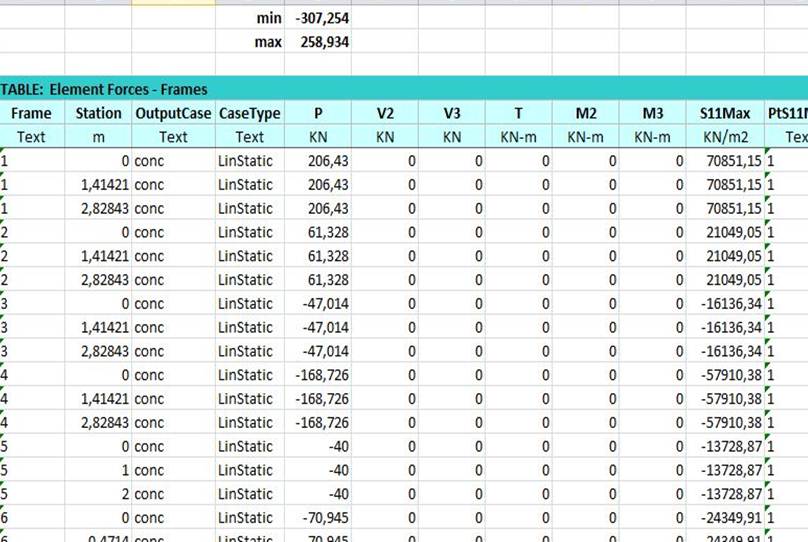
Abbiamo trovato il valore massimo di compressione pari a 307 kN sull'asta diagonale (n°244) e il valore massimo di trazione sull'asta diagonale (n°44) pari a 259 kN.

3.       Dimensionamento delle aste                

- progetto a trazione

Noto lo sforzo massimo di trazione, scelgo un materiale e trovo l'area minima che posso utilizzare mediante  σ=fD= N/A --> A=N/fD   

Scelgo un acciaio di tipo Fe 510, ottengo una tensione di progetto

fD = fyk/γ     con γ=1,05 --->    510/1,05 N/mm^2= 486 N/mm^2

A =259000N x mm^2/486N = 533 mm^2 = 5,33 cm^2

Ottengo così l'area minima che mi consente di rimanere distante dalla crisi del materiale (snervamento) per cui prenderò un'area superiore.

 

 

 

 

 

 

 

 

 

 

Scelgo un tubolare con sezione pari a 5,74 cm^2, di diametro 60,3 mm e spessore pari a 3,2 mm.

Nel progetto a trazione domina la verifica alla resistenza e la lunghezza delle aste non è importante.

 

-progetto a compressione

In questo caso il procedimento è lo stesso, ma il massimo sforzo di compressione è pari a 307 kN. Per cui avrò che

A =307000N x mm^2/486N = 632 mm^2 = 6,32 cm^2

Scelgo un tubolare di sezione pari a 7,33 cm^2, momento d'inerzia pari a 48,80 cm^4.

Oltre a tener conto dello sforzo massimo per il progetto della sezione, terrò in considerazione la lunghezza dell'asta. Nella compressione è insito, infatti, il rischio dell'instabilità euleriana dovuta all'eccesso di snellezza dell'elemento.  Un elemento strutturale, soggetto a compressione, può infatti inflettersi e sbandare non a causa della resistenza del materiale ma causa della sua snellezza, ossia a causa di un alto rapporto tra altezza e lunghezza dell'oggetto.  Domina la verifica al carico di punta, per cui devo verificare che  Nmax < Pcritico

          N_cr = π² x 210000 N/mm² x 1920000 mm⁴ / 7840000 mm² = 507065 N = 507 KN

          Nmax<Pcrit    la sezione risulta verificata