blog di Francesco.Leoni

TRAVATURA RETICOLARE SIMMETRICA

Le strutture reticolari sono composte da aste, solitamente metalliche vincolate tra loro da cerniere. Le aste sono soggette a solo sforzo normale e si dividono in puntoni, nel caso la normale sia di compressione, e tiranti se è di trazione. Sono utilizzate soprattutto per le travature che coprono luci considerevoli, per il loro ottimo rapporto tra peso proprio e resistenza.

Seguono alcuni esempi che mettono in luce il comportamento di queste strutture soggette a carichi gravitazionali.

Ci troviamo di fronte ad una struttura doppiamente appoggiata dove l=2m, sottoposta a tre carichi di 20KN concentrati nei nodi B, D, F. Per geometria e anche per i carichi la struttura è simmetrica quindi bastera analizzare solo metà della struttura per risolverla interamente.

1_Verifica di isostaticità

Per prima cosa verifichiamo se la struttura è isostatica. Ricordiamo che una struttura è isostatica se il numero dei gradi di vincolo è uguale al numero dei gradi di libertà.

-Il numero dei gradi di vincolo è dato dalla somma dei vincoli esterni e dei vicoli interni: V = Ve + Vi -Il numero dei gradi di libertà è dato dal numero dei corpi moltiplicato per 3 (traslazione orizzonate, traslazione verticale, Rotazione) : l = n x 3

gradi di vincolo:

La cerniera nel nodo A blocca 2 gradi di libertà, Il carrello nel nodo G blocca 1 grado di libertà: Ve = 3

I gradi di vincolo interni sono dati da 2(n-1), dove n è il numero di aste che arrivano a ciascun nodo. Quindi per ogni nodo:

A-G 2(2-1) = 2 , B-F 2(3-1) = 4 , C-D-E 2(4-1) = 6 ---> Vi = 2+2+4+4+6+6+6 = 30

V = Ve+Vi = 3+30 = 33

gradi di liberà

La trave è composta da 11 aste quindi: l = 11 x 3 = 33

La struttura è isostatica se: V = l --> 33 = 33 VERIFICATO!

2_ Calcolo delle reazioni vincolari

Adesso possiamo procedere con il calcolo delle reazioni vincolari dei nodi A e G.

Come prima considerazione diamo per certo che RuA=0, la reazione orizzontale della cerniera, sia uguale a zero in quanto non esistono nel sistema forze orizzontali da bilanciare.

Imponendo l'equilibrio alla traslazione Verticale Rv=0, troviamo invece i valori di RvA e RvG, alle quali viene ripartito simmetricamente il carico totale di 60 KN che devono bilanciare.

Quindi come nella trave appoggiata: RvA=RvG= Q/2 = 30 KN

3_ Calcolo delle reazioni di contatto.

La struttura è in equilibrio, ma noi vogliamo sapere come si distribuiscono gli sforzi al suo interno. In particolare essendo una travatura reticolare l'unica reazione di contatto agente sarà la Normale. Per determinarla su ogni asta ricorriamo al Metodo delle sezioni di Ritter.

Il metodo di Ritter consiste nel "sezionare" virtualemte la struttura tagliando, per ogni sezione, 3 aste che non convergono allo stesso nodo. In questo modo possiamo imporre per ogni parte, l'equilibrio alla traslazione e alla rotazione uguale a zero.

essendo la struttura simmetrica eseguiremo tre sezioni fino all'asse di simmetria della struttura in modo da sezionare almeno una volta tutte le aste:

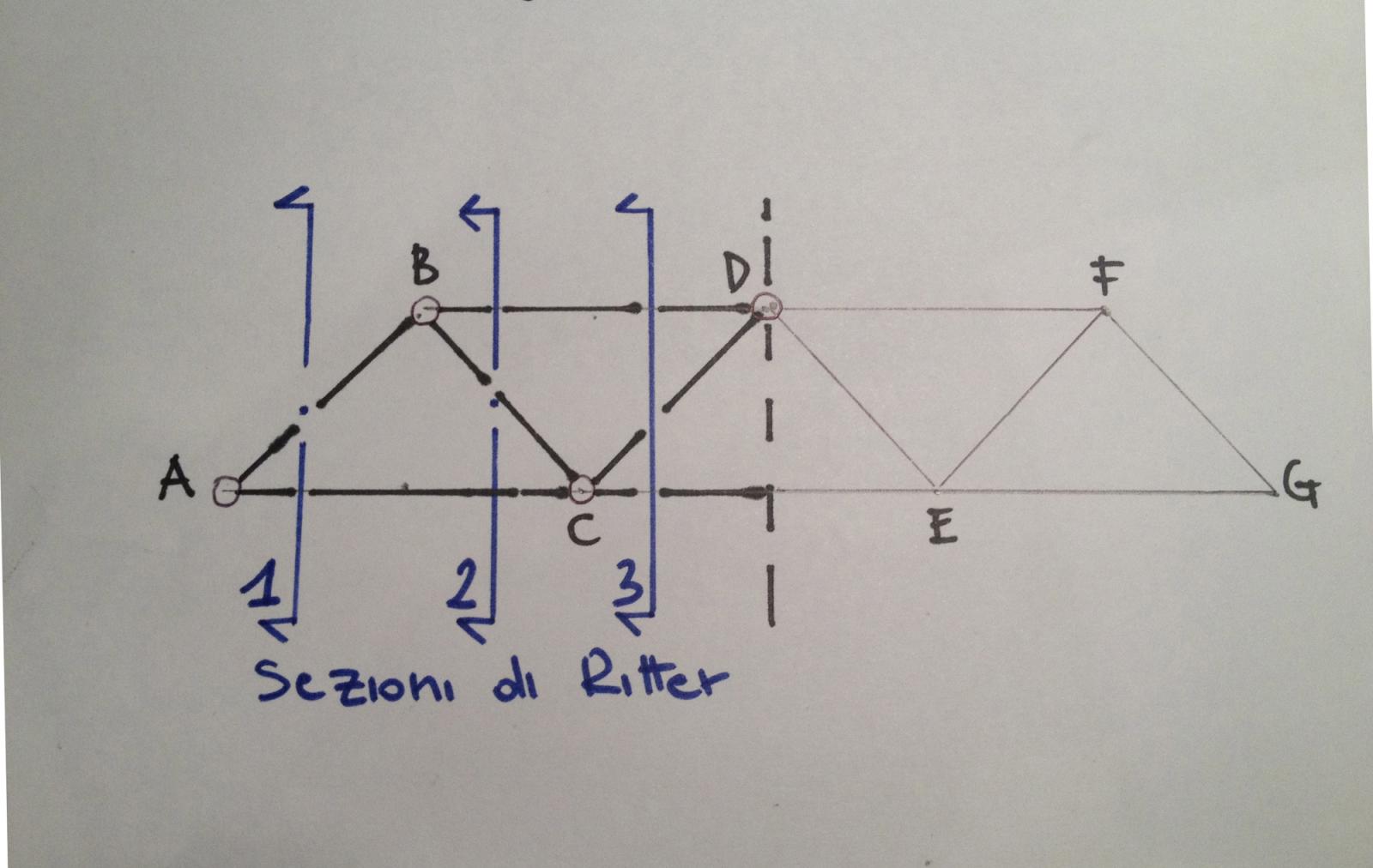
Analizziamo singolarmente ogni sezione:

Da ogni asta sezionata parte una freccia che indica lo sforzo Normale, per iniziare ipotizziamo che questi siano di verso uscente, quindi che sia uno sforzo normale di trazione, dopo aver effettuato l'equilibrio assegneremo verso entrante alle aste compresse.

Adesso eseguiamo l'equilibrio di ogni singola sezione considerando che se la struttura è in equilibrio lo sarà anche una sua parte.

Iniziamo da dalla sezione_2 (perchè ho meno forze da prendere in considerazione). Le incognite da espicitare sono ovviamente le Nn nelle equazioni dell'equilibrio alla traslazione verticale ΣFY=0, alla traslazione orizzontale ΣFX=0 e l'equilibro alla rotazione in un qualsiasi polo scelto x, ΣMx=0. si tratta quindi di impostare le equazioni più convenienti ed effettuare qualche sostituzione per le aste inclinate a 45°, dove se l'asta è Nn le sue componenti ortogonali sono (Nn)√2/2.

n.b. (I vari passaggi non verranno svolti passo per passo data per scontata la conoscenza di base al lettore)

sezione_2

ΣMC = 0 --> (-30kN)2L + (20KN)L + (N4)L =0 --> N4 = -40 KN *compressa

ΣFY =0 --> -20KN + 30KN + (N3)√2/2 =0 --> N3 = 10√2 KN *tesa

ΣMB =0 --> (-30KN)L + (N2)L =0 --> N2 = 30 KN *tesa

sezione_1

ΣFX =0 --> 30 KN + (N1)√2/2 =0 --> N1 = -30√2 KN *compressa

sezione_3

ΣMD =0 --> (20KN)2L -(30KN)3L + (N5)L =0 --> N5 = 50 KN *tesa (asta maggiormente sollecitata)

ΣFY =0 --> 30KN -20KN + (N6)√2/2 =0 --> N6 = -10√2 KN *compressa

A questo punto l'esercizio è terminato, per simmetria possiamo dedurre che il resto della struttura si comporterà in maniera speculare a quella analizzata.

Ecco il quadro di tutti gli sforzi normali con i versi corrispondenti (entrante=compresso ; uscente=teso ):

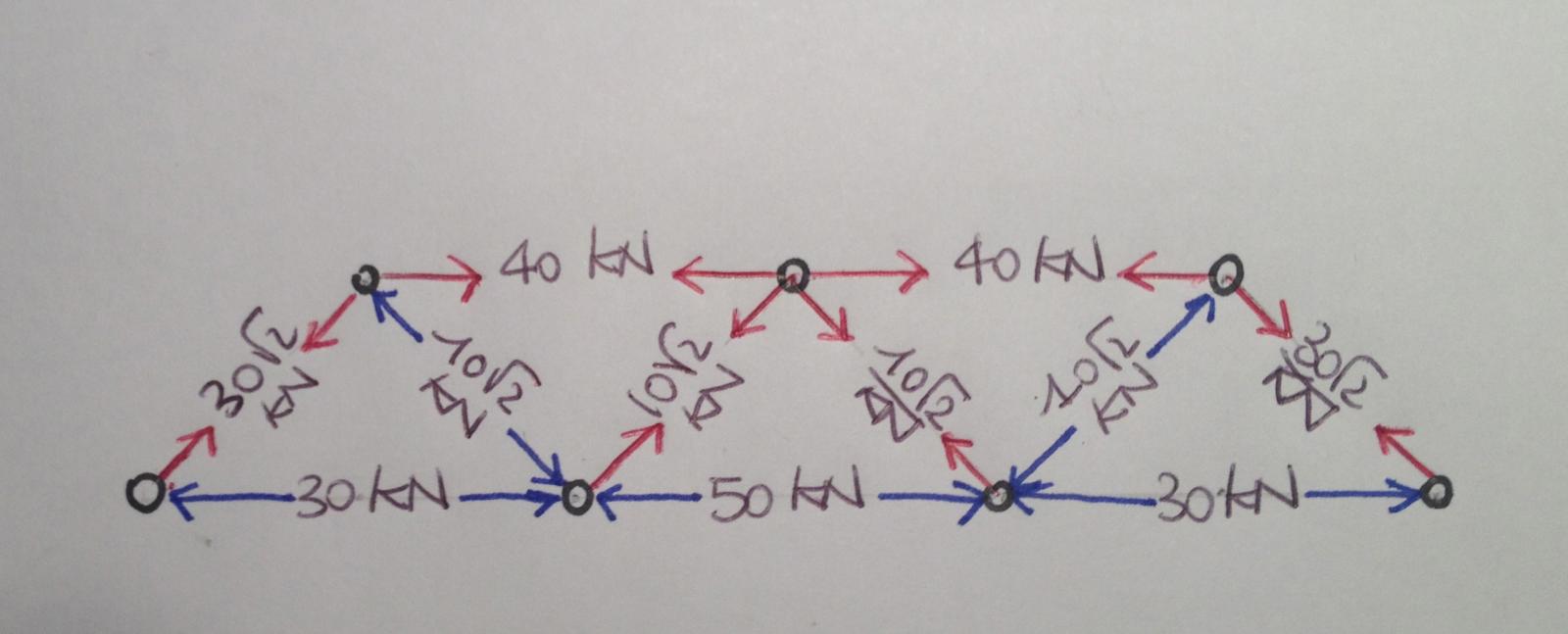
TRAVATURA RETICOLARE ASIMMETRICA

In questo caso ci troviamo sempre di fronte ad una travatura reticolare, ma al contrario della precedente questa non è simmetrica, quindi dovremo risolvere tutta la struttura per poter conoscere gli sforzi agenti su ogni asta. Procediamo per gradi.

1_Verifica di isostaticità

Per verificare l'isosostacità della struttura ricorriamo alla formuna Ve + n°aste = 2(n°nodi) da verificare, dove:

- Ve = 3 sono i vincoli esterni (2 della cerniere nel nodo B e 1 nel carrello nel nodo G)

- n°aste = 11 è il numero delle aste

- 2(n°nodi) = 14 sono il numero dei nodi moltiplicato per 2

3 + 11 = 7 x 2 --> 14 = 14

verificato! la struttira è isostatica.

2_Calcolo delle reazioni vincolari

- Intuivamente deduciamo che la reazione verticale RvB è l'unica che puo bilanciare i carichi concentrati nei nodi C ed E, quini sarà uguale alla loro somma con verso opposto: RvB = 20 KN

- Le reazioni orizzontali RuB e RuG saranno uguali ed opposte e si bilanceranno a vicenda, per trovarne i valori impostiamo un equilibrio alla rotazione nel polo B annullando l'effetto di RuB ed RvB:

ΣMB =0 --> -(10KN)1 -(10KN)2 +(RuG)1 = 0 --> RuG = 30KN

- di conseguenza RuB = 30KN

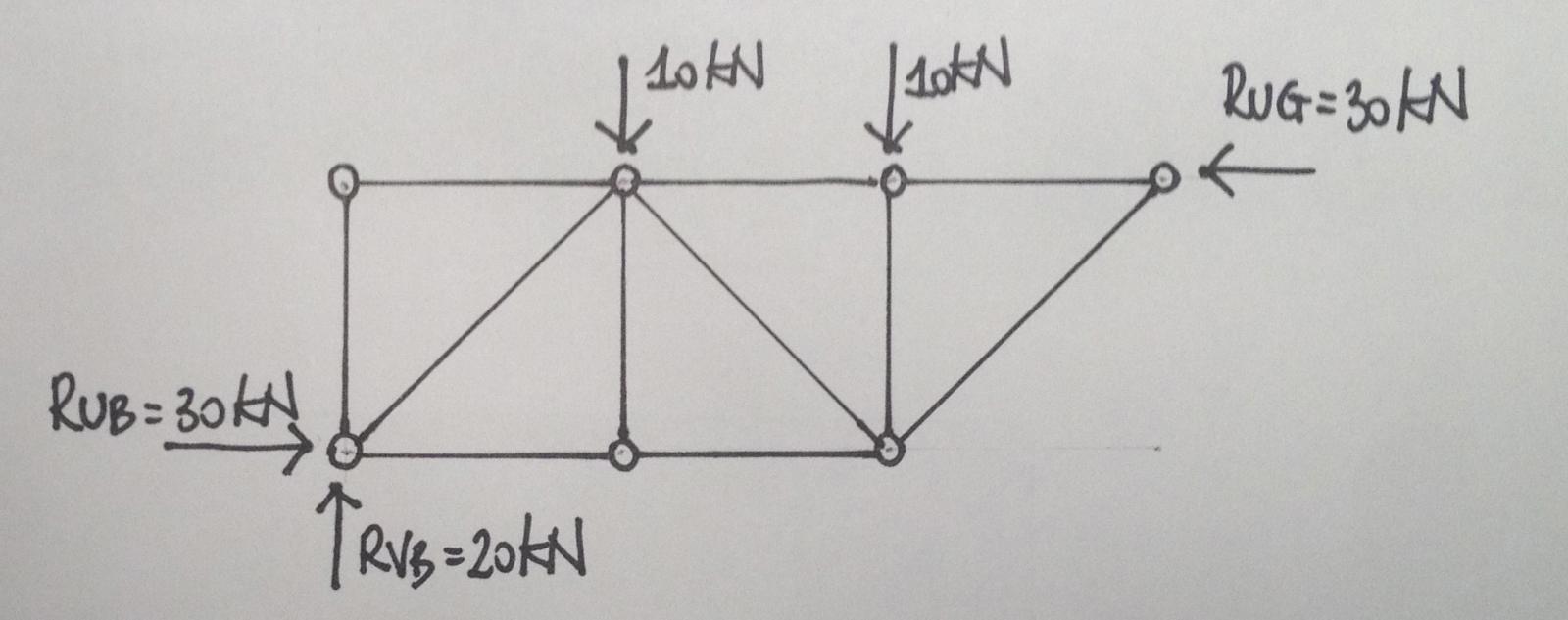
3_Calcolo delle reazioni di contatto

Per conoscere lo sforzo normale agente su ogni asta in questo esercizio utilizzeremo il metodo dei nodi, che consiste nell'equilibrare singolarmente ogni nodo individuando quali sono le reazioni di contatto con cui il nodo risponde alla sollecitazione proveniente da ogni asta. Procediamo metodicamente all'analisi di ogni nodo impostando le equazioni di equilibri alla traslazione verticale ed orizzontale:

Nodo A

ΣFx =0 --> N1 = 0 [asta scarica]

ΣFy =0 --> N2 = 0 [asta scarica]

Nodo B

ΣFx =0 --> N3 + 30KN + (N4)√2/2 = 0 --> N3 = -10KN [asta scarica]

DIMENSIONAMENTO DI UNA TRAVE

L’impalcato preso in esame è uno stralcio dell’ipotesi di progetto per una abitazione a Fiumicino (RM). Il telaio di travi e pilastri è previsto in CLS ma in questa esercitazione lo utilizzeremo come base per dimensionare una trave in diverse tecnologie, Acciaio, Legno e CLS.

La trave che andremo a dimensionare è quella che in questo stralcio di pianta sopporta il carico maggiore, la trave A-B, 2 che ha un area di influenza pari a 28mq con un interasse 4,80m, e una luce di 6,00m.

Per le tre tecnologie procederemo per gradi:

1_Scelta del pacchetto del solaio, individuando i pesi di ogni mareriale in KN/mq

2_Dimensionamento dei travetti tramite foglio excel, determinando qs, qp e qa.

qs = carico strutturale (porzione di solaio strutturale)

qp = carico permanente non strutturale (porzione di solaio non strutturale, impianti e

tramezzi)

qa = carico accidentale (2KN/mq, dipende dalla funzione dell’edificio, in questo caso

una biblioteca)

3_Dimensionamento della trave tramite foglio excel, aggiungendo il peso dei travetti al carico

strutturale qs.

4_Verifica della trave tramite foglio excel, aggiungendo al carico strutturale qs il peso proprio della

trave.

SOLAIO IN ACCIAIO

1_a) Scelta del pacchetto solaio.

1_ b) Peso dei materiali al mq.

Pavimento in gres porcellanato 0,4 KN/mq
Massetto alleggerito Foacem (per impianti) 1,4 KN/mq
Soletta = cls(c25/30)+lamiera (sp8/10) 2,4 KN/mq
Incidenza impianti 0.5 KN/mq
Incidenza tramezzi 1 KN/mq

2_Dimensionamento dei travetti

qs_carico permanete strutturale:

2,4 KN/mq (soletta+lamiera grecata)

- qp carico permanente non strutturale:

3,36 KN/mq = 0,4 KN/mq (pavimento) + 1,4 KN/mq (massetto) + 0,5 KN/mq (impianti) +

1 KN/mq (tramezzi) + 0,06 (controsoffitto)

- qa carico accidentale

2 KN/mq (abitazione)

- Qtot = qs + qp + qa = (2,4 + 3,36 + 2) KN/mq = 7,76 KN/mq

prendiamo come interasse approissimativo dei travetti 1m e calcoliamo il carico totale linearizzato:

- Qtot linearizzato = Qtot x interasse = 7,76 KN/mq x 1m = 7,76 KN/m

- Scelgo la classe di resistenza dell’acciaio --> S275

Adesso disponendedo di tutti i valori necessari posso procedere con il calcolo della dimensione del travetto attraverso un foglio di calcolo exel tenendo conto che:

M, momento massimo della trave è pari a ql²/8 come il modello della trave appoggiata

fD, resistenza a flessione di progetto e pari a fy,K/1,05(coefficiente di sicurezza)

Wx, modulo di resistenza minimo della trave, che ci permettere di scegliere il nostro profilo da tabella.

- Wx = 65,33 cm^3 --> scelgo il travetto in modo che il Wx si maggiore di 65,33 cm^3

IL travetto scelto è un IPE140 S275 Wx= 77,3 cm^3

3_Dimensionamento della trave

Per dimensionare la trave procederemo come per i travetti cambiando la luce e l'interasse, logicamente differente da quello dei travetti e aggiungendo al qs il peso dei travetti, essendo questi parte strutturale del solaio.

qs_carico permanete strutturale:

2,53 KN/mq = 2,4KN/mq (soletta+lamiera grecata) + 0,13 KN/mq (travetti)

- qp carico permanente non strutturale:

3,36 KN/mq = 0,4 KN/mq (pavimento) + 1,4 KN/mq (massetto) + 0,5 KN/mq (impianti) +

1 KN/mq (tramezzi) + 0,06 (controsoffitto)

- qa carico accidentale

2 KN/mq (abitazione)

- Qtot = qs + qp + qa = (2,53 + 3,36 + 2) KN/mq = 7,89 KN/mq

- Qtot linearizzato = Qtot x interasse = 7,89 KN/mq x 4,8m = 37,9 KN/m

- Classe dell'acciaio--> S275

Calcoliamo la trave tramite il foglio excel:

Wx = 650,71 cm^3 --> scelgo il profilo con Wx maggiore di 650,71 cm^3

La trave scelta è un IPE 330 S275 con Wx = 713,0 cm^3

4_Verifica del dimensionamento della trave

Come gia anticipato, per la verifica della trave ci limiteremo ad aggiungere al qs(carico strutturale) il peso proprio della trave ed eseguiremo di nuovo il calcolo con il foglio excel por controllare che il Wx minimo non superi quello del profilo scelto:

-Peso della trave:

49,1 Kg/m = 0,48 KN/ m (peso della trave linearizzato) --> 0,48KN/m x 4,8m = 0,1 KN/mq (peso della trave al mq)

-qs = 2,63 KN/mq

-qp = 3,36 KN/mq

-qa = 2 KN/mq

Calcolo di verifaica:

Wx = 658,96cm^3 (Wx minimo) < Wx = 713,0 cm^3 (Wx della IPE330 S275)

Il Wx minimo è minore di quello del profilo scelto --> La trave è Verificata!

SOLAIO IN LEGNO

1_a) Scelta del pacchetto solaio.

Il solaio preso in considerazione è un solaio rustico in legno massello. Le dimensioni dell'impalcato non si prestano molto a questa tecnologia ma sarà comunque interessante eseguire l'esercizio anche per capire quali sono i litimi del materiale.

1_ b) Peso dei materiali al mq.

-Pavimento in cotto levigato 0,48 KN/mq

-Massetto tradizionale SA300T (per impianti) 1,16 KN/m

-Tavolato 6KN/mc = 6KN/mc x (0.02x1x1) = 0,12 KN/mq

-Incidenza impianti 0.5 KN/mq

-Incidenza tramezzi 0,06 KN/mq

2_Dimensionamento dei travetti

qs_carico permanete strutturale:

0,12 KN/mq (tavolato)

- qp carico permanente non strutturale:

3,14 KN/mq = 0,48 KN/mq (pavimento) + 1,16 KN/mq (massetto) +

0,5 KN/mq (impianti) + 1 KN/mq (tramezzi)

- qa carico accidentale

2 KN/mq (abitazione)

- Qtot = qs + qp + qa = (0,12 + 3,14 + 2) KN/mq = 5.26 KN/mq

interasse da manuale del recupero del restauro di strutture orizzonatali: 0,55m

- Qtot linearizzato = Qtot x interasse = 5.26 KN/mq x 0,55m = 2,89 KN/m

Scelgo per la realizzazione dei travetti il legno lamellare BS14 con classe di resistenza GL28

Andiamo ad eseguire il calcolo con il foglio excel, considerando che:

M, momento massimo della trave è Ql^2/8

fm,k è la resistenza del legno, valore tabellato dato dalle caratteristiche del materiale 28 N/mmq

K,mod, coefficiente correttivo che tiene conto della permanenza del carico e dell'usura della struttura 0,5

ym, coefficiente di sicurezza 1,45

fD , resistenza di progetto data la fm,k*Kmod / ym = 28N/mmq x 0,5 / 1,45 = 9,66 N/mmq

b , è la base del travicello che prendiamo 10 cm

h , è l'altezza del travetto con la quale possiamo dimensionare il nostro elemento

h = 19,91 cm --> il travicello scelto è il BS14 Gl28 10 x 22 cm

3_Dimensionamento della trave

qs_carico permanete strutturale:

peso travicelli --> (0,1x0,22x1)m x 6 KN/mc = 0,13 KN/mq

0,25 KN/mq (tavolato + travicelli)

- qp carico permanente non strutturale:

3,14 KN/mq = 0,48 KN/mq (pavimento) + 1,16 KN/mq (massetto) +

0,5 KN/mq (impianti) + 1 KN/mq (tramezzi)

- qa carico accidentale

2 KN/mq (abitazione)

- Qtot = qs + qp + qa = (0,25 + 3,14 + 2) KN/mq = 5.39 KN/mq

- Qtot linearizzato = Qtot x interasse = 5.39 KN/mq x 4,80m = 25,9 KN/m

-classe di resistenza del legno lamellare GL28

Calcoliamo la sezione della trave con il foglio excel:

h = 49,11 --> la trave scelta è il BS14 Gl28 30 x 55 cm

4_Verifica del dimensionamento della trave

-Peso della trave:

(0,3x0,55x1)m x 6 KN/mc = 0,99 KN/mq

-qs = 1,24 KN/mq

-qp = 3,14 KN/mq

-qa = 2 KN/mq

Calcolo di verifica:

h = 53,43 < 55 (h della trave scelta)

h della sezione trovata aggiungendo il peso proprio della trave non supera quella della sezione scelta, la trave è Verificata!

SOLAIO IN CLS

1_a) Scelta del pacchetto solaio.

Il solaio preso in considerazione è un solaio tradizionale di pignatte e travetti in cemento precompresso, per l'analisi dei carici ci affidiamo ai valori tabellati forniti dal produttore in questo caso EDILTACCONI s.p.a.

1_ b) Peso dei materiali al mq

-Pavimento in gress porcellanato 0,4 KN/mq

-Isolante acustico 0,62 KN/mq

-pacchetto : caldana

pignatte

travetti

getto di completamento 2,8 KN/mq (valore tabellato)

-Intonaco 0,3 KN/mI

-Incidenza impianti 0.5 KN/mq

-Incidenza tramezzi 1 KN/mq

2_Dimensionamento della trave

qs_carico permanete strutturale:

2,8 KN/mq (valore tabellato)

- qp carico permanente non strutturale:

2,82 KN/mq = 0,4 KN/mq (pavimento) + 0,62 KN/mq (isolante) + 0,3 KN/mq (intonaco) +

0,5 KN/mq (impianti) + 1 KN/mq (tramezzi)

- qa carico accidentale

2 KN/mq (abitazione)

- Qtot = qs + qp + qa = (2,8 + 2,82 + 2) KN/mq = 7,62 KN/mq

- Qtot linearizzato = Qtot x interasse = 7,62 KN/mq x 4,8m = 36,5 KN/m

Adesso devo scegliere la classe di resistenza del materiale, nel calcestruzzo sia l'acciao che il cemento svolgono un importante ruolo

strutturale quindi dobbiamo scegliere

-classe di resistenza delle barre d'acciaio B450A fy,k = 450 MPa (utilizzata in zona sismica)

-classe di resistenza del calcestruzzo C40/50 (40=Fck resistenza cilindrica - 50=Rck resistenza cubica)

Effettuiamo il dimensionamento della trave tenendo conto che:

M, è il momento massimo della trave Ql^2/8 dato dal modello della trave appoggiata

fy, è la resistenza delle barre 450 MPa

fy,k è la resistenza diviso il coefficiente di sicurezza dell'accio per armature 450Mpa/ 1,15 = 391,30 N/mmq

Rck è la resistenza cunica del cemento 50 N/mmq

Fcd è la tensione di progetto data Rck/1, 5 (coefficiente di sicurezza)

b è la base della sezione della trave 25cm

delta sono i centimetri di cemento destinati al copriferro che non hanno funzione strutturale

H infine è l'altezza della sezione della trave

H = 34,43 --> scelgo una trave 25x40 cm

4_Verifica del dimensionamento della trave

-Peso della trave:

il foglio excel mi fornisce il peso al metro lineare, dividendolo per l'interasse ottengo il peso al metro cuadro

2,15 KN/m / 4,8m = 0,45 KN/mq

-qs = 3,25 KN/mq

-qp = 2,82 KN/mq

-qa = 2 KN/mq

Calcolo di verifica:

H = 35,29 cm < H = 40 cm (altezza della sezione scelta)

L'altezza della sezione ricalcolata con il peso proprio della trave è minore dell'altezza scelta in precedenza

la trave è Verificata!

STRUTTURA RETICOLARE SPAZIALE

In questa esercitazione ci occuperemo del disegno l’analisi e il dimensionamento di una struttura reticolare spaziale con modulo cubico (2x2x2)m e dimensioni (8x12x2h)m. Disegneremo la nostra struttura utilizzando come base Autocad, importeremo poi il disegno su SAP2000 per eseguirne l’anasisi strutturale e il dimensionamento.

1_disegno della struttura

Apriamo un nuovo file di Autocad e creiamo un nuovo layer che rinomineremo “aste”.

Questa operazione ci permettera di assegnare al layer la funzione Frames su SAP.

Sul layer appena creato iniziamo a disegnare la struttura partendo dall’ origine degli assi (0,0,0) in modo da ritrovare facilmente il disegno una volta importato su SAP.

Il modulo di base della reticolare spaziale sarà un cubo di lato 2m. Disegnamo quindi con il comando “Plilinea” tre lati e una diagonale lasciando appositamente aperto un lato del quadrato.

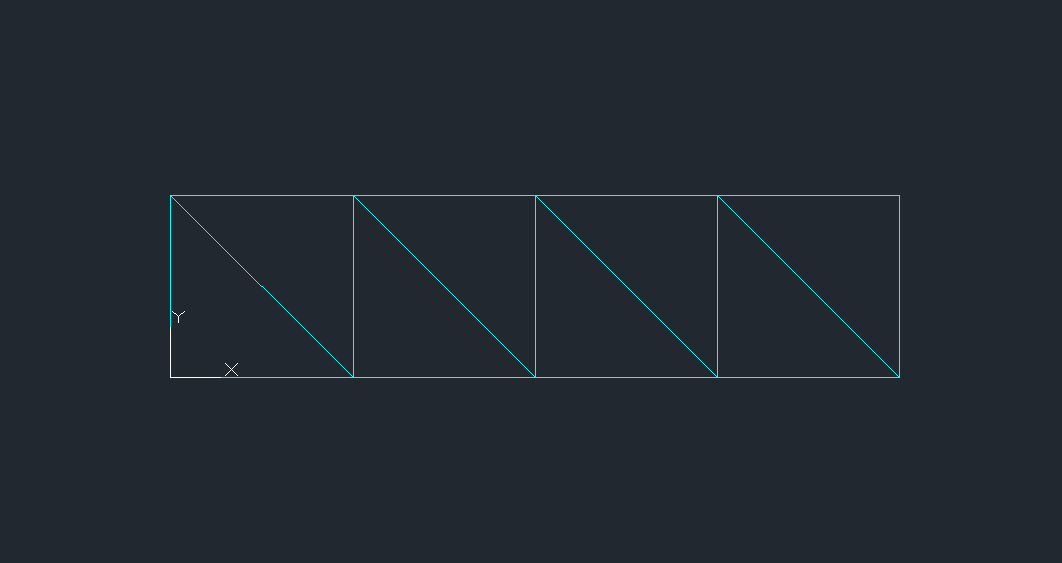
Utilizzando il comando “Arrey” ripetiamo lungo l’asse X il disegno di base per quattro con distanza 2m in modo da definire i moduli del lato corto della nostra piastra pari a 8m ossia 4 moduli.

Da questa operazione possiamo renderci conto dell’importanza di aver lasciato aperto un lato del quadrato iniziale, così facendo non avremo sovrapposizioni di polilinee nel disegno.

Passiamo ora al disegno in tre dimensioni utilizzando il comando “orbita” (o più facilemente Shift+Rotellina).

Utilizzando il comando “Ruota3d” ruotiamo intorno all’asse X di 90° in modo da avere l’intero disegno sul piano X,Z.

Abbiamo definito lungo l’asse Z altezza della nostra piastra pari 2m ossia un modulo.

Cambiano il sistema di riferimendo UCS sul piano Y,Z disegnamo le aste rimanenti per completare il modulo cubico lasciando aperto questa volta un intera faccia del cubo.

Ancora utilizzando il comando Arrey ripetiamo il disegno per 4 volte lungo X con distanza 2m.

Abbiamo disegnato un intera riga della nostra piastra.

Concludiamo il disegno ancora una volta con il comando “arrey” questa volta lungo Y sempre con distanza 2m ripetendo la riga per 6 volte.

Cancelliamo le linee aste in eccesso con l’accortezza che ogni modulo della piastra sia completo su ogni faccia.

Abbiamo disegnato la nostra piastra reticolare spaziale.

2_definizione della struttura su SAP2000

Per effettuare l'analisi della struttura ci affideremo come gia detto a SAP2000.

Salviamo il file di Autocad con estenzione .dxf 2007 in modo da poterlo importare su SAP.

Apriamo quindi SAP e scegliamo subito come unità di misura KN,m,C°

Una volta importato il file SAP ci chiede se qualche layer corrisponde ad eventuali elementi strutturali, assegneremo al nostro unico layer “Aste” la funzione di frames.

Per poter analizzare il comportamento strutturale della nostra piastra reticolare spaziale dobbiamo prima definirla come modello strutturale in modo che SAP possa riconoscerla.

Procediamo con ordine definendo :

vincoli esterni
vincoli interni
materiale delle aste
sezione delle aste
eventuali carichi (per poter apprezzare la deformata della struttura)

-vincoli esterni

Selezioniamo i 4 vertici inferiori della piastra e assegnamo a questi come vincoli esterni le Cerniere.

-vincoli interni

Esssendo una Reticolare spaziale dobbiamo imporre che agli estremi delle aste siano rilasciati i momenti simulando in questo modo la presenza di una cerniera interna in prossimità dei nodi della struttura.

Selezioniamo tutte le aste e imponiamo il rilascio dei momenti 2,2 e 3,3 in tutti i nodi della struttura.

-materiale delle aste

Per assegnare il materiale alle aste dobbiamo prima definirlo.

Creiamo un nuovo materiale “acciaio” assegnando come tipo di materiale “Steel”.

Una volta definito possiamo assegnarlo alle nostre aste.

-sezione delle aste

Allo stesso modo definiamo prima una sezione, in questo caso “tubolare”, alla quale possiamo assegnare il materiale “acciaio”.

Una volta definita la sezione possiamo assegnarla alle aste.

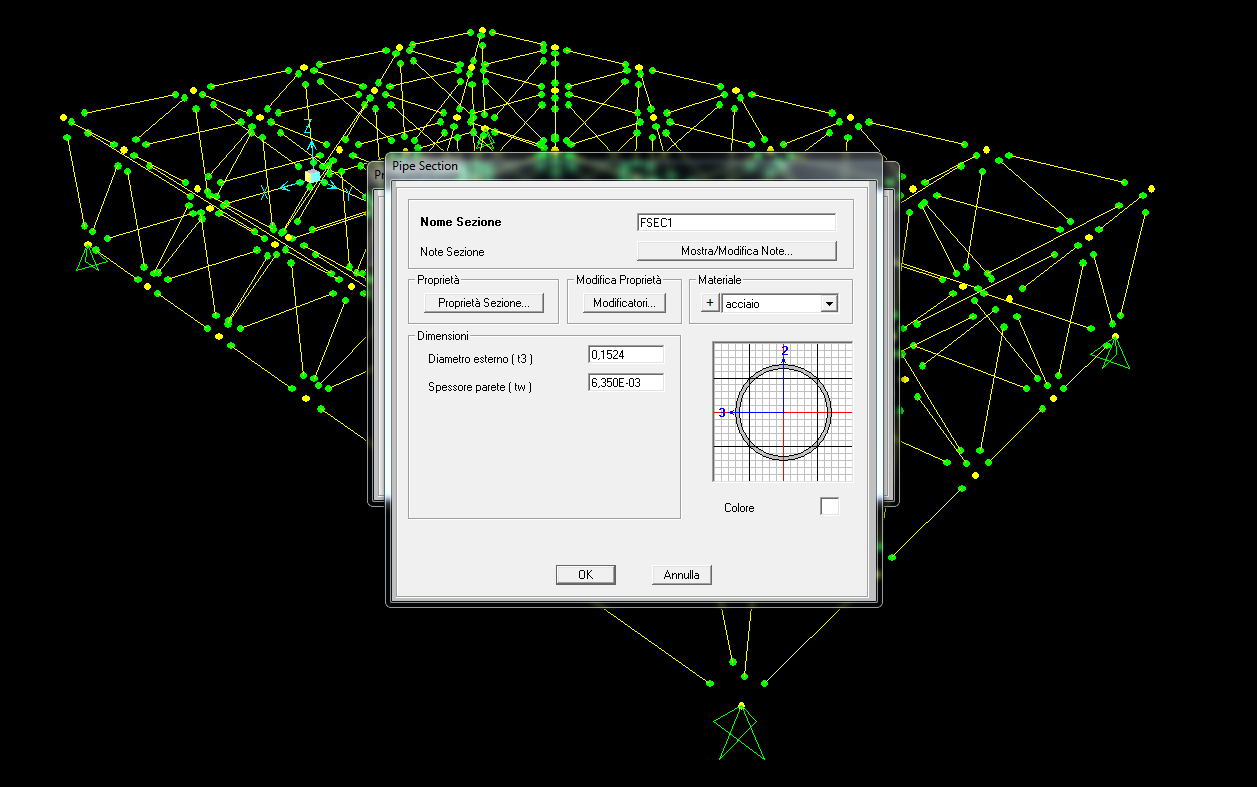
Una volta terminate queste operazioni la nostra struttura appare in questa maniera con tutte le aste definite con sezione e materiale.

-carichi

Anche i carichi prima di essere assegnati devono essere definiti.

Quindi definiamo un carico gravitazionale di -40kN (segno meno in modo da averla rivolta verso il basso),

che chiameremo “Forza Concentrata”.

Una volata definito il carico dobbiamo assegnarlo alla struttura, ovviamente essendo una struttura reticolare dobbiamo assegnarlo sui nodi superiori. Per selezionarli dobbiamo spegnere momentaneamente le aste attraverso il comando “set display options” --> “frame not in view” e “joints not invisible”.

Selezionando la vista 2D del piano Z,X possiamo facilmente selezionare i nodi superiori della struttura.

Adesso possiamo assegnare ai seguenti nodi il carico “forza concentrata” gia definito in precedenza.

Dalla vista 3d possiamo osservare la distribuzione delle forze concentrate su tutti i nodi superiori della struttura.

La struttura è modellata in maniera corretta affinché SAP possa riconoscerla, quindi procediamo lanciando l’analisi.

3_analisi della struttura

Lanciamo l'analisi ricordando di far analizzare i carichi di default.

SAP ci chiederà di salvare il file, dopo di che sarà subito possibile osservare la deformata della struttura sotto l'azione delle

forze concentrate.

Seguono i diagrammi dello sforzo Normale, rosso se di compressione e giallo se di trazione.

In oltre SAP ci offre le tabelle dove vengono specificati gli sforzi normali agenti su ogni asta, individuiamo l’asta più compressa e quella più tesa, e procediamo con il loro dimensionamento.

4_predimensionamento

Nmax (trazione)= 263,469 KN

Nmax (compressione)= -385,631 KN

-progetto dell’asta tesa

Per prima cosa definiamo la tensione di progetto --> fD = fy / γm

fD = tensione di design

fy = tensione di snervamento = dipende dal tipo di acciano in questo caso scegliamo S275

fy=275 MPa

γm = coefficiente di sicurezza = 1,05

fD = 275 MPA / 1,05 = 261,9 MPa

Definita la tensione di progetto possiamo definire anche l’area della sezione utilizzando la formula

fD = N / A --> A = N / fD

A = area della sezione

N = Sforzo normale massimo di trazione --> 263,469 KN = 263469 N

fD = tensione di progetto --> 261,9 MPA = 261,9 N/mm^2

A = 263469 N / 261,9 N/mm^2 = 1005,99 mm^2 = 10,06 cm^2

Scelgo quindi dalle tabelle una sezione con un area maggiorne di quella calcolata:

IL profilo scelto ha :

diametro 114,3 mm

spessore 3,6 mm

Area della sezione 12,50 cm^2

-progetto dell’asta compressa

Per il progetto dell’asta compressa eseguo lo stesso procedimento dell’asta tesa cambiando N, che questa volta sarà quello di compressione N = 385,631 KN, quindi:

A = 385631 N / 261,9 N/mm^2 = 1472,4 mm^2 = 14,72 cm^2

IL profilo scelto ha :

diametro 139,7 mm

spessore 3,6 mm

Area della sezione 15,40 cm^2

Per il progetto dell'asta compressa ci preoccuperemo di esguire anche la verifica a stabilità o Verifica del carico critico Euleriano.

Dobbiamo quindi verificare che il carico di punta P ,ovvero il nostro sforzo massimo di compressione Nmax

sia inferiore al carico critico euleriano P_crit, per il quale l'asta tenderebbe a sbandare e risulterebbe quindi instabile.

P < P_{crit -->}P_crit= π² x E x Jmin / l0²

dove: E = modulo elastico a compressione

Jmin = momento di inerzia minimo della sezione, in questo caso uguale in tutte e due le direzione in quando

la sezione è circolare.

lo = luce libera di inflessione, ossia la distanza tra due flessi dell'onda di sbandamento, questo valore dipende

dalla lunghezza dell'elemento e da i suoi vincoli esterni, in questo caso due cerniere quindi lo = l ,

l = √2 m = 2,8 m.

P_{crit =}π²x210000 N/mm2 x 357000 mm⁴/ 7840000 mm²= 942,824 KN

385,631 KN< 942,824 KN

asta verificata!

RIPARTIZIONE DELLE FORZE SISMICHE

(Esercitazione svolta in collaborazione con Davide Troiani)

Una struttura deve essere progettata per resistere ai carichi gravitazionali e allo stesso tempo reagire agli effetti di un eventuale carico orizzontale, come ad esempio un sisma o l’ azione del vento.

In una struttura ad occuparsi della spinta delle forze orizzontali sono i controventi. Per analizzare la ripartizione del carico orizzontale sui vari controventi dobbiamo ipotizzare che in un impalcato:

1) Il solaio sia un corpo rigido, non deformabile soggetto a traslazioni e rotazioni.
2) I telai si comportino come corpi elastici che reagiscono alla forza orizzontale con una spinta pari a f= K_t ∙ δ

Prenderemo come esempio il seguente impalcato in cemento armato, composto da 17 pilastri, 6 controventi verticali e 3 orizzontali, e analizzeremo il suo comportamento sotto l’ effetto delle forze sismiche:

- Qtot = qs + qp + qa = (2,4 + 3,36 + 5) KN/mq = 10,76 KN/mq

prendiamo come interasse approissimativo dei travetti 1m e calcoliamo il carico totale linearizzato:

- Qtot linearizzato = Qtot x interasse = 10,76 KN/mq x 1m = 10,76 KN/m