blog di JLARIA.VOLPI

Il principale obiettivo dell’esercitazione consiste nella ricerca del centro delle rigidezze e nel confronto tra la posizione di quest’ultimo e del centro di massa della struttura in analisi.

La soluzione ideale sarebbe che i due centri coincidessero, o fossero il più vicino possibile in modo da evitare rotazioni relative in caso di sisma.

La nostra struttura è composta da un solaio in cemento armato e da pilastri in acciaio che reggono la struttura mediante il collegamento con una travatura reticolare posta all’ultimo piano dell’edificio, che poggia su due ulteriori strutture in cemento armato, contenenti le scale e gli ascensori dell’edificio.

 

Procedendo su SAP abbiamo disegnato la struttura di un piano: i pilastri, le travi e le superfici dei vani scala/ascensori. Assegnato loro le relative sezioni con i materiali e ad ogni punto di base il vincolo di incastro.

Successivamente è necessario trovare il centro delle masse. L’operazione è stata svolta secondo il metodo geometrico, ossia tracciando le diagonali dell’edificio, essendo un rettangolo, e ponendo nell’intersezione di quest’ultime, alla quota delle travi, un punto (centro delle masse).

Abbiamo selezionato tutti i punti alla quota delle travi ed il centro di massa ed abbiamo assegnato loro la condizione di corpo rigido, facendo si che questi appartengano all’impalcato e che si evitino rotazioni e spostamenti relativi.

 

 

Per calcolare il peso proprio della struttura abbiamo impostato una condizione di carico ed avviato l’analisi.

 

Successivamente abbiamo sommato tutte le reazioni verticali in modo da calcolarci il peso proprio della struttura: 5740,25 KN

 

Per poter definire i carichi sismici, come percentuale del peso proprio, applichiamo al peso proprio della struttura un coefficiente di 0,2 in quanto Roma è una zona a basso rischio. In tal modo otteniamo un valore di : 1148,05 KN

 

Trovate le forze possiamo assegnare 2 carichi, uno in direzione x e uno in direzione y, pari alla forza sismica, al centro delle masse.

 

Avviamo l’analisi prima per la direzione x.

Notiamo che l’impalcato non subisce rotazioni relative.

Successivamente avviamo l’analisi in direzione y.

Anche qui notiamo che l’impalcato non subisce rotazioni relative.

In conclusione, dato che il nostro edificio presenta solo traslazioni relative, possiamo affermare che la struttura è perfettamente equilibrato e che il centro delle masse coinciderà con il centro delle rigidezze.

 

Jlaria Volpi e Giulia Mellano

 

Abbiamo, per prima cosa, costruito la travatura reticolare su SAP, avete modulo 3m x 3m e perimetro di 45m x 18m.

Successivamente abbiamo assegnato a tutti i nodi delle cerniere interne per impedire il passaggio del momento.

 Come terzo passaggio abbiamo assegnato la sezione in acciaio con profilato tubolare.

Per assegnare le forze su ogni nodo abbiamo calcolato il peso del singolo solaio ed infine il peso totale dei solai che la struttura dovrà sorreggere. Sui nodi di bordo il valore della forza assegnata è pari alla metà in quanto lavorano su metà area di influenza.

 

Abbiamo scelto un solaio in Latero-cemento di 645 m² per piano:

Carichi permanenti strutturali:

 

-Soletta: altezza: 4cm, peso specifico 25N/m³:

q_s,s =0.4 m x 25KN/m³ =1KN/m²

 

-Pignatta in laterizio: dim 20cm x 38cm, peso specifico 8KN/m², interasse 0,5m: q_s,pi =[( 0,38 x 0,2)/0.5] x 8KN/m²=1,2KN/m²

 

-Travetti.: dim 12x20cm, peso specifico 25KN/m³

q_s,t r= [(0,12 x 0,2) x 0,5]  x 25 KN/m³ = 1,2KN/m²

 

Il carico strutturale totale: q_s = q_s,tr + q_s,pi + q_s,s  = (1,2 + 1,2 + 1)KN/m² = 3,4KN/m²

 

Carichi permanenti non strutturali:

 

-Pavimento in gres porcellanato: spessore 2cm, peso specifico 20KN/m³

q_p,pa = 0,02m x 20KN/m³ = 0,40KN/m²

 

-Isolante acustico: spessore 3cm, peso specifico 1KN/m³

q_p,is = 0,03m x 1KN/m³ = 0,03KN/m²

 

-Allettamento più massetto: spessore 8+4cm, peso specifico 20KN/m³

q_p,ma = 0,12m x 20KN/m³ = 2,4KN/m²

 

-Intonaco: spessore 2cm, peso specifico 20 KN/m³

q_p,in = 0,02m x 20KN/m³ = 0,4KN/m²

 

Il carico permanente non strutturale totale a cui aggiungo l'incidenza di impianti e tramezzi:

q_p = q_p,is +q_p,ma+q_p,pa +q_p,im +q_p,in =(0,03+2,4+0,4+1,6+0,4)KN/m²=4,16KN/m²

 

Carichi accidentali:

 

-Lla destinazione d'uso è quella di uffici aperti al pubblico (categoria B2), quindi il carico accidentale q_a = 3KN/m²

 

Peso per m² di ogni piano:

q_u = 10,56 KN/m²

 

Peso totale di 1 piano:

10,56 KN/m² x 645 m² = 6811,2 KN

 

Peso dei 7 piani:

6811,2 KN x 7 = 47678,4 KN

 

Forza su ogni nodo:

47678,4 KN / 112(n nodi) = 425,7 KN

 

Deformata in 3D e 2D

Dopo aver assegnato la forza su ogni nodo abbiamo avviato l’analisi e successivamente estratto la tabella dei valori su Excel, da cui abbiamo ottenuto il valore massimo dello Sforzo Normale.

Asta tesa massima

 

 

Asta compressa massima

 

Il passo successivo sarà quello di dimensionare le aste tese e le aste compresse.

 

ASTE COMPRESSE

 

Abbiamo effettuato il dimensionamento delle aste compresse prendendo in esame le più sollecitate.

Prendiamo in considerazione alcuni fattori: lunghezza dell'asta (l); modulo di elasticità (E);  resistenza di design(f_yd)e la tipologia del vincolo (β). Per le aste compresse dobbiamo calcolare il modulo di inerzia minima (Imin), l'area minima (Amin), ed il raggio di inerzia (ρ_min), ed inoltre verificare che la snellezza (λ) non sia superiore a 200. 

 

ASTE TESE

Per dimensionare le aste tese sono dati necessari soltanto il valore dello sforzo normale e quello della resistenza di progetto, variabile a seconda del tipo di acciaio utilizzato (in questo caso, acciaio S275).

Conoscendo questi due dati, si può ricavare l’area minima necessaria a sopportare quel valore dello sforzo normale:

A_min = N / f_yd    

Anche in questo caso abbiamo preso in considerazione le aste più sollecitate (quelle che riportano il valore positivo dall'analisi su SAP).

Dopo aver calcolato i profilati per tutte le sezioni, utilizzando l procedimento sopra esposto, si procede all'analisi su SAP inserendo le dimensioni corrette.

 

Jlaria Volpi e Giulia Mellano

Lo scopo dell'esercitazione è progettare e verificare la trave più sollecitata, soggetta a flessione e il pilastro più sollecitato, soggetto a sforzo normale, del telaio, utilizzando sezioni in legno, acciaio e c.a.

                                                                              TELAIO:TRAVE PIU’ SOLLECITATA                                                                                                                                                                                                                                               TELAIO: PILASTRO PIU’ SOLLECITATO

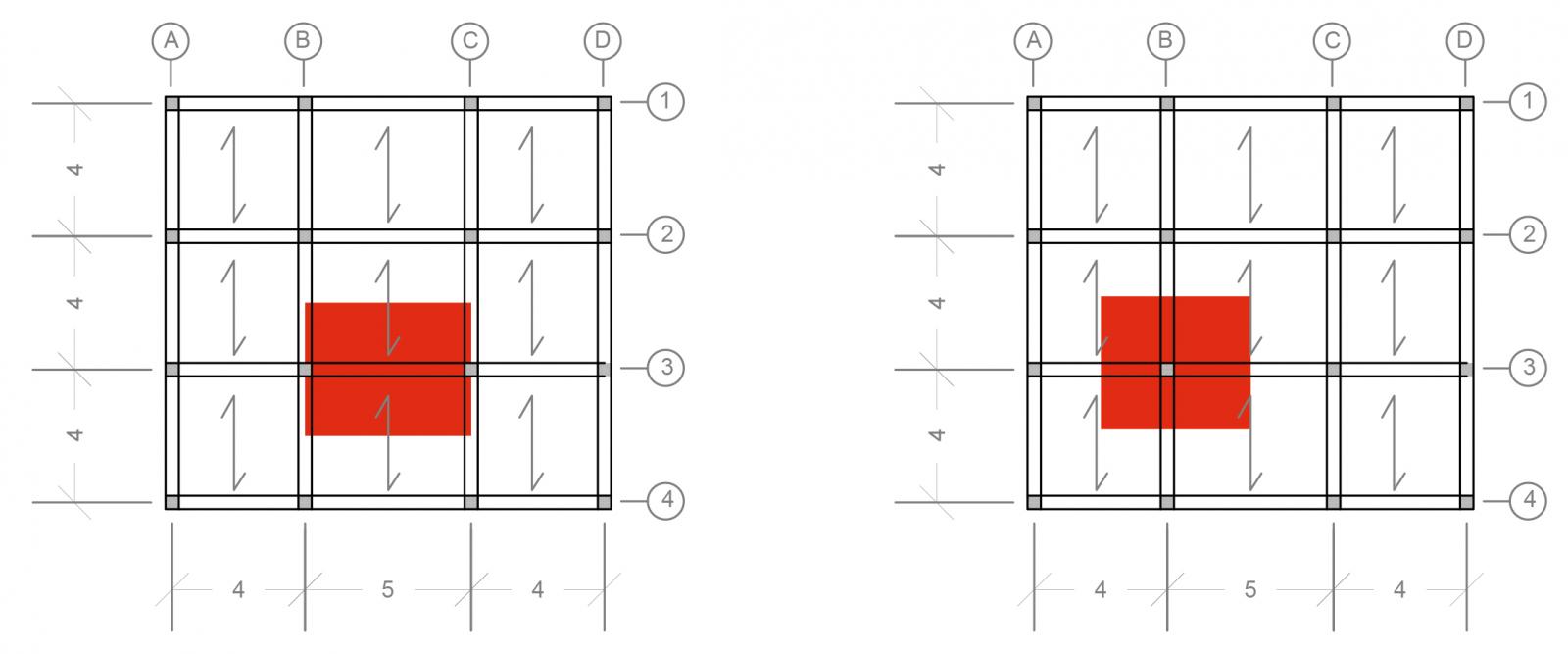
PREDIMENSIONAMENTO DELLA TRAVE PIU' SOLLECITATA

La trave evidenziata in figura è la più sollecitata dell'impalcato ed ha un'area di influenza di 4,00m x 5,00m = 20,00m²

TABELLA MOMENTI MASSIMI PER LE TRAVI PIU’ SOLLECITATE

 

1.     Legno

 

Come prima operazione calcoliamo i carichi permanenti strutturali(trascurando il peso proprio della trave), permanenti non strutturali ed accidentali

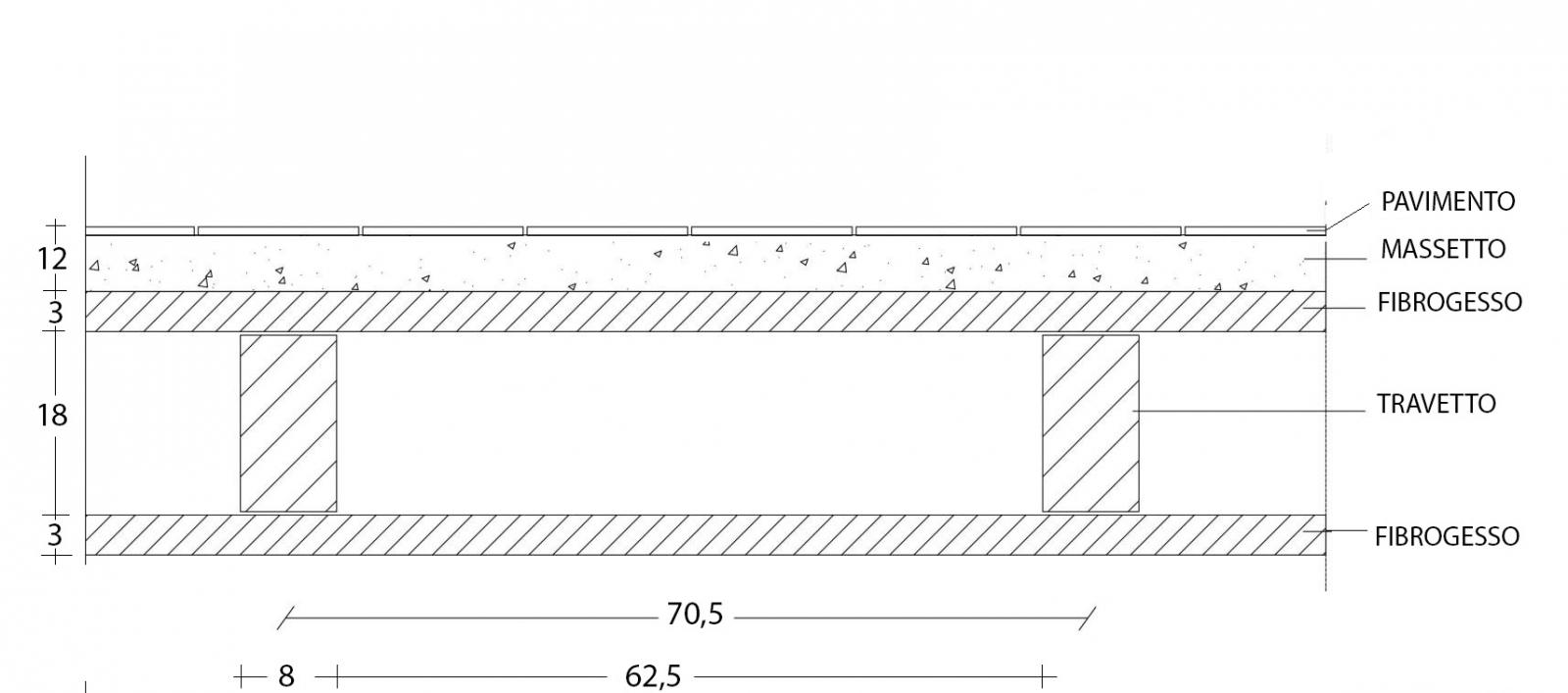
Carichi permanenti strutturali:

 

-Travetto in legno: (8x18)cm, peso specifico 5,5KN/m³, interasse 70,5cm

q_s,tr = (0,18m x 0,08m)/m² x 5,5KN/m³ = 0,08KN/m²

 

-Soletta in Fibrogesso: spessore 3 cm, peso specifico 11,5KN/m³

q_s,f = 0,03m x 11,5KN/m³ = 0,35KN/m²

Moltiplico per 2 avendo 2 solette: 0,35 x 2= 0,69 KN/m³

 

Il carico strutturale totale:

q_s = q_s,tr + q_s,f = (0,08+0,69)KN/m²  = 0,8KN/m²

 

Carichi permanenti non strutturali:

 

-Massetto di allettamento in malta di cemento: spessore 10cm, peso specifico 20KN/m³

q_p,ma = 0,1m x 20KN/m³ = 2KN/m²

 

-Pavimento in gres porcellanato: spessore 2cm, peso specifico 20KN/m³

q_p,pa = 0,02m x 20KN/m³ = 0,40KN/m²

 

Il carico permanente non strutturale totale a cui aggiungo l'incidenza di impianti, tramezzi e controsoffitto:

q_p = q_p,ma + q_p,pa + q_p,im  + q_p,tr  + q_p,c   = (2+0,40+0,1+1,6+0,06)KN/m²  = 4,16KN/m²

 

Carichi accidentali:

-Ipotizziamo che la destinazione d'uso sia quella di civile abitazione, quindi il carico accidentale q_a = 2KN/m²

 

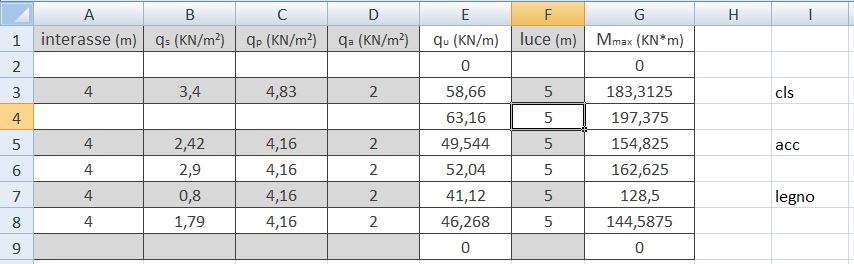
• Inserendo tutti i dati ricavati nel foglio di calcolo excel ricaviamo il carico

     q_u = 41,12KN/m agente sulla trave.

Introducendo come valore la luce di 5m otteniamo il valore del M_max = 128,5KN*m        

Scelgliamo la tipologia di legno C24, inserisco il valore caratteristico di resistenza f_m,K=24N/mm², il coefficiente diminutivo K_mod=0,6 (dipende dalla classe d’uso della trave, è un coefficiente correttivo dei valori di resistenza del materiale considerando l'aggravio delle condizioni esterne d'esercizio come particolari condizioni di carico e umidità) e il coefficiente parziale di sicurezza γ_m=1,45 in modo che il foglio di calcolo mi restituisca la tensione di progetto f_d=9,9310345N/mm² tramite la formula: f_md = k_mod x f_mk /γ_m = 13,24 N/mm²

 

Come passo successivo scegliamo la base della trave b=30cm e ricavo l'altezza minima h_min=50,87cm tramite la formula H_min = √6 M_max / fmd x b

Ingegnerizzando la sezione ricavata scegliamo una trave 30x55cm.

Calcoliamo il peso proprio della trave e lo aggiungiamo al carico permanente strutturale q_s: 

q_s,trave = (0,30m x 0,55m )/m² x 6KN/m³ = 0.99KN/m²

quindi

q_s  + q_s,trave = (0,8+0.99)KN/m²= 1,79KN/m²

inserendo il nuovo q_s verifico che il nuovo h_min=53,96cm<h=55cm  

VERIFICATA

TABELLA CALCOLO DEL PREDIMENZIONAMENTO DELLA SEZIONE DELLA TRAVE IN LEGNO

1. Acciaio

 

Come prima operazione calcoliamo i carichi permanenti strutturali(trascurando il peso proprio della trave), permanenti non strutturali ed accidentali.

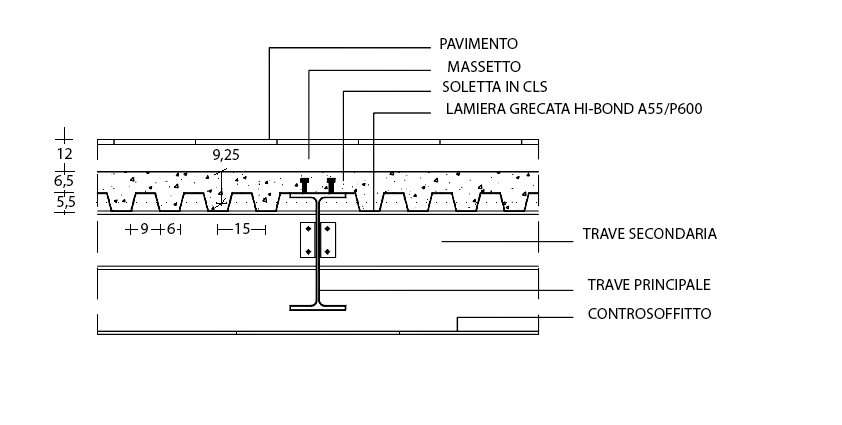
Carichi permanenti strutturali:

 

-Lamiera grecata: altezza 5,5 cm, spessore 8mm

q_s,la = 0,11 KN/m²

 

-Soletta in cls.a.: altezza: 0,65+0,55 peso specifico 25KN/m³

q_s,ca = [(0,65+0,55)/2] x 25 KN/m³ = 2,32KN/m²

 

Il carico strutturale totale:

q_s = q_s,la + q_s,ca  = (0,11+2,32)KN/m² = 2,42KN/m²

 

 

Carichi permanenti non strutturali:

 

-Massetto di allettamento in malta di cemento: spessore 10cm, peso specifico 20KN/m³

q_p,ma = 0,1m x 20KN/m³ = 2KN/m²

 

-Pavimento in gres porcellanato: spessore 2cm, peso specifico 20KN/m³

q_p,pa = 0,02m x 20KN/m³ = 0,40KN/m²

 

Il carico permanente non strutturale totale a cui aggiungo l'incidenza di impianti, tramezzi e controsoffitto:

q_p = q_p,ma + q_p,pa + q_p,im  + q_p,tr  + q_p,c   = (2+0,40+0,1+1,6+0,06)KN/m²  = 4,16KN/m²

 

Carichi accidentali:

 

-Ipotizziamo che la destinazione d'uso sia quella di civile abitazione, quindi il carico accidentale q_a = 2KN/m²

 

Inserendo tutti i dati ricavati nel foglio di calcolo excel ricavo il carico

q_u = 49,544KN/m agente sulla trave.

 

Introducendo come valore la luce di 5m otteniamo il valore del momento massimo

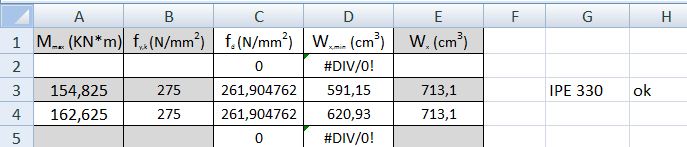
M_max = 154,825KN*m         

 

Scelgo la tipologia di acciaio S275, inserisco il suo valore di tensione di snervamento f_y,K=275MPa, si trova così la tensione di progetto 

f_d = f_yk /γ_s = 275/1,15 = 261,9 N/mm ²

dove γ_s = 1,15 coefficiente parziale di sicurezza dell'acciaio.

 

Ricavare dal foglio di calcolo il modulo di resistenza a flessione minimo rispetto all'asse x.

W_x,min = M_max / f_d = 591,15 cm³

 

Considerando W_x,min troviamo nella tabella dei profilati metallici un profilato con W_x > W_x,min

 

IPE 330 con W_x = 713,1 cm³

 

Calcolo il peso proprio della trave e lo aggiungo al carico permanente strutturale q_s:

q_s,trave = (0,006261m² )/m² x 78,5KN/m³ = 0, 49KN/m²

 

 

quindi

q_s  + q_s,trave = (2,42+0,49)KN/m²=2.9KN/m²

 inserendo il nuovo q_s verifico che il nuovo W_x,min=620,93cm³<W_x=713,1cm³ 

 

VERIFICATA

TABELLA CALCOLO DEL PREDIMENZIONAMENTO DELLA SEZIONE DELLA TRAVE IN ACCIAIO

1. Calcestruzzo armato

 

Come prima operazione calcolo i carichi permanenti strutturali(trascurando il peso proprio della trave), permanenti non strutturali ed accidentali

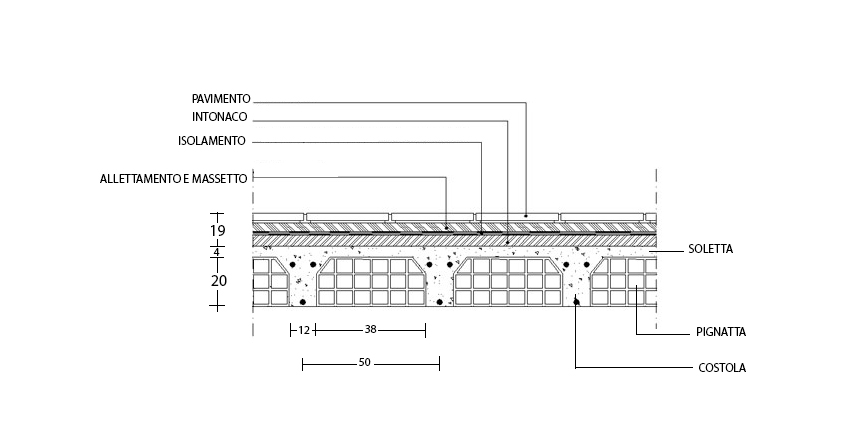
Carichi permanenti strutturali:

 

-Soletta: altezza: 4cm, peso specifico 25N/m³:

q_s,s =0.4 m x 25KN/m³ =1KN/m²

 

-Pignatta in laterizio: dim 20cm x 38cm, peso specifico 8KN/m², interasse 0,5m: q_s,pi =[( 0,38 x 0,2)/0.5] x 8KN/m²=1,2KN/m²

 

-Travetti.: dim 12x20cm, peso specifico 25KN/m³

q_s,t r= [(0,12 x 0,2) x 0,5]  x 25 KN/m³ = 1,2KN/m²

 

Il carico strutturale totale: q_s = q_s,tr + q_s,pi + q_s,s  = (1,2 + 1,2 + 1)KN/m² = 3,4KN/m²

Carichi permanenti non strutturali:

 

-Pavimento in gres porcellanato: spessore 2cm, peso specifico 20KN/m³

q_p,pa = 0,02m x 20KN/m³ = 0,40KN/m²

 

-Isolante acustico: spessore 3cm, peso specifico 1KN/m³

q_p,is = 0,03m x 1KN/m³ = 0,03KN/m²

 

-Allettamento più massetto: spessore 8+4cm, peso specifico 20KN/m³

q_p,ma = 0,12m x 20KN/m³ = 2,4KN/m²

 

-Intonaco: spessore 2cm, peso specifico 20 KN/m³

q_p,in = 0,02m x 20KN/m³ = 0,4KN/m²

 

Il carico permanente non strutturale totale a cui aggiungo l'incidenza di impianti e tramezzi:

q_p = q_p,is +q_p,ma+q_p,pa +q_p,im +q_p,in =(0,03+2,4+0,4+1,6+0,4)KN/m²=4,16KN/m²

 

Carichi accidentali:

 

-Ipotizziamo che la destinazione d'uso sia quella di civile abitazione, quindi il carico accidentale q_a = 2KN/m²

 

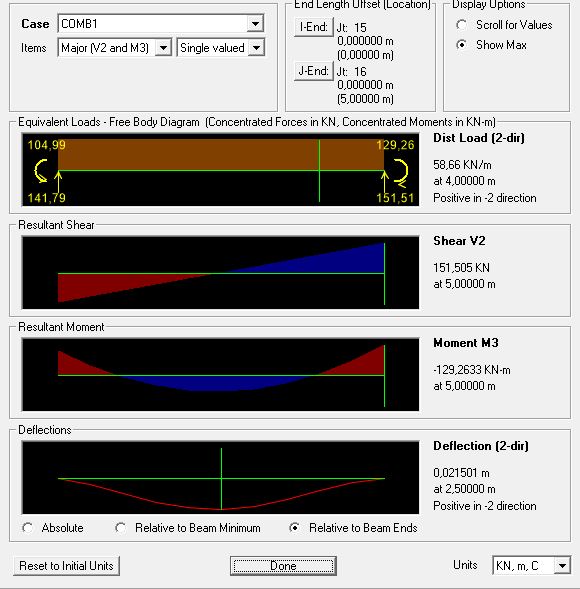
Inserendo tutti i dati ricavati nel foglio di calcolo excel ricavo il carico q_u = 58,66KN/m agente sulla trave.

Introducendo come valore la luce di 5m otteniamo il valore del M_max = 183,3125KN*m      

   

Scelgliamo la tipologia di cemento C25/30 con resistenza caratteristica f_cK=25MPa, quindi ricavo la resistenza di progetto f_cd=19,83MPa calcolata mediante la formula: f_cd = α_cc f_ck /γ_c = 14,16 N/mm2 servendosi del coefficiente riduttivo per le resistenze di lunga durata α_cc = 0,85 e del coefficiente parziale di sicurezza del calcestruzzo γ_c = 1,5.

La scelta dell’acciaio è condizionata dalla normativa, in questo caso viene scelto il B450C con 450 MPa di limite di snervamento. Inserendo questi dati nelle caselle apposite si trova il valore f_yd. La tensione di progetto dell'acciaio f_yd = f_yk /γ_s = 450/1,15 = 391,3 N/mm 2  con il coefficiente parziale di sicurezza dell’acciaio γ_s = 1,15.

Il passaggio successivo è la scelta di una dimensione per la base della sezione b=30cm che, insieme a resistenza di progetto f_cd e parametri β e r serve per trovare l'altezza utile h_u=52,69cm che addizionata al coprifilo δ=4cm determina l'altezza minima H_min=56,69cm.

Una volta ricavata l'altezza minima andiamo ad ingegnerizzare la sezione e scegliamo un'altezza di design H_design=60cm. 

Aggiungiamo ora  il peso della trave, prima trascurato, al carico totale che diventa q_u=63,16KN/m in modo da ricavare di nuovo H_min=58,68cm e se quest'ultima dimensione è inferiore a H_design la struttura è verificata.

H_min=58,68cm< H_design=60cm  

 

VERIFICATA

TABELLA CALCOLO DEL PREDIMENZIONAMENTO DELLA SEZIONE DELLA TRAVE IN CEMENTO ARMATO

 

PREDIMENSIONAMENTO DEL PILASTRO PIU' SOLLECITATO

Per quel che concerne il predimensionamento del pilastri nei vari materiali i valori dei carichi rimangono invariati. Per calcolare lo Sforzo Normale su di essi è stata applicata la formula per calcolare lo Sforzo Normale su ogni piano:

 

N_{1 piano}=(A_inf x q_u) + peso_travi

 

Il peso delle travi era stato precedentemente calcolato nel foglio Excel sulle travi. 

L’area di influenza è pari a l_a x l_b= 4 x 4,5=18m²

 

Per calcolare lo Sforzo Normale sul pilastro più sollecitato abbiamo moltiplicato lo Sforzo Normale per ogni piano per il numero di piani.

Cls: N_max=906,66 KN

Acciaio: N_max=681,25 KN

Legno: N_max=548,57 KN

 

TABELLA SFORZI NORMALI PER I PILASTRI PIU’ SOLLECITATI

 

TABELLA PREDIMENZIONAMENTO PILASTRO IN ACCIAIO

TABELLA PREDIMENZIONAMENTO PILASTRO IN  LEGNO

TABELLA PREDIMENZIONAMENTO PILASTRO IN CLS

 

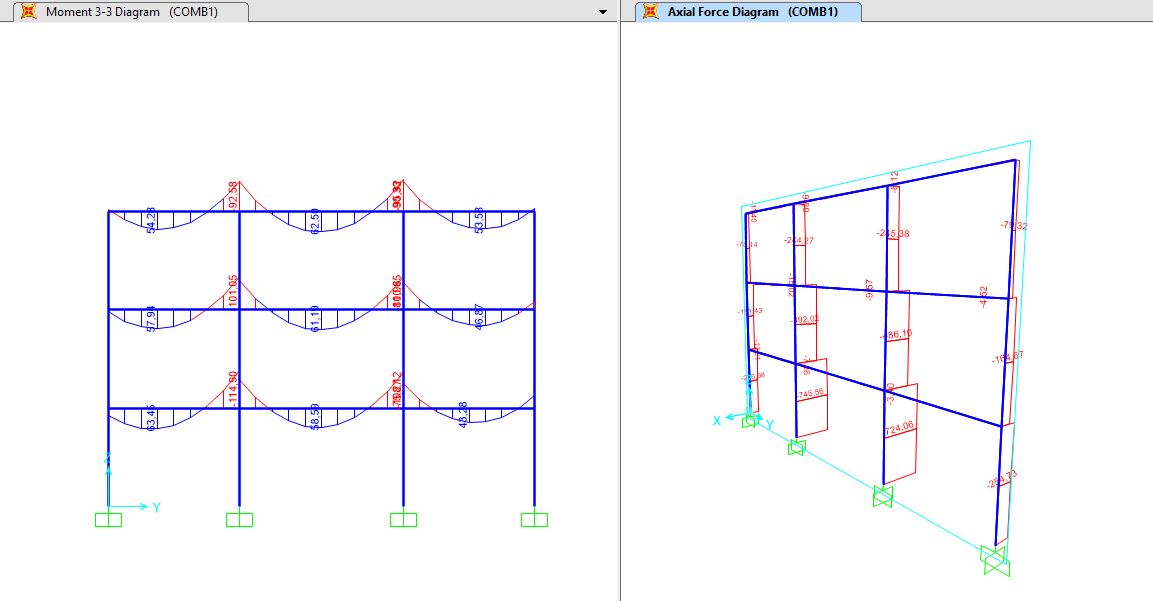
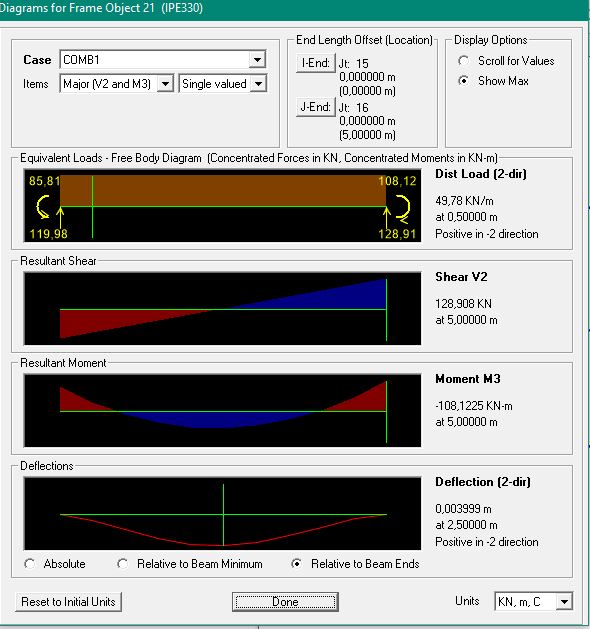
Dopo aver effettuato i calcoli su Excel abbiamo ricostruito i vari telai per ogni materiale in Sap e abbiamo controllato che i dati scelti fossero verificati.

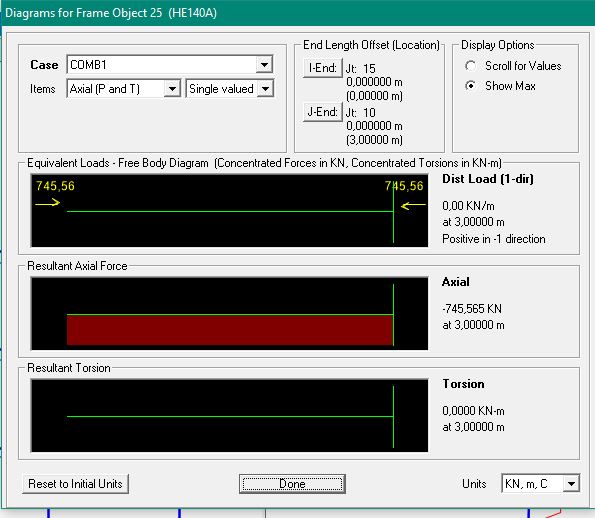
STUDIO DELLA STRUTTURA IN ACCIAIO SU SAP

 

STUDIO DELLA STRUTTURA IN LEGNO SU SAP

 

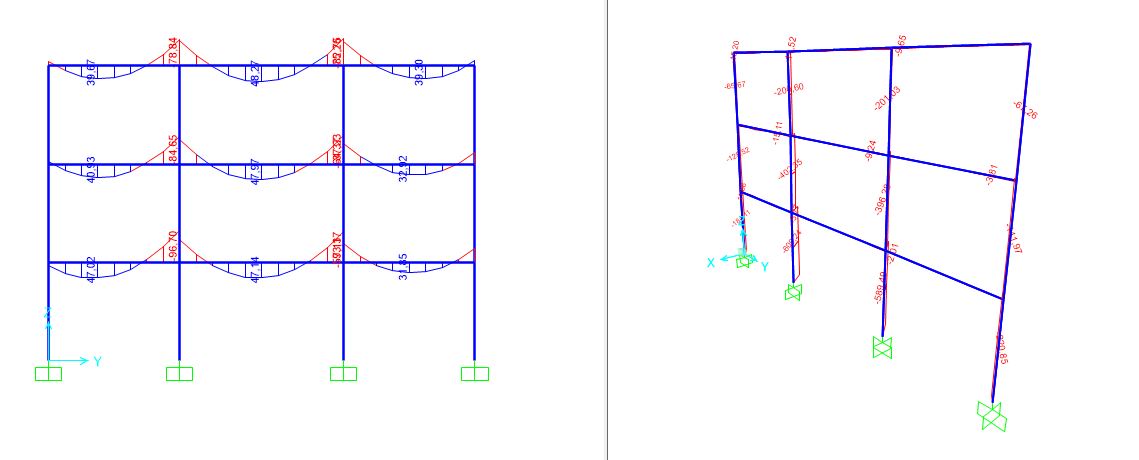
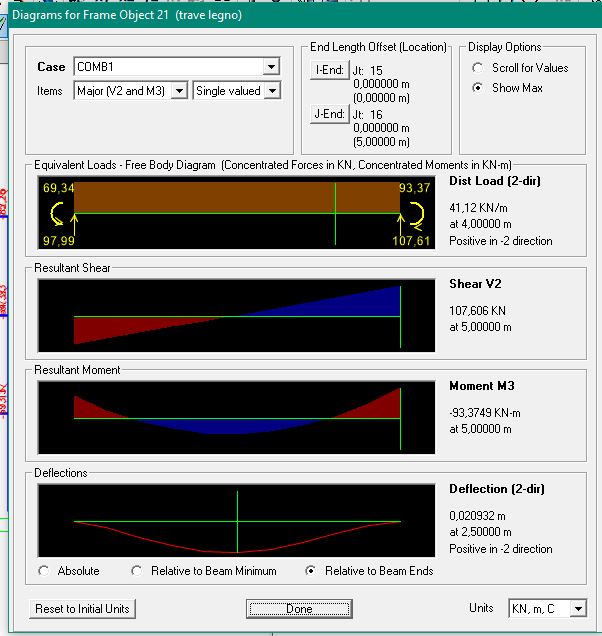
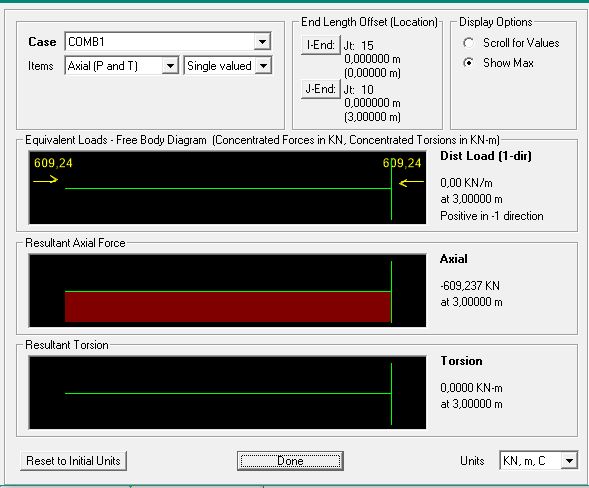
STUDIO DELLA STRUTTURA IN CLS SU SAP

 

 

 

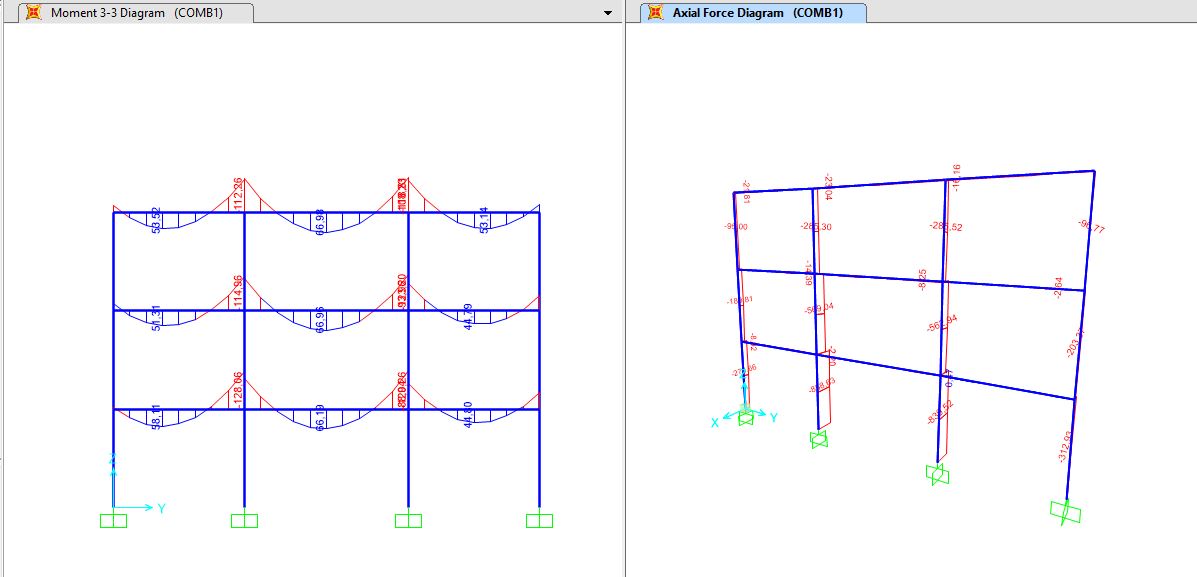
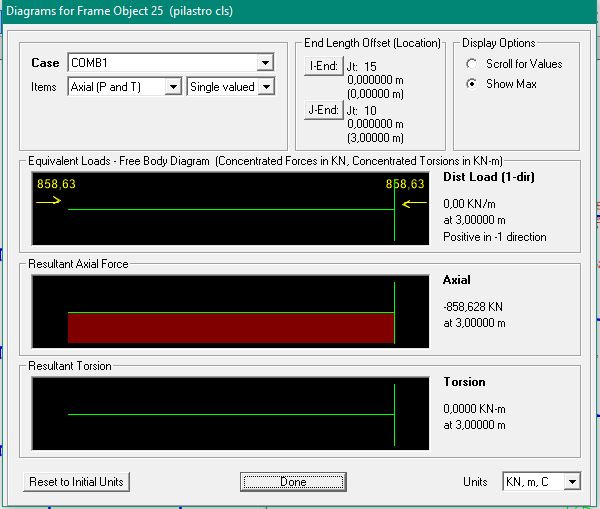
Nel caso dell’acciaio abbiamo riscontrato che il valore dello sforzo normale per il pilastro non era verificato. Allora abbiamo riportato il valore trovato in Sap nel foglio Excel e abbiamo scelto un profilato HEA 160, nonostante il profilato scelto in precedenza (HEA 140) avesse comunque un’area superiore all’area minima calcolata con il nuovo valore trovato su Sap.

Nel caso del pilastro in legno, abbiamo riscontrato che il valore dello sforzo normale per il pilastro non era verificato e allora abbiamo riportato il valore trovato da sap su excel ricalcolandoci la dimensione del pilastro in legno ma anche in questo caso abbiamo visto che nonostante l'aumento dello sforzo normale, il pilastro è comunque verificato per le dimensioni scelte in precedenza.

 

Stud.sse Jlaria Volpi e Giulia Mellano