blog di marta.massacesi

Esercitazione svolta con Angelo Mizzon e Alessandra Tagliatesta

 

In questa esercitazione dobbiamo studiare un piano di un edificio e trovare la posizione del centro delle rigidezze, e vedere che sia il più possibile vicina al centro di massa, in modo che, in caso di sisma, vengano evitate le rotazioni dell’edificio.

L’edificio analizzato presenta una struttura di travi in acciaio che poggiano su due blocchi scala/ascensore in cemento armato, che svolgono una funzione portante. 

 

 

Disegno la struttura su SAP2000 e assegno le sezioni ai vari elementi strutturali: per le travi scelgo delle travi IPE400 in acciaio S355, mentre per i setti portanti ipotizzo il calcestruzzo C35/45 con uno spessore di 30 cm. Poi vincolo la struttura a terra attraverso degli incastri.

 

 

Per calcolare il carico relativo al sisma devo prima calcolare il peso proprio della struttura, poi moltiplico il peso strutturale per 0,2 (coefficiente per zone a basso rischio sismico).

 

 

Successivamente calcolo il centro di massa dell’edificio scomponendolo in figure semplici e calcolando il baricentro di ogni figura, con cui poi posso calcolare il baricentro totale della figura.

Xg = 26,71 m

Yg = 8,33 m 

 

 

Una volta disegnato il centro di massa su SAP2000 imposto nei nodi trave-trave e trave-setto la condizione di impalcato rigido, in modo che la struttura del solaio si comporti come un corpo rigido.

Dopo di che assegno il carico alla struttura nel centro di massa lungo l’asse x e lungo l’asse y. Poi faccio partire l’analisi per vedere come reagisce la struttura ai carichi orizzontali. 

Come possiamo vedere dai risultati dell’analisi la struttura subisce solo traslazioni orizzontali e verticali, per cui possiamo dedurre che il centro di massa coinciderà con il centro delle rigidezze.

 

Esercitazione svolta in parte con Alessandra Tagliatesta

 

Scopo di questa esercitazione è il dimensionamento della trave e del pilastro più sollecitati di un telaio, analizzato in tre differenti tecnologie di costruzione: acciaio, legno, cemento armato.

Per fare ciò andremo ad utilizzare il programma di calcolo Excel unito al software di calcolo strutturale SAP2000.  In particolare, il procedimento prevede:

1. analisi dei carichi agenti sulla struttura
2. predimensionamento trave/pilastro più sollecitato su Excel
3. inserimento dei dati in SAP2000
4. verifica tramite Excel

 

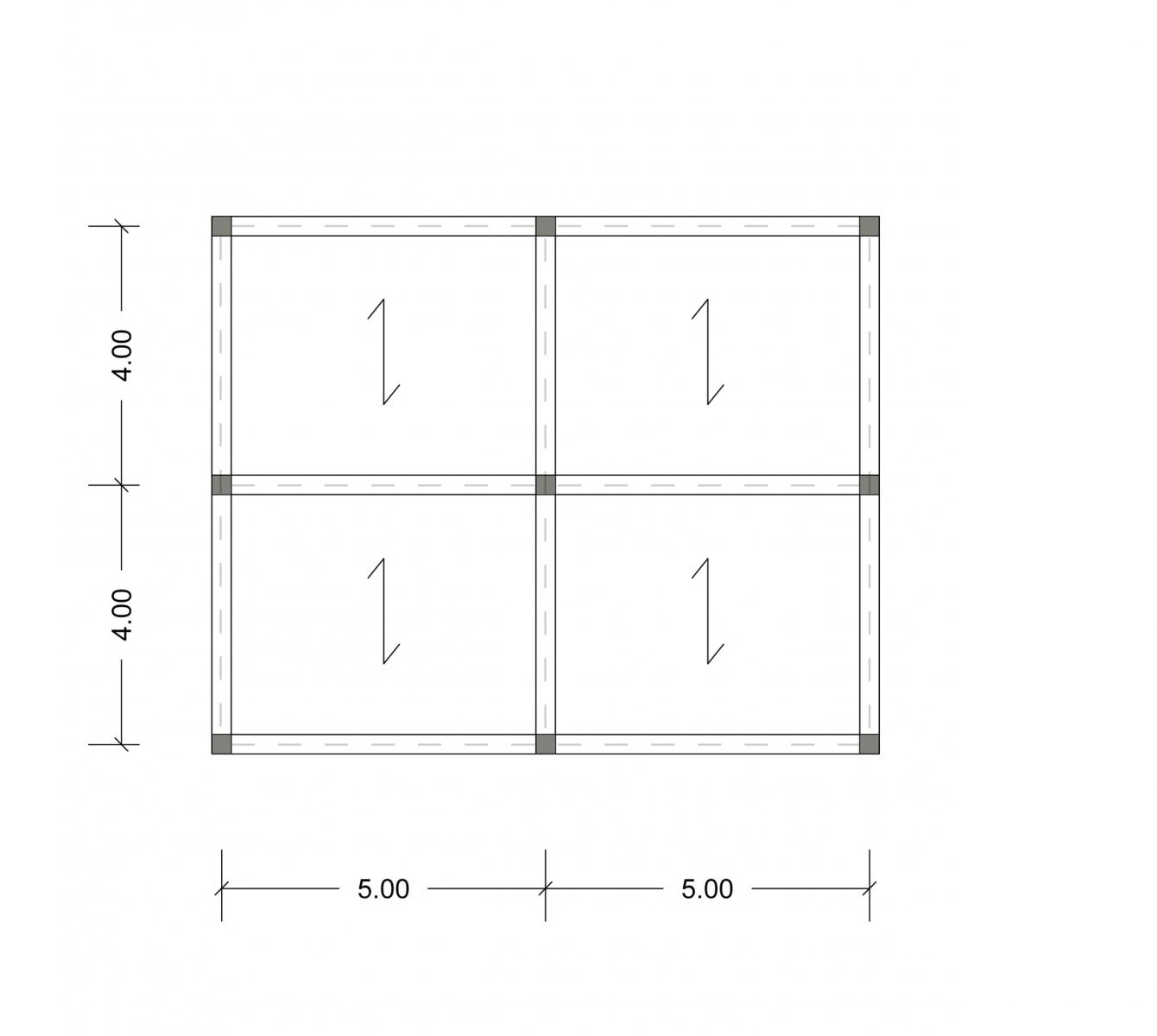
Per l'esercitazione si è scelto di andare a considerare un edificio a telai piani ad uso residenziale di 4 piani. 

• luce: 5m
• interasse: 4m

 

1) L'analisi dei carichi è data dalla somma dei vari carichi agenti sulla struttura moltiplicati per i loro coefficienti di sicurezza, che incrementano il carico per incertezza:

                                   qtot = qs x 1,3 + qa x 1,5 + qp x 1,5 = kN/m²

• qs rappresenta il carico strutturale, ovvero il carico degli elementi che hanno funzione portante
• qp rappresenta il carico permanente, ovvero il carico degli elementi che gravano sulla struttura ma non svolgono ruolo portante
• qa rappresenta il carico accidentale, legato alla destinazione d'uso dell'edificio e regolati dalla normativa (NTC2008- Norme tecniche per le costruzioni- D. M. 14 Gennaio 2008)

 

Per ottenere il valore del carico lineare qu, andrò a moltiplicare il carico totale agente per l'interasse:

                                               qu = qtot x i = kN/m

 

Per effettuare l'analisi dei carichi dobbiamo quindi considerare le stratigrafie dei tre solai presi in considerazione e valutare i carichi agenti

 

(a) SOLAIO IN ACCIAIO

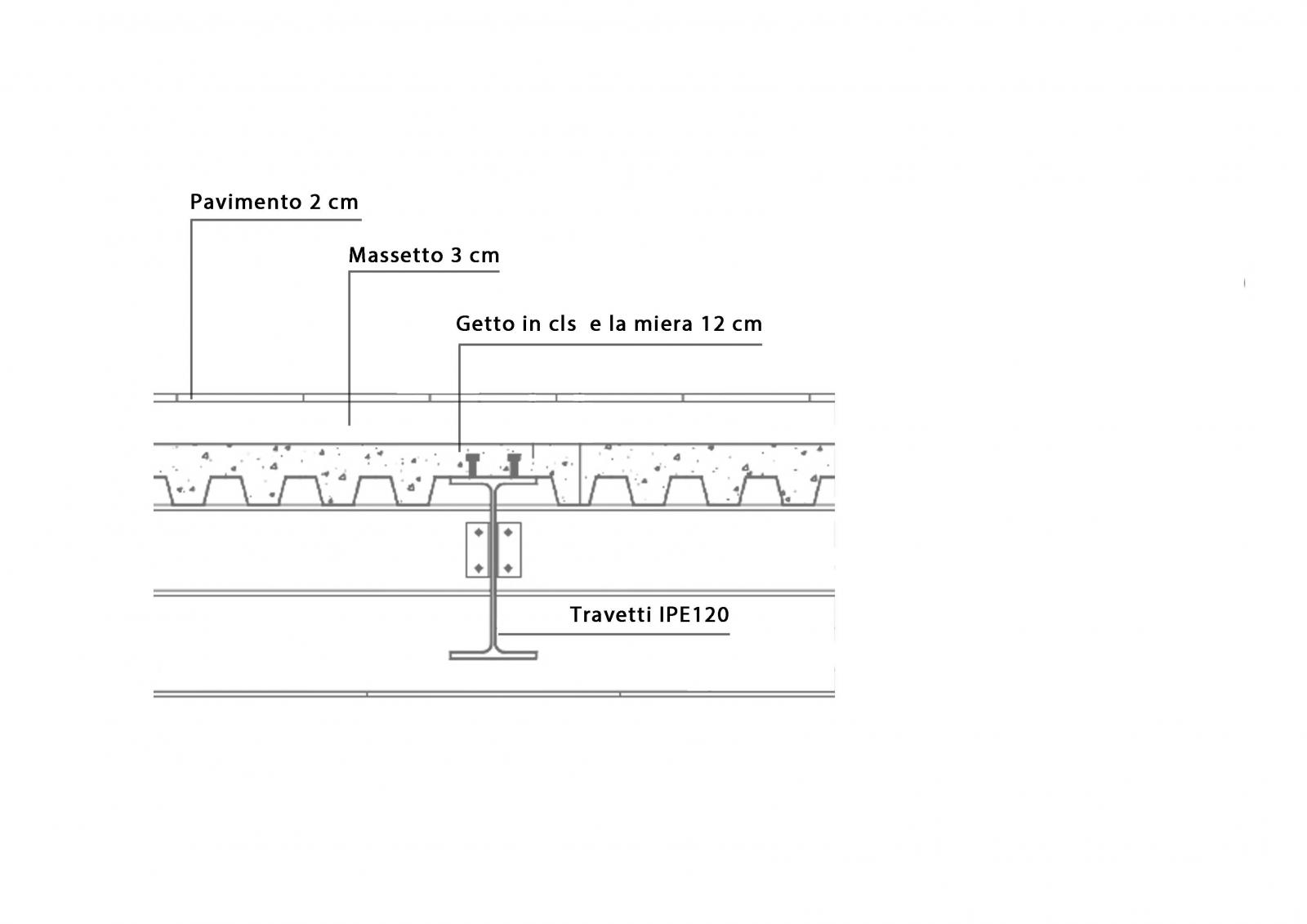
qs

• travetti: γacciaio x A x incidenza (1m/ interasse)= 78,5 kN/m³ x 0,001321m² x (1/0,08)= 0,13 kN/m²
• lamiera: 10,47 kg/m² x 9,8 m/s²= 0,10 kN/m²
• getto: γca x smedio = 25 kN/m³ x 0,0092= 2,32 kN/m²

tot: 2,55 kN/ m²

 

qp

• pavimento: 0,4 kN/m²
• massetto: γcls x smedio = 20 x 0,3 m = 0,6 kN/m²
• impianti: 0,1 kN/m²
• tramezzi: 1,6 kN/m²

tot: 2,7 kN/m²

 

qa

• civile abitazione: 2 kN/m²

 

(b) SOLAIO IN LEGNO

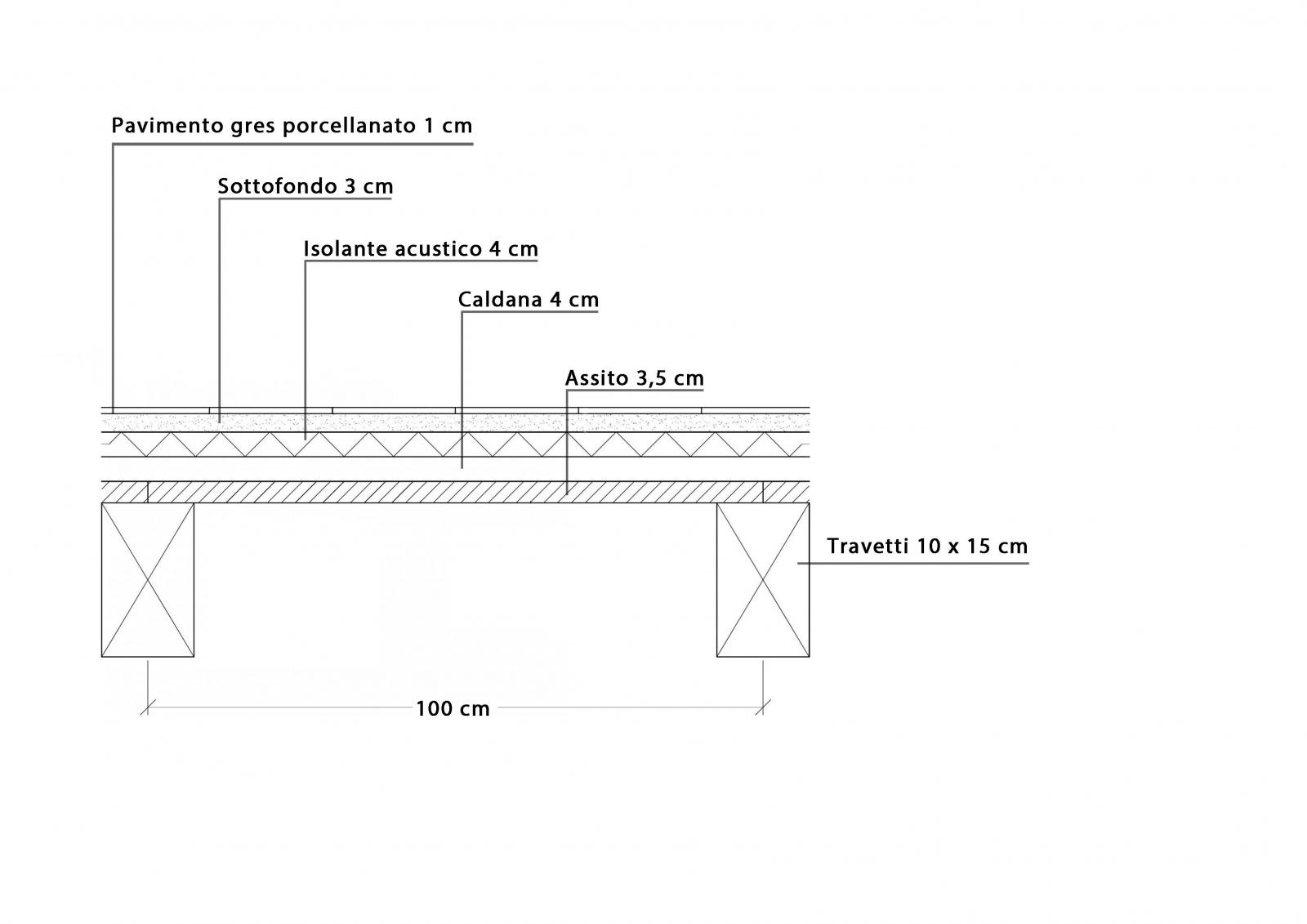
qs

• travetti: γlegno x A x i = 8 kN/m³ x (0,15 m x 0,10 m) x 1m= 0,015 kN/m²
• assito: 0,21 kN/m²
• caldana: 0,28 kN/m²

tot: 0,61 kN/m²

 

qp

• isolante: 0,0072 kN/m²
• sottofondo: 0,54 kN/m²
• pavimento: 0,2 kN/m²
• impianti: 0,1 kN/m²
• tramezzi: 1 kN/m²

tot: 1,85 kN/m²

 

qa

• civile abitazione: 2 kN/m²

 

(c) SOLAIO IN LATEROCEMENTO

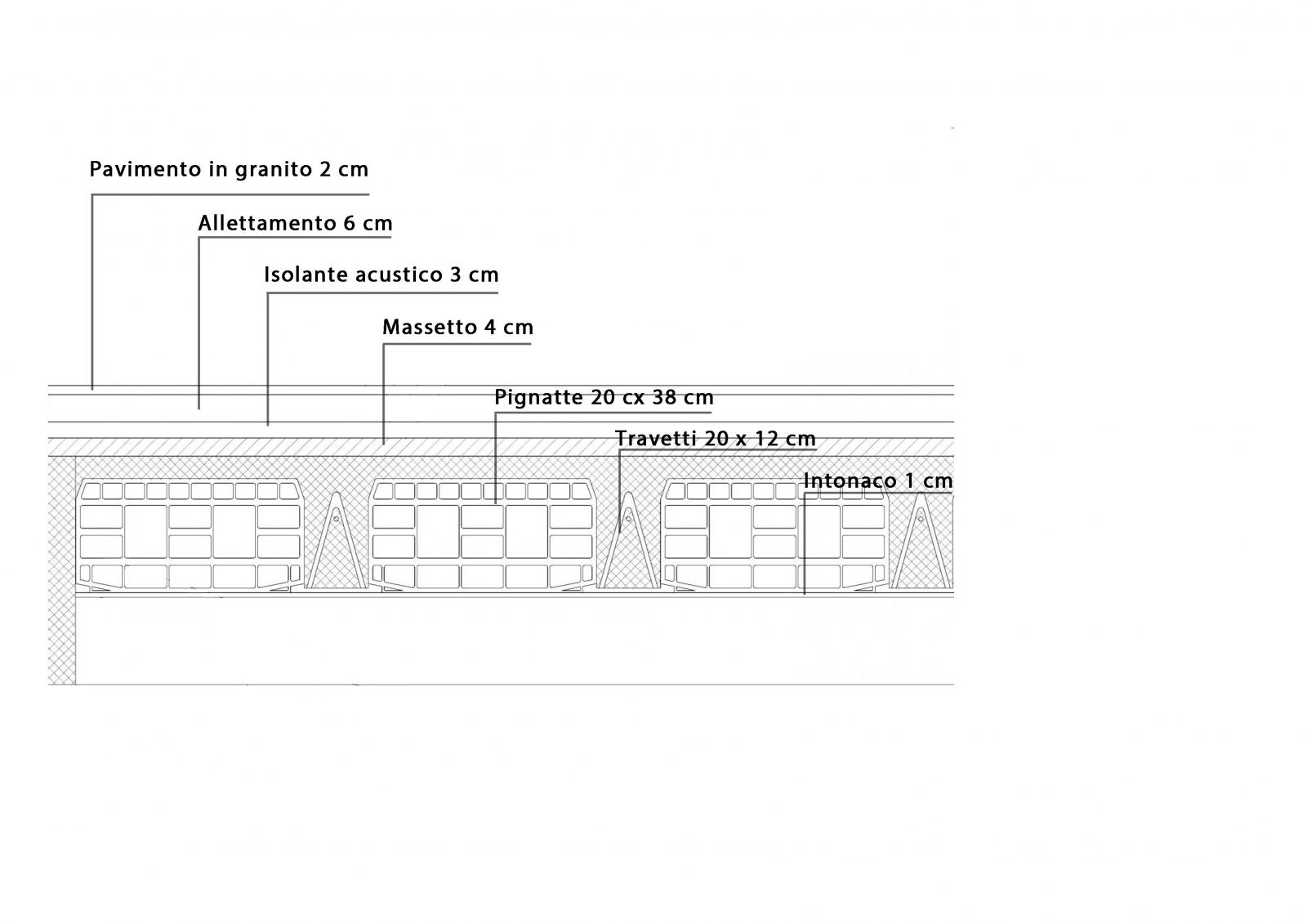
qs

• soletta in c.a.: γca x s = 25 kN/m³ x 0,04 m= 1 kN/m²
• travetti: γca x A x i = 25 kN/m³ x 0,12 m x (1/0,5) = 1,20 kN/m²
• pignatte: γlaterizio  x A x i = 6 kN/m³ x (0,38 x 0,20)m x (1/0,5)= 0,92 kN/m²

tot: 3,21 kN/m²

 

qp

• pavimento: 0,40 kN/m²
• allettamento e massetto: 2,40 kN/m²
• isolante acustico: 0,03 kN/m²
• intonaco: 0,40 kN/m²
• tramezzi: 1,60 kN/m²

tot: 4,83 kN/m²

 

qa

• civile abitazione: 2 kN/m²

 

 

2) Prima di andare a dimensionare la trave nelle varie tecnologie, assumiamo che:

- il modello di trave in esame viene considerato quello di semplice trave doppiamente appoggiata

- la tensione massima della trave viene posta come tensione di progetto (σmax= fd)

 

Si va ad individuare la trave più sollecitata e la sua area di influenza.

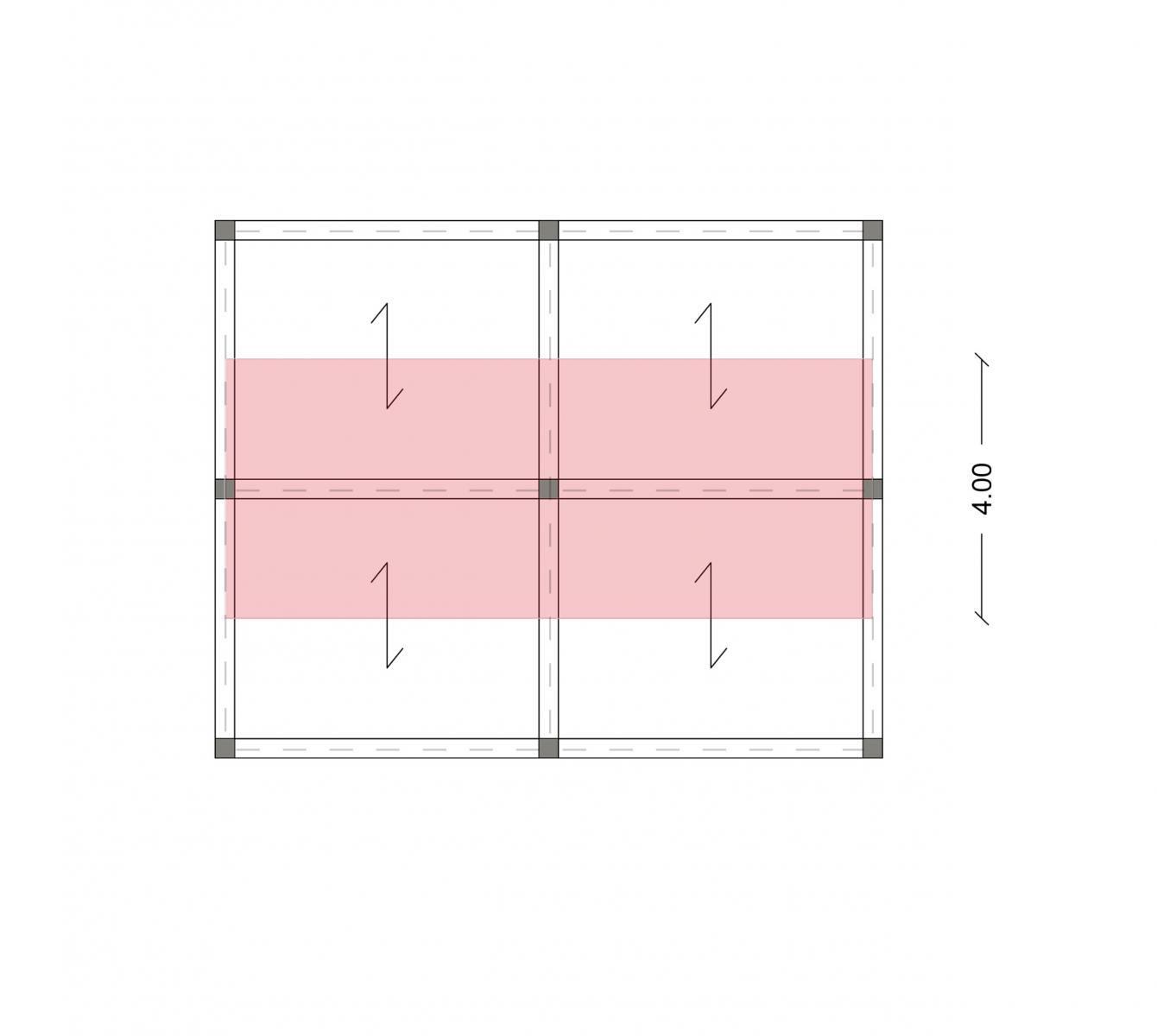
• interasse: 4m
• area di influenza: 20m²

 

Una volta effettuata l'analisi dei carichi e conoscendo la luce della trave, andiamo a progettare sul foglio di calcolo la trave a flessione tramite formula del momento per trave doppiamente appoggiata:

                                         Mmax = (qu x l²)/8

 

Per semplicità di lavoro, si è preferito distinguere le tabelle del foglio di calcolo in bianco, per i risultati, e in azzurro, per i dati in possesso. 

 

Ora su tre fogli di calcolo distinti per ciascun materiale andiamo a dimensionare la trave.

 

(a) ACCIAIO

La tensione di progetto fyd si calcola tramite tensione di snervamento dell'acciaio scelto (fyk=450 MPa), diviso per un coefficiente di sicurezza γs pari a 1,05:

                                                        fyd = fyk/γs

 

Per progettare la sezione in acciaio abbiamo bisogno del modulo di resistenza a flessione Wx:

                                                    Wxmin =  Mmax / fyd

 

Questo è il valore minimo che la nostra sezione può avere affinché non superi lo snervamento di progetto, per cui mi basterà prendere un profilo che abbia modulo di resistenza superiore a questo valore.

 

 

(b) LEGNO

La tensione di progetto fd si calcola moltiplicando la resistenza caratteristica a flessione del legno scelto (fm,k = 24 kN/mm²) per un coefficiente diminutivo kmod che tiene conto della durata del carico o delle condizioni ambientali e poi dividendo per un coefficiente di sicurezza γm = 1,45

                                               fd =  (fm,k  x kmod) / γm

 

Fissata la base della sezione, si può calcolare l'altezza minima:

                                          hmin= ( Mmax / b) ^ ^0,5 x (6 / fd)^ ^0,5

 

 

(c) CEMENTO ARMATO

Essendo questo un materiale composto sia da calcestruzzo che da barre di acciaio, avrò bisogno sia della resistenza caratteristica dell'acciaio (fyk) che di quella del calcestruzzo (fck) per poter quindi ricavare le due tensioni di progetto. Per quella del calcestruzzo occorre conoscere un coefficiente riduttivo pari a αcc=0,85 e un coefficiente di sicurezza γc , più alto di quello dell'acciaio pari a 1,5:

                                           fcd = αcc  x (fck/γc)

 

Fissata la base della sezione, calcolo quindi l'altezza utile della sezione hu= r x (Mmax/b)^^0,5, da cui ottengo

                                               Hmin = hu + δ,

in cui δ rappresenta la distanza tra baricentro dell'armatura e calcestruzzo teso.

 

Per la trave in cemento armato tuttavia, non possiamo trascurare il peso proprio della trave. Moltiplicando l'area della trave per il peso specifico del calcestruzzo armato (25 kN/m³), ottengo il peso unitario della trave. Vado a sommare al carico totale trovato in precedenza, il peso unitario moltiplicato per il coefficiente di sicurezza e svolgo nuovamente i calcoli. Nel caso in esame, posso mantenere la sezione scelta in precedenza. 

 

 

 

Per andare a dimensionare i pilastri, dobbiamo calcolare lo sforzo normale massimo Nmax.

Come prima, bisogna andare ad individuare il pilastro più sollecitato e la sua area di influenza. Questo corrisponderà al pilastro al piano terra, perché è quello su cui gravano tutti i carichi dell'edificio.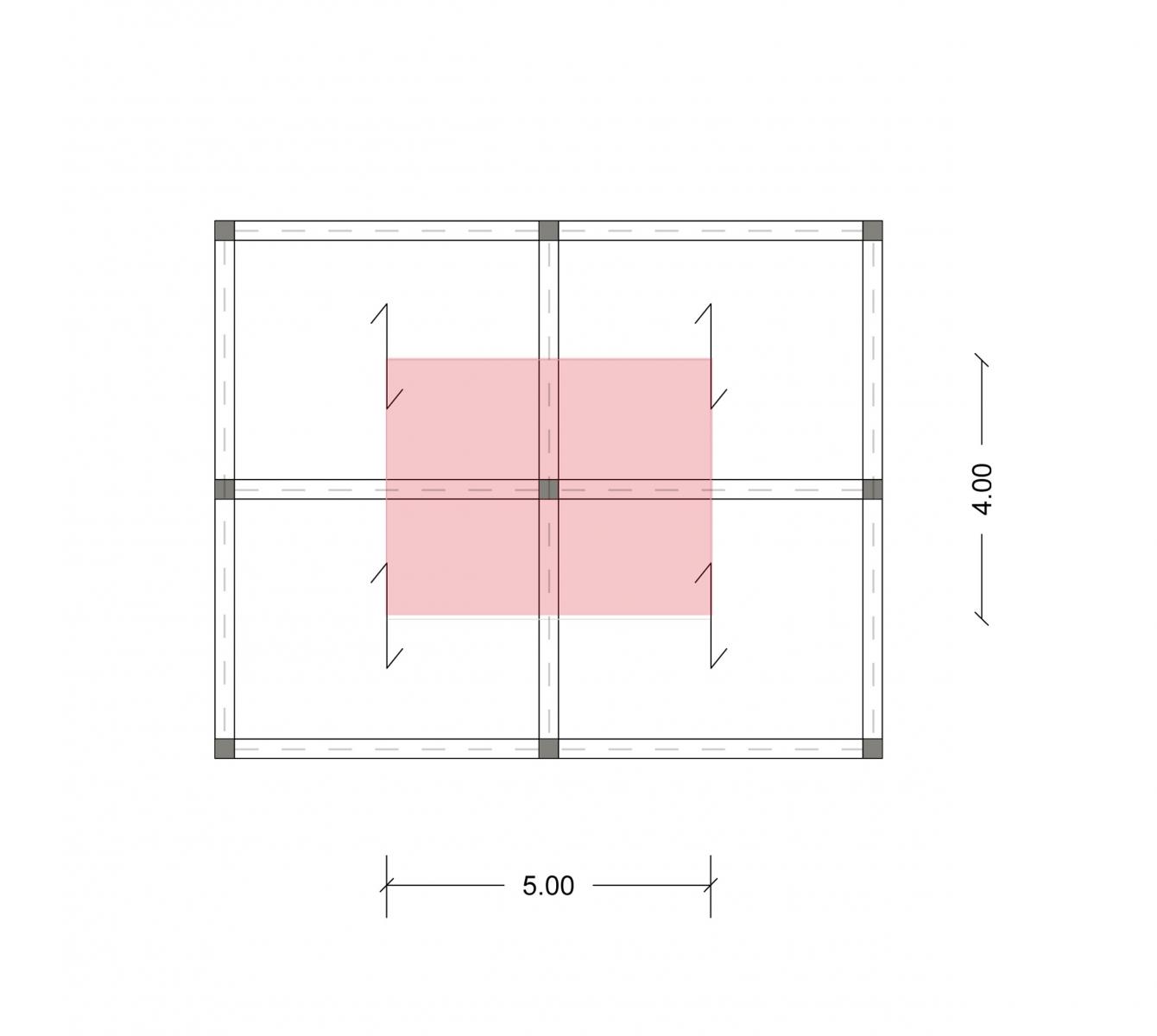 

• luce: 5m
• interasse: 4m
• area di influenza: 20m²

 

Il peso delle travi che poggiano sul pilastro più il carico del solaio, moltiplicati per il numero di piani della mia struttura, mi darà lo sforzo normale massimo Nmax:

                                                Nmax = (qtravi+qsolaio) x npiani

 

 

(a) ACCIAIO

Calcolando la tensione di progetto fyd, trovo l'area minima della sezione tramite sforzo nomale:

                                               Amin = Nmax / fyd.

 

Lo step successivo è quello di trovare il massimo valore di snellezza λmax e il raggio di inerzia minimo ρmin, in modo da calcolare l'inerzia minima Imin:

                                                     Imin = A ρmin²

 

Come per la trave, andrò a scegliere un profilo di acciaio con un valore di inerzia superiore. Una volta scelto il profilo, avrò anche l'Adesign e il Idesign tramite sagomario.

 

(b) LEGNO

Anche in questo caso posso trovare l'area minima tramite Amin = N/fyd, il massimo valore di snellezza λmax e il raggio di inerzia minima ρmin. Essendo la sezione rettangolare, in questo caso potrò ricavare direttamente la base della sezione

                                                          b = 2 x (3)^^0,5 x ρmin

per poi calcolare l'altezza

                                                                  h = Amin/b.

 

 

(c) CEMENTO ARMATO

Il calcolo del pilastro in cemento armato si effettua come quello del legno, quindi tramite calcolo della base della sezione a partire dall'area minima Amin, snellezza λmax e raggio di inerzia ρmin.

 

 

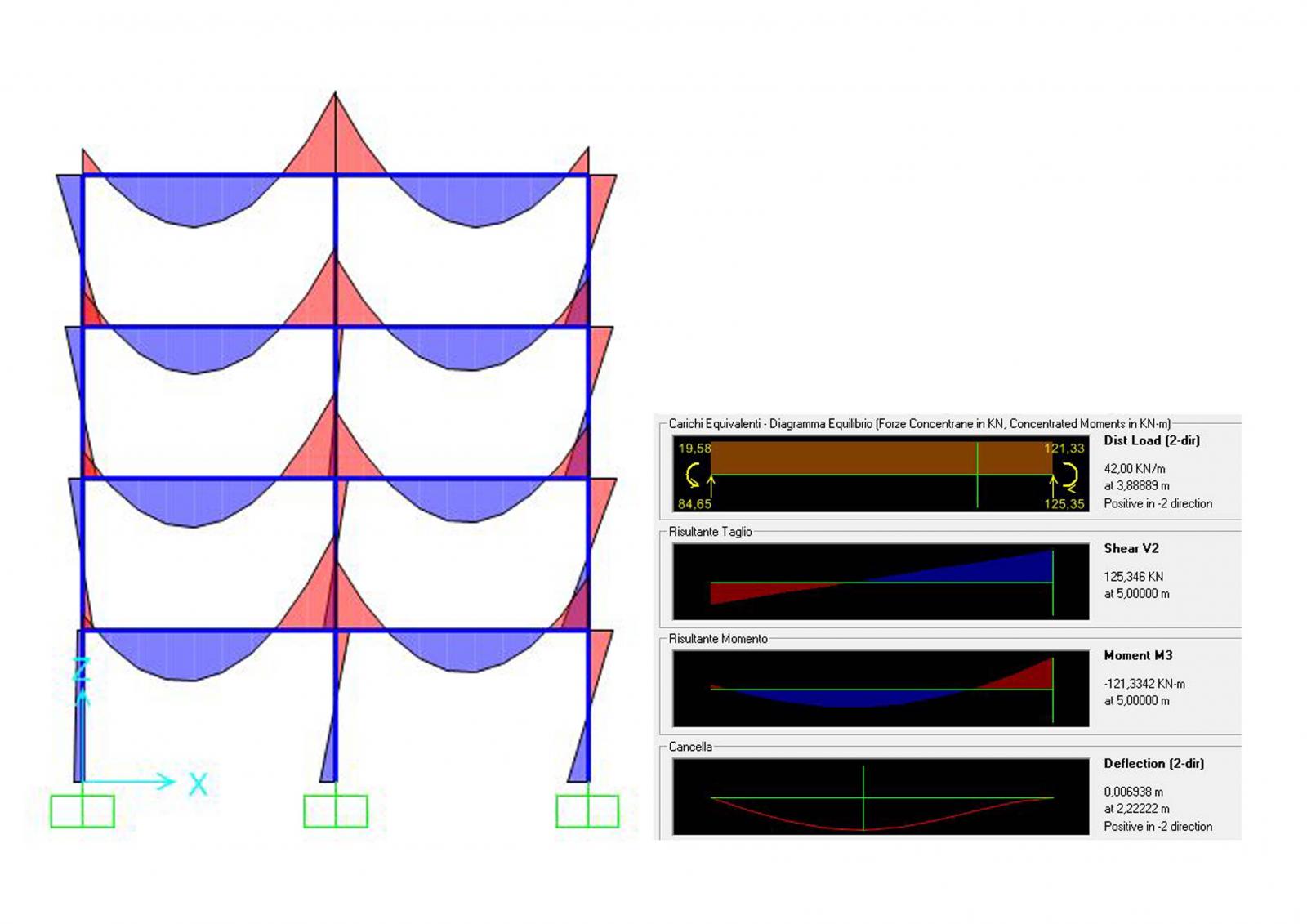
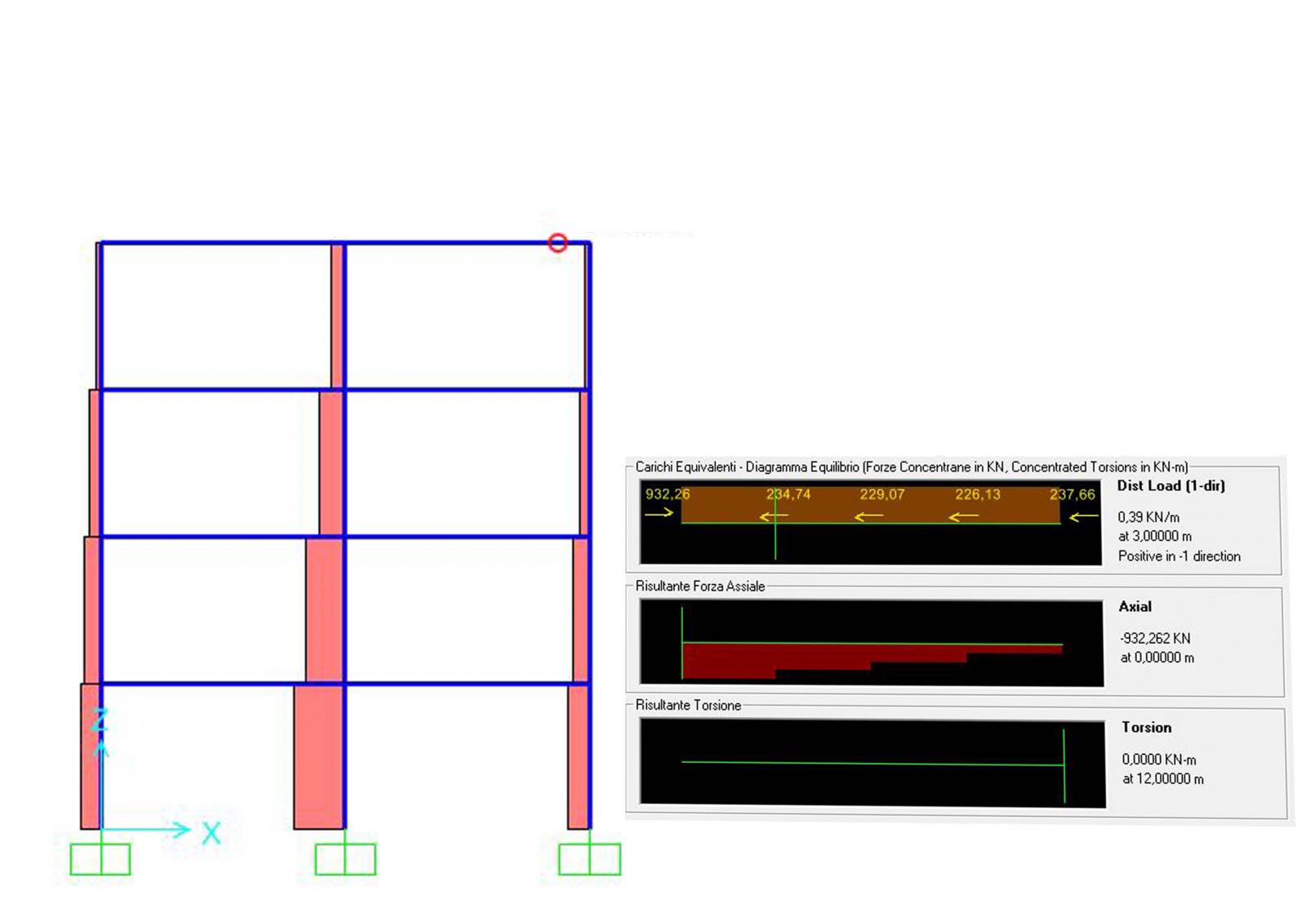
3) Una volta dimensionati le travi e i pilastri nelle tre tecnologie posso effettuare una verifica disegnando la struttura in SAP2000 come la si è progettata e applicandovi i carichi utilizzati. Inserirò inoltre il carico del vento e il peso delle travi che agiscono sui pilastri.

(a) ACCIAIO

• trave: IPE300
• pilastro: HEA160

(b) LEGNO

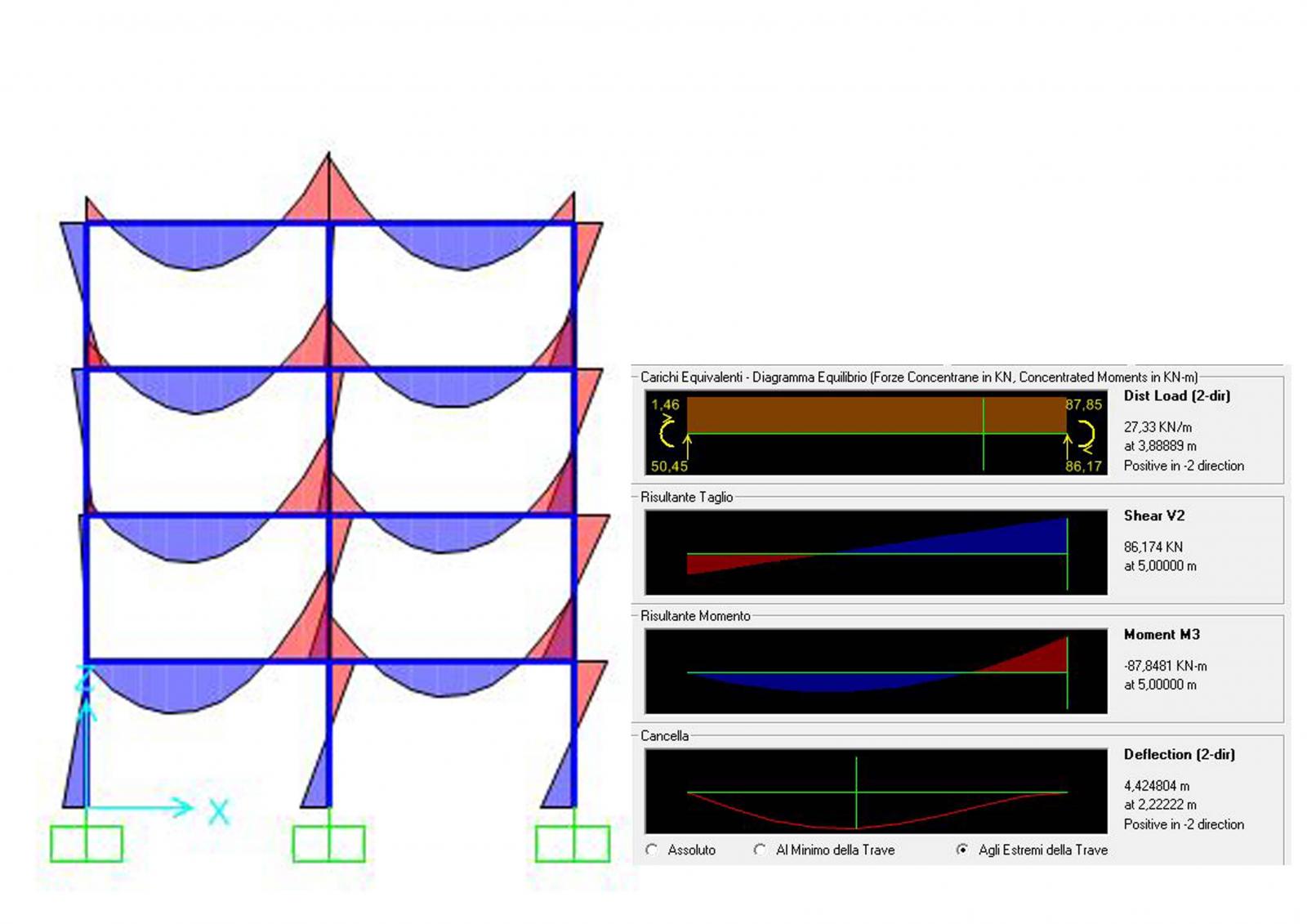
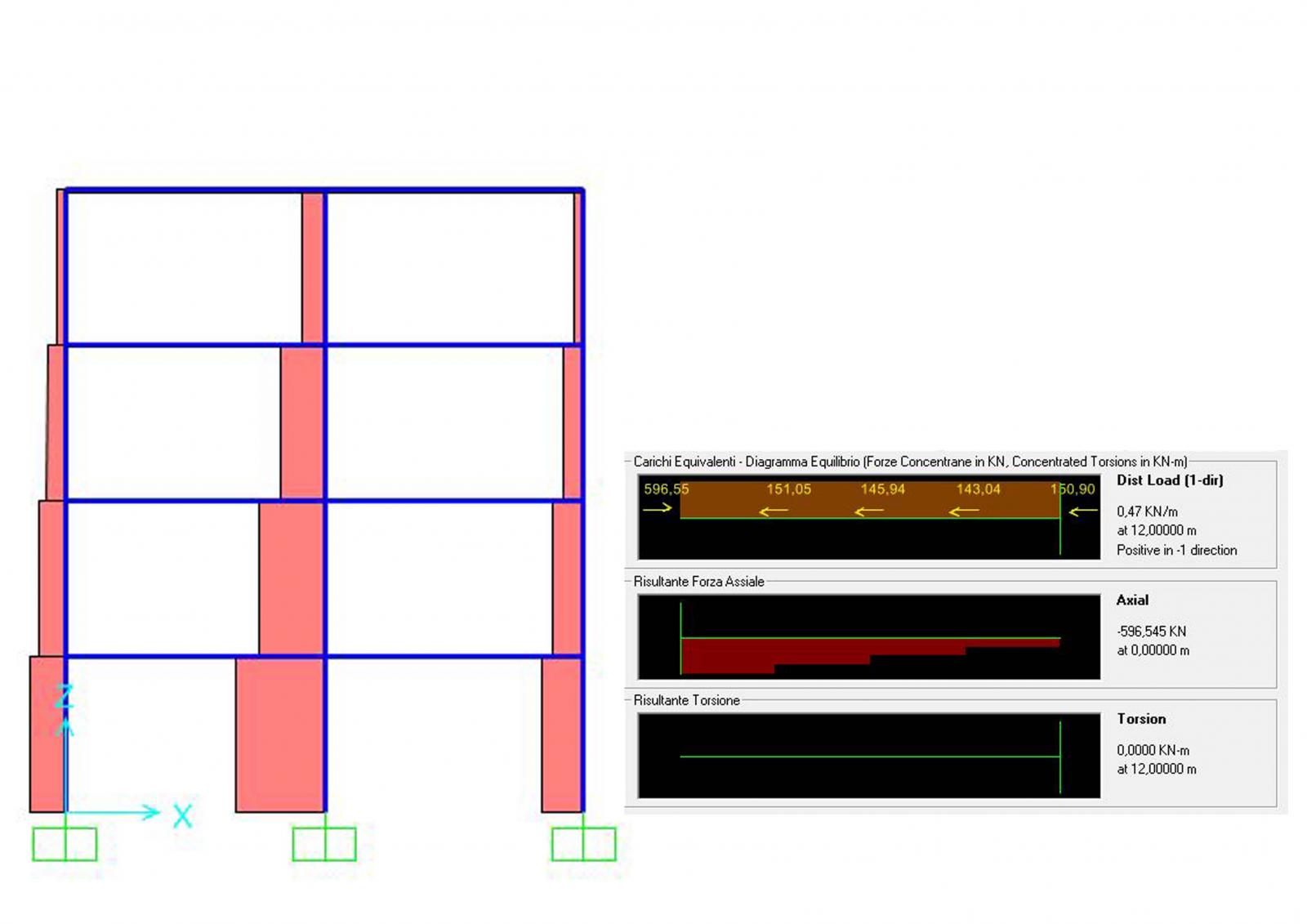
• trave: 30cm x 45cm
• pilastro: 30cm x 20cm

(c) CEMENTO ARMATO

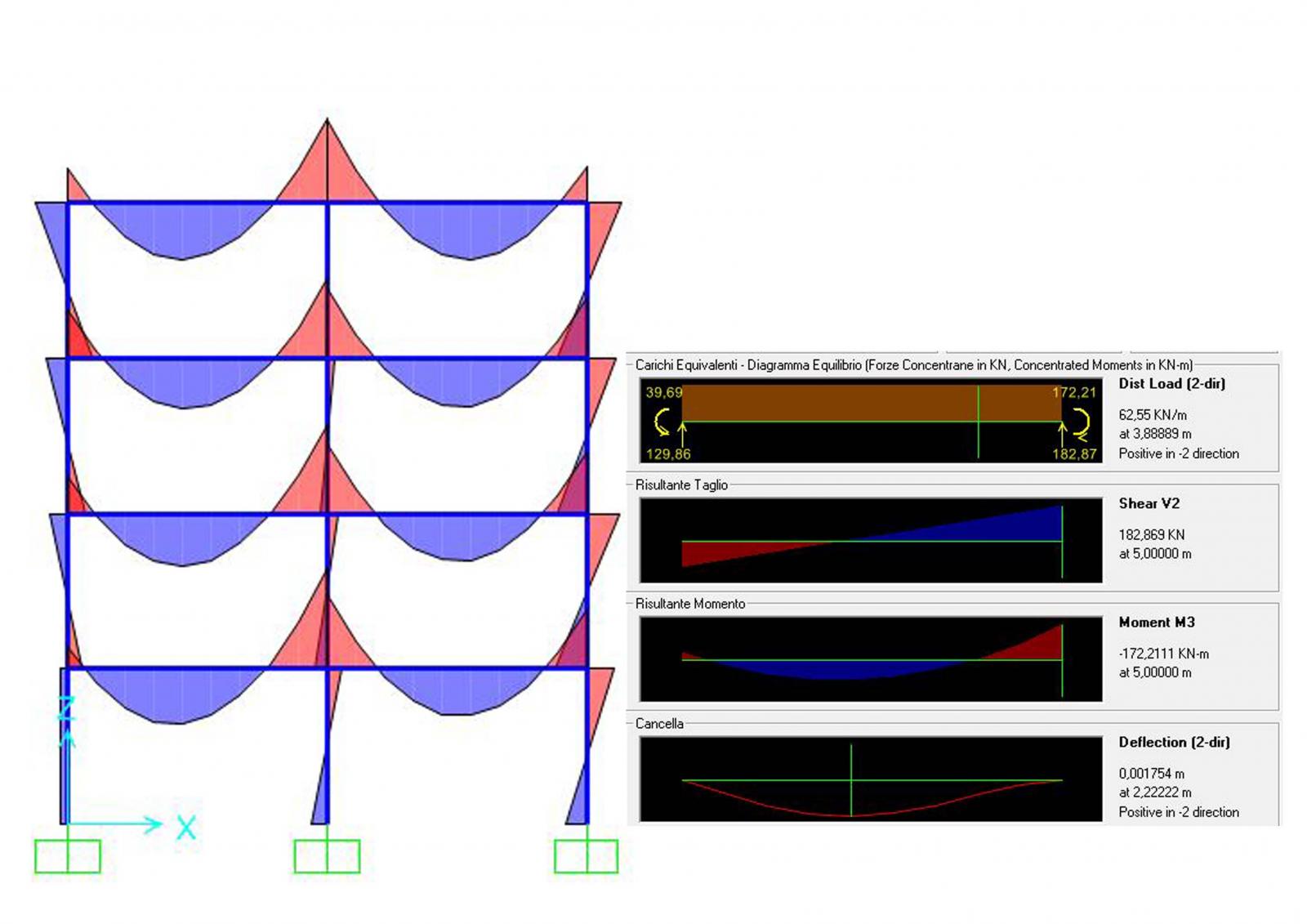
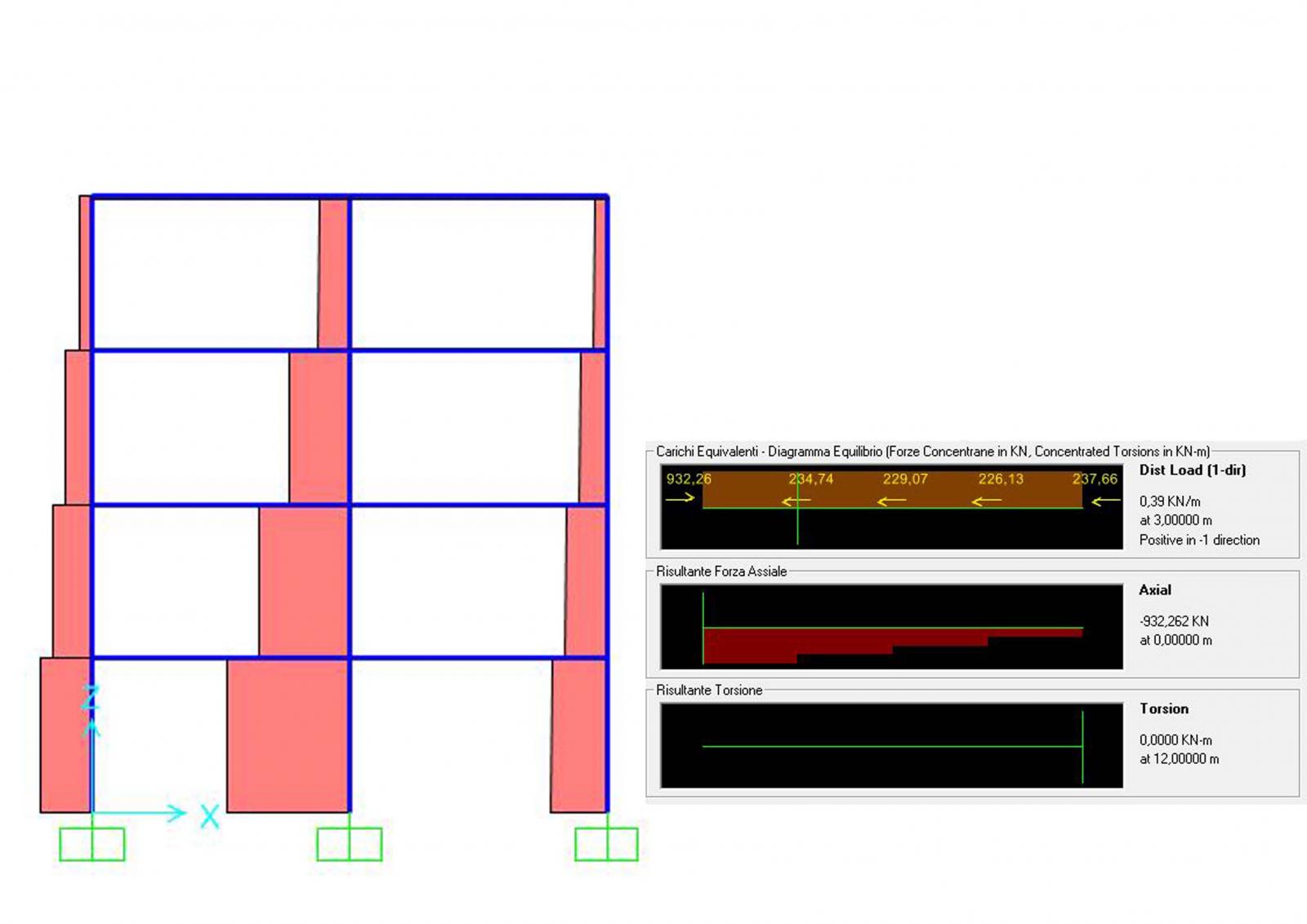
• trave: 30cm x 50cm
• pilastro: 30cm x 30cm

4) A questo punto posso confrontare i risultati ottenuti con SAP2000 con quelli del foglio di calcolo.

 

(a) ACCIAIO

 

La trave è verificata, mentre lo sforzo normale risulta maggiore di quello calcolato. La sezione tuttavia rimane invariata in quanto Adesign (IPE300) > Amin.

(b) LEGNO

Il momento risulta maggiore rispetto a quello calcolato con Excel, ma posso mantenere invariata la sezione della trave in quanto hdesign>hmin. Il pilastro invece viene leggermente ingrandito e la nuova sezione risulterà 30cm x 25cm.

(c) CEMENTO ARAMTO

Il momento viene verificato, mentre lo sforzo normale risulta più grande ma mantiene inalterata la sezione.

Nella sezione in calcestruzzo armato, tuttavia, dobbiamo considerare che il pilastro è sottoposto non solo a compressione ma a presso-flessione, per cui occorrerà effettuare anche la verifica a presso-flessione:

                                                                                                                                                                                                   σ = (N / A) + (Mt / Wmax)

                                                         σmax < fcd

In questo caso, la verifica non viene soddisfatta quindi bisognerà comunque modificare la sezione del pilastro e sceglierne uno più grande.