ESERCITAZIONE I_GRONDONA_PESCHIERA
L’ esercitazione 1 prevede il progetto di una struttura dimensionando gli elementi pilastri e travi; la struttura sarà studiata nei materiali: legno, acciaio, calcestruzzo.
Come prima cosa abbiamo definito il piano di carpenteria con:
-Luce: 6 m
-Interasse: 5 m
-Area di influenza: 30 m2
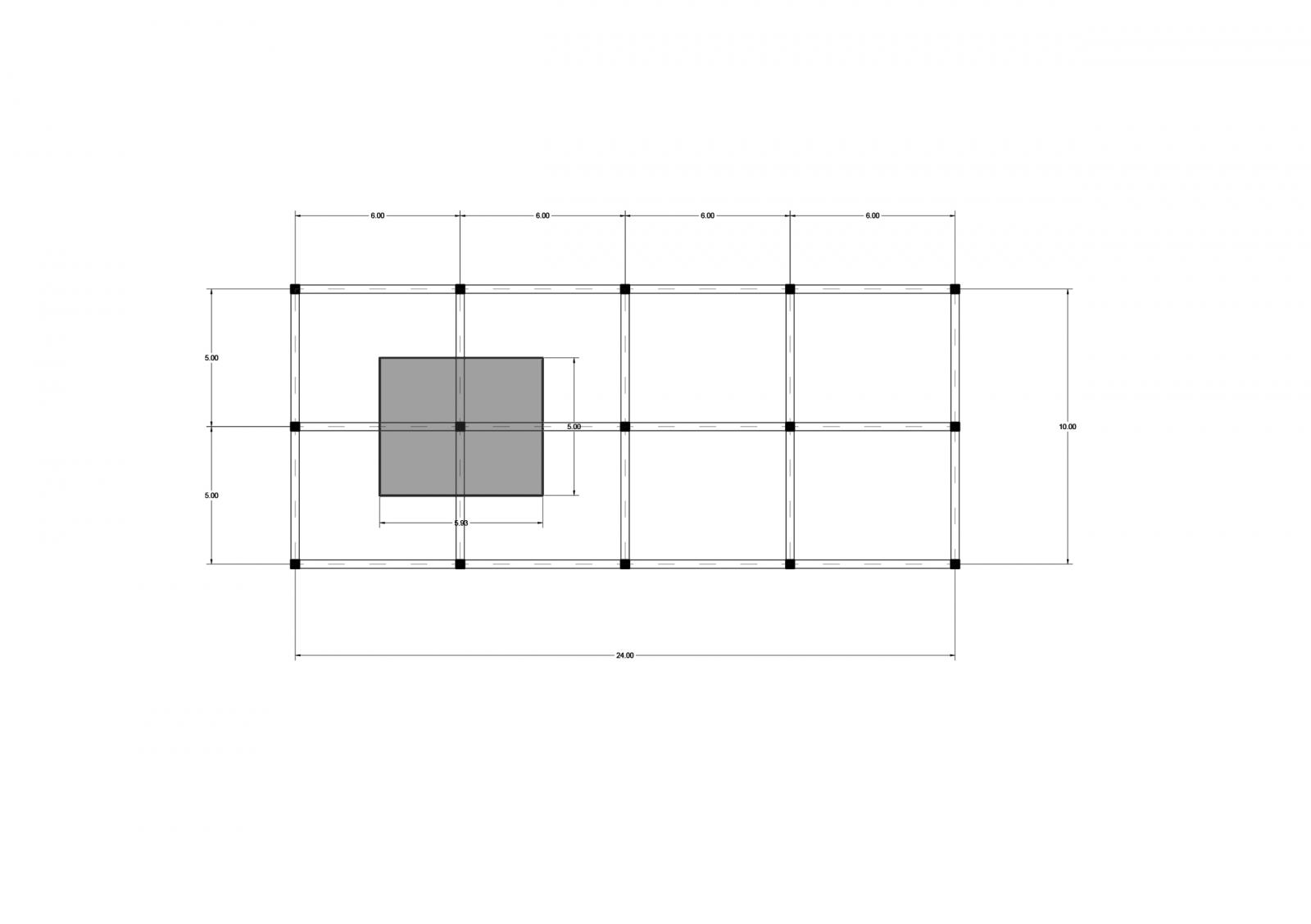
Il carico che imponiamo alla struttura è quello chiamato carico totale: Qu che è composta dalla somma del carico strutturale Qs ( carico dal peso proprio degli elementi portanti), il carico permanente Qp ( dato dal peso proprio degli elementi portati, non strutturali ) ed il carico accidentale Qa (carichi variabili nel tempo, accidentali, insieme ai carichi di esercizio).
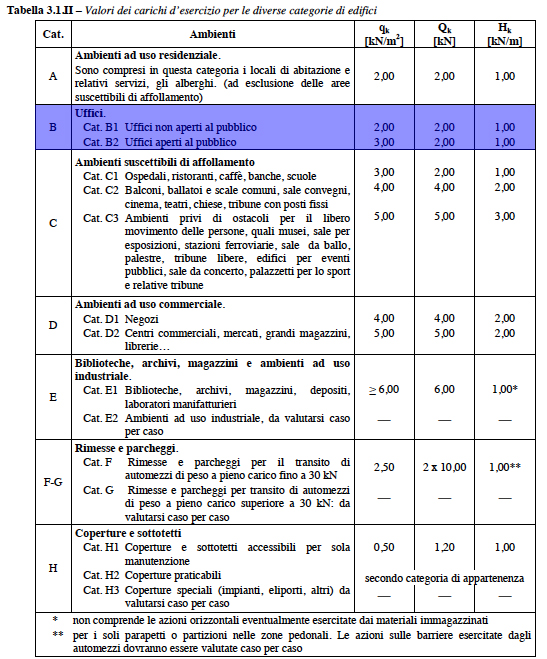
Nel nostro caso avendo preso in esame un edificio con uffici avremo considerandolo aperto al pubblico.
Abbiamo anche definito subito il carico Qp come il carico somma di:
-intonaco: 0.3 kn/m2
-tramezzi: 1 kn/m2
-impianti: 0.5 kn/m2
-pavimento in rovere:peso per unità di volume=720kg/m3 che sappiamo equivalere a 7.2 kN/m3;
quindi qpavimento=7.2kn/m3*0.18m=1.3 kn/m2
- massetto: peso per unità di volume=1750kg/m3=17.5 kN/m3, lo spessore è di 0.04 m; quindi qmassetto=17.5kn/m3x0.04m=0.7 kn/m
- Qp= (0.3+1+0.5+1.3+0.7)=3.8 [kN/m2]
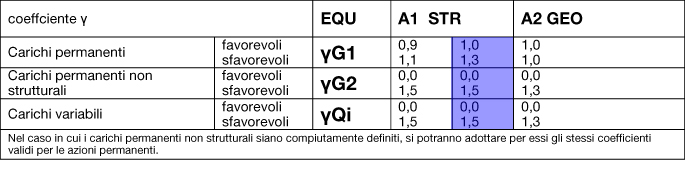
Tutti questi carichi per Norma vengono moltiplicati da dei coefficienti a seconda che si studi la condizione di carico allo SLE (stato limite di esercizio) o allo SLU (stato limite ultimo). Nel caso di studio li consideriamo allo SLU e per la combinazione di carico fondamentale.
- Qu = γG1*Qs + γG2*Qp + γQ1*Qa
Questi dati ci servono per il dimensionamento degli elementi strutturali nei tre casi presi in esame: legno, acciao, calcestruzzo, che andremo ora ad analizzare.
CLS
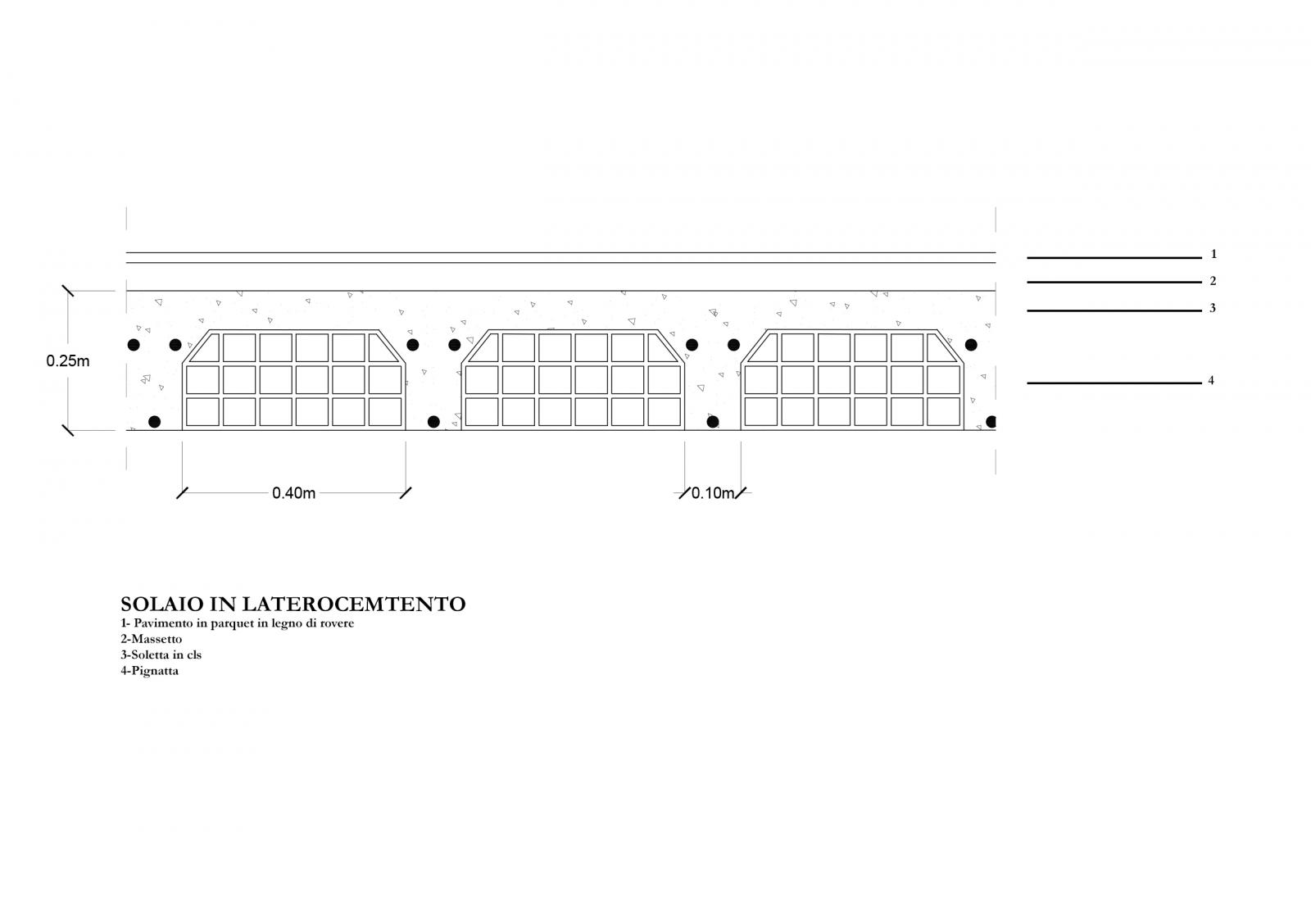
Per calcolare il carico strutturale Qs del solaio in laterocemento calcoliamo il carico in un metro quadro di solaio:
[Vcls x γcls]x1/ i ={[(0.05 x 0.2)x 2 +(0.05 x 0.5)] x 2 }x 2.5 = 2.25 [kN/m2 ]
[Vlat x γlat ]x1/ i =[(0.04 x 0.2)x 2 ]x 12= 1.92 [kN/m2 ]
- Qs = 2.25 +1.92 = 4.17 [kN/m2 ]
- Qu = 1.3 Qs + 1.5 Qp + 1.5 Qa = 5.42 +5.7 +4.5 = 15.62 [kN/m2 ]
1)TRAVI
Il foglio di calcolo relativo al cemento armato ha bisogno di più informazioni per dimensionare l’altezza della sezione rettangolare di una trave; questo può essere spiegato dal fatto che si tratta di un materiale non omogeneo, composto da calcestruzzo e da acciaio. Proprio per questo motivo in fase progettuale è necessario scegliere sia la resistenza caratteristica dell’acciaio (fyk) , che quella del calcestruzzo (fck).
**********
Una volta stabilite le tensioni di progetto abbiamo calcola l'altezza utile Hu e ẟ (la distanza fra il il baricentro dell’armatura e il filo del calcestruzzo teso) e la base per trovare l'altezza min di progetto.
L'altezza min identifica la sezione min del calcestruzzo che va poi ingegnerizzata. Inoltre nel calcolo finale una volta trovata l'area della sezione di progetto va calcolato il peso della singola trave che andrà a modificare le soluzioni già trovate dei carichi e riverificati tutti i dati.
2)PILASTRI
Per dimensionare i pilastri abbiamo riportato i valori ottenuti su excel e calcolato lo sforzo Normale per tutti i piani del nostro telaio, considerando in questo calcolo il peso della trave stessa. In base al tipo di cls scelto abbiamo trovato la tensione di compressione caratteristica che ci permetterà di ricavare la tensione di design dove αα è un fattore riduttivo che tiene conto degli effetti del tempo nel materiale pari a 0.85 e delle sue iterazioni con l'ambiente, mentre γm è un fattore di sicurezza che per le strutture in calcestruzzo è pari a 1.5.
- fck = 40 [Mpa]
- fcd = fck αα / γ m
Una volta calcolato sforzo normale per la pilastrata e tensione di desing possiamo calcolare l'area e la base minima del pilastro. Infatti la tensione di design può essere considerata in fase di progetto uguale a Ϭ max
- Ϭ max = N/A quindi fd = N/A Amin = N/ fd
Abbiamo poi considerato l'instabilità euleriana a seguito dello sforzo di compressione che agisce sul pilastro e dunque anc la snellezza λ .
Dove
- N eul =(π2 E Imin )/l02 l0 = β x l Imin = A ρ2 min λ = l0 /ρmin
Possiamo quindi definire una tensione critica, poichè il carico critico è una forza di compressione che agisce sulla sezione, e metterla in relazione con la tensione massima
E' più sicuro pensare che la tensione all'interno dell'elemento raggiungerebbe per prima la resistenza a schiacciamento del materiale, poichè l 'instabilità euleriana è un fenomeno imprevedibile e dunque non si riesce a controllare.
Abbiamo poi verificato a presso-flessione il pilastro così ottenuto
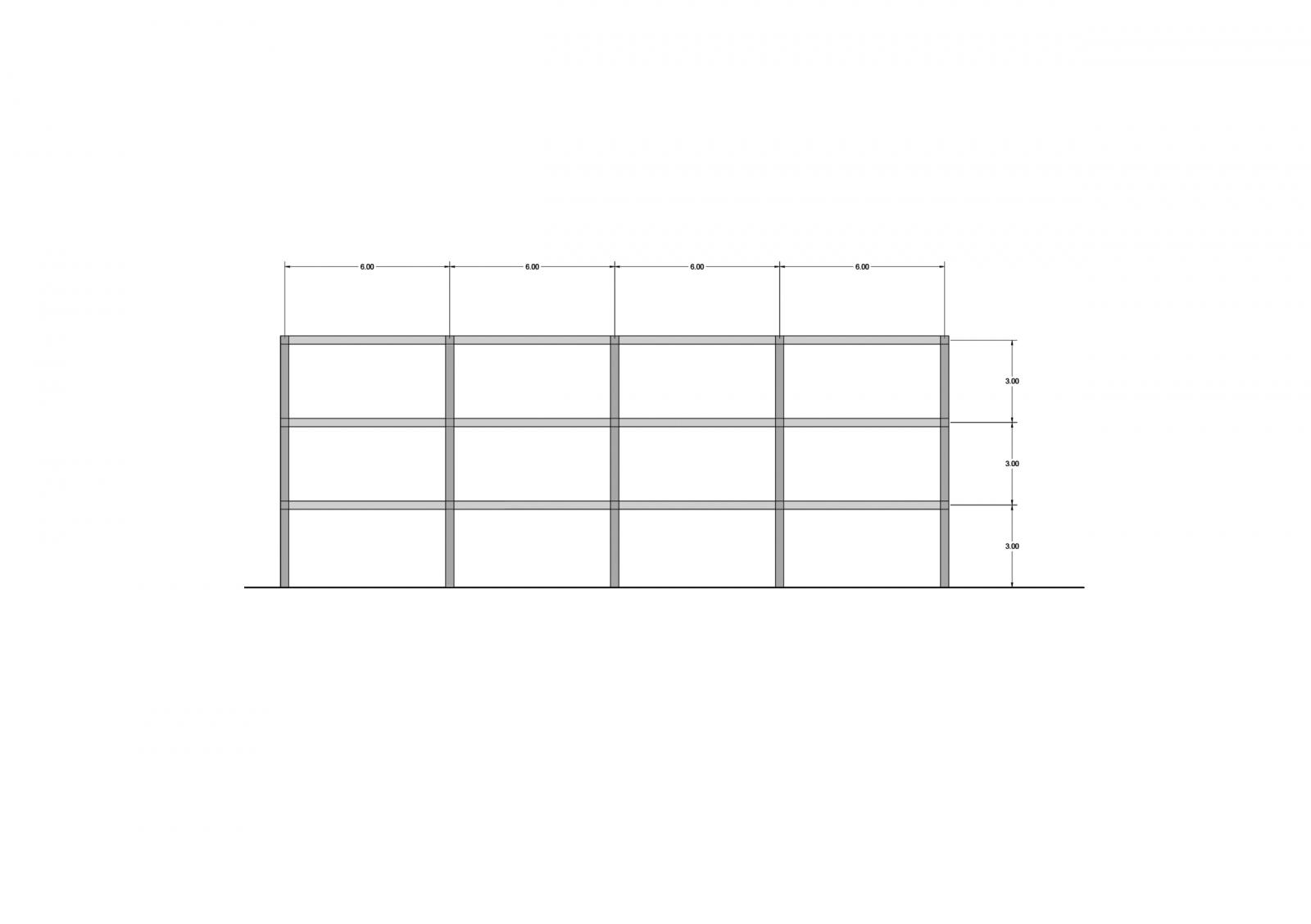
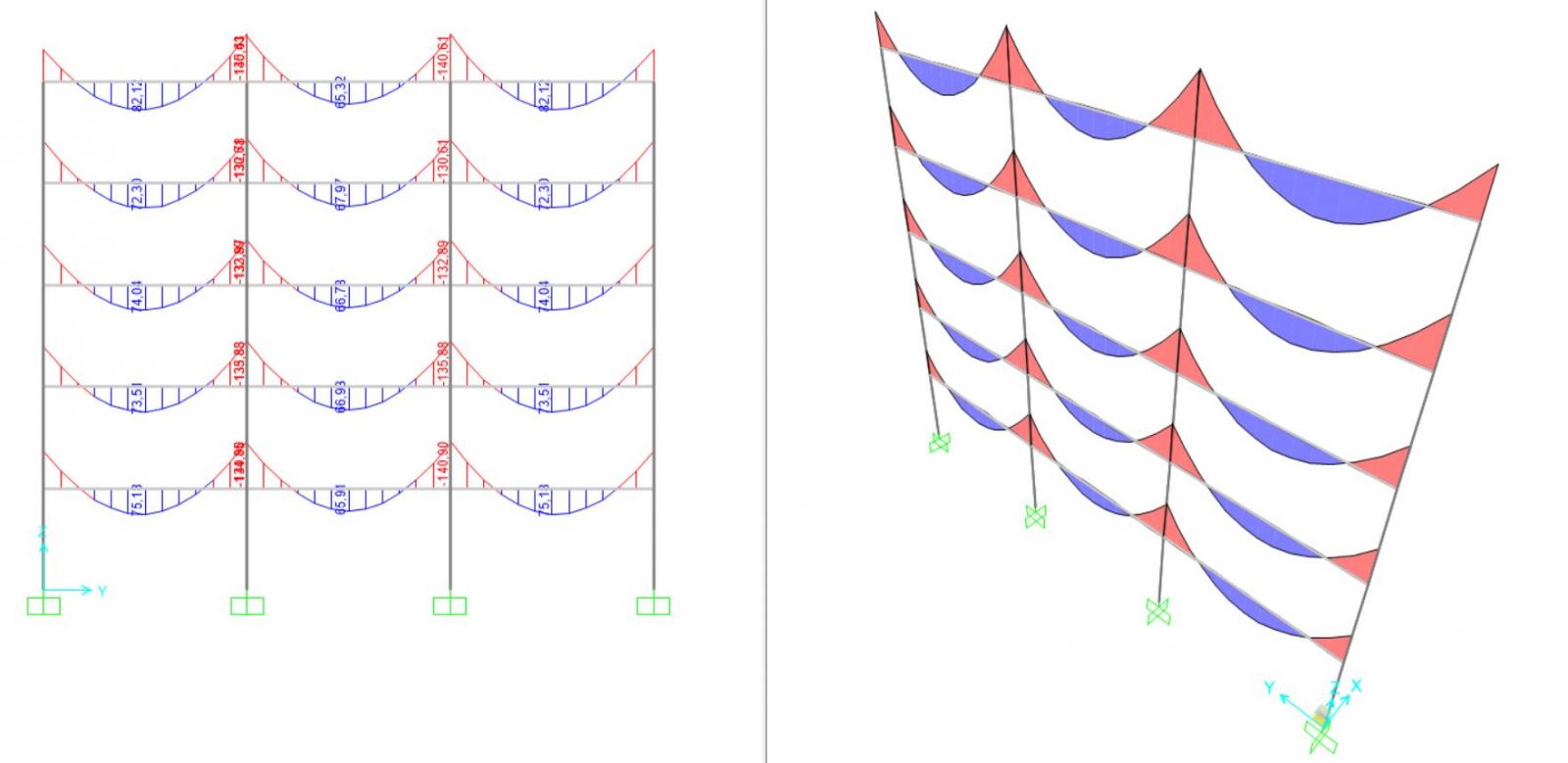
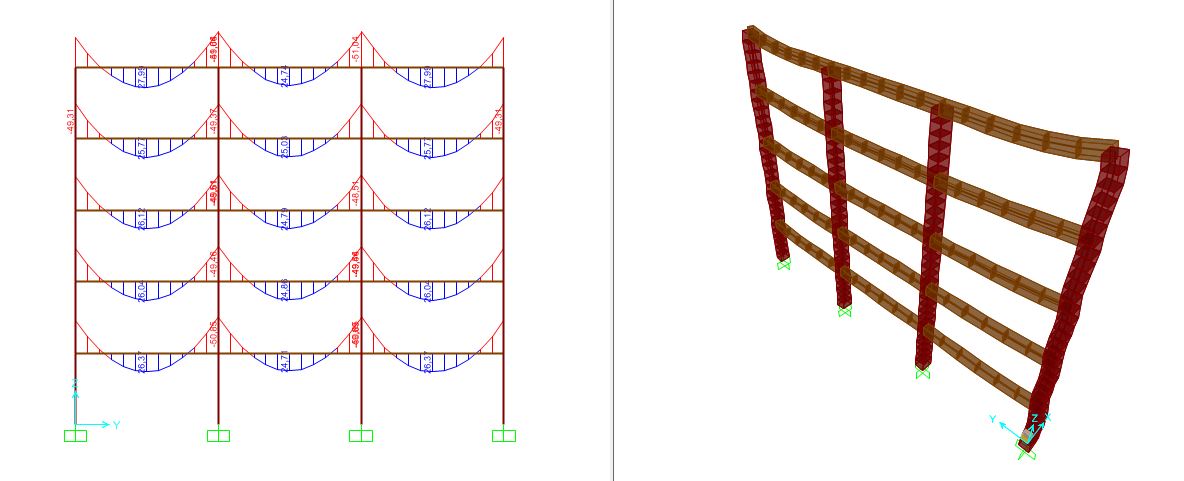
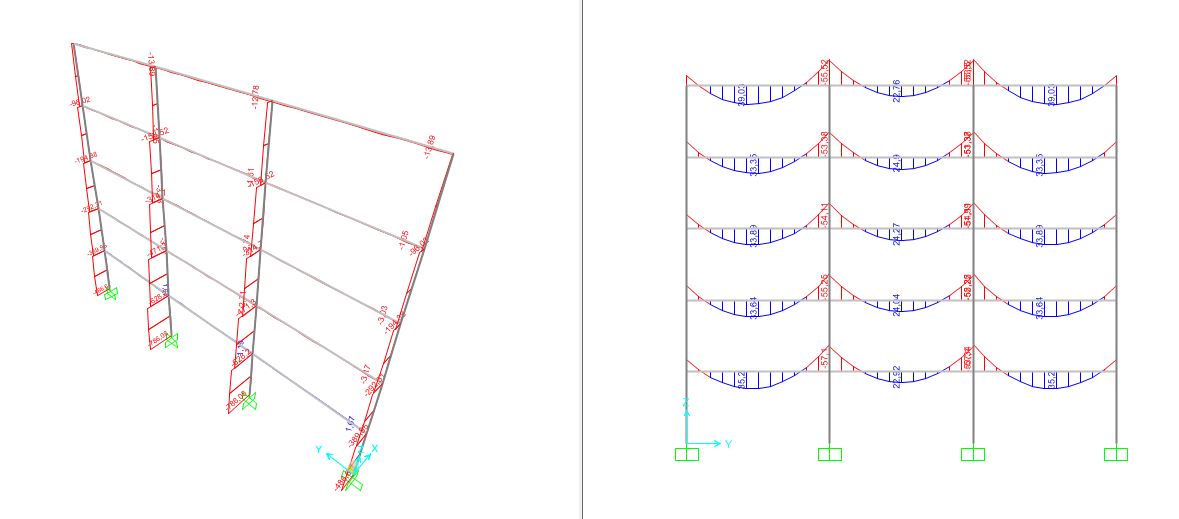
Una volta calcolato la base e l'altezza del pilastro abbiamo verificato la struttura su sap2000
Dai diagrammi dello sforzo normale del telaio abbiamo ottenuto uno sforzo normale nel pilastro più sollecitato inferiore al volere ottenuto su excel e dunque la pilastrata è verificata.
LEGNO
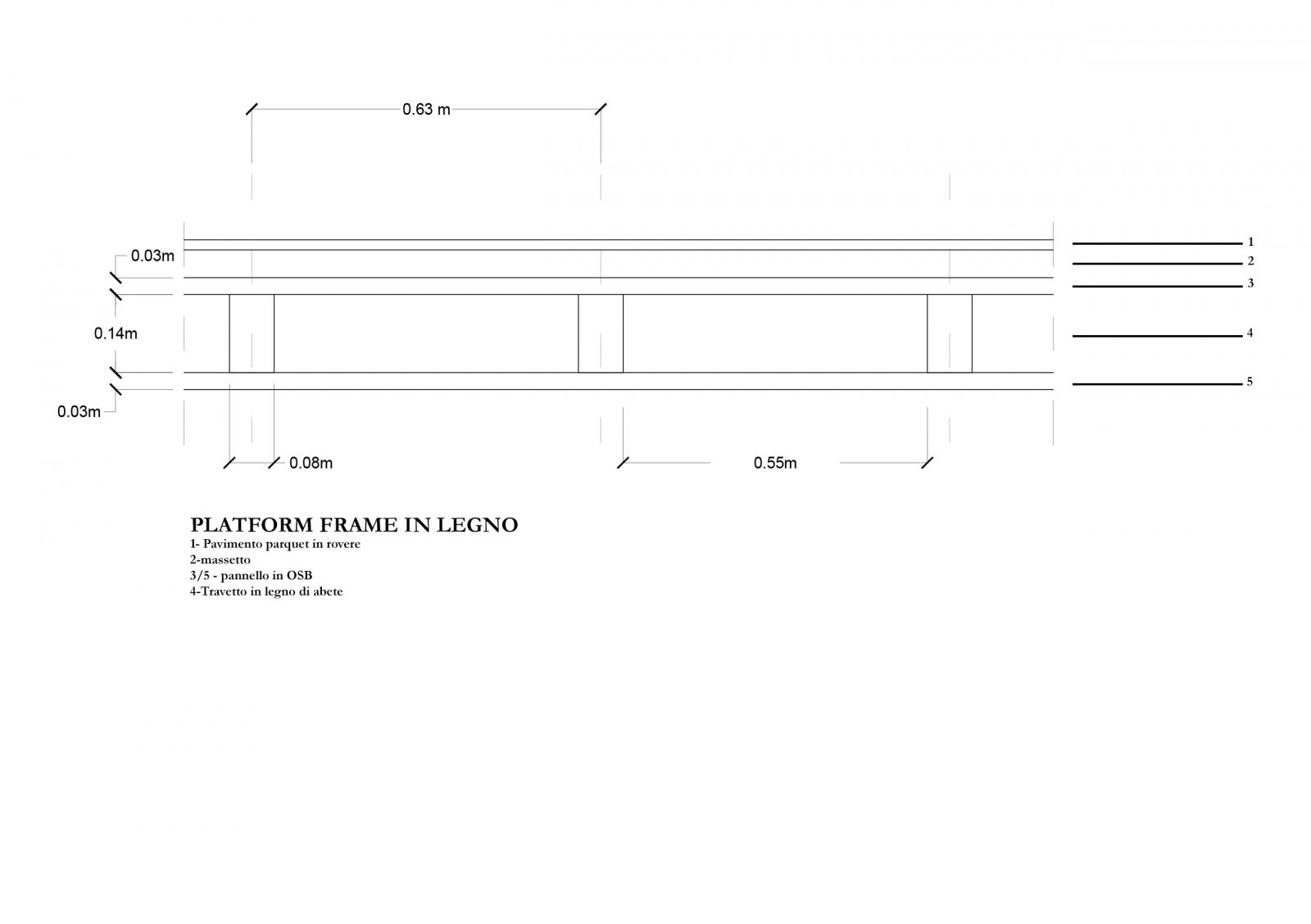
In base alla composizione di questo solaio avremo per i travetti:
(V*γ )*1/i = {[(0.08*0.14) *1]*5.50 }*1/0.625 = 0.0616*1/0.625[kN/m2]
Per il pannello OSB:
(V*γ )*1/i = {[(0.03*0.625)*1*2]*8 }*1/0.625 = 0.3*1/0.625[kN/m2]
- Qs=0.578[kN/m2]
- Qu=1.3*Qs+1.5*Qp+1.5*Qa=10.95 [kN/m2]
1)DIMENSIONAMENTO DELLE TRAVI
Avendo definito il tipo di solaio ed i carichi li abbiamo riportati su excel utilizzandolo come foglio di calcolo; dopo aver definito il carico sull’interasse ed il momento massimo , in base al tipo di legno abbiamo trovato la tensione di progetto fd.
La tensione di progetto tiene conto delle azioni del tempo che influiscono sul materiale e sulla durata del carico , di un valore di sicurezza imposto dalla normativa e dalla classe di resistenza del legno scelto
- Mmax= Qu*l2/8
- fcd = Kmod fyk / γ m dove Kmod < 1
In fase di progetto una volta trovata la tensione di design fcd è possibile ricavare Hmin e modulo elastico di resistenza Wx
- Hmin=[6*Mmax*1000/(b*fd)]^0.5
- Wx=b*h2/6
Per la verifica abbiamo controllato che la tensione massima Ϭmax risultante sia minore di quella di progetto fcd, risulta così verificata.
2)DIMENSIONAMENTO PILASTRI
Per quanto riguarda i pilastri abbiamo calcolato lo sforzo normale, definito la tensione di progetto, area minima della sezione.
Definiti modulo elastico e lunghezza libera di inflessione lo = β x l si calcolano: snellezza λ tenendo conto dell'instabilità euleriana , raggio d’inerzia e base minima ed altezza minima che ci aiutano a scegliere i valori che scegliamo per la base e l’altezza della sezione; calcoliamo anche l’area e inerzia di design come:
- Adesign=b*h
- Idesign=h*b3/12.
La verifica si ottiene calcolando la tensione come lo sforzo normale sull’area, che deve essere minore della tensione di progetto: la sezione risulta verificata.
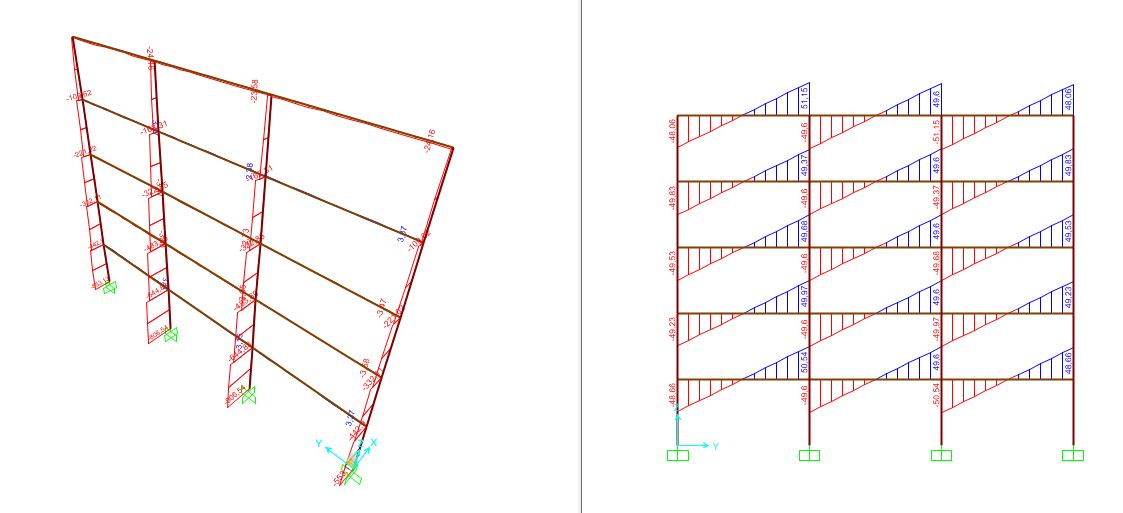
Abbiamo utilizzato SAP per verificare che i valori ottenuti sui fogli fossero corretti e per visualizzare gli schemi di carico sulla struttura ed i grafici dei carichi. Una volta disegnata la struttura, assegnato il materiale e definiti i carichi con la combinazione di carico finale, si vanno a definire le tipologie di sezioni; nel caso del legno le abbiamo definite come rettangolari in concrete ma abbiamo variato i valori per fare in modo che siano reali. Assegnate travi e pilastri abbiamo studiato la deformata ed i valori dei carichi e risulta che lo studio fatto in precedenza è corretto.
ACCIAIO
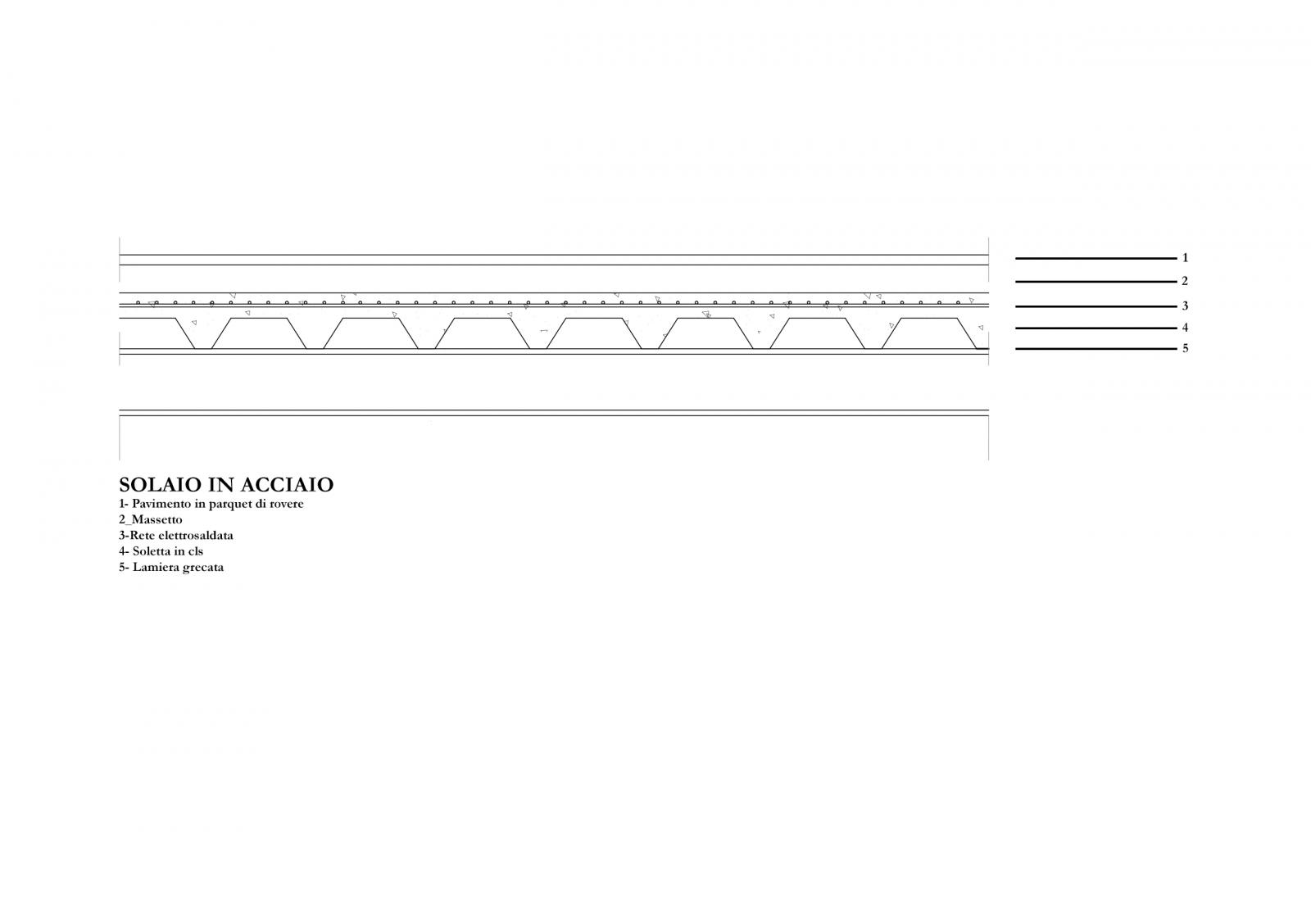
In base alla composizione del solaio abbiamo calcolato il carico strutturale sommando i carichi della soletta in calcestruzzo, della rete elettrosaldata e della lamiera grecata.
- Per la soletta in calcestruzzo :
- γCLS=2300 [kg/m3]=23[kN/m3]
- VCLS * γCLS = 23 *0.1 =2.3 [kN/m2]
- Per la rete elettrosaldata:
- γRETE=3.1 [kg/m2] = 0.031[kN/m2]
- Per la lamiera grecata:
- spessore = 1 mm
- γLAM = 9.58[kg/m2]=0.09[KN/m2]
Perciò il carico strutturale risulta:
- Qs=2.3 +0.031 +0.09 =2.421[KN/m2]
La combinazione di carico risulta quindi:
- Qu= 1.3Qs+1.5Qp+1.5Qa=13.35 [KN/m2]
1)DIMENSIONAMENTO TRAVI
Per la verifica ci siamo calcolate sul foglio excel il momento massimo Mmax
- Mmax=Qu*i*l2/8
- fcd = fyk / γ m dove fyk = 275 [N/mm2] γ m=1.05
- Wxmin=Mmax/fd
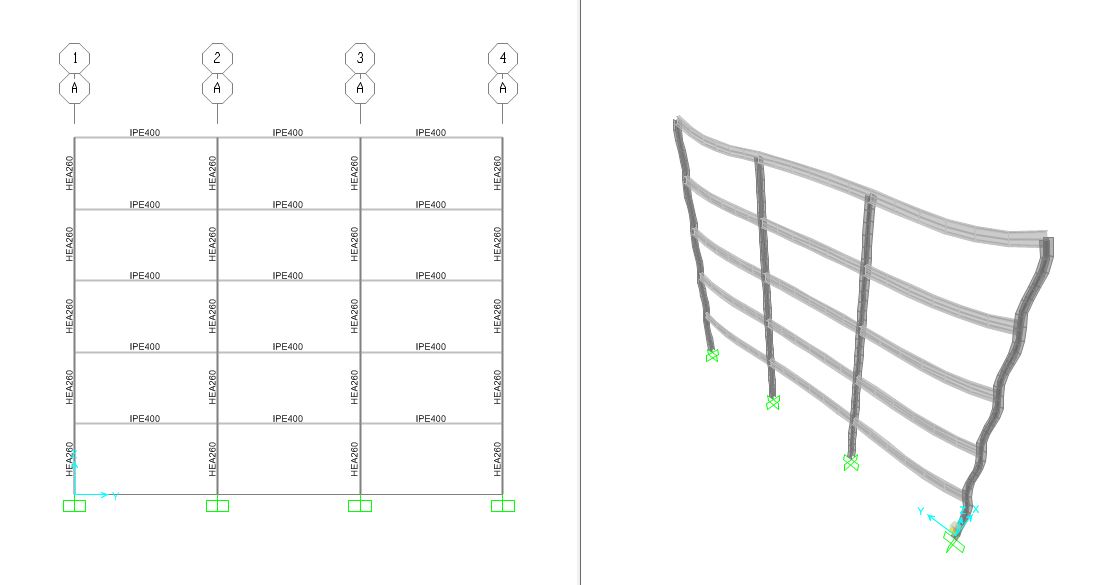
definita la tensione di progetto andiamo a calcolato il modulo elastico minimo: Wxmin=Mmax/fd*1000. Da questo valore andiamo a scegliere una sezione IPE dal tabellario che rispetti il valore trovato; scegliamo la IPE400 e verifichiamo che la tensione, calcolata sostituendo al modulo elastico precedente quello di quest'ultima , sia minore di quella di progetto. Risulta perciò verificata.
2)DIMENSIONAMENTO PILASTRI
Per dimensionare i pilastri abbiamo calcolato lo sforzo normale dei pilastri ci calcoliamo la tensione di progetto e l’area minima.
- N=(Qs+Qtrave)*npiani
- Amin=N/fyd
- λ=π*rad(E/fyd)
Ottenuto il raggio di inerzia minima è possibile ricavare il profilo HE corretto.
- ρMIN=β*l/λ
- IMIN=Amin* ρMIN 2
In base ai valori ottenuti scegliamo il profilato d’acciaio HEA260 e calcoleremo nuovamente la snellezza della trave sostituendo i valori:
La sezione è verificata avendo la tensione Ϭmax=N/Adesign<fyd minore di quella di progetto.
I risultati ottenuti sul modello di sap2000 danno uno sforzo normale sulla pilastrata inferiore rispetto a quelli ottenuti dunque i profili scelti sono verificati.
Posso osservare come la struttura subisca non solo una traslazione ma anche una rotazione oraria.
Osservo come anche in questo caso la struttura non solo subisca una traslazione lungo l'asse y ma anche una rotazione.
Possiamo dedurre che centro delle masse e centro delle rigidezze non coincidono dunque bisognerà ridisegnare l'impalcato.
Commenti recenti