blog di fabrizio.pontico

TELAIO

Per il dimensionamento di una struttura portante, che dipende dalle dimensioni dell’edificio, si fa fede in Italia alle NTC (Norme Tecniche di Costruzione) del 2008. La normativa prevede la progettazione della struttura portante, per la "vita utile" dell'edificio", in due stati:

- Stati Limite di Esercizio (SLE): sono associati ad una perdita di funzionalità dell’opera, ad esempio danneggiamenti locali di fessurazione. Lo SLE considera la struttura in fase elastica (fase in cui un corpo soggetto ad un’azione temporanea, mantiene la sua geometria senza deformarsi al termine dell’Azione).

- Stati Limite Ultimo (SLU): sono legati al collasso di un’intera opera oppure di una sua parte. Lo SLU considera la struttura in fase plastica (fase in cui un corpo soggetto ad una azione temporanea, al termine di essa rimane deformato, cambiando le sue proprietà meccaniche).

Il superamento dello stato limite ultimo genera il collasso della struttura e nel caso in esame la struttura portante verrà dimensionata allo SLU.

Nella figura sottostante è disegnata una struttura a telaio composta da un sistema di elementi verticali (pilastri) ed elementi orizzontali (travi) che successivamente verrà dimensionata nel  punto in cui la trave è più caricata con 3 materiali e tecniche costruttive diverse: Cemento Armato (CA), Acciaio e Legno.

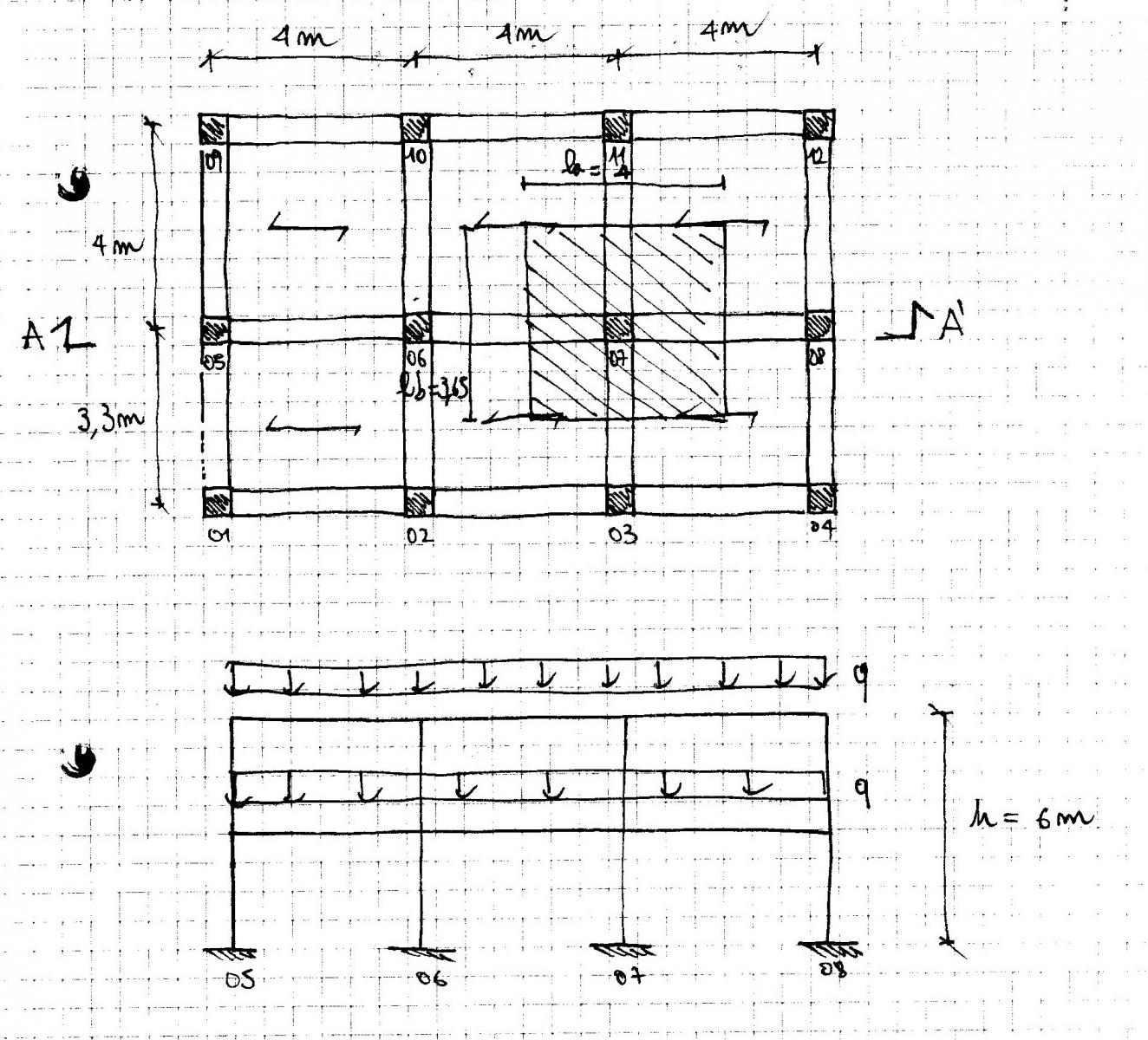
I numeri rappresentano i singoli pilastri, il simbolo nella campata segna l’andamento dei travetti che scaricano il peso sulle travi principali che a loro volta scaricano il peso sull’esterno. La travi secondarie collegano le travi principali e collaborano alla stabilità della struttura. Le quote esterne ci permettono di calcolarci l’area d’influenza del probabile pilastro più sollecitato.

Procedo con il dimensionamento del pilastro 07 e della trave principale 03-11 che risentono di una maggiore area d’influenza di carico. Il dimensionamento di travi e pilastri verrà eseguito usando un modello semplificato di struttura.

Tramite l’analisi dei carichi si determina un’area di un metro quadro tipo di solaio. Moltiplicando l’area tipo di solaio per l’interasse della trave si ottiene il carico distribuito.

ANALISI DEI CARICHI

Prendo in considerazione tre tipologie differenti di solaio: solaio in latero-cemento, solaio in acciaio e solaio in legno.

La Normativa suddivide il solaio in tre differenti carichi: carico strutturale Gk1, carico permanente Gk2 e carico variabile Qk.

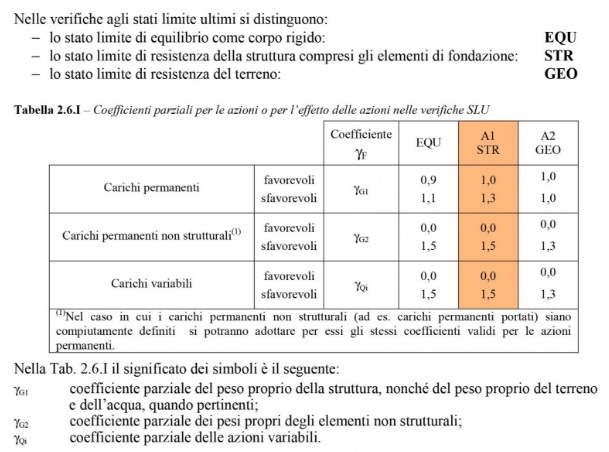
Lo SLU considera la possibilità che i carichi siano superiori a quelli effettivamente agenti e che le resistenze dei materiali siano inferiori a quelle considerate. Le resistenze sono determinate da prove sperimentali secondo un metodo probabilistico, quindi non avendo sempre la certezza che il materiale si comporti allo stesso modo, vengono introdotti dei coefficienti di sicurezza che amplificano il carico e dei coefficienti che riduco le resistenze. Seguendo le tabelle della normativa il carco ultimo risulta Qu= γg1*Gk1 + γg2*Gk2 + γqi*Qk  dove Gk1 è il carico strutturale (peso proprio della struttura), Gk2 è il carico permanente non strutturale (carico degli elementi non strutturali), e Qk sono i carichi variabili, dettati nella Tabella 3.1.II delle NTC 2008.

CEMENTO ARMATO trave

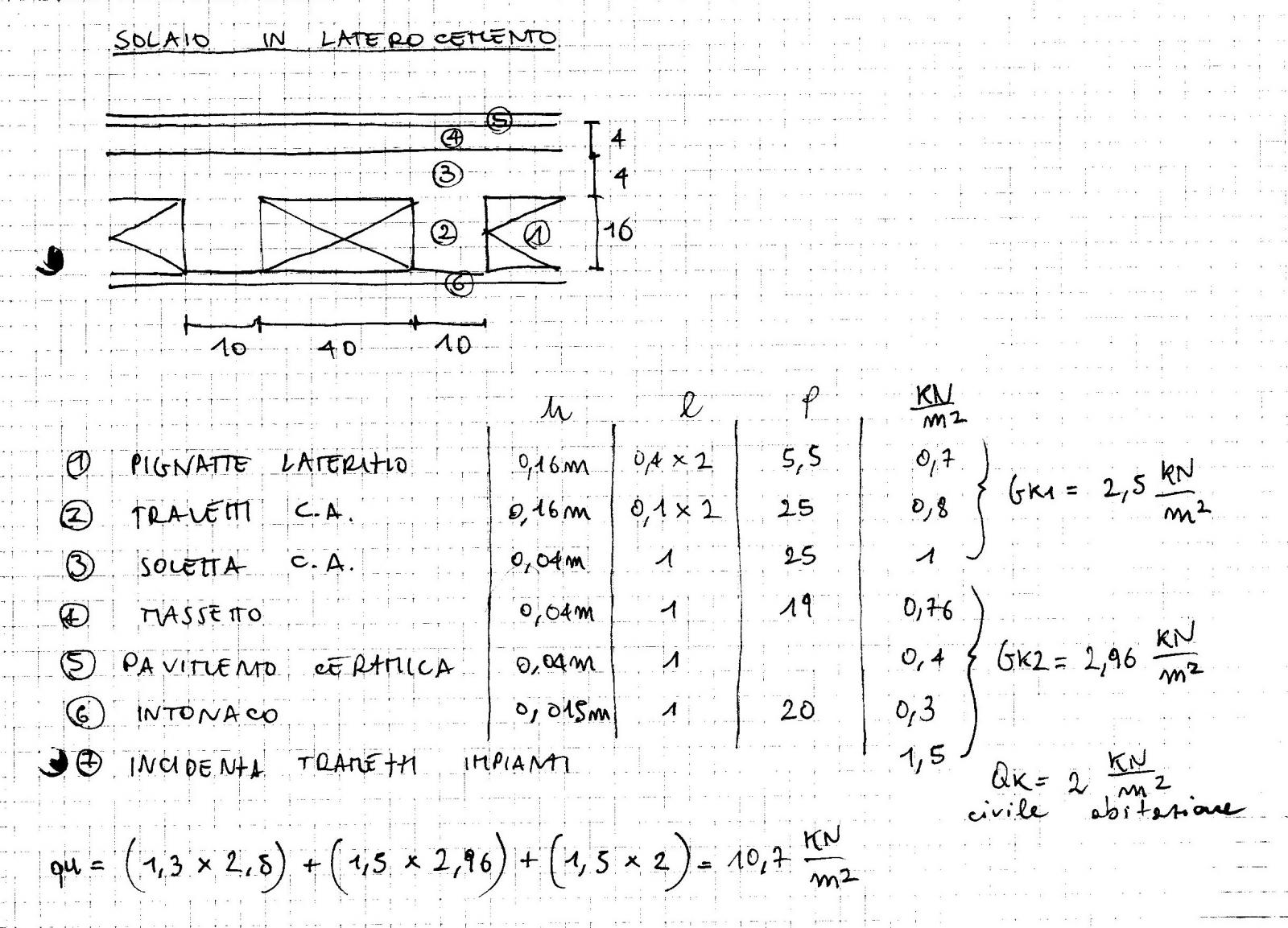
Prendiamo in considerazione 1 mq di solaio in latero-cemento. La figura mostra una sezione perpendicolare all'orditura dei travetti di cemento armato per mostrare i singoli materiali. Il carico ultimo che se ne ricava è uguale a Qu= 10,7 KN/m^2

Per il dimensionamento della trave è stato utilizzato un foglio elettronico che ci permette di ricavare l’altezza utile della sezione. Essendo il cemento un materiale che resiste bene a compressione e quasi niente a trazione ha bisogno dell’aiuto dell’acciaio per colmare questo gap. Il Cls e l’Acciaio hanno un comportamento meccanico diverso ma la deformazione deve essere la stessa per via del fattore di omogeneizzazione. Dato che i moduli elastici sono differenti viene introdotto questo coefficiente definito come il rapporto tra i moduli elastici dei due materiali. Dato che con il tempo il Cls abbassa la rigidezza per effetto della viscosità si accorcia e quindi n=15.

Tralasciando la dimostrazione diamo per buono che l’altezza utile della sezione è la radice quadrata del momento fratto una la base e diversi coefficienti.

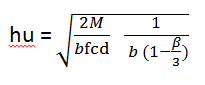
Inserendo i dati relativi:

-alle geometrie del telaio (La;Lb;luce)

-ai risultanti dell’analisi dei carichi (qs;qp;qa; con qu=luce*10,7)

-al momento massimo in mezzeria pari a ql^2/8

-a dei valori che troviamo (fyk;fyd;fcd;Es;Ec) e scegliamo (fck) in linea di massima dalla normativa

Troviamo un’altezza utile di 428mm, considerando un copriferro di 40 mm per coprire le barre d'acciaio risulta necessaria una trave principale alta almeno 468mm.
Per una facilità di realizzazione della trave, la sezione viene ingegnerizzata, quindi verrà utilizzata una trave con un’altezza pari a 500mm.
 

ACCIAO trave

Prendiamo in considerazione 1 mq di solaio con lamiera grecata che moltiplicato per la luce e l'interasse della Trave Principale ci darà il carico dell'Area di influenza (qu). La figura mostra una sezione perpendicolare all'orditura della lamiera grecata il carico ultimo ricavato è Qu= 12,25 KN/m^2

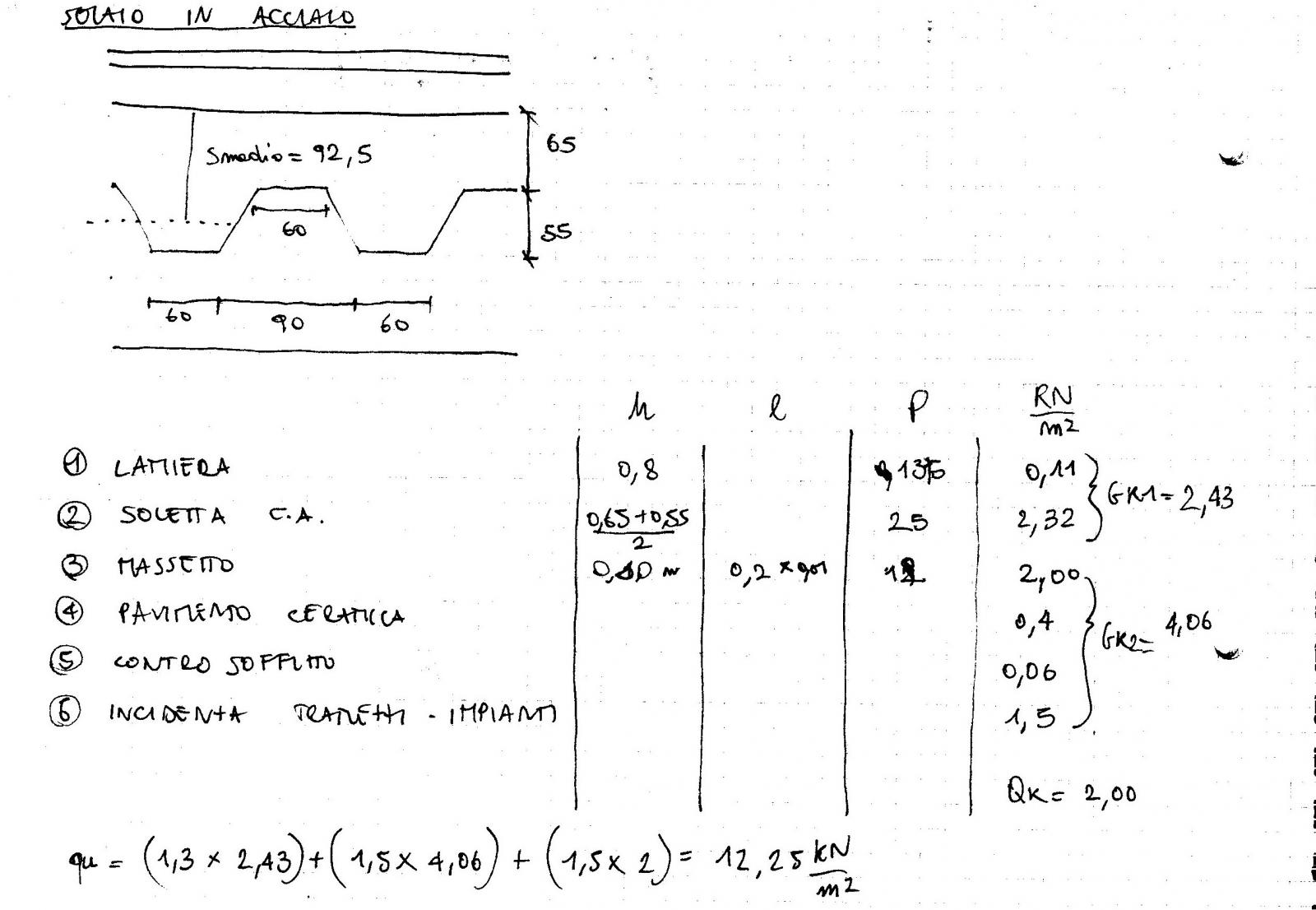
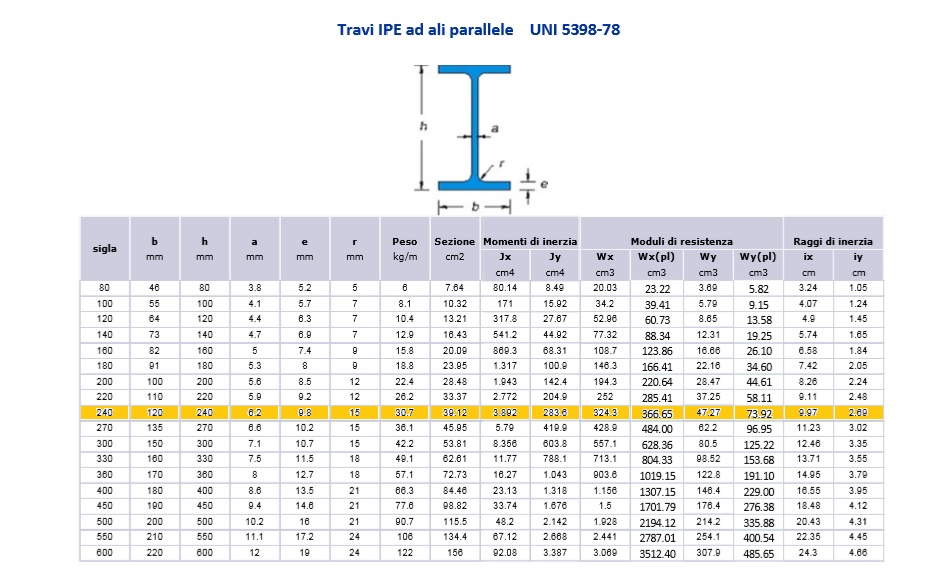
Anche per il dimensionamento della trave d’acciaio è stato utilizzato un foglio elettronico, ma stavolta non dobbiamo ricavarci l’altezza utile ma il procedimento è più veloce. Si considera al posto della tensione σ(y) la resistenza di progetto (Fyd) che serve per ricavarci attraverso il rapporto tra Momento massimo (ql^/8) e Fyd stesso il modulo di resistenza a flessione Wpl. Esso è il rapporto tra Mmax e Fyd, ma bisogna stare attenti alle equivalenze. Trovato il valore minimo Wpl=316,5 cm^3 della trave si prende il sagomario delle Ipe e si ricerca il valore Wx che supera quello trovato.

Dalla tabella si sceglie un’IPE 240 con Wx=366,65cm^3.

LEGNO trave

Come nei casi precedenti prendiamo in considerazione 1mq di solaio ma in legno. La figura mostra una sezione perpendicolare all’orditura dei travetti in legno ed il carico ultimo risultante è Qu= 7,6 KN/m^2

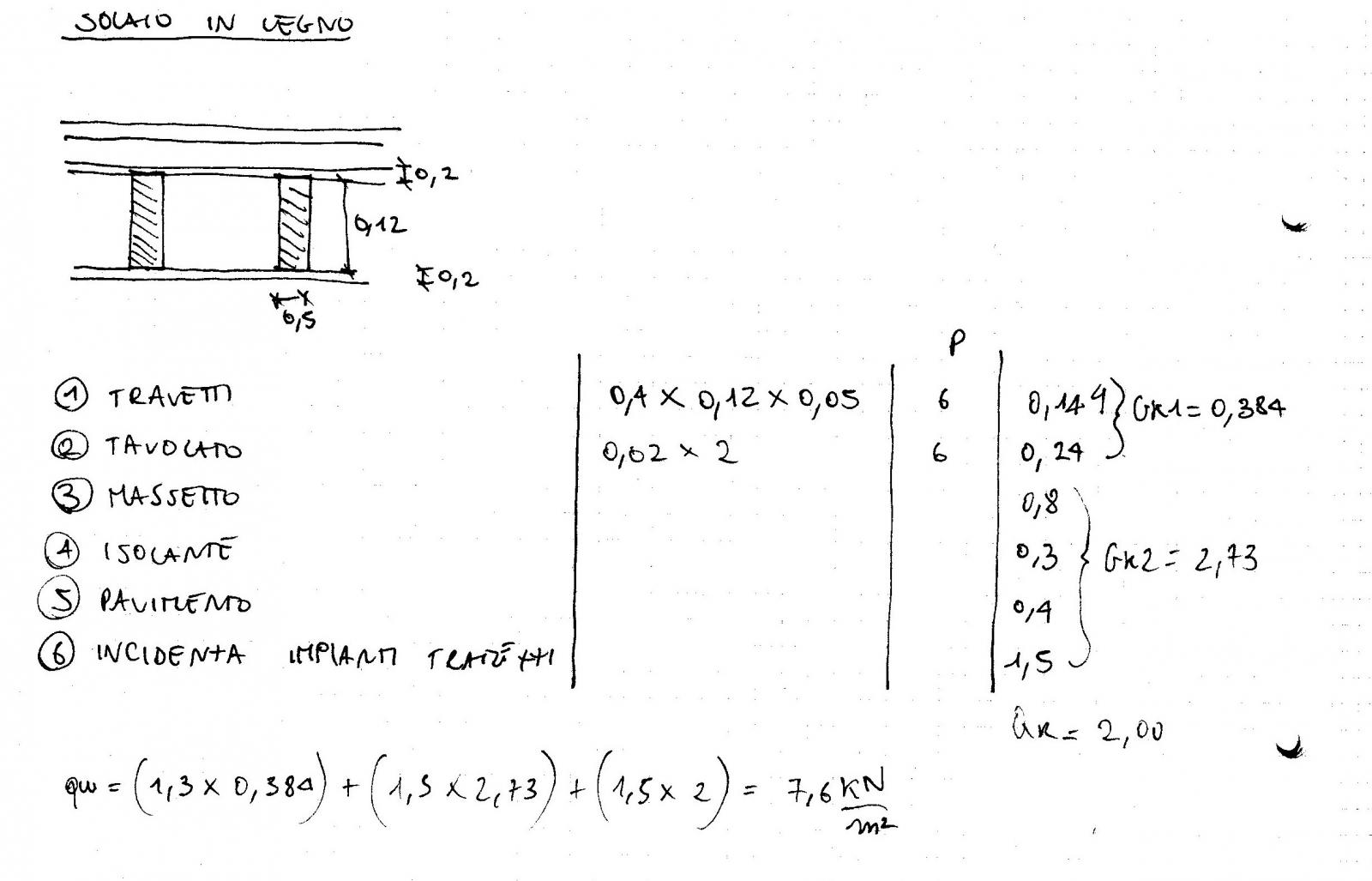
Ricorrendo sempre al foglio elettronico per il dimensionamento della trave il procedimento è simile a quello utilizzato per la trave in acciaio. Si parte dalla formula di Navier dove la tensione σ(y) è il rapporto tra il Momento Massimo (Mmax) e il modulo di resistenza a flessione (Wx). Da questa formula si ricava la Wx=3441cm^3 e poi si trova facilmente l’altezza utile della sezione facendo la radice quadrata del rapporto tra 6Wx e la base sapendo che il modulo di resistenza a flessione per una sezione rettangolare è Wx=bh^2/6. I valori non ancora citati(Fc0,k;kmod,γ) si ricavano dalla normativa.

Il risultato ottenuto mostra che l'altezza minima devo essere di 35,9 cm, che ingegnerizzato da un'altezza della trave di 40 cm.

PILASTRI

Nella costruzione del telaio, dopo aver determinato l’altezza della trave più sollecitata si dimensionano i pilastri. Per semplificare considero soltanto l’area d’influenza segnalata, ma per un dimensionamento più accurato dovrei dimensionare anche le altre campate. In ogni caso basterebbe aggiungere i dati ai fogli excel che li calcolerebbero automaticamente. Dunque così come nella trave si prende in esame l’area d’influenza maggiore (ricavata dividendo a metà le luci delle campate più grandi) che risente del maggior carico.

La sollecitazione principale a cui è sottoposto il pilastro è lo sforzo normale, ma nel nostro caso considereremo anche la flessione dovuta alle forze che esercita il vento sulle facciate.
Per dimensionare il pilastro bisogna verificare che lo sforzo normale non superi la resistenza del materiale.
Prendendo in esempio il modello di trave di Eulero-Bernoulli la relazione del legame costitutivo è σ = N/A.
Per ottenere l'area minima, sostituisco alla tensione σ la resistenza del materiale ( ovvero la resistenza caratteristica fk se sto progettando allo Stato Limite di Esercizio altrimenti la resistenza di progetto fd  per lo Stato Limite Ultimo).

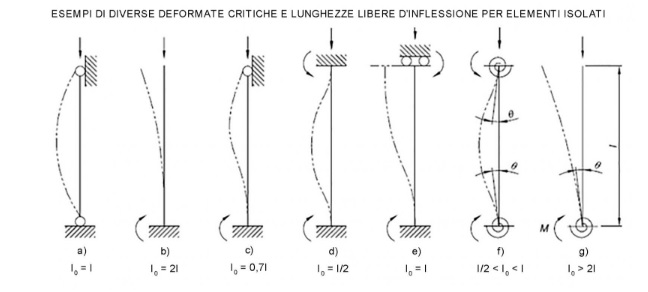
Il problema principale dei pilastri è la possibilità per elementi snelli di potersi inflettere,  per questo bisogna verificare l’instabilità. L'acciaio è il materiale che tra i tre proposti ha la resistenza più alta e permette di avere elementi molto snelli. Più è snello un elemento più risente dell’instabilità. L'elemento snello sottoposto a un carico verticale può inflettersi in diversi modi a seconda della condizioni ai bordi del pilastro (vincoli). La snellezza viene definita come il rapporto tra la luce libera di inflessione (distanza tra due flessi della deformata) e il raggio di inerzia minimo (definisce come le componenti di un oggetto sono distribuite attorno al suo asse di rotazione). Avendo scelto una struttura isostatica con cerniera e carrello come attacco a terra, dalla normativa troviamo che β=1.

CEMENTO ARMATO

Per progettare e verificare i pilastri si utilizza nuovamente excel, questa volta si creano 6 fogli relativi allo sforzo Normale e al dimensionamento per ogni tipologia costruttiva. Il procedimento per trovare la Nmax dipende dal numero di piani (n) e lo sforzo Normale relativo ad ogni piano (che si ottiene dal prodotto dell’area d’influenza (Ainf) per il peso delle travi espresso in KN per il carico ultimo (qu) derivante dall’analisi dei carichi). Trovato Nmax=359,5KN si riporta nella tabella relativa al dimensionamento. Anche qui, l’obiettivo è raggiungere la base e l’altezza di design per passare poi alla verifica della struttura. Dai fogli elettronici risulta che il pilastro al piano terra deve avere un’area minima di 264cm^2 e di conseguenza la base (ricavata moltiplicando ρmin*radice di 12) e l’altezza devono essere superiori rispettivamente a 8,4cm e 31,4cm. Scelgo un pilastro avente base e altezza uguali pari a 35cm evitando i problemi di inflessione poiché l’Area di design= 1225cm^2 supera l’Area minima=264cm^2.

ACCIAIO

Per il dimensionamento dei pilastri in acciaio utilizzo i profili HE in quanto più tozzi ed adatti di quelli IPE usati per la trave. Come per il Cemento Armato trovo lo Sforzo Normale Massimo=542,2KN che mi serve per trovare la geometria del pilastro. Essendo molto simile il procedimento, anche se nell’acciaio come detto in precedenza va considerato che avendo sezioni snelle c’è rischio di instabilità, mi limito a dire che nei fogli elettronici rispetto al c.a. cambiano i valori delle resistenze del materiale e per scegliere il profilato dal sagomario ho bisogno di trovare un’Inerzia minima che si ricava Imin=ρmin^2*Amin=235cm^4.

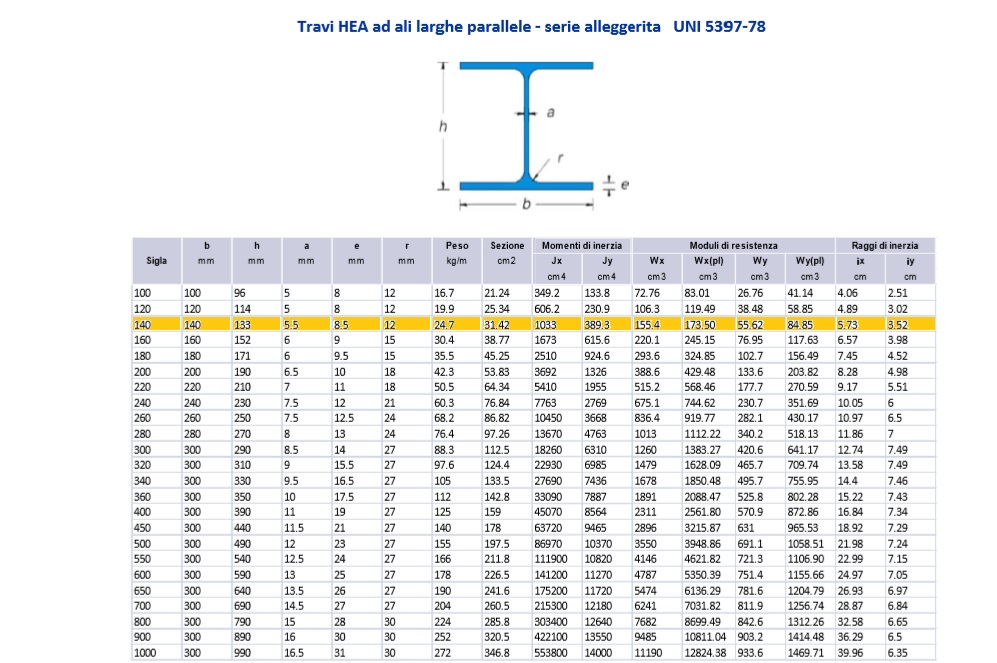
La resistenza molto elevata dell’acciaio permette di utilizzare un HEA140 che ha ovviamente un’inerzia maggiore di quella minima; inoltre per l’instabilità è verificato che λ<λc.

LEGNO

Il dimensionamento del legno ha lo stesso procedimento dell’acciaio in quanto anch’esso ha delle sezioni molto snelle. La Nmax=235,5KN è più bassa rispetto alle altre perché chiaramente il legno è un materiale che peso molto meno degli altri due 6KN/m^3 e addirittura pesa anche meno dell’acqua. Dalla tabella si evince chiaramente che il procedimento e simile e la sezione verificata viene di 15cmX15cm.

Dopo aver eseguito il predimensionamento della struttura si crea il tealio su SAP2000 dove si inseriscono per ogni tipologia costruttiva utilizzata i carichi linearmente distribuiti Qu al fine di ricavarci i diagrammi delle sollecitazioni e quindi i punti in cui sono massimi lo sforzo Normale e il Momento. Ottenuti questi valori si passa alla verifica a presso-flessione perché va considerata anche la pressione che il vento esercita sulle facciate.