blog di susanna.terreri

L'esercitazione è stata in .jpeg perchè il blog non salva gli avanzamenti, ma solo una parte dell'esercitazione caricata.

Esercitazione svolta con Francesco Petrelli.

L'esercitazione è stata caricata in .jpeg perchè il blog non salva gli avanzamenti, ma solo una parte dell'esercitazione caricata.

 

ESERCITAZIONE 01 
Esercitazione svolta con Francesco Petrelli.
 

Dimensionamento di un telaio in tre tecnologie (cemento armato, acciaio, legno)

La struttura analizzata è una struttura a telaio composta da un sistema di travi e pilastri, prendendo in esame gli elementi orizzontali e verticali più sollecitati (Fig.1) che saranno dimensionati nelle tre tecnologie richieste: cemento armato, acciaio e legno.

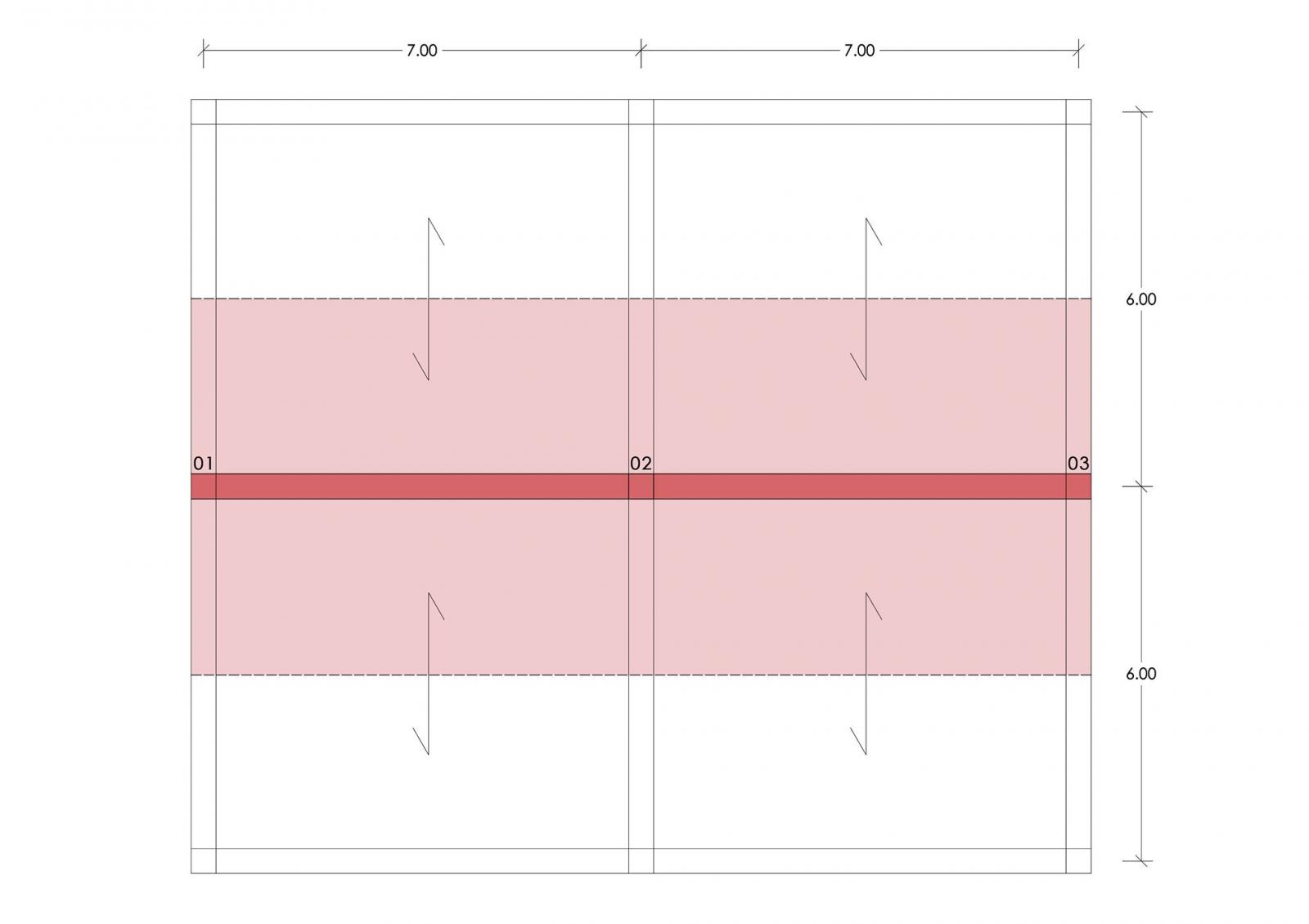
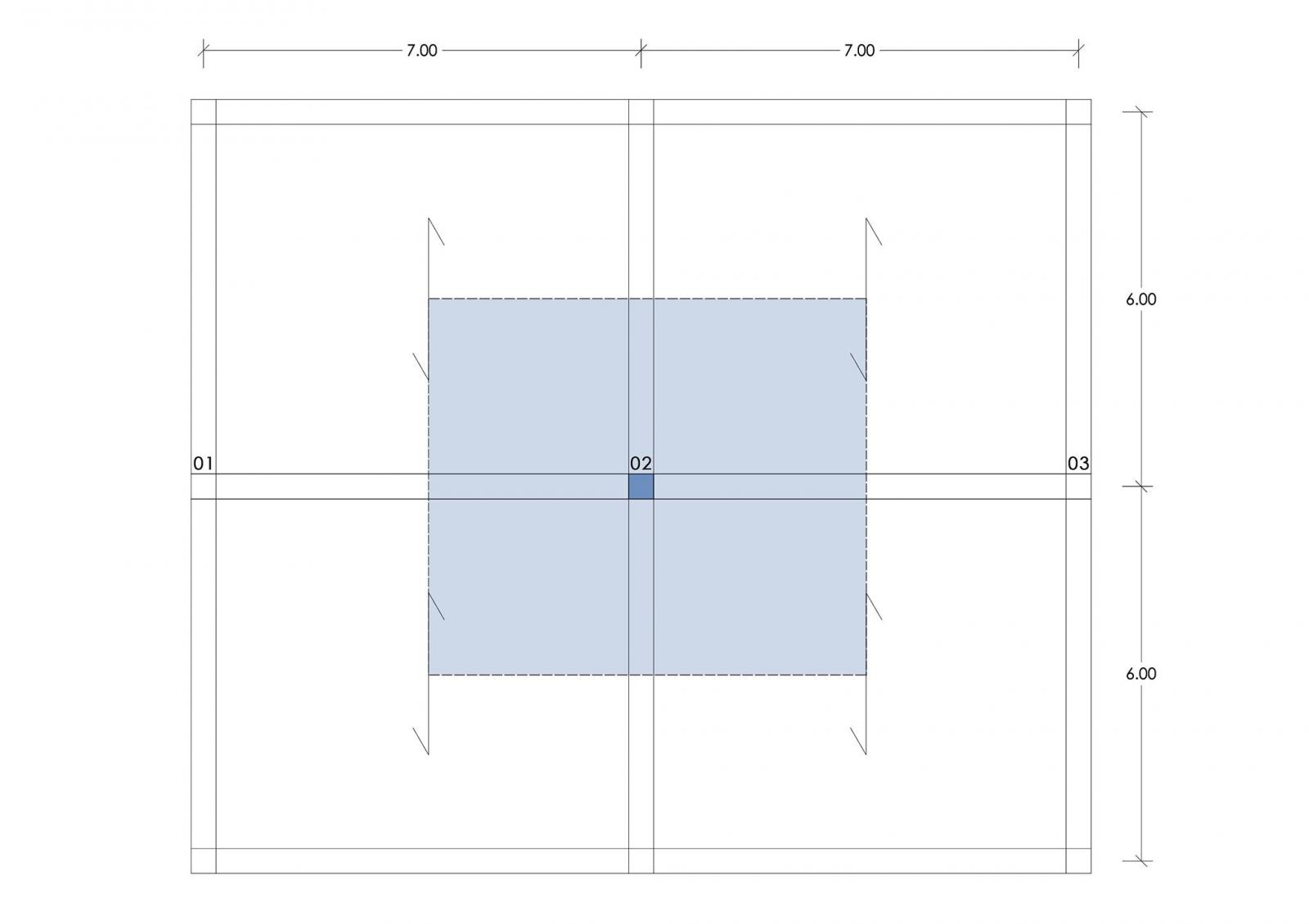Fig.1

 

ANALISI CARICHI

Il primo step per il predimensionamento è l’analisi dei carichi delle tre tipologie di solaio (solaio in latero-cemento, solaio in lamiera grecata e solaio in legno), secondo quanto stabilito dalla normativa che prevede l’analisi delle tre tipologie di carico (carico strutturale q_s, carico permanente non strutturale q_p, carico accidentale q_a) combinate tramite i coefficienti di sicurezza γ per ottenere il valore del carico ultimo q_u:

q_u=γ₁*q_s + γ₂*q_p +γ₃*q_a

dove i coefficienti di sicurezza γ₁,γ₂ e γ₃ hanno valori rispettivamente pari a 1,3, 1,5 e 1,5.
Il carico accidentale q_a è tabellato nella normativa ed ha un valore variabile a seconda della destinazione d’uso dell’edificio. In questo caso specifico è stato ipotizzato che il telaio studiato appartenga ad un edificio ad uso residenziale, per il quale la normativa prevede un carico accidentale q_a del valore di 2,00 kN/m².

CEMENTO ARMATO

Si considera il solaio in latero-cemento rappresentato nella F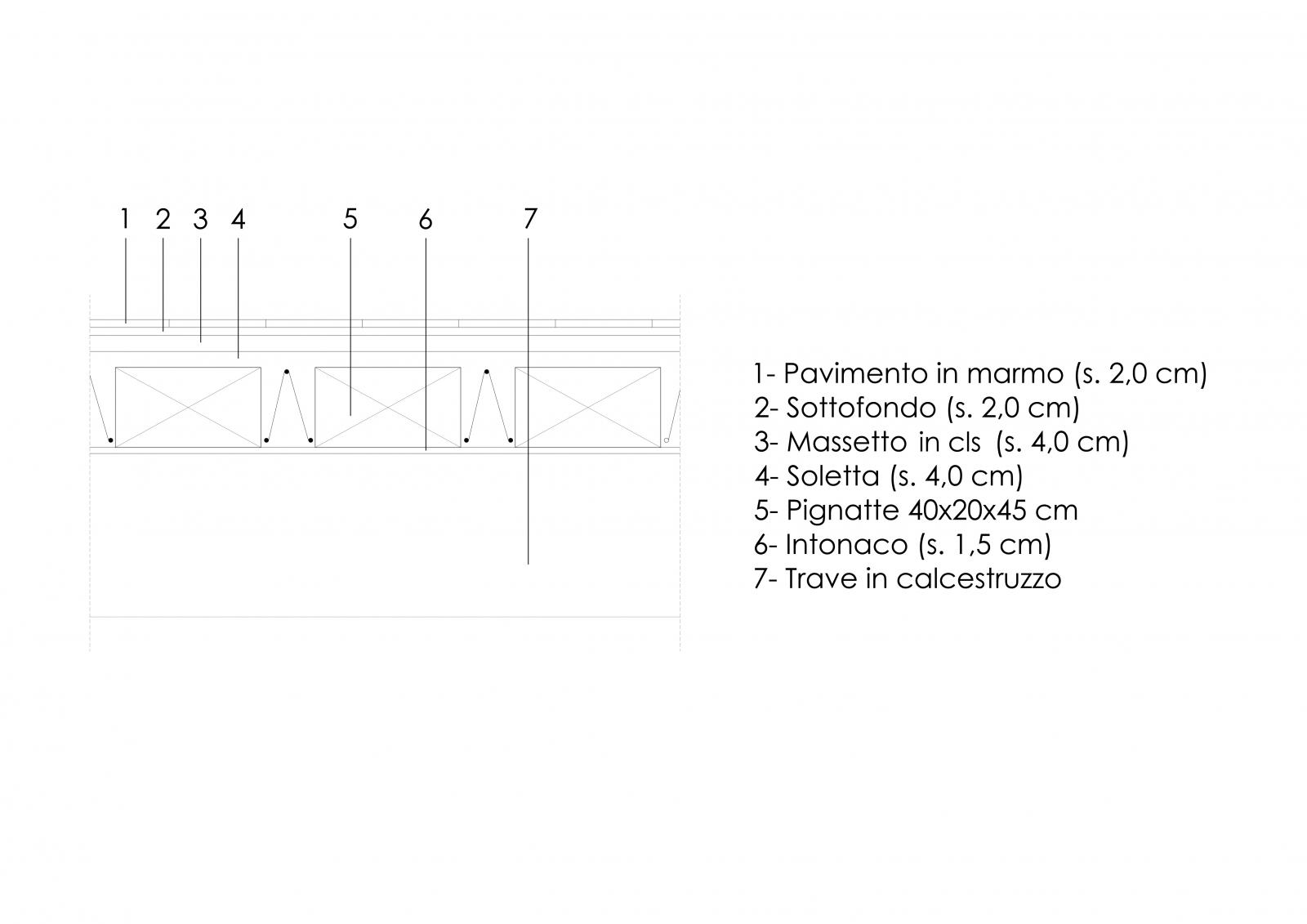ig.2

Fig.2

Nel calcolo del carico strutturale q_s vengono inseriti i carichi dati da:
- pignatte q_pignatte
- soletta in cls q_soletta
- travetti q_travetti

q_pignatte = V_pignatta /m² * γ_laterizio * (1m/interasse) = 0,08 m³/m² * 8 kN/m³ * 1m/0,50m = 1,28 kN/m²

q_soletta = s _soletta * γ_cls = 0,04m * 25 kN/m³ = 1 kN/m²

q_travetti = V_travetti /m² * γ_cls * (1m/interasse) = 0,02 m³/m² * 25 kN/m³ * 1m/0,50m = 1 kN/m²

q_s = q_pignatte + q_soletta + q_travetti = 3,28 kN/m²

Nel calcolo del carico permanente non strutturale q_p vengono inseriti i carichi dati da:
- massetto q_massetto
- sottofondo q_sottofondo
- pavimento q_pavimento
- intonaco q_intonaco
- incidenza dei tramezzi
- incidenza degli impianti

q_massetto = s _massetto * γ_cls = 0,04m * 25 kN/m³ = 1 kN/m²

q_sottofondo = s _sottofondo * γ_cls = 0,02m * 25 kN/m³ = 0,5 kN/m²

q_pavimento = s _pavimento * γ_marmo = 0,02m * 28 kN/m³ = 0,56 kN/m²

q_intonaco = s _intonaco * γ_{malta di calce} = 0,015m * 18 kN/m³ = 0,27 kN/m²

incidenza tramezzi = 1 kN/m²

incidenza impianti = 0,5 kN/m²

q_p = q_massetto + q_sottofondo + q_pavimento + q_intonaco + incidenza tramezzi + incidenza impianti = 3,77 kN/m²

 

q_u=γ₁*q_s + γ₂*q_p +γ₃*q_a = (3,28 kN/m² * 1,3) + (3,77 kN/m² * 1,5) + (2,00 kN/m² * 1,5) = 77,514 kN/ m²

 

ACCIAIO

Si considera il solaio in lamiera grecata rappresentato nella F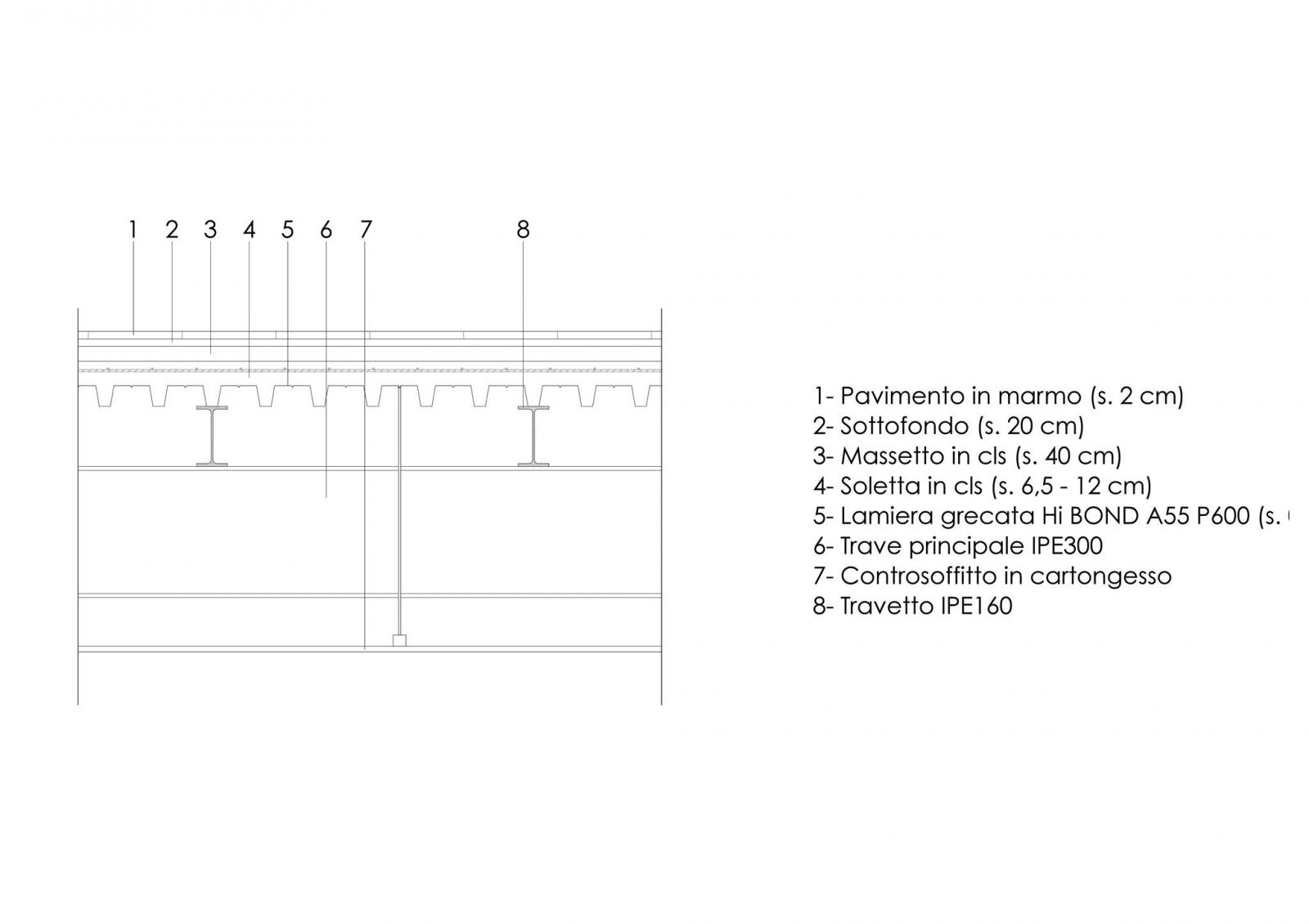ig.3

Fig.3

Nel calcolo del carico strutturale q_s vengono inseriti i carichi dati da:
- lamiera q_lamiera
- soletta in cls q_soletta
- travetti q_travetti

q_lamiera = 0,1045 kN/m²    (valore tabellato)

q_soletta = s _soletta * γ_cls = (0,065m – 0,055m/2) * 25 kN/m³ = 2,3125 kN/m²

q_travetti = n°_travetti /m² * Peso _travetto/m = (1m/interasse) * Peso _travetto/m = (1m/0,80m) * (0,158 kN/m / 1m) =
           = 0,1975 kN/m²

q_s = q_lamiera+ q_soletta + q_travetti = 2,6145 kN/m²

Nel calcolo del carico permanente non strutturale q_p vengono inseriti i carichi dati da:
- massetto q_massetto
- sottofondo q_sottofondo
- pavimento q_pavimento
- inincidenza dei controsoffitti
- incidenza dei tramezzi
- incidenza degli impianti

q_massetto = s _massetto * γ_cls = 0,04m * 25 kN/m³ = 1 kN/m²

q_sottofondo = s _sottofondo * γ_cls = 0,02m * 25 kN/m³ = 0,5 kN/m²

q_pavimento = s _pavimento * γ_marmo = 0,02m * 28 kN/m³ = 0,56 kN/m²

incidenza controsoffitti = 0,35 kN/m²

incidenza tramezzi = 1 kN/m²

incidenza impianti = 0,5 kN/m²

q_p = q_massetto + q_sottofondo + q_pavimento + incidenza controsoffitti + incidenza tramezzi + incidenza impianti =
= 3,91 kN/m²

 

q_u=γ₁*q_s + γ₂*q_p +γ₃*q_a = (2,6145 kN/m² * 1,3) + (3,91 kN/m² * 1,5) + (2,00 kN/m² * 1,5) = 73,5839kN/ m²

 

LEGNO

Si considera il solaio in legno lamellare rappresentato nella F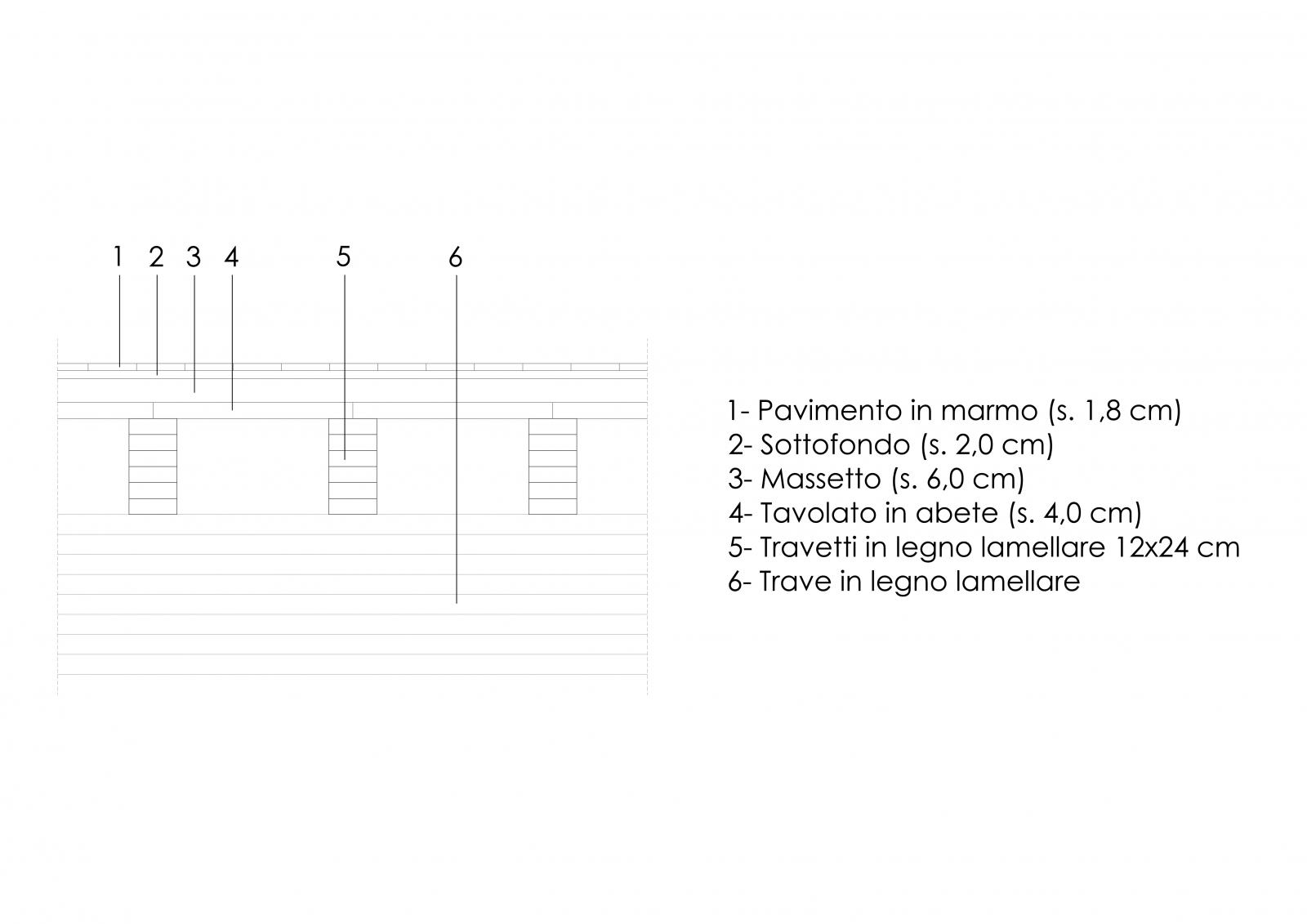ig.4

Fig.4

Nel calcolo del carico strutturale q_s vengono inseriti i carichi dati da:
- tavolato q_tavolato
- travetti q_travetti

q_tavolato = s _tavolato * γ_abete = 0,04m * 4,5 kN/m³ = 0,18 kN/m²

q_travetti = V_travetti /m² * γ_abete * (1m/interasse) = 0,0288 m³/m² * 4,5 kN/m³ * 1m/0,50m = 0,2592 kN/m²

q_s = q_tavolato + q_travetti = 0,4392 kN/m²

 

Nel calcolo del carico permanente non strutturale q_p vengono inseriti i carichi dati da:
- massetto q_massetto
- sottofondo q_sottofondo
- pavimento q_pavimento

q_massetto = s _massetto * γ_cls = 0,06m * 25 kN/m³ = 1,5 kN/m²

q_sottofondo = s _sottofondo * γ_cls = 0,02m * 25 kN/m³ = 0,5 kN/m²

q_pavimento = s _pavimento * γ_rovere = 0,018m * 7,5 kN/m³ = 0,135 kN/m²

q_p = q_massetto + q_sottofondo + q_pavimento = 2,135 kN/m²

 

q_u=γ₁*q_s + γ₂*q_p +γ₃*q_a = (0,4392 kN/m² * 1,3) + (2,135 kN/m² * 1,5) + (2,00 kN/m² * 1,5) =
= 40,6408 kN/ m²

 

I valori dei carichi strutturale, permanente non strutturale e accidentale e le combinazioni di carico sono stati riportati in un foglio di calcolo excel (fig.5) per valutare i momenti massimi M_max agenti sulle travi di ogni tecnologia.

M_max = q_u*l²/8

 

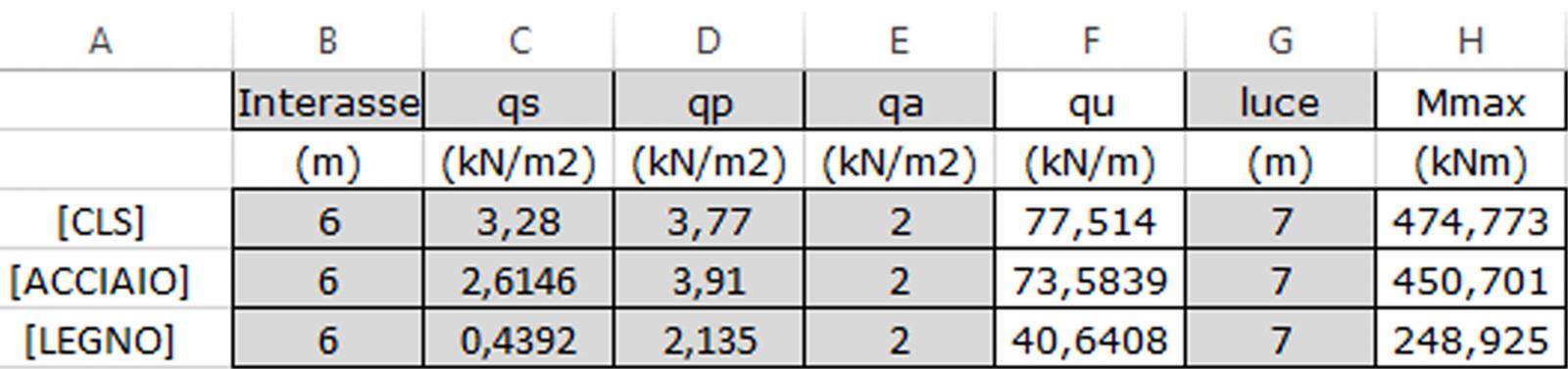
Fig.5

 

DIMENSIONAMENTO TELAI

I valori di M_max trovati sono stati a loro volta inseriti in altri fogli di calcolo per effettuare il predimensionamento delle travi di ogni tecnologia.

 

TELAIO in CEMENTO ARMATO

Date f_yk e f_ck, calcoliamo le resistenze di progetto dell’acciaio (B450) e del calcestruzzo (C30/37):

f_yd = f_yk/γ_M1 = 450 MPa / 1,15

f_cd = (α_cc* f_ck)/ γ_c = (0,85 * 30) / 1,5

dove γ_M1 e γ_c sono i coefficienti parziali di sicurezza rispettivamente di acciaio e cls, e α_cc il coefficiente riduttivo per le resistenze di lunga durata.

Con i valori ottenuti sono stati calcolati i coefficienti β e r, necessari per definire l’altezza utile della sezione della trave:

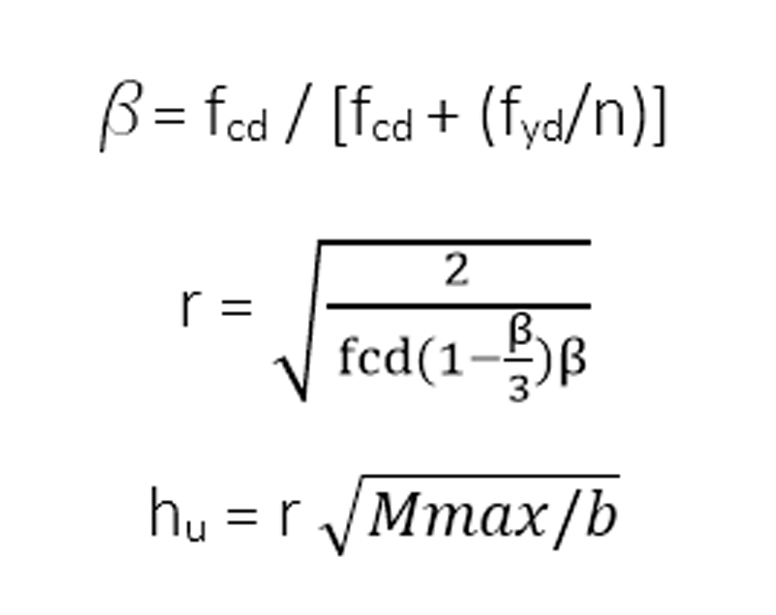
dove M_max è il valore del momento trovato in precedenza e b è il valore della base della sezione della trave scelta in modo arbitrario.

L’altezza della sezione sarà ottenuta sommando l’altezza del copriferro δ all’altezza utile h_u.

Una volta trovata l’altezza della trave in funzione della base, si può calcolare l’area della sezione e quindi il peso unitario della trave, moltiplicando il valore dell’area della sezione (A_trave = b*h) per il peso specifico del calcestruzzo (γ_cls = 25kN/m³).

Fig. 6

 

Il predimensionamento della trave, permette di poter dimensionare il pilastro del telaio in un nuovo foglio di calcolo excel.
Conoscendo le dimensioni geometriche della sezione della trave, quindi il suo peso, e la combinazione di carico agente distribuita superficialmente, si può calcolare la forza concentrata che agisce sul pilastro di un singolo piano moltiplicando la somma dei due carichi per l’area di influenza del pilastro (A_inf):

N₁ = (q_u + Peso_trave)*A_inf

Moltiplicando questo valore per il numero di piani n (n=4) si ottiene quindi la forza normale agente sul pilastro.

N_max = N₁*n

Fig.7

Determinato il valore della sollecitazione massima, si può dimensionare il pilastro.

Dati N_max e f_ck, si può calcolare f_cd, quindi l’area minima che dovrà avere il pilastro:

f_cd = (α_cc* f_ck)/ γ_c = (0,85 * 30) / 1,5

A_min = N_max / f_cd

Ipotizzando il pilastro con una sezione quadrata, possiamo definire b_min come la radice quadrata dell'area minima A_min e l’altezza minima h_min come A_min/b. Ingegnerizzando le dimensioni di b_min e h_min appena ottenute si ottengono le dimensioni geometriche di progetto della sezione del pilastro.

Fig.8

 

Una volta dimensionati le travi e i pilastri del telaio tramite i fogli di calcolo excel, si riportano le sezioni e i carichi su SAP2000.

Qui si disegna un telaio avente le caratteristiche geometriche e i materiali appena definiti e su questo telaio verranno applicate le condizioni di carico calcolate in precedenza, più un carico orizzontale dovuto alla forza del vento.

Facendo l’analisi di questo telaio si ottengono la configurazione deformata (Fig.9) e i diagrammi delle sollecitazioni del momento (Fig.10a - Fig.10b) e dello sforzo normale (Fig.11a - Fig.11b).

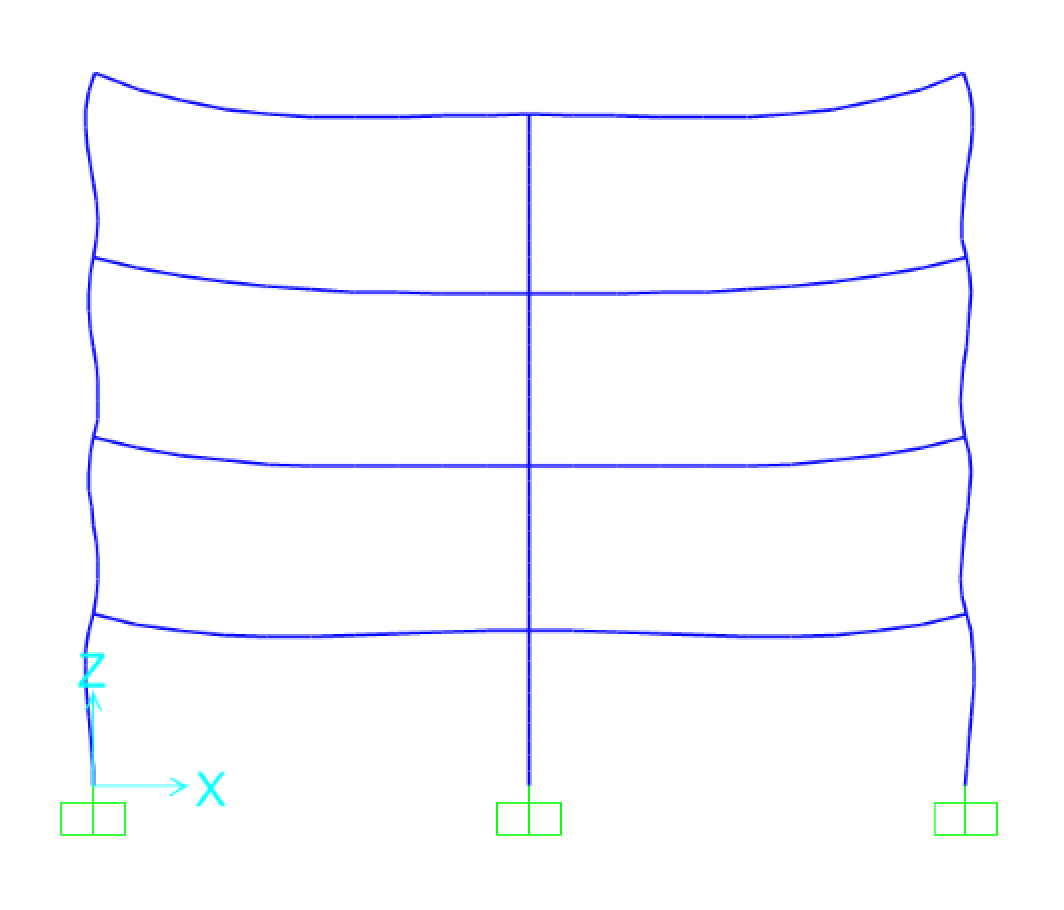Fig.9

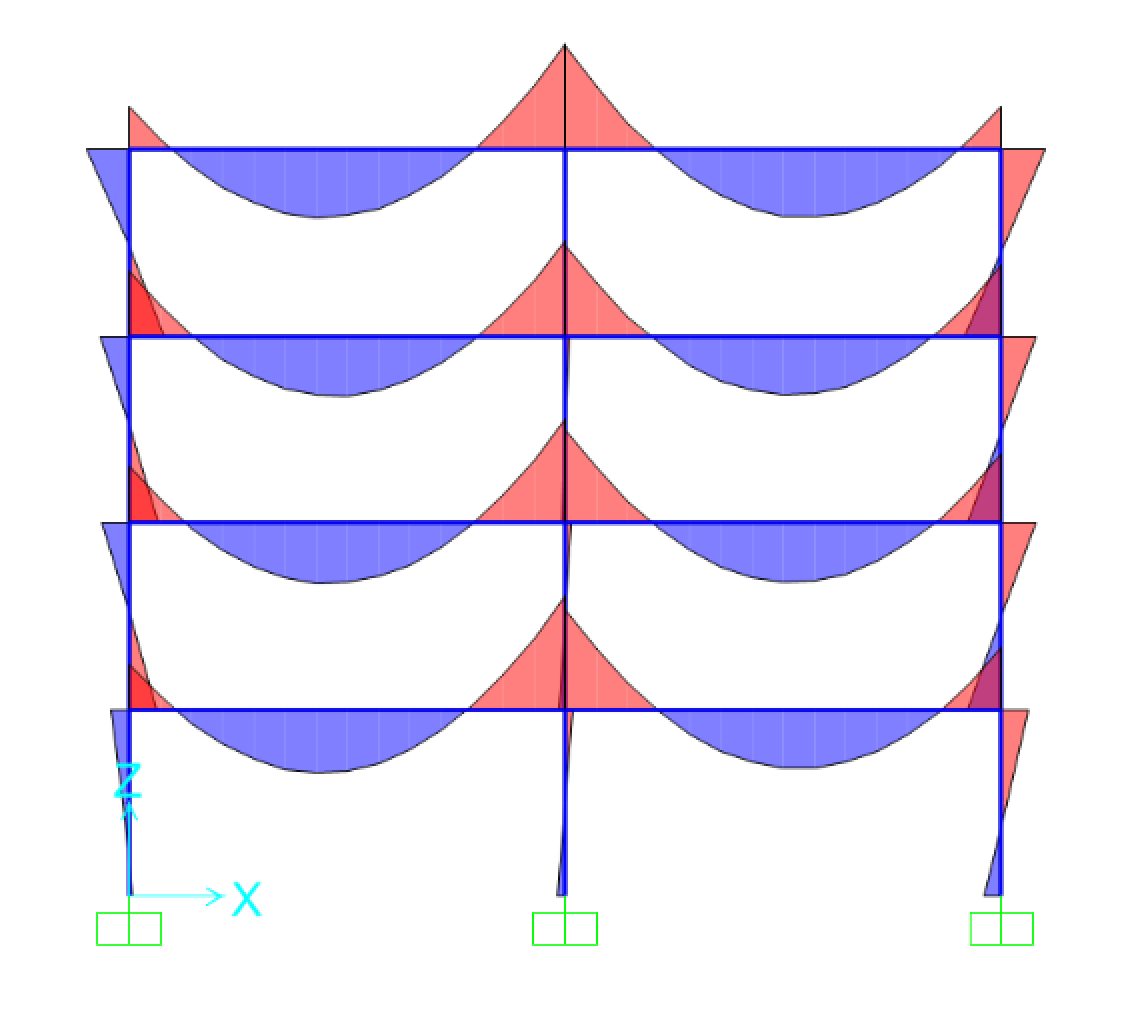Fig.10a

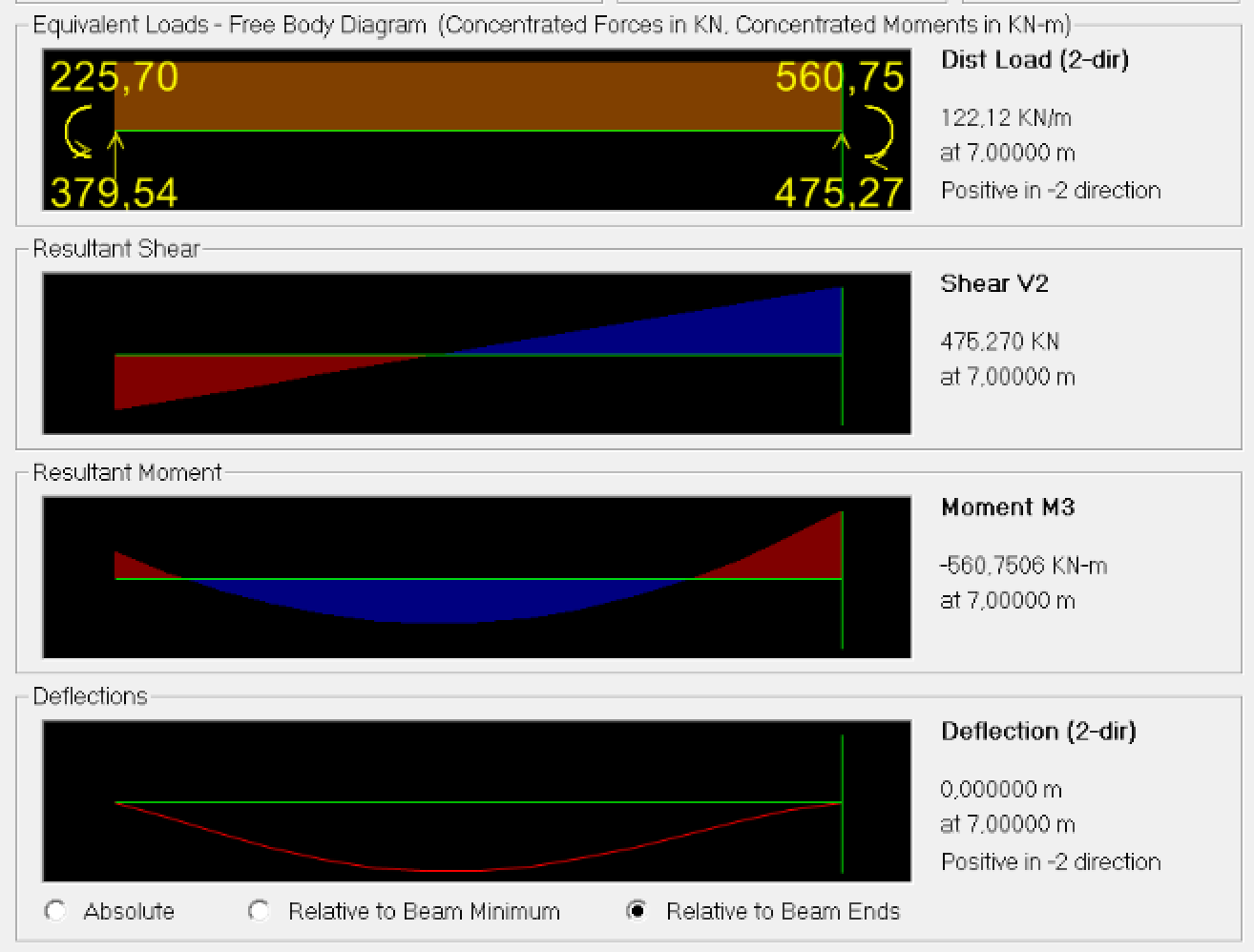
Fig.10b
 

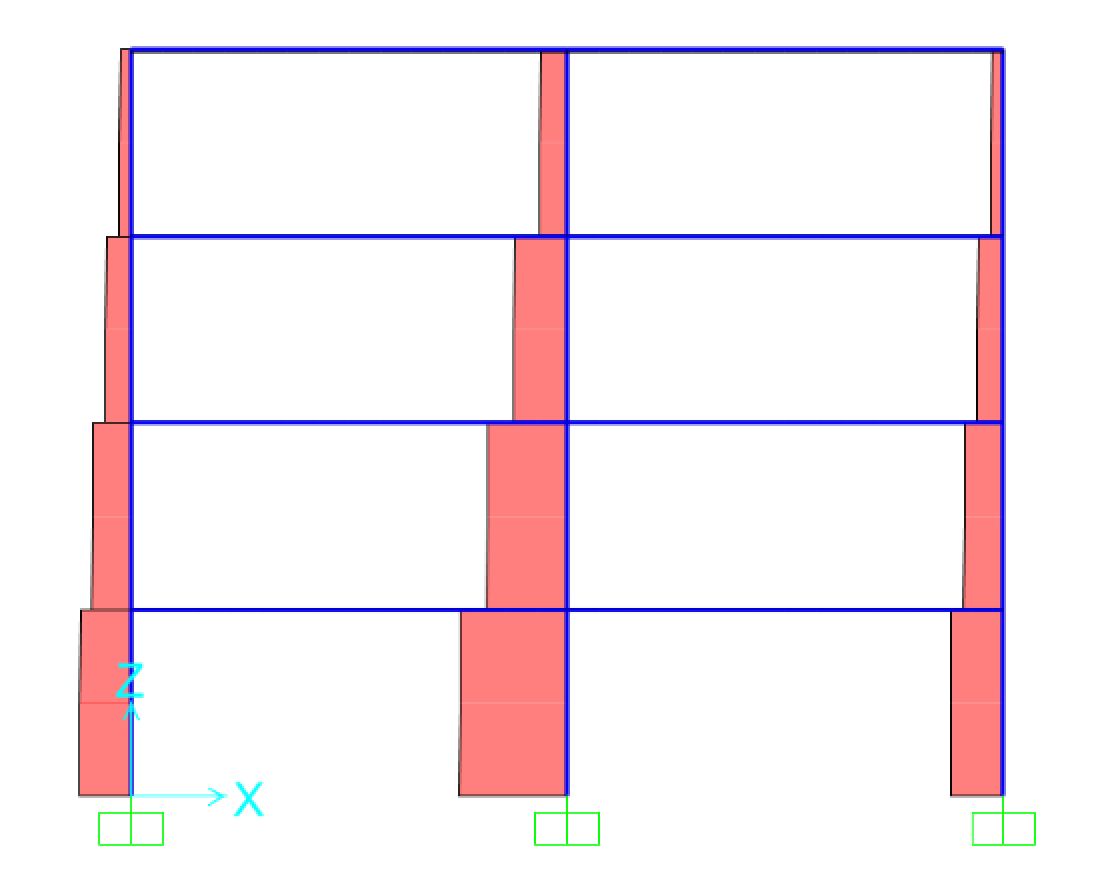Fig.11a

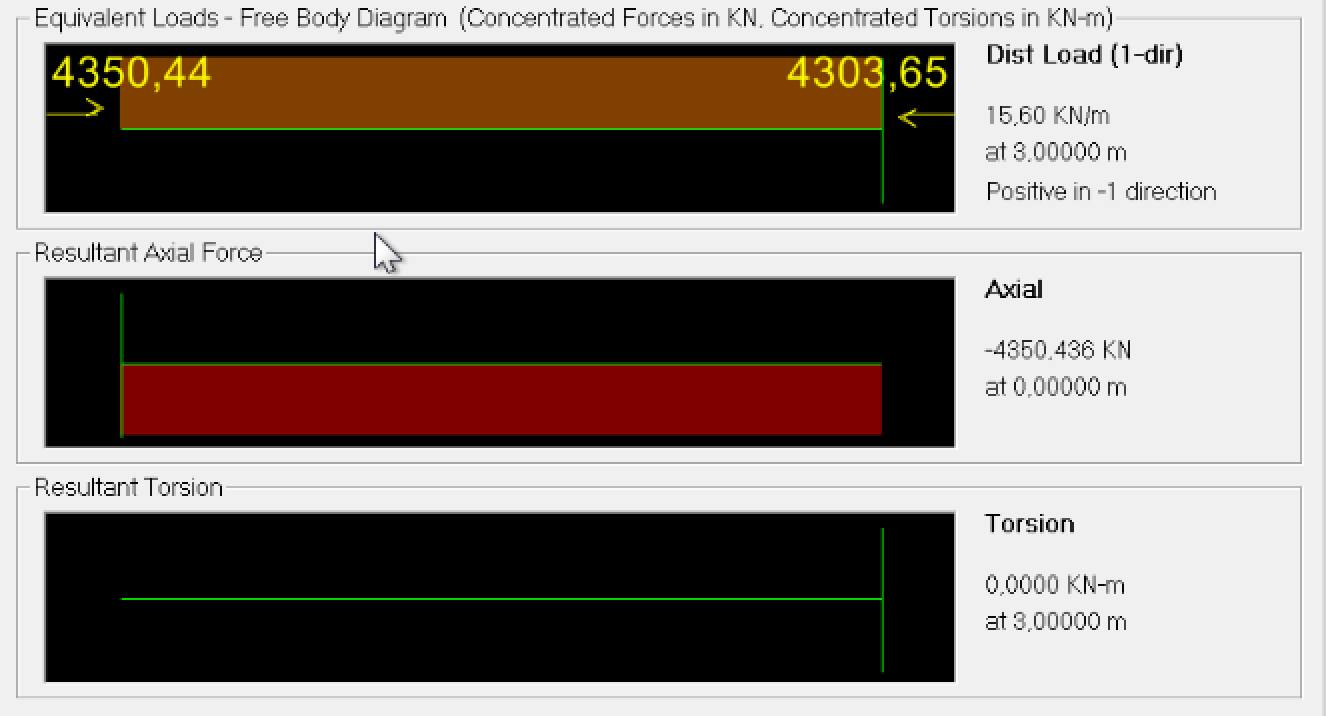
Fig.11b

 

Per verificare il dimensionamento del telaio, bisogna riportare nei fogli di calcolo excel costruiti in precedenza i valori massimi del momento e dello sforzo normale ricavati dall’analisi su SAP ed, eventualmente, modificare le dimensioni delle sezioni delle travi (Fig.12) e dei pilastri (Fig.13) calcolate durante il predimensionamento.

Fig.12

Fig.13

Nella Fig.13, le ultime tre celle del foglio di calcolo (q_t, M_t e σ_max) servono per la verifica a presso-flessione del pilastro.

Un pilastro è verificato a presso-flessione se la tensione massima provocata dai carichi è minore della resistenza di progetto:

σ_max < f_cd

La tensione massima è data da:

σ_max = (N_max/A) + (M_t/W_x)

dove N_max è lo sforzo normale massimo agente sul pilastro, A è l’area di design del pilastro, W_x è il modulo di resistenza a flessio e M_t è il momento trasferito sul pilastro dalla trave, che è dato da:

M_t = q_t*(l²/12)

Dove q_t è il carico del solaio linearmente distribuito sulla trave:

q_t = q_u*l

 

TELAIO in ACCIAIO (S 275)

Dati il M_max e f_yk, si possono definire f_yd e il modulo di resistenza a flessione W_x,min della sezione della trave in acciaio:

f_yd = f_yk/γ_M1 = 275 MPa / 1,05

W_x,min = M_max / f_yd

Conoscendo W_x,min si può scegliere la sezione della trave dal profilario delle sezioni di acciaio (Fig.14), scegliendo un profilo che presenti un valore di W_x > W_x,min
 

Fig.14

Fig.15

Una volta scelta la sezione e definite le caratteristiche geometriche della trave, con lo stesso procedimento utilizzato per il telaio in cemento armato si può calcolare lo sforzo normale massimo agente sul pilastro in acciaio.

Fig.16

 

Conoscendo N_max, f_yk e f_yd= f_yk/γ_M1, si può definire l’area minima del pilastro di acciaio:

A_min = N_max / f_yd

Dati il modulo di elasticità E, il coefficiente di vincolo β e la lunghezza del pilastro l, si può calcolare la snellezza massima del pilastro λ*, il raggio di inerzia minimo ρ_min e il momento di inerzia minimo I_min:

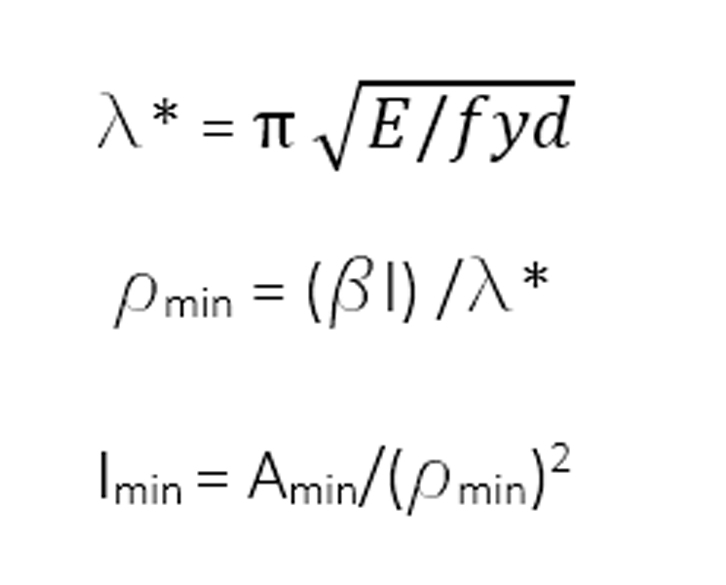
Conoscendo questi valori, si può scegliere la sezione del pilastro dal profilario delle sezioni di acciaio (Fig.17) tale che l’area del profilo scelto sia maggiore dell’A_min calcolata.

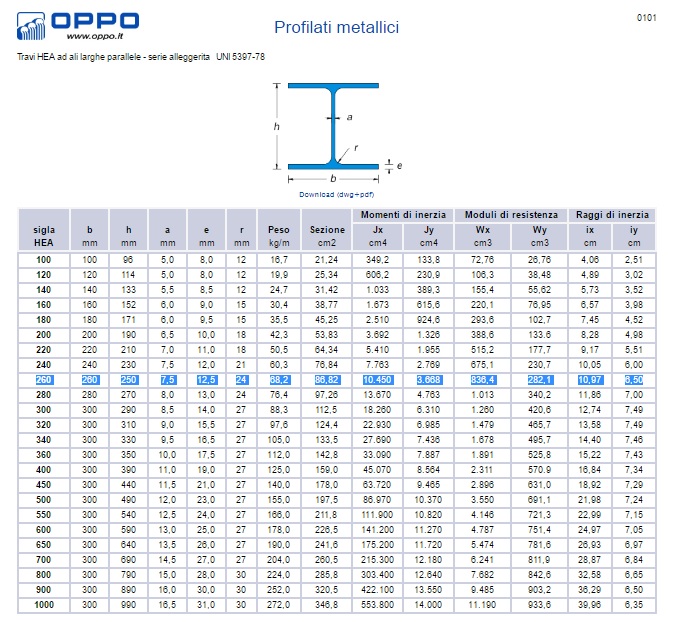
Fig.17

Fig.18

 

Una volta dimensionati le travi e i pilastri del telai, si riportano le sezioni e i carichi su SAP.

Si disegna un telaio avente le caratteristiche geometriche e i materiali appena definiti e verranno applicate le condizioni di carico, più il carico orizzontale dovuto alla forza del vento.

Facendo l’analisi di questo telaio si ottengono la configurazione deformata (Fig.19) e i diagrammi delle sollecitazioni del momento (Fig.20a - Fig.20b) e dello sforzo normale (Fig.21a - Fig.21b).

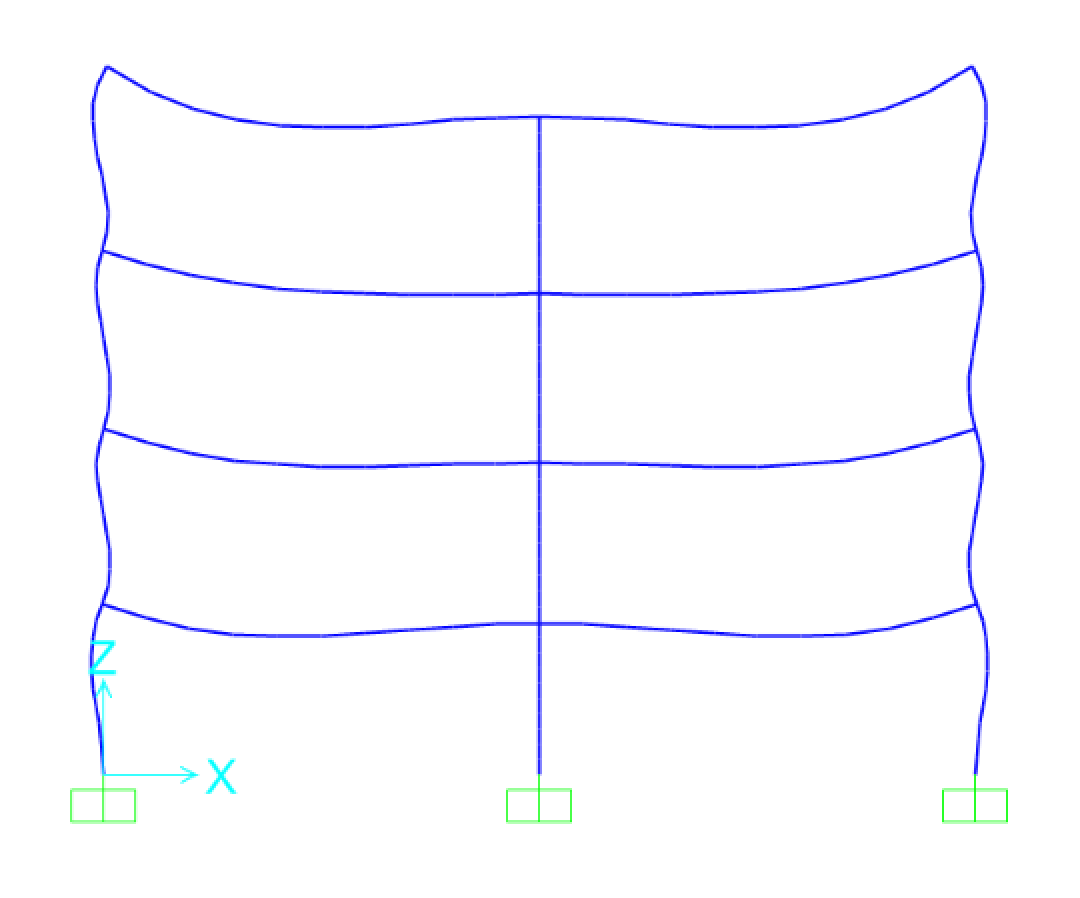Fig.19

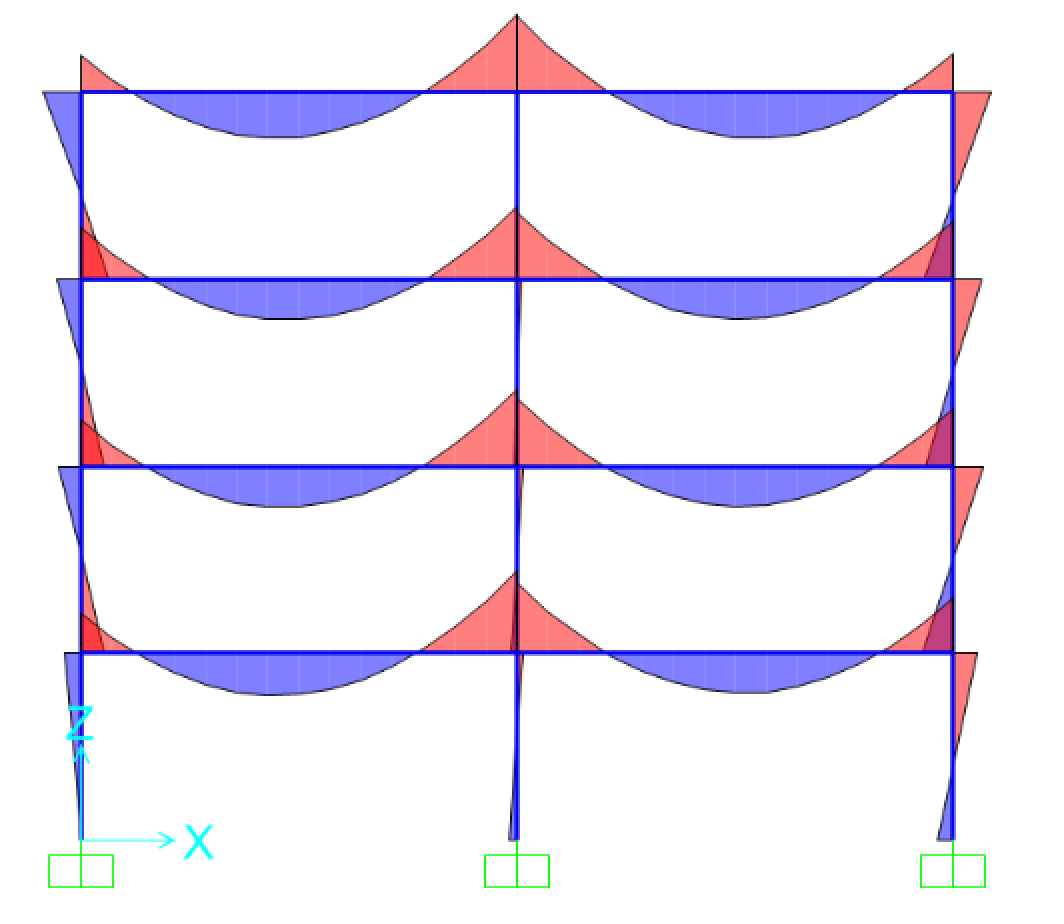Fig.20a

Fig.20b

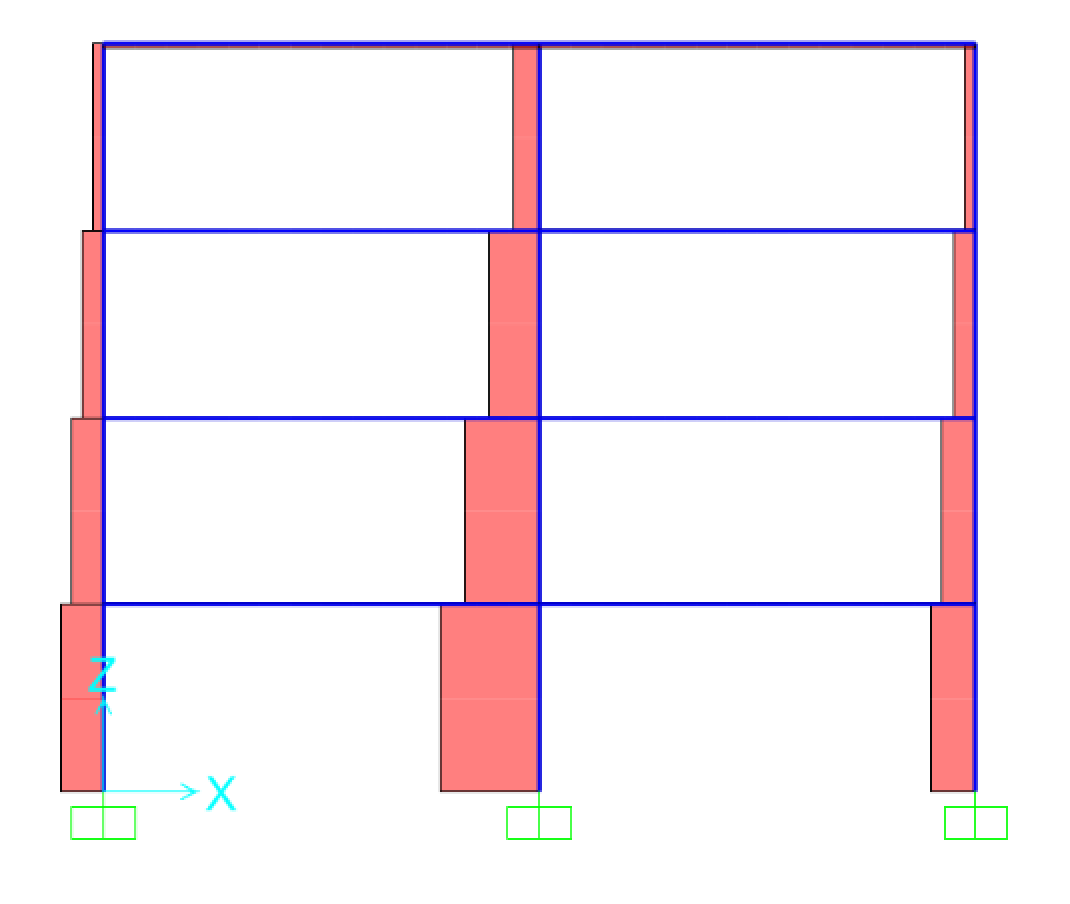Fig.21a

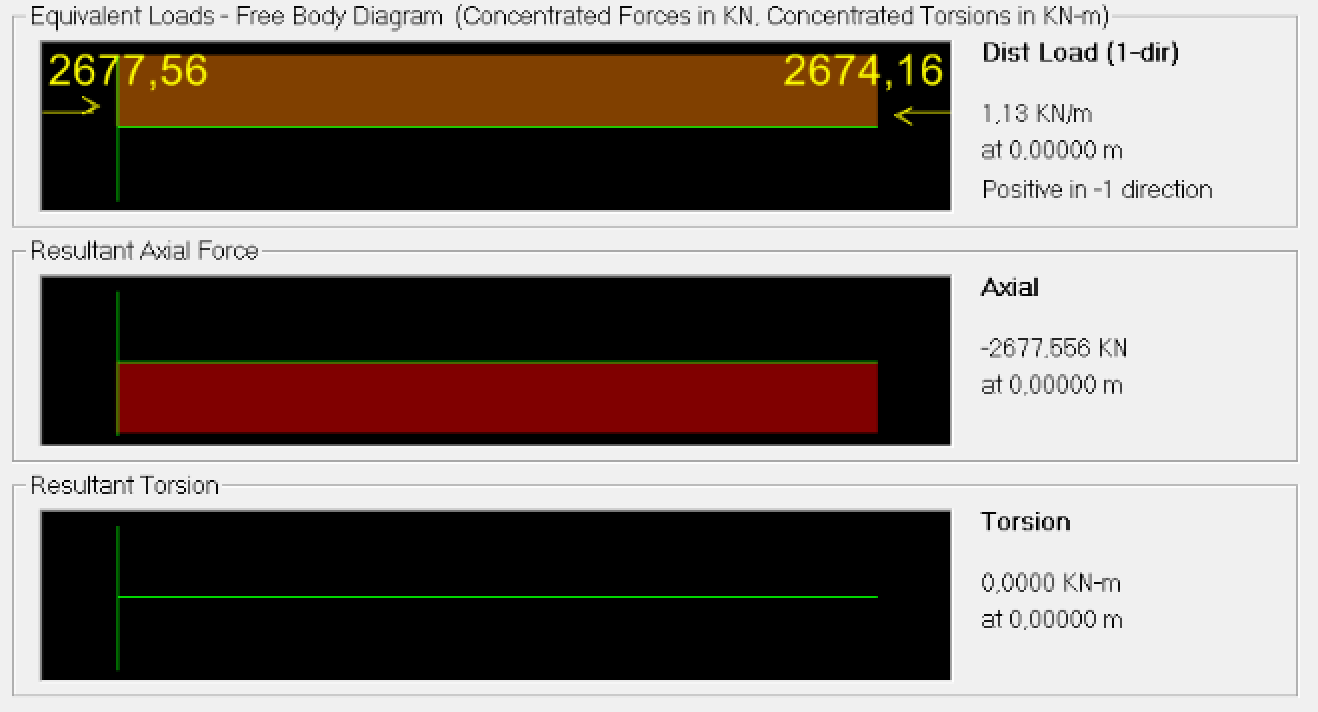
Fig.21b

 

Per verificare il dimensionamento del telaio, si riportano nei fogli di calcolo excel i valori massimi del momento e dello sforzo normale ricavati dall’analisi su SAP ed, eventualmente, si modificano le dimensioni delle sezioni delle travi (Fig.22) e dei pilastri (Fig.23) calcolate durante il predimensionamento.

Fig.22

Fig.23

 

TELAIO in LEGNO (GL 28h)

Dati il momento massimo M_max, la resistenza f_m,k, coefficiente diminutivo della resistenza del materiale k_mod e il coefficiente parziale di sicurezza γ_m, si può calcolare la geometria della trave.

Fissando una dimensione arbitraria della base b, si trova la dimensione dell’altezza minima della trave:

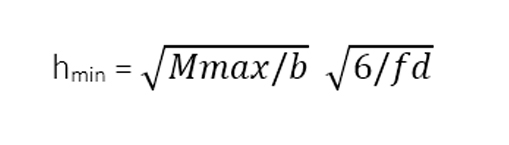
dove f_d = (k_mod * f_m,k) / γ_m.

Ingegnerizzando il valore di h_min ottenuto si trova il valore di h, quindi l’area della sezione.

Fig.24

Una volta scelta la sezione e definite le caratteristiche geometriche della trave, con lo stesso procedimento utilizzato per i telai in cemento armato e in acciaio si può calcolare lo sforzo normale massimo agente sul pilastro in legno.

Fig.25

Conoscendo N_max, f_m,k, f_d,  k_mod e γ_m, si calcola l’area minima del pilastro:

A_min = N_max / f_d

Dati il modulo di elasticità E, il coefficiente di vincolo β e la lunghezza del pilastro l, si può calcolare la snellezza massima del pilastro λ*, il raggio di inerzia minimo ρ_min:

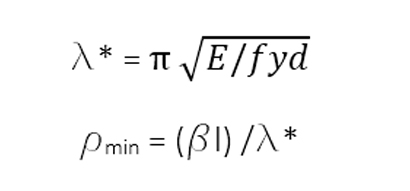
Si può allora calcolare la base minima della sezione:

Ingegnerizzando il valore ottenuto, si ricava b. Si può allora calcolare l’altezza minima della sezione:

h_min = A_min / b

Ingegnerizzando anche questo valore, si ottiene l’altezza della sezione.

Fig.26

Una volta dimensionati le travi e i pilastri del telai, si riportano le sezioni e i carichi su SAP.

Si disegna un telaio avente le caratteristiche geometriche e i materiali appena definiti e verranno applicate le condizioni di carico, più il carico orizzontale dovuto alla forza del vento.

Facendo l’analisi di questo telaio si ottengono la configurazione deformata (Fig.27) e i diagrammi delle sollecitazioni del momento (Fig.28a - Fig.28b) e dello sforzo normale (Fig.29a - Fig.29b).

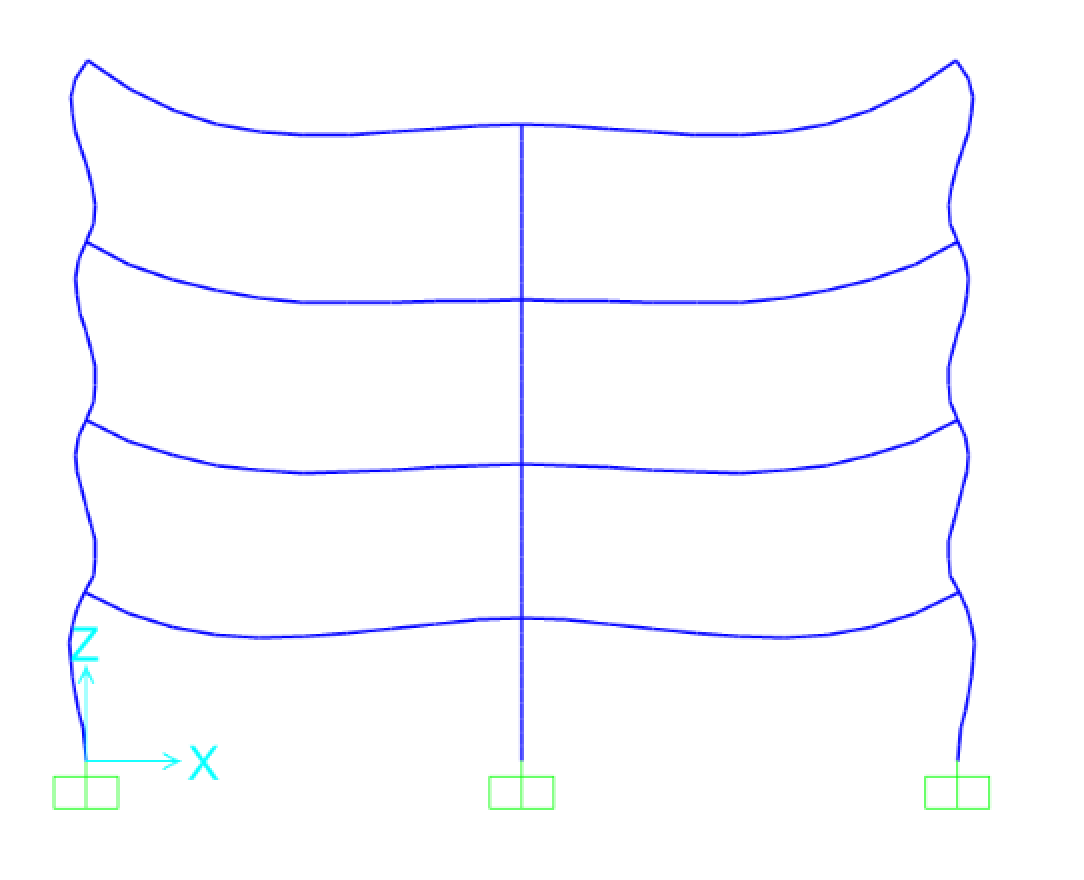Fig.27
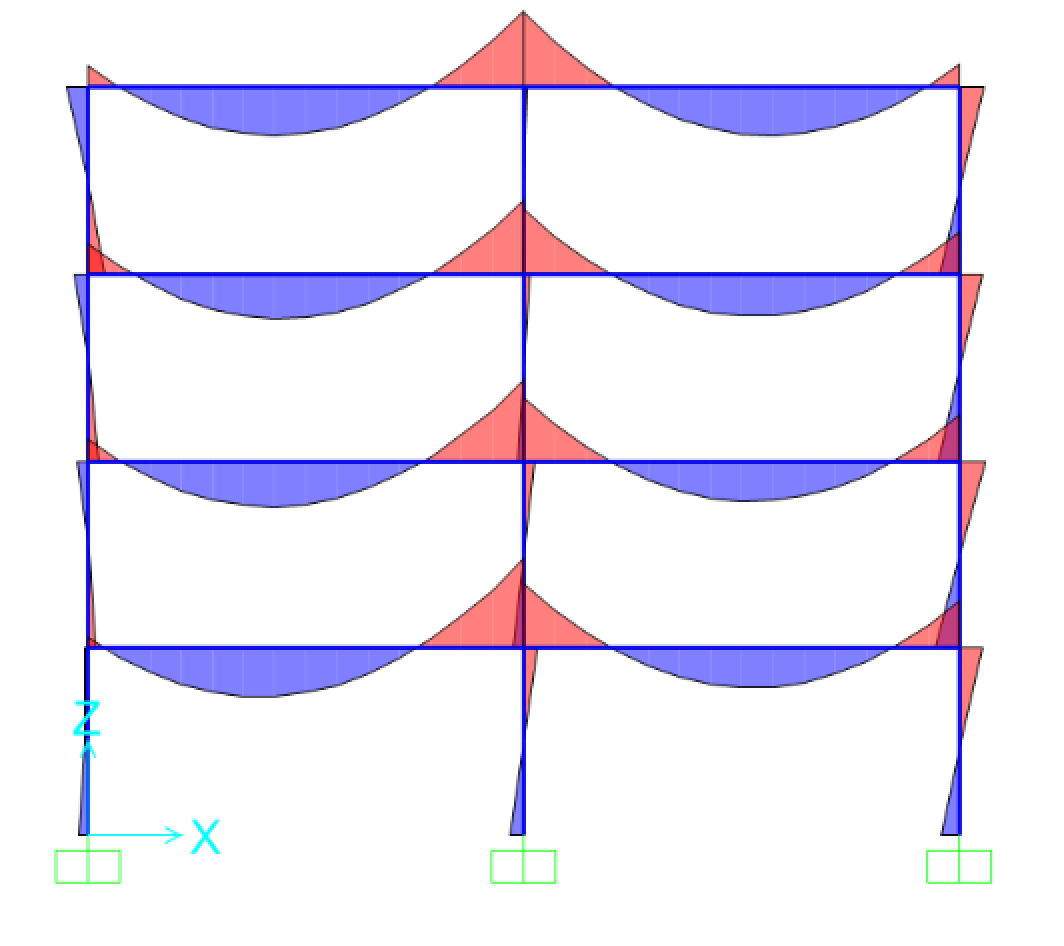Fig.28a

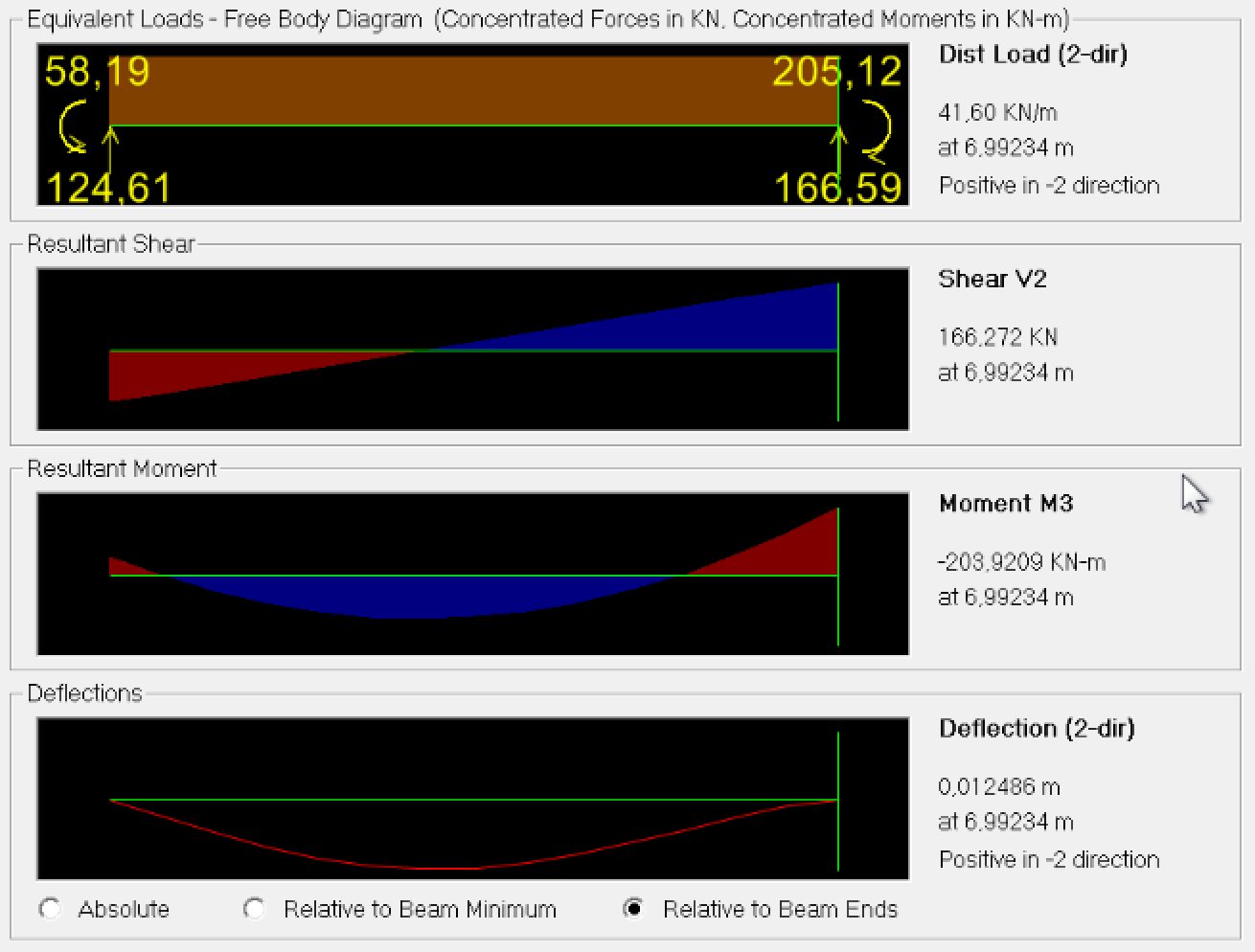
Fig.28b

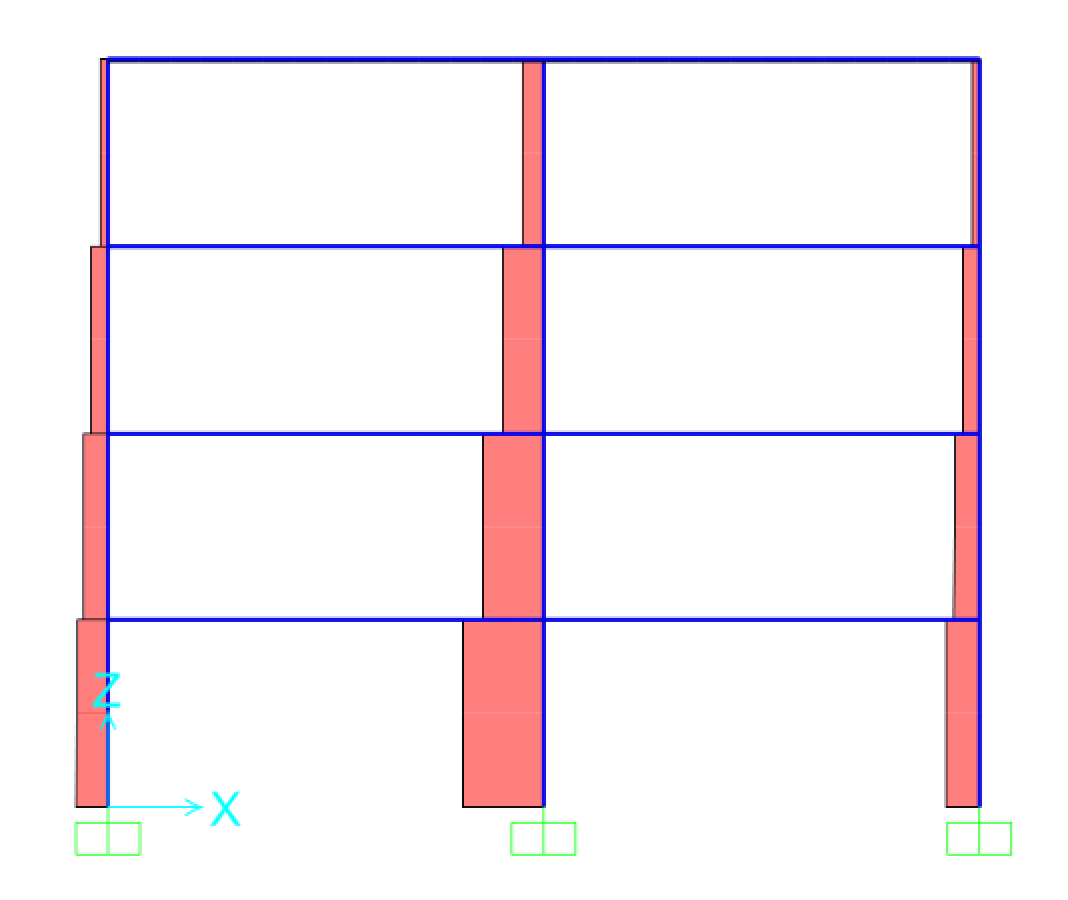Fig.29a

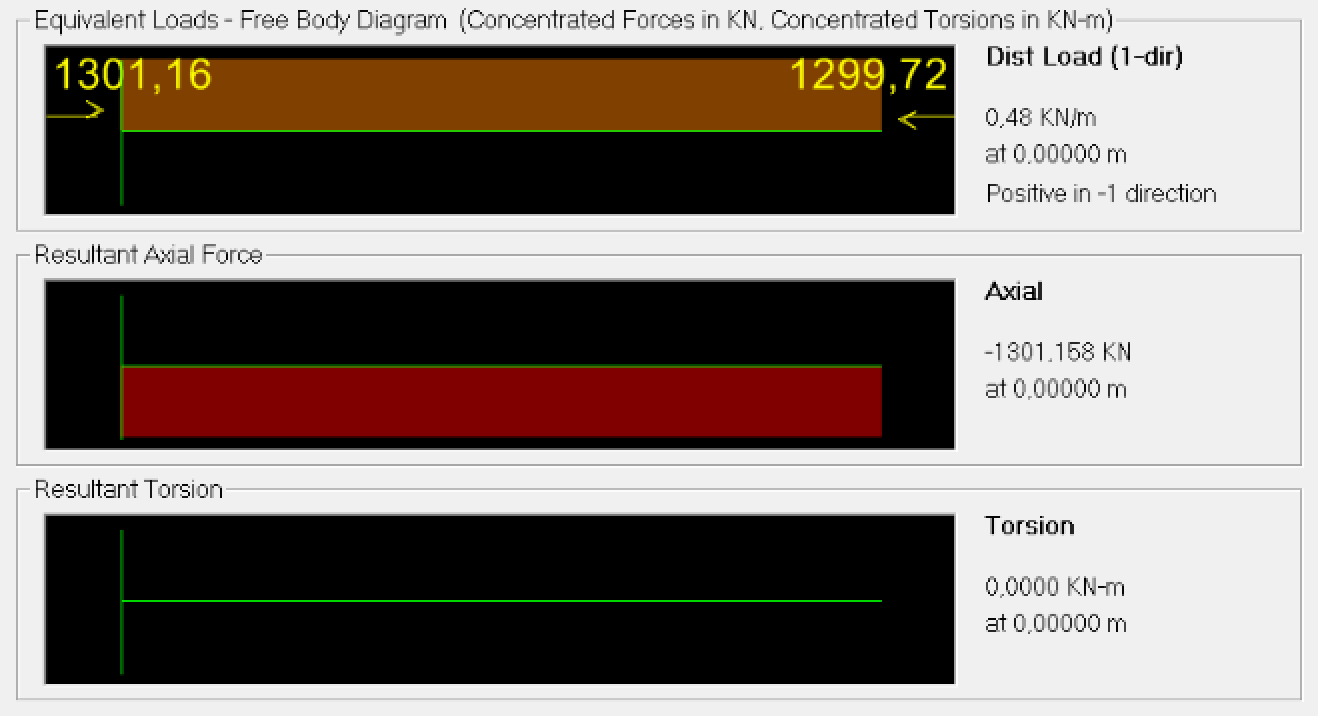
Fig.29b

 

Per verificare il dimensionamento del telaio, si riportano nei fogli di calcolo excel i valori massimi del momento e dello sforzo normale ricavati dall’analisi su SAP ed, eventualmente, si modificano le dimensioni delle sezioni delle travi (Fig.30) e dei pilastri (Fig.31) calcolate durante il predimensionamento.

Fig.30

Fig.31