TELAIO IN ACCIAIO
1)
Disegno il telaio della mia struttura, che avrà una luce massima di 8 m e un'altezza di tre piani.


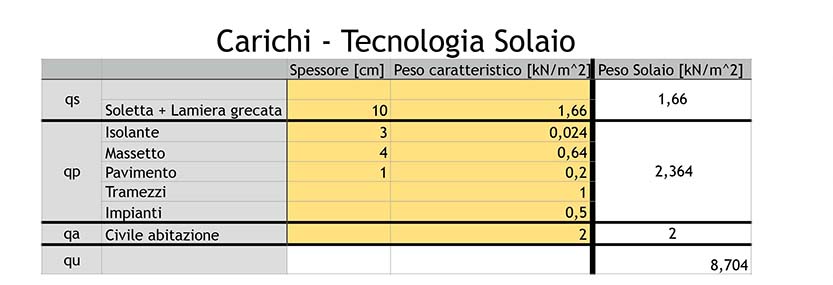
Scelgo la tecnologia del solaio, composta da travetti in travi di acciaio IPE140, sormontati da una pacchetto composto da una lamiera gregata e da una soletta. Il carico strutturale sarà calcolato dal prodotto tra volume e peso specifico dei materiali del solaio a metro quadro. 2)
qs=(V1* γ1 + ... + Vn* γn)*1/i
Il carico permanente sarà calcolat con lo stesso criterio, considerando la pavimentazione del solaio, isolante, massetto, pavimentazione, a cui saranno aggiunti i carichi di 1kN/m2 per i tramezzi, e di 0,5 kN/m2 per gli impianti.
Il dato del carico accidentale lo leggo sempre nella normativa vigente, e nel nostro caso è pari a 2 kN/m2
Posso trovare il qu, dalla seguente somma
qu=(1,3*qs+1,5*qp+1,5*qa)
il peso sarà maggiorato da coefficenti di sicurezza che mi obbligano ad aumentare il valore del mio peso considerato.
3)
Il peso a metro quadro del solaio, mi serve nel predimensionamento della trave, in quanto questo, moltiplicato per l'interasse di interessa e poi spalmato per la lunghezza della trave mi fornisce il carico distribuito sulla mia trave.
Per cui la prima operazione da fare sarà quella di trovare q, espresso in kN/m. Per calcolare il Momento massimo della trave, che considero come se fosse una trave doppiamente appoggiata, applicherò la formula
M=(q*l2)/8 (kN*m)
Una volta trovato M max, per scegliere il profilo più adeguato da utilizzare per predimensionare la mia trave, utilizzerò la formula fd=M/W , dove fd, è la tensione di progetto che io scelgo dal materiale. Nello specifico fd si calcola conoscendo la tensione di snervamento dell’acciaio prescelto,considerando di un coefficiente parziale di sicurezza γs, pari a 1,05.
fd=fk/1,05
In questo modo posso ricavare il modulo di resistenza a flessione
W=M/fd
scegliendo un W uguale o maggiore da una tabella di profilati IPE, avrò ottenuto un primo dimensionamento della mia trave.

4)
Il dimensionamento del pilastro parte da ragionamenti simili, in questo caso conosco già il peso del mio solaio e metro quadro, e devo fissare altri valori. Primo tra tutti l'area di influenza del solaio sul pilastro più sollecitato, che per l'appunto sarà quello su cui grava un'area di influenza maggiore. Avendo poi scelto una trave, aggiungo al peso qu, anche il peso lineare della trave scelta, moltiplicato per i metri degli interassi all'interno sempre dell'area di influenza interessata.
Ora, conoscendo anche il numero dei piani, posso calcolare lo sforzo N del pilastro più sollecitato con la seguente formula
Nmax=((qu*Ainf)*qt)*np
Trovato lo sforzo normale, posso trovare una prima area minima con la seguente formula
Amin=Nmax/fd
Tuttavia, l'area di questo pilastro terrebbe conto solo della compressione esercitata sul pilastro, e non della flessione a cui questo viene sottoposto con un carico verticale. Per non ovviare a questo problema, dovrò quindi tenere conto anche del carico critico Euleriano, e di conseguenza non avrò solo un'area minima, ma anche un'altro valore, cioè, quello del momento di inerzia minimo affinché la sezione del pilastro consenta a quest'ultimo di resistere a flessione.
Sapendo che la formula del momento di inerzia minimo è la seguente, posso calcolarlo, sapendo che y è un coefficiente di sicurezza, E il modulo elastico, e l0, la lunghezza libera di inflessione, che conosco conoscenso i vincoli agli estremi del mio pilastro.
Jmin > N*l0/γ*π^2*E
Altro valore da tenere in considerazione è il raggio di inerzia minimo che ricavo conoscendo l0 e la snellezza, in quanto la snellezza λ è il raggorto tra la lunghezza libera di inflessione e il raggio di inerzia minimo. E sapendo che la normativa mi impone di porre λ non minore di 200, scrivo:
imin > 200/l0
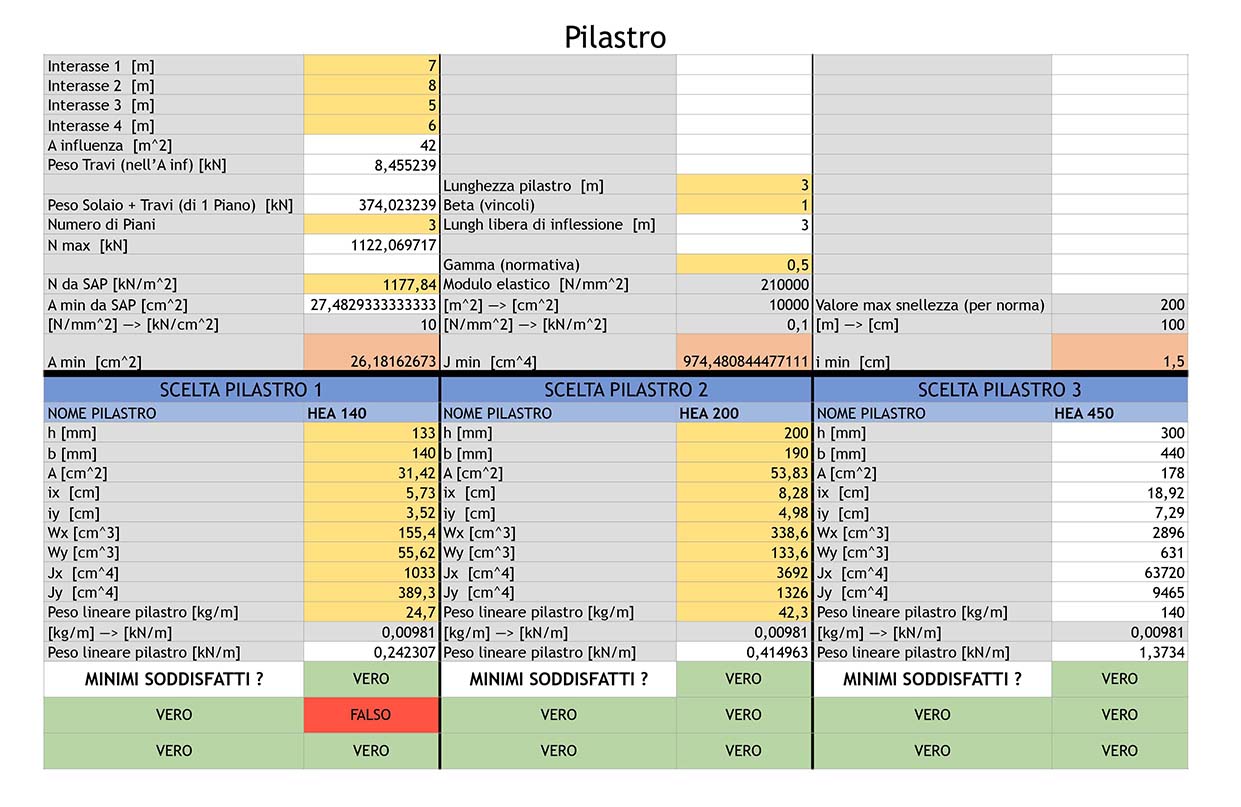
Dalla scelta del momento di inerzia minimo, scelgo nella tabella, il pilastro HEA con le caratteristiche corrispondenti ai tre valori minimi che devo soddisfare.
Il primo pilastro scelto, HEA140, tuttavia non soddisfa uno dei valori richiesti, come si vede nella figura 04.
Si passa alla scelta di un secondo pilastro, HEA200, che apparentemente soddisfa le nostre richieste prestazionali.
5)
Passo alla fase in cui devo verificare se effettivamente gli elementi strutturali predimensionati soddisfano o meno le reali richieste prestazionali.
per la trave utilizzo la formula
σ=Mmax/W
La trave è verificata se fd, cioè la tensione di progetto è maggiore della tensione trovata
fd>σ
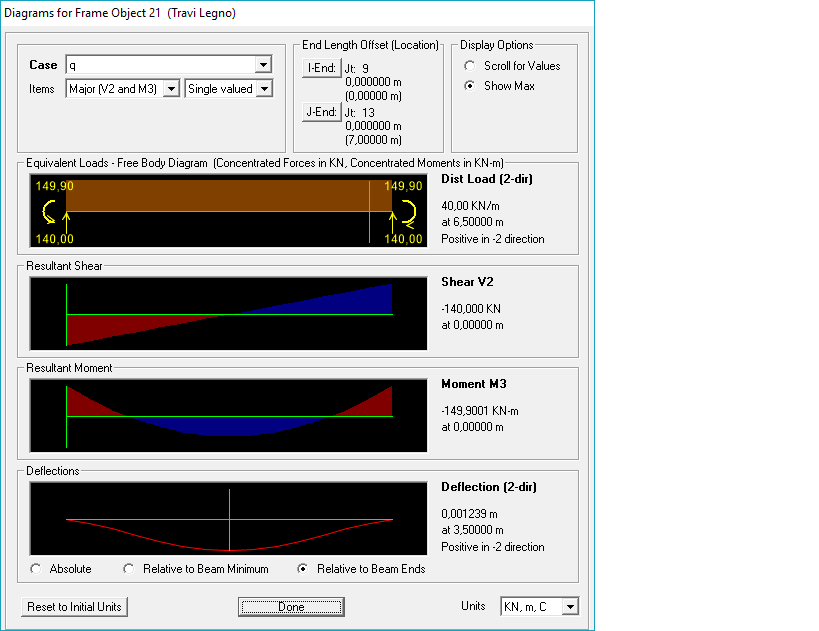
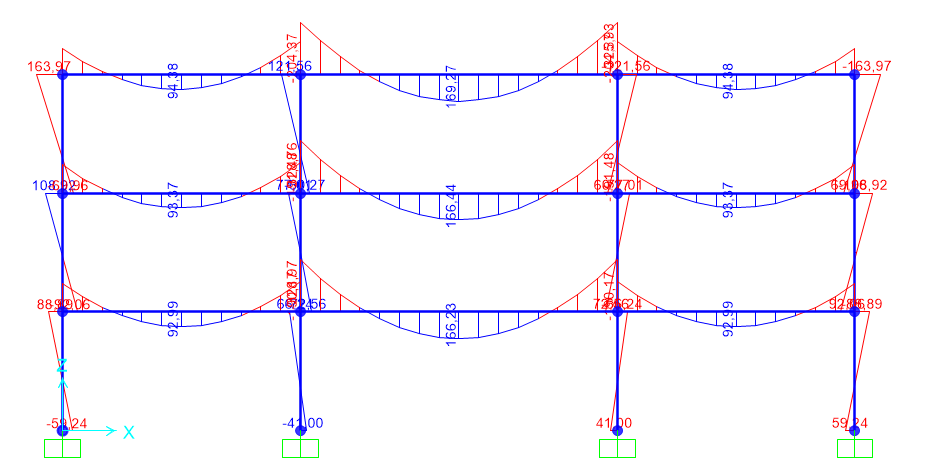
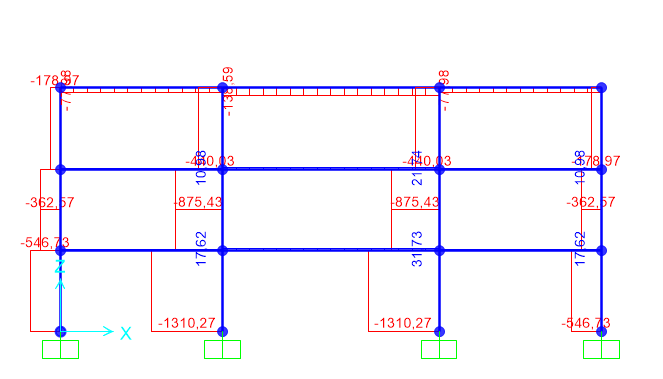
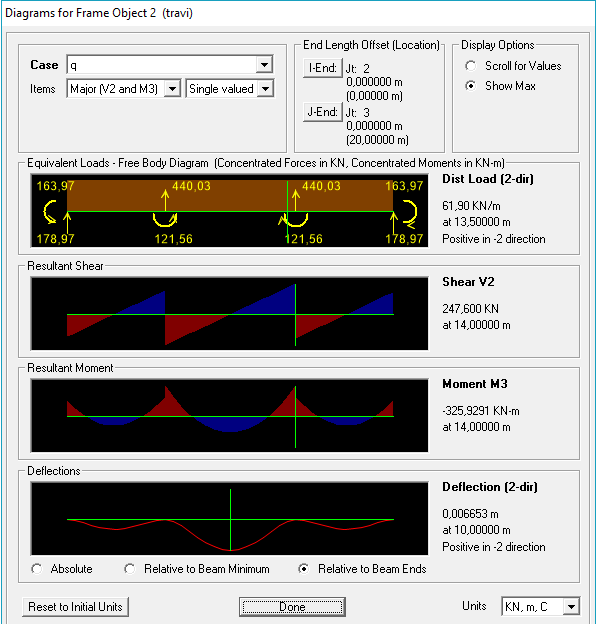
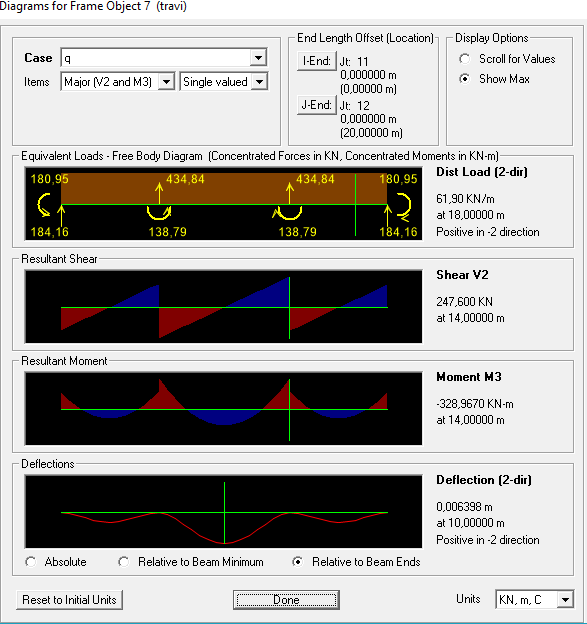
Nel nostro caso la trave è stata sovradimensionata, avendo considerato un momento massimo, quello della trave doppiamente appoggiata, di molto superiore al momento massimo reale trovato su sap, corrispondente al modello di una trave a doppio incastro.
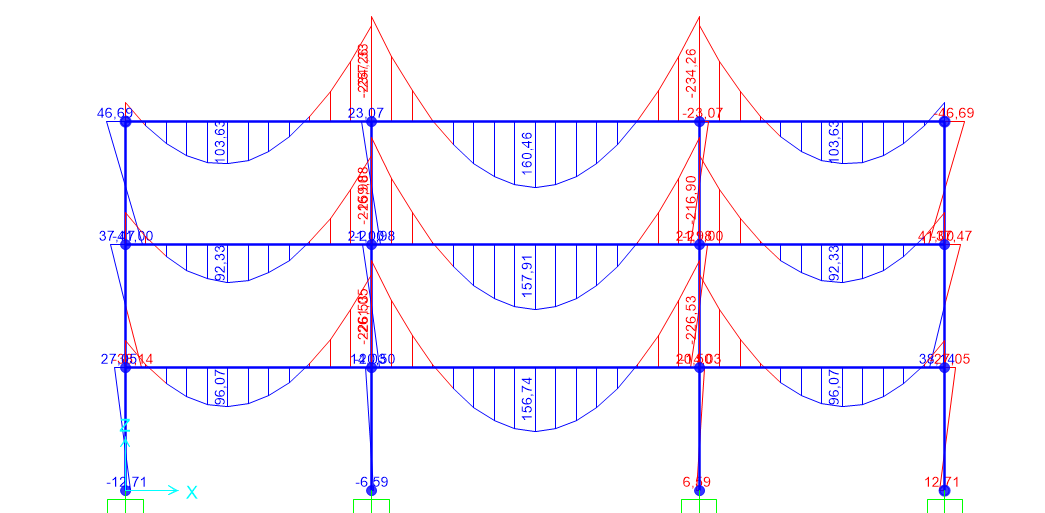
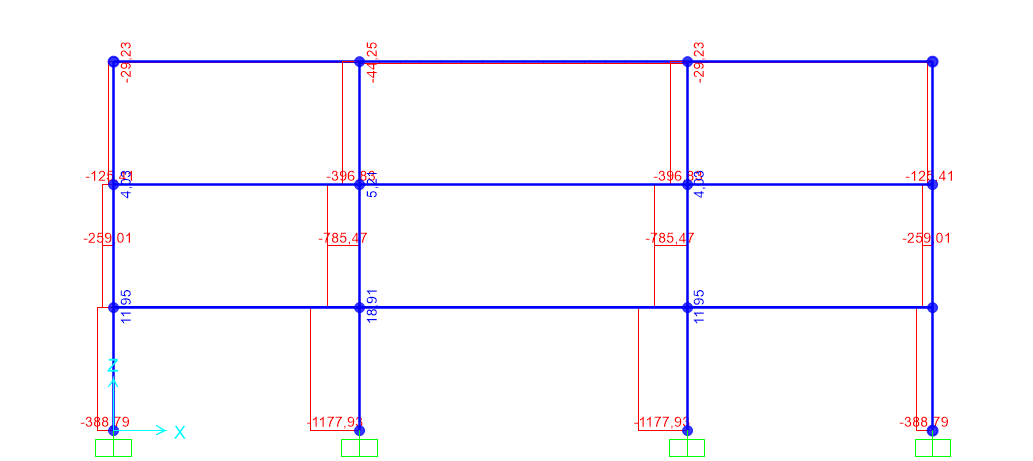
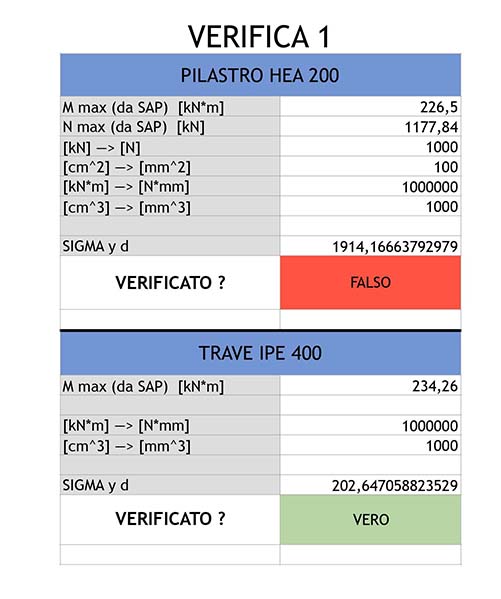
La verifica per il pilastro utilizza invece la seguente formula dovendo tener conto sia dello sforzo normale sia della flessione
σ=(Nmax/Ad)+(Mmax/W)
Il pilastro preso in considerazione non soddisfa la verifica, in quanto σ>>fd
Si cambiano quindi i paramenti presi in considerazione per il dimensionamento del pilastro, fino a trovare uno adeguato.

TELAIO IN LEGNO
1) Disegno il mio telaio, che avrà una luce massima di 7 m e un'altezza di tre piani.
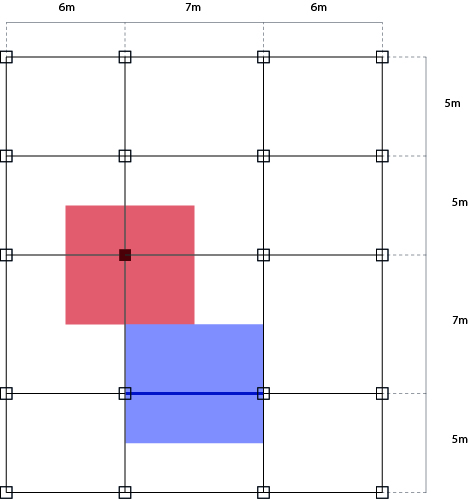
2) Scelgo la tecnologia del mio solaio come fatto precedentmente e calcolo il suo carico
qs=(V1* γ1 + ... + Vn* γn)*1/i

Vi aggiungo i carichi permanenti e accidentali, e trovo qu sommando.
qu=(1,3*qs+1,5*qp+1,5*qa)
3) Con il qu, moltiplicato per l'interasse, posso trovare M max della trave, considerandola sempre come se fosse una trave doppiamente appoggiata
M=(q*l2)/8 (kN*m)
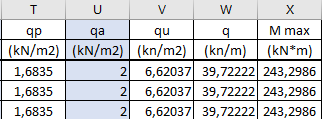
4) Per dimensionare la sezione della trave necessaria, devo applicare al seguente formula
h= l * ((3/4)*q/(b*fd))^0,5
Ho tutte i dati, la base la inserisco io come variabile, mentre fd, è la tensione di progetto, che ricavo dalla scelta del materiale. Nello specifico dalla sua tensione caratteristica, con la seguente formula:
fd=kmod*fk/γ
dove kmod è un coefficiente che tiene conto del tempo, quindi dell'agire di alcune condizioni quali l'umidità sulla resistenza del materiale, pari a 0,8, mentre gamma è un'altro coefficiente di sicurezza, pari a 1,5.
Fissata la mia base, trovo la rispettiva altezza, e le ingegnerizzo per ricavare una trave reale.
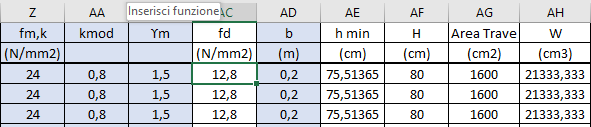
5) Per il dimensionamento dei pilastri, si seguono gli stessi criteri di cui ci siamo serviti per predimensionare il pilastro in acciaio, quindi considereremo la resistenza sia a compressione, sia a presso/flessione.
Considero quindi l'area minima necessaria ricavando lo sforzo N massimo, che trovo con la somma:
Nmax = ((qu*Ainf) + qt)* np
Dove qt è il peso delle travi, e np, il numero di piani del mio edificio.
Da qui trovo l'Area minima per resistere alla compressione

Diverso è il caso, analogamente per il primo calcolo che abbiamo considerato per la struttura in acciaio, per determinare l'area necessaria, in funziona del momento di inerzia minimo della sua sezione, nel caso in cui consideriamo il pilastro flettersi per effetto della compressione di punta esercitato su di esso.
considero per ricavare il mio momento di inerzia necessario, il raggio minimo di inerzia, che desumo dalla formula:
ρmin=l0/λ
dove l0 è la lunghezza libera di inflessione, seguendo gli stessi ragionamenti per l'acciaio.
Posso allora ricavare λ dalla seguente formula:
λ=π *(E/fd)^0,5
I restanti dati, sono dati che conosco e che determino io.
conoscendo quindi il raggio minimo di inerzia, posso desumere la base, quindi il lato più corto del pilastro, necessario per raggiungere l'area interessata.
b=2*((3)^0,5)*ρmin
Ora posso trovare l'altro lato, mettendo in rapporto tra loro l'area trovata inizialmente e la base.

6)
Una volta trovati su sap i momenti massimi reali, faccio la verifica tensionale, utilizzando le stesse formule usate per il dimensionamento del telaio in acciaio, e se le sezioni non sono verificate, le cambio fino ad ottenere un risultato corretto.



TELAIO IN C.A.
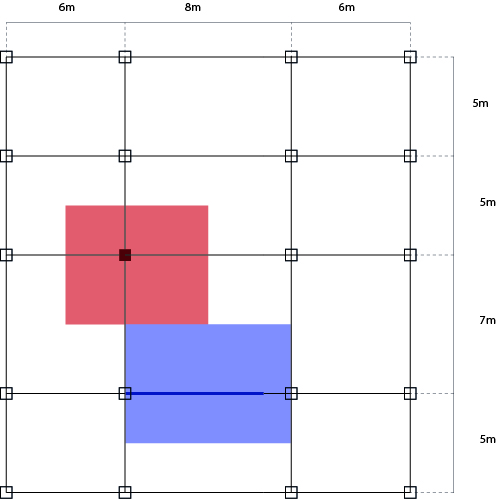
1) Si parte come nei casi precedenti dal disegno del telaio, che in pianta avrà le seguenti dimensioni.
2) Scelgo la tecnologia del mio solaio come fatto precedentmente e calcolo il suo carico
qs=(V1* γ1 + ... + Vn* γn)*1/i
Vi aggiungo i carichi permanenti e accidentali, e trovo qu sommando.
qu=(1,3*qs+1,5*qp+1,5*qa)

3) Con il qu, moltiplicato per l'interasse, posso trovare M max della trave, considerandola sempre come se fosse una trave doppiamente appoggiata
M=(q*l2)/8 (kN*m)
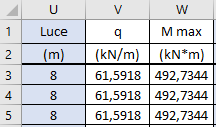
4) Il dimensionamento della trave, cambia di impostazione rispetto a quella applicata nel caso del telaio di legno Nel caso del calcestruzzo, ho più variabili da considerare, date dal fatto anche che sono in presenza di due materiali aventi caratteristiche differenti tra loro, e tensioni caratteristiche peculiari.
La formula dell'altezza di una sezione di trave in calcestruzzo è infatti la seguente:
h=( M/(r*fcd*b/2))^0,5
dove M è il momento massimo, fcd la tensione di progetto, che nel caso del calcestruzzo armato calcolo con la seguente:
fcd=fck*0,85/1,5
mentre r è un valore adimensionale dato dalla seguente formula:
r =α*(1-(α/3))
e α, è un altro valore adimensionale dato da uno specifico rapporto tra le tensioni di progetto dei materiali componenti il c.a.
α= (fcd/E)/(fcd/E)+(fyd/E)
Conoscendo i seguenti valori, e imponendo una base, posso ricavare un'altezza per la mia sezione a cui dovrò aggiungere lo spessore del copriferro, e ingegnierizzando i valori avrò ottenuto il predimensionamento della trave.

5) Per il dimensionamento dei pilastri, si seguono gli stessi criteri di cui ci siamo serviti per predimensionare il pilastro in legno, quindi considereremo la resistenza sia a compressione, sia a presso/flessione.
Considero quindi l'area minima necessaria ricavando lo sforzo N massimo, che trovo con la somma:
Nmax = ((qu*Ainf) + qt)* np
Dove qt è il peso delle travi, e np, il numero di piani del mio edificio.
Da qui trovo l'Area minima per resistere alla compressione
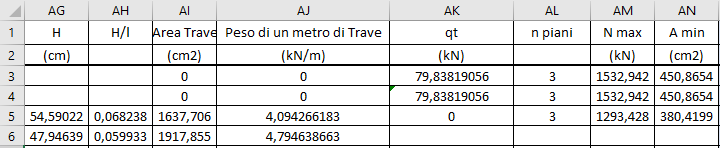
Diverso è il caso, analogamente per il primo calcolo che abbiamo considerato per la struttura in legno, per determinare l'area necessaria, in funziona del momento di inerzia minimo della sua sezione, nel caso in cui consideriamo il pilastro flettersi per effetto della compressione di punta esercitato su di esso.
considero per ricavare il mio momento di inerzia necessario, il raggio minimo di inerzia, che desumo dalla formula:
ρmin=l0/λ
dove l0 è la lunghezza libera di inflessione, seguendo gli stessi ragionamenti per l'acciaio.
Posso allora ricavare λ dalla seguente formula:
λ=π *(E/fd)^0,5
I restanti dati, sono dati che conosco e che determino io.
conoscendo quindi il raggio minimo di inerzia, posso desumere la base, quindi il lato più corto del pilastro, necessario per raggiungere l'area interessata.
b=2*((3)^0,5)*ρmin
Ora posso trovare l'altro lato, mettendo in rapporto tra loro l'area trovata inizialmente e la base.

6) Una volta trovati su sap i momenti massimi reali, faccio la verifica tensionale, utilizzando le stesse formule usate per il dimensionamento del telaio in acciaio, e se le sezioni non sono verificate, le cambio fino ad ottenere un risultato corretto.

Commenti recenti