Esercitazione 1 :
Travatura reticolare simmetrica (metodo di Ritter)
Trovare il valore delle reazioni vincolari e disegnare i diagrammi delle sollecitazioni agenti sulla trave:
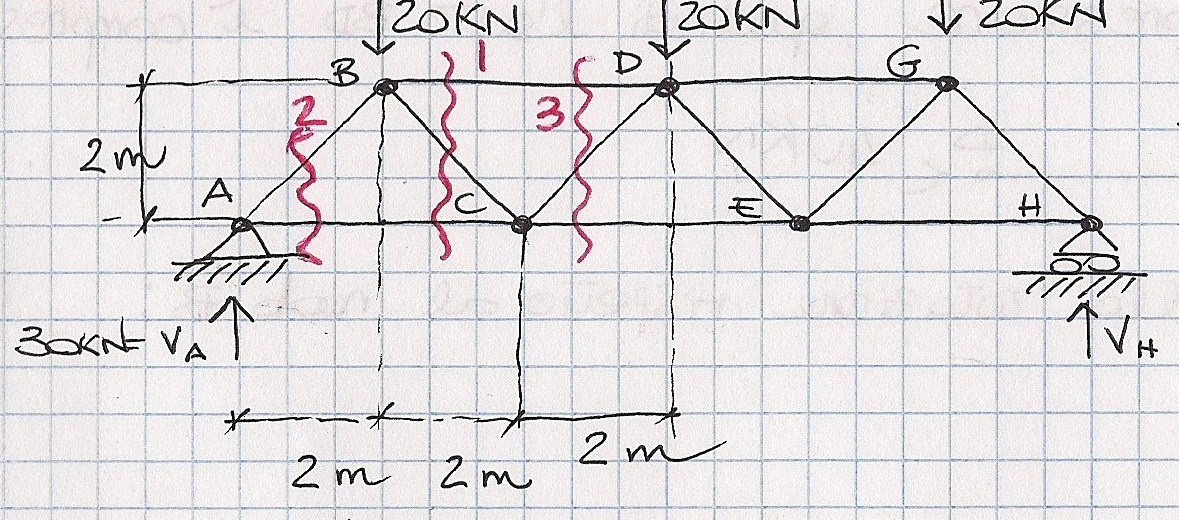
Per cominciare l'analisi della struttura occorre verificare che la trave sia isostatica, ovvero il numero dei vincoli esterni rispetto al numero dei nodi deve rispettare la seguente relazione:
Ve+a(numero aste) = 2nodi
3+11=14 ; dunque è verificato.
Si procede quindi con l'individuazione del verso e del modulo delle reazioni vincolari:
Imponendo l'equilibrio alla traslazione verticale
Σfy=0
Va+ Vb = 3F Va = Vb = 3/2 F
Poiché la struttura è simmetrica non devo calcolare il momento rispetto al polo A o al polo B per determinare le reazioni vincolari.
Una volta trovate le reazioni si procede con l'analisi delle aste (che possono essere tese o compresse, poiché in una struttura reticolare agisce solo la forza normale di trazione o di compressione).
Utilizziamo il metodo di Ritter (metodo che, attraverso un taglio ci permette di analizzare le forze interne di ciascuna asta):
Considero la sezione 1(ipotizzo tutte e tre le aste tese):
.jpeg)
Calcolo N1, N2, N3
Per farlo, impongo la condizione di equilibrio alla rotazione rispetto al nodo C :
ΣMc= 0
-3/2F2L + FL - N1L = 0
da cui N1 = -2FL, dunque di compressione(poiché di verso opposto a quello ipotizzato).
quindi l'asta BD risulta compressa.

Per trovare N3 impongo la condizione di equilibrio alla rotazione rispetto al nodo B:
ΣMb= 0
-3/2FL + N3L = 0
da cui N3 = 3/2 F, dunque di trazione (come da ipotesi), quindi l'asta AC risulta tesa.
.jpeg)
Per detrminare N2 impongo l'equilibrio alla traslazione verticale, scomponendo N2 secondo le diagonali:
Σfy=0
3/2F - F - N2√2/2 = 0
N2 = F√2/2, di trazione(come da ipotesi), dunque l'asta BC risulta tesa.
.jpeg)
Ridisegno la sezione 1 con i versi delle forze trovate:
.jpeg)
Ora considero la sezione 2(ipotizzo l'asta AB tesa):
.jpeg)
Impongo l'equilibrio alla traslazione orizzontale :
Σfx=0
30KN + N4√2/2 = 0
N4 = -30√2/2 = -30KN√2, dunque di compressione, quindi l'asta AB risulta compressa:
.jpeg)
Considero la sezione 3 :
.jpeg)
Impongo l'equilibrio alla rotazione rispetto al nodo D:
ΣMd= 0
N52m + 20KN4m -30KN6m = 0
N5 = 50 KN, dunque di trazione, quindi l'asta CE risulta tesa :
.jpeg)
Impongo l'equilibrio alla traslazione verticale :
Σfy=0
N6√2/2 + 30KN -20KN = 0
N6 = -10√2 KN, dunque di compressione, quindi l'asta CD risulta compressa.
.jpeg)
Poiché la struttura è simmetrica, mi basta aver calcolato le forze agenti sulla prima metà della trave.
Per concludere rappresento il grafico delle sollecitazioni normali che agioscono sulla trave:
.jpeg)
Verifica con SAP
Una volta trovate le sollecitazioni si esegue la verifica con SAP:
Si assegnano i carichi puntuali sui nodi del corrente superiore:

Mando l'analisi e ottengo la deformata:

Ottengo in seguito il diagramma delle sollecitazioni numerico e grafico :

Travatura reticolare asimmetrica (metodo dei nodi)
Trovare il valore delle reazioni vincolari e disegnare i diagrammi delle sollecitazioni agenti sulla trave.

Occorre verificare che la struttura sia isostatica, ovvero il numero dei vincoli esterni rispetto al numero dei nodi deve rispettare la seguente relazione :
Ve + a (numero aste) = 2 nodi
3 + 11 = 14, è verificato.
A questo punto si trovano le reazioni vincolari facendo l’equilibrio alla traslazione verticale e l’equilibrio dei momenti rispetto al nodo A. Si ricavano quindi la reazione verticale e orizzontale dell’appoggio e la reazione orizzontale del carrello.
ΣFy = 0
VB – F –F = 0 VB = 2F
ΣMA = 0
uBl – Fl –2Fl = 0 uB = 3F = uH

Si ricavano le azioni di contatto utilizzando il metodo dei nodi, ovvero facendo l’equilibrio delle sole forze verticali e orizzontali rispetto al nodo, per ottenere lo sforzo assiale che agisce sulla cerniera. Occorre analizzare tutti i 7 nodi presenti, non essendo questa una struttura simmetrica.

Dall’analisi del nodo A si evince come entrambe le aste che arrivano in esso sono scariche. N1 = N2 = 0
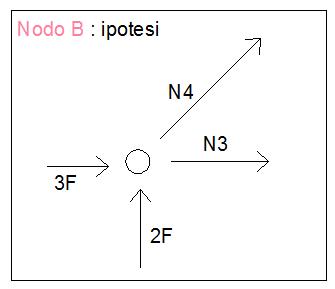
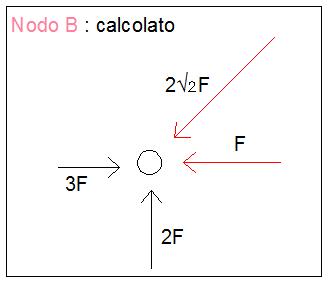
Dall’equilibrio delle forze verticali al nodo B si ricava lo sforzo assiale N4 = - 2√2 F e lo sforzo assiale N3 = -F. Dunque il verso precedentemente ipotizzato è errato, l’asta BC e l’asta BD infatti non sono tese ma compresse.
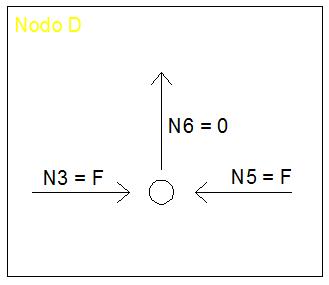
Dall’analisi al nodo D si ricavano la forza assiale N6 = 0 (poiché non ci sono forze verticali) e N5 = F.


Dall’analisi al nodo C si ricavano N7 = 3F e N8 = √2 F. N7 è stata ipotizzata nel verso sbagliato, l’asta CE risulta dunque compressa.

Dall’analisi del nodo E si ricavano N9 = 3F e N10 = F
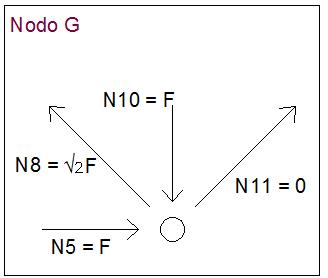
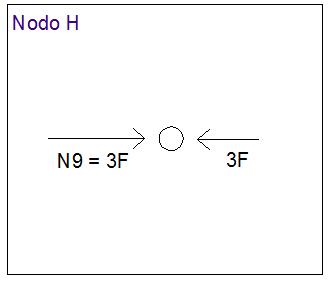
Dall’equilibrio al nodo G e H si evince come l’asta GH sia scarica(N11 = 0), poiché il nodo risulta già equilibrato dalle altre forze agenti.
La struttura presenta così tutte le aste compresse tranne l’asta CG che risulta tesa.
Attraverso il software di SAP si analizza la struttura per visualizzarne il diagramma degli sforzi assiali presenti:
Mediante l’aiuto della griglia si disegnano le aste della struttura :

Dopo aver selezionato i punti di appoggio si assegnano i vincoli : un appoggio e un carrello.
Successivamente si seleziona l'inera struttura per il rilascio dei momenti flettente e torcenre nei nodi.

A questo punto è possibile creare il carico F e assegnarlo nei nodi superiori.

Ora è possibile lanciare l'analisi e osservare la deformata :

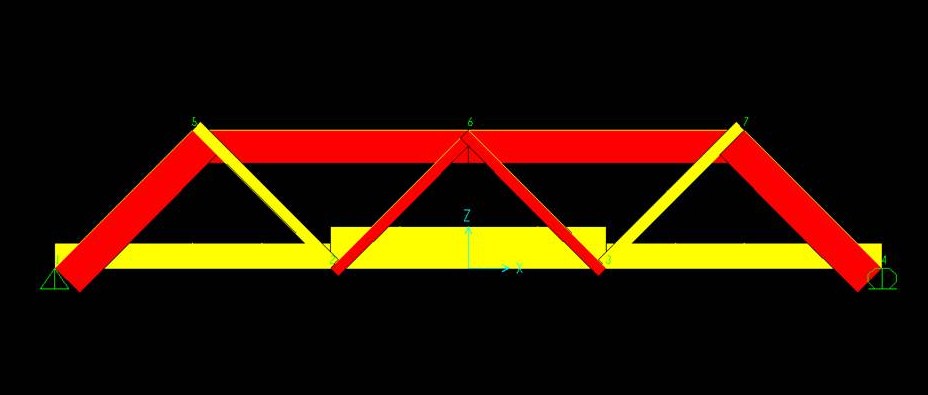
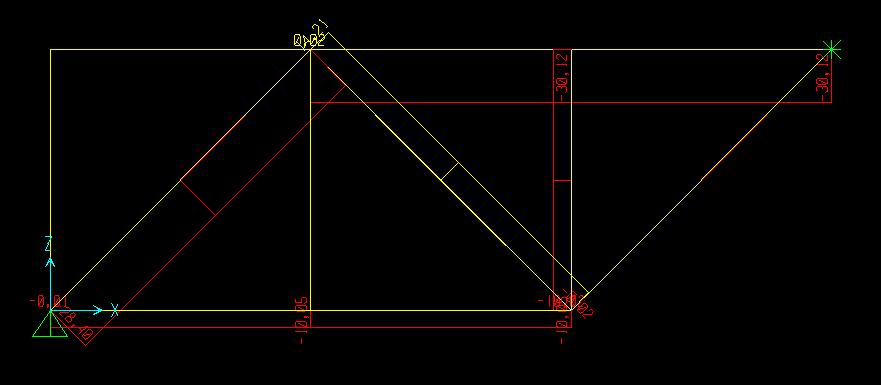
Dal diagramma degli sforzi assiali si osserva quanto già affermato, ovvero che l'unica asta tesa è la diagonale CG (in giallo) :

Assumendo la forza F = 10 del carico assegnato, si osserva lo stesso diagramma ma con i valori dei songoli sforzi interni :
Esercitazione 2
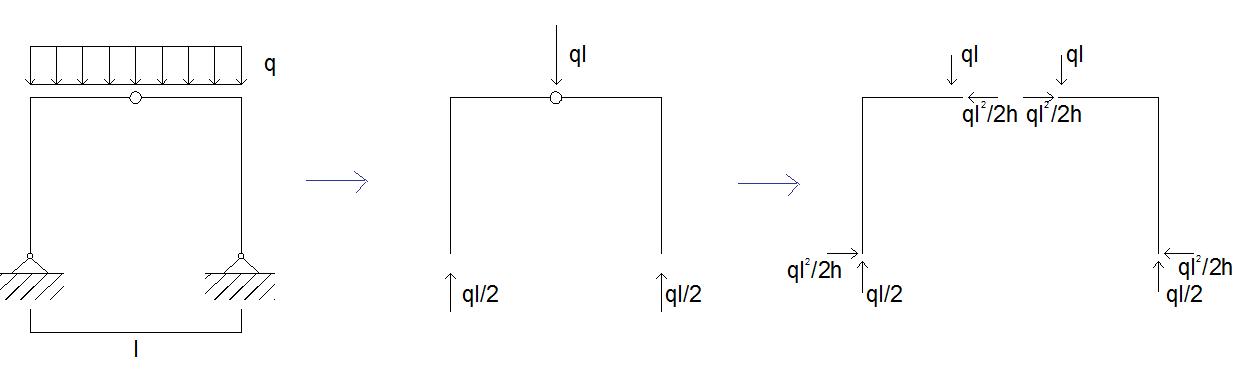
Arco a tre cerniere non allineate (SAP)
Si analizza il portale in figura,precedentemente risolto manualmente dal punto di vista statico, detto arco a tre cerniere non allineate (se fossero allineate sarebbe un arco degenere) mediante il software di SAP, per verificarne la deformata e i diagrammi delle sollecitazioni (Normale,Taglio,Momento).
Si disegna la struttura avvalendosi dell'uso di una griglia di partenza e assegnando il numero di campate e la distanza fra queste:

Una volta comparsa la griglia si disegna sulla stessa mediante il comando linea i diversi tratti del portale, fino ad ottenere la struttura desiderata

Si selezionanop quindi i punti di appoggio per assegnare i vincoli (traslazione verticale e orizzontale bloccata) assign>joint>restraints . Si rilascia il momento flettente nella prima asta orizzontale dopo averla selezionata. (assign>frame>releases/partial fixity > moment 33 end, che indica la fine dell’asta).Infine si rilascia il momento anche nella seconda, ma all'inizio di questa(moment 33 start). I vincoli saranno così configurati :

Una volta definita la forza agente sull'arco di -40 KN verso il basso distribuita si seleziona l'intera struttura e si assegna il carico:
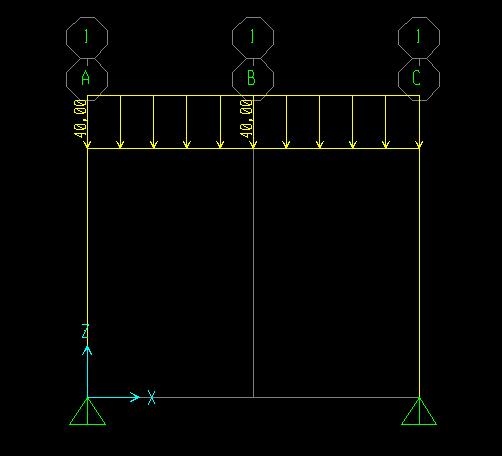
A questo punto è possibile lanciare l'analisi, ricordandosi di spuntare nella lista delle forze agenti sulla struttura quelle date da default nel programma (DEAD e MODAL) in modo che non vengano visualizzate.Si ottiene dunque la deformata :

I diagrammi delle sollecitazioni N,T,M rispettivamente :
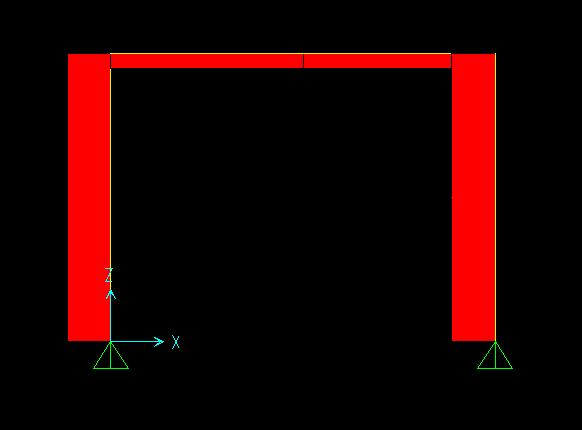
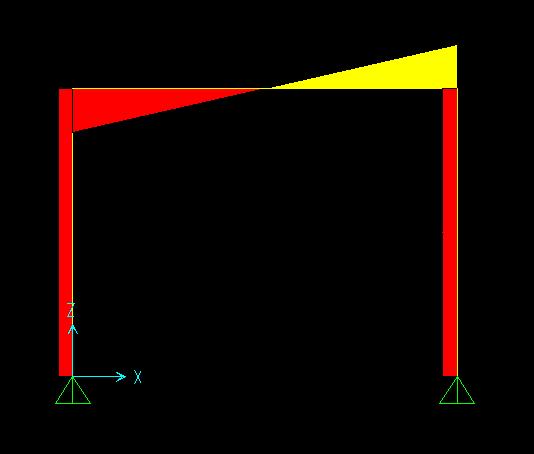

Esercitazione 3 (con Giulia Savarese):
Dimensionamento travi (mediante foglio di calcolo excel)
L'esercitazione prevede il dimensionamento di una trave in 3 diversi materiali : legno, acciaio e calcestruzzo.
Il progetto scelto è quello di case a schiera a Fiumicino su due piani con modulo 6m x 12m.
La pianta del solaio intermedio mostra la trave scelta che risulta doppiamente appoggiata e quindi con un momento massimo pari a ql2/8.

LEGNO

Dimensionamento travetto in legno
Calcolo carichi permanenti:
-Carico strutturale qs
Tavolato in castagno : 840 Kg/m3(Peso specifico ) x 0,03 m (Spessore) = 25,2 Kg/m2 ----> 0,25 KN/m2
-Carico non strutturale qp
Massetto : 2000 Kg/m3 x 0,05 m = 100 Kg/m2----> 1 KN/m2
Parquet in rovere : 720 Kg/m3x 0,02 m = 14,4 Kg/m2---->0,144 KN/m2
Incidenza tramezzi : 1KN/m2
Incidenza impianti : 0,5 KN/m2
qp = 1 KN/m2 + 0,144 KN/m2 + 1KN/m2 + 0,5 KN/m2 = 2,644 KN/m2
Calcolo carichi accidentali :
Destinazione d’uso abitativa : qa = 2 KN/m2
Dati:
Legno GL28h ---->fk = 28 MPa
Interasse = 0,9 m
Luce = 3 m
b = 0,1 m

L'altezza minima dei travetti in legno è di 17, 65, arrotondando la sezione risulta 10 cm x 20 cm.
Dimensionamento trave in legno
Calcolo carichi permanenti:
-Carico strutturale
Travetti in legno: 500 Kg/m3 x 0,1 x 1 = 50 Kg/m2---->0,5 KN/m2
Tavolato 0,25 KN/m2
qs = 0,5 KN/m2 + 0,25 Kn/m2 = 0,75 KN/m2
-Carico non strutturale
qp = 2,644 KN/m2
Calcolo carichi accidentali
qa = 2 KN/m2
Dati:
Legno GL28h----> fk = 28 MPa
Interasse = 3 m
Luce = 6 m
b = 0,2 m

L'altezza minima della trave è di 47, 81 m, arrotondando la sezione risulta 50 cm x 20 cm.
ACCIAIO

Dimensionamento trave IPE in acciaio
Calcolo carichi permanenti
-Carico strutturale
Lamiera grecata
Si è scelta una lamiera di 0,075 m di altezza per un totale di 0,13 m considerando anche il getto di calcestruzzo.
Il peso totale è 2,00 KN/m2

-Carico non strutturale
Isolante termoacustico 360 Kg/m3 x 0,01 m = 3,6 Kg/m2 ----> 0,036 KN/m2
Massetto 2000 Kg/m3 x 0,04 m = 80 Kg/m2 ----> 0,8 KN/m2
Piastrelle in Gres Porcellanato 1540 Kg/m3 x0,013 m = 20 Kg/m2---->0,2 KN/m2
Controsoffitto 800 Kg/m3 x 0,03 m = 24 Kg/m2 ---->0,24 KN/m2
Incidenza tramezzi : 1KN/m2
Incidenza impianti : 0,5 KN/m2
qp = 0,036 KN/m2 + 0,8 KN/m2 + 0,2 KN/m2 + 1KN/m2 + 0,5 KN/m2 = 2, 536 KN/m2
Calcolo carichi accidentali
Destinazione d’uso abitativa : qa = 2 KN/m2

Wx trovato = 350, 51 cm3
Si adotta un profilo IPE 270 con Wx = 429 cm3
CALCESTRUZZO ARMATO

Dimensionamento trave in cls
Calcolo carichi permanenti
-Carico strutturale
Travetti 2500 Kg/m3 x 0,18 m x 0,1 m = 45 Kg 0,45 KN x 2 (n° travetti in 1 m2)= 0,9 KN/m2
Pignatte 550 Kg/m3 x 0,18 m x 0,4 m = 40 Kg 0,4 KN x 2 (n° pignatte in 1 m2) = 0,8 KN/m2
Caldana 2500 Kg/m3 x 0,04 m = 1 KN/m2
qs = 0,9 KN/m2 + 0,8 KN/m2 + 1 KN/m2 = 2,7 KN/m2
-Carico non strutturale
Massetto 2000 Kg/m3 x 0,04 m = 80 Kg/m2----> 0,8 KN/m2
Isolante termoacustico 360 Kg/m3 x 0,01 m = 3,6 Kg/m2 ---->0,036 KN/m2
Piastrelle in Gres Porcellanato 1540 Kg/m3 x0,013 m = 20 Kg/m2---->0,2 KN/m2
Intonaco 200 Kg/m3 x 0,01 m =2 Kg/m2---->0,02 KN/m2
qp = 0,8 KN/m2 + 0,036 KN/m2 + 0,2 KN/m2 + 0,02 KN/m2 = 1,056 KN/m2
Dati :
Calcestruzzo C 25/30
fck = 30 MPa
base = 25 cm
copri ferro = 3 cm

L'altezza utile della trave risulta 28,8 cm + copriferro (3cm) = 31, 8 cm ----> 35 cm.
Esercitazione 4 :
Travatura reticolare spaziale : rappresentazione, analisi e dimensionamento
-
Rappresentazione (Autocad)
Per la prima fase ci si avvale dell’utilizzo di Autocad. Si disegna una polilinea su un layer che chiameremo “aste” tale da configurare il modulo base della reticolare, ovvero 2m x 2m x 2m.
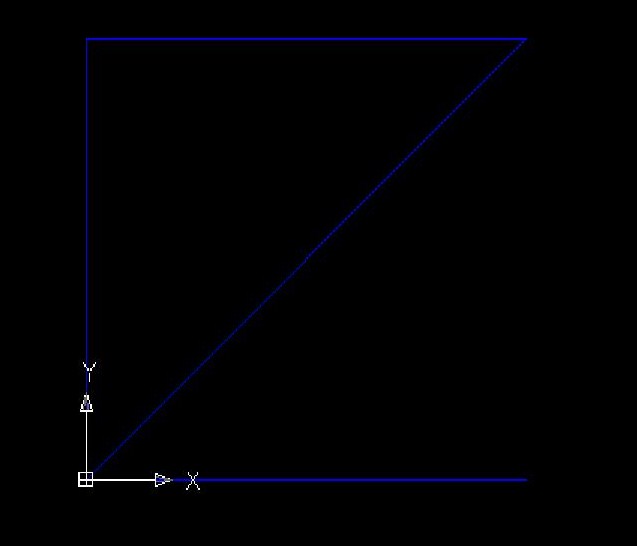
Successivamente ci si sposta in tre dimensioni e si ruota l’UCS, disponendo il modulo lungo l’asse x per poterlo replicare con il comando array.

Lo riproduciamo 4 volte, con distanza tra le colonne di 2 m.

Chiudiamo quindi la prima serie, che è rimasta aperta, con una linea e procediamo alla serie successiva.

Si disegna il modulo base delle 3 aste e diagonale anche nella direzione dell’asse y e si riproduce in serie nello stesso modo usato precedentemente( con il comando serie/array); e’ necessario cambiare l’UCS, mettendo l’asse X lungo la direzione del nuovo array (UCS > invio > seleziona origine > seleziona direzione asse x > seleziona direzione asse y).
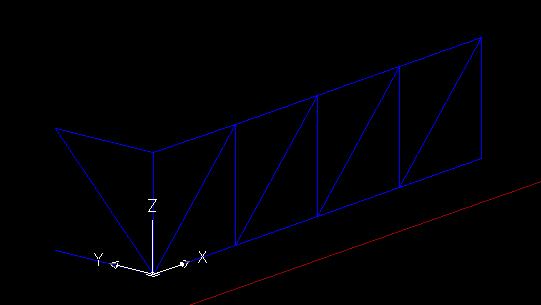

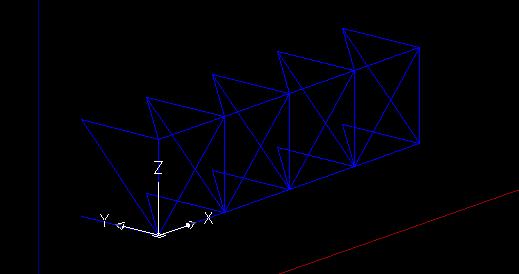
Per terminare la prima campata occorre disegnare le aste oblique superiori e inferiori.
Si procede con il completamento della struttura mediante la riproduzione seriale dell’intera riga appena disegnata.Questa volta ruotiamo l’UCS in modo da poter riprodurre la nostra struttura in senso ortogonale al precedente. Sempre mediante il comando array riproduciamo l’oggetto per 7 volte.

La settima fila, rimasta aperta, verrà poi eliminata, in modo da ottenere una piastra 6 x 4 moduli come desiderato.

Ora che si è disegnata la struttura, si esporta in formato .dxf , compatibilmente al software di SAP.
2. Analisi (SAP)
Verificato di utilizzare lo stesso layer “aste” , che si seleziona durante l’importazione del file(vedi immagine successiva) e la stessa unità di misura KN, m, C, si procede assegnando i vincoli ai 4 spigoli inferiori, ovvero 4 appoggi.( assign >joint> restraints, e selezionando il comando di appoggio >traslation 1,2,3);


Si ottiene così la seguente struttura

Infine si rilasciano i momenti torcente e flettente nella struttura dopo averla selezionata. (assign>frame>releases/partial fixity >moment 22, moment 33 start e end, che indicano l’inizio e la fine dell’asta).


A questo punto si definisce il materiale.(define> materials> add new materials) e la sezione delle aste(define>section properties>frame section>add new property) ------> Si sceglie un tubolare d’acciaio:
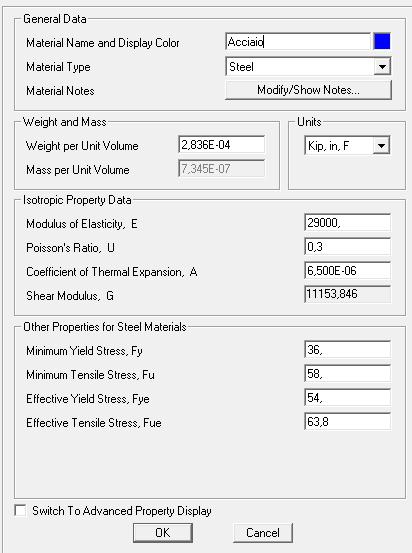

Per poter studiare la struttura occorre definire(define>load patterns) e assegnare (assign> joint loads>forces) un carico verticale distribuito sui nodi. Aiutandoci con il comando seguente : set display option> frame/cables/tendons>frame not in view si rendono invisibili le aste e si può selezionare più facilmente i nodi sui quali grava il carico. Si assegna alla forza DEAD, ovvero il peso proprio della struttura, il valore zero in modo da valutare solo gli effetti del sovraccarico appena creato, al quale si attribuisce un valore di 40KN diretti verso il basso (-40 KN).

Ora è possibile lanciare l’analisi e visualizzare la deformata:
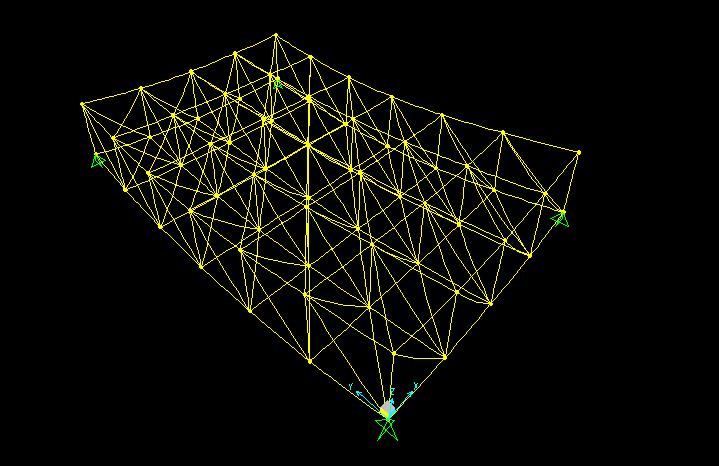
Si visualizzano anche i singoli sforzi di trazione e compressione che incidono sulla struttura, poiché in caso di strutture reticolari, sono i soli sforzi in gioco:



Questi si possono analizzare e classificare attraverso una tabella (display> show tables> analysis results> element output> file> export current table> to excel) esportabile in formato excel che risulta molto utile per l’individuazione delle aste maggiormente sollecitate, oggetto dell’ultima parte dell’esercitazione, ovvero il dimensionamento.
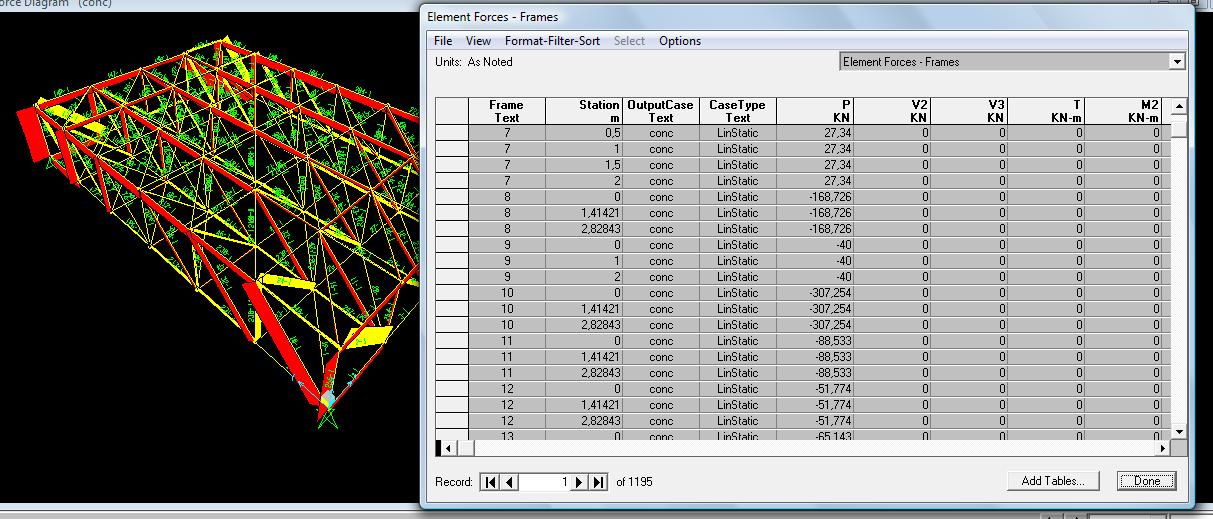
Per ciascuna asta sono presenti 3 valori che corrispondono alle sollecitazioni alle due estremità e nel mezzo. Alcune aste sono lunghe 2m ed avranno i 3 valori sotto la voce “station” di 0-1-2m, mentre altre(quelle diagonali) sono lunghe 2√2m ed avranno come misure 0-1,41-2,83m.I valori dello sforzo di taglio e momento come previsto risultano nulli.
3. Dimensionamento:
Per il progetto delle aste si scelgono quelle maggiormente sollecitate (la più tesa e la più compressa) che permettono di mantenersi in sicurezza rispetto al resto delle aste. Per quanto riguarda l’asta tesa, si effettuerà solo un dimensionamento mediante la formula di Navier e una successiva verifica a resistenza. Per quel che riguarda l’asta compressa il procedimento è più complesso. Essa infatti, può essere soggetta al carico di punta, o carico critico euleriano, il quale potrebbe portare l’asta ad un’eccessiva inflessione, fino al collasso. Perciò, per l’asta compressa, si effettuerà anche una verifica a snellezza(rapporto tra lunghezza e sezione dell’elemento)e stabilità.
Progetto asta tesa
L’asta che risulta avere più sforzo normale di trazione presenta un valore di N paria a 258,93 KN.
Si sceglie un acciaio S275
Si utilizza la formula di Navier:
fyd = N/A
dove:
-fyd è la tensione di progetto, data da fyk /γm0
· fyk = 275 MPa (tensione di snervamento del tipo di acciaio scelto)
· γm0 = 1,05 coefficiente di sicurezza del materiale
fyd = 275/1,05 = 262 MPa
-N lo sforzo normale
-A l’area del tubolare.
Dalla formula inversa di Navier si ricava l’area minima che il tubolare deve avere per resistere allo sforzo di trazione di 258,93 KN.
A=258934 N/ 262 =988 mm2 ___--> 9,88 cm2
Nel profilario dei tubi in acciaio a sezione circolare si cerca un area maggiore di quella trovata.
Si sceglie perciò il profilo: d x s = 88,9 mm x 4,0 mm (diametro x spessore)
A’= 10,7 cm2 > 9,88 cm2.

Si procede con la verifica a resistenza per accertarsi di aver scelto una sezione adeguata :
N/A’ < fyd
258934 N/1070 mm2= 242 MPa < 262 MPa
La sezione è verificata.
Progetto asta compressa
L’asta che risulta avere più sforzo normale di compressione ha un valore di N pari a -307,25 KN.
Si sceglie una acciaio S275
Si utilizza la formula di Navier per ricavare l’area minima:
A=N/fyd
A=307254 N/ (275 MPa/1.05) = 1173 mm2 ___--> 11,73cm2
Nel profilario dei tubi in acciaio a sezione circolare si cerca un area maggiore di quella trovata.
Scelgo perciò il profilo: d x s = 114,3x3,6 mm
A’= 12,50cm2 > 11,73cm2.
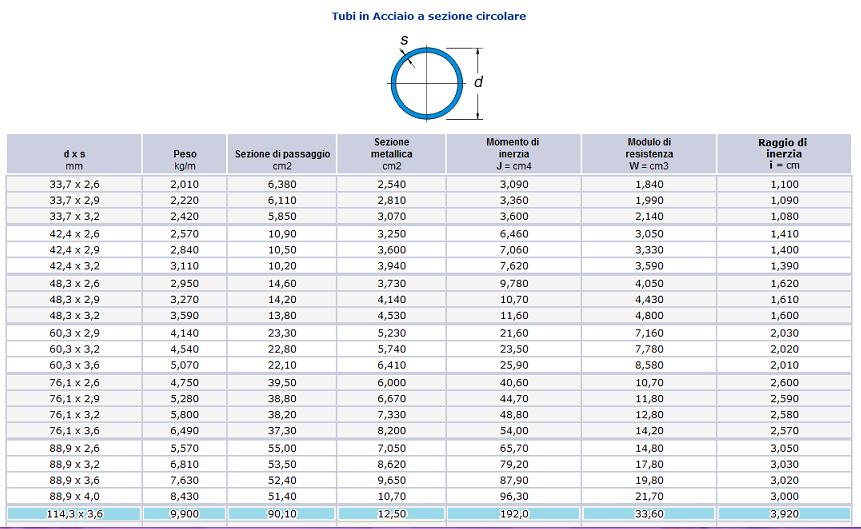
Si procede con la verifica a resistenza per accertarsi di aver scelto una sezione adeguata :
N/A’ < fyd
307254 N/1250 mm2= 245,80 MPa < 262 MPa
La sezione è verificata a resistenza.
Ora occorre verificare l’asta a snellezza :
si impone la condizione di λ<200 (condizione valida per gli elementi primari di una struttura)
sapendo che λ = lo/ρ :
lo = l*β (luce libera di inflessione)
ρ = 3,92 (raggio d’inerzia, valore tabellato)
La lunghezza dell’asta è pari a 200√2 cm = 283 cm
Occorre determinare β la quale dipende dal tipo di vincolo dell’asta in esame : in questo caso si tratta di una doppia cerniera, perciò β= 1
lo = 283*1 = 283 , λ = 283/3,92 = 72,19 < 200
Dunque l’asta è verificata a snellezza.
Per essere certi di aver dimensionato correttamente l’asta è necessario fare un’ultima verifica : la stabilità.
In questo caso il bisogna verificare che la resistenza a compressione Nd sia minore della resistenza che tiene conto dell’instabilità Nbrd
Nbrd= χ Afyk/ γm0
χ = 1 / (φ+ √φ 2 – λ2)
φ = 0,5[1 +α (λ̄ -0,2 ) + λ̄2]
α = 0,21 (coefficiente di imperfezione, dipende dal tipo di acciaio e di profilo)
λ̄ = √ (Afyk / Ncr) (snellezza critica)
Ncr =π2 E J/lo2 (carico critico euleriano)
Dove: E = modulo elastico a compressione = 210 000 N/mm2
J = momento di inerzia minimo della sezione (da profilario) = 192 cm4 = 1920000 mm4
lo = β* l luce libera di inflessione, ovvero quanto è larga l'onda sinusoidale che definisce lo sbandamento, che dipende dai vincoli. In questo caso i vincoli sono cerniere (β=1)perciò
= 1*l*√2 cm = 2√200 cm = 283 cm (asta diagonale).
Si calcola il carico critico euleriano Ncr = 9,86 x 210 000 N/mm2 x 1920000 mm4 / 8008900 mm4
Con l'aiuto di un foglio di calcolo excel si ricava il valore di Ncr e successivamente Nbrd

Nbrd = 254 310 N = 254,31 KN < 307,25 KN
L'asta scelta non è verificata a stabilità!
Occorre riprogettarla utilizzando un profilo con una sezione maggiore. Con l'utilizzo del foglio excel si possono effettuare diverse prove fino a trovare il profilo con un valore di Nbrd tale da soddisfare la verifica.
Tentativo n° 1
Si sceglie la sezione successiva che risulta 13,90 cm2

Inserendo i dati nel foglio di calcolo excel si ottiene :

Nbrd 281,71 KN < 307,25 KN ----> ancora un valore troppo basso.
Tentativo n°2 :
La sezione successiva ha un area di 15,50 cm2

Inserendo i dati nel foglio di calcolo si ottiene :

Nbrd 313,57 KN > 307,25 KN
L’asta è verificata anche a stabilità.
Esercitazione 5 (con Giulia Savarese) :
Ripartizione delle forze sismiche (mediante foglio di calcolo excel)
La progettazione strutturale di un edificio, soprattutto se in Italia, non può prescindere dal calcolo delle forze sismiche. La forza sismica è una grandezza proporzionale al peso dell’oggetto in questione (dunque maggiore sarà la massa dell’edificio, maggiore sarà la forza sismica agente su di esso) infatti si esprime come F= cP con c detto coefficiente di intensità sismica tale che c < 1.
Infatti, sapendo che F = ma (massa per accelerazione) e conoscendo l’accelerazione sismica al suolo pari a
a =cg (con g= accelerazione di gravità) ricaviamo la forza sismica F = mcg ,ma mg = forza peso P, dunque si ottiene F = cP.
Per contrastare e resistere per quanto possibile alla forza sismica occorre prevedere nell’edificio una serie di controventi, ovvero dei telai che possano resistere a sollecitazioni verticali e orizzontali.
Nota sui "centri" e la loro collocazione
Nel collocare i controventi all'interno di una struttura è necessario tenere presente le diverse rigidezze degli stessi, poiché attraverso di esse è possibile determinare il centro delle rigidezze, che cadrà sempre vicino al controvento più rigido, ma che deve essere il più vicino possibile al centro di massa, punto di applicazione della forza sismica. Questo per evitare la rotazione dell'impalcato dovuta alla presenza di un momento che si genera automaticamente, che ha per braccio la distanza tra i due centri.
L’esercitazione seguente prevede il calcolo della ripartizione delle forze sismiche nei diversi controventi di una struttura semplice, attraverso la ricerca del centro delle rigidezze e del centro di massa.
Si prende in esame la seguente struttura in acciaio:


Essa presenta 5 controventi verticali e 4
controventi orizzontali: le molle rappresentano le
diverse rigidezze.
La sezione dei pilastri è una HE 160 con valori di momento d’inerzia:
Ix = 1673 cm4
Iy = 616 cm4
_Step 1 : CALCOLO DELLE RIGIDEZZE TRASLANTI DEI CONTROVENTI DEL’EDIFICIO
Attraverso l’utilizzo di un foglio di calcolo excel si trovano i valori di rigidezza traslante dei 9 telai presenti nella struttura. Il calcolo deve tenere conto dei diversi momenti d’inerzia dei pilastri.
KT =( 12E *Σi Ii ) / h3

_Step 2 : TABELLA SINOTTICA CONTROVENTI E DISTANZE
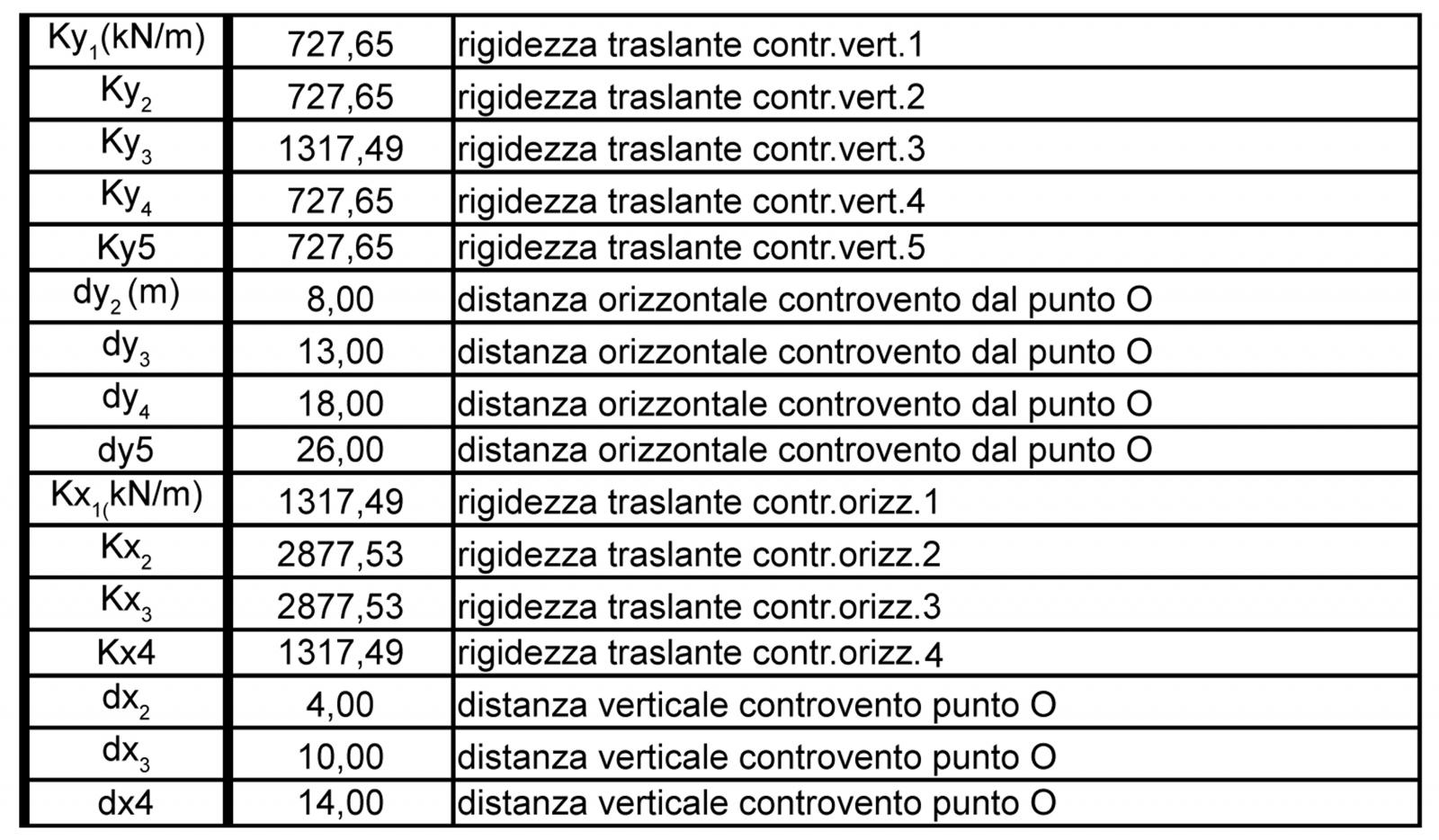
La tabella mostra tutti i valori delle rigidezze trovate e le relative distanze dal punto O, come riportato nella seguente immagine:

_Step 3 : CALCOLO DEL CENTRO DI MASSA

Si calcola il centro si massa, punto di applicazione della forza sismica. Si considerano le tre aree e si trovano i rispettivi centri di massa sul piano xy. Per calcolare le coordinate del centro di massa dell’area totale dell’impalcato si effettua la somma dei prodotti delle tre aree per le rispettive coordinate x e y e si divide per l’area totale.
Con X e Y coordinate del centro di massa :
X = ΣiAi*xi/ Atot
Y = ΣiAi*yi/ Atot

_Step 4 : CALCOLO DEL CENTRO DELLE RIGIDEZZE E DELLE RIGIDEZZE GLOBALI
Si effettua il calcolo delle rigidezze orizzontali e verticali:
ΣiKxi = rigidezza totale orizzontale (Kx tot)
ΣiKyi = rigidezza totale verticale (Ky tot)
E delle relative coordinate nel piano xy:
Xc = ΣiKxi*dyi (sommatoria delle rigidezze dei controventi orizzontali per le relative distanze verticali dal punto 0 );
Yc = ΣiKyi*dxi (sommatoria delle rigidezze dei controventi verticali per le relative distanze orizzontali dal punto 0 );
Xc e Yc così trovate sono le coordinate del centro delle rigidezze.
Si calcola ora la rigidezza torsionale totale :
Kφtot = ΣiKyi*ddyi2 + ΣiKxi*ddxi2

_Step 5 : ANALISI DEI CARICHI SISMICI
Come già affermato, la forza sismica è c * P ovvero il peso della struttura per il coefficiente di intensità sismica sempre minore di 1. Occorre trovare il peso P della struttura dato da
-somma dei carichi permanenti * l’area totale = G
+
-carico accidentale * area totale = Q
P = G + ΥQ , con Y coefficiente di contemporaneità pari a 0,80
Possiamo quindi ricavare la forza sismica F = cP , assumendo c = 0,20.

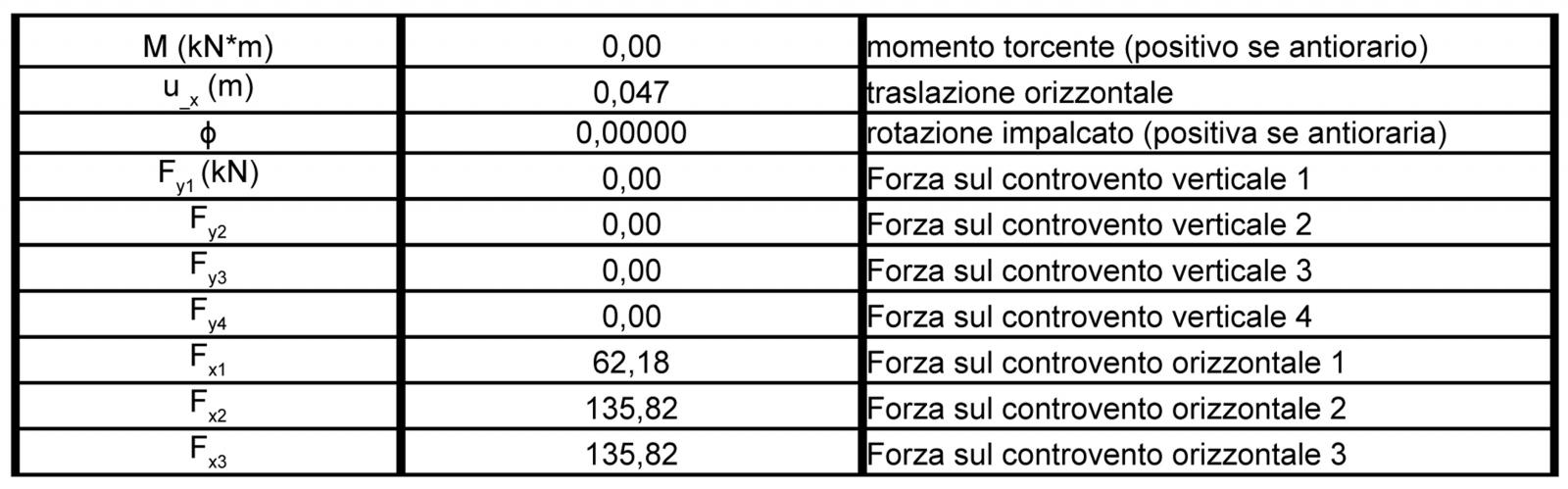
_Step 6 : RIPARTIZIONE DELLA FORZA SISMICA LUNGO x :
Si calcola la traslazione orizzontale dovuta dalla forza sismica appena trovata :
ux = F/Kx tot
Si calcola la rotazione dell’impalcato (momento torcente/ rigidezza totale)
φ = F*b / Kφtot , che risulta nulla.
Ora è possibile ricavare le diverse reazioni dei controventi
Rxi = Kxi (ux + φ ddxi)
Ryi = Kyi ( φ ddyi)
Essendo la rotazione φ nulla, ne possiamo concludere che è nullo il braccio tra il centro di massa (punto di applicazione della forza sismica) e il centro delle rigidezze: questi infatti coincidono, poiché la struttura è simmetrica.
La reazione nei controventi orizzontali è data solo dal contributo della traslazione orizzontale.
La reazione nei controventi verticali è nulla.
_Step 7 : RIPARTIZIONE DELLA FORZA SISMICA LUNGO y
Si calcola la traslazione verticale dovuta alla forza sismica :
uy = F/Ky tot
Sapendo già che il momento torcente è nullo,e dunque anche la rotazione dell’impalcato, ne calcoliamo solo le reazioni nei controventi verticali :
Ryi = Kyi uy
La reazione nei controventi orizzontali è nulla.

Commenti recenti