Il modello di graticcio è un modello fisico-matematico che ci consente, attraverso un linguaggio matematico, di comprendere comportamenti fisici attraverso un lavoro di astrazione. Il graticcio è una buona soluzione utilizzata per coprire luci ampie. E' formato da travi poste generalmente ortogonalmente le une con le altre. Non vi sono perciò travi principali o secondarie ma tutte lavorano sullo stesso piano.
Propongo qui la risoluzione di un problema per capire come si comporta il graticcio.
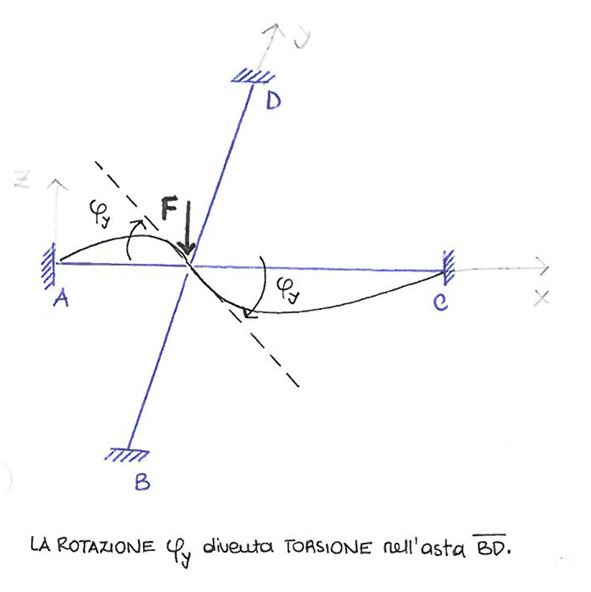
Il nodo in 3D ha 6 gradi di libertà, ma per semplificazioni le variabili si riducono a due: infatti non sussistono le variabili di traslazione verticale e orizzontale ma solo la traslazione sull'asse z, questo perché per ipotesi le aste non si possono né allungare né accorciare. Alla traslazione sull'asse z si somma quindi la rotazione.
Le variabili incognite sono quindi:
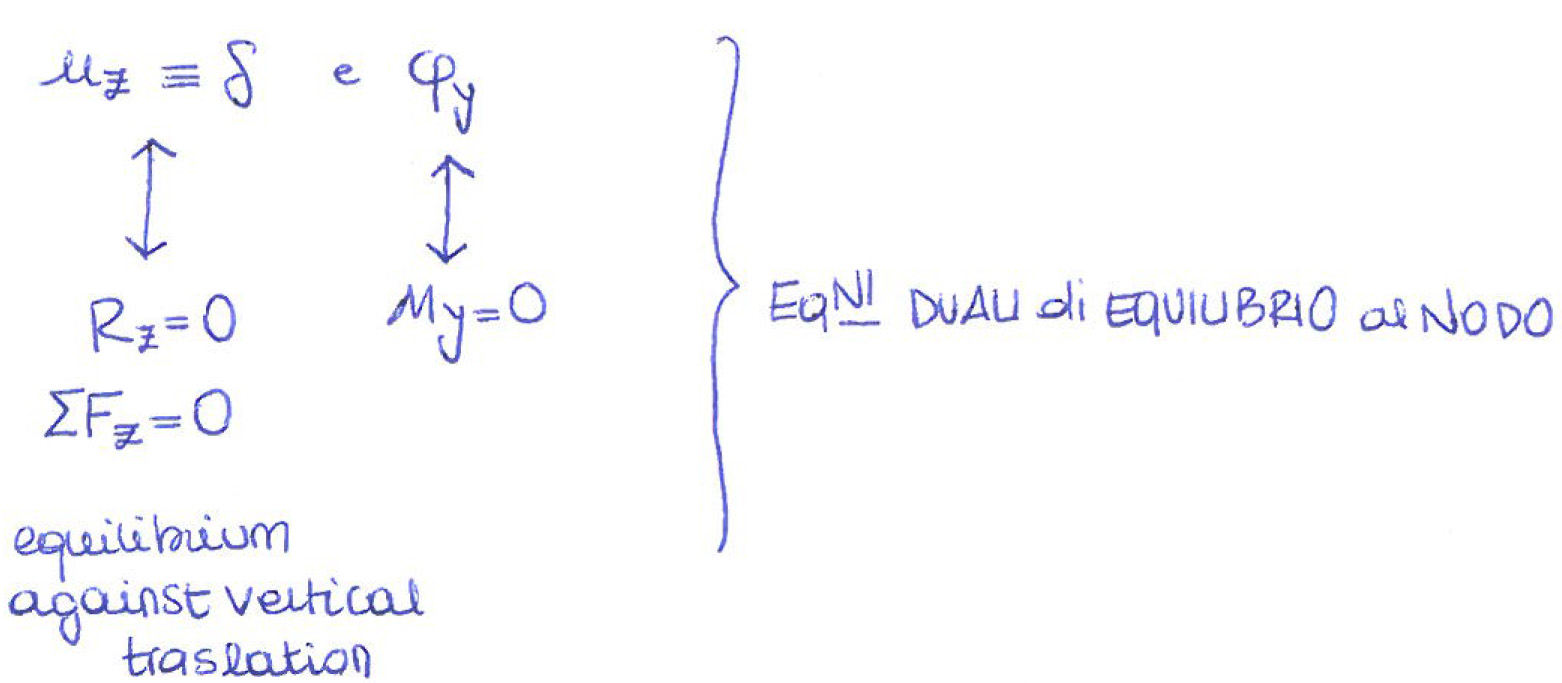
Analizzo ora le due cause su entrambe le aste:
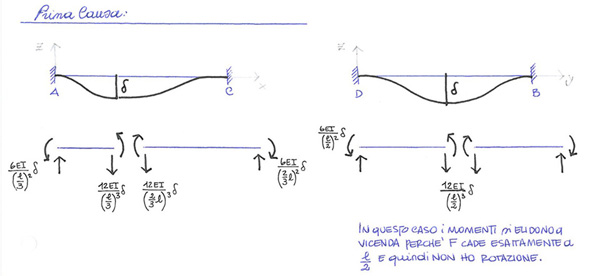
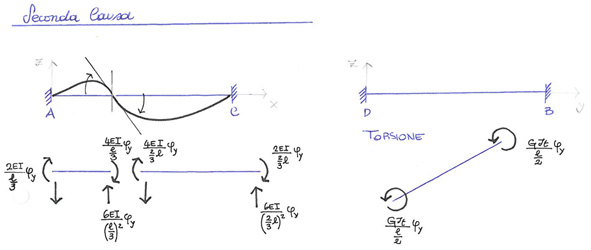

Nel procedimento sopra illustrato sono analizzati i contributi degli sforzi a Taglio e a Momento Flettente ed è risolta l'equazione di bilancio per i Momenti. Ottengo però un parametro che dipende da l'altra variabile incognita. Come in un sistema, vado quindi a sostituire il valore trovate nell'espressione in alto e trovo:

Questa teorizzazione sarà oggetto di verifica della prossima esercitazione. Impostando la scelta del materiale e delle sezioni delle aste, sarò in grado di valutare numericamente il comportamento del graticcio, verificando con il programma SAP 2000 i risultati così ottenuti.
Commenti recenti