Studentesse: Nicole Michelena e Marta Sacristán
Introduzione:
In questa esercitazione simuleremo il comportamento di un graticcio di travi inflesse in c.a., di dimensioni 30x30 metri, appoggiato su pilastri di h. 4 metri posizionati lungo il suo perimetro, ipotizzando che il questo sostenga 4 piani superiori (stimeremo un peso di 10 KN/ m2 per ogni piano.
Il graticcio di travi inflesse che dimensioneremo è composto da travi a-gerarchiche (con un nodo rigido tra loro) ordite secondo un passo costante e perpendicolari fra loro.
Al fine di semplificare la progettazione della sezione delle travi che lo compongono, ci serviremo della teoria della piastra intesa come un continuo bidimensionale, sollecitata al di fuori del suo piano medio (questo implica uno spostamento che inflette e torce.
Il graticcio e la piastra sono molto simili tra loro, infatti se infittissimo la trama di questo, il risultato è quello di un comportamento di piastra.
I passaggi che faremo sono i seguenti:
- Consideriamo una piastra in cls, altezza 100 cm. (soletta piena).
- Applichiamo i carichi agenti su di essa considerando anche il peso proprio, non trascurabile.
- Analizziamo il momento max e ci interessiamo di una striscia di essa di dimensioni 100 x 100 cm
Verifiche:
- Verifichiamo gli abbassamenti ( d Max < = 1/200 L)
- Verifichiamo la tensione normale Max
Se entrambe le verifiche sono soddisfatte, sapremo la altezza di una soletta piena in cls.
Ci interessiamo del momento di inerzia di una striscia, lo calcoliamo, e lo useremo quindi come strumento per ricavare l’area della sezione di una trave in c.a. del graticcio.
Sostituiremo infine la piastra in Sap con un graticcio di travi inflesse che abbiano il momento di inerzia equivalente a quello della piastra, avendo precedentemente deciso il passo strutturale che dovranno avere.
- Modellazione di una piastra (soletta piena in cls):
Iniziamo col definire le dimensioni di una griglia > Grid Only> 30 x 30 metri h pilastri 4 mt.


Definizione dei pilastri:
Definiamo il materiale: Define > Materials> Add New Material> Concrete> C50/60
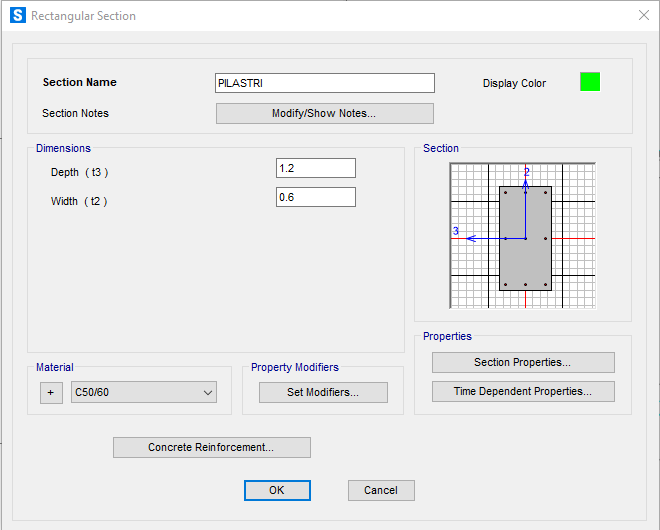
Definiamo le sezioni: Define> Frame Sections> Rectangular>Concrete>
- Pilastri Angolari 1x1m
- Pilastri :1,2 x 0,6 m

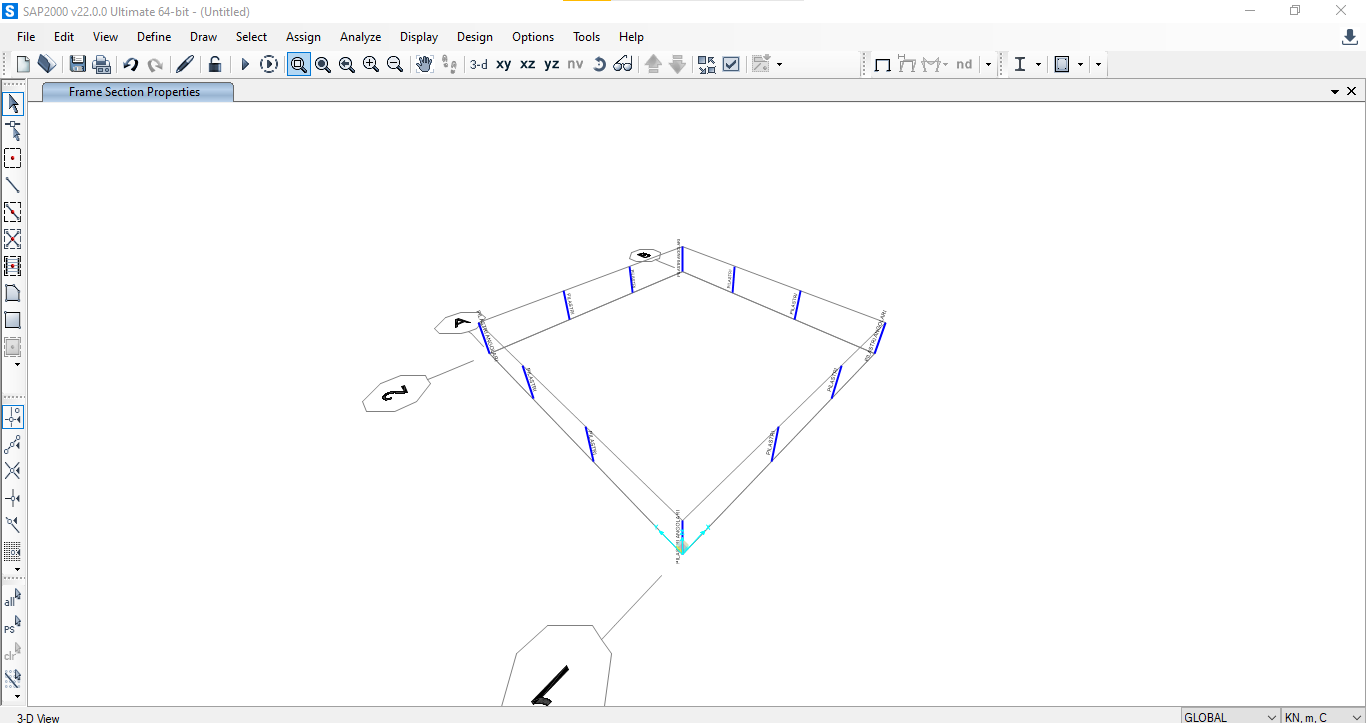
Ora vedremo i pilastri nella loro visualizzazione estrusa e capiremo quali sono i loro assi locali, in modo tale da posizionarli correttamente, cioè con la loro inerzia maggiore nella direzione dello sviluppo del graticcio.
Selezioniamo quali devono essere ruotati e effettuiamo questa operazione con il comando Assign>Frame>Local Axes.

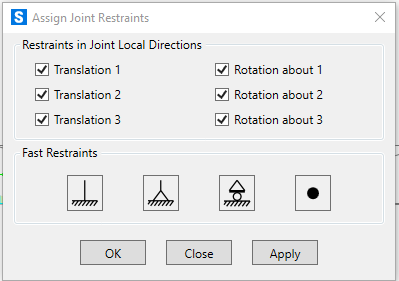
- Ora che i pilastri sono disposti nella maniera corretta, gli assegniamo i vincoli di incastro a terra.
Assign>Joints>Restaints>Incastro.
Modellazione della piastra:
Prima di disegnarla come SHELL, definiamo un materiale cls 50/60 con la differenza che in questa esercitazione non considereremo il coefficiente di Poisson, pertanto lo imposteremo = 0

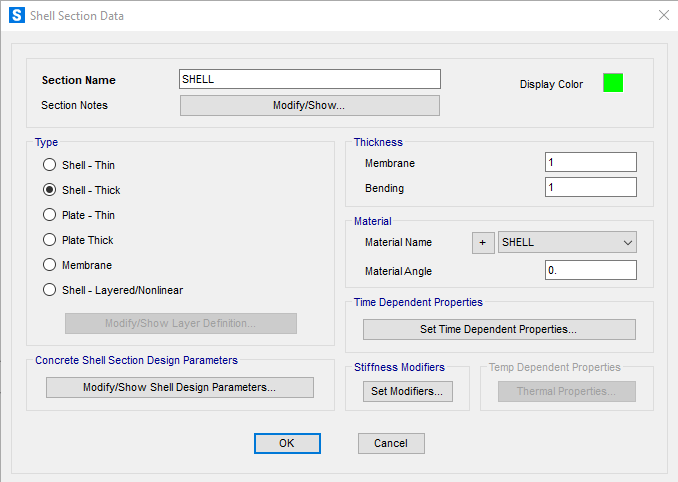
Ora definiamo la sezione >Define >Area Section>SHELL>Shell Thick >Materiale creato precedentemente>Dimensioni 1x1 m.
Chiaramente il PP della piastra va sempre considerato in quanto non è trascurabile, trattandosi di queste dimensioni e del cls.
Definiamo quindi un nuovo load pattern che chiameremo F con un self weight multiplier =1.
Disegniamo la piastra con il comando Draw Poly Area, la sezione sarà SHELL, precedentemente creata.
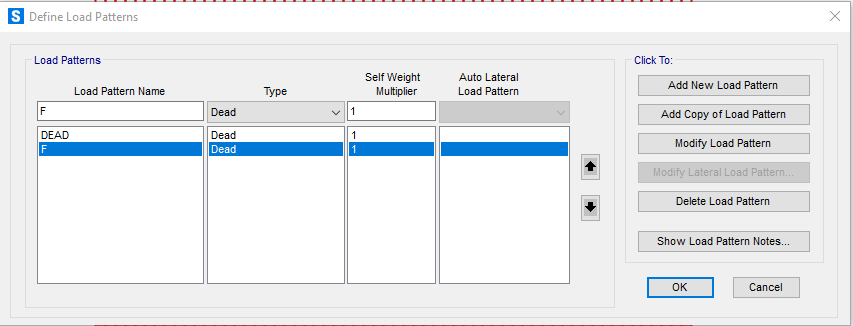
Facciamo ora l’operazione di discretizzare questa area, in modo tale che Sap consideri molte piccole aree al suo interno al fine di avere una maggiore precisione di calcolo.
Edit > Areas>Divide Areas> 0,50 x 0,50 m.


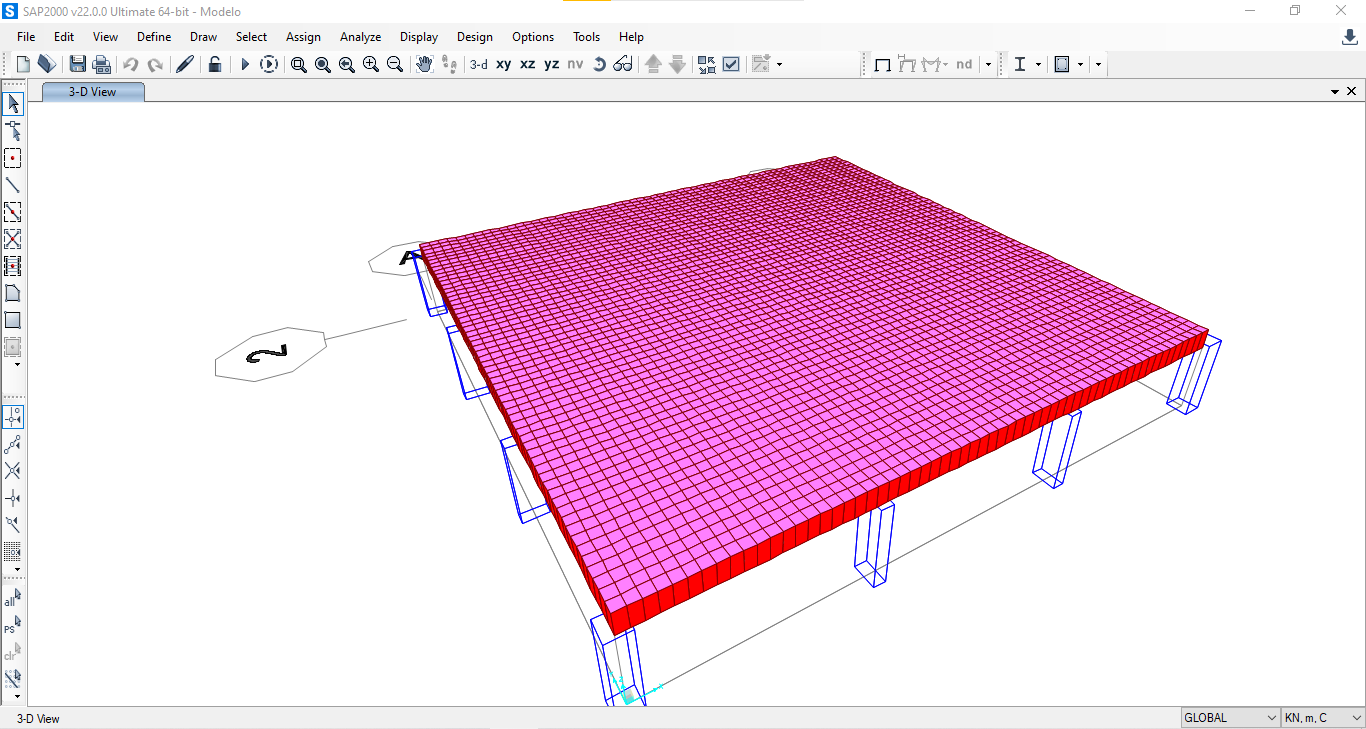
Seleziono l’area discretizzata e gli riassegno la sezione SHELL.
Ora dobbiamo assegnare i carichi agenti sulla piastra, ma per farlo bisogna distinguere i carichi che agiscono su i nodi posti in posizione perimetrale, centrale o angolare, in quanto porteranno una percentuale differente di carico concentrato.
Define>Groups>- NODI ANGOLARI e NODI PERIMETRALI (tutti gli altri rimarranno su ALL, gruppo di default di Sap). Selezioniamo i nodi e li assegno al gruppo corrispondente.
Consideriamo che la piastra modellata porti un peso di 10 KN/m2 per piano, e consideriamo 4 piani in totale.
30x30m = 900 m2 x 10 kN/m2 x 4 piani = 36000 kN .
Selezioniamo tutta la shell >Deselect Groups> togliamo i nodi angolari e perimetrali per assegnare il carico a quelli centrali. Faremo questa operazione ogni volta fino ad aver assegnato correttamente il carico puntuale sui tre gruppi di nodi.
Riassumendo:
- Nodi Centrali: carico di 10 KN
- Nodi Perimetrali: carico di 5 KN
- Nodi Angolari: carico di 2,5 KN


-Lanciamo l’analisi : per trovare il momento massimo .
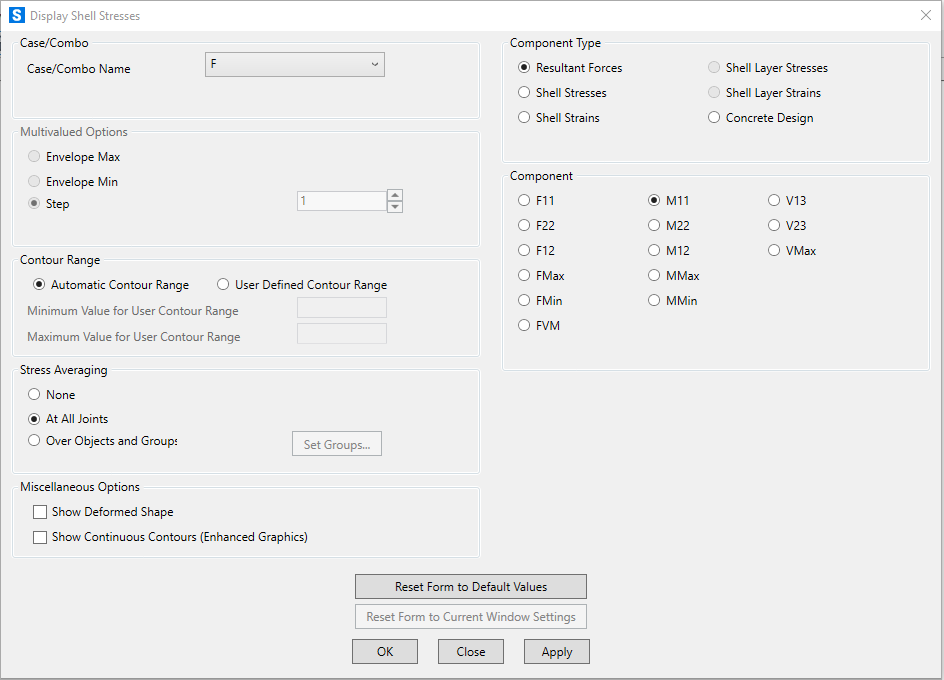
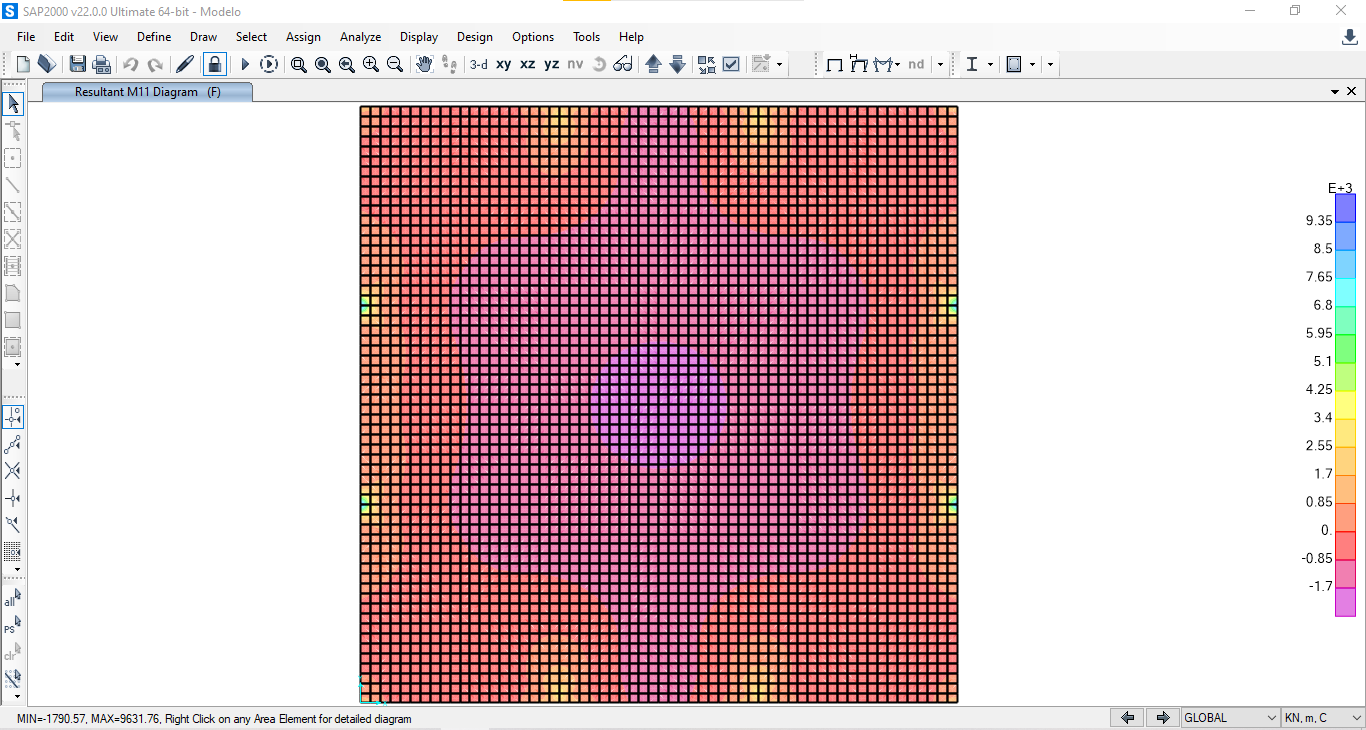
Consultiamo i risultati dell’analisi e vediamo che il comportamento alle sollecitazioni di momento è piuttosto regolare e il momento M1-1, intorno all’asse 1 (x) ci aspettiamo che sia uguale al momento M2-2, essendo un sistema simmetrico.
Faremo attenzione al Valore del Momento flettente massimo perché è il valore che più ci interessa per la progettazione delle travi inflesse del graticcio.
Il Valore è = 9631,76 Kn m. (vicino ai pilastri).
Passiamo a Excel (foglio di dimensionamento di una trave soggetta a flessione)
Inseriamo il valore del momento massimo ottenuto, e altri valori noti che abbiamo utilizzato per la piastra, per poter verificare l’altezza della sezione che dovrà avere ogni trave del graticcio.
L’altezza utile a sostegno del Mmax ottenuto è circa di 130 cm.
Prendiamo questo valore accettabile, considerando che si discosta dall’altezza iniziale che avevamo dato alla piastra avendo una maggiorazione del 30 %.
Nella progettazione esecutiva però, bisognerebbe avvicinarsi già da questo primo dimensionamento ad un’altezza che non si discosti molto da quella impostata di partenza.

Calcoliamo ora l’inerzia di una striscia pari a 1 x 1 metro. Risulta essere Ix = 0,833333 cm^4.
Sappiamo che la formula del momento di inerzia è
Ix = bh^3/12 e la formula inversa per ricavare l’h = rad^3 Ix * 12/ b.
Possiamo utilizzare questa formula per ricavare il momento di inerzia che dovrà avere la sezione della trave del graticcio equivalente a quello della piastra.
Per fare questo però dobbiamo fissare il passo strutturale che vogliamo che abbia il graticcio e rifare il calcolo di Ix per una striscia di 1 m x la dimensione del passo.
Passo strutturale scelto: 2,5 m.
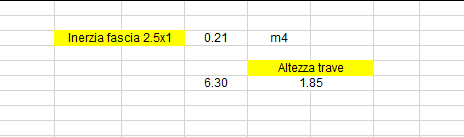
Da qui ricaviamo l’altezza che deve avere la trave: risulta essere pari a 1,85 m.
La trave avrà dimensioni h. 1,85 m x 0,40 m base.
MODELLAZIONE TRAVI DEL GRATICCIO IN SAP.
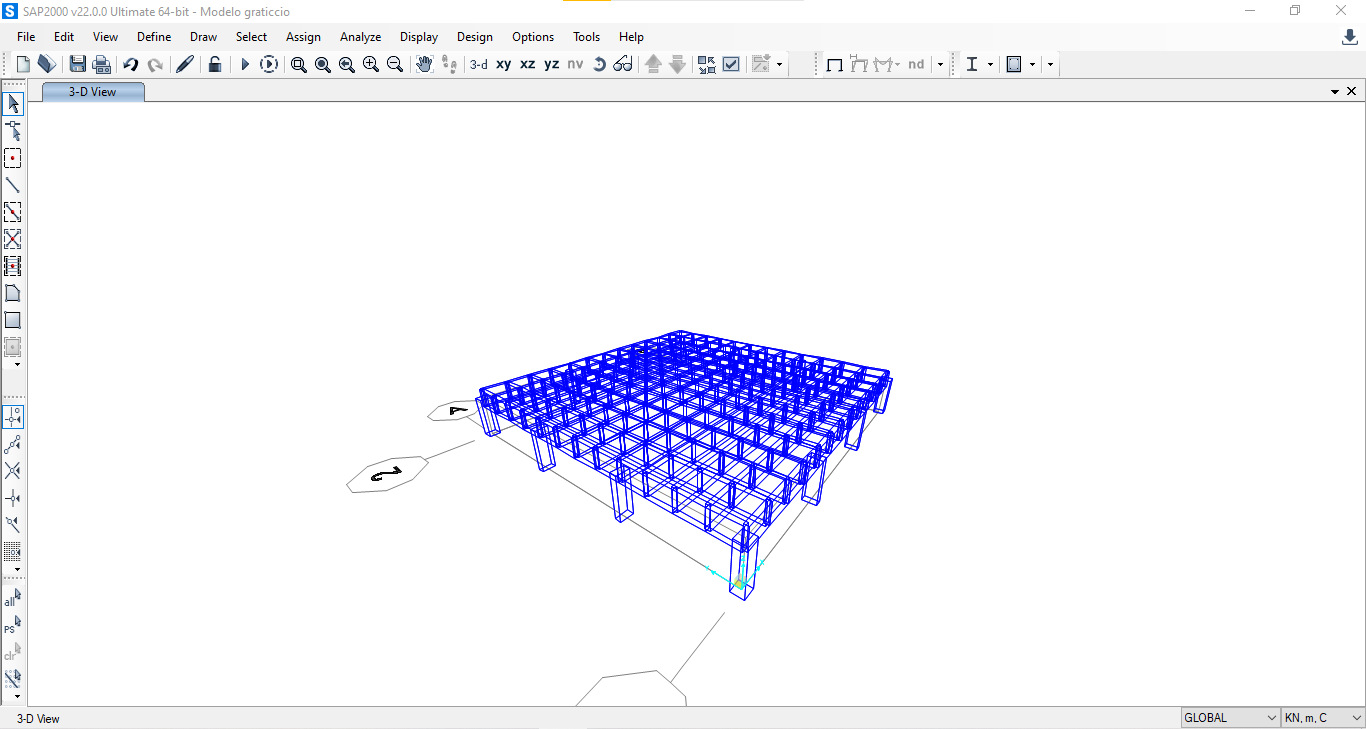
Cancelliamo ora la piastra e iniziamo a disegnare in Sap le travi del graticcio dimensionate precedentemente.
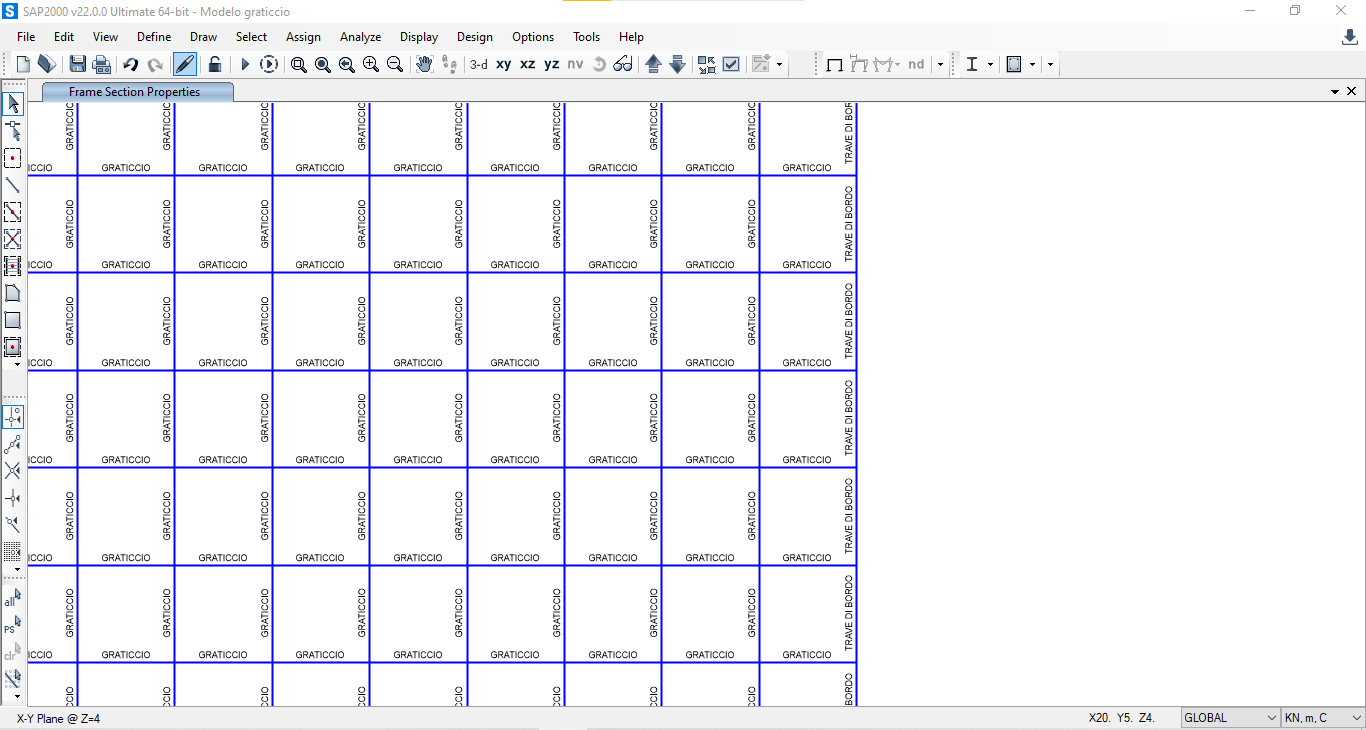
Creiamo ora la sezione delle travi a- gerarchiche del graticcio: Define >Section Properties> New Section > Trave GRATICCIO> C50/60 dimensioni 1,8 x 0,4 m.

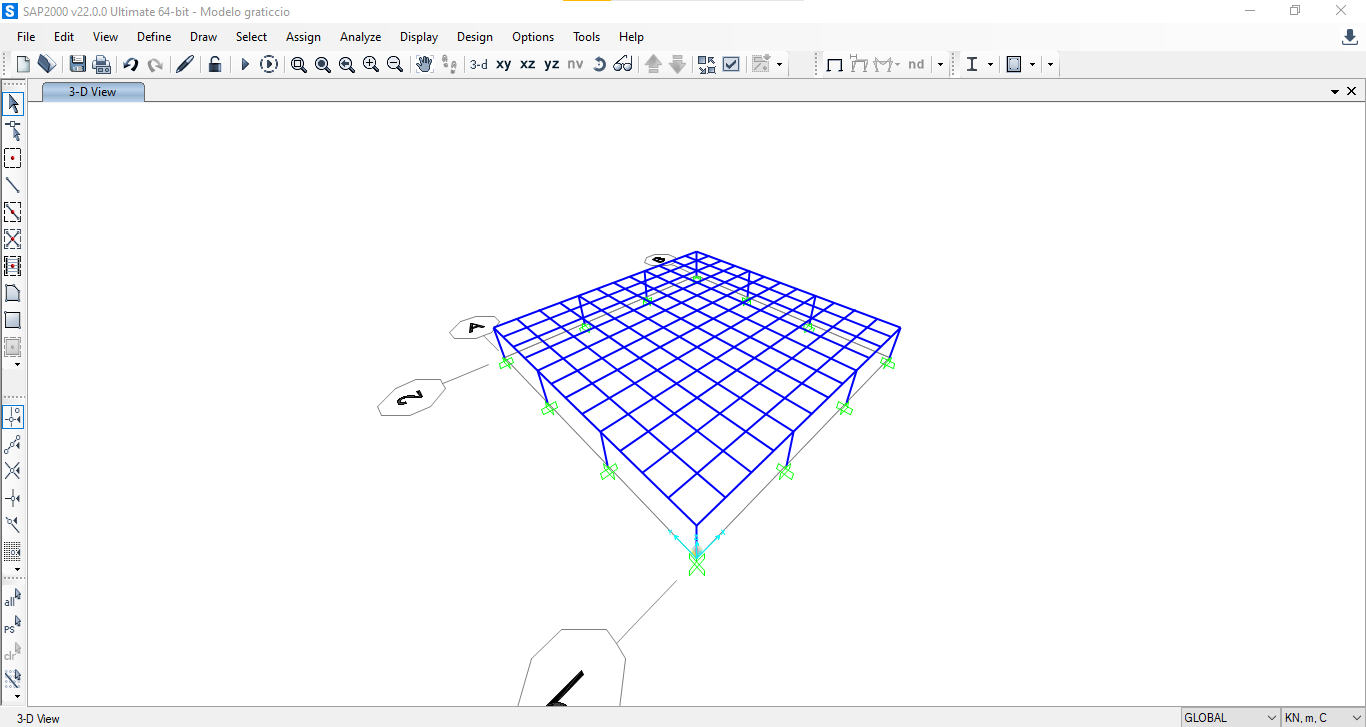
Con CTRL+ R Replicate copio le travi nelle due direzioni per completare il disegno del graticcio.
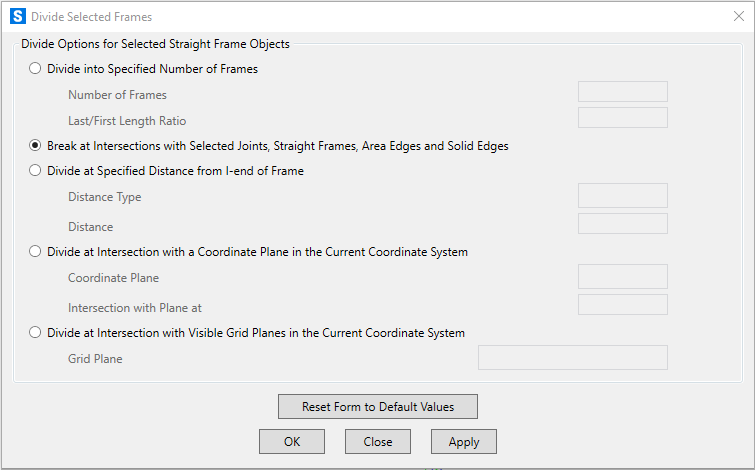
Ora bisogna suddividere le travi affinchè abbiamo il comportamento di un graticcio, ovvero un nodo rigido tra loro. Edit> edit lines> divide frames.
Ora riassegniamo i carichi, dividendo il carico totale per il numero dei nodi, a seconda de sono Centrali, perimetrali o angolari.
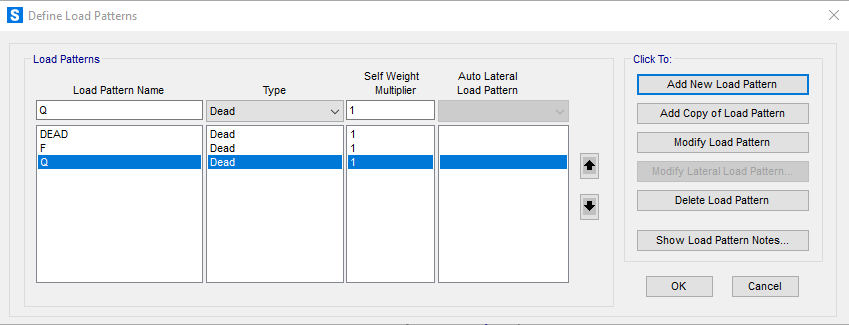
Creiamo quindi un nuovo Load Pattern “Q”. E assegnamo i carichi ai nodi
- Nodi centrali : carico 250 kn
- Nodi perimetrali : carico 125 kn
- Nodi Angolari : carico 62,5 kn
Riavviamo l’analisi su Q, considerando anche il peso proprio .
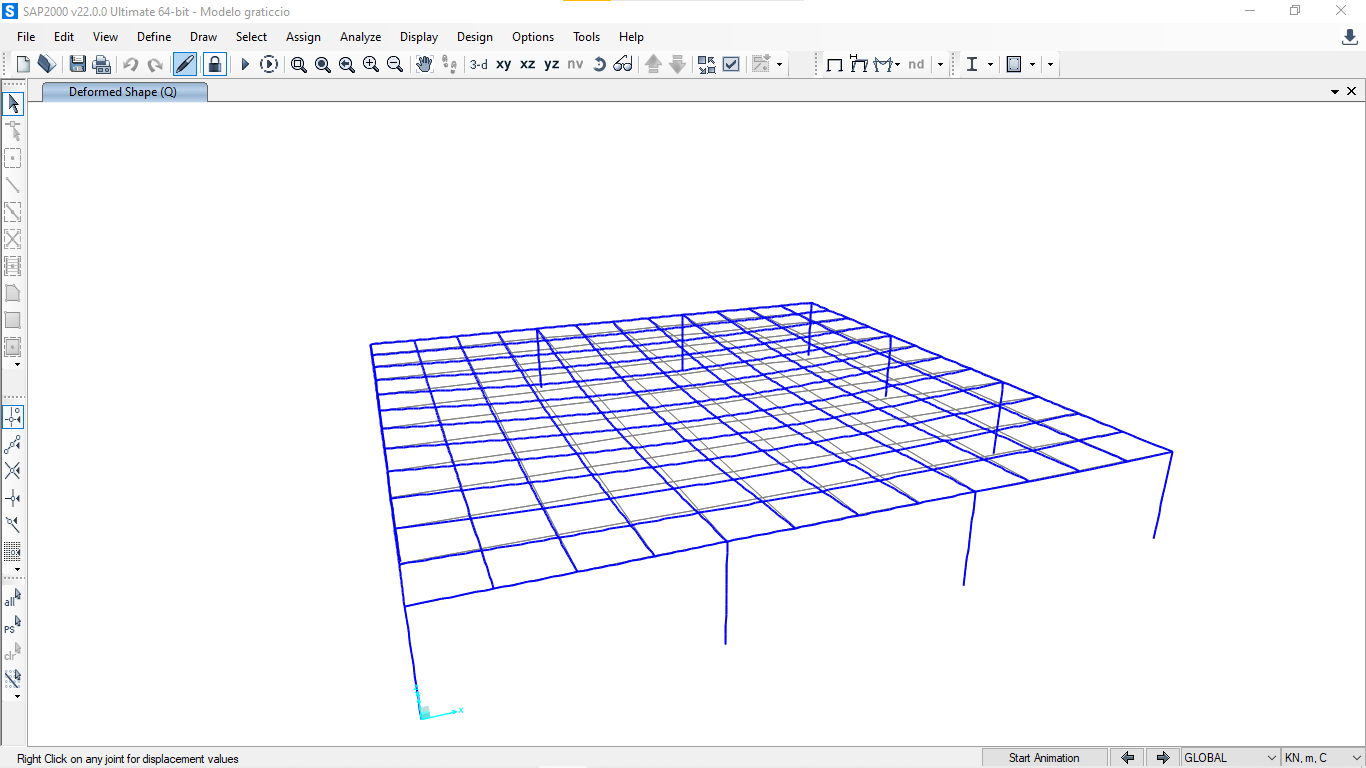
Controlliamo l’abbassamento massimo (si verifica in uno dei punti centrali).
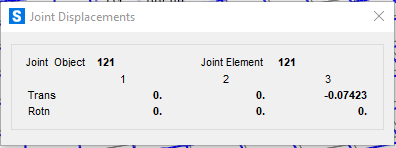
Risulta essere di circa 7 cm, è ammissibile in quanto rispettiamo il valore max di abbassamento consentito dalla normativa allo S.L.U. ( Max < = 1/200 L)
Inoltre, dalla visualizzazione deformata notiamo che i pilastri si incurvano in quanto il nodo tra trave e pilastro è rigido.
Vediamo i risultati del momento lineare in corrispondenza del pilastro e capiamo cosa succede alle travi di bordo, dobbiamo quindi lavorare sulla loro rigidezza torsionale.
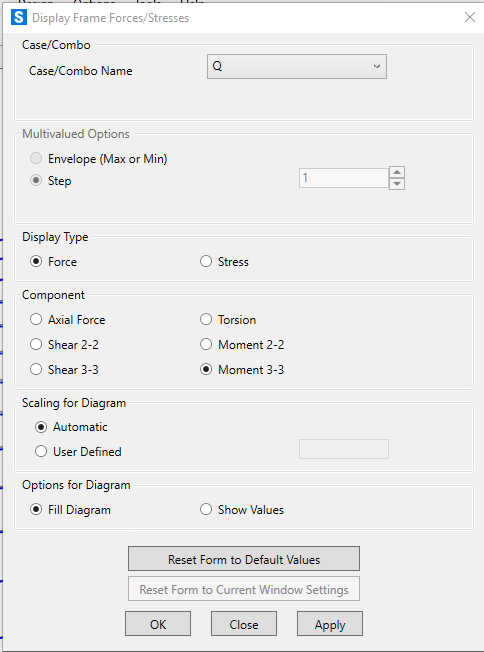

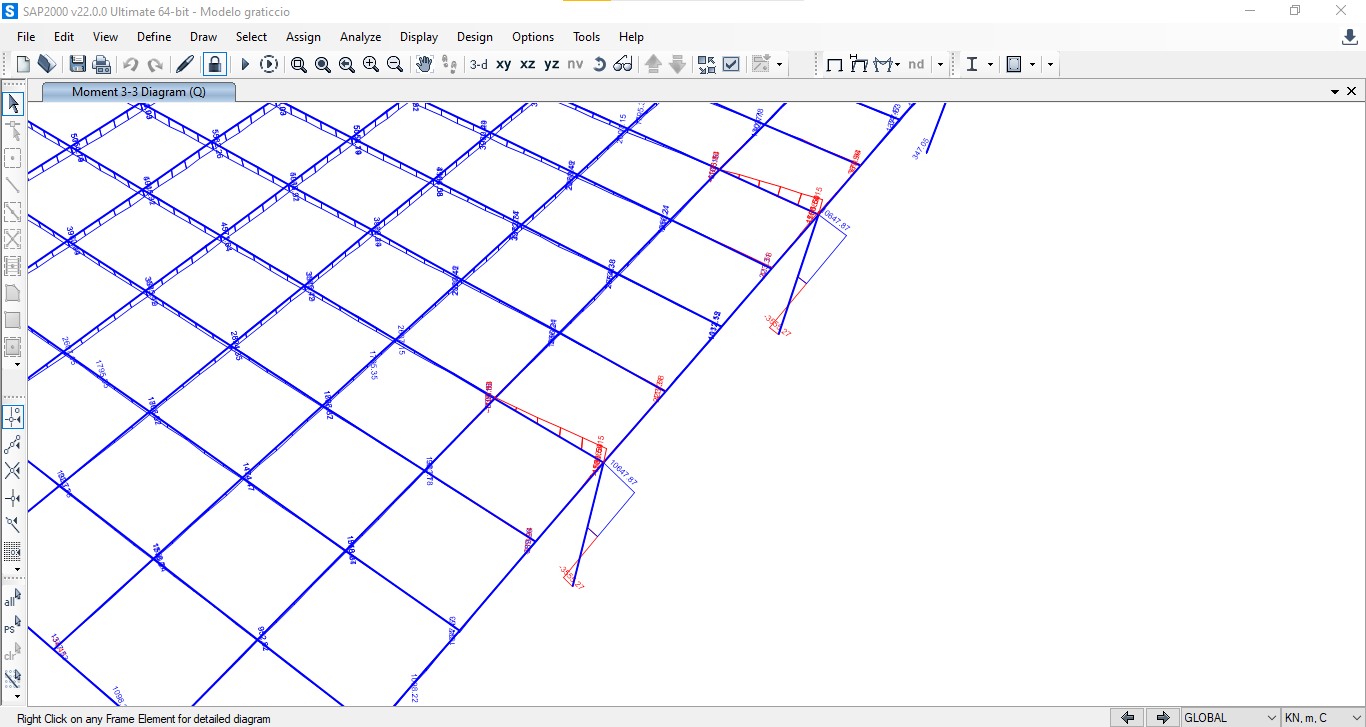
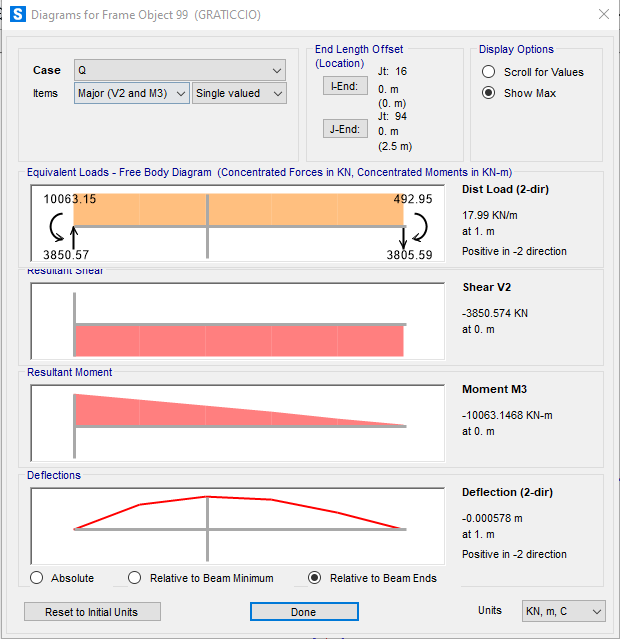
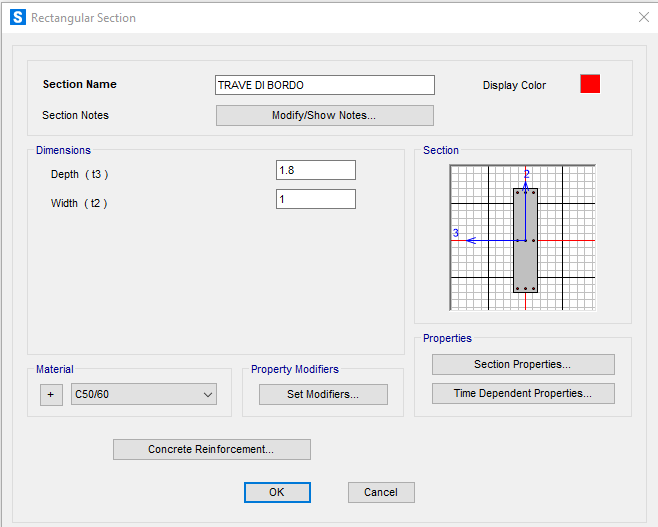
Dimensioniamo la trave di bordo con il foglio di calcolo per assegnarle una sezione adatta a contrastare il più possibile la torsione alla quale è soggetta.
Vefica trave di bordo :

Seleziono le travi di bordo , per cambiare la loro sezione . Assign>Frame>Frame Sections>trave di bordo > 1,8 X 1 METRI
Rilanciamo l’analisi .
Controlliamo ora i pilastri, verifichiamo la loro sezione con la tabella di calcolo .
Verifica pilastri :

La sezione verificata è pari a 180x60 cm , creiamo quindi una nuova sezione e la riassegniamo in Sap.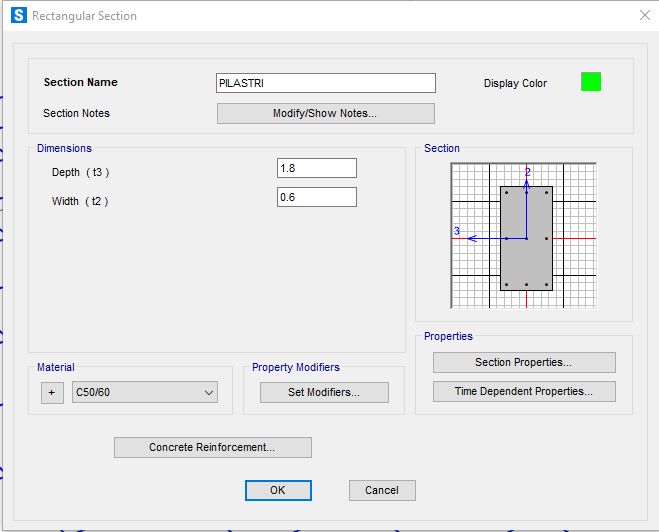

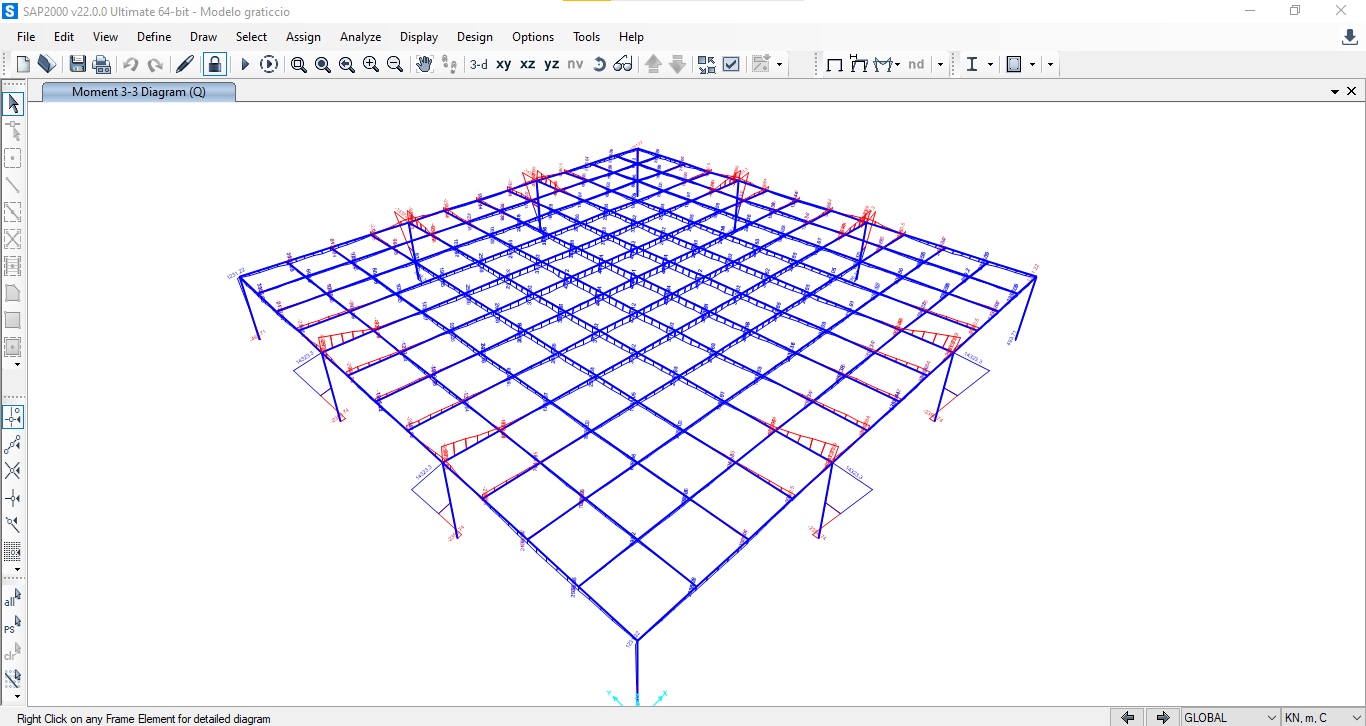
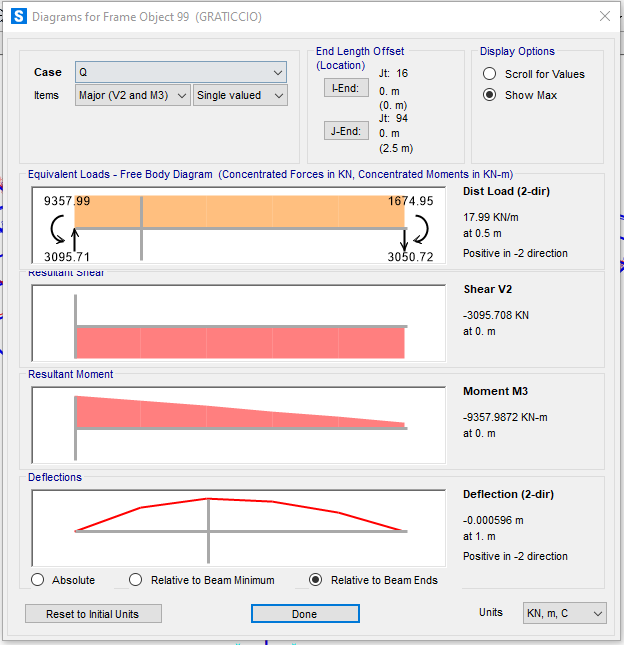
Consultando nuovamente le sollecitazioni, si nota chiaramente che con questo processo di reiterazione i valori migliorano notevolmente, stressando sempre meno la struttura .
Notiamo però che questo processo necessita di criteri specifici e di una consapevolezza tale da non creare ulteriori problemi alla struttura (se si aumenta la sezione delle travi o dei pilastri, aumenterà anche il peso della stessa, e questo porta ad altre problematiche).
Per questo motivo, si potrebbe considerare un cambio di sezione e di materiale per la trave di bordo, ad esempio una sezione tubolare o scatolare cava, che possiede una elevata rigidezza torsionale. Risulta essere un esercizio complesso, volto a “trovare un equilibrio”.
Nella progettazione esecutiva si continua con questo modus operandi fino ad ottenere i risultati ottimali, considerando in maniera sempre più specifica ed attenta quelle sopra citate (e non solo).
Concludiamo l’esercitazione avendo compreso l’importanza e la precisione che richiede la progettazione di morfologie strutturali speciali come questa, anche ad uno stato di primo dimensionamento da noi studiato e simulato con il programma di calcolo.
Commenti recenti