Lo scopo dell'esercitazione è quello di progettare e dimesionare una trave reticolare spaziale.
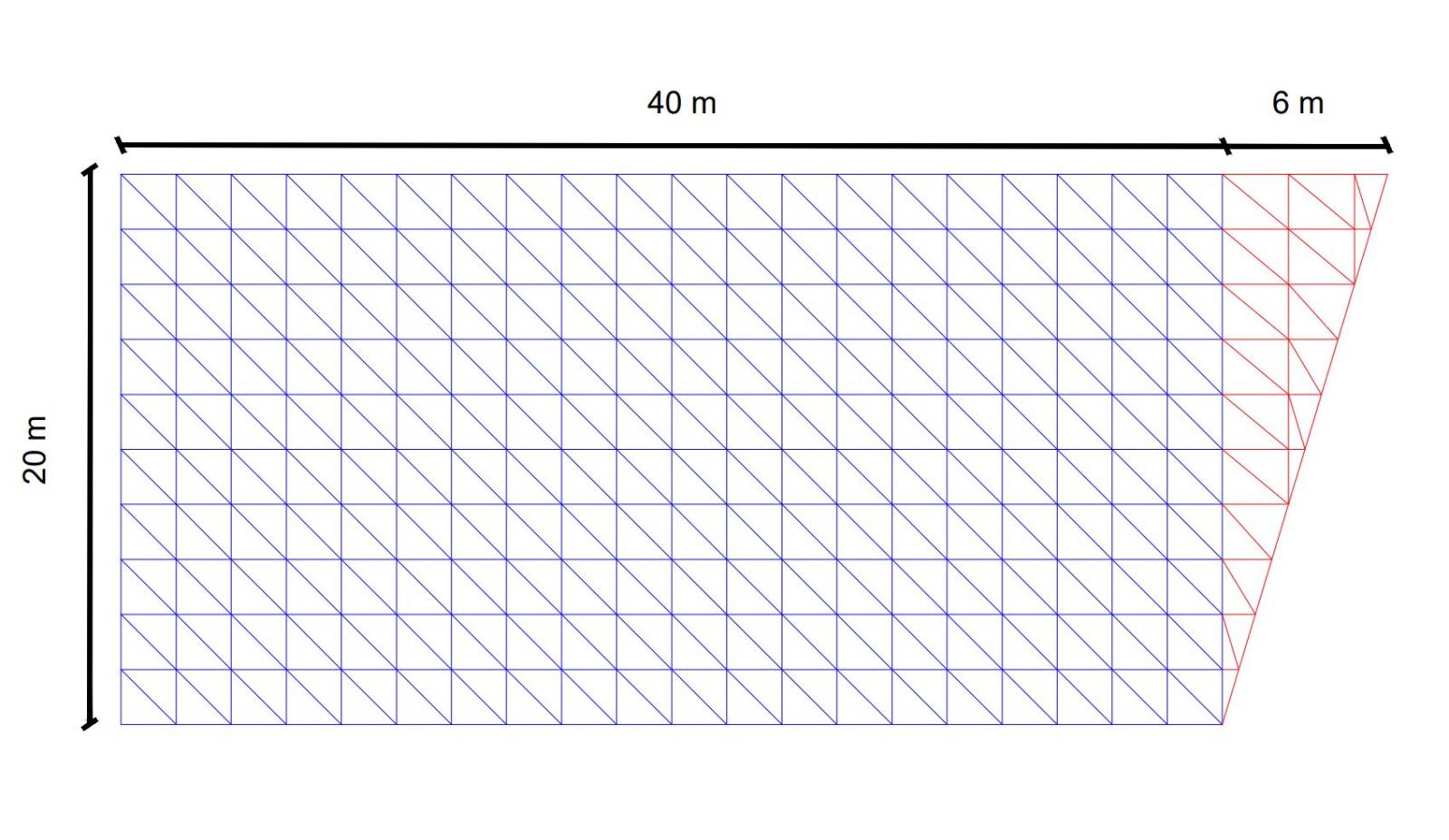
Prima di tutto abbiamo deciso le misure della trave reticolare spaziale e successivamente disegnata su Autocad per analizare la forma e gli ingombri.
 Lo scopo dell'esercitazione è quello di progettare e dimesionare una trave reticolare spaziale.
Lo scopo dell'esercitazione è quello di progettare e dimesionare una trave reticolare spaziale.
Prima di tutto abbiamo deciso le misure della trave reticolare spaziale e successivamente disegnata su Autocad per analizare la forma e gli ingombri.
 Dopo avere in mente la forma della reticolare spaziale siamo passati sul software Sap2000, dove come primo passaggio abbbiamo disegnato un cubo, a cui abbiamo assegnato un valore d 2m per ogni lunghezza delle aste sui tre assi X, Y, Z.
Dopo avere in mente la forma della reticolare spaziale siamo passati sul software Sap2000, dove come primo passaggio abbbiamo disegnato un cubo, a cui abbiamo assegnato un valore d 2m per ogni lunghezza delle aste sui tre assi X, Y, Z.
Sul cubo abbiamo assegnato gli elementi strutturali costituiti da elementi verticali, orizzontali e controventi.

 Successivamente abbiamo copiato il cubo fino a costruire la nostra reticolare spaziale, il lato irregolare è stato costruito in base alla forma scelta precedentemente durante la prima fase di studio.
Successivamente abbiamo copiato il cubo fino a costruire la nostra reticolare spaziale, il lato irregolare è stato costruito in base alla forma scelta precedentemente durante la prima fase di studio.
Il passaggio successivo è stato quello di attribuire il vincolo di cerniera nelle posizioni in cui ipoteticamente giaciono le due strutture verticali (FORMA A C) a setti e i pilastri.

Analisi su Sap2000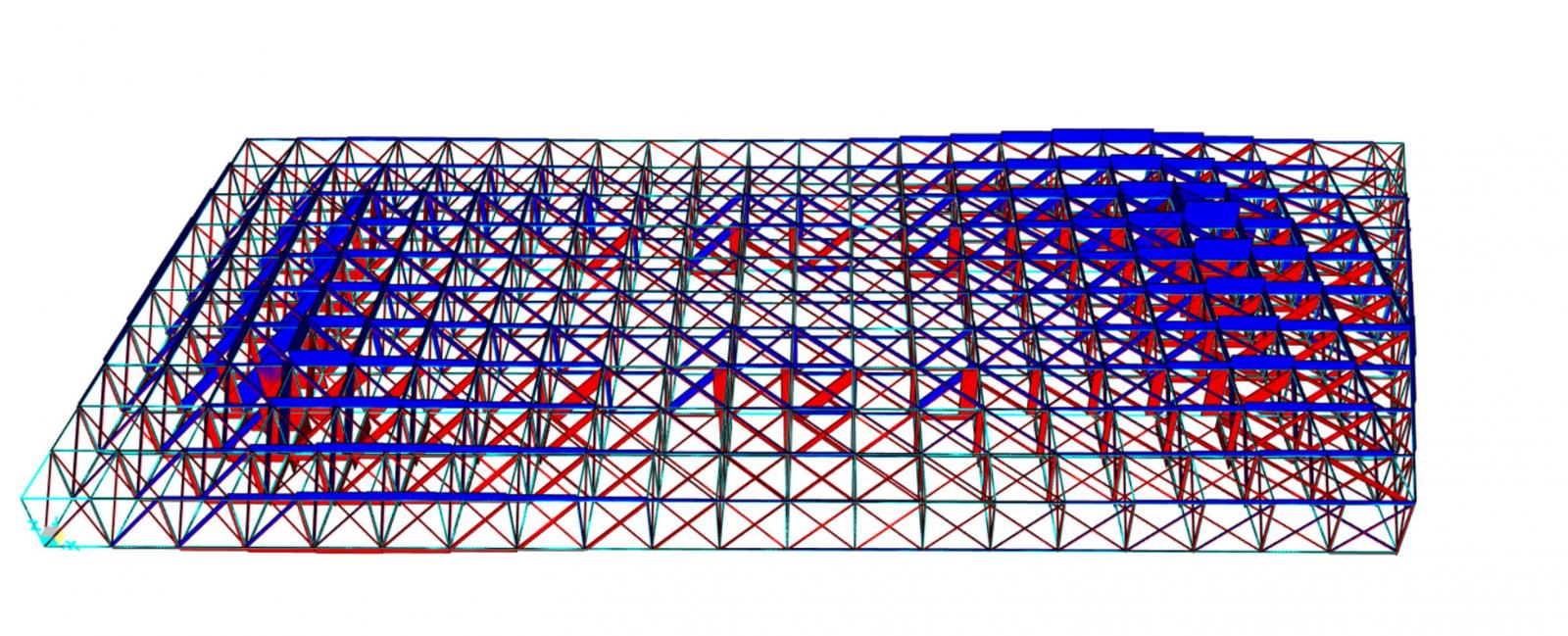

Per il peso del solaio al m^2 abbiamo utilizzato 10KN ed un numero di piano pari a 4, trovando così il peso proprio del telaio che la reticolare deve sostenere.
Con il software abbiamo inoltre calcolto il peso proprio della reticolare sommmando tutti i contributi delle reazioni vincolari.
P.P = 2.331 kN approssimiamo a 2.500 KN
Fp= 2550 KN
A= (20 x 40) + (6 x 20/ 2) = 800 + 60= 860 m^2
F= (10 x 860) x (n=4)= 8600 x 4= 34.400 KN
Ftot= 36.900 KN
Successivamente abbiamo individuato il numero di nodi centrali
Nc= 186
Np= 59
Na= 4
Ftot= 186F + 59/2F + 4 F/4
Ftot= (215,5) F
Fnodo= 36900/215,5= 171,23 KN


Dopo aver fatto partire l'analisi su Sap2000 abbiamo verificato i punti di abbassamento più critici:
Nodo 535: L=11,66 X ≤ 36900/250 = 0,046 Vmax = 0,09 NON RISPETTATA
Nodo 548: L=7,6 X ≤ 7,6/250 = 0,3 Vmax = 0,049 NON RISPETTATA
Nodo 117: L=7,48 X ≤ 7,48/250 = 0,029 Vmax = 0,009 RISPETTATA
La verfica di abbassamento nel nodo con Vmax non viene rispettata.
Più precisamente per i nodi vicini posizionati nella parte di telaio irregolare la verifica non viene rispettata, questo perchè giaciono lontani dagli appoggi.
Tuttavia per i nodi angolari restanti la verifica viene rispettata.
Da questa considerazione ne consegue che si aggiunge un vincolo in corrispondenza delle zone maggiormente deformate dalla reticolare.

RIPETIAMO ANALISI SLE
Vmax = 0,039 L= 6V2/250= 0,033
Risutando ancora non verificata, ma qesta volta per poco, scegliamo di ripetere la verifica una volta assegnata le sezioni dimensionate.
L'elemento più sollecitato è quello in corrispondenza della distanza maggiore dal vincolo più vicino, l'elemento in questione è il numero 3909.
----
DIVISIONE DELLE SEZIONI:
Abbiamo dviso la struttura in tre gruppi:
Struttura regolare
Struttura aste parte non regolare
Struttura diagonali parte non regolare
Per ogni gruppo abbiamo esportato in Excel due tabelle: Frame Section Assignment e Element forces frame.
Per la Tabella Element forces Frame abbiamo assegnato grupp di sezioni a seconda dello sforzo di compressione e di trazione.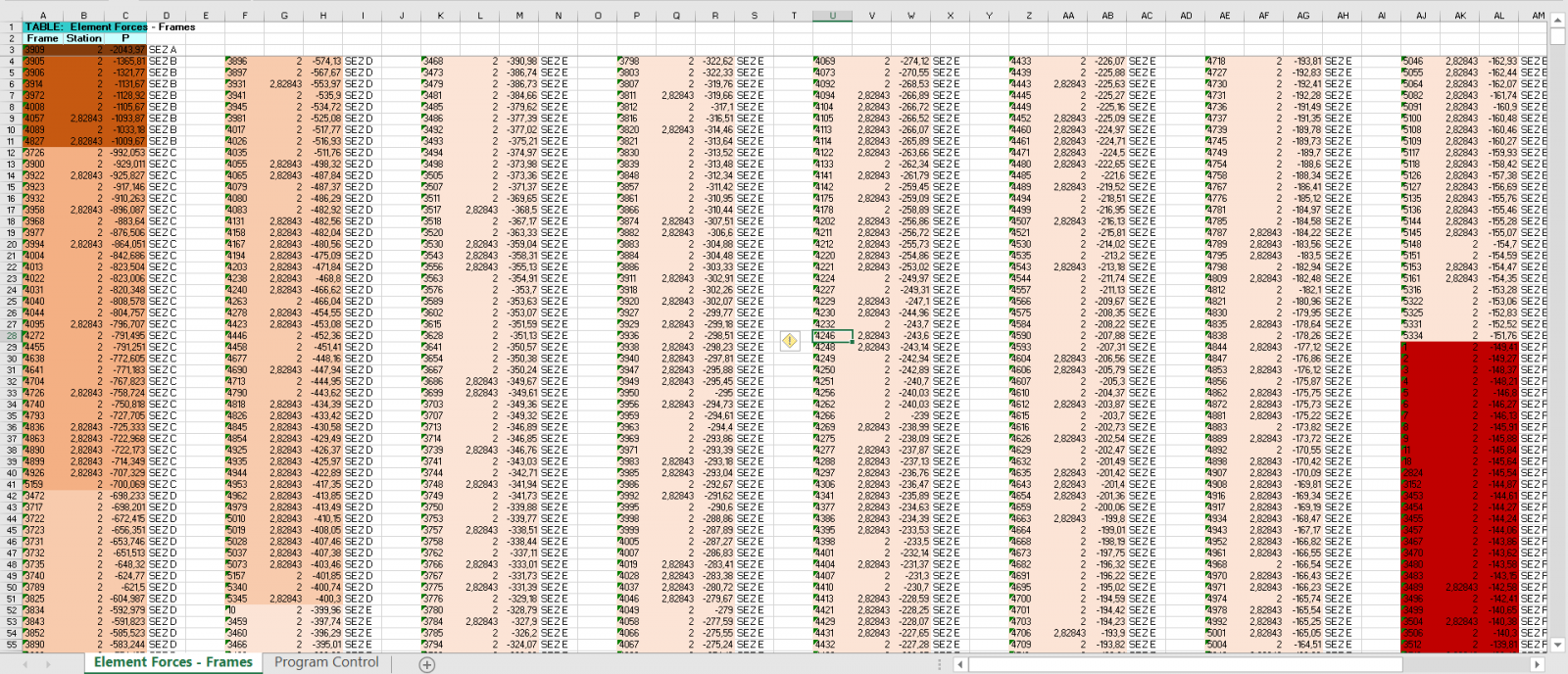
Qui sopra alleghiamo un esempio dell'assegnazione delle varie sezioni nella parte regolare della struttura.
Successivamente abbiamo usato la Tabella_AcciaioAsteReticolare per dimensionare, utilizzando la sollecitazione massima per ogni sezione.
Dopo di questo abbiamo assegnato le sezioni sulla tabella aperta in precendeza denominata "Frame Section Assignment".
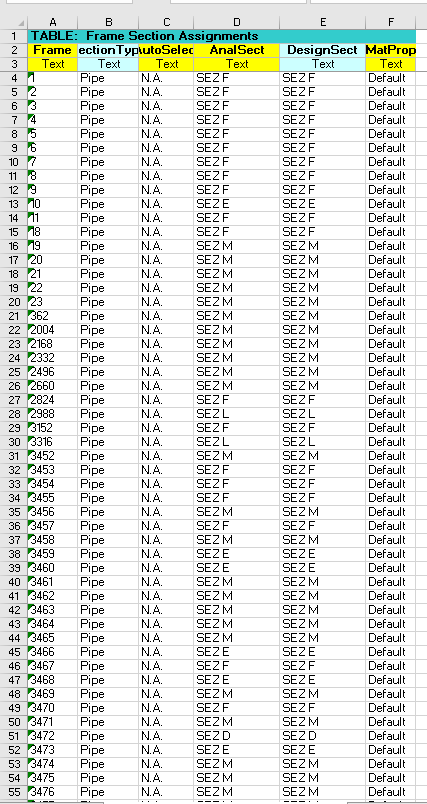
Qui sopra un esempio della Assegnazione sezione struttura parte irregolare.
---
ASSEGNAZIONE SEZIONI DA EXCEL A SAP2000
Nel momento di assegnazione delle sezioni su SAP2000 per la parte di reticolo regolare per ogni gruppo di sezioni /aste e diagonali) abbiao scelto le sezioni avente l'area maggiore tra l'aste e le diagonali più sollecitata.
Nel momento della verifica, successiva al dimensionamento, abbiamo sempre considerato la sezione maggiore tra il gruppo di aste e diagonali.
Nell'ultima foto un esempio.
Abbiamo importato per ogni gruppo la Tabella Excel per andare a segnare le varie sezioni su Sap2000:
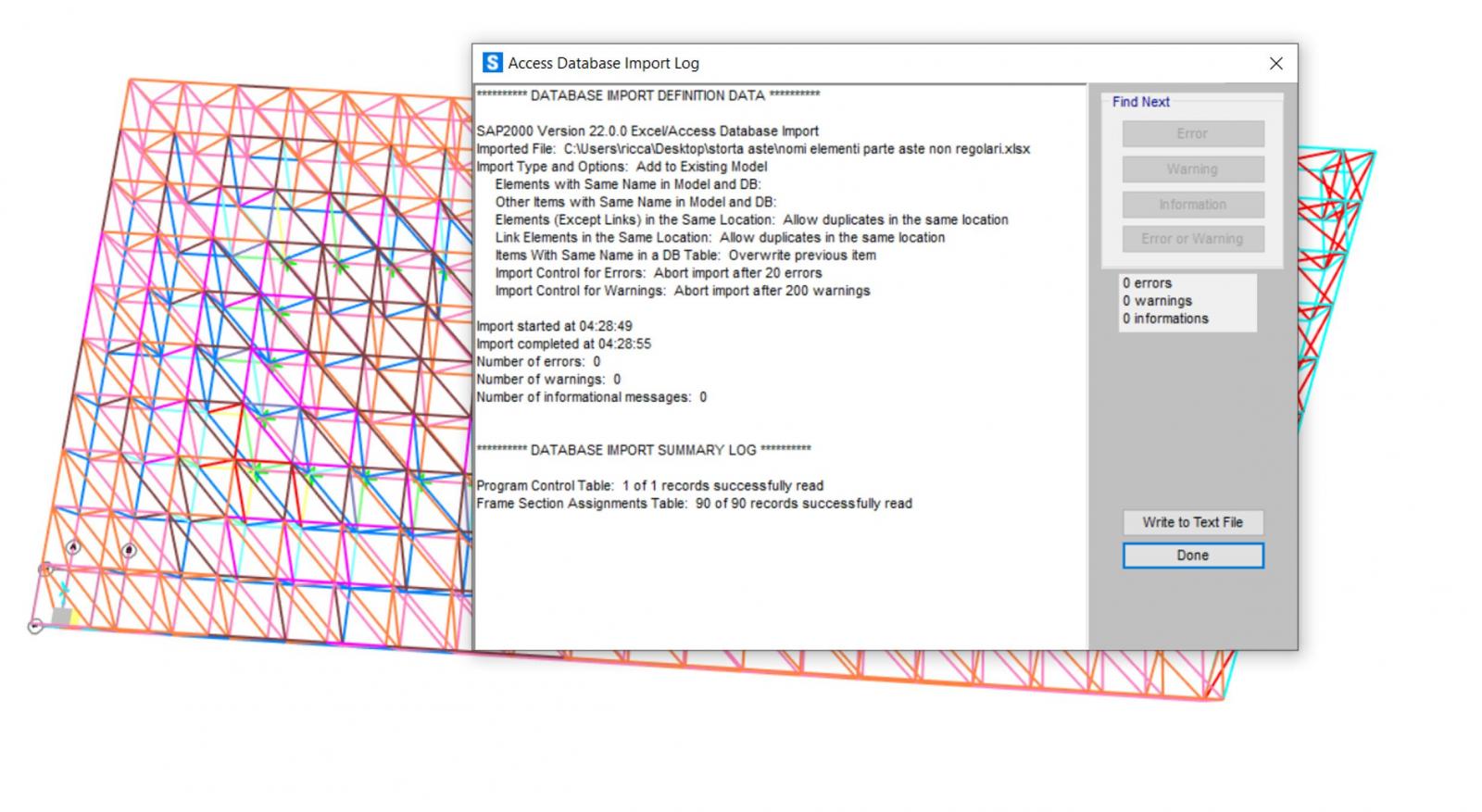
Dopo aver assegnato le nuove sezioni, abbiamo ricalcolato il Peso Proprio della Struttura reticolare attraverso la sommatoria delle Reazoni Vincolari
Joint reactios 2 calcolato con dead
F= 1669,193 KN ---> F= 1700 KN
Nc= 186
Np= 59
Na= 4
Abbiamo creato le nuove creazioni di Carico allo SLU e allo SLE e abbiamo nuovamente verificato l'abbassamento e le sezioni.
Fsolai= 34.400 KN
Ftot= 186F + 59/2 F+ 4/4F
Ftot= 215,5F
Ftot= 34400+ 1700= 36100 KN
Fnodo= 36.100/215,5= -167,5 KN
FNp= -83,75 KN
FNa= -41, 875 KN
SLE
Fc= 117, 5
Fp= 58, 75
Fa= 29, 375
Conclusioni:
-Per quanto riguarda l'abbassamento la verifica non è stata soddisfatta in alcuni punti della struttura reticolare Spaziale.
-Per quanto riguarda le sezioni del primo processo iterativo, nella maggior parte dei casi le prime sezioni da noi scelte risultano non verificate per la nuova considerazione di carico allo SLU.
Infine alleghiamo le varie tabelle con il dimensionamento e la verifica divise per gruppi assegnate precedentemente.
TABELLA CON VERIFICA GRUPPO STRUTTURA REGOLARE (COMPRESSIONE)

TABELLA CON VERIFICA GRUPPO STRUTTURA REGOLARE (TRAZIONE)
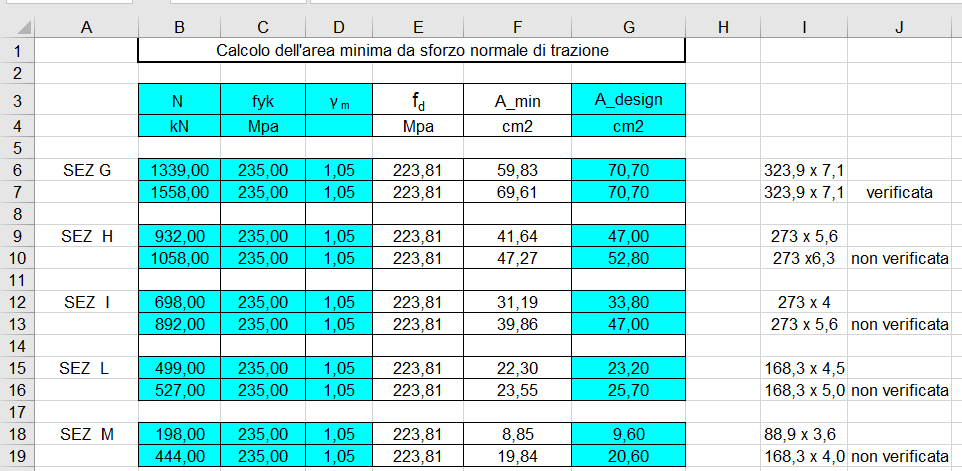
TABELLA CON VERIFICA GRUPPO STRUTTURA NON REGOLARE ASTE (COMPRESSIONE)
TABELLA CON VERIFICA GRUPPO STRUTTURA NON REGOLARE ASTE (TRAZIONE)
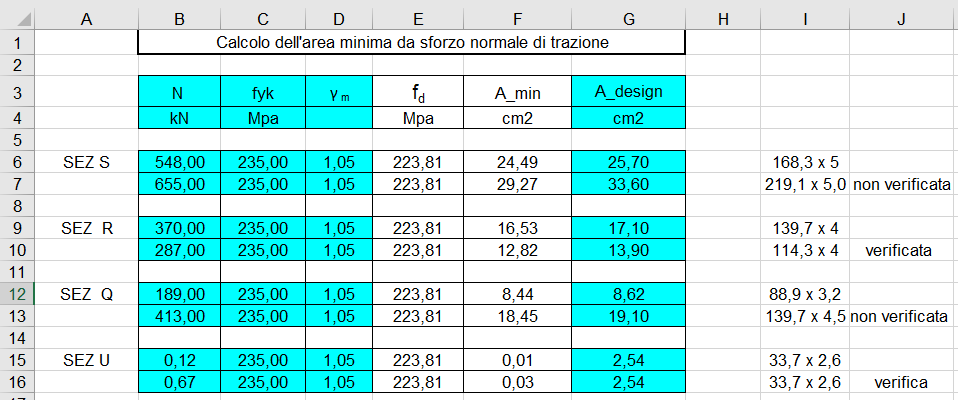
TABELLA CON VERIFICA GRUPPO STRUTTURA NON REGOLARE DIAGONALI (COMPRESSIONE)

TABELLA CON VERIFICA GRUPPO STRUTTURA NON REGOLARE DIAGONALI (TRAZIONE)
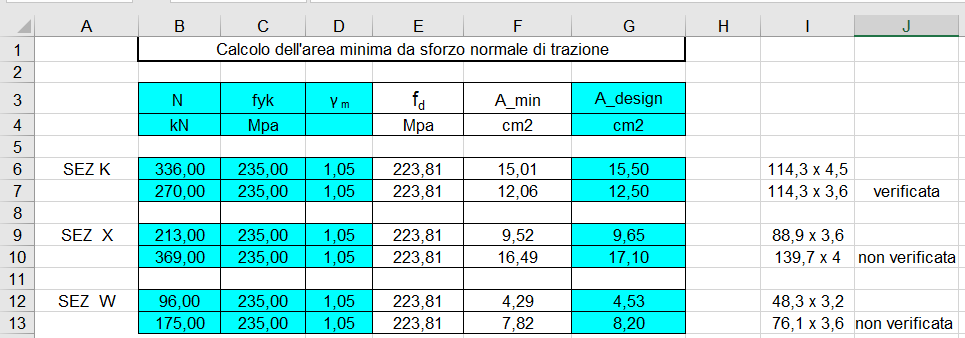
Commenti recenti