Scopo di questa esercitazione è quello di effettuare l’analisi dei carichi in tre differenti solai (legno, acciaio, calcestruzzo) al fine di dimensionare la sezione della trave più sollecitata.
Per ottenere il carico totale portato dalla trave, si devono sommare i carichi strutturali (qs), i carichi permanenti (qp) e i carichi accidentali (qa).
Questi carichi verranno inseriti insieme alle misure della struttura, all'interno di un foglio excel che calcolerà l'altezza necessaria della trave in base alla misura della base e delle caratteristiche del materiale in questione
Primo passo è quello di ipotizzare un solaio di una struttura. Si individua l'area di influenza della trave maggiormente sollecitata. Il solaio in questione presenta una trave centrale maggiormente sollecitata con un'area di influenza di 24 metri quadri.
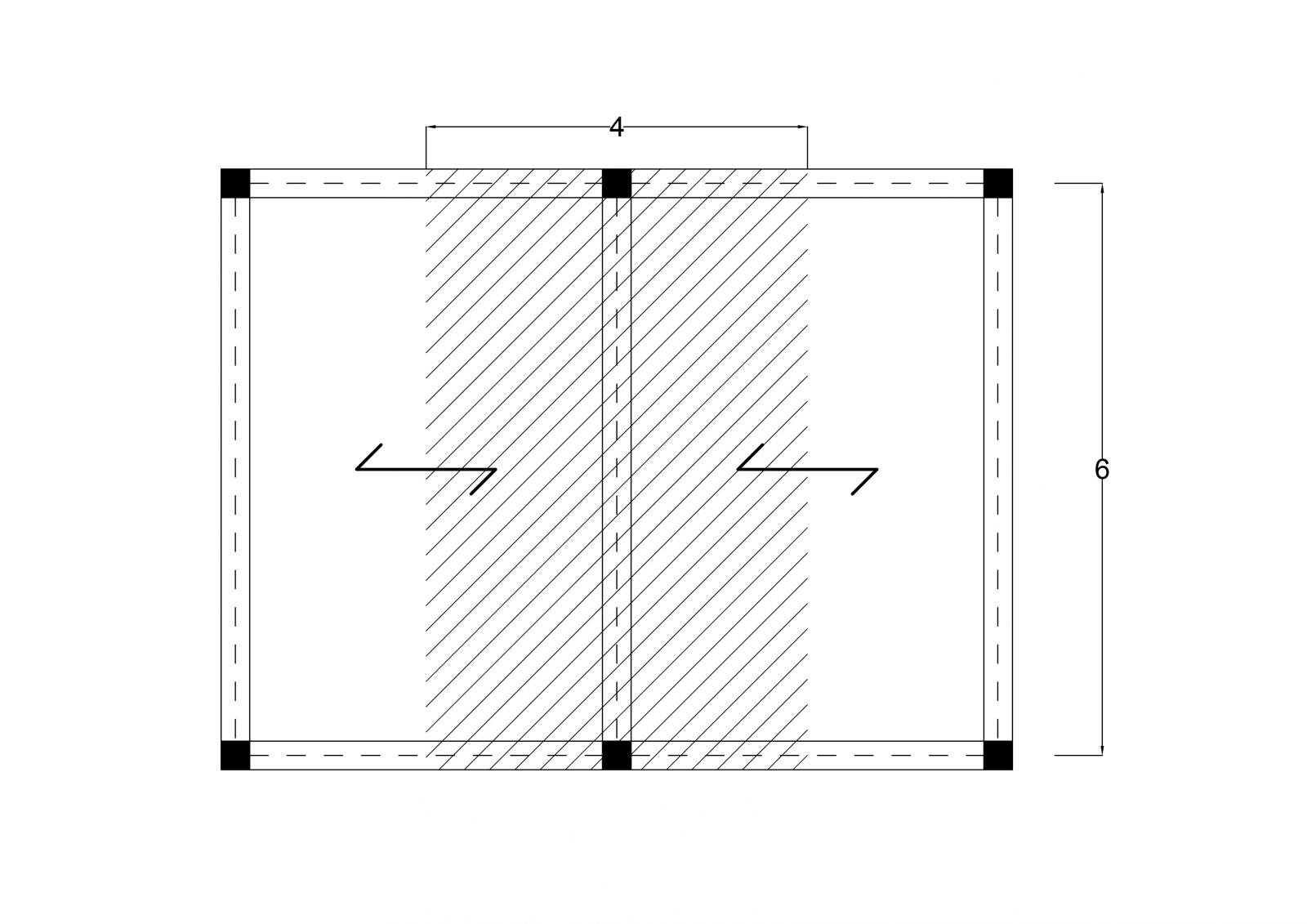
_Solaio in legno:
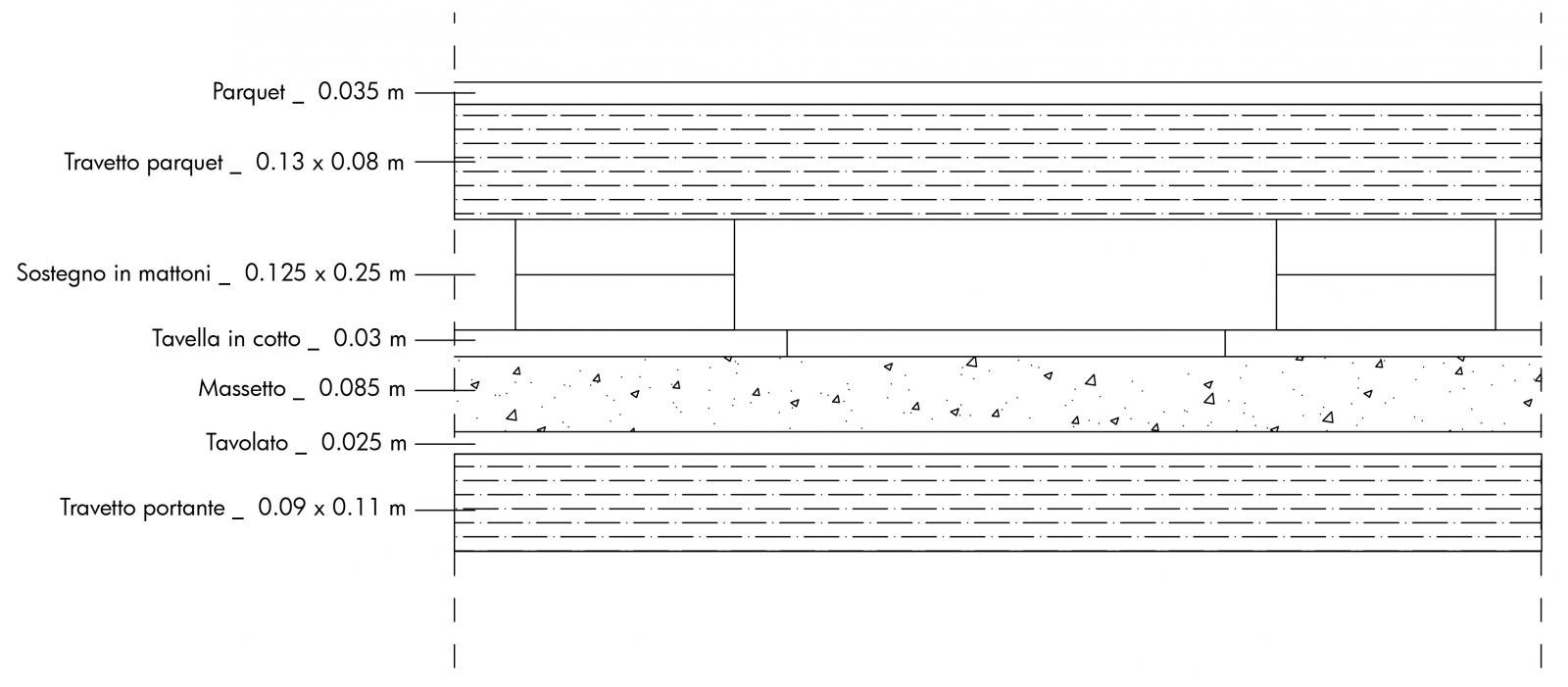
Carico strutturale (qs)
- Travetto 4 x (0,09m x 0,11m) x 8KN/m³ = 0,32 Kn/ m²
Carico permanente (qp)
- Parquet 0,025m x 7,2 KN/m³ = 0,18 KN/m²
- Travetto parquet 3 x (0,13m x 0,08m) x 6 KN/m³ = 0,187KN/m²
- Sostegno in mattoni 12 x (0,125m x 0,25m) x 18KN/m³ = 0,563 KN/m²
- Tavella in cotto 0,03m x 18KN/m³= 0,54 KN/m²
- Massetto 0,085m x 20KN/m³ = 1,7 KN/m²
- Tavolato in pioppo 0,025m x 7KN/m³ = 0,175 KN/m²
- Da normativa di aggiungono dei carichi dei tramezzi (1KN/m²) e degli impianti (0,5KN/m²)
Somma carichi permanenti: 4.85 KN/m²
Carico accidentale (qa)
- Definito da normativa a seconda della destinazione d'uso 2 KN/m²
Dopo aver inserito i carichi nella tabella Excel, si sceglie il legno tipo GL 24h con resitenza a flessione fm,k = 24MPa, e si ottiene quindi la sigma ammissibile. Impostando la base di 25 cm si troverà l'altezza di 51,40cm.

Dato il risultato di ipotizza una trave di progetto di 25 cm x 60 cm e si ipotizza il peso della trave.
Trave portante (0.25m x 0.60m) x 7KN/m³ = 1.05 KN/m
Aggiungo il peso della trave con un coefficiente di 1.3 al carico totale

Data l'altezza di 57.30 cm la trave può dirsi verificata.
_Solaio in acciaio:
Carico strutturale (qs)
- Travi secondarie (IPE 200) 2 x 0,00285 m² x 78,50 KN/m³ = 0,45 KN/m²
- Lamiera grecata 0,10 KN/m²
- Getto in calcestruzzo 0,10 m² x 24 KN/m² = 2,4 KN/m²
Somma carichi strutturali 2,95 KN/m²
Carico permanente (qp)
- Strato di isolante 0,04 m x 0.18 KN/m² = 0,072
- Strato in calcestruzzo alleggerito 0,04 m x 18 KN/m³ = 0,72 KN/m²
- Pavimento 0,015 x 11 KN/m² = 0.165 KN/m²
- Da normativa di aggiungono dei carichi dei tramezzi (1KN/m²) e degli impianti (0,5KN/m²)
Somma carichi permanenti 2.46 KN/m²
Carico accidentale (qa)
- Definito da normativa a seconda della destinazione d'uso 2 KN/m²
Per dimensionare la trave è necessario confrontare il modulo di resistenza Wx dato dalla tabella Excel con i moduli di resistenza dati dal profilario.
Possiamo quindi prendere come trave una IPE 360 con Wx=904 cm³.
Si inserisce il peso della trave con il profilo deciso
Trave portante 0.00727 m² x 78,50 KN/m³ = 0,57 KN/m
Aggiungo il peso della trave con un coefficiente di 1.3 al carico totale
Dato che il modulo di resistenza non supera quello del profilato, la sezione è verificata
_Solaio in cemento armato:
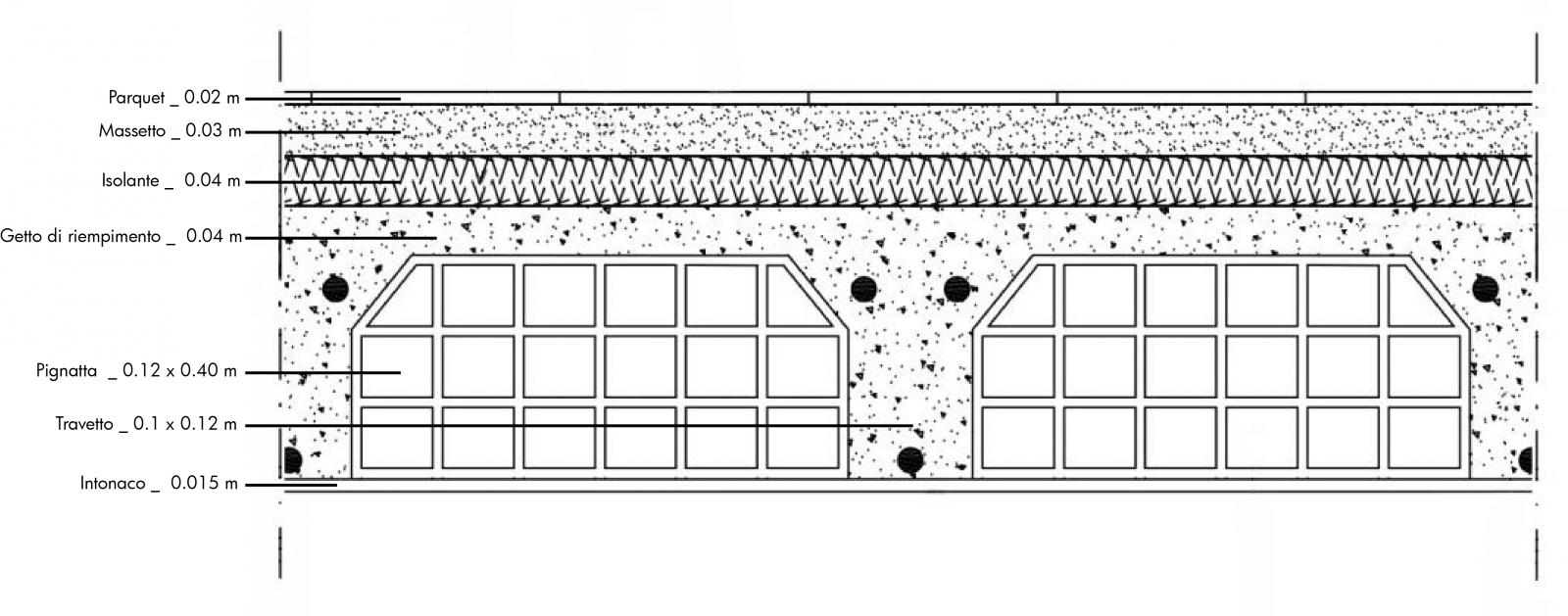
Carico strutturale (qs)
- Travetti in cemento armato 2 x 0,1 m² x 0,12 m² x 25 KN/m³ = 0,6 KN/m²
- Getto di riempimento in malta di cemento 0,04 m² x 21 KN/m² = 0,84 KN/m²
Somma carichi strutturali 1,44 KN/m²
Carico permanente (qp)
- Pignatte 2 x 0,40 m x 0,12 m x 5.5 KN/m² = 0,528 KN/m²
- Isolante 0,04 m x 9 KN/m³ = 0,36 KN/m²
- Getto di riempimento 0,03 x 18 KN/m² = 0.54 KN/m²
- Pavimento in parquet 0,02 x 8 KN/m² = 0.16 KN/m²
- Intonaco di calce 0,015 x 11.5 KN/m² = 0.17 KN/m²
- Da normativa di aggiungono dei carichi dei tramezzi (1KN/m²) e degli impianti (0,5KN/m²)
Somma carichi permanenti 3.30 KN/m²
Carico accidentale (qa)
- Definito da normativa a seconda della destinazione d'uso 2 KN/m²
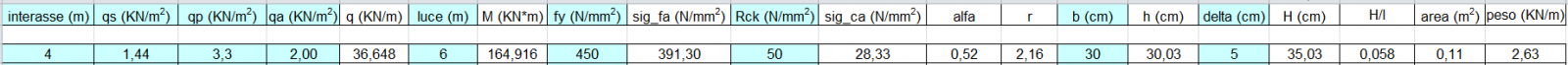
Dato che l'altezza rusultante è di 35.03 cm, si ingegnerizza a 40 cm
Si inserisce il peso della trave con l'altezza decisa
Trave portante 0,30 m x 0,40 m x 25 KN/m² = 3 KN/m²
Si aggiunge al q totale il peso della trave con un coefficiente di sicurezza di 1.3

Dato che l'altezza risultante è di 36.59, e quindi NON è maggiore di quella ingegnerizzata precedentemente, la sezione è verificata
Commenti recenti