blog di Tommaso

L'esercitazione mira a verificare che un arco è "più arco" (cioè si configura come una struttura spingente) quando la propria freccia diminuisce in rapporto alla luce, questa variazione di dimensione fa sì che il carico applicato sull'arco si trasformi prevalentemente in sforzo assiale a discapito dello sforzo di taglio e del momento flettente all'interno delle sezioni che compongono l'arcata.

Per quanto riguarda la tipologia dell'arco parabolico, ci aspettiamo di ottenere risultati dai diagrammi di taglio e momento flettente nulli, in quanto questa tipologia di arco, per la sua particolare forma geoemetrica è ingrado di trasformare tutto il carico gravante sull'arco in sforzo assiale.

Cominciamo con l'arco a tutto sesto, luce 12m, freccia 6m.

Importiamo il file IGES della struttura all'interno dell'ambiente sap20014.

Assegniamo INCASTRO alle imposte dell'arco, e in chiave CERNIERA interna selezionando le due aste più vicine al nodo e assegnando che rilasci il momento da sinistra a destra.

Definiamo le sezioni rettangolari (0,4m x 0,3m) del concio che compone l'arco. 

[vista estrusa]

Definiamo il carico distribuito assegniamo 0 a peso proprio.

Selezioniamo tutte le aste.

Asseganiamo il carico distribuito con un valore di 10 KN in modalità Gravity Projected.

Selezioniamo la combinazione di carico, carico distribuito e lanciamo l'analisi.

Deformata dell'arco.

Reazioni vincolari, notiamo come la componente Y è perfettamente il doppio della componente X che rappresenta la forza di spinta(ql²/2f).

Sforzo assiale:

all'imposta 52,21 KN DI COMPRESSIONE.

Momento flettente.

Sforzo di taglio.

Vediamo come si comporta l'arco a sesto ribassato ricordando che la luce è la stessa, così come il carico distribuito e che invece la freccia è la metà dell'arco a tutto sesto.

Deformata dell'arco.

Reazioni vincolari, notiamo come la componente X (della spinta) comincia a crescere rispetto a quella Y pareggiandola essendo la freccia in questo caso la perfetta metà della luce.

Sforzo assiale:

all'imposta 84,75 KN DI COMPRESSIONE. Questo valore è aumentato considerevolmente rispetto all'arco a tutto sesto.

Momento di flettente.

Sforzo di taglio.

Infine studiamo il comportamento dell'arco parabolico.

Ci attendiamo che essendo un arco funicolare e non catenario lavori solo a sforzo normale.

Deformata dell'arco.

Reazioni vincolari.

Sforzo assiale.

Con quest’esercitazione vogliamo studiare il comportamento di un impalcato quando esso è sollecitato da forze esterne di tipo orizzontale e di come i suoi controventi, progettati per questa struttura, rispondano a quest’ultime. La rappresentazione grafica, «l’avatar» dei controventi si configura come una molla, tesa alla più immediata fruizione del comportamento dei controventi, elastico reversibile. L’obiettivo, una volta calcolata la rigidezza delle molle, è quello di calcolare il centro di tutte le rigidezze dei controventi, luogo dei punti in cui le forze esterne applicate avranno un momento pari a zero, con conseguente rotazione rigida nulla di tutto l’impalcato.

Dunque, una volta effettuato il dimensionamento e la scelta della tipologia costruttiva (in questo caso abbiamo preferito una tecnologia in c.l.s. armato), attraverso uno strumento di calcolo elettronico, un foglio excel, riusciremo ad inserire tutti i dati e ad ottenere i risultati cercati: CALCOLO DEL CENTRO DELLE RIGIDEZZE. 

Pianta dell’impalcato in c.l.s. armato-Sezione impalcato

Rappresentazione «avatar» delle rigidezze K dell’impalcato in esame:

Definiamo un sistema di riferimento cartesiano, assi X-Y, e calcoliamo la distanza di ogni singolo controvento dall’origine degli assi, siano essi disposti in senso verticale (dv) sia in senso orizzontale (do):

dv1: 0 cm

dv2: 6 cm

dv3: 12 cm

dv4: 18 cm

dv5: 24 cm

dv6: 30 cm

do1: 0 cm

do2: 6 cm

do3: 12 cm

Sezione dei pilastri = 30x30 cm

Altezza dei pilastri in c.l.s. armato: H = 400 cm

Modulo di Young (E) = 21000 N/mm

È importante, a questo punto, nominare numericamente ogni pilastro così da poter definire ogni telaio, rispetto al numero dei pilastri che lo compongono sia nella direzione x che nella direzione y:

Telaio:                    n° pilastri:

    1                          1-6-12

    2                          2-7-13

    3                          3-8-14

    4                            9-15

    5                         4-10-16

    6                         5-11-17

    7                       1-2-3-4-5

    8                    6-7-8-9-10-11

    9                12-13-14-15-16-17

Iniziamo ora a compilare la tabella excel:

STEP1: calcolo delle rigidezze traslanti dei controventi dell'edificio: data dalla somma delle rigidezze di ciascun pilastro che compone ciascun telaio.

STEP2: Tabella sinottica dei controventi e delle loro distanze dell’origine.

• STEP3: CALCOLO DEL CENTRO DI MASSA: dopo aver suddiviso la pianta dell’impalcato in macro aree, geometricamente riconducibili a figure semplici, come rettangoli o quadrati, si procede alla determinazione del baricentro:

• STEP4: calcolo del centro di rigidezze e delle rigidezze globali: sommo tutte le rigidezze dei controventi, prima nella direzione orizzontale e poi in quella verticale. A questo punto posso determinare il centro delle rigidezze, rispetto alla sua coordinata x e y, facendo il rapporto tra la sommatoria del prodotto, di ogni singola rigidezza per il proprio braccio, per la rigidezza totale, sia verticale sia orizzontale. Il passo successivo sarà quello di calcolare la rigidezza torsionale (K): la sommatoria dei prodotti delle rigidezze di ciascun telaio per la distanza al quadrato di ognuno di essi rispetto a C = (x,y).

• STEP5: ANALISI DEI CARICHI SISMICI: Individuo il carico Q del solaio (somma di qs+qp+qa) e lo moltiplico per il coefficiente di contemporaneità (y), ottenendo così i pesi sismici. Successivamente moltiplico tale valore per il coefficiente d’intensità sismica (c), ottenendo così il valore della forza sismica orizzontale.

• STEP6/7: Ripartizione della forza sismica lungo X e Y: adesso posso capire come la forza sismica potrebbe ripartirsi lungo le due direzioni dell’impalcato. Il foglio excel, così concepito, mi permette di trovare direttamente la traslazione orizzontale e quella verticale e conseguentemente la rotazione dell’impalcato. È ora possibile, dunque, individuare come ogni forza sismica si ripartisce per ciascun telaio, ricavandone infine le reazioni di contrasto che ogni impalcato esercita al fine di contrastare la suddetta forza sismica orizzontale. 

Per avere una successiva verifica dei calcoli appena studiati, possiamo ora disegnare su Sap2000 la struttura dell’impalcato analizzata, così da verificarne la corrispondenza dei valori e visualizzare la deformazione messa in atto dall’azione del sisma orizzontale. 

Importiamo il modello dell’impalcato, disegnato su rhinoceros, in ambiente Sap2000, ricordandosi di prestare attenzione alla coerenza delle unità di misura. 

Assegniamo i vincoli esterni di tipo incastro alla base di ogni pilastro. 

Assegnami ai pilastri una sezione in cemento armato 0,3 x 0,3 m.

Assegniamo alle travi una sezione in cemento armato 0,3 x 0,7 m. Modifichiamo le proprietà della sezione della trave con l’obiettivo di renderla infinitamente rigida, tipicamente Shear-Type. A tal fine aumentiamo spropositatamente i valori del momento d’inerzia in asse 2 (y) e 3 (x).  

Definiamo l’impalcato rigido del “solaio”: selezioniamo tutti i nodi dell’impalcato, compreso il centro delle rigidezze. Assegna>nodi>vincoli interni>tipo di vincolo>Diaphragm che conferisce all’intera aria selezionata rigidezza tale da non avere dilatazioni né accorciamenti, ma solo traslazioni.

Definiamo lo schema di carico della forza sismica orizzontale: Definisci>schemi di carico>agg. Nuovo schema carico>peso proprio moltiplicat. = 0 à OK.

Selezioniamo il centro delle rigidezze e assegniamoli lo schema di carico appena definito nella direzione y, con valore 230,40 KN.

Lanciamo l’analisi e verifichiamone gli spostamenti.  

Con essa prendiamo coscienza del fatto che l’unico spostamento rigido di cui tener conto è quello in asse y, nella direzione della forza sismica orizzontale. La rotazione rigida risulta quasi nulla e, perciò, trascurabile.

Roma 4-06-2014                                                                           T.R.

In collaborazione con Alessandro Petroni

In riferimento allo schema strutturale di carpenteria di sopra verifichiamo che l'abbassamento della trave che sostiene lo sbalzo del solaio rientri nel rapporto: abbassamento<luce dello sbalzo/250. Nelle diverse tecnologie già studiate di Legno Lamellare, Acciaio, Cemento Armato.

Il foglio excell realizzato per la verifica richiede l'inserimento dei seguenti dati: interasse tra le travi portanti, luce dello sbalzo, carico strutturale, carico portato, carico accidentale. E la definizione dell'altezza ingegnerizzata della trave, il foglio excell a questo punto calcola il peso proprio della trave e lo somma ai carichi di sopra.

Il rapporto abbassamento<luce dello sbalzo/250 è verificato.

Il foglio excell realizzato per la verifica richiede l'inserimento dei seguenti dati: interasse tra le travi portanti, luce dello sbalzo, carico strutturale, carico portato, carico accidentale. E la definizione dell'altezza ingegnerizzata della trave, il foglio excell a questo punto calcola il peso proprio della trave e lo somma ai carichi di sopra.

Il rapporto abbassamento<luce dello sbalzo/250 è verificato.

Il foglio excell realizzato per la verifica richiede l'inserimento dei seguenti dati: interasse tra le travi portanti, luce dello sbalzo, carico strutturale, carico portato, carico accidentale. E la definizione dell'altezza ingegnerizzata della trave, il foglio excell a questo punto calcola il peso proprio della trave e lo somma ai carichi di sopra.

Il rapporto abbassamento<luce dello sbalzo/250 è verificato.

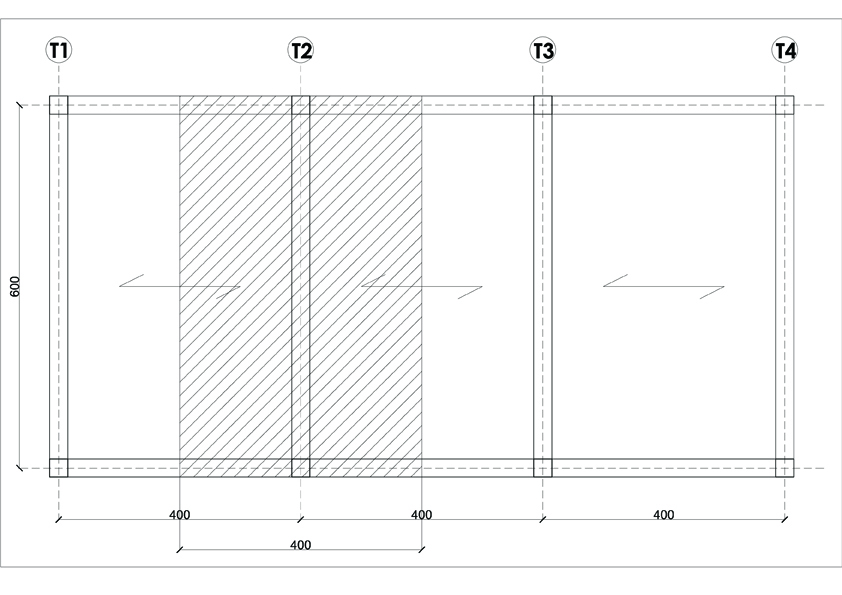
CONSIDERATO IL SEGUENTE SCHEMA DI CARPENTERIA CON INTERASSE TRA LE TRAVI DI 4,00 m E LUCE DI 6,00 m.

LE TRAVI T2 E T3 SONO QUELLE CHE PORTANO UN MAGGIORE PESO CON UN AREA DI INFLUENZA DI 24 mq.

CONSIDERATA LA SEGUENTE TECNOLOGIA DI SOLAIO IN LEGNO, SI PROGETTI LA TRAVE IN LEGNO LAMELLARE GL24c

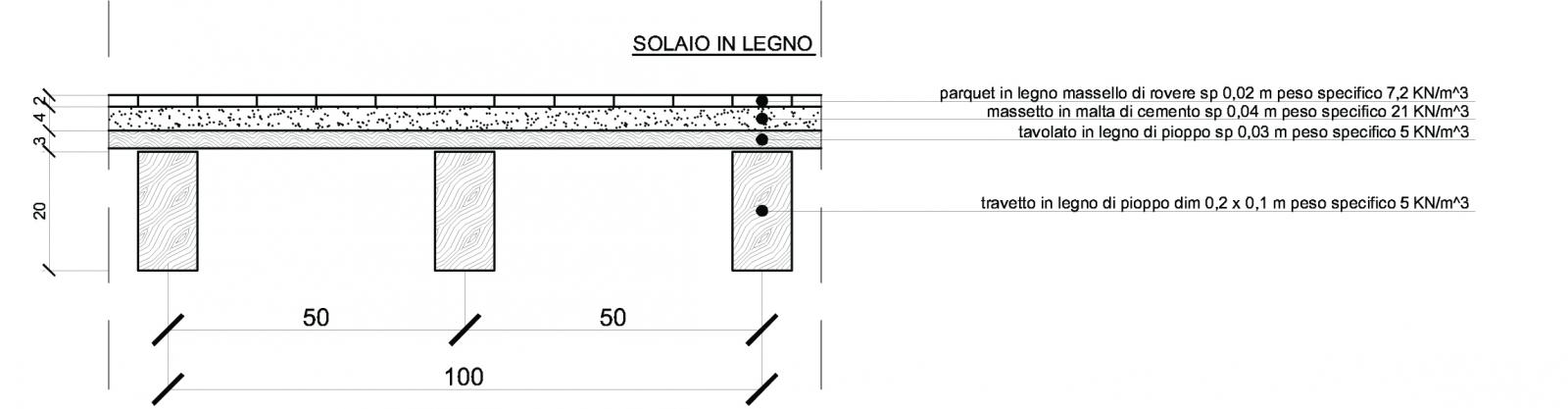
Qs=2 TRAVETTI IN LEGNO DI PIOPPO + TAVOLATO IN LEGNO DI PIOPPO

Qp=MASSETTO IN MALTA DI CEMENTO + PAVIMENTAZIONE parque in massello di rovere + TRAMEZZI/IMPIANTIdaNTC

Qa=CIVILE ABITAZIONEdaNTC

Qs=2x(0,20mx0,10mx1,0mx5KN/mc)/mq+(0,03mx1,0mx1,0mx5KN/mc)/mq=0,35KN/mq

Qp=(0,04mx1,0mx1,0mx21 KN/mc)/mq+(0,02mx1,0mx1,0mx7,2KN/mc)/mq+1,0KN/mq+0,5KN/mq=2,484KN/mq

Qa=2KN/mq

INSERISCO I VALORI DI INTERASSE, DI LUCE, DI Qs, DI Qp, DI Qa, DI b.

L'ALTEZZA DELLA TRAVE NECESSARIA DEVE ESSERE SUPERIORE A 42, 63 CM. QUINDI SUFFICENTE UNA TRAVE DI DIMENSIONI: 30CM X 45CM_LEGNO LAMELLARE GL24c

CONSIDERATA LA SEGUENTE TECNOLOGIA DI SOLAIO IN ACCIAIO, SI PROGETTI LA TRAVE IPE-275

Qs=IPE 160 (peso specifico 78,5 KN/mc area 20,09 cm^2) + SOLETTA IN CLS E LAMIERA GRECATA

Qp=MASSETTO IN MALTA DI CEMENTO + PAVIMENTAZIONE in cotto + TRAMEZZI/IMPIANTIdaNTC

Qa=CIVILE ABITAZIONEdaNTC

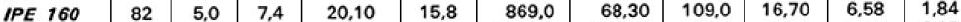
Qs=2x(0,00201m^2x1mx78,5KN/mc)/mq+(0,12mx1,0mx1,0mx24KN/mc)/mq=3,196KN/mq

Qp=(0,01mx1,0mx1,0mx2,8KN/mc)/mq+(0,02mx1,0mx1,0mx21KN/mc)/mq+1,0KN/mq+0,5KN/mq=1,948KN/mq

Qa=2KN/mq

INSERISCO I VALORI DI INTERASSE, DI LUCE, DI Qs, DI Qp, DI Qa, DI fyK.

IL PROFILO IPE-275 DEVE POSSEDERE UN VOLERE DI MODULO DI RESISTENZA A FLESSIONE MAGGIORE DI 729,18CM^3.

LA IPE360 E' IL PROFILO DI PROGETTO_

CONSIDERATA LA SEGUENTE TECNOLOGIA DI SOLAIO IN LATERO CEMENTO GETTATO IN OPERA, SI PROGETTI LA TRAVE IN C.A.

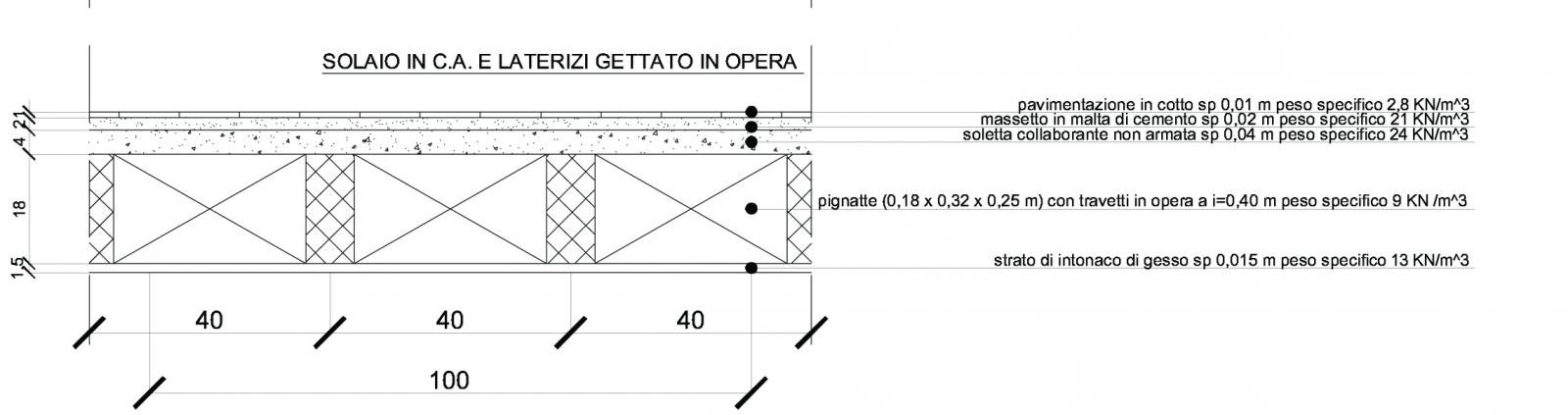
Qs=PIGNATTE CON TARVETTI IN OPERA + SOLETTA IN CLS COLLABORANTE NON ARMATA

Qp=INTONACO +MASSETTO IN MALTA DI CEMENTO + PAVIMENTAZIONE in cotto + TRAMEZZI/IMPIANTIdaNTC

Qa=CIVILE ABITAZIONEdaNTC

Qs=(0,18mx1,0mx1,0mx9KN/mc)/mq+(0,04mx1,0mx1,0mx24KN/mc)/mq=2,58KN/mq

Qp=(0,015mx1,0mx1,0mx13KN/mc)/mq+(0,02mx1,0mx1,0mx21KN/mc)/mq+(0,01mx1,0mx1,0mx2,8KN/mc)/mq+1,0KN/mq+0,5KN/mq=2,115KN/mq

Qa=2KN/mq

INSERISCO I VALORI DI INTERASSE, DI LUCE, DI Qs, DI Qp, DI Qa, DI RcK.

CON UNA BASE DI 30 CM E' NECESSARIA UN ALTEZZA TOTALE MAGGIORE DI 48,31 CM.

TRAVE DI CEMENTO ARMATO CON FERRI DI CLASSE 450 E CALCESTRUZZO Rck 30, RISULTA 30CM X 50 CM.

PER LA TECNOLOGIA DEL CEMENTO ARMATO, CONSIDERANDO IL RAPPORTO PESO/RESISTENZA DEL MATERIALE, E' OPPORTUNO ACCERTARSI CHE LA TRAVE PROGETTATA SIA VERIFICATA AGGIUNGENDO ANCHE IL PESO PROPRIO DELLA TRAVE.

QUINDI:

(0,30mx0,50mx1,0mx25KN/mc)/m=3,75KN/m

SOMMIAMO QUESTO CARICO NELLA CASELLA DEL CARICO TOTALE RIPARTITO RICORDANDOCI DI MOLTIPLICARLO PER IL COEFFICENTE DI SICUREZZA DEL CARICO STRUTTURALE:

LA TRAVE NON RISULTA VERIFICATA, ED E' RICHIESTA UNA ALTEZZA MINIMA DI 51CM CHE INGEGNERIZZATA DIVENTA 55CM.

VERIFICHIAMO QUESTA NUOVA SEZIONE CON LA STESSA PROCEDURA:

(0,30mx0,55mx1,0mx25KN/mc)/m=4,125KN/m

SOMMIAMO QUESTO CARICO NELLA CASELLA DEL CARICO TOTALE RIPARTITO RICORDANDOCI DI MOLTIPLICARLO PER IL COEFFICENTE DI SICUREZZA DEL CARICO STRUTTURALE:

LA TRAVE QUESTA VOLTA RISULTA VERIFICATA.

MODELLO STRUTTURA

PIANTA

PROSPETTO LATERALE

PROSPETTO FRONTALE

ASSONOMETRIA

SAP 200 V.14 FILE NUOVO

UNITA DI MISURA KN, M,C. SPAZIO VUOTO

FILE-IMPORTA-FILE IGES

IMPOSTAZIONI DI IMPORTAZIONE FILE IGES

STRUTTURA IN AMBIENTE SAP

SELEZIONA STRUTTURA-EDITA-EDITAPUNTI-UNISCI PUNTI

TOLLERANZA VALORE PREDEFINITO

SELEZIONA STRUTTURA-ASSEGNA FRAME-RILASCIA/SEMINCASTRI

RILASCIA MOMENTI CREA CERNIERE INTERNE 

CERNIERE INTERNE

SELEZIONA NODI LATERALI-ASSEGNA-NODO-VINCOLI ESTERNI CERNIERE ESTERNE

STRUTTURA VINCOLATA

DEFINISCI-SCHEMI DI CARICO

CARICO SU NODO PESO PROPRIO STRUTTURA 0

DEFINISCI SEZIONE

SEZIONE DEFINITA TUBOLARE ACCIAIO 0,60 X 0,05 M

SELEZIONA STRUTTURA-ASSEGNA-FRAME-SEZIONE FRAME

SEZIONE ASSEGNATA

SELEZIONA-SELEZIONA-SPECIFICAZIONE COORDINATE-CLICCA NODO NEL PIANO XY

ASSEGNA-CARICO NODO-FORZE

FORZE SU NODI -200 KN SU ASSE GLOBALE Z

STRUTTURA CARICATA

IMPOSTA VISUALIZZAZIONE

NOMINA ASTE E NODI DESIGNAZIONE

LANCIA ANLISI

IMPOSTA CASI DI CARICO

STRUTTURA DEFORMATA

ORDINA DI VISUALIZZARE REAZIONI VINCOLARI

ORDINA DI VISUALIZZARE TENSIONI

ASTE COMPRESSE 

VISUALIZZA-MOSTRA TABELLE

SPUNTA DATI DA TABELLARE

SCEGLI ELEMENT FORCES-FRAME

FILE-ESPORTA TABELLA CORRENTE-SU EXCEL

ORDINA RISULTATI TENSIONI SU EXCEL DAL PIU GRANDE AL PIU PICCOLO

VERIFICA STRUTTURA IN ACCIAIO

LA STRUTTURA E' VERIFICATA

--FINE--