L’obiettivo di questa prima esercitazione, è il dimensionamento della trave più sollecitata della seguente pianta di carpenteria. Tale operazione è da considerarsi solo in relazione al carico che interessa la trave, e prevede il dimensionamento della stessa in relazione a tre ipotesi tecnologiche relative all’utilizzo di tre materiali: una prima in legno, una seconda in acciaio ed infine la terza in calcestruzzo.
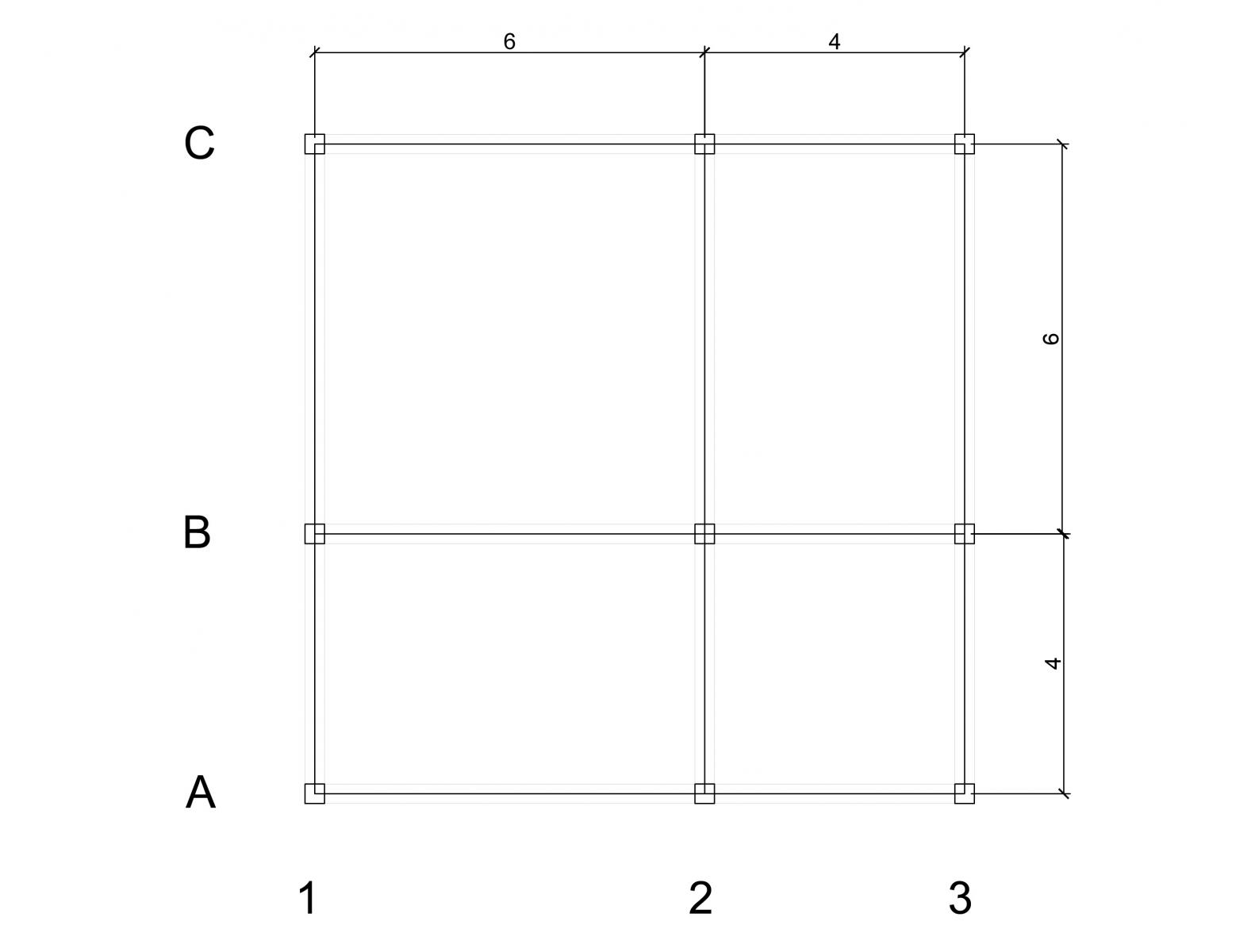
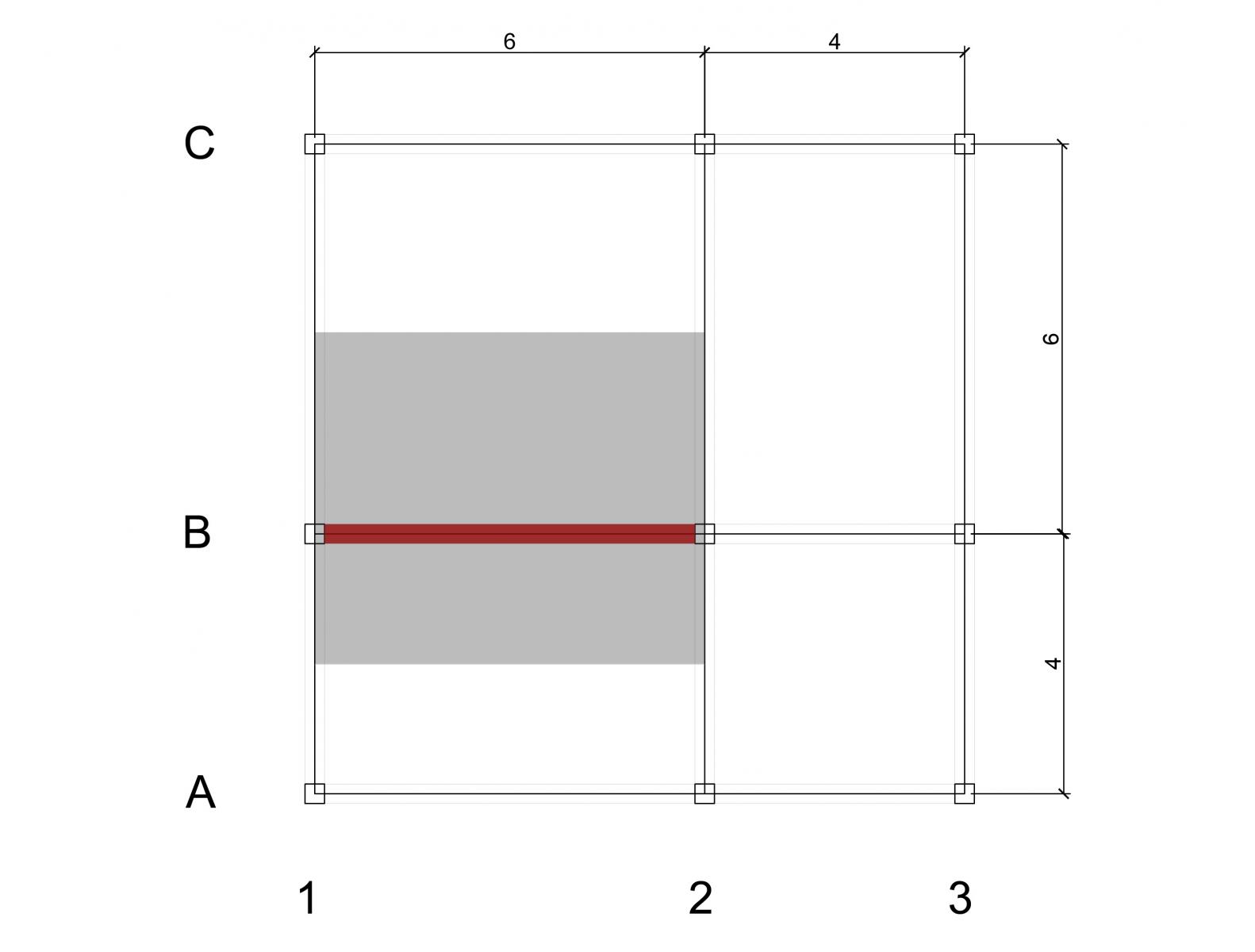
Prima di procedere, occorre individuare la trave maggiormente sollecitata. Si individua facilmente che la trave deputata a sostenere il carico maggiore è la B, nel tratto 1-2 di luce 6m. Quest’ultima è soggetta un’area di influenza pari a 30mq, ossia la somma delle metà delle campate a sx e dx della trave (INTERASSE: 3m+2m=5m) moltiplicate per la luce che interessa la trave (5mx6m=30mq).
Considero dunque un progetto di solaio in LEGNO:
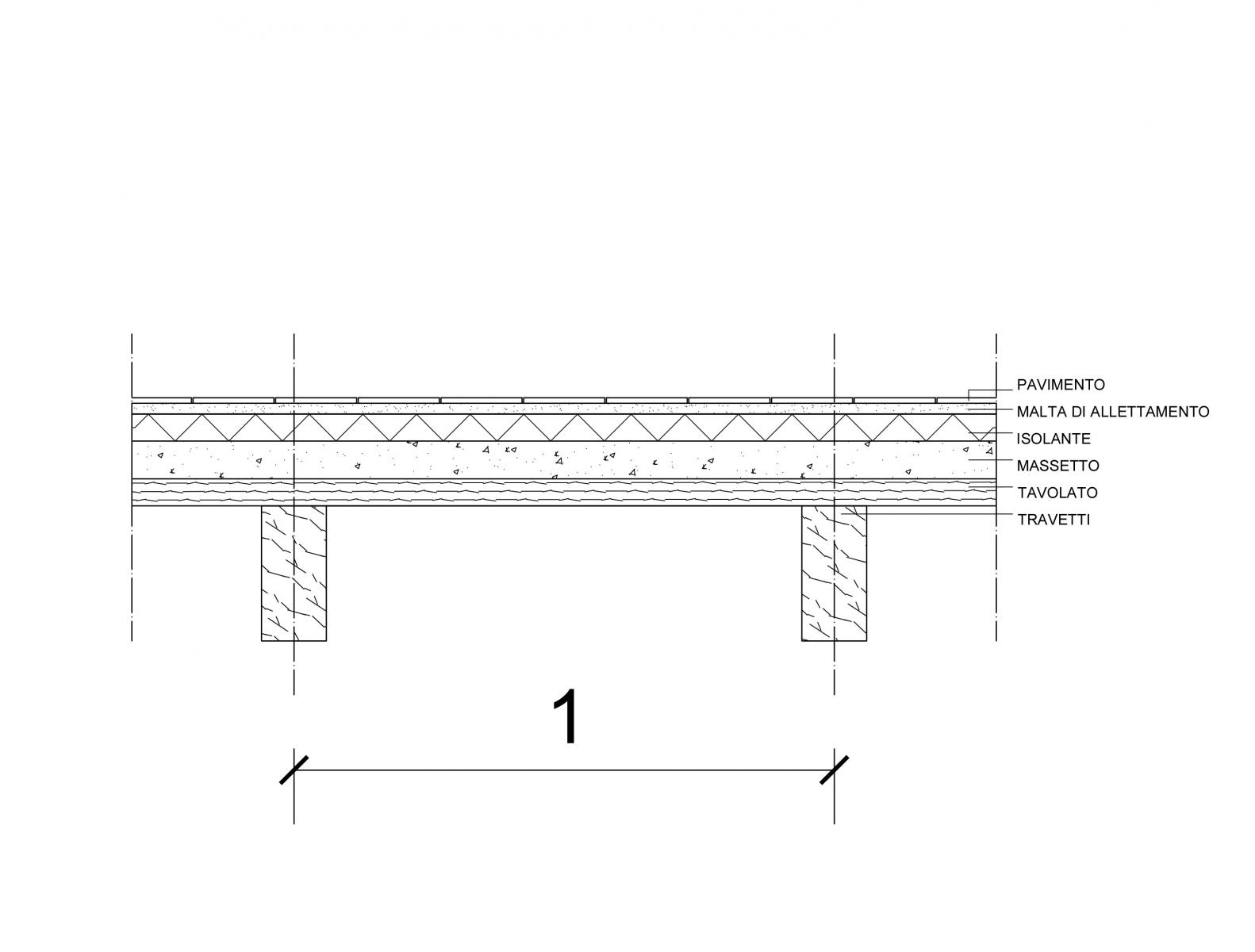
È composto da elementi costruttivi distinguibili in strutturali e non strutturali che caratterizzeranno il carico permanente (qp) esercitato sulla trave.
Seguendo queste due categorie calcolo il carico degli elementi strutturali (qs):
TRAVETTI: dimensione: 0,12x0,25 m
peso specifico: 6kN/mc
peso per mq di solaio: (0,12x0,25x1,00)mc/mq x 6kN/mc = 0,18kN/mq
TAVOLATO: dimensione: 0,05m (spessore)
peso specifico: 6kN/mc
peso per mq di solaio: (0,05x1,00x1,00)mc/mq x 6kN/mc = 0,3kN/mq
SOMMANDO RISPETTIVI PESI PER MQ DI SOLAIO OTTENGO: qs = 0,18+0,3 = 0,48kN/mq
Quindi si passa al calcolo del carico degli elementi non strutturali (qp):
MASSETTO (in cls): dimensione: 0,07x1,00x1,00 m
peso specifico: 21kN/mc
peso per mq di solaio: (0,07x1,00x1,00)mc/mq x 24kN/mc = 1,68kN/mq
ISOLANTE (fibra di legno): dimensione: 0,05x1,00x1,00 m
peso specifico: 0,6kN/mc
peso per mq di solaio: (0,05x1,00x1,00)mc/mq x 0,6kN/mc = 0,03kN/mq
MALTA DI ALLETTAMENTO (malta di cemento): dimensione: 0,02x1,00x1,00 m
peso specifico: 21kN/mc
peso per mq di solaio: (0,02x1,00x1,00)mc/mq x 21kN/mc = 0,42kN/mq
PAVIMENTAZIONE (gres): dimensione: 0,01x1,00x1,00 m
peso specifico: 8kN/mc
peso per mq di solaio: (0,01x1,00x1,00)mc/mq x 8kN/mc = 0,08kN/mq
IMPIANTI: peso per mq di solaio secondo normativa: 0,5kN/mq
TRAMEZZI: peso per mq di solaio secondo normativa: 1 kN/mq
SOMMANDO RISPETTIVI PESI PER MQ DI SOLAIO OTTENGO: qp = 1,47+0,03+0,42+0,08+0,5+1 = 3,50 kN/mq
Nel valutare la somma dei carichi esercitati sulla trave vanno considerati anche i carichi accidentali (qa). Secondo normativa, per destinazione d’uso a civile abitazione: qa=2kN/mq
Inizio dunque ad inserire i valori dei carichi all’interno del foglio di calcolo.

Un dato importante è l’interasse della trave, che serve a definire in valore esatto del carico del solaio agente sulla trave. Fino ad ora infatti conosco il carico agente su un mq di solaio, ma sulla trave grava un interasse di 5m, per ogni “unità lineare di luce”.
Un’altra cosa da ricordare, è che ogni carico (qs, qp, qa) va moltiplicato per un coefficiente di sicurezza imposto dalla normativa, che consente di ridurre fattori accidentali o incertezze di ordine probabilistico relative all’utilizzo della struttura ed al materiale utilizzato.
Dunque: qu= (qs x 1,3 + qp x 1,5 + qa x 1,5)kN/mq x 5m
Ottengo dunque un carico unitario qu= 44,37 kN/m
Dal momento che mi trovo davanti ad una trave appoggiata, il momento massimo agente (Mmax) sarà pari a ql^2/8.
Mmax = [44,37 kN/m x (6m)^2]/8 =199,67Knm
Considero di realizzare la trave in legno lamellare. Il legno lamellare di conifera, di classe GL24C possiede una resistenza caratteristica a flessione pari a f m,k =24 N/mmq
Tale valore va moltiplicato per un coefficiente diminuitivo, relativo alla durata di utilizzo della struttura ed alle condizioni di umidità, che ne alterano le prestazioni nel tempo poiché causano deformazioni nelle travi. Considero una durata di carico permanente ed una classe di servizio 2 (che identifica la presenza di umidità elevata solo per poche settimane l’anno ed una temperatura media mite) .
Per legno lamellare, alle suddette condizioni:
K mod= 0,60
Ma il prodotto di K mod x f m,k va diviso per il coefficiente di sicurezza del materiale, che per legno lamellare è pari a 1,45
Ottengo così: fd =(24 N/mmq x 0,60) / 1,45
Stabilisco la base della sezione della trave (in coerenza con il pilastro) e svolgendo i calcoli, ricordando che il momento è espresso in kNm, incompatibile con fd espresso invece in N/mmq, e pertanto va convertito in N/mmq moltiplicando x 1000.
Ottengo h min = 63,41 cm (in cm poiché la base attribuita è in cm)
Utilizzando una trave ingegnerizzata, ottengo una sezione pari a b = 30 cm; h =65 cm
A questo punto verifico se la trave resiste considerando non solo il carico che il solaio esercita su di essa, ma anche il peso proprio.
Calcolo il peso della trave per m lineare:
qt=(0,35x0,65x1)mc/m x6kN/mc = 1,37kN/m
Moltiplico quindi per il coefficiente di sicurezza:
qut= 1,37 x 1,3= 1,78kN/m
sommando tale valore al qu precedentemente ottenuto verifico se la dimensione della trave scelta sia adeguata al carico strutturale ottenuto dopo il dimensionamento della trave.
L’h min ottenuta è aumentata a 69,48cm. Ne consegue che il profilo ingegnerizzato da scelto non è adeguato.
Verifico nuovamente:
qt=(0,35x0,70x1)mc/m x6kN/mc = 1,41kN/m
qut= 1,37 x 1,3= 1,91kN/m
Ottengo un’ h di 69,65cm. Essendo minore di H = 70, risulta verificata numericamente, tuttavia lo scarto di meno di mezzo cm in un materiale come il legno mi sembra irragionevole. Decido di aumentare la sezione del pilastro così da compensare meglio i problemi di sforzo normale e conseguente snellezza relativi al pilastro.
Allo stesso tempo compenso la proporzione i base ed altezza della sezione della trave: b=40cm; h=65 ottengo:
qt=(0,40x0,65x1)mc/m x6kN/mc = 1,56kN/m
Con I valori attribuiti, ottengo una h min = 60,87 cm (considerando anche il peso proprio della trave) ed una H = 65cm

La trave con sezione rettangolare di 40 x 65 cm risulta così VERIFICATA.
ACCIAO:
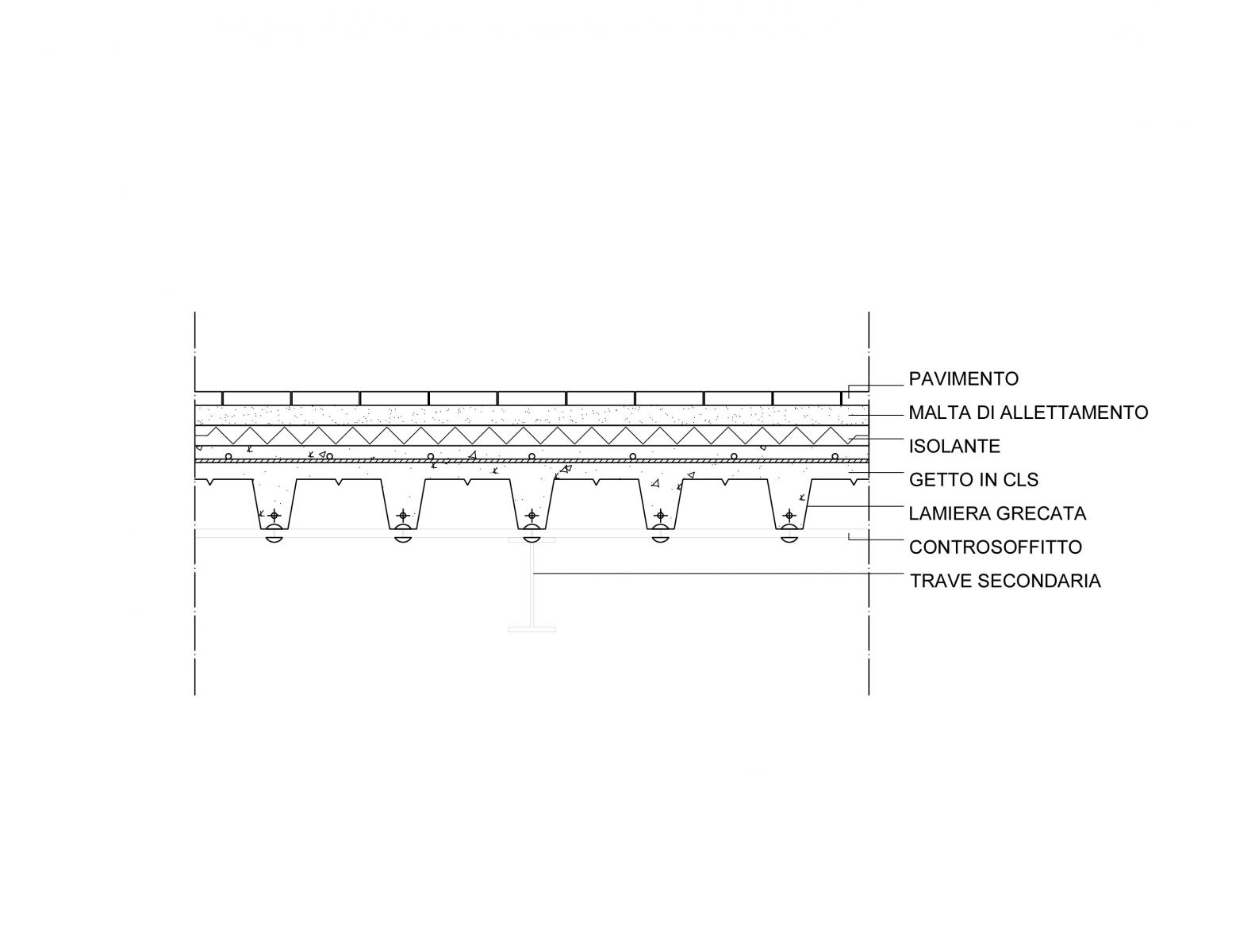
calcolo il carico degli elementi strutturali (qs):
TRAVI SECONDARIE: dimensione: 0,00285 m
peso specifico: 78,5kN/mc
peso per mq di solaio: (0,00285x1,00)mc/mq x 78,5kN/mc = 0,22kN/mq
LAMIERA GRECATA: peso per mq di solaio: 0,11kN/mq
GETTO IN CLS (caldana): dimensione: 0,0675 (AREA SEZIONE DI 1m)
peso specifico: 21kN/mc
peso per mq di solaio: (0,0675x1,00)mc/mq x 21kN/mc = 1,41kN/mq
SOMMANDO RISPETTIVI PESI PER MQ DI SOLAIO OTTENGO: qs = 0,22+0,11+1,41 = 1,74kN/mq
Quindi si passa al calcolo del carico degli elementi non strutturali (qp):
ISOLANTE (fibra di legno): dimensione: 0,03x1,00x1,00 m
peso specifico: 0,6kN/mc
peso per mq di solaio: (0,03x1,00x1,00)mc/mq x 0,6kN/mc = 0,018kN/mq
MALTA DI ALLETTAMENTO (malta di cemento): dimensione: 0,03x1,00x1,00 m
peso specifico: 21kN/mc
peso per mq di solaio: (0,03x1,00x1,00)mc/mq x 21kN/mc = 0,63kN/mq
PAVIMENTAZIONE (gres): dimensione: 0,01x1,00x1,00 m
peso specifico: 8kN/mc
peso per mq di solaio: (0,01x1,00x1,00)mc/mq x 8kN/mc = 0,08kN/mq
CONTROSOFFITTO: dimensione: 0,012x1,00x1,00 m
peso specifico: 13kN/mc
peso per mq di solaio: (0,012x1,00x1,00)mc/mq x 8kN/mc = 0,16kN/mq
SOMMANDO RISPETTIVI PESI PER MQ DI SOLAIO OTTENGO: qp = 0,018 +0,63+0,8+1,16 = 2,61 kN/mq
Nel valutare la somma dei carichi esercitati sulla trave vanno considerati anche i carichi accidentali (qa). Secondo normativa, per destinazione d’uso a civile abitazione: qa=2kN/mq
Inizio dunque ad inserire i valori dei carichi all’interno del foglio di calcolo.

Scelgo un acciaio S275
A questo punto il valore di resistenza dell’acciaio viene diviso per il coefficiente di sicurezza 1,05 ottenendo fyd.
Dividendo il Momento max per il valore di fyd ottengo il mio Wxmin=788cmc.
Tale valore va ingegnerizzato, e pertanto scelgo un profilo IPE 360 CON Wx=904
La trave possiede un peso proprio al metro pari a 57,1kg/m. Converto in kN, 0,571kN/m per fare la verifica. Moltiplico al solito per il coefficiente di sicurezza ed ottengo che Wxmin =801. Wx>wxmin, quindi la trave è VERIFICATA.

CALCESTRUZZO:
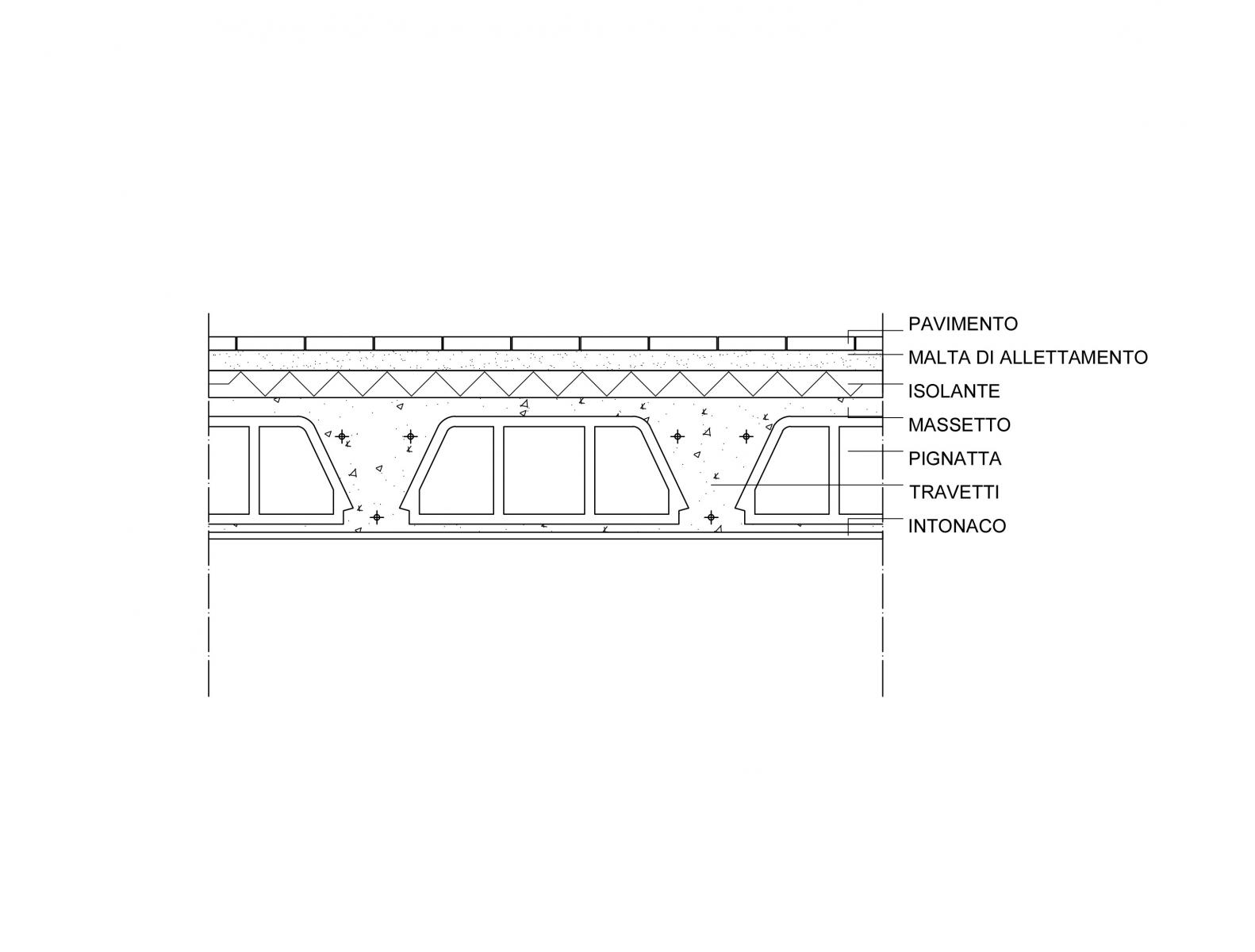
calcolo il carico degli elementi strutturali (qs):
TRAVETTI: dimensione: area sezione: 0.021mq
peso specifico: 21kN/mc
peso per elemento: (0,021x1,00)mc/mq x 21kN/mc = 0,44kN/mq
numero travetti per mq di solaio: 2
peso totale per mq di solaio: 2x0.44kN/mq= 0,88kN/mq
PIGNATTA: dimensioni: 0,16x0,42x0,50 m (area frontale: 0,059 mq)
peso per elemento: 18,1kg (0,18N)
numero pignatte per mq di solaio: 4
peso totale per mq di solaio: 4x0,18kN/mq= 0,72kN/mq
SOLETTA COLLABORANTE: dimensione: 0,03
peso specifico: 21kN/mc
peso per mq di solaio: (0,03x1,00X1,00)mc/mq x 21kN/mc = 0,63kN/mq
SOMMANDO RISPETTIVI PESI PER MQ DI SOLAIO OTTENGO: qs = 0,88+0,72+0,63 = 2,23kN/mq
Quindi si passa al calcolo del carico degli elementi non strutturali (qp):
ISOLANTE (fibra di legno): dimensione: 0,04x1,00x1,00 m
peso specifico: 0,6kN/mc
peso per mq di solaio: (0,03x1,00x1,00)mc/mq x 0,6kN/mc = 0,024kN/mq
MALTA DI ALLETTAMENTO (malta di cemento): dimensione: 0,03x1,00x1,00 m
peso specifico: 21kN/mc
peso per mq di solaio: (0,03x1,00x1,00)mc/mq x 21kN/mc = 0,63kN/mq
PAVIMENTAZIONE (gres): dimensione: 0,01x1,00x1,00 m
peso specifico: 8kN/mc
peso per mq di solaio: (0,01x1,00x1,00)mc/mq x 8kN/mc = 0,08kN/mq
INTONACO: dimensione: 0,01x1,00x1,00 m
peso specifico: 18kN/mc
peso per mq di solaio: (0,01x1,00x1,00)mc/mq x 18kN/mc = 0,18kN/mq
IMPIANTI: peso per mq di solaio secondo normativa: 0,5kN/mq
TRAMEZZI: peso per mq di solaio secondo normativa: 1 kN/mq
SOMMANDO RISPETTIVI PESI PER MQ DI SOLAIO OTTENGO: qp = 0,024 +0,63+0,08+0,18+0,5+1 = 2,41kN/mq
Destinazione d’uso a civile abitazione: qa=2kN/mq
Inserisco i valori nel foglio elettronico:

Dopo aver ottenuto il carico unitario, attribuisco i miei valori di resistenza caratteristica, relativi alla scelta del materiale: acciao B450 (fy=450N/mmq) ed un CLS C45/55 (fc=45N/mmq). Moltiplicando per gli opportuni coefficienti di sicurezza si ottengono i valori di progetto.
Ottengo un hu di 36,82cm, cui sommando la dimensione del copriferro arriverò ad una hmin=40,82cm
Da qui la scelta di una H ingegnerizzata pari a H =45cm.
A questo punto il foglio excel povvede al calcolo del peso unitario per ogni metro di trave considerando il volume per il peso del CLS
Inserendo il peso proprio della trave (moltiplicato per il coefficiente di sicurezza 1,3), al carico unitario supportato dalla trave, sono in grado di capire se l’H scelta consente alla trave di resistere al carico portato + il carico proprio.

La sezione (30x45)cm risulta VERIFICATA
Commenti recenti