Esercitazione 4_Metodo delle Forze

Introduzione

Il metodo delle Forze è uno dei metodi per risolvere i sistemi strutturali iperstatici.

Ricordiamo che una struttura si dice iperstatica quando i gradi di vincolo sono maggiori dei gradi di libertà. In questo caso le equazioni di equilibrio non sono sufficienti per determinare le reazioni vincolari. Perciò se ci basiamo esclusivamente sulle equazioni cardinali della statica, i sistemi di travi iperstatici sono equilibrati da infinite soluzioni di reazioni vincolari.

Quindi tra le infinite soluzioni di equilibrio statico dovrò scegliere quella che, oltre l’equilibrio, implichi anche la congruenza, ovvero il rispetto dei vincoli esterni ed interni iperstatici nonostante le deformazioni indotte nella struttura dai carichi esterni.

Step_1: Verifica Iperstaticità della Trave

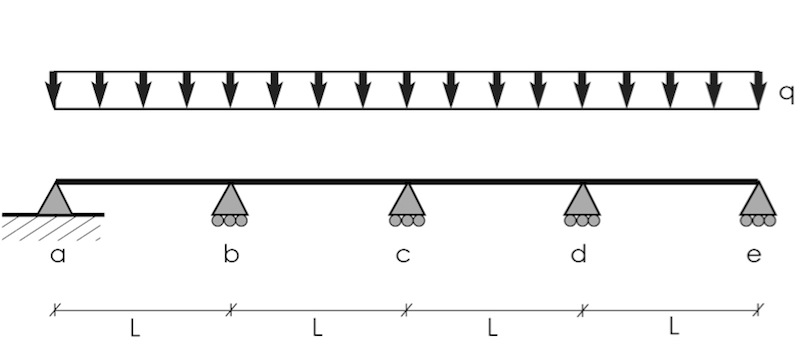
La trave presa in considerazione ha 3 gradi di libertà e 6 gradi di vincolo e quindi è 3 volte iperstatica. 

Step_2: Scegliere la struttura isostatica di riferimento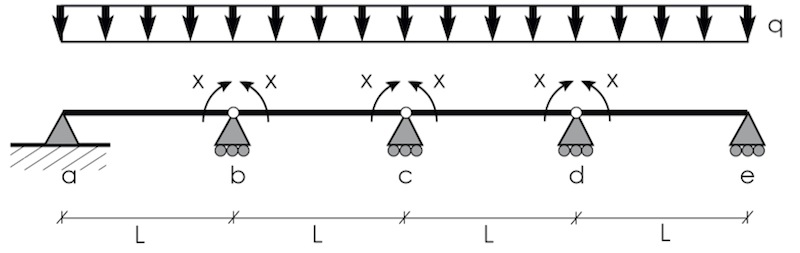

Introducendo 3 momenti in B,C e in D  e separando la struttura otteniamo la nostra isostatica di riferimento. I momenti X sono ovviamente incogniti e rappresentano le nostre incognite iperstatiche.

Step_3: Imporre la congruenza

I momenti X ed il carico Q adesso provocheranno delle rotazioni delle sezioni della trave a destra e a sinistra del carico opposte. Questa ipotesi tuttavia è puramente ipotetica perchè come sappiamo benissimo la trave in realtà è continua. Perciò adesso impostiamo che la rotazione data dai momenti e dal carico a destra e a sinistra dei carrelli sia uguale: 

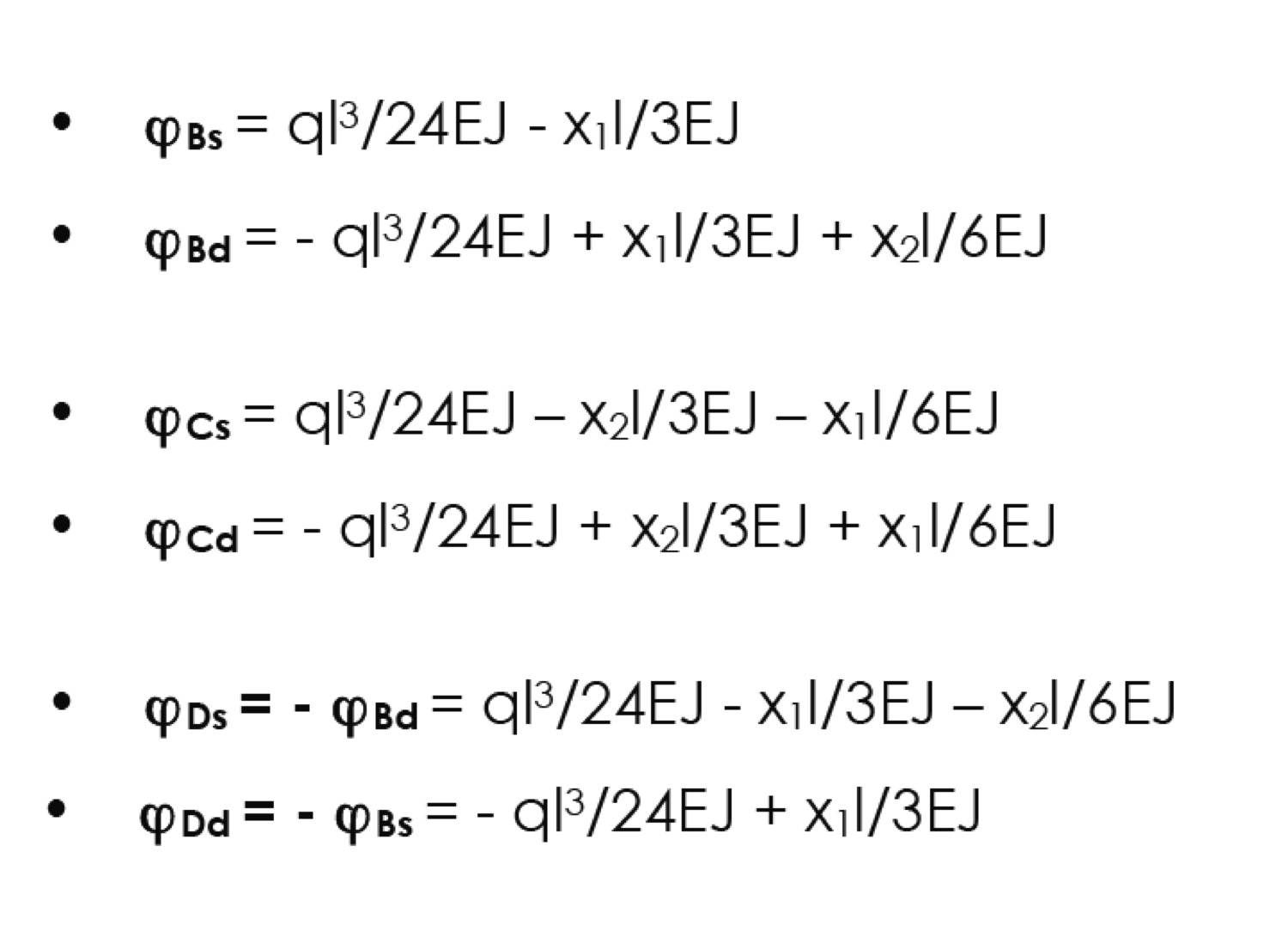
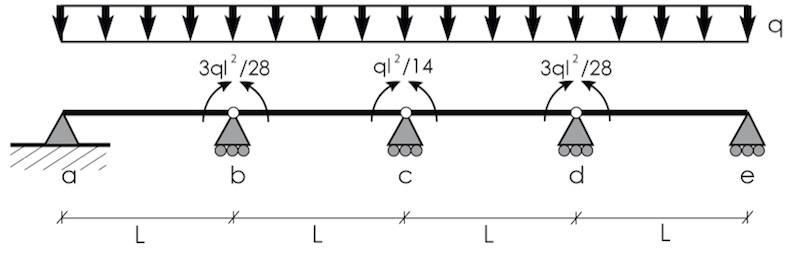
Avendo risolto i momenti adesso possiamo trovare le reazioni vincolari.

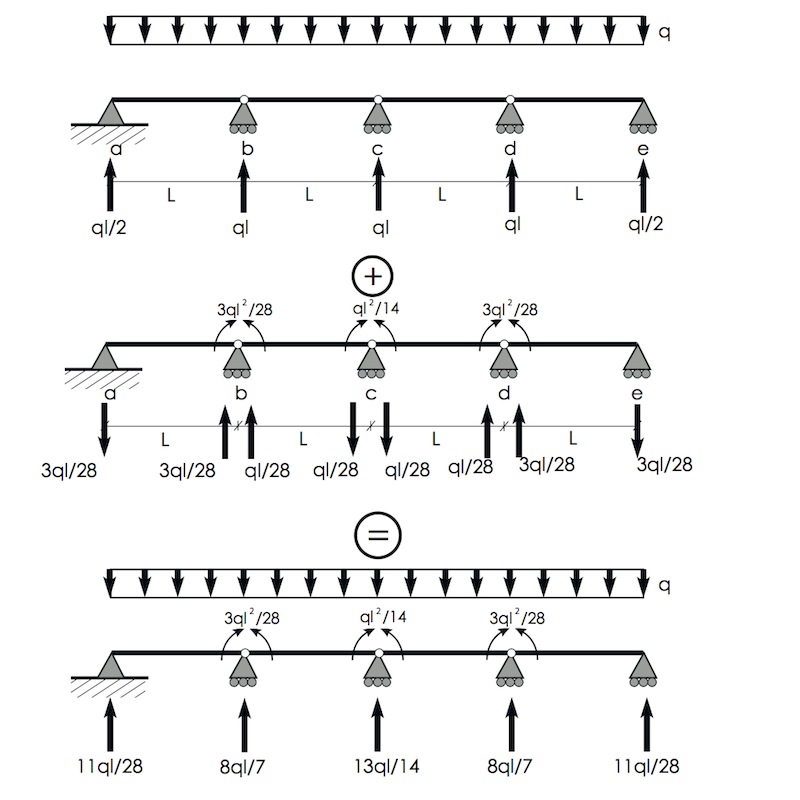
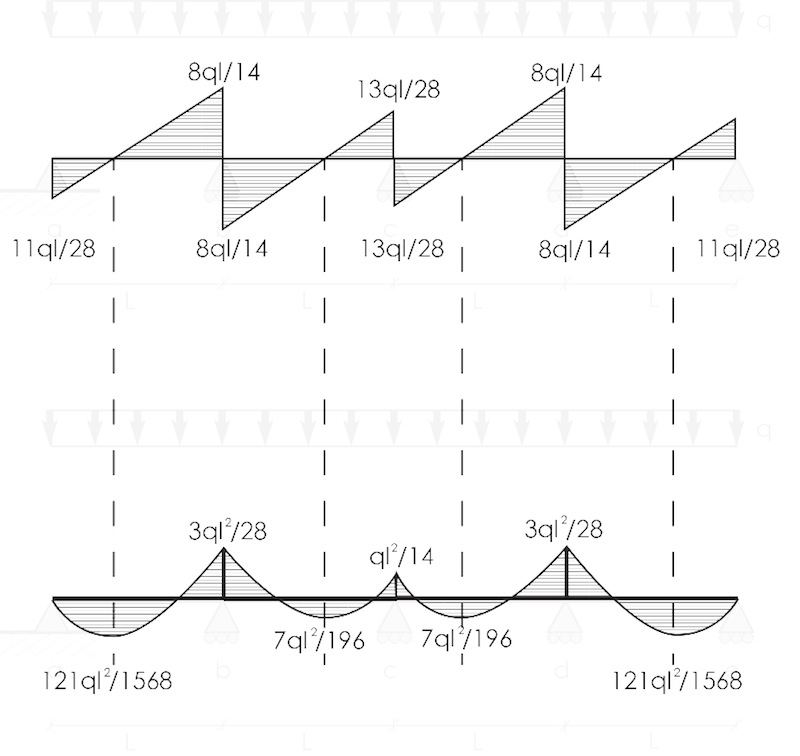
Step_4: Determinare i diagrammi delle sollecitazioni