Introduzione
Il metodo delle rigidezze è un metodo per risolvere strutture iperstatiche ed in particolare abbiamo studiato tale metodo per calcolare portali, telai, telai shear type e travi Virendeel.
Come sappiamo la rigidezza è la forza necessaria a produrre uno spostamento unitario.
Per questa esercitazione vogliamo applicare il metodo delle rigidezze ad una trave Virendeel.

Step_1: Deformata
Conoscendo la deformata di una trave incastro-incastro con cedimento strutturale, o il comportamento deformativo di un telaio shear type possiamo facilmente dedurre la deformata di una Virendeel.

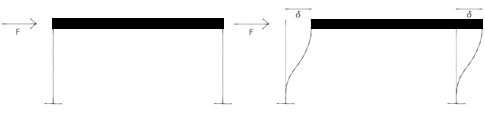
Essendo una trave Virendeel una sovrapposizione di telai shear type possiamo disegnare la deformata.

Step_ 2: Calcolo Taglio e Momento nelle travi
Dallo studio dello shear type sappiamo che il taglio si ripartisce in maniera proporzionale alla rigidezza e alla luce. Perciò ogni pilastro contrasterà metà del carico.
Tp1= F/2
Tp2= F
Tp3= 3F/2
Tp4= 2F
Tp5= 5F/2
Tp6= 3F

Per il calcolo del momento agli incastri basterà moltiplicare il taglio per metà della luce:
Mp1= F/2 * L/2 = FL/4
Mp2= F * L/2 = FL/2
Mp3= 3F/2 * L/2 = 3FL/4
Mp4= 2F * L/2 = FL
Mp5= 5F/2 * L/2 = 5FL/4
Mp6= 3F * L/2 = 3FL/2
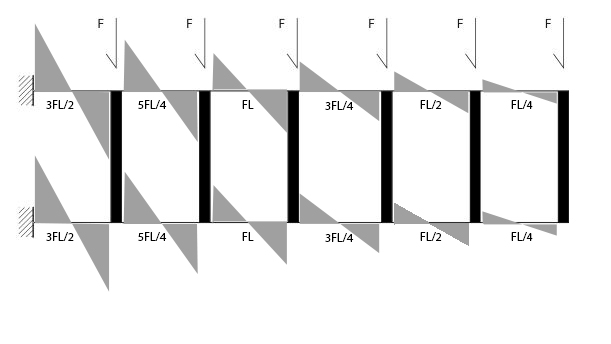
Step_3: Equilibrio al nodo di incastro
Per verificare il comportamento delle travi infinitamente rigide dobbiamo innanzitutto verificare l'equilibrio ai nodi.


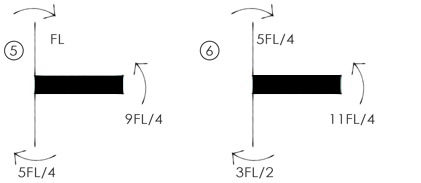
Step_4: Momento nella Trave
Ora possiamo facilmente disegnare il diagramma dei momenti sulle travi.

Step_5: Taglio della Trave
Essendo il momento della trave lineare, avremo un taglio costante che sarà dato dalla somma dei momenti ai bordi diviso la luce della trave.
Tt1 = (FL/4 + FL/4)/H = FL/2H
Tt2= (3FL/4 + 3FL/4)/H = 3FL/2H
Tt3= (5FL/4 + 5FL/4)/H = 5FL/2H
Tt4= (7FL/4 + 7FL/4)/H = 7FL/2H
Tt5= (9FL/4 + 9FL/4)/H = 9FL/2H
Tt6= (11FL/4 + 11FL/4)/H = 11FL/H
Step_6: Verifica su SAP
Per la verifica su SAP costruisco un "2D Frames" con la stessa geometria di cui sopra.

Per simulare la rigidezza infinita bisogna impostare un materiale che abbia o altezza infinita o modulo di elasticità infinito.
DEFINE-FRAME-FRAME SECTION-ADD NEW PROPERTY-NEW MATERIAL
Importante: in LOAD PATTERN ricordarsi di mettere al carico DEAD il SELF MULTIPLIE WEIGHT pari a O.

A questo punto possiamo far partire l'analisi (RUN NOW)



Commenti recenti