Progettazione di una trave in CA, Acciaio e Legno Lamellare di una struttura a telaio

Le dimensioni di una struttura portante dipendono dalle dimensioni dell'edificio. Più è grande l'edificio maggiore sarà il peso che dovrà essere sostenuto e maggiori saranno le dimensioni della struttura. In Italia la Normativa che regola le dimensioni della struttura portante è la NTC (Norme Tecniche per le Costruzioni) del 2008.
La normativa prevede la progettazione della struttura portante, per la "vita utile" dell'edificio", in due stati:

- Stati Limite di Esercizio (SLE): capacità di garantire le prestazioni previste per le condizioni di esercizio.
lo stato limite di esercizio considera la struttura in fase elastica (fase in cui un corpo soggetto ad un azione temporanea, mantiene la sua geometria senza deformarsi al termine dell'Azione)

- Stati Limite Ultimo (SLU): capacità di evitare crolli, perdite di equilibrio e dissesti gravi, totali o parziali, che possano compromettere l’incolumità delle persone ovvero comportare la perdita di beni, ovvero provocare gravi danni ambientali e sociali, ovvero mettere fuori servizio l’opera.
Lo stato limite ultimo considera la struttura in fase plastica (fase in cui un corpo soggetto ad una azione temporaneo, al termine dell'azione rimane deformato, cambiando le sue proprietà meccaniche).

Il superamento dello stato limite ultimo genera il collasso della struttura.

In questo caso sotto proposta la struttura portante verrà dimensionata allo SLU.

Nella figura sottostante è mostrata una struttura a telaio (struttura composta da un sistema di elementi verticali, pilastri, ed elementi orizzontali, travi) e successivamente verrà dimensionata la trave più caricata con 3 materiali e tecniche costruttive diverse: Cemento Armato (CA), Acciaio e Legno Lamellare.

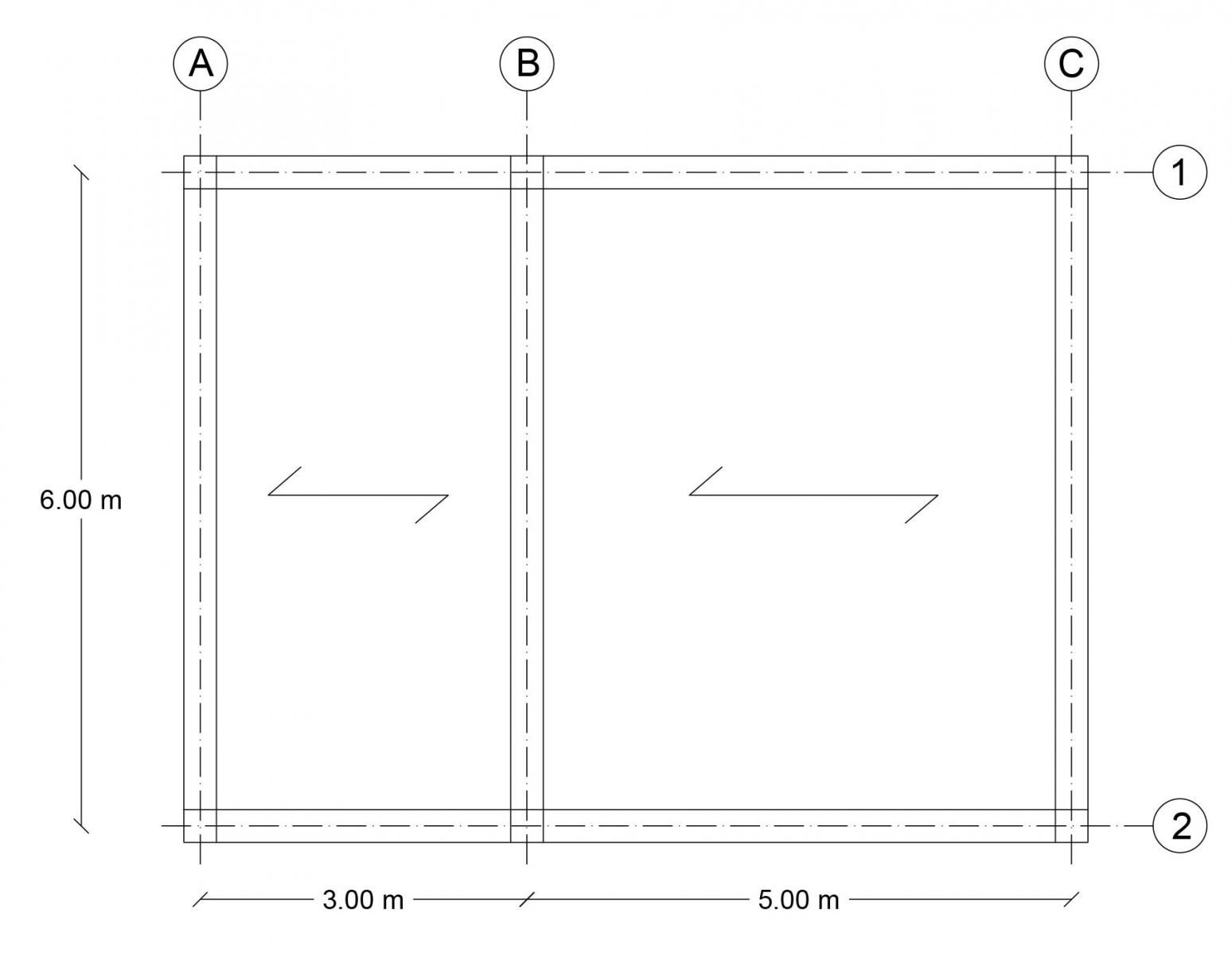
Le lettere rappresentano l'orditura della travi principali che scaricano i pesi dei solai sui pilastri che a loro volta scaricano i pesi al terreno. I numeri, invece, rappresentano l'orditura delle travi secondarie che collegano le travi principali e collaborano alla stabilità della struttura. Il simbolo nella campata rappresenta l'orditura dei travetti che scaricano il peso sulla trave principale

In figure sono mostrate le Aree di Influenza di carico dei solai sulle travi principali

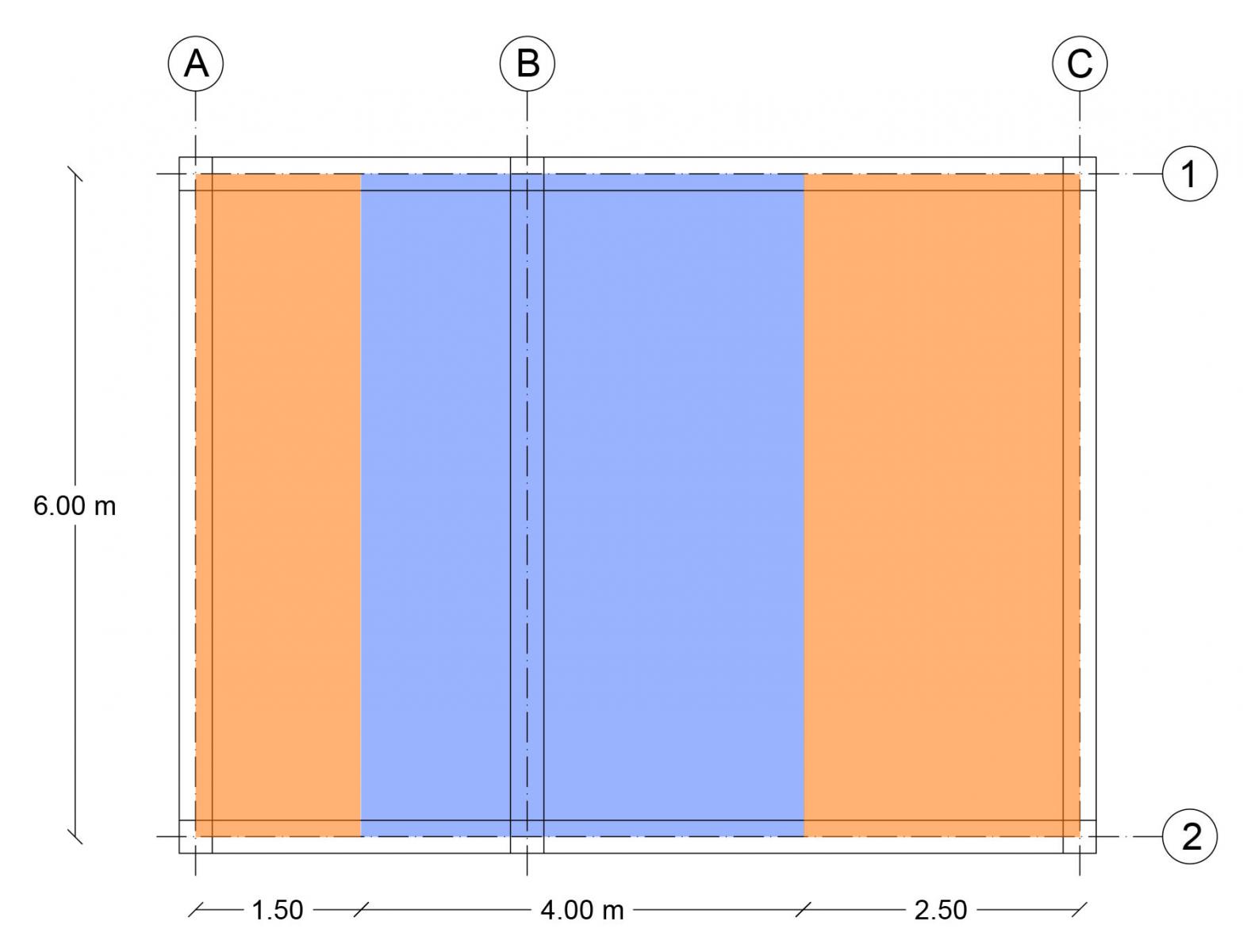
Dimensioniamo la Trave B perchè è la trave principale che risente di una maggiore area di influenza di carico.

Il dimensionamento di travi e pilastri verrà eseguito usando un modello semplificato di struttura isostatica appoggiata – appoggiata.

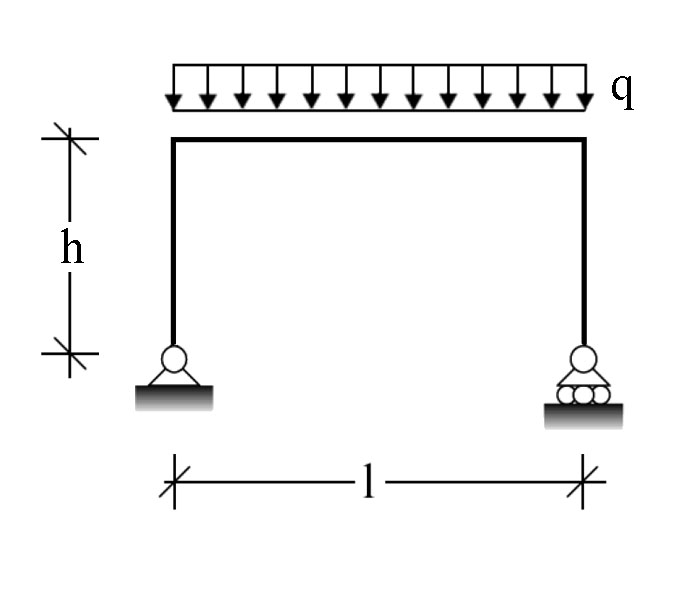
Tramite l’analisi dei carichi si determina un area di un metro quadro tipo di solaio. Moltiplicando l’area tipo di solaio per l’interasse della trave si ottiene il carico distribuito.

ANALISI DEI CARICHI

Prendiamo in considerazione tre tipologie di solaio: solaio in laterocemento, solaio in acciaio e solaio in legno.

La Normativa divide il solaio in tre differenti carichi: carico strutturale G1, carico permanente G2 e carico aggiunto (o variabile) Qa.

Lo stato limite ultimo considera la possibilità che i carichi siano superiori a quelli effettivamente agente e che le resistenze dei materiali siano inferiori a quelle considerate. Le resistenze sono determinate da prove sperimentali secondo un metodo probabilistico, quindi non avendo sempre la certezza che il materiale si comporti allo stesso modo, vengono introdotti dei coefficienti di sicurezza che amplificano il carico e dei coefficienti che riduco le resistenze. 

Nella seguente immagine vengono mostrati i coefficienti che amplificano il carico agente a seconda del tipo di carico

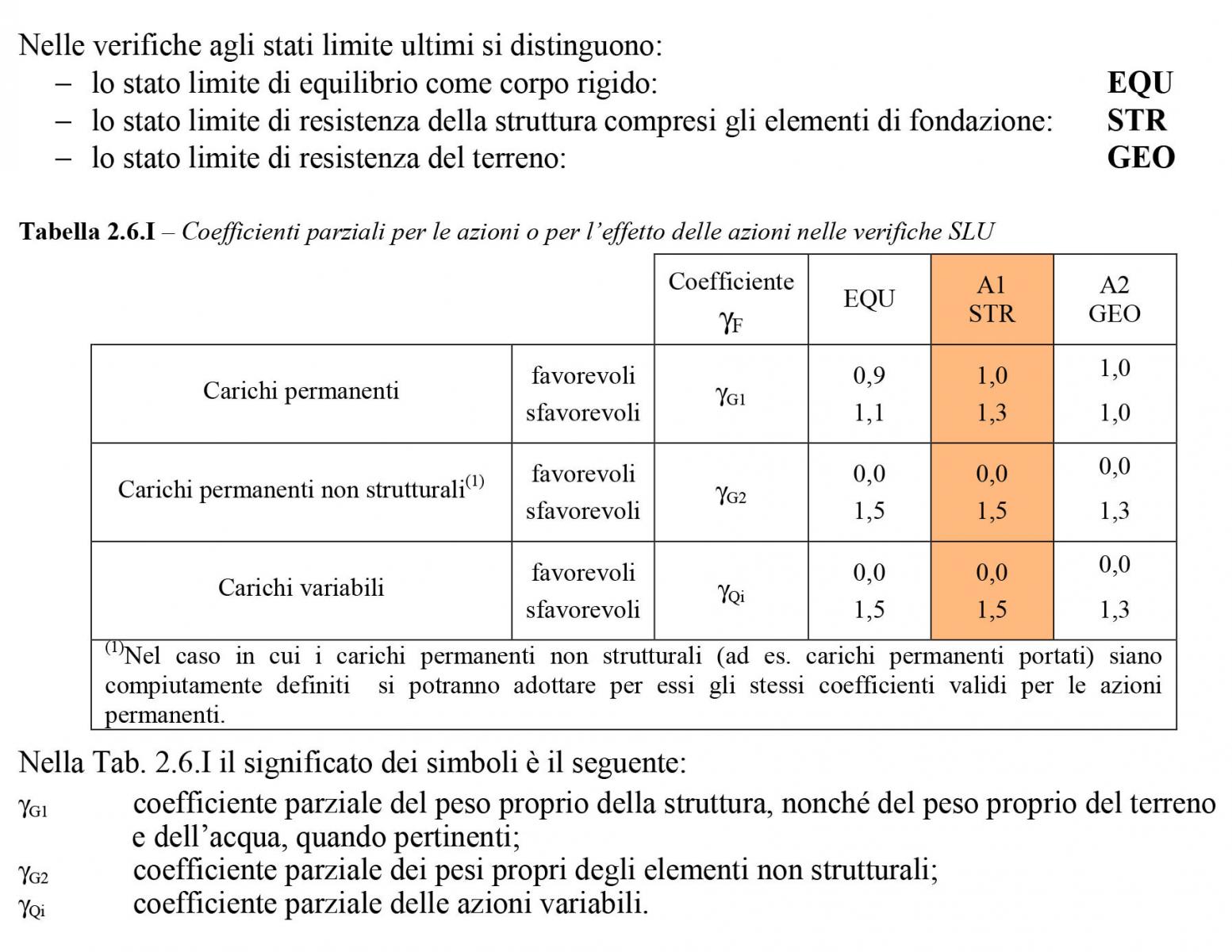
Quindi il carico ultimo risulta Qu = γG1 Qs + γG2 Qp + γQi Qa
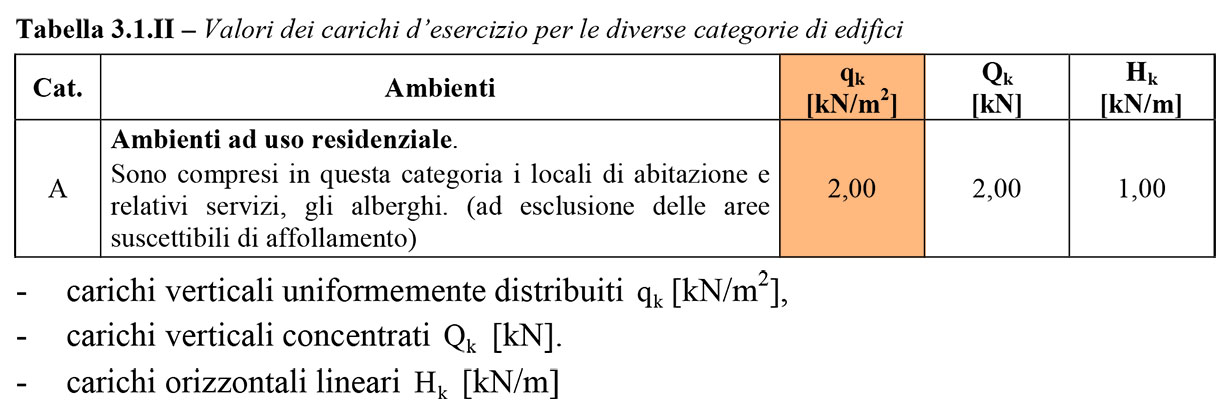
(dove Qs è il carico strutturale (peso proprio della struttura), Qp è il carico permanente non strutturale (carico degli elementi non strutturali), e Qa sono i carichi variabili, dettati nella Tabella 3.1.II delle NTC 2008)
 

Per il dimensionamento di travi e pilastri usiamo dei modelli di travi e pilastri semplificate e ridotte a una struttura isostatica (in cui le possibilità di movimento, gradi di libertà, sono bloccate da vincoli , gradi di vincolo. Pero ogni elemento ci sono 3 gradi di libertà) appoggiata - appoggiata

 

DIMENSIONAMENTO DELLA TRAVE IN CEMENTO ARMATO:

Analisi dei Carichi

Prendiamo in considerazione in 1 mq di solaio in laterocemento.

La figura mostra una sezione perpendicolare all'orditura dei travetti di cemento armato per mostrare i materiali del solaio in latero cemento tipico

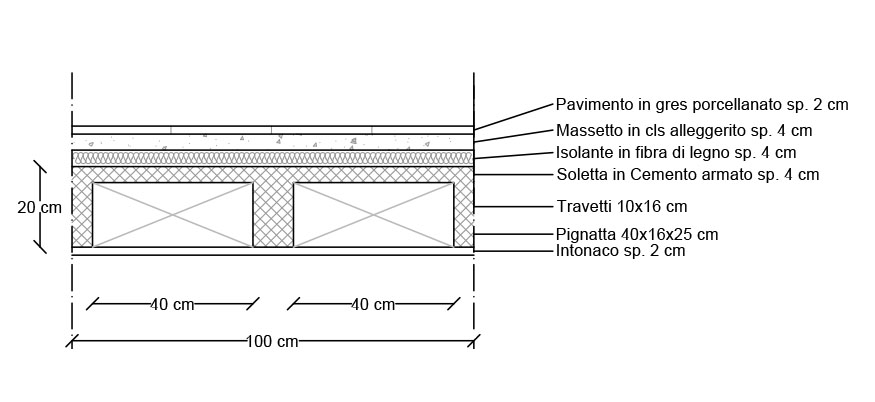
Pavimento in Greso Porcellanto
dimensioni: (1m x 1m x 0,02m)
Q/mq = 0,4 kN/mq

Massetto in Calcestruzzo alleggerito tipo "MCS edilizia"
dimensioni: (1m x 1m x 0,04m)   densità = 18 Kn/mc
Q/mq = 0,72 kN/mq

Isolante in pannelli di Fibra di Legno 140 SD tipo "Fassa Bortolo"
dimensioni: (1m x 1m x 0,04m)    densità = 1,4 kN/mc
Q/mq = 0,056 kN/mq

Soletta in cemento armato tipo "MCS edilizia"
dimensioni: (1m x 1m x 0,04m)   densità = 25 kN/mc
Q/mq = 1 kN/mq

Pignatte in laterizio tipo "RipaBianca"
dimensioni: (40cm x 16cm x 25cm)     Q/Cad. = 8 kg (x8 pignatte)
Q/mq = 0,64 kN/mq
                                                  

Travetti in cemento Armato
dimensioni: (10cm x 16cm x 1m)   densità = 25 kN/mc (x2 travetti)
Q/mq = 0,8 kN/mq
                                                                          

Intonaco
dimensioni: (1m x 1m x 0,015m)
Q/mq = 1 kN/mq

sono stati utilizzati un calcestruzzo C 35/45 con una resistenza caratteristica fck = 35 MPa ( Mpa = Mega Pascal)
e barre d'acciaio FeB 450C con una resistenza caratteristica di 450 MPa
che risultano avere resistenze di progetto di fcd = 19,83 Mpa e fyd = 391,30 MPa

Per il dimensionamento della trave è stato utilizzato un foglio elettronico che considera:
- la struttura come una isostatica appoggiata - appoggiata
- Sollecitazione massima a Momento Flessionale in mezzeria della trave pari a q l^2/8
- resistenze caratteristiche e di progetto di calcestruzzo e acciaio
- la dimensione fissa della base della trave principale (b)

Qs =  Q travetti + Q soletta + Q  pignattE
Qs = 0,8 kN/mq + 1 kN/mq + *0,64 kN/mq  = 2,44 kN/mq
 

Qp = Q intonaco + Q isolante + Q massetto + Q pavimento + Q muri interni* + Q impianti

Qp = 1 kN/mq +0,056 kN/mq +0,72 kN/mq +0,4 kN/mq +1 Kn/mq* +0,5 kN/mq*  = 
=3,076 KN/mq = 3,08 kN/mq

*muri e impianti sono consederati con dei valori forfettari perchè ci possono essere delle modifiche durante in tutta la vita utile dell'edificio

Qa = 2 kN/mq    valore dipendente dalla Tabella 3.1.II delle NTC per un ambiente ad uso residenziale

il carico ultimo risulta quindi essere:
Qu = (2,44 kN/mq * 1,3   +   3,08 kN/mq * 1,5   +   2 kN/mq * 1,5) x 4 (interasse)  =  43,14 kn/mq

 

Per il dimensionamento della trave è stato utilizzato un foglio elettronico che considera:
- la struttura come una isostatica appoggiata - appoggiata
- Sollecitazione massima a Momento Flessionale in mezzeria della trave pari a q l^2/8
- resistenze caratteristiche e di progetto di calcestruzzo e acciaio
- la dimensione fissa della base della trave principale (b)

Il C.A. è un materiale composito da Cemento e Acciaio. Il cemento è un materiale che resiste molto alla compressione mentre ha una resistenza quasi nulla alla trazione. L’acciaio compensa la scarsa resistenza a Trazione. Il Calcestruzzo e l’acciaio hanno un comportamento meccanico diverso, ma la deformazione di un punto della trave deve essere la stessa per via della Omogeneizzazione

ε(P)cls = ε(P)s

σ(P)cls x Ecls = σ(P)s x Es

dato che i Moduli elastici di acciaio e Cls sono diversi, viene introdotto un coefficiente di omogeneizzazione che è definito come il rapporto dei moduli elastici dei due materiali.

σ(P)cls = n σ(P)s

n viene considerato uguale a 15.

 

Per via dell’omogeneizzazione  le tensioni di cls

Yn : hu = fcd : fyd

Dove:
Yn è l’asse neutro
hu è l’altezza utile. È il punto della sezione in cui si trovano le armature di acciaio.

Per l’omogeneizzazione fyd = come (fcd + fyd/n)

Yn : hu = fcd : (fcd + fyd/n)

Yn = hu x fcd/((fcd + fyd/n))

Consideriamo β come Il rapporto tra le resistenze cosi che la posizione dell’asse neutro risulti

Yn = β X hu

Quando una trave è soggetta a un carico perpendicolare al suo asse, si generano delle sollecitazioni di Momento. A causa del Momento si generano delle tensioni in ogni punto della sezione della trave. Una parte della sezione si comprime mentre una parte si tende.

Facendo l’equilibrio del momento possono presentarsi due possibiltà:

M = T x B                                            M = C x B

Dalla risultante di Compressione è possibile determinare l’area di calcestruzzo, mentre dalla risultante di Trazione è possibile determinare l’area minima di Acciaio.

Il foglio di calcolo utilizzato di sotto dimensiona l’area di calcestruzzo.

La risultante di Compressione vale:

C = (Yn x fcd)/2  x b

Il braccio B risulta

B = hu – yn/3                                    B = hu -(β X hu)/3                           B = β ( 1 – β/3) hu

Quindi la formula del Momento può essere riscritta come

M = (Yn x fcd)/2  x b    x β ( 1 – β/3) hu

Dando un valore fisso alla base della sezione e considerando la hu come incognita possiamo trovare l’altezza minima dalla trave  H = hu + δ                              dove δ è il copriferro

Inserendo i dati del carico risulta necessaria una trave con altezza utile alte 42,01 cm
considerando un copriferro di 5 cm per coprire le barre d'acciaio risulta necessaria una trave principale alta 47,1 cm.
Per una facilità di realizzazione della trave, la sezione viene ingegnerizzata, quindi verrà utilizzata una trave con un altezza di 55 cm.
La seconda riga di calcolo riesegue i calcoli considerando nel carico ultimo l'aggiunta del peso della trave. Nonostante l'aggiunta al carico strutturale di peso della trave, la sezione ingegnerizzata risulta comunque verificata.

 

DIMENSIONAMENTO DELLA TRAVE IN ACCIAIO:

Analisi dei Carichi

Prendiamo in considerazione in 1 mq di solaio con lamiera grecata che moltiplicato per la luce e l'interasse della trave Principale ci darà il carico dell'Area di influenza.

La figura mostra una sezione perpendicolare all'orditura della lamiera grecata.

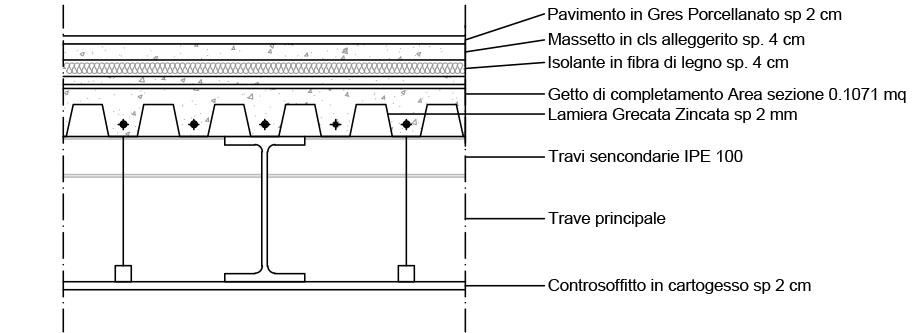
Pavimento in Greso Porcellanto
dimensioni: (1m x 1m x 0,02m)
Q/mq = 0,4 kN/mq

Massetto in Calcestruzzo alleggerito tipo "MCS edilizia"
dimensioni: (1m x 1m x 0,04m)    densità = 18 Kn/mc
Q/mq = 0,72 kN/mq

Isolante in pannelli di Fibra di Legno 140 SD tipo "Fassa Bortolo"
dimensioni: (1m x 1m x 0,04m)    densità = 1,4 kN/mc
Q/mq = 0,056 kN/mq

Getto di completamento in il cemento armato
dimensioni: (1m x 1m x 0,04m)   densità = 25 kN/mc
Q/mq = 1 kN/mq

Lamiera Grecata Zincata
dimensioni: (10cm x 16cm x 1m)
Q/mq = 0,157 kN/mq

IPE 100
dimensioni: (0,00103m^2 x 1m)   densità = 78,5 kN/mc
Q/mq = 0,081 kN/mq

Intonaco in cartongesso tipo "Knauf"
dimensioni: (1m x 1m x 0,02m)
Q/mq = 0,078 kN/mq

Si progetta la trave Principale con un acciaio S275 con una resistenza carattestica fyk di 275 MPa con un coefficiente 
γm0 = 1,05. La resistenza di progetto fyd = 261,90 MPa. Si è scelto di utilizzare un profilo IPE per il migliore momento di inerzia della sezione. 

Qs = Q getto di completamento + Q lamieera + Q IPE100
Qs = 1 kN/mq   +   0,157 kN/mq    +   0,081 kN/mq  = 1,238 kN
 = 1,24 kN/mq 
   

Qp = Q controsoffitto + Q isolante + Q massetto + Q pavimento + Q muri interni* + Q impianti*
Qp = 0,078 kN/mq + 0,056 kN/mq + 0,72 kN/mq + 0,4 kN/mq  + 1 Kn/mq* + *0,5 kN/mq
= 2,75 KN/mq

*muri e impianti sono consederati con dei valori forfettari perchè ci possono essere delle modifiche durante in tutta la vita utile dell'edificio

Qa = 2 kN/mq    valore dipendente dalla Tabella 3.1.II delle NTC per un ambiente ad uso residenziale

il carico ultimo risulta quindi essere:
Qu = 1,24 kN/mq * 1,3   +   2,75 kN/mq * 1,5   +   2 kN/mq * 1,5   =  34,97 kn/mq

Ricordando  la Formula di Navier
σ(y) = Mmax  y
              Ix        
Per il dimensionamento della trave d'acciaio, si considera al posto di σ(y) la resistenza di progetto, per determinare sezione minima della trave. dove Mmax è il valore del Momento massimo, Ix è il momento di Inerzia della sezione e y è la distanza dall'asse neutro della sezione.

Per stabilire la Geometria della trave è importante ricordare che Wx = Ix/y dove Wx è un modulo di resistenza geometrico della trave

Il risultato del calcolo della prima riga mostra come il Wx minimo della trave debba essere 600,88 cm^3 dunque la sezione minima della trave risulta essere un IPE 33O con un Wx di 713 cm^3.

Poichè anche la trave Principale ha un proprio peso, nella seconda riga del foglio di calcolo al carico ultimo (Qu) è stato aggiunto il peso al metro lineare dell' IPE 330 (0,491 kN/m x γG1=1,3 per elementi strutturali). Nonostante l'aumento del carico, il Wx minimo è comunque minore del Wx dell'IPE 330, dunque non è necessario avere un profilato più grande

dove

DIMENSIONAMENTO DELLA TRAVE IN LEGNO LAMELLARE:

Analisi dei Carichi

Prendiamo in considerazione in 1 mq di solaio in Legno Lamellare che moltiplicato per la luce e l'interasse della trave Principale ci darà il carico dell'Area di influenza.

La figura mostra una sezione perpendicolare all'orditura dei travetti di Legno Lamellare

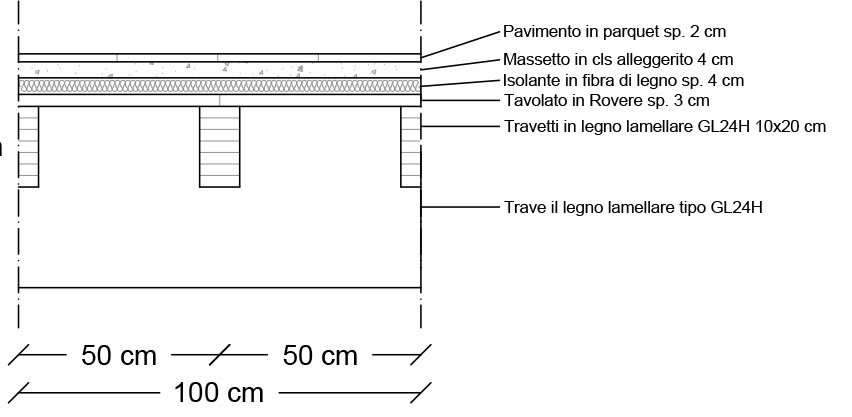
Pavimento in parquet in rovere tipo "metroquadro"
dimensioni: (1m x 1m x 0,02m)   densità = 7,2 Kn/mc
Q/mq = 0,144 kN/mq

Massetto in Calcestruzzo alleggerito tipo "MCS edilizia"
dimensioni: (1m x 1m x 0,04m)    densità = 18 Kn/mc
Q/mq = 0,72 kN/mq

Isolante in pannelli di Fibra di Legno 140 SD tipo "Fassa Bortolo"
dimensioni: (1m x 1m x 0,04m)
/mq = 0,056 kN/mq

tavolato in lego di rovere  tipo "metroquadro"
dimensioni: (1m x 1m x 0,03m)   densità = 7,2 kN/mc
Q/mq = 0,216 kN/mq

travetti in legno lamellare GL 24 H
dimensioni: (0,1m x 0,2m x 1m)   densità = 3,80 kN/mc
Q/mq = 0,078 kN/mq

E' stata utilizzata un Legno Lamellare con una 

Qs = Q travetti + Q tavolato
Qs = 0,078 kN/mq   +   0,216 kN/mq   = 0,292 kN/mq
= 0,3 kN/mq  

Qp = Q isolante +  Q massetto + Q pavimento + Q muri interni* + Q impianti
Qp =  0,056 kN/mq  +  0,72 kN/mq  + 0,144 kN/mq  +  *1 Kn/mq   +  *0,5 kN/mq
= 2,26 kN/mq 

*muri e impianti sono consederati con dei valori forfettari perchè ci possono essere delle modifiche durante in tutta la vita utile dell'edificio

Qa = 2 kN/mq    valore dipendente dalla Tabella 3.1.II delle NTC per un ambiente ad uso residenziale

il carico ultimo risulta quindi essere:
Qu = 0,3 kN/mq * 1,3   +   2,26 kN/mq * 1,5   +   2 kN/mq * 1,5   =  27,12 kn/mq 

il legno lamellare GL 24 H ha una resistenza di 24 MPa
Nella progettazione della trave in legno lamellare bisogna tenere presenti alcuni fattori.
- Cosi come per il cemento bisogna fissare la dimensione della trave per determinare l'altezza della trave
-la classe di servizio

-la durata del carico

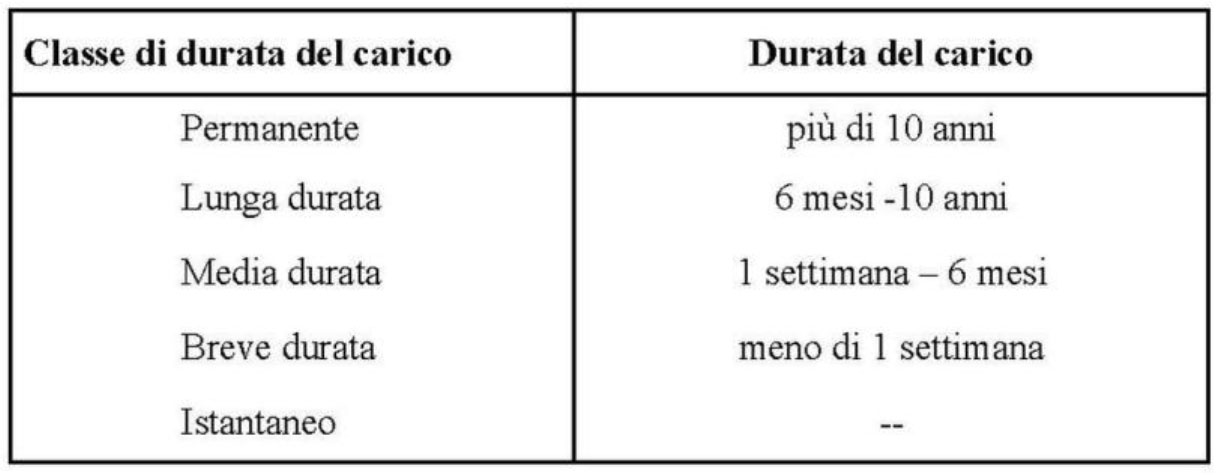
- il Legno lamellare nella determinazione della resistenza di progetto considera un fattore Kmod che è un coefficiente correttivo tenente conto dell’effettosi della classe di servizio sia della classe di durata del carico.

Il dimensionamento della sezione della trave avviene con lo stesso procedimento utilizzato per la sezione di acciaio.

Partendo dalla Formula di Navier
σ(y) = Mmax
            Wx        

Considerando che il Modulo di resistenza geometrica della trave W per una sezione rettangolare risulta essere

E fissando il valore della base della sezione b, risulta che l’altezza minima della sezione è

Il risultato ottenuto mostra che l'altezza minima devo essere di 43,97 cm, che ingegnerizzato danno un'altezza della trave di 45 cm.
Così come per l'Acciaio, anche con il legno la prima riga indica il dimensionamento della trave senza considerarne il peso. In questo caso però l'aggiunta del peso della trave (0,4275 kN/m x γG1=1,3 per elementi strutturali) richiede un aumento dell'altezza minima da 42 a 46 cm quindi, ingegnerizzando la sezione, l'altezza della sezione della trave in legno diventa 50 cm